Automatic Control and Health Monitoring of a 3-Dimentional
Overhead Crane with Minimally Required Sensor Devices
Minami Kumarawadu
1a
and Logeeshan Velmanickam
2b
1
Engineering Design Department, Electro Metal Pressings Pvt Ltd., Panagoda, Sri Lanka
2
Department of Electrical Engineering, University of Moratuwa, Moratuwa, Sri Lanka
Keywords: Overhead Crane, Controller-Observer, Health Monitoring.
Abstract: This paper presents a controller-observer scheme for linear position tracking control of the load of an overhead
crane in the 3-D space and also investigates the possibility of actuator health monitoring with minimal sensor
requirement. This way, admissible position tracking accuracy and system transient behaviour both are
achieved only using position sensors. Closed-loop stability of the plant-controller-linear velocity observer
system is guaranteed using Lyapunov method. A trajectory planning method is proposed based on standard
exponential functions that enables defining the distance to the destination, maximum linear velocities and
accelerations in the parameters of the function itself. The methods proposed are validated using computer
numerical simulations in the presence of model parameter uncertainties and external disturbances. We also
investigate the potential of using observer outputs to improve the early detection of actuator faults.
1 INTRODUCTION
Owing to ever increasing operational, maintenance,
and safety requirements of industrial multi-motor
systems, predictive maintenance (PdM) has received
increasing attention. PdM is a data-driven approach
to identify operational anomalies and potential
equipment defects, enabling timely repairs before
failures occur. However, additional sensor and data
communication requirements add up to cost and
maintenance. To this end, much emphasis has been
placed on automatic control and monitoring of
systems using minimally required sensor devices
(Suzuki and Fujii, 2006, Gowrienanthan et al., 2023,
Gao et al., 2015, Kumarawadu et al., 2007).
3-dimensional overhead cranes are widely used in
industry for transportation of heavy loads. Accurate
position tracking feedback control of the 3 degrees-
of-freedom requires three position sensors. Velocity
feedback is required in order to ensure admissible
transient performance. As a result, total number of
sensor requirement for automatic position tracking
control of a 3D overhead crane will be six. Finite
difference estimation of the velocity has no
theoretical grounds and is also vulnerable to position
a
https://orcid.org/0009-0004-1065-0725
b
https://orcid.org/0000-0003-3767-8280
measurement noise. Controller-observer schemes can
be used to minimize the number of sensors required
or to estimate unmeasurable variable for feedback
control purposes.
Many controller-observer schemes with
guaranteed stability have been proposed for robotic
systems (Kumarawadu et al., 2007, Ji et al., 2019) to
estimate the robot joint angular velocities. In
Kumarawadu and Lee, 2009, a velocity observer has
been used to estimate the lateral velocity of self-
driving vehicles that is unmeasurable.
In this paper, a controller-observer scheme is used
for automatic tracking control with guaranteed
closed-loop stability using minimally required sensor
devices. This is achieved by a velocity observer that
estimates the linear velocities of the moving
components in the travel, traverse, and hoist motions.
Closed-loop stability of the plant-controller-observer
system is guaranteed using Lyapunov method. Our
future research includes investigation into how to
incorporate the estimated velocity profiles by the
observer in identification and localization of
anomalies in PdM applications of multiple motor
systems. This way, automated health monitoring of
engineering systems to be achieved exclusively using
Kumarawadu, M. and Velmanickam, L.
Automatic Control and Health Monitoring of a 3-Dimentional Overhead Crane with Minimally Required Sensor Devices.
DOI: 10.5220/0013041200003822
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 21st International Conference on Informatics in Control, Automation and Robotics (ICINCO 2024) - Volume 1, pages 453-461
ISBN: 978-989-758-717-7; ISSN: 2184-2809
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
453

the control sensor feedbacks and the estimated motion
parameters only.
We also present a trajectory planning method
using a combination of exponential functions to
ensure smooth tracking trajectories. This is important
to ensure minimal swing of the load. In our approach,
the desired linear velocity trajectories are planned
based on the distance to the destination. Maximum
velocity and acceleration are defined using standard
exponential functions. As a result, the desired
position trajectories can be obtained by simply
integrating the smooth varying time function profiles
of the desired velocities.
Using frequency domain, correlation, and
sensitivity analysis, we investigate the potential of
using the position tracking error and the velocity
observer output for actuator health monitoring.
This paper is organized as follows: Section 2
presents our feedback controller-linear velocity
observer scheme and the trajectory planning
approach. Closed-loop stability is established using
Lyapunov method. Section 3 presents the simulation
results. Actuator fault simulation and analysis is
presented in Section 4. Section 5 concludes the paper.
2 CONTROLLER-OBSERVER
SCHEME
2.1 System Equations of Motion
In the 3D overhead crane, travel motion refers to the
movement of the entire crane along a fixed runway
beam. See Fig. 1. Traverse motion refers to the
movement of the crane trolley allowing the crane to
position itself horizontally perpendicular to the
direction of travel. Hoist motion refers to the vertical
movement of the crane's hook-block or lifting
mechanism. With reference to an 𝑥-𝑦-𝑧 orthogonal
set, travel, traverse, and hoist linear motions take
place in the 𝑥≥0,𝑦≥0 and 𝑧≤0 regions,
respectively. See Fig. 2.
The model-based controller-observer design
approach is based on the linearized equations of
motion that ignore the swing dynamics of the load.
Let 𝑀

,𝑀

,𝑀

are the travelling, traversing, and
hoisting down components of the crane mass. Load
mass is 𝑚. By applying Newton’s 2
nd
law of motion
to the 𝑥-direction, 𝑦-direction, and 𝑧-direction we get
𝐹

,𝐹

,𝐹

are the driving forces, 𝐷

,𝐷

,𝐷

are the
viscous friction coefficients, and 𝑑

,𝑑

,𝑑

are the
unknown bounded time-varying external disturbance
forces for the motions in the 𝑥,𝑦,𝑧 directions.
Figure 1: A 3-D overhead crane (Khatamianfar, 2015).
Figure 2: Coordinate system of the 3-D overhead crane.
(
𝑀

+𝑚
)
𝑥

(𝑡)+ 𝐷

𝑥(𝑡) + 𝑑

(𝑡)=𝐹

(𝑡)
(1)
𝑀

+𝑚𝑦

(𝑡)+ 𝐷

𝑦(𝑡) + 𝑑

(
𝑡
)
=𝐹

(𝑡)
(2)
(
𝑀

+𝑚
)
𝑧

(
𝑡
)
+𝐷

𝑧
(
𝑡
)
−𝑚𝑔+𝑑

(
𝑡
)
=𝐹

(𝑡)
(3)
The disturbance force, 𝑑(𝑡) is a bounded quantity
satisfying |𝑑(𝑡)|≤𝑑

, where 𝑑

is a constant
denoting the upper bound. Such disturbance can be
considered as energy bounded random noise, which
widely exists in practical systems (Jin et al., 2022).
2.2 The Controller-Observer Scheme
Automatic controller tracks a planned trajectory to
move the load attached to the hook-block of the
overhead crane to the final destination in the 𝑥-𝑦-𝑧
space and return to the original position. Controller-
observer scheme and the stability proof are presented
for the 𝑧 (hoist) motion. Travel and traverse (𝑥 and 𝑦)
that do not have a 𝑚𝑔 term in the dynamics may be
considered as special cases.
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
454

In the sequel, (∙)

denotes the estimated value of (·
) and 𝑧̃ =𝑧−𝑧̂. It is assumed that the desired
position, 𝑧

, and its time derivatives, 𝑧

, 𝑧

, are
known. The control objective is to regulate the
tracking error, 𝑒=𝑧−𝑧

. Implicit in it are
simultaneously keeping the observer estimation error
small. Consider the following combined controller-
velocity observer system:
Controller:

𝐹=𝑀𝜈+𝐷𝑧
̂

−𝑚𝑔
𝜈=𝑧


−𝑘

𝑧
̂

−𝑧

−𝑘

(
𝑧−𝑧

)
(4)
Observer:

𝑧
̂

=𝑟+𝐿

(
𝑧−𝑧
̂
)
𝑟 =𝜈+𝐿

(
𝑧−𝑧
̂
)
(5)
Here, 𝑀=𝑀

+𝑚. The positive adjustable
controller-observer gains, 𝑘

,𝑘

,𝐿

,𝐿

, are to be
chosen by the designer. 𝑟 denotes a reference
acceleration input, which is obtained by modifying
the resolved acceleration with position estimation
error. Integrating 𝑟 and further modifying it by
position estimation error yield the estimated velocity.
Consider the controller-observer system defined by
(4) and (5) in a closed loop with the controlled system
with the plant (3). The closed-loop system can be
made to be UUB by suitably selecting the controller-
observer gains, 𝑘

,𝑘

,𝐿

,𝐿

.
Stability proof of the closed-loop system is given
in the Appendix.
2.3 Trajectory Planning
The desired velocity trajectory for the forward motion
is defined as
𝑥
,
(
𝑡
)
=
𝑉
(
1−𝑒

)
;0≤𝑡<𝑇
𝑉𝑒

(

)
;𝑇≤𝑡≤𝑇+7
(6)
For the return path, 𝑥
,
(
𝑡
)
=−𝑥
,
(
𝑡
)
.
Here, 𝑉 is the maximum velocity and 𝑎𝑉 is the
maximum acceleration. Time interval, 𝑇, is selected
to match the distance between the starting point and
the final destination. For example, the desired
velocity trajectories for the roundtrip motion are
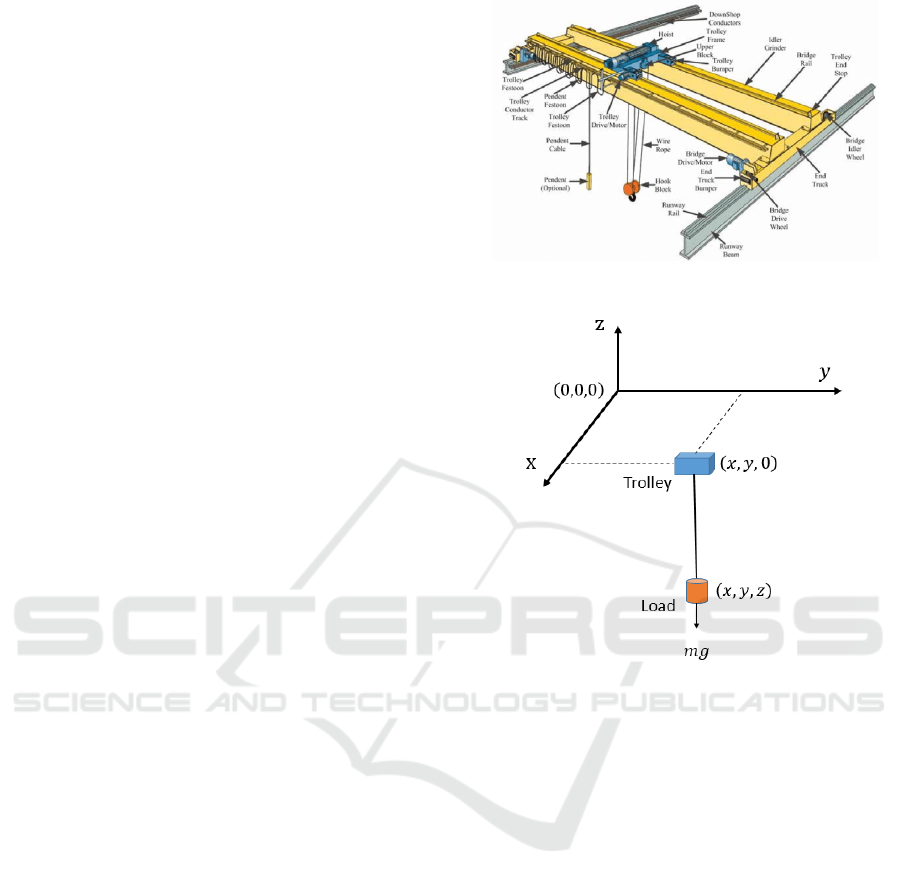
given in Fig. 3. Here, 𝑉,𝑎𝑉,𝑇 are 0.5, 0.5, 20 for
travel, 0.4, 0.4, 15 for traverse, and -0.2, -0.2, 5 for
hoist motions. When the maximum acceleration and
velocity are known, distance travelled can be
obtained by time integrating (6) as a function of 𝑇.
Hence, the distance travelled can be pre-set by setting
the value 𝑇.
Figure 3: Desired velocity: travel (dashed line), traverse
(dotted line), and hoist (dash-dot).
Figure 4: Desired acceleration: travel (dashed line), traverse
(dotted line), and hoist (dash-dot).
Desired acceleration trajectories given in Fig. 4
can be obtained by time differentiating the desired
velocities. Likewise, desired positions are obtained
by time integrating the velocities. As a result, the
desired position trajectories and their time derivatives
that are required in the control method presented in
Section 2.2 can be obtained completely analytically
without needing numerical calculus.
3 SIMULATION STUDY OF THE
HEALTHY SYSTEM
Crane workspace is 12 meters long, 8 meters wide,
and 2 meters deep. Its maximum accelerations and
velocities are 2 m/s

and 0.5 m/s for traveling, 1.5
m/s

and 0.3 m/s for traversing, and 1.5 m/s

and
0.1 m/s for load hoisting, respectively.
Dynamic model parameters are 𝑀

=
1440 kg ,𝐷

=400 kgs

, 𝑀

=110 kg ,𝐷

=
40 kgs

,𝑀

=20 kg,𝐷

=5 kgs

. Load mass,
𝑚=150 kg. Acceleration due to gravity, 𝑔=
9.81 ms

.
Automatic Control and Health Monitoring of a 3-Dimentional Overhead Crane with Minimally Required Sensor Devices
455

The overhead crane system is disturbed by
random external disturbance forces formulated by
𝑑

(
𝑡
)
= 20×
(
2×rand
(
1
)
−1
)
N
𝑑

(
𝑡
)
=𝑑

(
𝑡
)
= 2×
(
2×rand
(
1
)
−1
)
N
all the time. Here, 0≤rand(1)≤1 is a random
number.
The hook-block moves from (𝑥,𝑦,𝑧)=(0,0,0)
position to (10,6,−1) meters with the load and
returns to the original position with no load.
Controller-observer gains are heuristically set as:
𝑘

=10,𝑘

=10,𝐿

=10,𝐿

=0.1; 𝑘

=
30,𝑘

=30,𝐿

=10,𝐿

=0.8; 𝑘

=
35,𝑘

=35,𝐿

=6,𝐿

=0.6.
Model parameter uncertainties of 15% is assumed
to be in the control law except for the mass of the
load, which is known accurately. Following logic is
used to reset the model parameter, load mass (𝑚), in
the control law, (4), for the return motion.
𝑚=
𝑚;𝑥

(
𝑡
)
≥0
0
;
Otherwise
(7)
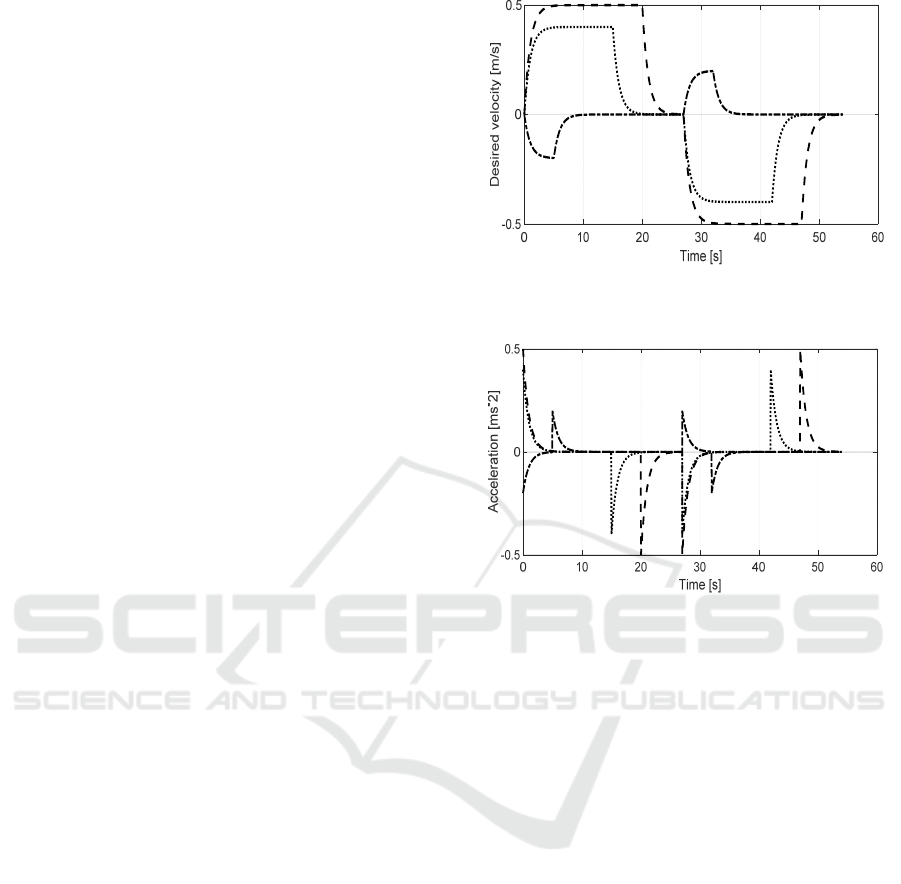
Desired and actual positions are shown in Fig. 5.
Fig. 6 presents the position tracking control errors.
These figures show small position tracking errors and
admissible transient performance. Driving forces are
given in Fig. 7.
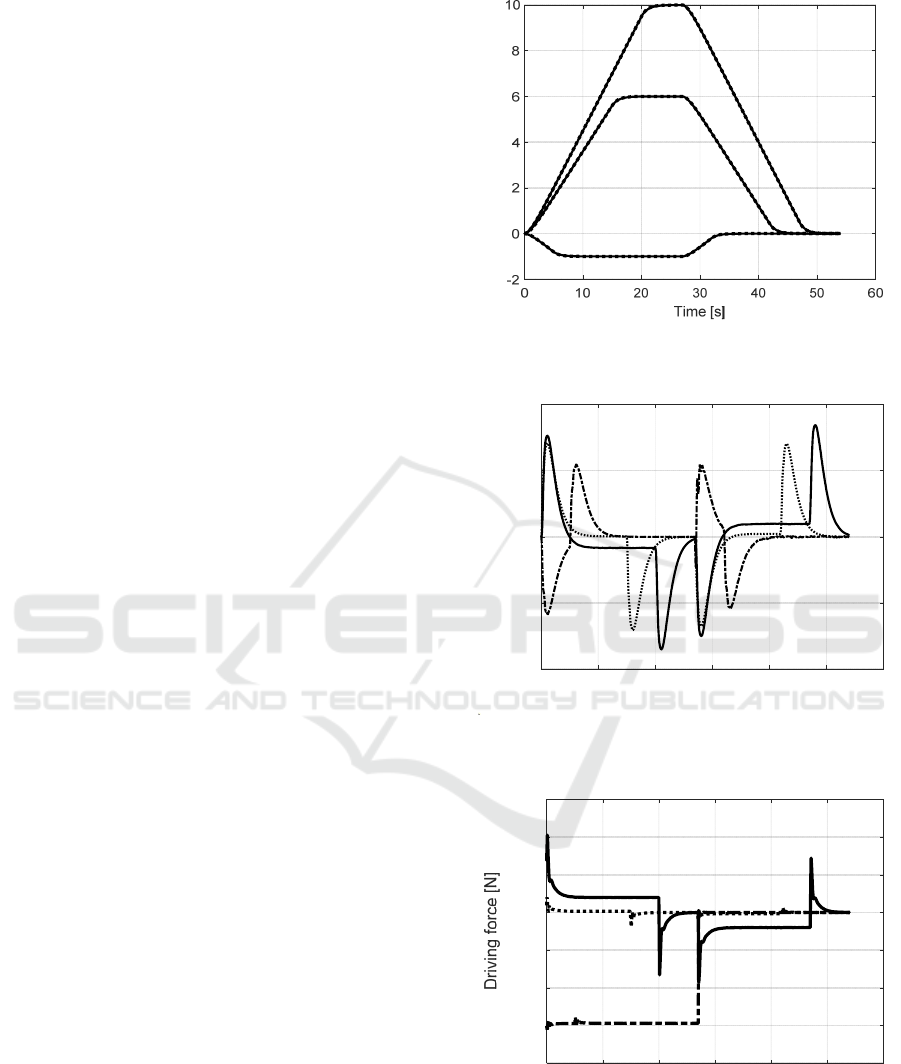
Actual and observer estimated velocities are
compared in Fig. 8. Velocity estimation errors are
given in Fig. 9. These figures show very good
velocity estimation accuracy and admissible transient
performance of the velocity observer.
Fig. 10 shows the position tracking error without
load mass parameter resetting as described in (7) in
the control law. As it can be seen, hoist position
tracking error increases significantly during the return
motion without load mass parameter resetting in the
control law. Percentage changes in the total mass
parameter in the motion dynamics, from the forward
motion (𝑚= 150 kg) to the return motion (𝑚= 0)
are 9.4%, 27.3%, 57.7%, for the travel, traverse, and
hoist motions, respectively. The result in Fig. 9
signifies the importance of load parameter resetting.
However, many published work on 3D overhead
cranes do not consider the no-load dynamics during
the return motion (Lee, 1998).
Figure 5: Desired and actual positions: desired (dotted line)
and actual (solid line).
Figure 6: Position tracking error: travel (solid line), traverse
(dotted line), and hoist (dash-dot).
Figure 7: Driving forces: travel (solid line), traverse (dotted
line), and hoist (dash-dot).
Desired and actual position [m]
0 102030405060
Time
[
s
]
-0.02
-0.01
0
0.01
0.02
Position tracking error [m]
0 102030405060
Time [s]
-2000
-1500
-1000
-500
0
500
1000
150
0
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
456

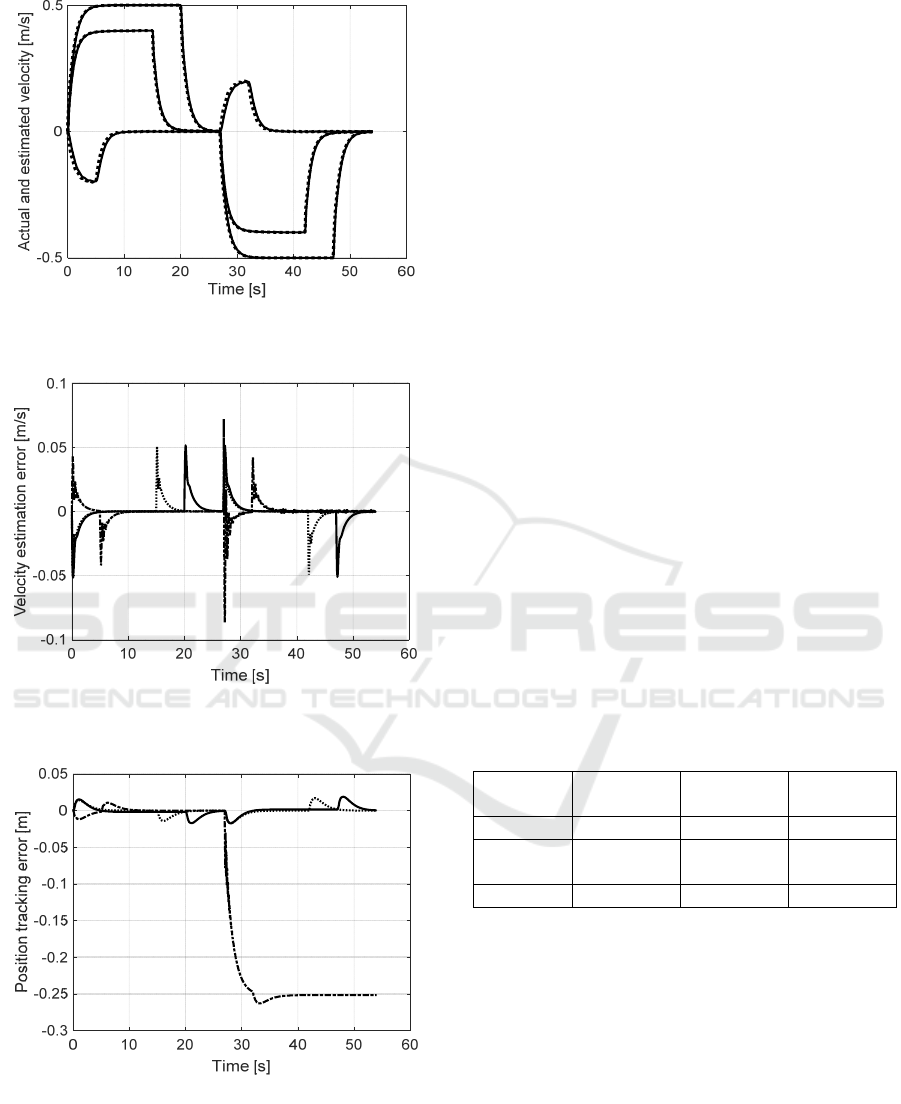
Figure 8: Actual (dotted lines) and observer estimated (solid
lines) velocities.
Figure 9: Velocity estimation error: travel (𝑥

, solid line),
traverse (𝑦

, dotted line), and hoist (𝑧̃

, dash-dot).
Figure 10: Position tracking error: travel (solid line),
traverse (dotted line), and hoist (dash-dot).
4 ACTUATOR FAULT
SIMULATION AND FAULT
ANALYSIS
4.1 Actuator Fault Model
Unknown, time-varying actuator fault is described
by
𝐹

(
𝑡
)
=𝛽
(
𝑡
)
𝐹
(
𝑡
)
+𝑏
(
𝑡
)
;𝑡≥0
(7)
where 𝐹

(𝑡) is the actuator output force and 𝐹(𝑡) is
the control command. The unknown time-varying
fault parameters, 𝛽(𝑡) and 𝑏
(
𝑡
)
, are actuator
efficiency factor and the actuator bias fault,
respectively. If 𝛽
(
𝑡
)
=1 and 𝑏
(
𝑡
)
=0 for all 𝑡≥0,
it implies that the actuator always works normally. In
practice, actuators have finite actuation effectiveness
and bias faults are bounded (Wang et al., 2021). If
𝑏
(
𝑡
)
≠0 and 0<𝛽
(
𝑡
)
<1, it represents an actuator
with a bias fault and actuator partial loss-of-control-
effectiveness. Actuator fault model in (7) is in
compliance with the models used in (Li et al., 2023,
Wang et al., 2021, Jin et al., 2022).
In this study, we consider bridge drive motor
actuator faults that is directly related to the travel
motion in the 𝑥-direction. Actuator loss of control
effectiveness, 1−𝛽, that corresponds to the different
stages of the unknown actuator fault development
from the healthy stage to the final stage are given in
Table 1.
Table 1: Stages of actuator fault development.
Stage Healthy Early Progressive
1
(1−𝛽)% 0 5 10
Stage Progressive
2
Progressive
3
Final
(
1−𝛽
)
% 15 20 25
4.2 Health Monitoring and Frequency
Domain Analysis
In this paper, we propose overhead crane automatic
control and health monitoring with minimally
required sensor devices. No sensors are used
specifically for health monitoring. Only sensors in the
system are the position sensors essential for the
feedback control of the 3 degrees-of-freedom of the
crane.
We investigate the possibility of using the
position tracking error waveform, 𝑒

=𝑥−𝑥

, or
the difference between the position sensor feedback
Automatic Control and Health Monitoring of a 3-Dimentional Overhead Crane with Minimally Required Sensor Devices
457

and the desired position to identify and classify the
faults. Furthermore, the velocity error waveform or
the rate-of-change of error is recommended to better
capture the transients related features. However, no
velocity sensors are used. Hence, we instead analyse
the difference between the observer estimated
velocity and the desired velocity (𝑥

=𝑥

−𝑥

). To
that end, by considering both the waveforms, we
intend to combine both the steady-state and transient
analysis in the fault diagnosis process.
4.3 Features, Correlation, and
Sensitivity
If the crane performs repetitive motions between the
same loading and unloading stations, its position and
velocity profiles may be considered stationary
waveforms. As a result, the position and velocity
error waveform are also stationary. Fast Fourier
transform (FFT) is a powerful technique to analyse
the stationary waveforms. Frequency spectra of the
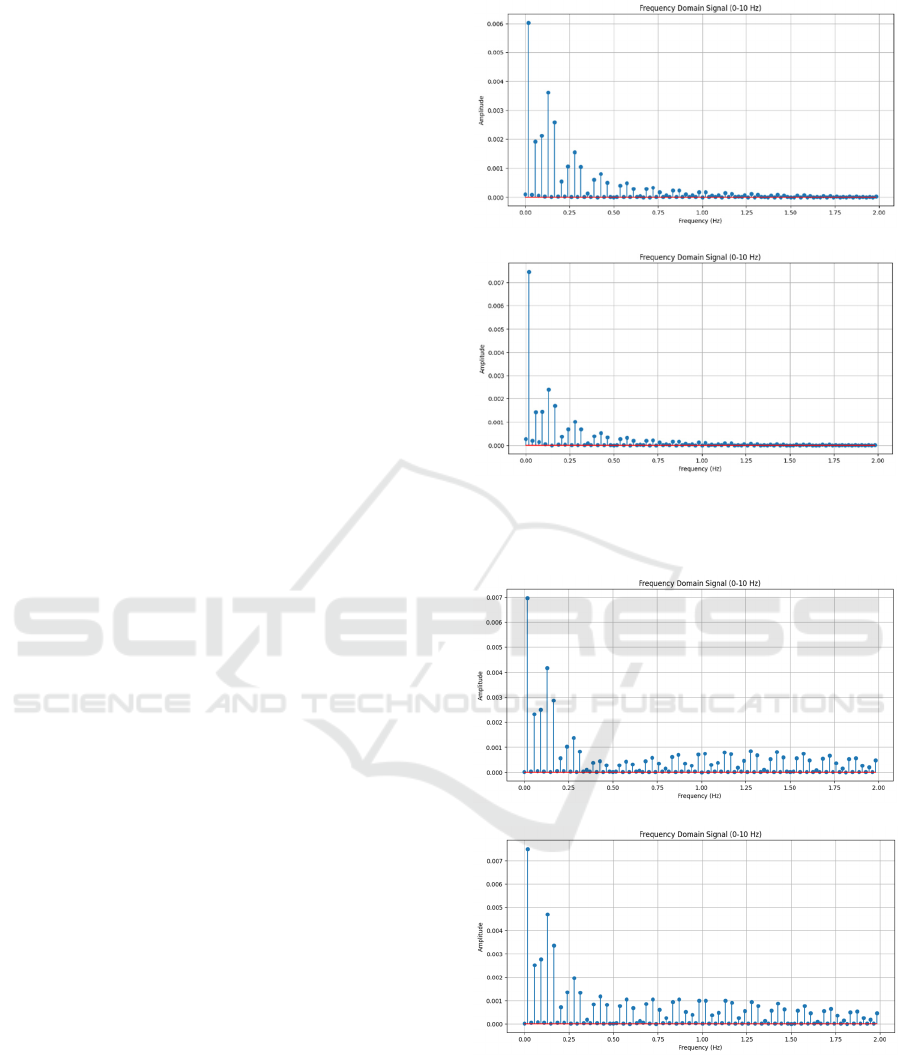
position error waveforms for the healthy actuator and
progressive3 stages are given in Fig. 11 and of the
velocity error for the same stages are given in Fig. 12.
Spectra for the early and final stages are not shown
for brevity.
Difference in magnitude of the FFT components
between the faulty stage and healthy stage may be
used to good effect as the features or inputs to a health
monitoring model. Because the values are small,
before taking the difference, all FFT component
magnitudes are multiplied by a scaling factor of 10

for better readability and round-off error. In the
sequel, 𝑑ℎ


denotes the difference in magnitude of
the 𝑖

FFT component between the faulty stage and
healthy stage of 𝑒

=𝑥−𝑥

and 𝑑ℎ


denotes that of
𝑥

=𝑥

−𝑥

. For instance, 𝑖=0,1,2,3 represent the
DC component, fundamental, 2
nd
harmonic, and 3
rd
harmonic, respectively.
For the purpose of health monitoring, actuator %
loss of control effectiveness is taken as the output.
When the actuator fault develops slowly over the
time, 𝑒

and 𝑥

waveforms vary in their features yet
preserving the stationarity. In this study, we consider
the first 100 FFT components of each waveform at all
different stages of the actuator fault outlined in Table
1. We first perform Spearman and Kendall Tau
correlation analyses to identify the 𝑑ℎ


and 𝑑ℎ


variables with the strongest correlation with the
output. The identified 𝑑ℎ


and 𝑑ℎ


variables are
then ranked according to the range.
(a)
(b)
Figure 11: Position error frequency spectra: (a) Healthy
stage (b) Progressive3 stage.
(a)
(b)
Figure 12: Velocity error frequency spectra: (a) Healthy
stage (b) Progressive3 stage.
Fig. 12 shows the variation of the 𝑑ℎ


and 𝑑ℎ


variables that have the highest range. They all have
correlation index of either 1 or -1. Here, 1 indicates a
perfect positive relationship, -1 indicates a perfect
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
458

negative relationship, and 0 indicates no relationship.
As it can be seen in Fig. 13, the 𝑑ℎ


and 𝑑ℎ


variables with the higher range have higher
sensitivity. Furthermore, their monotonic and non-
linear nature justifies our choice of the type of the
correlation, namely, Spearman and Kendall Tau.
Figure 13: Variation of 𝑑ℎ


and 𝑑ℎ


with the development
of the fault.
Table 2 shows the 𝑑ℎ


and 𝑑ℎ


variables in the
ascending order in terms of the range and sensitivity
with the output.
Table 2: The 𝑑ℎ


and 𝑑ℎ


variables in the ascending order
in terms of the range and sensitivity with the output.
Variable Range Order of
sensitivit
y
Correlation
𝑑ℎ


2.51855504
1 +1
𝑑ℎ


-1.62332400 2 -1
𝑑ℎ


-1.17462186 3 -1
𝑑ℎ

0.98634920 4 +1
𝑑ℎ


-0.88233157 5 -1
𝑑ℎ

0.84783237 6 +1
𝑑ℎ

0.84783237 7 +1
𝑑ℎ

0.84769452 8 +1
𝑑ℎ

0.76450033
9 +1
𝑑ℎ

0.73262167
10 +1
Sensitivity analysis helps determine how sensitive the
output is to the variations of different inputs. This
helps identify which input variable the most critical
in the input-output relationship. As seen in Table 2,
the highest ranked input variables in terms of
sensitivity is a mixture of 𝑑ℎ


and 𝑑ℎ


variables.
Furthermore, in Fig. 13, it can be seen that the
sensitivity of 𝑑ℎ


, which has the largest range, is
small in the early stages of the actuator fault. To this
end, we conclude that consideration of the error
waveform, 𝑥

=𝑥

−𝑥

, enhances the chances of
early detection of the actuator fault.
5 CONCLUSIONS
This paper presented a controller-observer scheme for
linear position tracking control of the hook-block of
an overhead crane in the 3-D space. Closed-loop
stability of the plant-controller-linear velocity
observer system has been guaranteed using Lyapunov
method.
The simple trajectory planning method proposed
here has enabled defining the times and distance to
the destination, maximum linear velocities and
accelerations in the parameters of the function itself
as well as ensuring smooth tracking trajectories. This
simplifies the meeting of operational and safety
requirements and meeting the actuator constraints.
Computer numerical simulations in the presence of
15% model parameter uncertainties and random
external disturbances have produced small position
tracking and velocity estimation errors as well as
admissible transient performance.
Using frequency domain, correlation, and
sensitivity analysis, we have also shown that position
tracking error, 𝑒

=𝑥−𝑥

, and velocity error, 𝑥

=
𝑥

−𝑥

, waveforms may be used successfully for
actuator health monitoring. As a result, only the
position measurements are required for the entire
purpose of automatic control and health monitoring in
PdM applications of multi-motor systems.
Future work involves investigation of wavelet
transforms, wavelet NNs architectures, and ensemble
techniques to address the health monitoring problem
when the motion trajectories are non-repetitive.
ACKNOWLEDGEMENTS
We would like to acknowledge the support extended
by the industry sponsor, Electro Metal Pressings Pvt.
Ltd and the University of Moratuwa for the assistance
in publishing this paper.
REFERENCES
Gao, Z., Cecati, C., Ding, SX. (2015). A Survey on Fault
Diagnosis and Fault Tolerant Techniques-Part II: Fault
Diagnosis with Knowledge-Based and Hybrid/Active
Approaches. IEEE Trans. Industrial Electronics, Vol.
62, pp. 3768-3774.
Gowrienanthan, B., Kiruthihan, N., Ratnayake, KDIN.,
Logeeshan, V., Kumarawadu, S. (2023). Deep-
Learning-Based Non-Intrusive Load Monitoring for 3-
Phase Systems. IEEE Access, Vol. 11, pp. 49337–
49347.
dh
pi
and dh
vi
Automatic Control and Health Monitoring of a 3-Dimentional Overhead Crane with Minimally Required Sensor Devices
459

Ji, L., Xu, Y., Zou, J., Wang, M. (2019). Sensorless Control
for PMSM With Novel Back EMF Observer Based on
Quasi-PR Controller. In Int. Conf. Electrical Machines
and Systems, Harbin, China.
Jin, XZ., Che, WW., Wu, ZG., Zhao, Z. (2022). Adaptive
Consensus and Circuital Implementation of a Class of
Faulty Multiagent Systems. IEEE Trans. Syst., Man,
Cybern. Syst., vol. 52, no. 1, pp. 226–237.
Kumarawadu, S., Lee, TT. (2009). Neuroadaptive Output
Tracking of Fully Autonomous Road Vehicles With an
Observer. IEEE Trans. Intelligent Transportation
Systems, Vol. 10, pp. 335-345.
Kumarawadu, S., Watanabe, K., Lee, TT. (2007). High-
Performance Object Tracking and Fixation With an
Online Neural Observer. IEEE Trans. Systems, Man,
and Cybernetics, Part B (Cybernetics), Vol. 37, pp.
213-223.
Khatamianfar, A. (2015). Advanced Discrete-Time Control
Methods for Industrial Applications. PhD Thesis,
Cornell Univ. (also available at www.researchgate.net).
Lee, HH. (1998). Modeling and Control of a Three-
Dimentional Overhead Crane. Journal of Dynamic
Systems, Measurement and Control, Vol. 120, pp. 471-
476.
Li, L., Zhang, Q., Liu, J. (2023). Consensus Tracking and
Vibration Control for Multiple Overhead Cranes with
Flexible Cables Under Time Varying Actuator Faults.
IEEE Trans. Automation Science and Engineering, pp.
1-11.
Wang, C., Wen, C., Guo, L. (2021). Adaptive Consensus
Control for Nonlinear Multiagent Systems with
Unknown Control Directions and Timevarying
Actuator Faults. IEEE Trans. Autom. Control, vol. 66,
no. 9, pp. 4222–4229.
Wen JT., Bayard, DS. (1988). New Class of Control Laws
for Robot Manipulators:Non-Adaptive Case. Int.
Journal of Control, vol. 47, pp. 1361–1385.
Suzuki, K., Fujii, T. (2006). Fault Diagnosis of Parameter
Change Type Faults and a Fault Tolerant System
Design for Servo Systems. In American Control
Conference, Minneapolis, Minnesota.
APPENDIX
Consider the Lyapunov function candidate
𝐿=
1
2
𝑧
̃


+𝜆𝑧
̃

𝑧
̃
+
1
2
𝐿

+𝜆𝐿

𝑧
̃

(A1)
+
1
2
𝑒

+𝜆𝑒𝑒+
1
2
𝑘

+𝜆𝑘

𝑒

which is positive definite for 𝜆 sufficiently small.
With (4), (5), and dynamics equation, (3), we get
𝑀𝑧
̃

+𝐿

𝑧
̃

+𝐿

𝑧
̃
=−𝐷𝑧
̃

−𝑑
(A2)
𝑀𝑒

+𝑘

𝑒+𝑘

𝑒−𝑘

𝑧
̃

=−𝐷𝑧
̃

−𝑑
(A3)
Time differentiating (A1) and using the results
(A2), (A3) yield
𝐿

=−𝐿

+
𝐷
𝑀
−𝜆𝑧
̃


−𝜆𝐿

𝑧
̃

−
(
𝑘

−𝜆
)
𝑒

−𝜆𝑘

𝑒

−
𝐷
𝑀
(
𝜆𝑧̃+𝑒+𝜆𝑒
)
𝑧̃

−
𝑑
𝑀
𝑧
̃

+𝜆𝑧
̃
+𝑒+𝜆𝑒
(A4)
+𝑘

(𝑒+𝜆𝑒)𝑧
̃

Following inequalities can be written for the terms
of (A4)
−

𝐿

+
𝐷
𝑀
−𝜆

𝑧
̃


−𝜆𝐿

𝑧
̃

−
(A5)
(
𝑘

−𝜆
)
𝑒

−𝜆𝑘

𝑒

≤0
−
𝐷
𝑀
(
𝜆𝑧
̃
+𝑒+𝜆𝑒
)
𝑧
̃

≤
𝐷
𝑀
(
𝜆
|
𝑧
̃
|
+
|
𝑒
|
+𝜆
|
𝑒
|)
𝑧
̃


(A6)
≤
𝐷
2𝑀
𝑒

+𝜆𝑒

+3𝑧
̃


+𝜆

𝑧
̃


−
𝑑
𝑀
𝑧
̃

+𝜆𝑧
̃
+𝑒+𝜆𝑒
≤
𝑑

𝑀
|𝑧
̃

|+𝜆
|
𝑧
̃
|
+
|
𝑒
|
+𝜆
|
𝑒
|

(A7)
≤
𝑑

2
𝑀
𝑧
̃


+𝜆

𝑧
̃

+𝑒

+𝜆

𝑒

+4
In (A6) and (A7), the fact that for any real scalars
𝑎 and 𝑏, 𝑎𝑏≤(𝑎

+𝑏

)/2 is used.
𝑘

(
𝑒+𝜆𝑒
)
𝑧
̃

≤𝑘

(|
𝑒
|
+𝜆
|
𝑒
|)

𝑧
̃


(A8)
≤
𝑘

2
2𝑧
̃


+𝑒

+𝜆

𝑒


Because of the inequalities (A5) through (A8),
there results
𝐿

≤−
𝑘

2
−𝜆−
1
2
𝐷
𝑀
−
1
2
𝑑

𝑀
𝑒

−𝜆𝑘

−
𝜆

2
𝑘

−
𝜆

2
𝐷
𝑀
−
𝜆

2
𝑑

𝑀
𝑒

−

𝐿

−𝑘

−𝜆−
1
2
𝐷
𝑀
−
1
2
𝑑

𝑀

𝑧
̃


−

𝜆𝐿

+
𝜆

2
𝐷
𝑀
−
𝜆

2
𝑑

𝑀

𝑧
̃

+2
𝑑

𝑀
According to 𝛽-ball lemma (Wen and Bayard, 1988),
it follows that
𝐿

≤−𝜅

𝑒

−𝜅

𝑒

−𝜅

𝑧̃


−𝜅

𝑧̃

+2
𝑑

𝑀
where 𝜅

>0;𝑖=1,2,3,4 for a 𝜆 sufficiently small
and suitably chosen set of controller-observer gains,
𝑘

,𝑘

,𝐿

,𝐿

>0. This allows us to write
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
460

−𝐿

𝑒,𝑒,𝑧̃

,𝑧̃≤−𝜅𝐿𝑒,𝑒,𝑧̃

,𝑧̃+𝛾
for some 𝜅>0. Here, 𝛾=2



.
Therefore, the Lyapunov function, 𝐿(𝑒,𝑒,𝑧̃

,𝑧̃), is
positive definite outside a compact set of 𝒪(𝛾) and
the closed-loop plant-controller-observer system, (3),
(4), (5), is uniformly ultimately bounded (UUB).
Automatic Control and Health Monitoring of a 3-Dimentional Overhead Crane with Minimally Required Sensor Devices
461