Personalization of Dataset Retrieval Results Using a Data Valuation

Method

Malick Ebiele

1 a

, Malika Bendechache

2 b

, Eamonn Clinton

and Rob Brennan

1 c

ADAPT, School of Computer Science, University College Dublin, Belﬁeld, Dublin, Ireland

School of Computer Science, University of Galway, Galway, Ireland

Tailte

Eireann, Phoenix Park, Dublin, Ireland

Keywords:

Data Valuation, Data Value, Personalized Data Value, Dataset Retrieval, Information Retrieval, Quantitative

Data Valuation.

Abstract:

In this paper, we propose a data valuation method that is used for Dataset Retrieval (DR) results re-ranking.

Dataset retrieval is a specialization of Information Retrieval (IR) where instead of retrieving relevant doc-

uments, the information retrieval system returns a list of relevant datasets. To the best of our knowledge,

data valuation has not yet been applied to dataset retrieval. By leveraging metadata and users’ preferences,

we estimate the personal value of each dataset to facilitate dataset ranking and ﬁltering. With two real users

(stakeholders) and four simulated users (users’ preferences generated using a uniform weight distribution), we

studied the user satisfaction rate. We deﬁne users’ satisfaction rate as the probability that users ﬁnd the datasets

they seek in the top k = {5, 10} of the retrieval results. Previous studies of fairness in rankings (position bias)

have shown that the probability or the exposure rate of a document drops exponentially from the top 1 to the

top 10, from 100% to about 20%. Therefore, we calculated the Jaccard score@5 and Jaccard score@10 be-

tween our approach and other re-ranking options. It was found that there is a 42.24% and a 56.52% chance on

average that users will ﬁnd the dataset they are seeking in the top 5 and top 10, respectively. The lowest chance

is 0% for the top 5 and 33.33% for the top 10; while the highest chance is 100% in both cases. The dataset

used in our experiments is a real-world dataset and the result of a query sent to a National mapping agency data

catalog. In the future, we are planning to extend the experiments performed in this paper to publicly available

data catalogs.

1 INTRODUCTION

Given rapidly rising data volumes, knowing which

data to keep and which to discard has become an

essential task. Data valuation has emerged as a

promising approach to tackle this problem (Even and

Shankaranarayanan (2005)). The primary focus of

data valuation research is the development of method-

ologies for determining the value of data (Khokhlov

and Reznik; Laney; Qiu et al.; Turczyk et al.; Wang

et al.; Wang et al. (2020; 2017; 2017; 2007; 2021;

2020)).

Data valuation methods have been applied to data

management, machine learning, system security, and

energy (Khokhlov and Reznik; Turczyk et al.; Wang

https://orcid.org/0000-0001-5019-6839

https://orcid.org/0000-0003-0069-1860

https://orcid.org/0000-0001-8236-362X

et al.; Wang et al. (2020; 2007; 2021; 2020)). There

have been no previous attempts to apply data valua-

tion to dataset retrieval. Dataset retrieval is a special-

ization of information retrieval where instead of re-

trieving relevant documents the Information Retrieval

system returns a list of relevant datasets (Kunze and

Auer (2013)). Dataset retrieval systems will return

relevant datasets according to a given query. The re-

trieved datasets are sorted alphabetically by name or

using another metadata like creation date or a ranking

algorithm incorporated in the dataset retrieval tech-

nique. However, they do not consider the user’s pref-

erences in terms of metadata. Some dataset retrieval

software allows users to sort the results by each meta-

data separately like creation date, usage, and last up-

date or ﬁltering the results using boolean operations.

However, none of them allow users to sort the results

by a combination of those metadata (see Equation 5

below). In this paper, we propose a metadata-based

122

Ebiele, M., Bendechache, M., Clinton, E. and Brennan, R.

Personalization of Dataset Retrieval Results Using a Data Valuation Method.

DOI: 10.5220/0013044100003838

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2024) - Volume 1: KDIR, pages 122-134

ISBN: 978-989-758-716-0; ISSN: 2184-3228

data valuation method that will allow users to sort

dataset retrieval results using a combination of meta-

data.

Position bias is the study of the relationship be-

tween the ranking or position of a retrieved document

and the exposure it receives (Agarwal et al.; Craswell

et al.; Jaenich et al.; Wang et al. (2019; 2008; 2024;

2018)). In other words, position bias is the study of

the probability of a document being consulted by a

user according to its position among the retrieved doc-

uments. Previous studies have shown that the proba-

bility or the exposure rate of a document drops ex-

ponentially from the top 1 to the top 10 and then

more logarithmically from the top 11 to the top 100

(Jaenich et al. (2024)). Jaenich et al. (2024) also

showed that the number of possible orderings of doc-

uments for rankings of size k = 1 ...100 grows expo-

nentially. Using a group of 6 job seekers as an ex-

ample, Singh and Joachims (2018) illustrated how a

small difference in relevance (used to order retrieved

documents or items) can lead to a large difference in

exposure (an opportunity) for the group of females.

They showed that a 0.03 difference in average rele-

vance (between the top 3 who are all male and the

bottom 3 who are all female) can result in a 0.32 dif-

ference in average exposure. The difference in aver-

age exposure (between the top 3 and the bottom 3) is

10 times the difference in average relevance.

The above studies show that putting the most rel-

evant information on top or providing a fair ranking

is crucial. Many fair ranking techniques have been

designed to attempt to solve the fairness problem in

rankings (Singh and Joachims; Zehlike et al.; Zehlike

et al. (2018; 2022a; 2022b)). To the best of our knowl-

edge, none of the existing ranking techniques inte-

grate the user’s preferences in the ranking algorithm

or use them as a post-retrieval step to re-rank the re-

trieved information. Here, we present a metadata-

based data valuation technique that takes in the re-

trieved datasets’ metadata and the user’s preferences

and outputs a re-ranking of the retrieved datasets. It

is worth noting that because data value is a relative

measure if a dataset d

is more valuable than d

the whole set of datasets D, then d

will always be

ranked higher than d

considering D or any subset of

D containing both datasets.

Many of the existing data valuation approaches

are subjective. This is due to the subject-dependent

nature of some dimensions (e.g. Utility dimen-

sion) that characterise data value (Attard and Brennan

(2018)) or the subject-dependent weighting tech-

niques (in the case of weighted averaging or sum-

ming) (Deng et al.; Odu (2023; 2019)). Subjective

metrics of data value dimensions (metadata are proxy

for data value dimensions, therefore usage metadata

and usage dimension mean the same thing) or weight-

ing techniques can only be deﬁned by individual users

or experts based on their personal views, experiences,

and backgrounds. These are opposed to objective

metrics that can be determined precisely based on a

detailed analysis of the data or extracted from the data

infrastructure (Bodendorf et al. (2022)). This makes

it challenging to develop a fully objective data val-

uation model because of the difﬁculty to objectively

measure some dimensions and also experts can be ex-

pensive. We believe that instead of generalizing sub-

jective metrics and weighting techniques, it would be

better to attempt to develop personalized data val-

uation models. The difference between subjective

data value and personalized data value is that the for-

mer assumes that subjective metrics and weights can

be applied to every user. Meanwhile, personalized

data value will request the subjective metrics and the

weights from each user representing their preferences

to calculate a personal data value.

Choosing a suitable weighting technique is an ad-

ditional challenge for weighted approaches to data

valuation. For instance, usage-over-time is one of the

ﬁrst data valuation methods and developed a weight-

ing technique based on recency (Chen (2005)). The

recency-based weighting technique is objective. The

only subjective decision is the choice of assigning

higher or lower weights to the more recent Usage

metadata. Chen (2005) assigned higher weights to

the more recency Usage metadata; which is logical

for their use case. In our case, the desired weighting

technique should be subjective, performant (have low

complexity for calculation), and straightforward for

the users to interact with.

The research question is: To what extent can

metadata-based data valuation methods improve the

results of dataset retrieval systems in terms of users’

satisfaction?

To answer this research question, we designed and

implemented a metadata-based data valuation method

and applied it to a dataset retrieval use case for a Na-

tional Mapping Agency. The goal is to improve the

users’ satisfaction by putting on top the datasets they

consider more valuable. This is done by taking into

account the customers’ dataset preferences to re-rank

the retrieved datasets.

The contributions of this paper are as follows:

• The ﬁrst application of a metadata-based data val-

uation method to dataset retrieval.

• Proposed a personalized and interactive data valu-

ation method. Extant methods are mainly subjec-

tive approaches.

Personalization of Dataset Retrieval Results Using a Data Valuation Method

123

The remainder of this paper is structured as fol-

lows. Section 2 gives a description of the use case.

Section 3 describes the related work. Our proposed

metadata-based data valuation method is explained in

Section 4. Section 5 explains our experimental de-

sign. In Section 6, the experimental results are shown

and discussed. Finally, the conclusion and future

work are presented in Section 7.

2 USE CASE DESCRIPTION AND

BACKGROUND

2.1 Project Description

This data valuation project is part of an ongoing col-

laboration between researchers from University Col-

lege Dublin (UCD) and Tailte

Eireann (TE). Tailte

Eireann (TE) is Ireland’s state agency for property

registrations, property valuation and national map-

ping services. It was established on 1 March 2023

from a merger of the Property Registration Author-

ity (PRA), the Valuation Ofﬁce (VO) and Ordnance

Survey Ireland (OSI). The end goal of this collab-

oration is to design and implement a data valuation

method for TE’s datasets from the customer’s per-

spective. They would like to apply a metadata-based

data valuation to re-rank the results of a query sent

to their dataset retrieval platform. The data valuation

method should take into account the customers’ pref-

erences in terms of metadata. At this stage, the goal

is to design and implement a proof of concept.

2.2 Current Dataset Retrieval Process

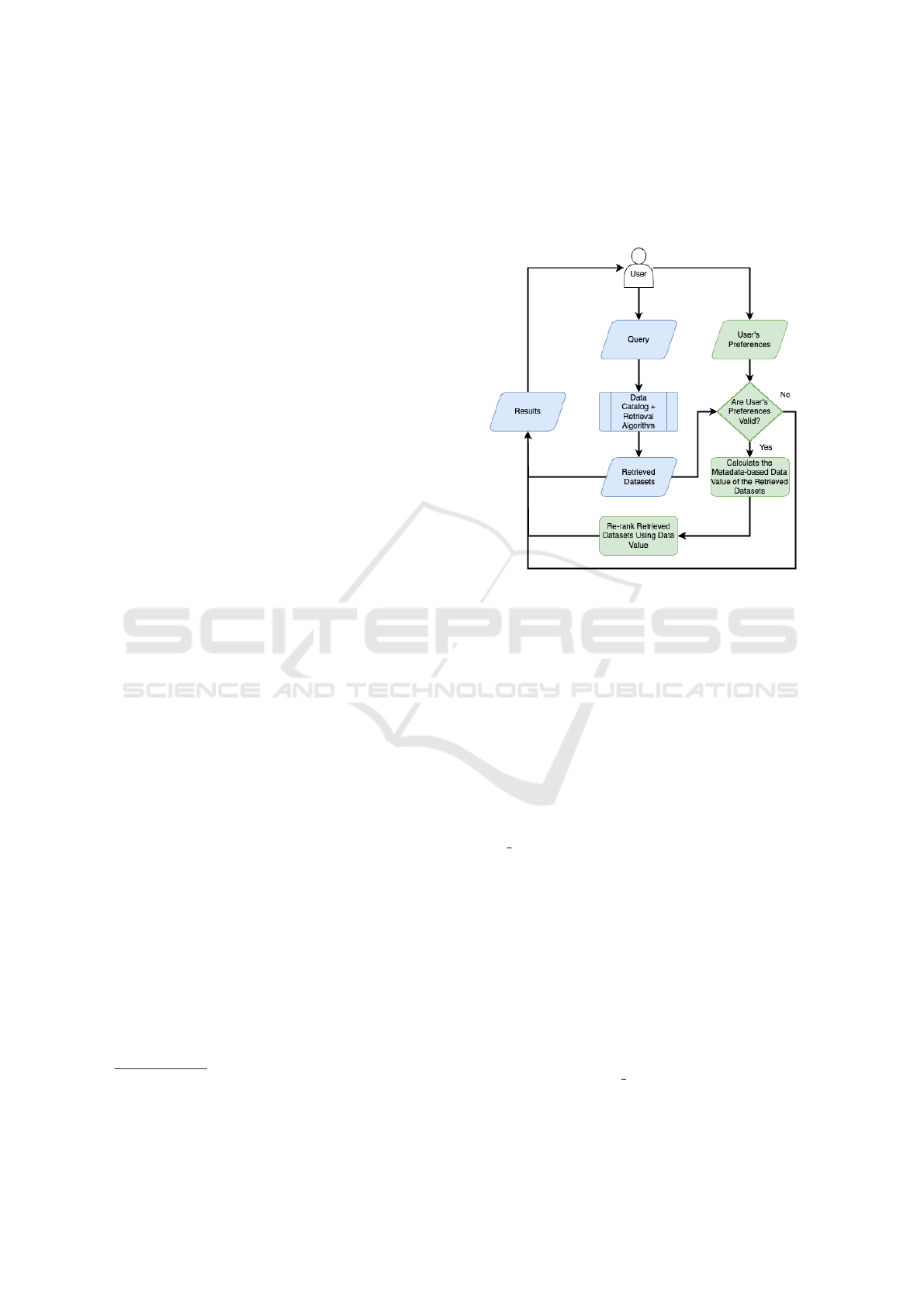
Figure 1 below displays the current dataset retrieval

process (in Blue, some examples here

123

) and our

proposed personalized dataset retrieval process (in

Green). In the current process, the user sends a query

to the data catalog. The query is then processed and

used to extract the relevant datasets from the data cat-

alog. The retrieved datasets are ﬁnally formatted in

a user-friendly way and sent to the user. In our pro-

posed approach, simultaneously or after the query is

sent, the user can specify their preferences in terms

of the retrieved datasets’ metadata. The user pref-

erences go through a validity test (to test if all of

the weights provided are not zeros). The retrieved

datasets’ metadata and the user preferences are then

used to compute the value of each retrieved dataset.

https://data.gov

https://www.kaggle.com/datasets

https://datasetsearch.research.google.com

The calculated data value is ﬁnally used to re-rank

the retrieval datasets before formatting them in a user-

friendly way and sending them to the user. If no pref-

erences are provided or if they are invalid, then the

retrieved datasets are presented alphabetically.

Figure 1: Personalized datasets retrieval using a metadata-

based data valuation. In Blue is the current dataset retrieval

process. In Green are the additional steps we proposed to

personalize dataset retrieval results.

2.3 Information and Dataset Retrieval

Performance Metrics

The Jaccard index also known as the Jaccard score has

been chosen to evaluate the users’ satisfaction. The

Jaccard score measures the similarity between at least

two ﬁnite sets and is deﬁned as the size their inter-

section divided by the size of their union (see Equa-

tion 1 below). The truncated Jaccard score at k (Jac-

card score@k), which only focuses on the top k el-

ements, is preferred for our use case. As shown in

Section 1, only the top k (with k ≤ 10) are most likely

to be consulted. Therefore, focusing mainly on the

top k elements makes sense.

However, Jaccard score does not take into account

the positions. So, the Normalized Discounted Cumu-

lative Gain (NDCG) has also been calculated. NDCG

is widely used and involves a discount function over

the rank while many other measures uniformly weight

all positions (see Equation 2 below). It measures the

matching degree between our ranking and other rank-

ings.

NDCG and Jaccard score@k range between 0 and

1, with 1 being the optimal performance. We used

the scikit-learn implementation of NDCG with the de-

KDIR 2024 - 16th International Conference on Knowledge Discovery and Information Retrieval

124

fault parameters

and a self implementation of Jac-

card score@k in Python.

J(A, B) =

|A ∩ B|

|A ∪ B|

|A ∩ B|

|A| + |B| − |A ∩ B|

(1)

NDCG

( f ,S

) =

DCG

( f ,S

)

IDCG

)

DCG

( f ,S

) =

∑

r=1

G(y

(r)

)D(r),

IDCG

) = max

′

∑

r=1

G(y

′

(r)

)D(r),

(2)

with D(r) =

log

(1+r)

(inverse logarithm decay with

base b) the discount function, S

is a dataset, f is a

ranking function, f

′

is the best ranking function on

, and G is the Gain. DCG

( f ,S

) is the Discounted

Cumulative Gain (DCG) of f on S

with discount D

and IDCG

) is the Ideal DCG.

3 RELATED WORK

This section describes the current state-of-the-art in-

formation and dataset retrieval approaches and their

limitations. Then, it highlights the challenges related

to weighted average approaches because the approach

proposed in this paper falls into that category.

3.1 Information and Dataset Retrieval

Tamine and Goeuriot (2021) deﬁne Information re-

trieval (IR) as a system that deals with the repre-

sentation, storage, organization and access to infor-

mation items. It has two main processes: Indexing

(which consists of building computable representa-

tions of content items using metadata) and Retrieval

(which consists of optimally matching queries to rel-

evant documents) (Tamine and Goeuriot (2021)). IR

models have evolved since the 1960s from Boolean

to Neural Networks (Lavrenko and Croft; Liu; Maron

and Kuhns; Miutra and Craswell; Robertson et al.;

Salton et al.; Salton and McGill; Tamine and Goeuriot

(2001; 2009; 1960; 2018; 1980; 1983; 1986; 2021)).

Hambarde and Proenc¸a (2023) argue that IR sys-

tems have two stages: retrieval and ranking. The re-

trieval stage consists of four main techniques: Con-

ventional IR, Sparse IR, Dense IR, and Hybrid IR

techniques. The latter is any combination of the for-

mer three. The ranking stage consists of two main

https : / / scikit - learn.org / stable / modules / generated /

sklearn.metrics.ndcg score.html

approaches: Learning To Rank and Deep Learning

Based Ranking approaches. For more details on this

categorization of IR techniques, please refer to Ham-

barde and Proenc¸a (2023).

Liu et al. (2020) argue that the IR research com-

munity has long agreed that major improvement of

search performance can only be achieved by taking

account of the users and their contexts, rather than

through developing new retrieval algorithms that have

reached a plateau. Three main approaches have been

employed to personalize IR results: Query expansion,

Result re-ranking, and Hybrid personalization tech-

niques (Liu et al. (2020)). Query expansion collects

additional information about user interest from het-

erogeneous sources, represents them by some terms,

and automatically adds these terms to the initial query

for a reﬁned search (Bai et al.; Belkin et al.; Bian-

calana et al.; Bilenko et al.; Bouadjenek et al.; Budzik

and Hammond; Buscher et al.; Cai and de Rijke; Chen

and Ford; Chirita et al.; Jayarathna et al.; Kelly

et al.; Kraft et al. (2007; 2005; 2008; 2008; 2013;

1999; 2009; 2016; 1998; 2007; 2013; 2005; 2005)).

Result re-ranking techniques reorder search results

for users according to document relevance (Gauch

et al.; Liu et al.; Liu and Hoeber; Tanudjaja and

Mui; Wang et al. (2003; 2002; 2011; 2002; 2013)).

Hybrid techniques combine query expansion and re-

sult re-ranking; they outperform either one individu-

ally but are under-explored (Ferragina and Gulli; Lv

et al.; Pitkow et al.; Pretschner and Gauch; Shen et al.

(2005; 2006; 2002; 1999; 2005)).

Most re-ranking systems are not interactive. They

have some sort of pre-settled weighting criteria for

re-ranking, giving heavier weight to those documents

that match user interests and push them to top ranks

(Liu et al.; Tanudjaja and Mui (2002; 2002)). The

ones that are interactive present the top k documents

to the users for feedback and then reﬁne ranking based

on the feedback (Gauch et al.; Liu and Hoeber; Wang

et al. (2003; 2011; 2013)).

Thus it can be seen that interactive IR result

re-ranking based on users’ preferences is under-

explored. The approach proposed in this paper is an

interactive dataset retrieval technique based on users’

preferences in terms of the retrieved datasets’ meta-

data.

3.2 Weighted Average Data Valuation

Methods

There were also previous attempts to calculate the

data value using weighted averaging of metadata de-

scribing data value dimensions (Chen; Ma and Zhang;

Qiu et al. (2005; 2019; 2017)). For instance, measur-

Personalization of Dataset Retrieval Results Using a Data Valuation Method

125

ing usage-over-time is one of the ﬁrst data valuation

methods and it estimates data value with the weighted

averaging approach of Chen (Chen (2005)). It con-

sists of splitting the usage data into a series of time

slots, assigning a weight to each time slot, and then

computing the data value using the weighted aver-

age. The weights are the normalized recency weights.

The more recent time slots are assigned the higher

weights (Chen (2005)). Ma and Zhang (2019) ex-

tended the usage-over-time model by adding the age

and size dimensions. Their Multi-Factors Data Valu-

ation Method (MDV ) is a trade-off between dynamic

and static data value. The dynamic data value is the

usage-over-time model of Chen. The static data value

is the weighted average of the normalized age and

size. The weights of the age and size dimensions are

assigned subjectively by experts.

Qiu et al. (2017) used the Analytic Hierarchy Pro-

cess (AHP) which is a different weighting approach.

AHP requires a subjective rating of the input dimen-

sions in pairs. These pairwise comparisons are then

arranged in a matrix (the Judgement matrix, see Ap-

pendix 7), from which a ﬁnal weighting of the dimen-

sions will be calculated. AHP is technically straight-

forward to implement and more importantly allows

to assess the transitivity consistency of the pairwise

comparisons matrix by assigning a consistency score

to it. However, experts are still needed for the pair-

wise rating of the input dimensions. Qiu et al. (2017)

use the measure of 6 dimensions in their model.

Those dimensions are: the size of the data (S), the

access interval (T ), the data read and write frequency

(F), the number of visits (C), the contents of the ﬁle

(D), and the potential value of the data (V ). For more

details on the dimensions used, please refer to Qiu

et al. (2017).

The challenge of applying weighted approaches

is the weighting technique. In our case, the desired

weighting technique must be straightforward for the

users to interact with and fast to compute as it is sup-

posed to be integrated into a live system for interac-

tive IR re-ranking. The weighting approach used in

this paper is detailed in Section 4.1.

To the best of our knowledge, the application of

a metadata-based data valuation approach to dataset

retrieval proposed in this study is unique. Also, none

of the studies described above validated the outputs of

their data valuation approaches. Our approach is val-

idated using preferences from two stakeholders and

four simulated users.

4 PROPOSED DATA VALUATION

METHOD

Our method has two main steps: ﬁrst dimension meta-

data weight determination and then data value calcu-

lation. These are described below.

4.1 Weight Determination

Analytic Hierarchy Process (AHP) was our ﬁrst

choice because of its sound mathematical basis (Saaty

(1987)). However, it was challenging to apply, as in-

stead of assigning a weight to each metadata or di-

mension, a pairwise comparison of the dimensions is

needed (Saaty (1987)). E.g. usage is twice as im-

portant as creation date, usage is 5 times more im-

portant than the number of spatial objects, or us-

age is twice less important than currency. This ex-

ercise was difﬁcult for the stakeholders who partic-

ipated in the experiments. They confessed being

more comfortable with a rating-like weighting ap-

proach e.g. 1 to 5 websites or products rating mech-

anism. Also, AHP assumes that preferences are tran-

sitive and has a transitivity consistency test. Saaty

(1987) advise to discard the current weights deduced

from the pairwise comparisons if the consistency ra-

tio is greater than 0.1. Previous studies showed

that preferences are not always transitive (Al

os-Ferrer

et al.; Al

os-Ferrer and Garagnani; Fishburn; Gendin

(2023; 2021; 1991; 1996)). Al

os-Ferrer et al. (2023)

shows using two preference datasets that no matter

the initial assumptions, even when the preferences are

supposed to be transitive, a maximum of 27.45% of

individual preferences are non-transitive. We believe

that assuming that all preferences are transitive im-

plies ignoring some individual preferences. There-

fore, we used a slider from 0 to 10 (with a step of 1)

as the weights determination technique; the presence

of a zero rating allows the individual to discard a par-

ticular metadata as not relevant to the use case or at

that time. This approach is straightforward and inclu-

sive because it was tested during the interviews with

the stakeholders. The only constraint in our weighting

approach is that at least one of the provided weights

should be non-zero.

4.2 Data Value Calculation

This is split into the following steps: Data preprocess-

ing and Data value calculation.

KDIR 2024 - 16th International Conference on Knowledge Discovery and Information Retrieval

126

4.2.1 Data Preprocessing

As the collected metadata values have different scales,

they must be normalized. The weights also must be

normalized. For the Number of spatial objects meta-

data (see Table 1 below for the description), the val-

ues are divided by the maximum value. For the Us-

age, because it is a time series data (collected monthly

from January 2017 to January 2023). It is normal-

ized by dividing each value by the maximum value

of each month. Then the current Usage value is the

6-month Exponential Moving Average (EMA). EMA

is widely used in ﬁnance to capture stock and bond

price trends while reducing noises like sudden sharp

moves. It was ﬁrst introduced by Roberts (1959) (see

Equation 3). The 6-month Exponential Moving Av-

erage was calculated using the Pandas implementa-

tion with default parameters

. As to the creation date,

we applied the probabilistic approach of calculating

data currency with a decline rate of 20%. This ap-

proach was proposed by Heinrich and Klier (2011)

and the data currency Q

Curr.

(ω,A) formula is shown

in the Equation 4 below. ω is a value in the Attribute

A. The motivation is that the currency of information

does not solely depend on its age but also on whether

the information is likely to change over time or not.

For instance, a satellite image of a mountain range

might still be relevant even if the image is 30 years

old. On the other hand, a 10-year-old satellite image

of road networks might be outdated.

EMA

(U, n) =

∑

i=0

(1 − α)

t−i

∑

i=0

(1 − α)

(3)

t is the current time, n the number of past periods, U

the time-series of usage metadata, U

the usage meta-

data at time t, α (0 < α ≤ 1) is the smoothing factor,

and EMA

(U, n) the EMA of usage metadata at time

t considering n previous periods.

Curr.

(ω,A) := exp(−decline(A) ·age(ω,A)) (4)

For the weights, the weight of each metadata has

been divided by the sum of the weights of all three

metadata per stakeholder.

4.2.2 Actual Data Value Calculation

The data value is then the weighted average of the

metadata values using the Equation 5 below.

V (d

) = w

× U

+ w

× Q

+ w

× O

, (5)

where w

{U, Q, O}

in [0,1] are the weights and V(d

) in

[0,1] the data value. U, Q, and O stand for Usage,

Currency (derived from the Creation date; see Equa-

tion 4), and Number of Spatial Objects, respectively.

https : / / pandas.pydata.org / docs / reference / api /

pandas.DataFrame.ewm.html

Table 1: Description of the metadata used in this paper.

Metadata /

Data Value

Dimension

Description

Usage

Access counts. It measures how many times a given

dataset has been accessed.

Creation date

Date the ﬁrst version has been made available for

the users or the last date it has been updated.

Number of

spatial objects

The number of geometric data (e.g. points, lines,

polygons, paths) in the dataset. It is a domain-relevant

measure of data volume and information content.

5 EXPERIMENTAL DESIGN

Figure 2 below shows the ﬂowchart of our experi-

mental design. The experiments consist of re-ranking

dataset retrieval results using a metadata-based data

valuation technique. It has four main steps: Metadata

extraction, User preferences request, Data value cal-

culation, and Re-ranking of the retrieved datasets.

5.1 Metadata Extraction

This consists of extracting metadata from the data cat-

alog system. For this use case, only three metadata

types have been extracted from 15 datasets: creation

date, number of spatial objects, and usage. The 15

selected datasets are the results of a query sent to the

data catalog system; they are ordered alphabetically

by default.

5.2 User Preferences Request

For this use case, the user preferences have been

requested during interviews with three stakeholders.

The stakeholders included in this study are managers

within the mapping agency with data management re-

sponsibilities for at least 3 years each.

The main goal of each interview (15-20 minutes)

was to get the stakeholders to assign weights to each

metadata ﬁeld. A slider from 0 to 10 (with a step of

1) is used to assign the weight to each metadata.

Table 3 shows the weights provided by each stake-

holder. Stakeholder 2 (SH2) provided an invalid set of

weights (all of the weights are zero) because all of the

metadata selected for this case study was irrelevant to

them. Therefore, the retrieved datasets will be alpha-

betically presented to Stakeholder 2.

5.3 Personal Data Value Calculation

The personal data value is calculated for each dataset

using the valid weights provided by stakeholders SH1

Personalization of Dataset Retrieval Results Using a Data Valuation Method

127

and SH3 and four randomly generated users’ prefer-

ences (using a uniform weight distribution) and Equa-

tion 5. The datasets are then ranked by data value.

The resulting personalized rankings are then com-

pared to the default alphabetic order, MDV and AHP-

based re-rankings. They were also compared to the

univariate rankings based on each metadata indepen-

dently (Usage, Number of Spatial Objects, and Cur-

rency; the current IR/DR data catalog re-ranking op-

tions).

6 EXPERIMENTAL RESULTS

6.1 Comparison with Other Data

Valuation Approaches

In this Section, we compare our approach with other

data valuation approaches: Chen (2005)’s usage-over-

time, Ma and Zhang (2019)’s MDV, and Qiu et al.

(2017)’s AHP-based data valuation techniques.

6.1.1 Our Approach vs Usage-over-Time Model

To computer the usage-over-time data value (see

Equation 6), we used a valuation period (vp) of 6

months, a lifestage length s of 1 month (usually in

terms of usage metadata granularity, here on monthly

basis), N

= 6 (N

is the number of lifestages per valu-

ation period), and x = 2 (x is a regularizer of the slope

of the weight distribution together with N

). Chen

(2005) suggest that signiﬁcantly ﬂat (too large x or N

)

or steep (too small x or N

) weight distributions should

be avoided. Chen (2005) also advised that a valid val-

uation period for long-lived information should be at

least a few months on a quarterly or semi-annual ba-

sis.

We chose x = 2 because, for the examples shown

by Chen (2005) with N

= 5, the weight distribution is

too ﬂat for x = 1.2, too steep for x = 3, and in between

for x = 2.

We have 13 valuation periods with a length of 6

months for the ﬁrst 12 periods and 1 month for the

last period. Therefore, for the last valuation period,

UT is equal to the collected usage data.

(d) =

∑

i=1

(w(i) × f (U

(d))), 0 ≤ f (U

(d)) ≤ 1,

w(i) =

(

)

∑

j=1

(

)

∑

i=1

w(i) = 1, x ≥ 1,

vp = [t − (N

× s),t],N

(6)

Figure 3 below shows the Usage metadata trends

of the retrieved datasets (Figure 3a), the usage-over-

time (Figure 3b), and 6-month Exponential Moving

Average (EMA-6, Figure 3c). We can see that both

usage-over-time (as per Chen) and our proposed 6-

month EMA capture the main usage trends with re-

duced noise (steep highs and lows). The main differ-

ence is that the 6-month EMA reduces the effects of

the noise on the present values while the usage-over-

time removes them completely. EMA is preferred be-

cause it captures every movement while usage-over-

time fails for the same valuation period.

To make the graphs below and in the remainder of

this paper easy to read, Table 2 has been generated. It

maps each dataset to a unique ID. The dataset names

have been sorted alphabetically and an ID starting

from 1 has been assigned to them.

Table 2: Dataset IDs and Names Mapping.

IDs Datasets

1 ig/basemap premium

2 itm/6inch cassini

3 itm/basemap premium

4 itm/basemap public

5 itm/digitalglobe

6 itm/historic 25inch

7 itm/historic 6inch cl

8 itm/national high resolution imagery

9 itm/ortho

10 itm/ortho 2005

11 wm/basemap eire

12 wm/basemap ms public

13 wm/basemap premium

14 wm/basemap public

15 wm/digitalglobe

6.1.2 Our Approach vs MDV and AHP Data

Valuation Approaches

MDV (Ma and Zhang (2019)) is a natural extension of

the usage-over-time model by adding the Age (Valu-

ation Date minus Creation Date) and the Size meta-

data to the Usage metadata. MDV is calculated using

the Equation 7 below. The weights of the age (W

age

)

and the size (W

size

), and the trade-off coefﬁcient k

are set to W

age

= W

size

= 0.5 and k = 0.2; the same

values as the example presented by (Ma and Zhang

(2019)). The Age and Size metadata are normalized

using the MinMax scaler (Scikit-learn implementa-

tion with default parameters

) then the resulting value

is subtracted from 1 because Ma and Zhang (2019) as-

sume that more recent and smaller sized datasets are

https : / / scikit - learn.org / stable / modules / generated /

sklearn.preprocessing.MinMaxScaler.html

KDIR 2024 - 16th International Conference on Knowledge Discovery and Information Retrieval

128

Figure 2: Experimental design for personalized metadata-based data valuation.

(a) Usage metadata

(b) Usage-over-time

Figure 3: Comparison of usage-over-time with a 6-month

EMA at capturing the usage metadata trends.

considered more valuable.

V = kV

+ (1 − k)V

= w

size

× f (S(d)) + w

age

× f (A(d)),

0 ≤ f (S(d)) ≤ 1,0 ≤ f (A(d)) ≤ 1,

= V

(d) (see Equation 6).

(7)

As we couldn’t collect pairwise comparisons of

the metadata from the stakeholders (see Section 4.1),

we will use the weights they provided (see Table 3)

to produce proxy pairwise comparisons. The pro-

vided weights are summed per metadata type and then

the inverse of the sum per metadata is multiplied by

the maximum of the sum (see Table 4 and Equation

8). The obtained pairwise comparison vector is used

to ﬁll out the AHP Judgement matrix using its reci-

procity and transitivity properties (see Appendix 7).

AHP

= [

′′

] = [1,

′′

Because w

′′

= Max(w

′′

With w

′′

∑

i=1

′

̸= 0,w

′′

∑

i=1

′

̸= 0,

′′

∑

i=1

′

̸= 0,

(8)

AHP

is the ﬁrst row vector of the judgement ma-

trix P because the diagonal elements of P are equal to

1. From V

AHP

, we can deduce the ﬁrst column vec-

tor of P using its reciprocity property. Then, ﬁll out

the rest of the matrix P using its transitivity property

For more details see Appendix 7.

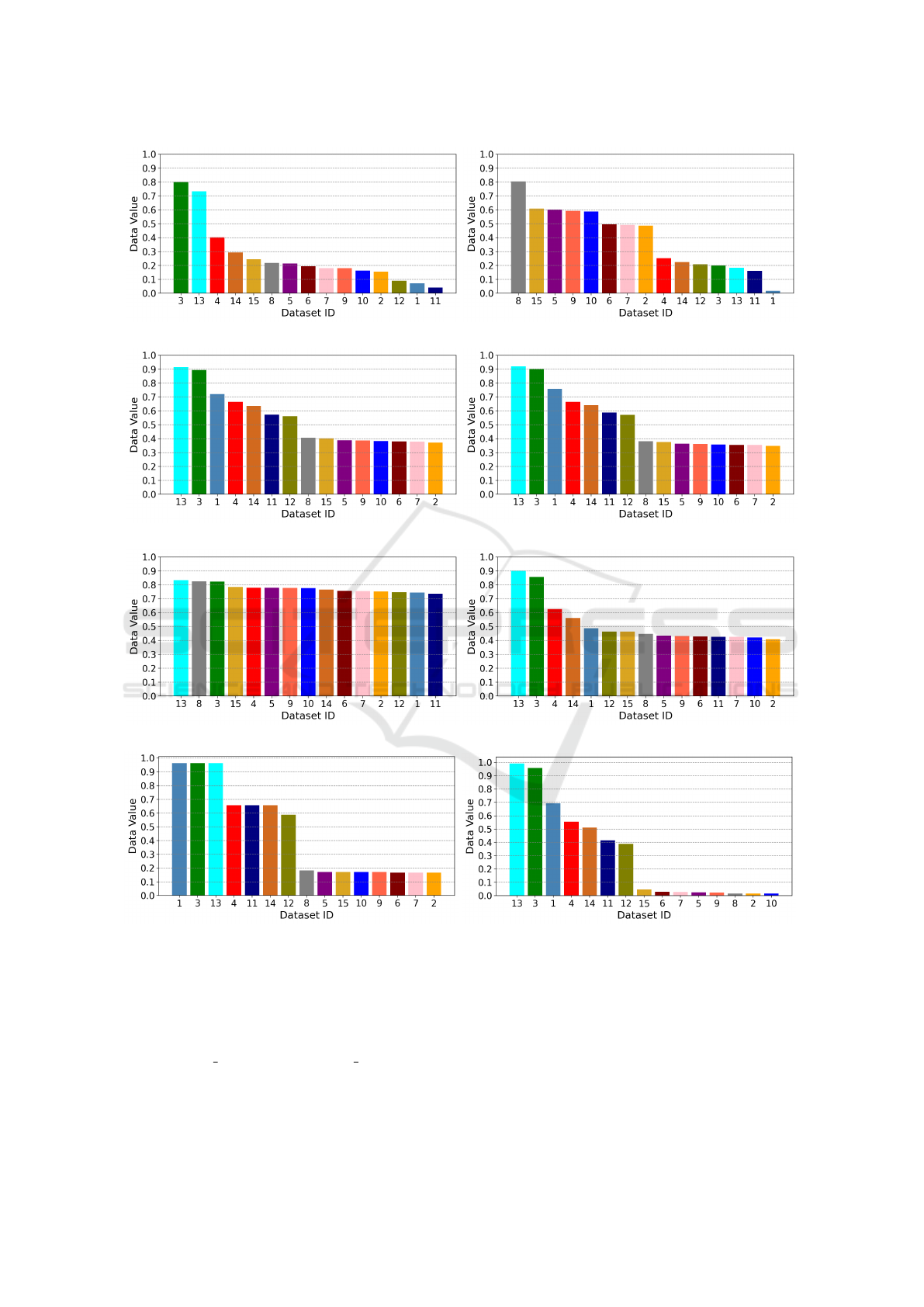
Figure 4 below shows the order in which the re-

trieved datasets are presented to the users based on

MDV, AHP, and ours (ties are broken using alpha-

betic order). Figures 4a and 4b display the order in

which the retrieved datasets are shown to all the users.

Figures 4c-4h show the order in which the results are

presented to each user according to their preferences.

One can see that the order is different from one user to

another and from each user to MDV and AHP-based

rankings.

It can also be seen that the data value varies ac-

cording to the weights assigned to each metadata.

Therefore, we are going to measure the users’ satis-

faction rate in Section 6.2 below.

6.2 Users’ Satisfaction Evaluation

We deﬁne a user satisfaction rate as the probabil-

ity that users ﬁnd the datasets they seek in the top

k = {5,10} of the retrieval results. Therefore, we cal-

culated the Jaccard score@5 and Jaccard score@10

between our approach and other re-ranking options.

We also computed NDCG which measures the degree

It works ﬁne considering V

AHP

as the ﬁrst column vec-

tor of P instead of its ﬁrst row vector. One just needs to

apply the reciprocity property of P then its transitivity prop-

erty.

Personalization of Dataset Retrieval Results Using a Data Valuation Method

129

(a) Re-ranking Based on MDV (b) Re-ranking Based on AHP

(e) Re-ranking Based on User1 Preferences (f) Re-ranking Based on User2 Preferences

(g) Re-ranking Based on User3 Preferences (h) Re-ranking Based on User4 Preferences

Figure 4: Retrieved Datasets’ Re-ranking Based on MDV, AHP, and Ours.

to which the results re-ranking using users’ prefer-

ences match the other re-rankings.

Table 5 presents the evaluation results regarding

NDCG, Jaccard score@5, and Jaccard score@10 per

user. The highest and the lowest scores per user and

metric are highlighted in bold and red. There is a

42.24% and a 56.52% chance on average that users

will ﬁnd the dataset they are seeking in the top 5 and

top 10, respectively. The lowest chance is 0% for the

top 5 and 33.33% for the top 10; while the highest

chance is 100% in both cases. On average, the dif-

ferent re-rankings match the users’ preferred ordering

81.81% of the time.

It can also be seen in Table 5 that the degree to

KDIR 2024 - 16th International Conference on Knowledge Discovery and Information Retrieval

130

Table 3: Dataset value dimension (metadata ﬁeld) weights

provided by stakeholders. SH2 provided an invalid set of

weights.

Stakeholders

(SH) / Users

Currency

#Spatial Objects

Usage

SH1 10 8 5

SH3 9 9 4

User1 9 0 1

User2 7 1 7

User3 2 8 0

User4 0 4 2

Table 4: From stakeholders’ provided weights to AHP

weights.

Steps

Currency

/ Age

#Spatial Objects

(Proxy for Size)

Usage

SH1 10 8 5

SH3 9 9 4

The Sum of

the provided

weights

19 17 9

A pairwise

comparison

1 19/17 19/9

AHP weights

0.4222 0.3778 0.2

which a given re-ranking technique matches a user’s

preferred ordering does not predict the probability

of the user ﬁnding what they are seeking. For in-

stance, for SH1, 6month EMA got the highest NDCG

score. However, 6month EMA got the same Jac-

card score@5 as #Objects, MDV, and UT and a lower

Jaccard score@10 than #Objects.

7 CONCLUSION

This paper introduces a data valuation method that

can be used to re-rank dataset retrieval results. It

showed, using 12 datasets (the result of a query sent to

a data catalog) and 6 users (including two stakehold-

ers and 4 randomly generated using the uniform dis-

tribution of the weights), that there is only a 42.24%

and a 56.52% chance on average that users will ﬁnd

the dataset they are seeking in the top 5 and top 10, re-

spectively. Users should ﬁnd the information they are

seeking in the top 10 because, as shown by Jaenich

et al. (2024), the probability of a document being con-

sulted drops exponentially from the top 1 (100%) to

the top 10 (about 20%). In other words, if a document

is not in the top 10, its chances of being consulted are

less than 20%. It is important to re-rank retrieval re-

sults according to users’ interests because, in addition

to the query sent to a data catalog, users also have

Table 5: Evaluation Results.

Users

Data Value

Dims/Methods

NDCG

Jaccard

score@5

Jaccard

score@10

SH1

#Objects 0.8035 0.6667 1.0000

6month EMA 0.8958 0.6667 0.6667

AHP (Qiu et al.) 0.7487 0.0000 0.3333

Alphabetic order 0.7506 0.4286 0.3333

Currency 0.8482 0.0000 0.3333

MDV (Ma and Zhang) 0.8445 0.6667 0.5385

UT (Chen) 0.8384 0.6667 0.6667

SH3

#Objects 0.8035 0.6667 1.0000

6month EMA 0.8958 0.6667 0.6667

AHP (Qiu et al.) 0.7487 0.0000 0.3333

Alphabetic order 0.7506 0.4286 0.3333

Currency 0.8482 0.0000 0.3333

MDV (Ma and Zhang) 0.8445 0.6667 0.5385

UT (Chen) 0.8384 0.6667 0.6667

User1

#Objects 0.7669 0.2500 0.5385

6month EMA 0.8418 0.4286 0.5385

AHP (Qiu et al.) 0.8170 0.4286 0.6667

Alphabetic order 0.8199 0.2500 0.5385

Currency 0.7846 0.4286 0.5385

MDV (Ma and Zhang) 0.8540 0.4286 0.8182

UT (Chen) 0.8320 0.4286 0.5385

User2

#Objects 0.8660 0.6667 0.8182

6month EMA 0.8051 0.6667 0.6667

AHP (Qiu et al.) 0.7857 0.0000 0.4286

Alphabetic order 0.7692 0.4286 0.4286

Currency 0.7215 0.0000 0.4286

MDV (Ma and Zhang) 0.7524 0.6667 0.6667

UT (Chen) 0.7493 0.6667 0.6667

User3

#Objects 0.9977 1.0000 1.0000

6month EMA 0.8225 0.4286 0.6667

AHP (Qiu et al.) 0.8040 0.0000 0.3333

Alphabetic order 0.7571 0.4286 0.3333

Currency 0.8128 0.0000 0.3333

MDV (Ma and Zhang) 0.8174 0.4286 0.5385

UT (Chen) 0.8239 0.4286 0.6667

User4

#Objects 0.8245 0.6667 0.6667

6month EMA 0.9062 0.6667 0.8182

AHP (Qiu et al.) 0.7434 0.0000 0.3333

Alphabetic order 0.8174 0.4286 0.3333

Currency 0.8891 0.0000 0.3333

MDV (Ma and Zhang) 0.8623 0.6667 0.5385

UT (Chen) 0.8556 0.6667 0.8182

preferences regarding the retrieved datasets’ proper-

ties or metadata. In fact, Liu et al. (2020) argue that

the IR scholars have agreed that major improvement

in search performance can only be achieved by con-

sidering the users and their contexts; thus their pref-

erences. This paper is a step in that direction by using

the users’ preferences to re-rank IR results.

In the future, we are planning to run a set

of queries on public data catalogs (e.g. Kaggle

Personalization of Dataset Retrieval Results Using a Data Valuation Method

131

datasets

) and collect the top k (k≤100) results sorted

by relevance and study the distribution of users’ sat-

isfaction through simulation.

ACKNOWLEDGEMENTS

This research has received funding from the ADAPT

Centre for Digital Content Technology, funded un-

der the SFI Research Centres Programme (Grant

13/RC/2106 P2), co-funded by the European Re-

gional Development Fund. For the purpose of Open

Access, the author has applied a CC BY public copy-

right licence to any Author Accepted Manuscript ver-

sion arising from this submission.

REFERENCES

Agarwal, A., Zaitsev, I., Wang, X., Li, C., Najork, M., and

Joachims, T. (2019). Estimating Position Bias without

Intrusive Interventions. In Proceedings of the Twelfth

ACM International Conference on Web Search and

Data Mining, WSDM ’19, pages 474–482, New York,

NY, USA. Association for Computing Machinery.

os-Ferrer, C., Fehr, E., and Garagnani, M. (2023). Iden-

tifying nontransitive preferences. Publisher: [object

Object].

os-Ferrer, C. and Garagnani, M. (2021). Choice consis-

tency and strength of preference. Economics Letters,

198:109672.

Attard, J. and Brennan, R. (2018). Challenges in Value-

Driven Data Governance. In Panetto, H., Debruyne,

C., Proper, H. A., Ardagna, C. A., Roman, D., and

Meersman, R., editors, On the Move to Meaning-

ful Internet Systems. OTM 2018 Conferences, volume

11230, pages 546–554. Springer International Pub-

lishing, Cham. Series Title: Lecture Notes in Com-

puter Science.

Bai, J., Nie, J.-Y., Cao, G., and Bouchard, H. (2007). Us-

ing query contexts in information retrieval. In Pro-

ceedings of the 30th annual international ACM SIGIR

conference on Research and development in informa-

tion retrieval, SIGIR ’07, pages 15–22, New York,

NY, USA. Association for Computing Machinery.

Belkin, N. J., Cole, M., Gwizdka, J., Li, Y. L., Liu, J. J.,

Muresan, G., Roussinov, D., Smith, C. A., Taylor, A.,

and Yuan, X. J. (2005). Rutgers information interac-

tion lab at TREC 2005: Trying HARD. In NIST Spe-

cial Publication. Institute of Electrical and Electronics

Engineers Inc. ISSN: 1048-776X.

Biancalana, C., Micarelli, A., and Squarcella, C. (2008).

Nereau: a social approach to query expansion. In

Proceedings of the 10th ACM workshop on Web in-

formation and data management, WIDM ’08, pages

95–102, New York, NY, USA. Association for Com-

puting Machinery.

https://www.kaggle.com/datasets

Bilenko, M., White, R. W., Richardson, M., and Murray,

G. C. (2008). Talking the talk vs. walking the walk:

salience of information needs in querying vs. brows-

ing. In Proceedings of the 31st annual international

ACM SIGIR conference on Research and development

in information retrieval, SIGIR ’08, pages 705–706,

New York, NY, USA. Association for Computing Ma-

chinery.

Bodendorf, F., Dehmel, K., and Franke, J. (2022). Scientiﬁc

Approaches and Methodology to Determine the Value

of Data as an Asset and Use Case in the Automotive

Industry.

Bouadjenek, M. R., Hacid, H., and Bouzeghoub, M. (2013).

LAICOS: an open source platform for personalized

social web search. In Proceedings of the 19th ACM

SIGKDD international conference on Knowledge dis-

covery and data mining, KDD ’13, pages 1446–1449,

New York, NY, USA. Association for Computing Ma-

chinery.

Budzik, J. and Hammond, K. (1999). Watson: Anticipating

and Contextualizing Information Needs.

Buscher, G., van Elst, L., and Dengel, A. (2009). Segment-

level display time as implicit feedback: a comparison

to eye tracking. In Proceedings of the 32nd interna-

tional ACM SIGIR conference on Research and devel-

opment in information retrieval, SIGIR ’09, pages 67–

74, New York, NY, USA. Association for Computing

Machinery.

Cai, F. and de Rijke, M. (2016). Selectively Personal-

izing Query Auto-Completion. In Proceedings of

the 39th International ACM SIGIR conference on Re-

search and Development in Information Retrieval, SI-

GIR ’16, pages 993–996, New York, NY, USA. Asso-

ciation for Computing Machinery.

Chen, S. Y. and Ford, N. (1998). Modelling user navigation

behaviours in a hyper-media-based learning system :

An individual differences approach. Knowledge Or-

ganization.

Chen, Y. (2005). Information valuation for information

lifecycle management. In Second International Con-

ference on Autonomic Computing (ICAC’05), pages

135–146. IEEE.

Chirita, P. A., Firan, C. S., and Nejdl, W. (2007). Person-

alized query expansion for the web. In Proceedings

of the 30th annual international ACM SIGIR confer-

ence on Research and development in information re-

trieval, SIGIR ’07, pages 7–14, New York, NY, USA.

Association for Computing Machinery.

Craswell, N., Zoeter, O., Taylor, M., and Ramsey,

B. (2008). An experimental comparison of click

position-bias models. In Proceedings of the 2008 In-

ternational Conference on Web Search and Data Min-

ing, WSDM ’08, pages 87–94, New York, NY, USA.

Association for Computing Machinery.

Deng, Y., Li, X., Yu, X., Fu, Z., Chen, H., Xie, J., and Xie,

D. (2023). Electricity Data Valuation Considering At-

tribute Weights. In 2023 3rd International Conference

on Intelligent Power and Systems (ICIPS), pages 788–

794.

Even, A. and Shankaranarayanan, G. (2005). Value-Driven

Data Quality Assessment. In ICIQ.

KDIR 2024 - 16th International Conference on Knowledge Discovery and Information Retrieval

132

Ferragina, P. and Gulli, A. (2005). A personalized search

engine based on web-snippet hierarchical clustering.

In Special interest tracks and posters of the 14th inter-

national conference on World Wide Web, WWW ’05,

pages 801–810, New York, NY, USA. Association for

Computing Machinery.

Fishburn, P. C. (1991). Nontransitive Preferences in De-

cision Theory. Journal of Risk and Uncertainty,

4(2):113–134. Publisher: Springer.

Gauch, S., Chaffee, J., and Pretschner, A. (2003). Ontology-

based personalized search and browsing. Web Intelli.

and Agent Sys., 1(3-4):219–234.

Gendin, S. (1996). Why Preference is Not Transitive. The

Philosophical Quarterly (1950-), 46(185):482–488.

Publisher: [Oxford University Press, University of St.

Andrews, Scots Philosophical Association].

Hambarde, K. A. and Proenc¸a, H. (2023). Information Re-

trieval: Recent Advances and Beyond. IEEE Access,

11:76581–76604. Conference Name: IEEE Access.

Heinrich, B. and Klier, M. (2011). Assessing data cur-

rency—a probabilistic approach. Journal of Informa-

tion Science, 37(1):86–100. Publisher: Sage Publica-

tions Sage UK: London, England.

Jaenich, T., McDonald, G., and Ounis, I. (2024). Query Ex-

posure Prediction for Groups of Documents in Rank-

ings. In Goharian, N., Tonellotto, N., He, Y., Lipani,

A., McDonald, G., Macdonald, C., and Ounis, I., ed-

itors, Advances in Information Retrieval, pages 143–

158, Cham. Springer Nature Switzerland.

Jayarathna, S., Patra, A., and Shipman, F. (2013). Min-

ing user interest from search tasks and annotations.

In Proceedings of the 22nd ACM international con-

ference on Information & Knowledge Management,

CIKM ’13, pages 1849–1852, New York, NY, USA.

Association for Computing Machinery.

Kelly, D., Dollu, V. D., and Fu, X. (2005). The loqua-

cious user: a document-independent source of terms

for query expansion. In Proceedings of the 28th

annual international ACM SIGIR conference on Re-

search and development in information retrieval, SI-

GIR ’05, pages 457–464, New York, NY, USA. Asso-

ciation for Computing Machinery.

Khokhlov, I. and Reznik, L. (2020). What is the value of

data value in practical security applications. In 2020

IEEE Systems Security Symposium (SSS), pages 1–8.

IEEE.

Kraft, R., Maghoul, F., and Chang, C. C. (2005). Y!Q:

contextual search at the point of inspiration. In Pro-

ceedings of the 14th ACM international conference on

Information and knowledge management, CIKM ’05,

pages 816–823, New York, NY, USA. Association for

Computing Machinery.

Kunze, S. R. and Auer, S. (2013). Dataset Retrieval. In 2013

IEEE Seventh International Conference on Semantic

Computing, pages 1–8.

Laney, D. B. (2017). Infonomics: how to monetize, manage,

and measure information as an asset for competitive

advantage. Routledge.

Lavrenko, V. and Croft, W. B. (2001). Relevance based

language models. In Proceedings of the 24th annual

international ACM SIGIR conference on Research

and development in information retrieval, SIGIR ’01,

pages 120–127, New York, NY, USA. Association for

Computing Machinery.

Liu, F., Yu, C., and Meng, W. (2002). Personalized web

search by mapping user queries to categories. In Pro-

ceedings of the eleventh international conference on

Information and knowledge management, CIKM ’02,

pages 558–565, New York, NY, USA. Association for

Computing Machinery.

Liu, H. and Hoeber, O. (2011). A Luhn-Inspired Vector Re-

weighting Approach for Improving Personalized Web

Search. pages 301–305. IEEE Computer Society.

Liu, J., Liu, C., and Belkin, N. J. (2020). Personal-

ization in text information retrieval: A survey.

Journal of the Association for Information Sci-

ence and Technology, 71(3):349–369. eprint:

https://onlinelibrary.wiley.com/doi/pdf/10.1002/asi.

24234.

Liu, T.-Y. (2009). Learning to Rank for Information Re-

trieval. Found. Trends Inf. Retr., 3(3):225–331.

Lv, Y., Sun, L., Zhang, J., Nie, J.-Y., Chen, W., and Zhang,

W. (2006). An iterative implicit feedback approach

to personalized search. In Proceedings of the 21st In-

ternational Conference on Computational Linguistics

and the 44th annual meeting of the Association for

Computational Linguistics, ACL-44, pages 585–592,

USA. Association for Computational Linguistics.

Ma, X. and Zhang, X. (2019). MDV: A Multi-Factors Data

Valuation Method. In 2019 5th International Con-

ference on Big Data Computing and Communications

(BIGCOM), pages 48–53.

Maron, M. E. and Kuhns, J. L. (1960). On Relevance, Prob-

abilistic Indexing and Information Retrieval. J. ACM,

7(3):216–244.

Miutra, B. and Craswell, N. (2018). An Introduction to

Neural Information Retrieval. Found. Trends Inf. Retr.,

13(1):1–126.

Odu, G. O. (2019). Weighting methods for multi-criteria de-

cision making technique. Journal of Applied Sciences

and Environmental Management, 23(8):1449–1457.

Pitkow, J., Sch

utze, H., Cass, T., Cooley, R., Turnbull, D.,

Edmonds, A., Adar, E., and Breuel, T. (2002). Per-

sonalized search: A contextual computing approach

may prove a breakthrough in personalized search efﬁ-

ciency. Commun. ACM, 45(9):50–55.

Pretschner, A. and Gauch, S. (1999). Ontology based per-

sonalized search. In Proceedings 11th International

Conference on Tools with Artiﬁcial Intelligence, pages

391–398. ISSN: 1082-3409.

Qiu, S., Zhang, D., and Du, X. (2017). An Evaluation

Method of Data Valuation Based on Analytic Hi-

erarchy Process. In 2017 14th International Sym-

posium on Pervasive Systems, Algorithms and Net-

works & 2017 11th International Conference on Fron-

tier of Computer Science and Technology & 2017

Third International Symposium of Creative Comput-

ing (ISPAN-FCST-ISCC), pages 524–528. ISSN:

2375-527X.

Roberts, S. W. (1959). Control Chart Tests Based on Ge-

ometric Moving Averages. Technometrics, 1(3):239–

250.

Personalization of Dataset Retrieval Results Using a Data Valuation Method

133

Robertson, S. E., van Rijsbergen, C. J., and Porter, M. F.

(1980). Probabilistic models of indexing and search-

ing. In Proceedings of the 3rd annual ACM confer-

ence on Research and development in information re-

trieval, SIGIR ’80, pages 35–56, GBR. Butterworth &

Co.

Saaty, R. W. (1987). The analytic hierarchy process—what

it is and how it is used. Mathematical Modelling,

9(3):161–176.

Salton, G., Fox, E. A., and Wu, H. (1983). Ex-

tended Boolean information retrieval. Commun. ACM,

26(11):1022–1036.

Salton, G. and McGill, M. J. (1986). Introduction to Mod-

ern Information Retrieval. McGraw-Hill, Inc., USA.

Shen, X., Tan, B., and Zhai, C. (2005). Implicit user mod-

eling for personalized search. In Proceedings of the

14th ACM international conference on Information

and knowledge management, CIKM ’05, pages 824–

831, New York, NY, USA. Association for Computing

Machinery.

Singh, A. and Joachims, T. (2018). Fairness of Exposure in

Rankings. In Proceedings of the 24th ACM SIGKDD

International Conference on Knowledge Discovery &

Data Mining, KDD ’18, pages 2219–2228, New York,

NY, USA. Association for Computing Machinery.

Tamine, L. and Goeuriot, L. (2021). Semantic Infor-

mation Retrieval on Medical Texts: Research Chal-

lenges, Survey, and Open Issues. ACM Comput. Surv.,

54(7):146:1–146:38.

Tanudjaja, F. and Mui, L. (2002). Persona: A Contextu-

alized and Personalized Web Search. pages 67–67.

IEEE Computer Society.

Turczyk, L., Groepl, M., Liebau, N., and Steinmetz, R.

(2007). A method for ﬁle valuation in information

lifecycle management.

Wang, B., Guo, Q., Yang, T., Xu, L., and Sun, H. (2021).

Data valuation for decision-making with uncertainty

in energy transactions: A case of the two-settlement

market system. Applied Energy, 288:116643.

Wang, H., He, X., Chang, M.-W., Song, Y., White, R. W.,

and Chu, W. (2013). Personalized ranking model

adaptation for web search. In Proceedings of the 36th

international ACM SIGIR conference on Research

and development in information retrieval, SIGIR ’13,

pages 323–332, New York, NY, USA. Association for

Computing Machinery.

Wang, T., Rausch, J., Zhang, C., Jia, R., and Song, D.

(2020). A principled approach to data valuation for

federated learning. Federated Learning: Privacy and

Incentive, pages 153–167. Publisher: Springer.

Wang, X., Golbandi, N., Bendersky, M., Metzler, D., and

Najork, M. (2018). Position Bias Estimation for Un-

biased Learning to Rank in Personal Search. In Pro-

ceedings of the Eleventh ACM International Confer-

ence on Web Search and Data Mining, WSDM ’18,

pages 610–618, New York, NY, USA. Association for

Computing Machinery.

Zehlike, M., Yang, K., and Stoyanovich, J. (2022a). Fair-

ness in Ranking, Part I: Score-Based Ranking. ACM

Comput. Surv., 55(6):118:1–118:36.

Zehlike, M., Yang, K., and Stoyanovich, J. (2022b).

Fairness in Ranking, Part II: Learning-to-Rank and

Recommender Systems. ACM Comput. Surv.,

55(6):117:1–117:41.

APPENDIX

AHP Explained

AHP stands for Analytic Hierarchy Process and was

ﬁrst introduced by Saaty (1987). It is used to cal-

culate the relative weights of the criteria in a multi-

criteria decision setting. For instance, a multi-criteria

decision consists of choosing the best dataset among

multiple datasets considering their currency, size, and

usage frequency, simultaneously.

AHP has 5 main components:

1. Criteria. Selection of the criteria to be considered

in the decision making.

2. Pairwise Comparisons of the Criteria. This

consists of comparing each criterion to all the

other criteria. There are

n(n−1)

comparisons

needed for n criteria.

3. Judgement Matrix P

• P is reciprocal: P(i, j) = 1/P( j,i)

• The diagonal elements of P are equal to 1

• Each element of P is a strictly positive real

number:

– P(i, j) = 1 means criteria i and j are equiva-

lent

– P(i, j) < 1 means criterion i is less important

than criterion j

– P(i, j) > 1 means criterion i is more important

than criterion j

4. Criteria Weights. The weights are calculated us-

ing the judgement matrix P. The details of the

calculation steps can be found in (Qiu et al.; Saaty

(2017; 1987)).

5. Consistency Ratio (CR). CR should be less than

or equal to 0.1 or 10%. It measures the transitive

consistency.

• Transitivity: if a = 2b and b = 3c, then a = 6c

• CR = 0 iff P is transitively consistent. Then

P(i, j) = P(i,k) ×P(k, j), for all i, j, and k.

With one row or column vector from the judge-

ment matrix P (a vector of n elements with at least

one element equal to 1), one can ﬁll out the rest of

the judgement matrix P using its reciprocity and tran-

sitivity properties. This is how we derived the AHP

weights shown in Table 4.

KDIR 2024 - 16th International Conference on Knowledge Discovery and Information Retrieval

134