Searching for Idealized Prototype Learning for Interpreting

Multi-Layered Neural Networks

Ryotaro Kamimura

Tokai University, Kitanakame, Hiratsuka, Kanagawa, 259-1292, Kanagawa, Japan

Keywords:

Prototype Learning, Non-Prototype Learning, Activation Function, Potentiality, Ratio Potentiality, Entropy,

Divergence, Interpretation.

Abstract:

The present paper aims to show that neural learning consists of two fundamental phases: prototype and non-

prototype learning in an ideal state. The prototype refers to a network with the simplest conﬁguration, ideally

determined without the inﬂuence of inputs. However, in actual learning, prototype and non-prototype learning

are mixed and entangled. To demonstrate the existence of these two phases in an ideal state, it is necessary

to explicitly distinguish between networks that are exclusively focused on acquiring the prototype and those

that target non-prototype properties. We use different activation functions, combined serially, to represent

the prototype and non-prototype learning phases. By combining multiple different activation functions, it is

possible to create networks that exhibit both prototype and non-prototype properties in an almost ideal state.

This method was applied to a business dataset that required improved generalization as well as interpretation.

The experimental results conﬁrmed that the ReLU activation function could identify the prototype with difﬁ-

culty, while the hyperbolic tangent function could more easily detect the prototype. By combining these two

activation functions within one framework, generalization performance could be improved while maintaining

representations that are as close as possible to those obtained during prototype learning, thus facilitating easier

interpretation.

1 INTRODUCTION

1.1 Idealized Prototype Learning

The concept of prototype learning has received sig-

niﬁcant attention over the years (Saralajew et al.,

2018). If an informative exemplar, or prototype, can

be identiﬁed, learning in neural networks becomes

much more efﬁcient, enabling faster training and eval-

uation. This could address the problem of massive

data requirements for training multi-layered neural

networks. Furthermore, prototypes offer greater inter-

pretability, which is crucial, given the black-box na-

ture of neural networks, especially as these networks

become larger and more complex.

As mentioned above, conventional methods have

typically focused on prototypes as representative ex-

amples of input data sets. In contrast, the proto-

type discussed in this paper is intended to serve as

the foundation for constructing basic neural networks,

from which actual multi-layered neural networks can

be derived. For instance, we can imagine a prototype

that is self-organized, utilizing network resources as

minimally as possible. This prototype should be

extracted or constructed at the beginning of learn-

ing, followed by ordinary, non-prototype learning to

achieve faithful representations of the inputs.

To explain the prototype more concretely in the

context of neural networks as discussed in this paper,

we assume that any multi-layered neural network can

be generated from a corresponding prototype, hidden

within the network. This prototype is a network with-

out hidden layers, where all components, such as neu-

rons and weights, are connected independently and

separately. It is important to note that this proto-

type is not intended to faithfully represent the inputs

but rather to represent the given network resources as

minimally as possible.

However, the distinction between prototype and

non-prototype learning is not always clear in ac-

tual learning processes. In practice, these two types

of learning are often intertwined, making it difﬁcult

to distinguish between them. To address this, we

ﬁrst attempt to differentiate between networks dedi-

cated to prototype learning and those focused on non-

prototype learning. Subsequently, we aim to combine

Kamimura, R.

Searching for Idealized Prototype Learning for Interpreting Multi-Layered Neural Networks.

DOI: 10.5220/0013047600003837

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Joint Conference on Computational Intelligence (IJCCI 2024), pages 475-487

ISBN: 978-989-758-721-4; ISSN: 2184-3236

475

these networks within a single framework to achieve

and examine the ideal learning process that incorpo-

rates both prototype and non-prototype learning.

Then, we need to identify a network where the

prototype is easily recognizable and another where

the prototype is not as easily identiﬁed. There are

various ways to create different conﬁgurations, and

in this context, we propose using multiple activation

functions within a single framework to realize differ-

ent properties. If our hypothesis of prototype and

non-prototype learning holds true, one of the major

challenges in selecting appropriate activation func-

tions lies in the pursuit of ﬁnding the best possible

function or an idealized activation function that works

across all scenarios, including both prototype and

non-prototype learning (Ramachandran et al., 2017).

Given that the properties of these two phases are

likely to be strongly interwoven, it may be impossi-

ble to ﬁnd a single appropriate activation function for

all situations.

In this paper, we attempt to generate networks

with different properties to enhance interpretation and

generalization by using different activation functions.

We then combine these activation functions to pro-

duce an idealized prototype for network conﬁgura-

tion. The primary objective of this paper is to examine

how the combination of different activation functions

can inﬂuence the performance of the corresponding

network, based on the assumption that every learning

process comprises both prototype learning and non-

prototype learning.

1.2 Main Contributions

The main contributions of this paper can be summa-

rized as follows.

• This paper shows that a prototype exists behind

complex multi-layered neural networks. The pro-

totype is assumed to be a network without hidden

layers, with components that are independently

and separately connected. Consequently, the

learning process of neural networks should con-

sist of both prototype and non-prototype learning.

Prototype learning aims to identify the simplest

possible network, while non-prototype learning

focuses on processing detailed information in the

inputs.

• Because pure prototype and non-prototype learn-

ing cannot be easily achieved, we attempt to pro-

duce networks that are relatively better at detect-

ing the prototype, and others that are not as proﬁ-

cient at doing so. To create these different net-

works, we introduce a method to vary the acti-

vation function and attempt to incorporate mul-

tiple activation functions within one framework.

We aim to demonstrate the effectiveness of this

method in improving generalization while main-

taining network conﬁgurations as close as possi-

ble to their simplest form. This can enhance inter-

pretability, which is the main objective of proto-

type learning.

1.3 Paper Organization

In Section 2, we present some related studies on the

activation function, few-shot learning, and U-shaped

learning, emphasizing the differences between our

method and conventional methods. In Section 3, we

show multiple activation functions, combining the

tangent and ReLU activation functions, correspond-

ing to prototype and non-prototype learning. In par-

ticular, we explain why prototype and non-prototype

learning correspond to the tangent and ReLU func-

tions. Then, after brieﬂy explaining the difference be-

tween prototype and non-prototype learning, the po-

tentiality is introduced, based on the absolute values

of connection weights. For comparing the prototype

and compressed networks, we introduce the ratio po-

tentiality of the compressed to the supposed prototype

network. In Section 4, we present results using a sim-

ple business dataset. The results conﬁrmed that the

combination of tangent and ReLU functions could de-

tect higher ratio potentiality in prototype learning and

higher generalization in non-prototype learning.

2 RELATED WORK

We explain three main related works: activation

functions, few-shot learning, and U-shaped learning

brieﬂy.

First, the activation function plays an important

role in creating prototype learning. According to

our hypothesis, prototype learning aims to extract

the prototype for network conﬁgurations, while non-

prototype learning focuses on processing detailed in-

formation from inputs and their relations to out-

puts. Therefore, it is natural that the activation func-

tion should change depending on the learning objec-

tive. There are numerous activation functions that

address computational issues such as vanishing gra-

dients, computational load, and sparsity (Ramachan-

dran et al., 2017; Nwankpa et al., 2018; Jagtap and

Karniadakis, 2023; Emanuel et al., 2024). Addition-

ally, activation functions have become adaptive with

parameters, and ensemble and combined activation

functions have been found to perform well (S

utfeld

et al., 2020; Apicella et al., 2021; Jagtap and Karni-

NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications

476

adakis, 2023).

Our method of idealized prototype learning is

based on the combination of different activation func-

tions. At present, the activation functions are ﬁxed-

type, but if trainable activation functions could be

used (S

utfeld et al., 2020), the method might ap-

proach idealized prototype learning. However, one

of the major differences is that, unlike most con-

ventional methods aimed at improving generalization,

our method seeks to interpret the inner workings of

neural networks by positing the existence of a proto-

type, which should exist for all neural networks. The

prototype is not obtained by training neural networks

but is assumed to exist behind any multi-layered neu-

ral network.

Second, the prototype learning proposed here dif-

fers from conventional methods. Prototype learn-

ing has received considerable attention recently, as

complex datasets require equally complex neural net-

works for learning. If many inputs are classiﬁed un-

der one prototype, learning can be signiﬁcantly eas-

ier (Kim et al., 2019; Song et al., 2023). Addition-

ally, in so-called “zero-shot” learning (Chao et al.,

2016; Pourpanah et al., 2022), the concept of a pro-

totype becomes more abstract, eventually leading to

no actual prototypes being used. Instead, semantic

features are introduced to relate seen and unseen in-

puts. Although the concept becomes more abstract to

improve generalization, these methods still focus on

input properties. The prototype in this paper becomes

increasingly abstract, minimizing or even excluding

semantic information about inputs as much as pos-

sible. The prototype is not for coming inputs but is

solely for the network conﬁguration itself. Within the

given network resources, neural networks attempt to

self-organize as simply and economically as possible.

Only after this prototype learning process should ac-

tual non-prototype learning begin. This suggests the

possibility of extending the concept of a prototype to

different areas.

Third, prototype learning can be viewed as an ex-

tended version of the well-known U-shaped learning.

Prototype learning is strongly related to U-shaped

learning, particularly in the context of language ac-

quisition problems (Westermann, 2022). This prob-

lem was initially associated with the attempt to unify

regular and irregular forms in natural language us-

ing neural networks or connectionist models (Rumel-

hart and McClelland, 1986; Pinker and Prince, 1988;

Kirov and Cotterell, 2018; Corkery et al., 2019). Chil-

dren initially use language rules correctly, then en-

ter a period of overgeneralization, where irregular

verbs are treated as regular ones. Eventually, they

learn to use both regular and irregular forms correctly.

U-shaped learning has been actively discussed not

only in cognitive development but also in many other

ﬁelds, particularly in computational learning (Car-

lucci and Case, 2013; Case and K

otzing, 2016; Vier-

ing and Loog, 2022).

In our framework, the phase of overgeneraliza-

tion corresponds to the phase of prototype learning.

Children do not initially try to extract abstract rules

of language but rather explore the permissible con-

ditions within given physical and mental constraints.

Within these constraints, they then attempt to simplify

and clarify these physical and mental components as

much as possible. We can say that rule acquisition

in language learning occurs during the phase of non-

prototype learning, which corresponds to the ﬁnal

phase of learning. This may explain why U-shaped

learning is observed in so many different ﬁelds.

3 THEORY AND

COMPUTATIONAL METHODS

3.1 Prototype and Non-Prototype

Learning

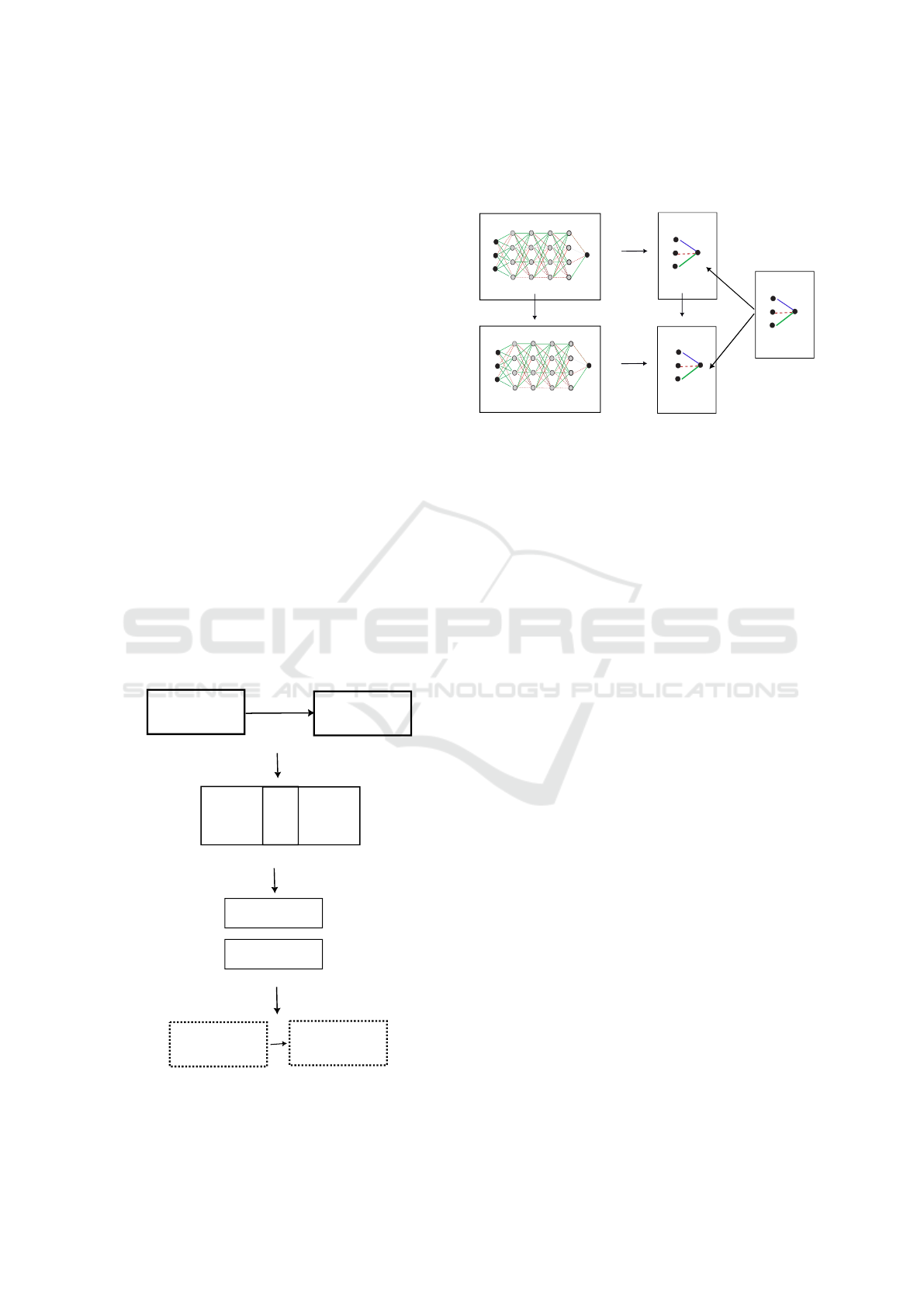
The idealized prototype learning is illustrated in Fig-

ure 1(a), where, at the beginning, a network attempts

to acquire its prototype, which is the minimal possible

network conﬁguration. After completing this proto-

type learning, non-prototype learning begins, aiming

to acquire as much detailed information about the in-

puts as possible. However, in actual situations, proto-

type learning is mixed or entangled with correspond-

ing non-prototype learning, making it sometimes im-

possible to separate them, as shown in Figure 1(b).

It is important to note that even in this entangled and

mixed case, prototype learning is assumed to exist at

the deepest level of learning. When it is almost im-

possible to extract the prototype, we attempt to train

several networks independently to search for candi-

date networks for prototype or non-prototype learn-

ing, as depicted in Figure 1(c). Finally, these indepen-

dently trained networks are serially arranged to esti-

mate the ideal prototype learning, as shown in Figure

1(d).

3.2 Multiple Activation Functions

We use different activation functions for different

learning schemes within one framework (S

utfeld

et al., 2020). Let us compute the input u

to the neu-

ron from the nth layer to the n + 1th layer, labeled

(n, n+1), using an idealized activation function. In an

ideal state, it is assumed that two distinct activation

Searching for Idealized Prototype Learning for Interpreting Multi-Layered Neural Networks

477

functions are used for the two types of learning:

(n,n+1)

= α Proto(u

(n,n+1)

) +(1 − α) NProto(u

(n,n+1)

(1)

where “Proto” and “NProto” represent the activation

functions for the prototype and non-prototype learn-

ing, respectively, and the parameter α is set to one for

prototype learning and zero for non-prototype learn-

ing.

This idealized prototype learning cannot be easily

realized because it is impossible to know which acti-

vation function is appropriate for the speciﬁc learning

phase. Therefore, as shown in Figure 1(c), we inde-

pendently train different networks with different ac-

tivation functions, searching for the appropriate ones

for the speciﬁc learning phase. For example, in the

experiments below, it is experimentally shown that

the hyperbolic tangent function can clearly extract the

prototype, while the ReLU activation function can-

not extract the prototype as effectively. However, this

may be speciﬁc to our experiments. We then combine

two conventional activation functions as follows:

(n,n+1)

= α Tanh(u

(n,n+1)

)+(1−α) ReLU(u

(n,n+1)

). (2)

In the actual learning process, as shown in Figure

1(d), the hyperbolic tangent function is used at the be-

ginning, followed by the ReLU activation function in

subsequent steps. In the actual learning, for the ﬁrst

ﬁxed number of learning steps, α is set to one, mean-

ing the hyperbolic tangent function is used initially.

Prototype learning

Non-prototype learning

(a) Idealized prototype learning

(b) Mixed prototype learning

(d) Estimated idealized prototype training

Figure 1: Concept of idealized prototype learning and its

actualization learning.

Afterward, the parameter is set to zero, meaning the

ReLU activation function is used for the remaining

learning steps.

Compression

Estimated

Supposed

Estimated

prototype

Prototype learning (tangent)

Non-prototype learning (ReLU)

Compression

Correlation coefficient

(1) i

(2) j

(3) k (4) l

(1) i

(2) j

(3) k (4) l

(5) m

(6)

(1)

(2)

Figure 2: Concept of supposed and estimated prototype

with prototype and non-prototype learning.

3.3 Prototype Network

We here show how to compute the prototype and mea-

sure the similarity between the estimated and sup-

posed prototypes. Figure 2 illustrates the concept

of the actual prototype and the supposed prototype.

The supposed prototype is composed of connection

weights, calculated as the normalized correlation co-

efﬁcients between inputs and outputs. This weight

conﬁguration does not aim to faithfully represent the

relationships between inputs and outputs but rather to

represent those relationships as minimally as possible.

The actual prototype can be obtained by com-

pressing the original network. In the ﬁgure, a multi-

layered neural network with a hyperbolic tangent acti-

vation function is trained and compressed into an esti-

mated prototype. In the later stage of learning, we use

the ReLU activation function. The multi-layered neu-

ral network with the ReLU activation function is then

compressed into another prototype. These estimated

prototypes are compared with the supposed one.

In evaluating the learning processes, we use po-

tentiality and ratio potentiality. Potentiality represents

the degree of organization of connection weights and

is akin to conventional entropy, while ratio poten-

tiality measures the similarity between estimated and

supposed prototypes. Speciﬁcally, ratio potentiality

aims to identify which input is more important than

others in terms of the strength of connection weights.

Thus, it is not necessary to estimate the similarity

of actual connection weights, but rather the similar-

ity of individual potentiality. For the computation

of entropy, divergence, and compression from multi-

layered neural networks to the prototypes, see Ap-

pendix.

The potentiality of a neural network is based on

NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications

478

the strength of connection weights. This simpliﬁ-

cation helps clarify the properties of the prototype.

Here, we show how to compute potentiality only for a

prototype network conﬁguration, i.e., a network with-

out hidden layers, as shown in Figure 2. The individ-

ual potentiality or absolute connection weight for the

estimated prototype is given by:

=| w

|, (3)

where w denotes the connection weights from the ith

neuron to the output neuron. For simplicity, we as-

sume that all individual potentialities are greater than

zero. Then, the relative individual potentiality is com-

puted for the estimated and compressed prototype, la-

beled (1,6):

(1,6)

max

′

(1,6)

′

. (4)

Next, the potentiality is computed by summing all

individual ones:

G =

∑

(1,6)

. (5)

The potentiality is bounded and can be normalized

for easier interpretation in the explanation of experi-

mental results. Additionally, we compute the relative

individual potentiality for the supposed prototype:

(1,2)

max

′

(1,2)

′

, (6)

where c denotes the individual potentiality, namely

the correlation coefﬁcients between inputs and the tar-

get in the training data set. We can also compute the

potentiality for the supposed prototype:

Z =

∑

(1,2)

. (7)

The potentiality is similar to the entropy function,

and it is developed to simplify the computation of en-

tropy. As with entropy, when all the relative poten-

tialities are the same, the potentiality reaches its max-

imum. On the other hand, if only one potentiality is

larger than any of the others, the potentiality becomes

smaller.

In addition to this standard potentiality, we intro-

duce the ratio potentiality for comparison between the

estimated and supposed prototypes. The ratio of com-

pressed individual potentiality to supposed individual

potentiality can be computed by:

(1,6)

(1,2)

. (8)

For this ratio r

, we compute the ratio potentiality:

(1,6)

∑

(1,6)

max

′

(1,6)

′

. (9)

When all the ratio potentialities are equal, the ra-

tio potentiality becomes larger. On the other hand, if

only one ratio potentiality is larger than the others, the

ratio potentiality becomes smaller. We should note

here that ratio potentiality is introduced primarily to

detect which input is more important than others in

terms of the corresponding potentialities. When used

as a measure of similarity, the corresponding connec-

tion weights should be carefully examined for actual

interpretation.

4 RESULTS AND DISCUSSION

4.1 Experimental Outline

The preliminary experiments used the bankruptcy

data (Shimizu, 2009). In this section, ﬁrst, we ex-

plain the experimental results using the tangent and

ReLU activation functions separately. The results

conﬁrmed that the tangent activation function could

more explicitly extract the prototype network than the

ReLU function. Then, by combining the tangent and

ReLU functions, we demonstrate how this combina-

tion could be used to improve generalization. Finally,

by examining individual connection weights as well

as the corresponding ratio potentialities, we show how

the combination of the two functions could extract

both prototype and non-prototype features.

The data was composed of 1,040 input patterns

and six input variables, augmented from the original

130 inputs. The data augmentation was only for sta-

bilizing our ﬁnal results. Without this data augmen-

tation, we could achieve similar results with some

instability in the ﬁnal outcomes. To facilitate easy

reproduction of these results, we used the Pytorch

neural network package with default parameter val-

ues, except for the activation function (hyperbolic tan-

gent and ReLU). These default parameters and stan-

dard activation functions were used to ensure that the

present results could be reproduced as easily as pos-

sible. Finally, all the values were averaged over ten

runs and normalized for easy interpretation.

Before delving into the details, we should summa-

rize the main results as follows:

• The networks with the tangent activation function

could clearly detect the prototype at the very be-

ginning of learning in Figure 3. On the other hand,

Searching for Idealized Prototype Learning for Interpreting Multi-Layered Neural Networks

479

Figure 3: The actual prototype with signed individual po-

tentialities (weights). The weights were actually normal-

ized correlation coefﬁcients between inputs and targets in

the training data set.

the ReLU activation function detected the proto-

type less clearly than the tangent activation func-

tion. This can be explained by the loss of infor-

mation on negative weights that occurred during

learning with the ReLU activation function.

• By combining the tangent and ReLU activation

functions in one framework, generalization could

be improved to an almost maximum level. This

demonstrates the utility of combining prototype

learning with non-prototype learning, which is

ideally supposed to exist behind any learning in

neural networks. Though our method did not aim

to improve generalization, we reported better gen-

eralization results because many methods similar

to our present method in multiple activation learn-

ing strive hard to improve generalization perfor-

mance.

• Because the non-prototype learning of the ReLU

activation was naturally inﬂuenced by the proto-

type learning with the tangent activation function,

the ﬁnal connection weights tended to be simi-

lar to those of the prototype obtained at the be-

ginning. This means that even though improved

generalization performance could be achieved by

considering detailed information of inputs in the

non-prototype learning with the ReLU activa-

tion function, the ﬁnal internal representation was

based on the prototype, making interpretation

much easier.

4.2 Single and Independent Activation

Learning

We used two different activation functions to improve

generalization performance, namely, the hyperbolic

tangent and ReLU activation functions. The experi-

ment conﬁrmed that the hyperbolic tangent function

showed better generalization performance. On the

other hand, the ReLU activation function produced

lower generalization performance. This is because the

potentiality decreased more rapidly than it did with

the hyperbolic tangent activation function. A decrease

in potentiality means that the number of effective con-

nection weights decreases.

Figure 4 shows the potentiality (left), divergence

(middle), and generalization accuracy (right) of net-

works with no hidden layers (a), with ten hidden

layers and the hyperbolic tangent activation func-

tion (b), and the ReLU activation function (c). As

shown in Figure 4(a), without hidden layers, the ac-

curacy (right) increased very gradually and could not

reach a high level of generalization. The potentiality

(left) and divergence (middle) increased and then de-

creased, indicating that connection weights were not

well-organized for improved generalization. When

the hyperbolic tangent activation function was used,

as shown in Figure 4(b), the potentiality decreased

slowly and consistently, while the divergence (mid-

dle) remained unchanged. Since the generalization

(right) showed higher values in the end, the decrease

in potentiality, corresponding to the organization of

connection weights, is one of the main reasons for

this improvement. Figure 4(c) shows the results of

using the ReLU activation function. The potential-

ity decreased more rapidly than with the hyperbolic

tangent activation function, indicating that connec-

tion weights were more organized than with the hy-

perbolic tangent activation. The divergence (middle)

decreased slightly but remained almost unchanged

throughout the entire learning process. The general-

ization accuracy (right) was slightly lower than that of

the hyperbolic tangent activation function.

The results show that the hyperbolic tangent ac-

tivation function could improve generalization better

than the ReLU activation function. This is due to

the more rapid decrease in potentiality and the corre-

spondingly overly organized connection weights pro-

duced by the ReLU function in terms of the number

of connection weights.

For the ratio potentiality, the hyperbolic tangent

function could detect it immediately at the beginning,

but the ReLU activation function failed to do so. Fig-

ure 5 shows the ratio (left), divergence (middle), and

correlation coefﬁcients between estimated and sup-

posed prototypes (right). One of the main results is

that the ratio potentiality (left) of the hyperbolic tan-

gent activation function produced much higher values

at the very beginning, as shown in Figure 5(b). In fact,

the highest value was 0.841, close to the maximum

value, and it was achieved in only 73 steps, as shown

in Table 1. The correlation coefﬁcient (right) also pro-

duced higher values at the beginning, but they were

not as explicit as the ratio potentiality. The divergence

(middle) did not show the lowest and optimal values

at the beginning. On the other hand, the networks

without hidden layers in Figure 5(a) and those with

NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications

480

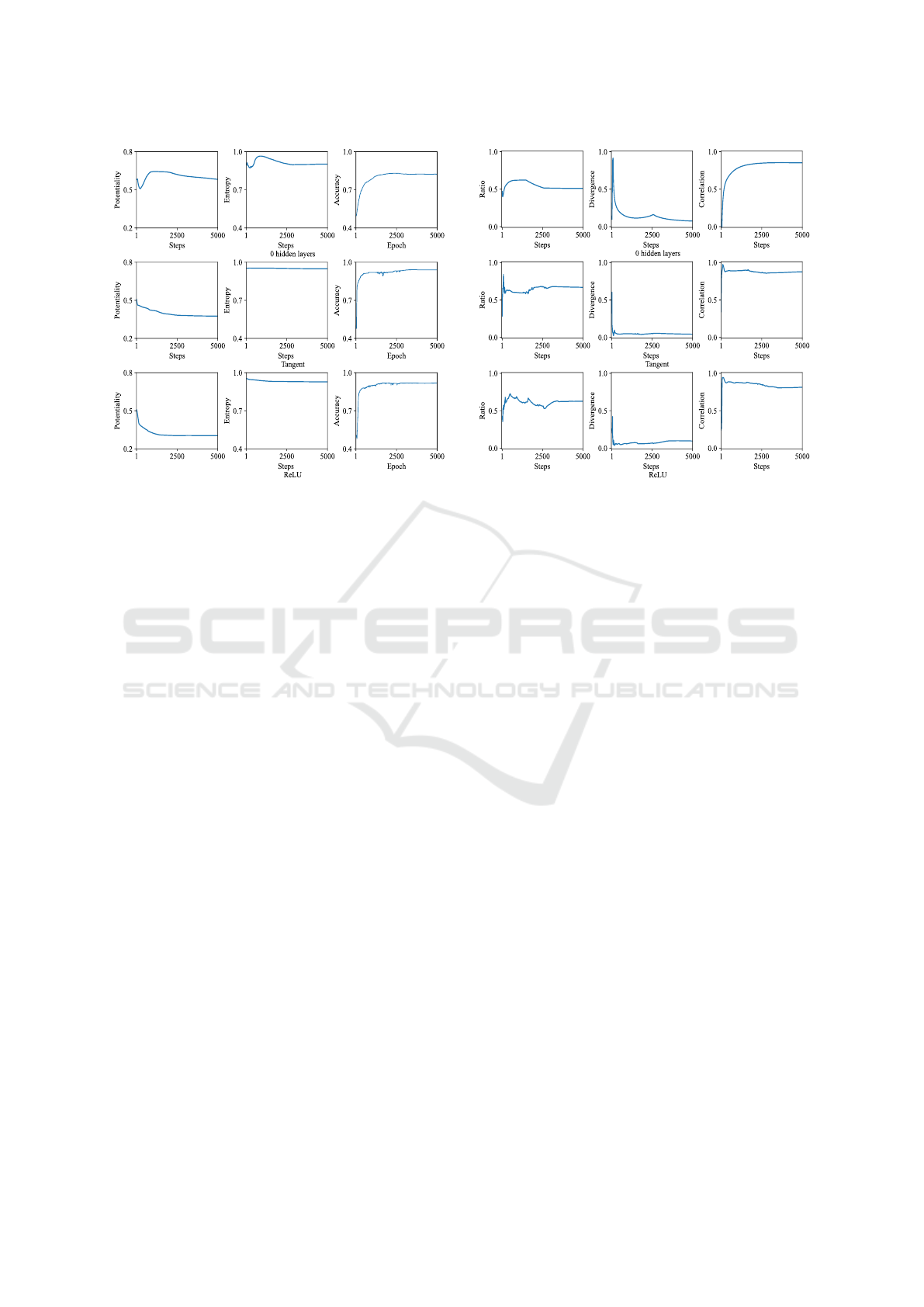
(a)

(b)

(c)

Figure 4: Potentiality (left), entropy (middle) and general-

ization accuracy (right) as a function of the number of learn-

ing steps (epochs) by networks with no hidden layers (a), 10

hidden layers with the hyperbolic tangent function (b), with

the ReLU function (c).

the ReLU activation function in Figure 5(c) showed

higher values for the ratio potentiality and lower val-

ues for the divergence at the beginning, but they were

not as explicit as those produced by the hyperbolic

tangent activation function. The correlation coefﬁ-

cients (right) showed higher values at the beginning,

but they were less clear than those produced by the

hyperbolic tangent activation function. This means

that the hyperbolic tangent activation function with

multi-layered neural networks could clearly detect the

prototype in terms of ratio potentiality.

4.3 Prototype and Prototype Learning

By using multiple activations with the hyperbolic tan-

gent and ReLU activation functions, the properties of

the tangent activation function seemed to be preserved

during learning with the ReLU activation function.

This combination effect should result in better gen-

eralization and, in particular, easier interpretation.

Figure 6 shows the results of using multiple acti-

vations with the hyperbolic tangent and ReLU activa-

tion functions when the number of prototype learning

steps increased from 500 (a) to 1500 (c). The poten-

tiality on the left decreased naturally, similar to that

of the hyperbolic tangent function, as shown in Figure

6(b). However, the entropy remained unchanged and

was not effective in describing the learning and orga-

nization processes. The generalization performance

on the right shows a rapid increase when the activa-

(a)

(b)

0.841(73 steps)

(c)

Figure 5: Ratio potentiality (left), divergence (middle) and

correlation coefﬁcient (right) as a function of the number of

learning steps (epochs) by networks with no hidden layers

(a), 10 hidden layers with the tangent hyperbolic function

(b), with the ReLU function (c).

tion function was switched to the ReLU function after

a sharp decline in generalization. In particular, when

the number of learning steps for the prototype learn-

ing with the tangent activation function was 1000, as

shown in Figure 6(b), the generalization accuracy was

close to the maximum value.

Figure 7 shows the ratio (left), divergence (mid-

dle), and correlation coefﬁcients (right) when the

number of learning steps increased from 500 (a) to

1500 (c). Naturally, at the beginning, higher ratio po-

tentiality and correlation coefﬁcient values were ob-

served due to the tangent activation function. When

the activation function was switched to the ReLU ac-

tivation function, the ratio and, less clearly, the cor-

relation coefﬁcient became slightly higher, while the

divergence remained small. The ratio potentiality

tended to increase when the activation was switched

to the ReLU function. In particular, when the number

of learning steps for prototype learning was 500, as

shown in Figure 7(a), the increase in ratio potential-

ity was more explicitly observed. This is expected, as

the effect of higher ratio potentiality persisted at the

beginning of learning. The ratio potentiality clearly

detected the effect of prototype learning at the begin-

ning, while the divergence and correlation coefﬁcient

detected this effect less clearly.

Searching for Idealized Prototype Learning for Interpreting Multi-Layered Neural Networks

481

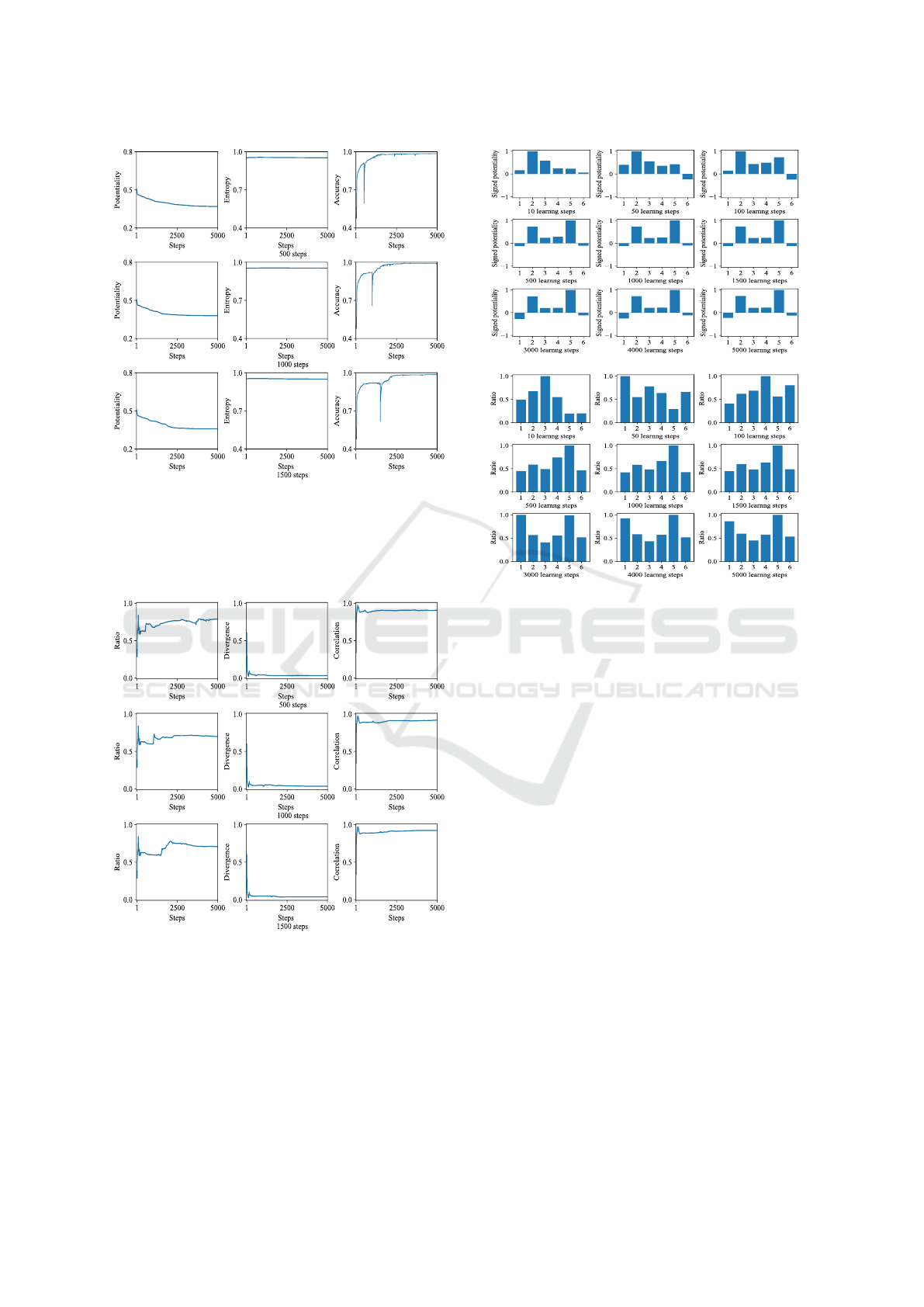
(a)

(b)

(c)

Figure 6: Potentiality (left), entropy (middle) and gener-

alization accuracy (right) as a function of the number of

learning steps (epochs) by the multi-activation with 500 (d),

1000 (e) and 1500 (f) learning steps for the ﬁrst learning

steps with the hyperbolic tangent and the remaining ones

with the ReLU function.

(a)

(b)

(c)

Figure 7: Ratio potentiality (left), divergence (middle) and

correlation coefﬁcient (right) as a function of the number of

learning steps (epochs) by the multiple activations with 500

(d), 1000 (e) and 1500 (f) learning steps for the ﬁrst learning

steps with the hyperbolic tangent and the remaining ones

with the ReLU function.

4.4 Individual Potentialities

The hyperbolic tangent activation function could de-

tect the prototype around the 100th learning step. At

(a) Signed potentiality

(b) Ratio potentiality

Figure 8: Signed ratio potentialities when the tangent ﬁc-

tion was used with the best generalization in the single acti-

vation.

this point, input No.5 was detected as important in a

linear manner, while input No.1 was detected as im-

portant in a non-linear manner.

Figure 8(a) shows the signed individual potential-

ities or connection weights when the number of learn-

ing steps increased from 10 to 5000 using only the hy-

perbolic tangent activation function. As can be seen

in the ﬁgure, the potentialities became most similar

to the prototype shown in Figure 3 around the 100th

learning step, where input No.2 had the largest po-

tentiality. Gradually, input No.5 surpassed input No.2

in potentiality. Figure 8(b) shows the individual ra-

tio potentialities as the number of learning steps in-

creased from 10 to 5000. Over time, input No.5, as

well as input No. 1, became more signiﬁcant than the

other inputs. Input No.5 had a higher correlation coef-

ﬁcient in the prototype, while input No.1 had a lower

correlation coefﬁcient. This indicates that the hyper-

bolic tangent activation function initially detected lin-

ear correlations most strongly, and later also identiﬁed

non-linear correlations for input No.1 as important.

The ReLU activation function produced outputs

based on inputs No.4 and No.6, which were not con-

sidered important in the supposed prototype. Figure

9(a) shows the signed individual potentialities or con-

NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications

482

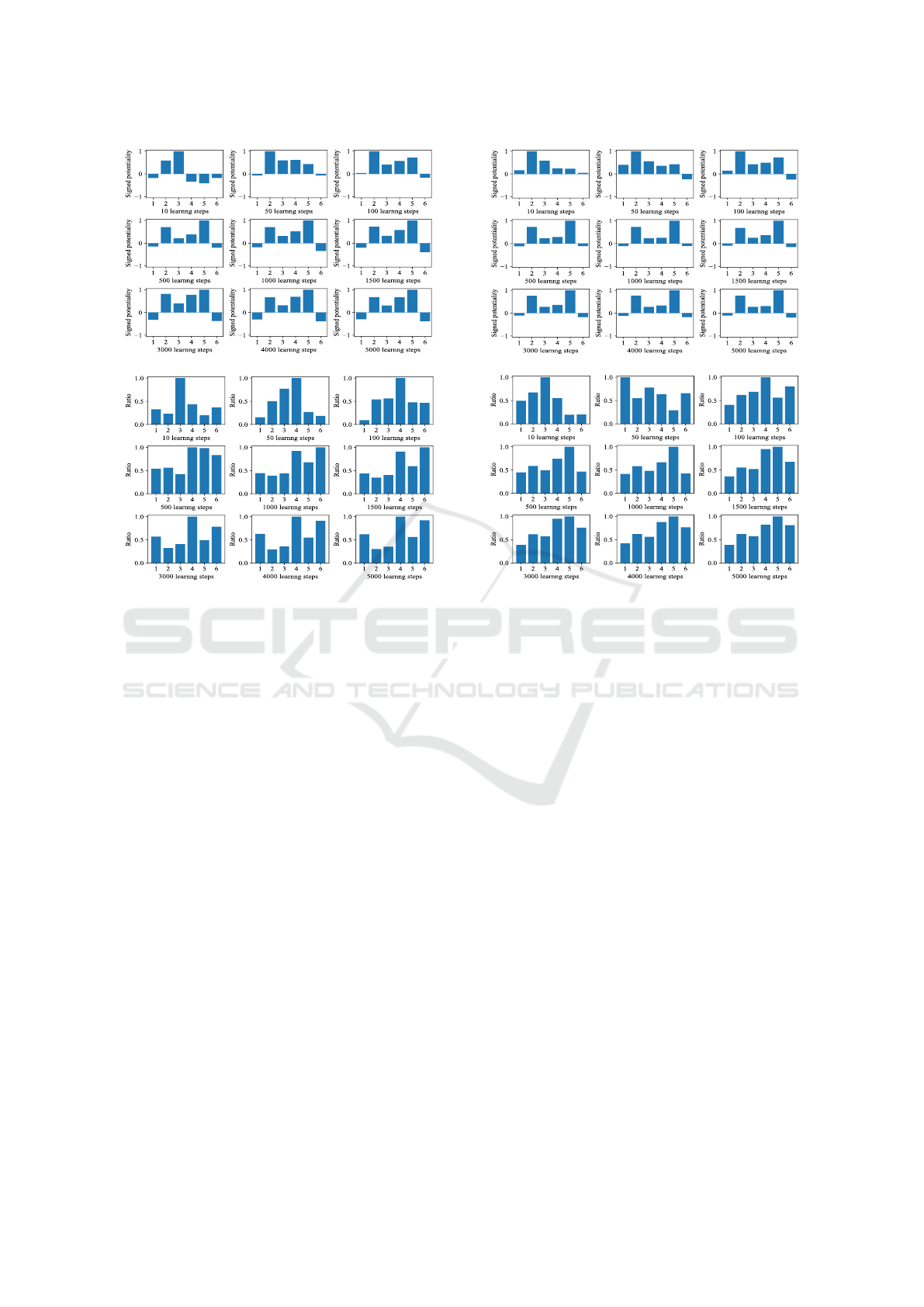
(a) Signed potentiality

(b) Ratio potentiality

Figure 9: Signed ratio potentialities when the ReLU func-

tion was used in the single activation.

nection weights with the ReLU activation function.

The potentialities became relatively similar to the

supposed prototype around the 100th learning step,

but the similarity was not very high. Gradually, in-

put No.5 became more prominent in the learning pro-

cess. Figure 9(b) shows the individual ratio poten-

tialities. One important point to note is that inputs

No.4 and No.6 had larger values by the end of the

learning process. However, these inputs did not have

large weights or correlation coefﬁcients in the proto-

type, indicating that they were not strongly linearly

connected to the outputs. This suggests that the ReLU

activation function learned the input patterns in a non-

linear manner.

The results from the multiple activations show that

combining two different activation functions allows

for the simultaneous use of linear and non-linear re-

lations, improving generalization while retaining the

simple properties of the prototype for easier interpre-

tation. Figure 10(a) shows the results of signed indi-

vidual potentialities or connection weights from mul-

tiple activation learning using tangent and ReLU ac-

tivation functions, achieving the best generalization.

Because the tangent activation function was used for

the ﬁrst 1000 learning steps, the signed potentialities

became naturally similar to those from the hyperbolic

(a) Signed potentiality

(b) Ratio potentiality

Figure 10: Signed ratio potentialities when the tangent

(1000 steps) and ReLU fuction were used with the best gen-

eralization.

tangent activation function. Moreover, in the remain-

ing learning steps, the individual potentialities were

close to those from the tangent activation function in

Figure 8.

Figure 10(b) shows the ratio potentialities when

multiple activation learning was used. Using the ratio

potentiality, different results were obtained. For ex-

ample, one key characteristic is that the ratio poten-

tiality increased with the input number. In particular,

the ﬁnal three inputs, namely inputs No.4 to No.6, had

larger potentialities. As explained in Figure 9, inputs

No.4 and No.6 had larger potentialities with the sin-

gle ReLU activation function. On the other hand, in-

put No.5 had relatively larger potentiality in the proto-

type, as shown in Figure 3. This indicates that multi-

ple activation learning aimed to strengthen both linear

and non-linear relations between inputs and outputs.

The results demonstrate that the tangent activation

function strongly detected linear and non-linear rela-

tions, while the ReLU function focused on non-linear

ones. By combining them in multi-activation, both

linear and non-linear relations could be detected. This

multiple activation learning approach improved gen-

eralization more effectively, with prototype learning

by the tangent activation function and non-prototype

Searching for Idealized Prototype Learning for Interpreting Multi-Layered Neural Networks

483

(a) Single activation (tangent)

(b) Multiple activations (tangent+ReLU)

Figure 11: Loss (error) and accuracy by the single activation

(tangent) and multiple activation learning (tangent+ReLU).

learning by the ReLU function contributing to the en-

hanced generalization. Additionally, because the ﬁ-

nal connection weights retain the characteristics of

the supposed prototype from the prototype learning,

it is much easier to understand the inner workings of

the neural network. The estimated idealized proto-

type learning, achieved by combining the tangent and

ReLU activation functions, clearly demonstrates the

existence and utility of the concept of idealized pro-

totype learning for interpreting multi-layered neural

networks.

4.5 Smaller Variation of Generalization

The reason why better generalization was achieved

can be explained by examining the error (loss) and ac-

curacy values computed over ten different runs. This

indicates that multiple activation learning can reduce

variations in accuracy.

Figure 11 shows the error (left) and accuracy

(right) for single activation and multiple activation

learning, with the number of steps for prototype learn-

ing set to 1000 for optimal generalization perfor-

mance. As seen in Figure 11(a), when only the hy-

perbolic tangent activation function was used, dis-

crepancies between validation (green) and testing val-

ues (red) increased from the beginning. In contrast,

when multiple activation learning was employed in

Figure 11(b), the discrepancy decreased immediately

after introducing the non-prototype learning with the

ReLU activation function, following the sharp de-

cline associated with the change in activation func-

tion. This reduction in the variation of generaliza-

tion errors and accuracies is clearly related to the im-

proved generalization.

Table 1: Summary of experimental results on average ra-

tio, divergency, correlation, and generalization accuracy by

networks without hidden layers, tangent, ReLU activation

function and three types of multiple activations(changing

the number of steps in the prototype learning from 500 to

1500). Bold type letters indicate optimal values. The up-

per and lower number represent the actual values and the

corresponding number of learning steps.

Activ Ratio Diverg Correl General

0.624 0.074 0.855 0.824

1460 5000 3710 4901

Tangent 0.841 0.024 0.973 0.941

73 96 103 3470

ReLU 0.729 0.035 0.945 0.917

492 165 87 4185

500 0.841 0.024 0.973 0.985

73 96 103 4514

1000 0.841 0.024 0.973 0.992

73 96 103 3047

1500 0.841 0.024 0.973 0.984

73 96 103 4253

4.6 Numerical Summary

Numerical results show that detecting the prototype

at the beginning of learning can contribute to im-

proved generalization. This implies that ideal learn-

ing with both prototype and non-prototype compo-

nents can enhance generalization. Additionally, non-

prototype learning is performed while maintaining the

trace of prototype learning. The interpretation of the

inner mechanism is much easier because the proto-

type represents the simplest network within the given

network resources.

Table 1 summarizes the numerical analysis. The

network without hidden layers produced the low-

est ratio potentiality (0.624), the largest divergence

(0.074), the lowest correlation coefﬁcient (0.855), and

the lowest generalization (0.824). This indicates that

without hidden layers, it is difﬁcult to disentangle the

relations between inputs and outputs, making it dif-

ﬁcult to extract the prototype. The tangent activa-

tion function produced the highest ratio potentiality

(0.841) and the highest correlation coefﬁcient (0.973),

along with the smallest divergence (0.024), except for

the generalization performance (0.941). The ReLU

activation function resulted in the second lowest ra-

tio potentiality (0.729), the second lowest correlation

coefﬁcient (0.945), and the second highest divergence

(0.035). Additionally, the generalization (0.917) was

the second lowest. When multiple activation learning

was introduced, the ratio potentiality, divergence, and

correlation coefﬁcient were similar to those obtained

with the tangent activation function. However, the

NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications

484

generalization performance reached the highest value

(0.992) when the number of learning steps in proto-

type learning was 1000. Even in other multiple activa-

tion learning cases, generalization (0.984 and 0.985)

was signiﬁcantly better than that of the single activa-

tion models (0.941 and 0.917).

The results conﬁrm that detecting and combining

prototype and non-prototype learning can contribute

to improved generalization and interpretation. In par-

ticular, interpretation is greatly facilitated because the

prototype, with its minimal network conﬁguration,

has a considerable effect on learning.

5 CONCLUSION

The present paper aimed to demonstrate that neural

learning should begin with the extraction of the pro-

totype, the simplest network within the given network

resources, followed by non-prototype learning on de-

tailed input information. The prototype is intended to

be determined as independently as possible from any

inputs, though ideally. The importance of the pro-

totype can be demonstrated by comparing a network

that easily acquires the prototype with one that does

not, using multi-activation techniques. By changing

the activation function from the hyperbolic tangent

at the beginning to the ReLU function in later learn-

ing steps, we observed a signiﬁcant improvement in

generalization performance. Additionally, the ﬁnal

weights retain the trace of the prototype learning from

the beginning and are easily understood. The extrac-

tion of the prototype should play a critical role in

training neural networks, making their internal repre-

sentations more comprehensible and enhancing gen-

eralization.

Finally, we should address several future direc-

tions. First, we need to resolve issues inherent to po-

tentiality and ratio potentiality. Due to its simplicity

and stability, potentiality is limited to the absolute val-

ues of connection weights. The ratio potentiality at-

tempts to estimate how much the estimated individual

potentiality exceeds the supposed potentiality. This

simpliﬁcation is used to highlight the importance of

inputs for easier interpretation, as larger weights are

considered more important. However, in actual sce-

narios discussed in this paper, negative weights ap-

pear to play signiﬁcant roles in some cases. Thus, it is

necessary to incorporate the negative effect or “nega-

tive potentiality” to make the potentiality framework

more general. Second, exploring different types of

activation functions for prototype extraction is pos-

sible. In the multiple activation learning, only two

standard activation functions were used for ease of

reproduction, but many other activation functions ex-

ist. It would be interesting to use them for extracting

the ideal prototype. Additionally, it may be possible

to identify a single activation function or an idealized

activation function that captures the properties of both

prototype and non-prototype learning. Finally, apply-

ing the method to larger and more practical datasets is

crucial to determine if our approach can address prac-

tical problems that require not only improved general-

ization but also enhanced interpretation. Understand-

ing the inner workings of neural networks is consid-

ered more important than merely improving general-

ization.

REFERENCES

Apicella, A., Donnarumma, F., Isgr

o, F., and Prevete, R.

(2021). A survey on modern trainable activation func-

tions. Neural Networks, 138:14–32.

Bucilu

a, C., Caruana, R., and Niculescu-Mizil, A. (2006).

Model compression. In Proceedings of the 12th ACM

SIGKDD international conference on Knowledge dis-

covery and data mining, pages 535–541. ACM.

Carlucci, L. and Case, J. (2013). On the necessity of u-

shaped learning. Topics in cognitive Science, 5(1):56–

88.

Case, J. and K

otzing, T. (2016). Strongly non-u-shaped lan-

guage learning results by general techniques. Informa-

tion and Computation, 251:1–15.

Chao, W.-L., Changpinyo, S., Gong, B., and Sha, F. (2016).

An empirical study and analysis of generalized zero-

shot learning for object recognition in the wild. In

Computer Vision–ECCV 2016: 14th European Con-

ference, Amsterdam, The Netherlands, October 11-14,

2016, Proceedings, Part II 14, pages 52–68. Springer.

Corkery, M., Matusevych, Y., and Goldwater, S. (2019).

Are we there yet? encoder-decoder neural networks

as cognitive models of english past tense inﬂection.

arXiv preprint arXiv:1906.01280.

Emanuel, R. H., Docherty, P. D., Lunt, H., and M

oller, K.

(2024). The effect of activation functions on accu-

racy, convergence speed, and misclassiﬁcation conﬁ-

dence in cnn text classiﬁcation: a comprehensive ex-

ploration. The Journal of Supercomputing, 80(1):292–

312.

Jagtap, A. D. and Karniadakis, G. E. (2023). How impor-

tant are activation functions in regression and classiﬁ-

cation? a survey, performance comparison, and future

directions. Journal of Machine Learning for Modeling

and Computing, 4(1).

Kim, J., Oh, T.-H., Lee, S., Pan, F., and Kweon, I. S.

(2019). Variational prototyping-encoder: One-shot

learning with prototypical images. In Proceedings of

the IEEE/CVF Conference on Computer Vision and

Pattern Recognition, pages 9462–9470.

Kirov, C. and Cotterell, R. (2018). Recurrent neural net-

works in linguistic theory: Revisiting pinker and

Searching for Idealized Prototype Learning for Interpreting Multi-Layered Neural Networks

485

prince (1988) and the past tense debate. Transac-

tions of the Association for Computational Linguis-

tics, 6:651–665.

Neill, J. O. (2020). An overview of neural network com-

pression. arXiv preprint arXiv:2006.03669.

Nwankpa, C., Ijomah, W., Gachagan, A., and Marshall, S.

(2018). Activation functions: Comparison of trends in

practice and research for deep learning. arXiv preprint

arXiv:1811.03378.

Pinker, S. and Prince, A. (1988). On language and con-

nectionism: Analysis of a parallel distributed process-

ing model of language acquisition. Cognition, 28(1-

2):73–193.

Pourpanah, F., Abdar, M., Luo, Y., Zhou, X., Wang, R.,

Lim, C. P., Wang, X.-Z., and Wu, Q. J. (2022). A re-

view of generalized zero-shot learning methods. IEEE

transactions on pattern analysis and machine intelli-

gence, 45(4):4051–4070.

Ramachandran, P., Zoph, B., and Le, Q. V. (2017).

Searching for activation functions. arXiv preprint

arXiv:1710.05941.

Rumelhart, D. E. and McClelland, J. L. (1986). On learn-

ing the past tenses of English verbs. In Rumelhart,

D. E., Hinton, G. E., and Williams, R. J., editors, Par-

allel Distributed Processing, volume 2, pages 216–

271. MIT Press, Cambrige.

Saralajew, S., Holdijk, L., Rees, M., and Villmann,

T. (2018). Prototype-based neural network layers:

incorporating vector quantization. arXiv preprint

arXiv:1812.01214.

Shimizu, K. (2009). Multivariate analysis (in Japanese).

Nikkan Kogyo Shinbun.

Song, Y., Wang, T., Cai, P., Mondal, S. K., and Sahoo, J. P.

(2023). A comprehensive survey of few-shot learn-

ing: Evolution, applications, challenges, and opportu-

nities. ACM Computing Surveys, 55(13s):1–40.

utfeld, L. R., Brieger, F., Finger, H., F

ullhase, S., and Pipa,

G. (2020). Adaptive blending units: Trainable activa-

tion functions for deep neural networks. In Intelligent

Computing: Proceedings of the 2020 Computing Con-

ference, Volume 3, pages 37–50. Springer.

Viering, T. and Loog, M. (2022). The shape of learning

curves: a review. IEEE Transactions on Pattern Anal-

ysis and Machine Intelligence.

Westermann, G. (2022). Emergent modularity and u-shaped

learning in a constructivist neural network learning the

english past tense. In Proceedings of the Twentieth

Annual Conference of the Cognitive Science Society,

pages 1130–1135. Routledge.

APPENDIX

Entropy and Divergence

As mentioned above, potentiality is computed to sim-

plify entropy and its corresponding divergence. We

(1) i

(2) j

(3) k (4) l

(5) m

(6)

1st compression

2nd compression

3rd compression

Estimated prototype

(5) m

(4) l

(3) k

(1) i

(1)i

(6)

Figure 12: Concept of compression prototype.

introduce the entropy and its related divergence mea-

sure here. The relative potentiality for the supposed

prototype network is computed by

(1,2)

∑

′

(1,2)

′

. (10)

Next, the relative potentiality for the compressed

and estimated prototype network is computed by

(1,6)

∑

′

(1,6)

′

. (11)

Entropy can be deﬁned by

(1,6)

= −

∑

(1,6)

log p

(1,6)

. (12)

Divergence, being the reverse type, is computed

(1,6)

∑

(1,6)

log

(1,6)

(1,2)

. (13)

This divergence decreases when the potentialities

of the two networks become more similar to each

other.

Compression

In the ﬁrst compression, the weights from the input

layer to the third layer, labeled (1,3), are compressed

as follows:

(1,3)

∑

(1,2)

i j

(2,3)

. (14)

By repeating these processes, we obtain the com-

pressed weights connecting the ﬁrst and ﬁfth layers,

denoted as w

(1,5)

. Using these connection weights, we

ﬁnally obtain the fully compressed weights for (1,6):

(1,6)

∑

(1,5)

(5,6)

. (15)

In the context of large multi-layered neural net-

works, there are many different types of compres-

sion methods. This compression method differs from

NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications

486

conventional and popular compression methods (Bu-

cilu

a et al., 2006; Neill, 2020). The majority of these

conventional methods attempt to compress the orig-

inal multi-layered neural networks without consider-

ing internal conﬁgurations, focusing instead on gen-

eralization performance. This paper aims to under-

stand the inner workings of neural networks, and thus

it is necessary to preserve the internal conﬁgurations

of the original multi-layered neural networks as much

as possible.

Searching for Idealized Prototype Learning for Interpreting Multi-Layered Neural Networks

487