Trade Data Harmonization: A Multi-Objective Optimization Approach
for Subcategory Alignment and Volume Optimization
Himadri Sikhar Khargharia, Sid Shakya and Dymitr Ruta
EBTIC, Khalifa University, Abu Dhabi, U.A.E.
Keywords:
Trade Data Harmonisation, Non-Dominated Sorting Genetic Algorithm II, Genetic Algorithm,
Population-Based Incremental Learning, Distribution Estimation Using MRF and Simulated
Annealing.
Abstract:
Aligning trade data from disparate sources poses challenges due to volume disparities and category nam-
ing variations. This study aims to harmonize subcategories from a secondary dataset with those of a pri-
mary dataset, focusing on aligning the number and combined volumes of subcategories. We employ a multi-
objective optimization approach using Non-dominated Sorting Genetic Algorithm II (NSGA-II) to facilitate
trade-off assessments and decision-making via Pareto fronts. NSGA-II’s performance is compared with single-
objective optimization techniques, including Genetic Algorithm (GA), Population-based Incremental Learning
(PBIL), Distribution Estimation using Markov Random Field (DEUM), and Simulated Annealing (SA). The
comparative analysis highlights NSGA-II’s efficacy in managing trade data complexities and achieving opti-
mal solutions, demonstrating the effectiveness of meta-heuristic approaches in this context.
1 INTRODUCTION
International trade significantly impacts global eco-
nomic stability by facilitating the exchange of essen-
tial resources such as energy, minerals, metals, and
agricultural products (Harding and Harding, 2020).
When countries lack key domestic resources, trade
shifts from being a strategic option to an economic
necessity (Hammoudeh et al., 2009) (Lewrick et al.,
2018).
Economists support free trade, highlighting its
benefits for growth and welfare (Berg and Lewer,
2015). Accurate and standardized trade data, man-
aged by customs authorities and international bod-
ies, are crucial for quantifying these benefits (Lewrick
et al., 2018) (Ferrantino et al., 2012). However,
data inconsistencies in volume and category naming
across datasets pose challenges, complicating policy
analysis and decision-making (Feenstra et al., 1999)
(Hansen and Prusa, 1997) (Torres-Esp
´
ın and Fergu-
son, 2022) (Khargharia et al., 2023).
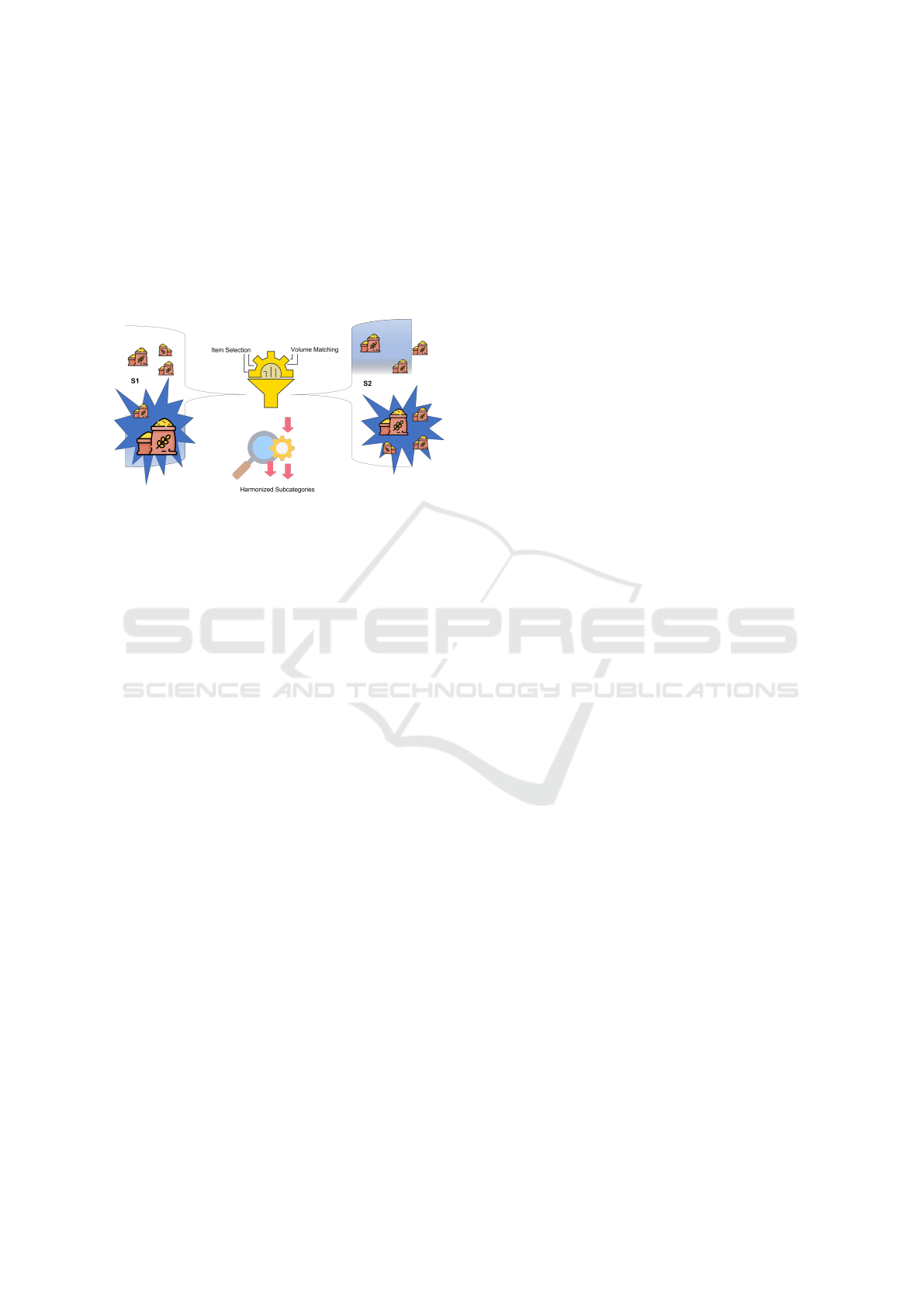
In (Khargharia et al., 2023), trade volume dis-
parities were addressed using a subset sum problem
framework. Building on this, our research focuses
on aligning subcategories across datasets S
1
and S
2
to harmonize traded volumes. Figure 1 illustrates this
approach, where rice subcategory volumes from S
1
are matched with those in S
2
. This study has two main
objectives: (1) aligning subcategory counts and (2)
harmonizing combined traded volumes. To achieve
this, we employ a multi-objective optimization us-
ing the Non-dominated Sorting Genetic Algorithm II
(NSGA-II) (Deb et al., 2002), which is widely used
for generating Pareto fronts to facilitate trade-off as-
sessments and informed decision-making.
To further assess the effectiveness of NSGA-
II, four single-objective optimization techniques
are implemented: Genetic Algorithm (GA) (Gold-
berg, 1989), Population-based Incremental Learning
(PBIL) (Baluja, 1994), Distribution Estimation using
Markov Random Fields (DEUM) (Shakya and Mc-
Call, 2007) (Shakya et al., 2021), and Simulated An-
nealing (SA) (Kirkpatrick et al., 1983). Scalarization
is applied to unify subcategory numbers and volumes
into a single optimization criterion. Although direct
comparison between single and multi-objective op-
timization is challenging due to differing cost func-
tions, it is common in EA literature to use the solution
closest to the ideal point (refer section 2.2) as a refer-
ence for comparison. Additionally, when a Pareto so-
lution outperforms the best single-objective solution
across all objectives, the comparison becomes clearer
and more meaningful.
For a comprehensive evaluation, we select the so-
338
Khargharia, H., Shakya, S. and Ruta, D.
Trade Data Harmonization: A Multi-Objective Optimization Approach for Subcategory Alignment and Volume Optimization.
DOI: 10.5220/0013052500003837
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 16th International Joint Conference on Computational Intelligence (IJCCI 2024), pages 338-345
ISBN: 978-989-758-721-4; ISSN: 2184-3236
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.

lution point in the Pareto front closest to the ideal
point (de la Fuente et al., 2018) as one of the refer-
ence point for the best solution for NSGA-II. We also
scan through the full Pareto set of solutions found by
NSGA-II to check if there are any solutions that are
better in both objectives in comparison to the best so-
lutions found by single objective algorithms, allowing
us to measure the relative performance of NSGA-II
against the single-objective optimization techniques.
Figure 1: Overview of trade volume harmonization.
The paper is organized as follows: Section 2 dis-
cusses the subset sum problem, Pareto fronts, and
ideal point calculation. Section 2.5 reviews recent
meta-heuristic literature. Section 3 defines the prob-
lem, constraints, and objectives with an example.
Section 4 covers data preparation. Section 5 presents
the methodology and techniques used. Section 6 de-
tails the experimental setup and results. Section 7
summarizes findings and suggests future work.
2 BACKGROUND
This section outlines the fundamental concepts for
our trade volume harmonization approach, utilizing
Pareto optimality, ideal point determination, scalar-
ization, and the subset sum problem for robust align-
ment of trade data.
2.1 Pareto Optimality
Pareto optimality is essential in multi-objective opti-
mization, where conflicting objectives are minimized.
It aligns the number of selected sub-categories and
their combined volume with a reference dataset’s total
import volume. A solution x dominates another solu-
tion y if x is less than or equal in all objectives and
strictly less in at least one:
Pareto Dominance: ∀i : x
i
≤ y
i
and ∃ j : x
j
< y
j
(x ≺ y)
Pareto Optimality: x
∗
is Pareto optimal ⇔ ∄y
such that y ≺ x
∗
2.2 Ideal Point Calculation
The ideal point in multi-objective optimization is de-
rived from the final population of solutions, typically
the non-dominated set forming the Pareto front. For
each objective f
i
, z
∗
i
is determined as the minimum or
maximum value across the final population:
z
∗
i
= min
x∈Final Population
f
i
(x) or z
∗
i
= max
x∈Final Population
f
i
(x)
The ideal point z
∗
is then defined as
(z
∗
1
,z
∗
2
,...,z
∗
m
). This point, though often theo-
retical due to conflicting objectives, serves as a
reference for evaluating Pareto optimal solutions.
2.3 Scalarization
Scalarization converts multiple objectives into a sin-
gle scalar function:
F(x) = w
1
· f
1
(x) + ... + w
k
· f
k
(x).
We use this method to balance selected sub-
categories and their combined volume.
2.4 Subset Sum Problem
The subset sum problem seeks a subset S
′
of a set S
that minimizes:
Minimize:





∑
v
i
∈S
′
v
i
− T





,
where T is a target value. It is computationally
complex and NP-complete.
2.5 Literature Review
Recent studies (2023-2024) illustrate the versatility
of meta-heuristic algorithms in complex optimization.
Hosseini et al. (Hosseini et al., 2024) integrated them
with deep learning for energy management, while Ak-
ter et al. (Akter et al., 2024) applied them to mi-
crogrid optimization. Mahmoodi et al. (Mahmoodi
et al., 2024) and Abid et al. (Abid et al., 2023) ex-
plored their use in financial modeling, improving pre-
dictive accuracy. Yahia and Mohammed (Yahia and
Mohammed, 2023) optimized UAV path planning.
In network optimization, Priyadarshi (Priyadarshi,
2024) focused on energy-efficient routing in sensor
networks, and Ghasemi et al. (Ghasemi et al., 2024)
introduced a new engineering optimization method.
Khargharia et al. (Khargharia et al., 2023) uniquely
applied these techniques to trade data harmoniza-
tion, balancing trade volumes across subcategories,
demonstrating their adaptability in new domains.
Trade Data Harmonization: A Multi-Objective Optimization Approach for Subcategory Alignment and Volume Optimization
339

3 PROBLEM DESCRIPTION
Khargharia et al. (Khargharia et al., 2023) modeled
the alignment of trade volumes between two datasets,
S
1
and S
2
, for various product categories in a spe-
cific country, C
1
, as a subset sum problem (see Sec-
tion 2.4). This section refines this by selecting sub-
categories from S
2
that match the total trade volume
and number of sub-categories in S
1
for each prod-
uct category. Product categories encompass broader
types like rice, edible oils, vegetables etc., while their
sub-categories refer to their specific types, such as
rice varieties, types of oils like coconut or mustard,
or different vegetables.
Let P
subc
denote the set of sub-categories for a
product category Pr
i
in S
1
:
P
subc
= {p
1
, p
2
,. .., p
i
} (1)
Similarly, let
ˆ
P
subc
represent the set of sub-
categories for the same product category Pr
i
in S
2
:
ˆ
P
subc
= { ˆp
1
, ˆp
2
,. .., ˆp
N
} (2)
3.1 Objective
The goal is to align sub-categories in S
2
with those
in S
1
by selecting a subset from S
2
whose combined
trade volume approximates that of S
1
while having a
similar number of sub-categories. This is expressed
mathematically as:
∃
ˆ
P
subc
⊂
ˆ
P
subc
:
∑
∀p
i
∈P
subc
T
v
(p
i
) ≈
∑
∀ ˆp
i
∈
ˆ
P
subc
T
v
( ˆp
i
) (3)
where T
v
is the traded volume,
ˆ
P
subc
is the selected
subset from
ˆ
P
subc
, and |
ˆ
P
subc
| ≈ |P
subc
|.
3.2 Constraints
• Subset Selection: The solution involves selecting
a subset of sub-categories from S
2
. This subset
must be chosen such that it aligns as closely as
possible with both the total trade volume and the
number of sub-categories in S
1
.
3.3 Example
Consider product rice in S
1
with three sub-categories:
Basmati (T
v
(p
1
) = 100), Jasmine (T
v
(p
2
) = 200),
and Long-grain (T
v
(p
3
) = 300), giving P
subc
=
{p
1
, p
2
, p
3
} and a total trade volume of 600.
Dataset S
2
has a more detailed breakdown into six
sub-categories: White Basmati (T
v
( ˆp
1
) = 80), Brown
Basmati (T
v
( ˆp
2
) = 100), Jasmine (T
v
( ˆp
3
) = 190), Or-
ganic Long-grain (T
v
( ˆp
4
) = 310), Parboiled Long-
grain (T
v
( ˆp
5
) = 270), and Glutinous rice (T
v
( ˆp
6
) =
40), forming
ˆ
P
subc
= { ˆp
1
, ˆp
2
, ˆp
3
, ˆp
4
, ˆp
5
, ˆp
6
}.
The goal is to select
ˆ
P
subc
⊂
ˆ
P
subc
such that the
trade volume and number of sub-categories match
S
1
. For example, { ˆp
2
, ˆp
3
, ˆp
4
} gives 100 + 190 +
310 = 600, matching S
1
in both volume and three
sub-categories. Another subset, { ˆp
2
, ˆp
3
, ˆp
5
, ˆp
6
}, also
sums to 600 but includes four sub-categories, making
it non-optimal.
4 DATA PREPARATION AND
ANALYSIS
This section describes the preparation and analysis of
two datasets, S
1
and S
2
, for trade data of country C
1
.
S
1
is a genuine dataset representing real trade data
from reliable sources, while S
2
is a simulated dataset
expanding the subcategories in S
1
to increase problem
complexity and test robustness.
Table 1: Product categories from S
1
with subcategories and
trade volumes.
Category |P
subc
| Trade Vol (KMT)
Pr
1
19 154.103
Pr
2
54 461.450
Pr
3
92 782.301
Pr
4
194 1641.841
Four key product categories are analyzed in S
1
:
Pr
1
, Pr
2
, Pr
3
, and Pr
4
, each with subcategories P
subc
(see Table 1). To increase complexity, S
2
expands
each product’s subcategories by approximately ten
times, denoted as
ˆ
P
subc
. This ensures controlled scal-
ing for computational efficiency, represented as:
N ≈ 10 · |P
subc
| :
ˆ
P
subc
= { ˆp
1
, ˆp
2
,. .., ˆp
N
} (4)
where P
subc
represents the set of subcategories for
any product Pr
i
from S
1
, and
ˆ
P
subc
denotes the ex-
panded subcategories in S
2
.
In S
1
, trade volumes T
v
(p
i
) for subcategories
range from 0 to 8 KMT, while T
v
( ˆp
i
) in S
2
ranges
from 7 to 10 KMT, increasing complexity and avoid-
ing exact matches. Mathematically, the ranges are:
p
i
∈ P
subc
: T
v
(p
i
) ∈ R[0,8]
ˆp
i
∈
ˆ
P
subc
: T
v
( ˆp
i
) ∈ R[7,10]
(5)
Table 2 provides details of S
2
with expanded sub-
categories and corresponding trade volumes.
ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications
340

Table 2: Product categories from S
2
with expanded subcat-
egories and trade volumes.
Category |
ˆ
P
subc
| Trade Vol (KMT)
Pr
1
200 762.399
Pr
2
600 2388.052
Pr
3
1000 3955.926
Pr
4
2000 8008.241
5 METHODOLOGY
This section outlines the methodology for model-
ing the problem from Section 3 as an optimization
task, including fitness evaluations for meta-heuristic
techniques, solution design, and the specific methods
used.
5.1 Solution Representation
To align trade data between datasets S
1
and S
2
(Sec-
tion 3), we utilize four single-objective binary meta-
heuristic techniques (Khargharia et al., 2023) and one
multi-objective binary metaheuristic technique (Deb
et al., 2002). Let X = {x
1
,...,x
n
}, where n = N =
|
ˆ
P
subc
| (from equations 4 and 2). The binary string X,
representing solutions, varies in length (SOL) as 200,
600, 1000, or 2000 (Table 2). Each x
i
∈ X can be 0 or
1.
In a practical example, if dataset S
2
includes eight
subcategories (P1, P2, P3, P4, P5, P6, P7, P8) and we
aim to select matching subcategories from S
1
such as
P2, P3, and P8, the binary solution from any meta-
heuristic method should resemble the example in Fig-
ure 2.
Figure 2: Illustration of Binary Representation of Solution
5.2 Fitness Evaluation
Fitness evaluation acts as a measure to assess the
effectiveness of identified subcategories in aligning
trade data, aiming to uncover meaningful patterns for
specific commodities.
Let m = |P
subc
|, representing the number of sub-
categories associated with any product category Pr
i
from dataset S
1
(as defined in equation 1). As men-
tioned before, T
v
is considered as the traded volume.
We mathematically model the problem discussed in
Section 3 as involving two functions:
f
1
(X) : Align the number of selected sub-categories.
f
2
(X) : Align the combined volume of selected
sub-categories.
such that:
f
1
(X) = |m −
n
∑
i=1
x
i
|
!
f
2
(X) = |
m
∑
i=1
T
v
(p
i
) −
n
∑
i=1
x
i
· T
v
( ˆp
i
)|
!
(6)
where the terms carry their usual meanings as defined
in Equation 3 and in Section 5.1.
5.2.1 Using Multi Objective Optimization
Techniques
While using a multi-objective optimization technique,
f
1
(X) and f
2
(X) represent the objectives that need to
be optimized simultaneously as mathematically rep-
resented below.
min
X={x
1
,...,x
n
}
f
1
(X) , min
X={x
1
,...,x
n
}
f
2
(X)
(7)
f
1
(X) and f
2
(X) are used to create a Pareto front
as follows:
Pareto Optimality. The goal is to find solutions X
that are not dominated by any other feasible solution
in terms of both objectives f
1
(X) and f
2
(X) (refer sec-
tion 2.1). A solution X
∗
is Pareto optimal if there does
not exist another feasible solution X
′
such that:
f
1
(X
′
) ≤ f
1
(X
∗
) and f
2
(X
′
) ≤ f
2
(X
∗
) (8)
with at least one strict inequality.
Pareto Front. The Pareto front consists of all non-
dominated solutions. It represents the trade-offs be-
tween f
1
(X) and f
2
(X) where improving one objec-
tive comes at the expense of the other. Points on
the Pareto front cannot be improved in one objective
without worsening the other.
5.2.2 Using Single Objective Optimization
Techniques
To consolidate multiple objectives f
1
(X) and f
2
(X)
into a single-objective form, scalarization is applied
using min-max normalization (see section 2.3). Given
a set V = {v
1
,v
2
,. ..,v
n
}, the normalization function
is:
Norm(v
i
) =
v
i
− min(V )
max(V ) − min(V )
(9)
The scalarized fitness function is defined as:
min
X
f (X ) = w
1
· Norm ( f
1
(X)) + w
2
· Norm ( f
2
(X))
(10)
where equal weights w
1
= w
2
= 1 are used. The
normalization ranges for f
1
(X) are 0 and |m − n|, and
for f
2
(X), 0 and
|
∑
m
i=1
T
v
(p
i
) −
∑
n
i=1
T
v
( ˆp
i
)
|
.
Trade Data Harmonization: A Multi-Objective Optimization Approach for Subcategory Alignment and Volume Optimization
341

5.3 Considered Meta-Heuristic
Techniques
To address the Trade Data Harmonization problem
(Section 3), both single and multi-objective optimiza-
tion techniques are considered, with NSGA-II (Deb
et al., 2002) used for multi-objective optimization.
5.3.1 Non-dominated Sorting Genetic Algorithm
II (NSGA-II)
A robust evolutionary algorithm for multi-objective
optimization problems, NSGA-II extends Genetic Al-
gorithms by efficiently handling conflicting objectives
using two core mechanisms: non-dominated sorting
and crowding distance.
• Non-Dominated Sorting. Solutions are ranked
into non-dominated fronts based on their domi-
nance relationships. A solution X dominates Y if:
∀i, f
i
(X) ≤ f
i
(Y ), ∃ j, f
j
(X) < f
j
(Y )
where f
i
denotes the objective value for i-th ob-
jective. NSGA-II assigns ranks F
1
,F
2
,. .. to solu-
tions, with lower ranks indicating better solutions.
• Crowding Distance. Maintains diversity in the
population. For each front F
n
, the distance D
i
for
each solution i is:
D
i
=
m
∑
j=1
f
j
(next
i
) − f
j
(prev
i
)
Range
j
where f
j
(next
i
) and f
j
(prev
i
) are neighboring ob-
jective values, and Range
j
is the range of j-th ob-
jective in F
n
.
NSGA-II evolves populations across generations
using selection, crossover, and mutation, balancing
convergence and diversity to approach Pareto-optimal
solutions. For further details, see (AlShanqiti et al.,
2019).
The single objective techniques from (Khargharia
et al., 2023) include:
5.3.2 Genetic Algorithm (GA)
GA mimics natural selection on a population of
solutions. Using crossover (cOper) and mutation
(mOper) operators with probabilities (cp, mp), it
evolves the population to preserve elites (e) and bal-
ance exploration (Goldberg, 1989).
5.3.3 Population-Based Incremental Learning
(PBIL)
PBIL updates a probability vector based on elite so-
lutions (e) using a learning rate (λ) and selection size
(ss), guiding the search in promising regions (Baluja,
1994).
5.3.4 Distribution Estimation Using Markov
Random Field (DEUM)
DEUM employs a Markov Random Field model to
estimate distributions, adjusting a temperature coeffi-
cient (β) for exploration-exploitation balance (Shakya
and McCall, 2007).
5.3.5 Simulated Annealing (SA)
SA uses a cooling schedule to control the tempera-
ture (τ), shifting from exploration to exploitation as τ
decreases (Kirkpatrick et al., 1983).
6 EXPERIMENT SETUP AND
ANALYSIS OF RESULTS
Experiments were conducted on a workstation with
an 11th Gen Intel Core i7-11800H @ 2.30GHz
processor and 32 GB RAM, using datasets S
1
and S
2
.
S
1
has product categories Pr
1
to Pr
4
with subcate-
gory counts of 19, 54, 92, and 194, while S
2
includes
sizes 200, 600, 1000, and 2000. Refer to Section 4
for dataset details and Section 3 for experiment de-
scriptions. Each experiment was repeated 15 times
with different solution sizes and parameter settings
(see Section 6.1).
6.1 Parameter Selection
Optimal parameters were selected empirically
through initial trials. Population sizes for GA, PBIL,
DEUM, and NSGA-II were set to half the solution
length (SOL/2) for SOL values of 200, 600, 1000,
and 2000. Maximum generations were set to 10
times the population size, except for SA, where it was
set to 10 times (SOL/2)
2
, due to its single-solution
approach.
GA used uniform crossover with 0.79 probability,
tournament selection, and 1-bit mutation with 0.034
probability. PBIL’s selection size was 0.47 and learn-
ing rate 0.16. DEUM had a selection size of 0.06
and a temperature coefficient of 0.86. SA was set
with a temperature of 0.023. NSGA-II used 1-point
crossover (0.7 probability) and 1-bit mutation (0.0121
probability), with tournament selection.
6.2 Experimental Analysis
In this section, the experimental results for the prob-
lem detailed in Section 3 are presented and summa-
rized in Table 3, covering 15 runs for each algorithm-
solution size combination. For the single-objective
ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications
342

Table 3: Results of difference in selected Items and volume.
SOL Algo
2000 GA PBIL DEUM SA IP (NSGA-II) B (NSGA-II)
α 55 27 389 216 24 25
β 0.000 0.000 119.871 0.001 0.007 0.000
θ 55.33 ± 0.577 27.0 ± 0.000 394.5 ± 7.778 229.67 ± 12.34 24.11 ± 0.87 25.428 ± 0.494
γ 0.000 ± 0.000 0.000 ± 0.000 123.658 ± 49.197 0.083 ± 0.128 0.026 ± 2.23 0.000 ± 0.000
1000 GA PBIL DEUM SA IP (NSGA-II) B (NSGA-II)
α 23 13 167 102 9 9
β 0.002 0.000 74.654 0.337 0.000 0.000
θ 23.0 ± 0.0 13.333 ± 0.577 184.0 ± 15.133 109.667 ± 6.658 9.476±0.67 10.457 ± 1.17
γ 0.086 ± 0.144 0.000 ± 0.000 121.076 ± 51.143 0.425 ± 0.184 1.30±2.43 0.003 ± 0.045
600 GA PBIL DEUM SA IP (NSGA-II) B (NSGA-II)
α 50 22 71 62 5 7
β 0.341 0.013 0.496 0.191 7.632 0.000
θ 54.867 ± 2.503 26.0 ± 2.673 73.333 ± 2.082 67.000 ± 4.359 4.78±0.63 7.928±0.593
γ 0.095 ± 0.141 0.034 ± 0.038 0.762 ± 0.258 0.277±0.100 9.23±4.50 0.001±0.003
200 GA PBIL DEUM SA IP (NSGA-II) B (NSGA-II)
α 22 9 11 19 2 3
β 0.013 0.022 0.024 0.259 0.888 0.000
θ 23.333 ± 1.155 11.6 ± 1.242 13.0 ± 2.0 24.133 ± 2.386 2.11±0.57 3.268±0.44
γ 0.110 ± 0.089 0.037 ± 0.059 0.035 ± 0.038 0.325 ± 0.116 1.53±2.35 0.004±0.034
optimization algorithms (GA, PBIL, DEUM, and
SA), discrepancies in selected sub-categories (Item
Diff, α) and differences in traded volumes (VOL Diff,
β) are computed using equation (10) based on the Best
Fitness run.
For the multi-objective NSGA-II, two solutions
from the Pareto front are reported: IP (NSGA-II),
which is the closest point to the ideal (see Section
2.2), and B (NSGA-II), which has superior values for
both objectives. The Euclidean distance, normalized
to [0,1], ensures equal weight for sub-category differ-
ences (Item Diff ) and volume differences (VOL Diff ).
Table 3 also provides the average discrepancies
(θ, Item Diff (Avg ± SD)) and volume differences (γ,
VOL Diff (Avg ± SD)) along with standard deviations
across 15 runs. For SOLs 200 and 600, all single-
objective algorithms achieve near-zero VOL Diff with
similar sub-categories. For SOLs 1000 and 2000,
PBIL achieves the lowest VOL Diff with the fewest
selected sub-categories. SA and DEUM select more
sub-categories for SOLs 1000 and 2000, with SA ef-
fectively reducing VOL Diff, while DEUM faces chal-
lenges in achieving optimal results.
NSGA-II competes effectively with single-
objective algorithms, as illustrated in Figures 3 and
4 for solution sizes 200, 600, 1000, and 2000 (based
on run 6 out of 15). These figures demonstrate the
trade-offs between Item Diff and VOL Diff, providing
insights for decision-makers. Ideal points, plotted as
reference points, highlight non-dominated solutions
in Front 0, with the closest solutions marked based
on Euclidean distance.
In Table 3, the B (NSGA-II) solution consistently
outperforms single-objective algorithms across all so-
lution sizes (200, 600, 1000, and 2000), showing su-
perior performance across both objectives compared
to the best results from single-objective techniques.
The IP (NSGA-II) solution prioritizes proximity to the
ideal point, yielding results that are generally better
or comparable to single-objective approaches. How-
ever, for solution size 600, the IP (NSGA-II) solution
shows a higher VOL Diff compared to the best single-
objective solution.
6.3 Analysis of Solution Quality
Variability
Further analysis of Table 3 is illustrated in Figure 5,
showing the distribution of average Item Diff (θ) and
VOL Diff (γ) with their standard deviations across dif-
ferent solution sizes and algorithms. DEUM’s outlier
performance is excluded to ensure a clear comparison.
Trade Data Harmonization: A Multi-Objective Optimization Approach for Subcategory Alignment and Volume Optimization
343

(a) SOL 200
(b) SOL 600
Figure 3: Pareto Front Representation by NSGA-II for
SOL.
(a) SOL 1000
(b) SOL 2000
Figure 4: Pareto Front Representation by NSGA-II for
SOL.
Results from B (NSGA-II) indicate that NSGA-II
consistently achieves superior outcomes with negligi-
ble variation for both Item Diff and VOL Diff across
all solution sizes and algorithms. Among the single-
objective algorithms, PBIL provides the best results
with minimal variability, while DEUM is less likely
to yield optimal results.
Figure 5: Spread of average Item Diff and Volume Diff
across all Solution Size.
7 CONCLUSION
This paper tackled a trade data harmonization prob-
lem with multiple optimization objectives, evaluat-
ing NSGA-II’s performance against single-objective
techniques. A Pareto front was generated to help
decision-makers balance trade-offs between sub-
category numbers and combined volumes. Scalar-
ization and normalization converted multiple objec-
tives into a single scalar form for fair comparison
with single-objective algorithms. Results showed that
NSGA-II consistently outperformed single-objective
methods, finding better solutions for both objectives.
Among the single-objective techniques, PBIL often
performed best, while DEUM had the lowest perfor-
mance.
In conclusion, this study demonstrates the effec-
tiveness of multi-objective techniques, particularly
NSGA-II, in trade data harmonization. These meth-
ods handle multiple objectives directly, avoiding the
need for normalization or scalarization, and produce
a Pareto set of solutions, giving users more flexibility
in selecting the optimal solution. Future work could
refine these methods, explore other multi-objective al-
gorithms, and apply them to real-world case studies to
address trade data harmonization challenges further.
REFERENCES
Abid, M., El Kafhali, S., Amzil, A., and Hanini, M.
(2023). An efficient meta-heuristic methods for travel-
ling salesman problem. In The International Confer-
ECTA 2024 - 16th International Conference on Evolutionary Computation Theory and Applications
344

ence on Advanced Intelligent Systems and Informat-
ics. Springer.
Akter, A., Zafir, E., Dana, N., Joysoyal, R., and Sarker,
S. (2024). A review on microgrid optimization with
meta-heuristic techniques: Scopes, trends and recom-
mendation. Energy Strategy Reviews.
AlShanqiti, K., Poon, K., Shakya, S., Sleptchenko, A., and
Ouali, A. (2019). A multi-objective design of in-
building distributed antenna system using evolution-
ary algorithms. In Artificial Intelligence XXXVI: 39th
SGAI International Conference on Artificial Intelli-
gence, AI 2019, Cambridge, UK, December 17–19,
2019, Proceedings 39, pages 253–266. Springer.
Baluja, S. (1994). Population-based incremental learning.
a method for integrating genetic search based func-
tion optimization and competitive learning. Technical
report, Carnegie-Mellon Univ Pittsburgh Pa Dept Of
Computer Science.
Berg, H. V. d. and Lewer, J. J. (2015). International trade
and economic growth.
de la Fuente, D., Vega-Rodr
´
ıguez, M. A., and P
´
erez, C. J.
(2018). Automatic selection of a single solution from
the pareto front to identify key players in social net-
works. Knowledge-Based Systems, 160:228–236.
Deb, K., Pratap, A., Agarwal, S., and Meyarivan, T. (2002).
A fast and elitist multiobjective genetic algorithm:
Nsga-ii. IEEE transactions on evolutionary compu-
tation, 6(2):182–197.
Feenstra, R. C., Hai, W., Woo, W. T., and Yao, S. (1999).
Discrepancies in international data: an application to
china–hong kong entrep
ˆ
ot trade. American Economic
Review, 89(2):338–343.
Ferrantino, M. J., Liu, X., and Wang, Z. (2012). Evasion
behaviors of exporters and importers: Evidence from
the us–china trade data discrepancy. Journal of inter-
national Economics, 86(1):141–157.
Ghasemi, M., Golalipour, K., Zare, M., and Mirjalili, S.
(2024). Flood algorithm (fla): an efficient inspired
meta-heuristic for engineering optimization. The
Journal of Supercomputing.
Goldberg, D. (1989). Genetic algorithms in search. Opti-
mization, and Machine Learning, Addison Wesley.
Hammoudeh, S., Sari, R., and Ewing, B. T. (2009). Re-
lationships among strategic commodities and with fi-
nancial variables: A new look. Contemporary Eco-
nomic Policy, 27(2):251–264.
Hansen, W. L. and Prusa, T. J. (1997). The economics and
politics of trade policy: An empirical analysis of itc
decision making. Review of Int. Economics, 5(2):230–
245.
Harding, R. and Harding, J. (2020). Strategic Trade as a
Means to Global Influence, chapter 6, pages 143–172.
John Wiley & Sons, Ltd.
Hosseini, E., Al-Ghaili, A., and Kadir, D. (2024). Meta-
heuristics and deep learning for energy applications:
Review and open research challenges (2018–2023).
Energy Strategy Reviews.
Khargharia, H., Shakya, S., and Ruta, D. (2023). Compar-
ative analysis of metaheuristics techniques for trade
data harmonization. In Proceedings of the 15th Inter-
national Joint Conference on Computational Intelli-
gence - Volume 1: ECTA, pages 206–213. INSTICC,
SciTePress.
Kirkpatrick, S., Gelatt Jr, C. D., and Vecchi, M. P.
(1983). Optimization by simulated annealing. science,
220(4598):671–680.
Lewrick, U., Mohler, L., and Weder, R. (2018). Produc-
tivity growth from an international trade perspective.
Review of International Economics, 26(2):339–356.
Mahmoodi, A., Hashemi, L., and Mahmoodi, A. (2024).
Novel comparative methodology of hybrid support
vector machine with meta-heuristic algorithms to de-
velop an integrated candlestick technical analysis
model. Journal of Capital Markets Studies.
Priyadarshi, R. (2024). Energy-efficient routing in wire-
less sensor networks: a meta-heuristic and artificial
intelligence-based approach: a comprehensive review.
Archives of Computational Methods in Engineering.
Shakya, S. and McCall, J. (2007). Optimization by esti-
mation of distribution with deum framework based on
markov random fields. International Journal of Au-
tomation and Computing, 4:262–272.
Shakya, S., Poon, K., AlShanqiti, K., Ouali, A., and
Sleptchenko, A. (2021). Investigating binary eas for
passive in-building distributed antenna systems. In
2021 IEEE Congress on Evolutionary Computation
(CEC), pages 2101–2108. IEEE.
Torres-Esp
´
ın, A. and Ferguson, A. R. (2022).
Harmonization-information trade-offs for sharing
individual participant data in biomedicine.
Yahia, H. and Mohammed, A. (2023). Path planning op-
timization in unmanned aerial vehicles using meta-
heuristic algorithms: A systematic review. Environ-
mental Monitoring and Assessment.
Trade Data Harmonization: A Multi-Objective Optimization Approach for Subcategory Alignment and Volume Optimization
345