An Approach for Fractional Commensurate Order Youla

Parametrization Using q-weighted Operator

Hanna Aboukheir

, Juan Romero

and Antonio Di Teodoro

Colegio de Ciencias e Ingenier

ıas, Universidad San Francisco de Quito, Quito, Ecuador

Keywords:

Fractional Order Control Systems, q-weighted Operator, Youla Parametrization.

Abstract:

The Youla-Kucera parametrization is a strategy widely used for robust control design and system identiﬁcation

of integer systems, but with the increasing interest in fractional order controllers, a new window for research

and development is widely open. In this work this parametrization is extended to fractional commensurate

order systems using the q-weighted operator; originally developed for the ﬁeld of theoretical physics, is pro-

posed as a tool for developing robust fractional order controllers, the proposal is evaluated in two simulated

processes and implemented in the TCLAB process.

1 INTRODUCTION

In industrial environments, controllers are essential

for meeting performance criteria like stabilization,

sensitivity, and robustness. Meeting all these re-

quirements simultaneously is challenging, leading to

the development of polynomial techniques for the

parametrization of controllers that stabilize a given

plant (Ku

cera, 2007). The parametrization proposed

by (Youla et al., 1976) has been widely utilized across

various applications, including closed-loop identiﬁ-

cation and adaptive control as found in(Anderson,

1998; Forssell and Ljung, 1999). Recently, Youla

parametrization has been used in applications such as

plug&play control and multi model adaptive control

among others, (Mahtout et al., 2020).

In the other hand, with the increasing interest in

industrial applications for fractional order controllers

as shown in (Tepljakov et al., 2021) one main chal-

lenge is the implementation of such controllers, this

is when the Youla Parametrization could serve as an

useful answer to implement such controllers in the in-

dustrial ﬁeld aided by the use of the q-weighted oper-

ator (paper developed by the third author of the cur-

rent article), originally developed to obtain a set of

fractional Einstein ﬁeld equations within 2+1 dimen-

sional spacetime, in the area of control systems this

operator aids in the design of stabilizing controllers

https://orcid.org/0000-0002-8214-511X

https://orcid.org/0000-0001-9558-6398

https://orcid.org/0000-0002-8766-0356

in fractional order independently and no limited to

ﬁrst order plus time delay (FOPDT) processes as the

methods shown in (Di Teodoro et al., 2022) and (Ran-

ganayakulu et al., 2016); in other words, allows the

design of different types of controllers including frac-

tional PID controllers for systems with models differ-

ent than the FOPDT.

In this ﬁrst approach in the use of the q-weighted

operator and Youla Parametrization this paper is

structured as follows: Section 2 presents a brief intro-

duction to Fractional Calculus in which fundamentals

of the q-weighted operator are presented, its relation

with the Youla Parameter and the basis for controller

design are presented in Section 3, followed by a set

of applications using the toolbox FOMCON (Tepl-

jakov and Tepljakov, 2017) in Section 4 including a

real time implementation in TCLAB from apmonitor

2 BRIEF INTRODUCTION TO

FRACTIONAL CALCULUS

Deﬁnition 2.1. The Riemann–Liouville fractional in-

tegral of order η > 0 is given by (see (Kilbas et al.,

2006; Podlubny, 1994; Kilbas et al., 1993))





(x) =

Γ(η)

h(t)

(x −t)

1−η

dt, x > a. (2.1)

We denote by I

) the class of functions h, repre-

sented by the fractional integral (2.1) of a summable

function, that is h = I

ϕ, where ϕ ∈ L

(a,b). A de-

scription of this class of functions was provided in

706

Aboukheir, H., Romero, J. and Di Teodoro, A.

An Approach for Fractional Commensurate Order Youla Parametrization using q-weighted Operator.

DOI: 10.5220/0013058700003822

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 21st International Conference on Informatics in Control, Automation and Robotics (ICINCO 2024) - Volume 1, pages 706-713

ISBN: 978-989-758-717-7; ISSN: 2184-2809

(Kilbas et al., 2006; Kilbas et al., 1993; Stein and

Shakarchi, 2009).

Theorem 2.2. A function h ∈ I

),η > 0, if and

only if its fractional integral I

s−η

h ∈ AC

([a,b]),

where s = [η] + 1 and (I

s−η

(k)

(a) = 0, for k =

0,..., s − 1.

In Theorem 2.2, AC

([a,b]) denotes the class of func-

tions h, which are continuously differentiable on the

segment [a,b], up to order s − 1 and h

(s−1)

is abso-

lutely continuous on [a,b]. By removing the last con-

dition in Theorem 2.2, we obtain a class of functions

that admit a summable fractional derivative. (See

(Kilbas et al., 2006; Kilbas et al., 1993))

Deﬁnition 2.3 (see (Kilbas et al., 1993)). A func-

tion h ∈ L

(a,b) has a summable fractional deriva-

tive





(x) if



s−η



(x) ∈ AC

([a,b]), where

s = [η] + 1.

Deﬁnition 2.4. Let





(x) denote the fractional

Riemann–Liouville derivative of order η > 0 (see

(Kilbas et al., 2006; Podlubny, 1994; Kilbas et al.,

1993))





(x) =





Γ(s − η)

h(t)

(x −t)

η−s+1







s−η



(x), (2.2)

where s = [η] + 1,x > a [η] denotes the integer part

of η and Γ is the gamma function. When 0 < η < 1 ,

then (2.2) takes the form





(x) =



1−η



(x). (2.3)

Note that, when η → 1, we recover the typical

derivative operator (Kilbas et al., 2006; Podlubny,

1994; Kilbas et al., 1993; Ceballos et al., 2020).

The semigroup property for the composition of frac-

tional derivatives does not hold generally (see (Pod-

lubny, 1994, Sect. 2.3.6)). In fact, the property:





= D

η+γ

h, (2.4)

holds if

( j)

) = 0, j = 0,1,..., s − 1, (2.5)

and h ∈ AC

s−1

([a,b]), h

(s)

∈ L

(a,b) and s = [γ] + 1.

Thus, we can write this result in the following:

Lemma 2.5. Consider h ∈ AC

s−1

([a,b]) and h

(s)

∈

(a,b) then,





h = D





h, (2.6)

holds whenever

( j)

) = 0, j = 0,1,..., s − 1, (2.7)

where s = [γ] + 1.

Proof. This proof can be found in (Podlubny, 1994,

Secton 2.3.6).

Remark 2.6. It is worth noticing that the Riemann-

Liouville derivative of a constant is not zero. How-

ever, in the limit process, it behaves as expected.

lim

η→1





(x) = lim

η→1

(x − a)

−η

Γ(1 − η)

= 0. (2.8)

Example. Consider α ∈ (0, 1), a

> 0 and for m ∈ N

(See (Kilbas et al., 2006; Kilbas et al., 1993; Ceballos

et al., 2022)).

(t − a)

(m+1)α−1

= (t − a)

mα−1

(t − a)

α−1

= 0 ifα < 1 and x > 0.

There are other types of derivatives, such as the Ca-

puto derivative (where the derivative of a constant

is zero), the Caputo-Fabrizio derivative, the Hilfer

derivative, among others. However, for this proposal,

we will use a modiﬁcation of the Riemann operator

that recently has applications in physics, speciﬁcally

in developing solutions for Fractional Einstein ﬁeld

equations. This is our primary motivation: starting

from an operator that has applications in physics and

exploring how it can contribute to control theory.

Now we will introduce the weighted fractional op-

erator, the central piece of all our subsequent develop-

ment.

Deﬁnition 2.7. Consider q

(x,η) a continuous func-

tion, q

(x,η) a continuously differentiable function

on x and let



)



(x) =





(x) de-

note the q-weighted fractional Riemann-Liouville

derivative of order η > 0. For q

∈ AC

(R)





(x) = q

(x,η)





(x,η)



s−η



(x),

(2.9)

where s = [η] + 1, x > a and [η] denotes the integer

part of η.

Remark 2.8. To recover the Riemann-Liouville

operator deﬁned in 2.2, it is sufﬁcient to take

lim

η→1

(x,η) = lim

η→1

(x,η) = 1, and to obtain the

classical derivative, it is enough to take α → 1.

An Approach for Fractional Commensurate Order Youla Parametrization using q-weighted Operator

707

Example. Consider 0 < η < 1 and taking q

(x,η) =

(x − a)

η−1

so then (2.9) takes the form





(x) = q

(x,η)





(x − a)

η−1



1−η



(x).

(2.10)

As a consequence of the form of q

, we have that for

any q

, the derivative of a constant is zero





(x) = 0 (2.11)

As in the case of the Riemann-Liouville operator, It is

not difﬁcult to see that the operator is linear and the

semigroup property for the composition of fractional

derivatives is generally not satisﬁed. Nonetheless, we

can obtain similar relation

Based on the operator (2.9), and considering numeri-

cal implementations with much greater simplicity and

computational ease, we slightly modify the structure

of the operator, keeping the form, but now thinking of

it in terms of convolutions.





(x) =

(t,η) ∗

(x,η) ∗



1−η



(t)+

(t,η) ∗ q

(t,η) ∗





(t) (2.12)

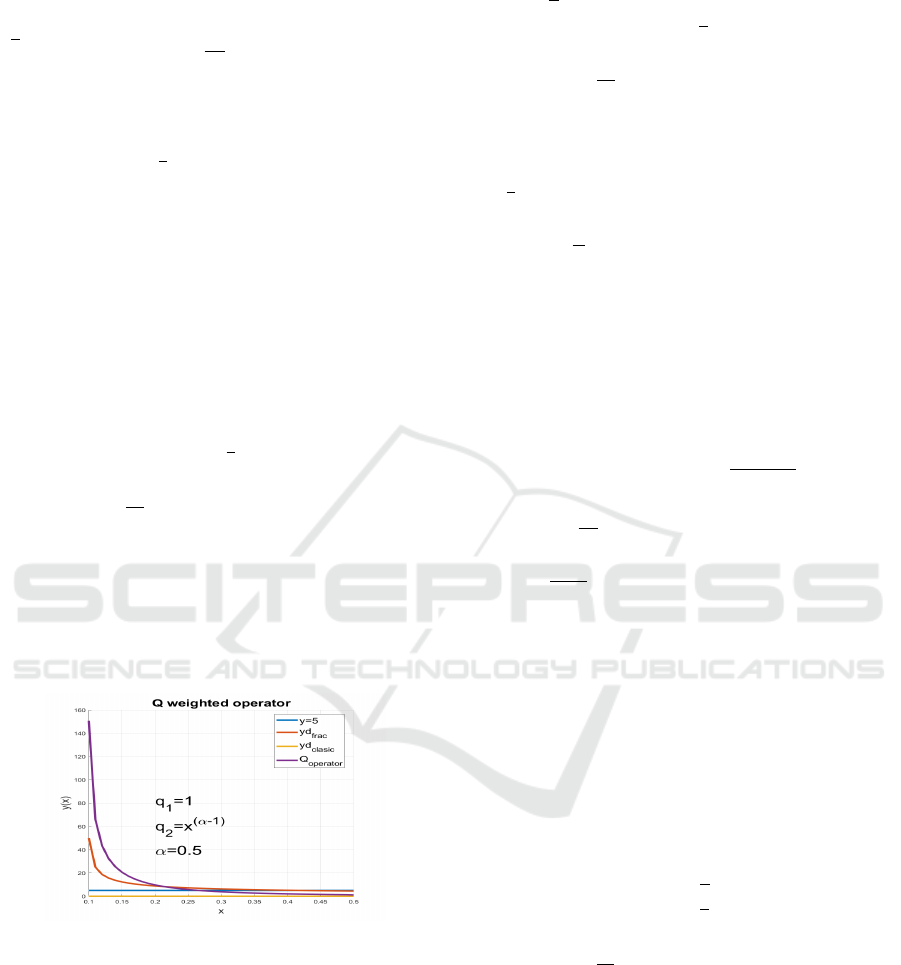
Example. Let’s consider in ﬁg:1 the case where α =

0.5 and the weights are deﬁned as q

= 1 and q

(x − a)

with a = 0 in the Q operator as deﬁned in

2.10. The weight q

is speciﬁcally chosen to cancel

the Q operator when the function f (t) is a constant.

Figure 1: Example Q operator.

2.0.1 Laplace Transform of Fractional-Order

Derivatives

Deﬁnition 2.9. Consider F(s) := (L f )(s) to rep-

resent the Laplace transform of certain function f ,

α ∈ (n − 1,n], and n ∈ N (See (Kilbas et al., 1993)).



L D



(s) = s

F(s) −

∑

k=1

k−1

α−k

f )(0)

It is clear that if α ∈ (0,1], then



L D



(s) = s

F(s) − (D

α−1

f )(0) (2.13)

By applying the Laplace transform to the following

modiﬁed q-weighted operator with 0 < η < 1.





(t) =

(t,η) ∗

(x,η) ∗



1−β



(t)+

(t,η) ∗ q

(t,η) ∗





(t) (2.14)

we obtain:





(s) = q

(s,η)q

(s,η)[s

+ s

]h(s) (2.15)

2.1 The q-weighted Gr

unwald-Letnikov

Derivative Version

The Gr

unwald-Letnikov derivative is deﬁned as (Pala-

cios et al., 2023):

Deﬁnition 2.10. Let η > 0, f ∈ C

[a,b], and a < x ≤

b. Then

f (x) = lim

N→∞

∆

f (x)

= lim

h→0

∞

∑

k=0

(−1)





f (x − kh), (2.16)

with h =

(x−a)

, N = 1,2,....

This deﬁnition involves a sum of values of the func-

tion f (x) at different points.

Remark 2.11. It is worth mentioning that the

unwald-Letnikov derivative can be seen as a dis-

crete approximation of the Riemann-Liouville deriva-

tive, and in the limit, as the step size goes to zero, the

unwald-Letnikov derivative becomes a continuous

fractional derivative.

Having the deﬁnition of the Gr

unwald-Letnikov,

we can deﬁne our version of the weighted operator,

which will be used for the numerical implementations

in this work.

The Gr

unwald-Letnikov q-weighted version





(t) =

(t,η) ∗

(x,η) ∗



1−η



(t)+

(t,η) ∗ q

(t,η) ∗





(t) (2.17)

Example. Let’s consider the case in ﬁg:2 where α =

0.5 and the weights are deﬁned as q

= (x − a)

and

= 1, with a = 0. The function f [t] = x

is cho-

sen to illustrate how the Qweighted operator func-

tions in a speciﬁc scenario. The analytical im-

plementation deﬁned in 2.10 is contrasted with the

unwald–Letnikov approximation deﬁned in 2.17,

revealing minor differences between the two ap-

proaches.

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

708

Figure 2: Example Q operator.

3 THE q-weighted OPERATOR

AND THE RELATION WITH

YOULA PARAMETRIZATION

In the previous section the generalized q-weighted op-

erator is presented, in this section, the operator is used

for fractional order control.

In order to further explain the proposed method,

it is necessary to keep in mind some necessary ba-

sic concepts that are formalized in the following para-

graphs.

Deﬁnition 3.1. A system P(s

) =

N(s

)

D(s

)

is said to be

proper if the degree of D(s

) is larger or equal than

the degree of N(s

)(Goodwin et al., 2001).

Deﬁnition 3.2. A system P(s

) is said to be com-

mensurate if the dynamics order of the fractional sys-

tem are equal; otherwise, is incommensurate (Tava-

zoei and Asemani, 2020).

Deﬁnition 3.3. A system is said to be BIBO stable

(bounded-input bounded-output) if every bounded in-

put excites a bounded output. This stability is deﬁned

for the zero-state response and is applicable only if

the system is initially relaxed (Chen, 1999).

Theorem 3.4. (Petr

s and Petr

s, 2011) A fractional

commensurate system P(s

) =

N(s

)

D(s

)

is said to be

stable if and only if considering a fractional opera-

tor α ∈ (0,2) then

| arg[eig(P(s

))] |> α

(3.1)

Deﬁnition 3.5. A fractional incommensurate sys-

tem G(s

) is said to be BIBO stable if and only if

α ∈ (0,2) satisfy the following inequality (Petr

s and

Petr

s, 2011):

| arg[eig(G(s

))] |< π



1 −



(3.2)

Two deﬁnitions for stability are presented in deﬁni-

tions 3.3,and 3.5 and one Theorem in 3.4 for con-

trol system purposes;with all this in mind, consider

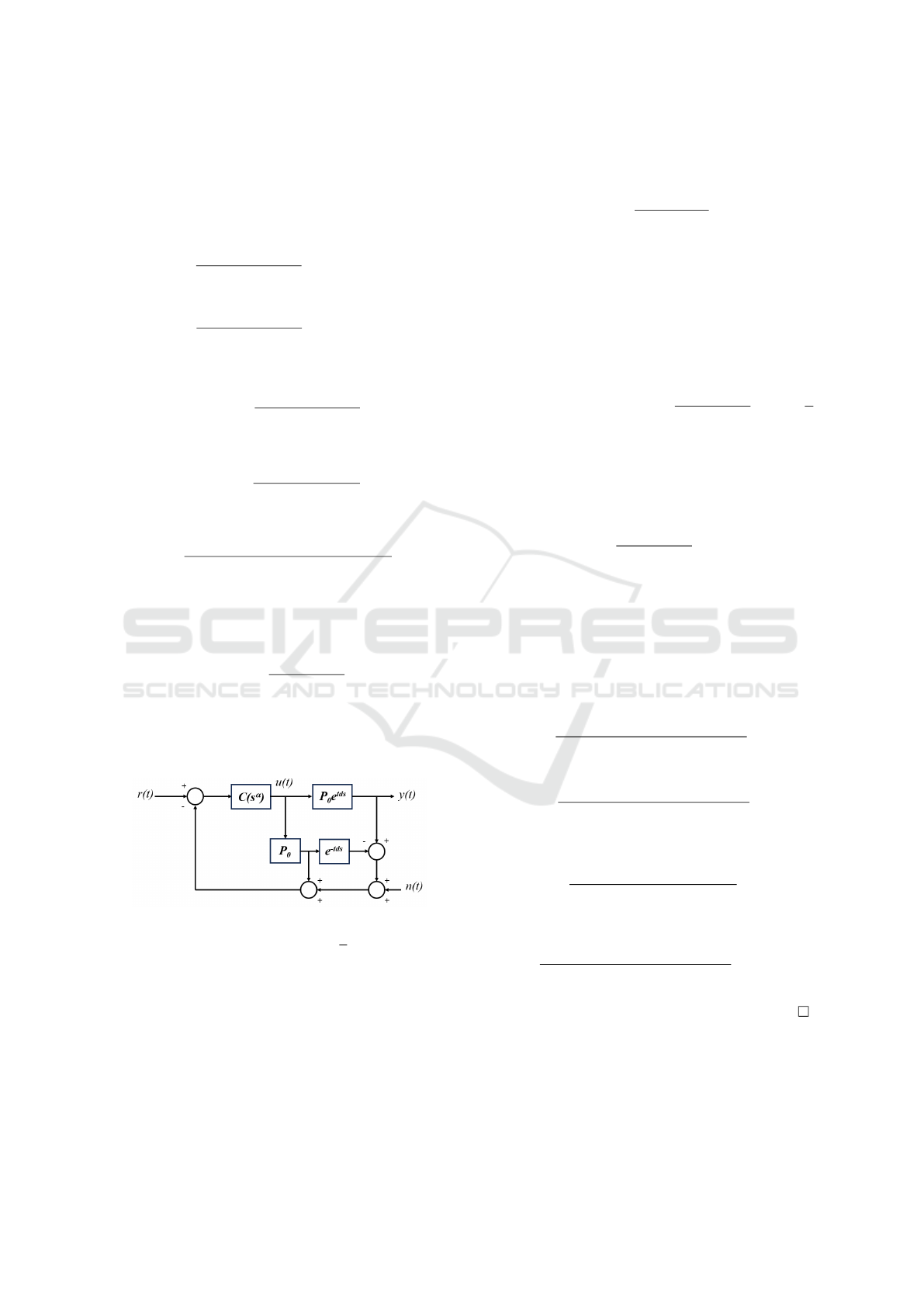
for instance the closed loop system shown in ﬁgure

3,where r(t),y(t), u(t) and n(t) are the reference sig-

nal, the output signal, control signal and the noise sig-

nal (white noise) respectively. P

is the real process

which for the moment is assumed stable in open loop

and C(s

) is the fractional controller to be estimated.

Figure 3: Closed loop linear fractional system with noise.

Following (Mahtout et al., 2020) The set of trans-

fer functions from n(s) and r(s) to y(s) are shown as

follows:

y(s) =

C(s

1 +C(s

r(s) −

C(s

1 +C(s

n(s), (3.3)

Now, the set of transfer functions from r(s),n(s) to

u(s) are estimated as follows:

u(s) =

C(s

)

1 +C(s

r(s) −

C(s

)

1 +C(s

n(s). (3.4)

Following (Keviczky and B

any

asz, 2007; Mahtout

et al., 2020) and adapting to this work it is clear that:

Q(s

) =

C(s

)

1 +C(s

(3.5)

Q(s

) in (3.5) is the Fractional Youla Parameter

(Aboukheir et al., 2006; Aboukheir, 2010; Keviczky

and B

any

asz, 2007; Mahtout et al., 2020).

Clearing for C(s

) in (3.5) it is possible to obtain

C(s

) =

Q(s

)

1 − Q(s

(3.6)

Replacing (3.6) in (3.3) following (Bars and Ke-

viczky, 2015) the closed loop is transformed into the

Internal Model Structure shown as follows

y(s) = P

Q(s

)[r(s) − n(s)] (3.7)

The Youla Parameter Q(s

) must be proper and stable

(Valderrama et al., 2020), and selected with commen-

surate order according to (Petr

s and Petr

s, 2011) by

the designer in order to guarantee the closed loop sta-

bility.

The control system presented in 3.7, is not the ideal

approach when P

is open loop unstable, or has a time

delay; which is the case to be analyzed as follows, ﬁrst

consider again the system presented in ﬁgure 3 with

An Approach for Fractional Commensurate Order Youla Parametrization using q-weighted Operator

709

= P

−tds

with P

a proper and stable open loop

model coupled with a time delay td, the closed loop

set of transfer functions from setpoint to output and

setpoint to control signal are shown as follows:

y(s) =

C(s

−tds

1 +C(s

−tds

[r(s) − n(s)] (3.8)

u(s) =

C(s

)

1 +C(s

−tds

[r(s) − n(s)] (3.9)

It is clear from (3.9) that Q(s

) is:

Q(s

) =

C(s

)

1 +C(s

−tds

(3.10)

Rearranging for C(s

) in (3.10) it is possible to ob-

tain:

C(s

) =

Q(s

)

1 − Q(s

−tds

(3.11)

It is possible to replace P

−tds

in (3.11) with:

C(s

) =

Q(s

)

1 − Q(s

)[P

−tds

− P

−tds

+ P

]

(3.12)

This modiﬁcation is the well known Smith Predictor

(Smith and Corripio, 2005) shown in Figure 4, which

leads to the following parametrization of controller

C(s

) =

Q(s

)

1 − Q(s

(3.13)

Which is similar to (3.6) with the difference that the

open loop model in (3.13) does not consider the full

dynamic of the plant as P

but only the stable open

loop part without delay P

Figure 4: Closed loop system with Smith Predictor.

In this paper it is proposed to use the q-weighted oper-

ator presented in (Contreras, ) as the Youla Parameter.

Using the laplace transform with zero initial condi-

tions presented in (2.15) and selecting f (s) = λe(s)

with e(s) the error signal between the output and the

reference and λ a parameter selected by the designer

it is possible to obtain:

Q(s

) = q

(s)q

(s)[s

+ s

]λe(s) (3.14)

This is formalized in deﬁnition 3.6.

Deﬁnition 3.6. The group of controllers C(s

) that

stabilize P

= P

and/or P

−tds

are parameterized by

C(s

) =

Q(s

α)

1 − Q(s

α)

(3.15)

with Q(s

α)

as presented in (3.14) must be proper,

commensurate order and stable.

Theorem 3.7. An open loop system represented with

the model P

= P

or P

−tds

is stabilized in closed

loop by C(s

) if it exist an operator with commensu-

rate order Q(s

) proper and stable that parameterize

C(s

) according to (3.6) and relocates the closed loop

poles of the system in such a way that:

| arg[eig(Q(s

))] |≡| arg



eig



C(s

1 +C(s



|> α

(3.16)

with α ∈ (0,2)

Proof. Consider an open loop system P

stable and

invertible and C(s

) the unknown controller to be es-

timated,the closed loop transfer function is:

y(s) =

C(s

)

1 + P

C(s

)

r(s) (3.17)

The parameter Q(s

) is selected with commensurate

order, proper and stable according Theorem 3.4 and

Deﬁnition 3.1 as follows:

Q(s

) = q

(s)q

(s)[s

+ s

]λ (3.18)

with q

(s) selected as (Bars and Keviczky, 2015):

λq

(s)[s

+ s

] = [P

]

−1

(3.19)

and q

(s) fulﬁlling Theorem 3.4 as:

(s) =

nα

+ a

(n−1)α

+ ... + a

+ 1

(3.20)

The proper and stable Q(s

) is represented as:

Q(s

) =

]

−1

nα

+ a

(n−1)α

+ ... + a

+ 1

(3.21)

using (3.6) or (3.13) it is possible to obtain the con-

troller C(s

C(s

) =

]

−1

nα

+ a

(n−1)α

+ ... + a

(3.22)

introducing the controller C(s

) in 3.17 it is possible

to obtain the controlled closed loop transfer function:

y(s) =

nα

+ a

(n−1)α

+ ... + a

+ 1

r(s) (3.23)

It is clear that the stabilized poles of the closed sys-

tems are the same as the poles of Q(s

)

Theorem 3.7 it is possible to extract the following

observation formalized in Lemma 3.8

Lemma 3.8. The value of α and β in (3.14) are re-

lated with the zeros of Q(s

) in order to fulﬁll theorem

3.7 it is necessary that α ≡ β.

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

710

4 APPLICATIONS

4.1 First Experiment

For the ﬁrst experiment is the mixing process, a hot

water stream F

(t) is manipulated to mix with a cold

water stream F

(t) to obtain an output ﬂow F

(t) at

the desired temperature T

(t). The temperature trans-

mitter is located at a distance L from the mixing tank

bottom. This highly nonlinear system has variable dy-

namic see (Aboukheir et al., 2021) for details.

For a given operating point, it is estimated the follow-

ing ﬁrst order plus dead time model (Aboukheir et al.,

2021):

(s) =

0.38

6.41s + 1

−25s

(4.1)

It is clear from (4.1) that a Smith Predictor is required

for the control calculations, using the scheme pre-

sented in ﬁgure 4, and taking into the account that

the system is ﬁlled up of uncertainties in gain, time

constant and time delay, it is necessary to build a con-

trollers that rejects disturbances while guaranteeing

setpoint tracking, using (3.13) the value of α = β =

0.5 and λ = 0.5 is selected with q

(s) and q

(s):

(s) = 0.5



6.41

0.5



0.5

= 6.41s + 1 (4.2)

(s) =

142.85s

1.1

+ 0.38

(4.3)

The proper and stable Q(s

) is presented for this sys-

tem according Deﬁnitions 3.1 and Theorem 3.4 as fol-

lows:

Q(s

) =

6.41s + 1

142.85s

1.1

+ 0.38

(4.4)

With this in mind, the controller C(s

) is:

C(s

) =

0.007(6.41s + 1)

1.1

(4.5)

The fractional controller obtained in (4.5) is com-

pared with a Fractional PI, tuned using Chen tuning

rules found in (Ranganayakulu et al., 2016), obtain-

ing the following controller:

FPID(s) = 0.9916 +

0.0615

1.1

(4.6)

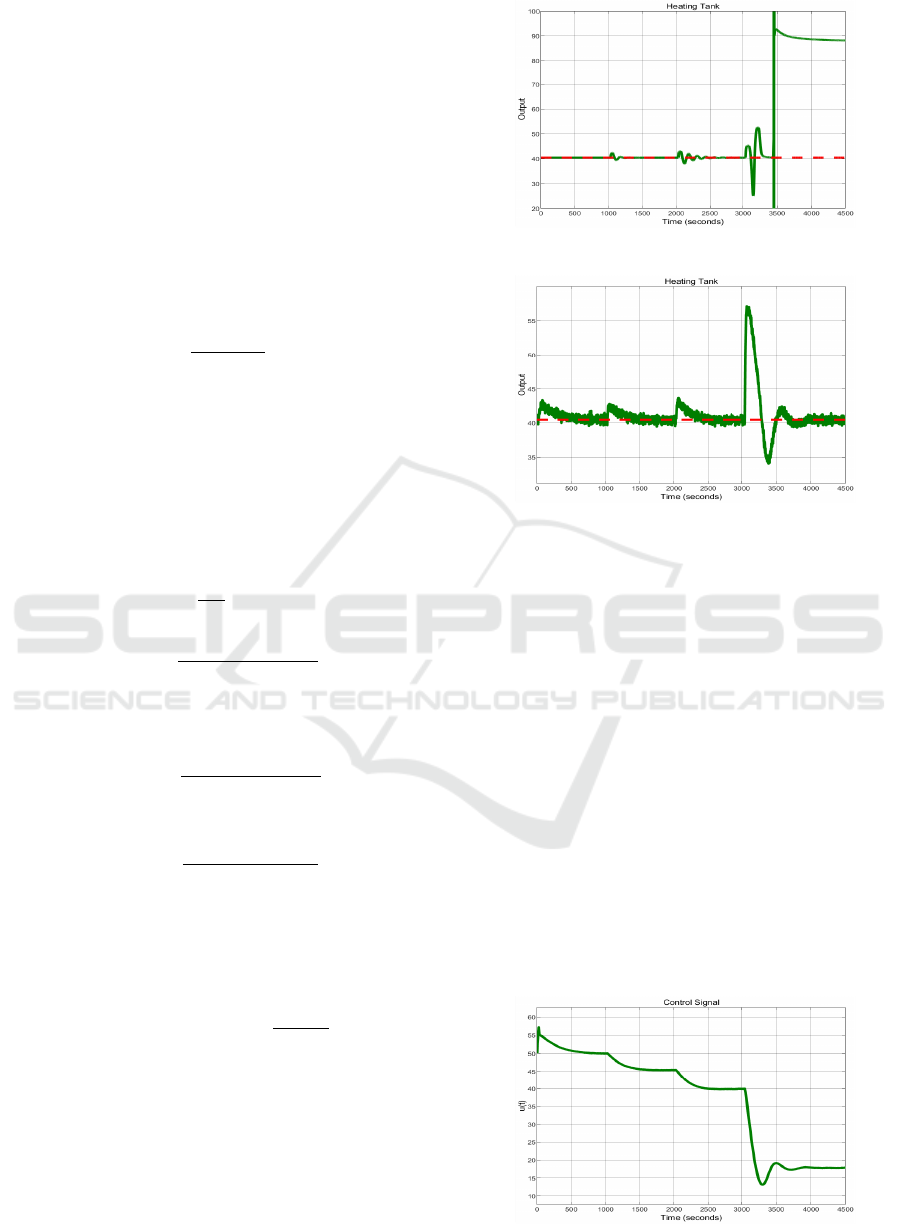
The output of the closed loop system with the FPID

is shown in ﬁgure 5, where it is possible to see that

the Fractional PID cannot handle the uncertainties of

the system, this result is similar than the Integer PID

found in (Aboukheir, 2023)

In ﬁgure 6 the controller C(s

) using the proposed

method is tested against the inherent uncertainties

of the system adding some large measurables distur-

bances and unmeasurable disturbances in the form of

Figure 5: Closed loop response of the system with FPID(s).

Figure 6: Closed loop response of the system with C(s

white noise. The output of the controller is shown in

ﬁgure 7

From ﬁgure 6 it is clear that the controller can han-

dle the large uncertainties and the variability in the

time delay, rejecting the measurables and unmeasur-

ables disturbances while keep the system following

the setpoints, but is in 7 when it is possible to observe

that the controller ﬁlters the noise, providing a ﬁltered

control signal, in the following experiment, the pro-

posed fractional controller is implemented in a real

system.

4.2 Second Experiment

The second experiment,is the temperature control lab

(TCLAB) from APMONITOR, this process is con-

nected with Matlab/Simulink where the proposed

controller is installed, ﬁgure 8 shows the connection

used for this test.

Figure 7: Output of the Fractional Controller C(s

An Approach for Fractional Commensurate Order Youla Parametrization using q-weighted Operator

711

Figure 8: Temperature control lab connected with simulink.

An estimated linear model is obtained for this nonlin-

ear system, which is presented as follows:

y(s) =

0.8265

165s + 1

−25s

u(s) (4.7)

This system has a delay so, a controller with smith

predictor is selected as the one presented in ﬁgure 4,

following the procedure shown in the previous exam-

ples, fulﬁlling deﬁnitions 3.1 and Theorem 3.4 Q(s

)

and C(s

) are respectively:

Q(s

) =

(165s + 1)

285.71s

1.1

+ 0.8265

(4.8)

C(s

) = 0.0035

(165s + 1)

1.1

(4.9)

Figure 9: Closed loop system with C(s

) (red) Setpoint

(blue) Implemented closed loop system.

Figure 10: Output of the fractional controller C(s

From ﬁgures 9 and 10 it is clear that the frac-

tional controller C(s

) must deal with uncertainties,

measurable and unmeasurables disturbances, the ro-

bustness of the proposed controller minimize the ef-

fects of these elements while provides setpoint track-

ing throughout the whole operating region. From

these experimnents it is clear that it is possible to

parametrize controllers using Youla Parametrization

through the use of the q-weighted operator.

5 CONCLUSIONS

In this paper a methodology for Youla parametrization

of fractional commensurate order controllers is pre-

sented; ﬁrst a model of the process is required, with

this model and the speciﬁed performance criteria the

Youla parameter is built Q(s

) using the q-weighted

operator, this parametrization allows to design a ro-

bust loop controller that deals with noise, measurable

disturbances and uncertainties while provides setpoint

tracking as shown in the previously presented exper-

iments, in future works the proposal is going to be

extended to incommensurate systems.

ACKNOWLEDGEMENTS

This work was supported by Universidad San Fran-

cisco de Quito USFQ (Ecuador), through the Cole-

gio de Ciencias e Ingenier

ıa and Decanato de Investi-

gaci

on.

REFERENCES

Aboukheir, H. (2010). Closed loop identiﬁcation using tak-

agi sugeno models. IEEE Latin America Transactions,

8(3):199–204.

Aboukheir, H. (2023). Data driven sliding mode con-

trol: A model-free approach. In 2023 IEEE Seventh

Ecuador Technical Chapters Meeting (ECTM), pages

1–6. IEEE.

Aboukheir, H., Herrera, M., Iglesias, E., and Camacho, O.

(2021). Dynamic sliding mode control based on fuzzy

systems for nonlinear processes. In 2021 IEEE Fifth

Ecuador Technical Chapters Meeting (ETCM), pages

1–6. IEEE.

Aboukheir, H., Rojas, K., Villa, G., and Romero, P. (2006).

Closed loop identiﬁcation with youla parameteriza-

tion and neural nets. In 2006 American Control Con-

ference, pages 6–pp. IEEE.

Anderson, B. D. (1998). From youla–kucera to identiﬁ-

cation, adaptive and nonlinear control. Automatica,

34(12):1485–1506.

Bars, R. and Keviczky, L. (2015). Introducing new

control paradigms in basic control education youla

parametrization.

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

712

Ceballos, J., Coloma, N., Di Teodoro, A., and Ochoa-

Tocachi, D. (2020). Generalized fractional cauchy–

riemann operator associated with the fractional

cauchy–riemann operator. Advances in Applied Clif-

ford Algebras, 30(5):1–22.

Ceballos, J., Coloma, N., Di Teodoro, A., Ochoa-Tocachi,

D., and Ponce, F. (2022). Fractional multicomplex

polynomials. Complex Analysis and Operator Theory,

16(4):1–30.

Chen, C.-T. (1999). Linear system theory and design. Ox-

ford University Press.

Contreras, E Di Teodoro, A. M. M. Fractional einstein ﬁeld

equations in 2+1 dimensional spacetime. preprint to

be published.

Di Teodoro, A., Ochoa-Tocachi, D., Aboukheir, H., and

Camacho, O. (2022). Sliding-mode controller based

on fractional order calculus for chemical processes.

In 2022 IEEE International Conference on Automa-

tion/XXV Congress of the Chilean Association of Au-

tomatic Control (ICA-ACCA), pages 1–6. IEEE.

Forssell, U. and Ljung, L. (1999). Closed-loop identiﬁca-

tion revisited. Automatica, 35(7):1215–1241.

Goodwin, G. C., Graebe, S. F., Salgado, M. E., et al. (2001).

Control system design, volume 240. Prentice Hall Up-

per Saddle River.

Keviczky, L. and B

any

asz, C. (2007). Future of the

smith predictor based regulators comparing to youla

parametrization. In 2007 Mediterranean Conference

on Control & Automation, pages 1–5. IEEE.

Kilbas, A. A., Marichev, O., and Samko, S. (1993). Frac-

tional integrals and derivatives (theory and applica-

tions).

Kilbas, A. A., Srivastava, H. M., and Trujillo, J. J.

(2006). Theory and applications of fractional differ-

ential equations, volume 204. elsevier.

cera, V. (2007). Polynomial control: past, present, and

future. International Journal of Robust and Nonlinear

Control: IFAC-Afﬁliated Journal, 17(8):682–705.

Mahtout, I., Navas, F., Milan

es, V., and Nashashibi, F.

(2020). Advances in youla-kucera parametrization: A

review. Annual Reviews in Control, 49:81–94.

Palacios, J., Teodoro, A. D., Fuenmayor, E., and Contreras,

E. (2023). A fractional matter sector for general rela-

tivity. The European Physical Journal C, 83(10):894.

Petr

s, I. and Petr

s, I. (2011). Stability of fractional-order

systems. Fractional-Order Nonlinear Systems: Mod-

eling, Analysis and Simulation, pages 55–101.

Podlubny, I. (1994). Fractional-order systems and

fractional-order controllers. Institute of Experimen-

tal Physics, Slovak Academy of Sciences, Kosice,

12(3):1–18.

Ranganayakulu, R., Babu, G. U. B., Rao, A. S., and Patle,

D. S. (2016). A comparative study of fractional or-

der piλ/piλdµ tuning rules for stable ﬁrst order plus

time delay processes. Resource-Efﬁcient Technolo-

gies, 2:S136–S152.

Smith, C. A. and Corripio, A. B. (2005). Principles and

practices of automatic process control. John wiley &

sons.

Stein, E. M. and Shakarchi, R. (2009). Real analysis: mea-

sure theory, integration, and Hilbert spaces. Princeton

University Press.

Tavazoei, M. and Asemani, M. H. (2020). On robust stabil-

ity of incommensurate fractional-order systems. Com-

munications in Nonlinear Science and Numerical Sim-

ulation, 90:105344.

Tepljakov, A., Alagoz, B. B., Yeroglu, C., Gonzalez, E. A.,

Hosseinnia, S. H., Petlenkov, E., Ates, A., and Cech,

M. (2021). Towards industrialization of fopid con-

trollers: A survey on milestones of fractional-order

control and pathways for future developments. IEEE

Access, 9:21016–21042.

Tepljakov, A. and Tepljakov, A. (2017). Fom-

con: fractional-order modeling and control toolbox.

Fractional-order modeling and control of dynamic

systems, pages 107–129.

Valderrama, F., Ruiz, F., Vicino, A., and Garulli, A. (2020).

A youla-kucera parametrization for data-driven con-

trollers tuning. IFAC-PapersOnLine, 53(2):3989–

3994.

Youla, D., Bongiorno, J., and Jabr, H. (1976). Modern

wiener–hopf design of optimal controllers part i: The

single-input-output case. IEEE Transactions on Auto-

matic Control, 21(1):3–13.

An Approach for Fractional Commensurate Order Youla Parametrization using q-weighted Operator

713