Third Order Super Twisting Based Robust Tracking of 2-DOF
Helicopter with State Estimation
Ratiba Fellag
a
and Mahmoud Belhocine
b
Industrial Automation and Robotics Division,
Centre de Développement des Technologies Avancées (CDTA), Algiers, Algeria
Keywords: 2-DOF Helicopter, Continuous Control Signal, Sliding Mode Control, State Observer, Robustness.
Abstract: This study proposes a third-order super-twisting sliding mode control algorithm combined with a Luenberger
state observer for robust trajectory tracking of a two-degree-of-freedom (2-DOF) experimental helicopter.
Validated on the inherently unstable and nonlinear Quanser Aero 2 platform, the method offers finite-time
convergence and continuous control signals while estimating unmeasured states. The controller demonstrates
accurate angular position tracking despite cross-coupling, limited measurements, uncertainties, and
disturbances, effectively reducing the chattering phenomenon typically seen in conventional sliding mode
control. Experimental results confirm the approach's efficacy and robustness in trajectory tracking the 2-DOF
helicopter system.
1 INTRODUCTION
Unmanned Aerial Vehicles (UAVs), particularly
helicopter-based systems, have experienced
remarkable growth in recent years due to their
adaptability and diverse applications. Helicopter-type
UAVs offer unique capabilities like hovering and
precise maneuvring in confined spaces. Nevertheless,
controlling helicopter dynamics presents significant
challenges due to the inherent nonlinearities and
coupled motions, necessitating advanced control
strategies to optimize their performance and exploit
their full potential in various operational scenarios
(Zuo et al., 2022).
Sliding mode control (SMC) is a widely used
technique for managing disturbance-affected
systems. It offers theoretical exact disturbance
compensation by maintaining zero-valued sliding
variables (Edwards & Spurgeon, 1998; Utkin, 2013).
This is achieved through infinite-frequency
switching. However, practical SMC implementation
encounters a phenomenon known as chattering,
characterized by high-frequency discontinuous
oscillations, which presents a significant challenge in
real-world applications (Levant, 1993).
a
https://orcid.org/0000-0002-2905-3988
b
https://orcid.org/0000-0003-3495-7444
This limitation necessitates further investigation
into chattering mitigation strategies while preserving
SMC's robust disturbance rejection capabilities.
Higher Order Sliding Mode Control (HOSMC) has
emerged as an effective strategy to eliminate
chattering. HOSMC extends the principle of driving
the sliding variable to zero to its higher-order
derivatives. For second-order systems with a relative
degree of two, representing most mechanical and
electrical systems, the second-order Super-Twisting
Algorithm (STA) has emerged, producing continuous
control signals and avoiding chattering (Levant,
2007). Kamal et al. (Kamal & Chalanga, 2014)
further generalized the STA for arbitrary relative
degree systems, preserving its key characteristics
while offering finite-time stabilization of both system
output and its derivatives. Furthermore, it generates a
continuous control signal, thereby reducing the
chattering problem (Fellag et al., 2021). This
approach simultaneously compensates for
disturbances and uncertainties, requiring only the
knowledge of the system’s output and its first
derivative.
In this study, we improve the control of systems
with only partial state information by adding a state
observer to the third-order super-twisting algorithm
480
Fellag, R. and Belhocine, M.
Third Order Super Twisting Based Robust Tracking of 2-DOF Helicopter with State Estimation.
DOI: 10.5220/0013059700003822
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 21st International Conference on Informatics in Control, Automation and Robotics (ICINCO 2024) - Volume 1, pages 480-485
ISBN: 978-989-758-717-7; ISSN: 2184-2809
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.

(3-STA) based controller. The integration of a state
observer addresses the practical challenge of
incomplete state measurements, providing accurate
estimates of the unmeasured states required for the
implementation of SMC. Additionally, the state
observer filters out noise and disturbances in the
measurements, resulting in cleaner state estimates and
improved control robustness (Luenberger, 1966).
This approach not only reduces the dependency on
physical sensors, thereby lowering system costs and
complexity, but also extends the applicability of SMC
to a wider range of systems (Chalanga et al., 2016).
The primary objective of this study is to analyze
and experimentally validate the combined 3-STA
controller with state estimation to stabilize the
Quanser Aero2 two degrees-of-freedom (2-DOF)
helicopter system under nonlinearities, cross-
coupling, uncertainties, and disturbances and enable
precise trajectory tracking.
2 SYSTEM DESCRIPTION AND
MODELING
The Aero 2 helicopter system, shown in Figure 1,
made by Quanser, consists of a base with an arm
supporting two thrusters powered by DC motors. It
includes high-resolution encoders, an IMU for precise
control of pitch and yaw, and a data acquisition
system (Quanser, 2022b). When voltage is applied to
the pitch motor, the front rotor generates a force
perpendicular to the body, causing torque around the
yaw-axis due to aerodynamic drag. Similarly, the rear
motor affects the body away from the yaw axis,
mimicking the action of a tail rotor in conventional
helicopters.
In order to obtain the dynamic model, Newton's
second law is used for each of the helicopter axes.
Friction, air resistance, and centrifugal forces are
ignored to create a simplified model. This simplified
model will require a robust controller to compensate
for uncertainties and disturbances.
() () () ()
() () ()
ppspp
yyy
JttDtK t
JtDt t
θθ θτ
ψψτ

++ =
+=




 
 
(1)
with:
() () ()
() () ()
ppptppyty
yyptpyyty
KDV KDV
tKDV
ttt
ttKDV
τ
τ




=+
=

+
(2)
All the parameters of the dynamic model (1) and
(2) are explicitly described in Table 1.
Figure 1: Quanser Aero2 helicopter system (Quanser,
2022a).
All the parameters of the dynamic model (1) and
(2) are explicitly described in Table 1.
By choosing a state vector as:
[]
() () () () ()
T
T
xt tttt θψθψ =


;
() () ()
T
T
py
tVtVt u =


the state space representation of the helicopter system
is given by:
13
24
313 1 2
43 1 2
11
22
sp p t pp t py
pp p p
ytyptyy
yy y
xx
xx
KDDK DK
xxxuu
JJ J J
DDK DK
xx u u
JJ J
yx
yx
=
=
=− − + +
=− + +
=
=

















(3)
Table 1: Quanser Aero2 helicopter parameters (Fellag &
Belhocine, 2024a).
Symbol Description Value
J
p
Pitch axis inertia 0.0232 Kg.m
2
J
y Yaw axis inertia 0.0238 Kg.m
2
D
p Pitch axis damping 0.0020 N.m/
V
D
y Yaw axis damping 0.0019 N.m/
V
K
s
p Pitch axis stiffness 0.0074
N
.m/
V
K
pp Pitch thrus
t
gain from fron
t
roto
r
0.0032 N/
V
K
py Pitch thrus
t
gain from rea
r
roto
r
0.0014 N/
V
K
yy Yaw thrus
t
gain from rea
r
roto
r
0.0061 N/
V
K
yp Yaw thrus
t
gain from fron
t
roto
r
-0.0032 N/
V
D
t Distance
b
tw pivo
t
& roto
r
cente
r
0.1674 m
3 CONTROLLER AND STATE
OBSERVER DESIGN
This section details the design of the combined 3-
STA based controller and the state observer. The
control objective is to produce torques that enable
precise regulation of pitch and yaw angles towards
specified setpoints with minimal deviations.
Third Order Super Twisting Based Robust Tracking of 2-DOF Helicopter with State Estimation
481

3.1 State Observer Design
The full-order observer is responsible for estimating
all system states, and comparing them with the
physical model by analysing the error using a gain
matrix (L) that multiplies the difference between the
states and their estimates (Radisavljevic-Gajic,
2015). This matrix is then integrated into the
theoretical model and adjusted until the error
approaches zero.
Using (3), we rewrite the system state space
representation as:
x
Ax Bu
yCxDu
=+
=+

(4)
With:
and
After checking the observability of our state space
model (4), we design the full-order observer as
follows (Fellag & Belhocine, 2024a):
() () ()
()
()
00
ˆ
ˆ
,
,
.
ˆ
ˆ
()
ˆ
ˆ
x
tAxtBut
xt x
yt Cx t
=+
=
=

(5)
With
0
ˆ
x
and t
0
initial conditions for the observer.
The estimation error
ˆ
() () ()et xt xt=−
is used to
construct the observation system:
()
() ()
ˆ
() () ( () ())
() ,
ˆˆ
ˆ
x
tAxtButLytyt
Ax t Bu t LCe t
=++ −
=+ +

(6)
where matrix L represents the observer gain matrix.
From (3) and (6), we obtain the dynamics of the error
as:
() ( ) ()
,et A LCet=−

(7)
3.2 3-STA Controller Design
Considering the desired state vector
[00]
TT
ddd
x θψ =
and initial states of the system
are null.
Let
e
θ
and
e
ψ
be pitch and yaw errors defined
using the estimated states and the desired states:
2
111
22
ˆ
()
(
ˆ
ˆˆ
)
d
d
e
e
t
x
t
x
x
x
ψ
θ




−
=−

=
(8)
Then, their derivatives are defined by:
333
444
ˆ
ˆˆ
ˆ
d
d
e
exx
x
x
θ
ψ




=

−
=−


(9)
The objective is to bring these errors to zero using
the 3-STA controller and the state observer.
Theorem:
For any system presented in general form:
2
12
(,)
zz
zufzt
=
=+


(10)
The proposed 3-STA approach builds upon the
second-order super-twisting algorithm, as presented
in the work of Kamal et al. (Kamal & Chalanga,
2014) .
1
2
1
3
||sign()
sign( )
uk P
Pk d
φφ
φ

=− +


=− +



(11)
Where:
and
1
k
,
2
k
, and
3
k
are positive gains suitably
designed, stabilizing the perturbed system in finite
time.
d is the perturbation satisfying
d ≤Δ
■
The detailed Lyapunov stability proof of the
controller is provided in (Kamal & Chalanga, 2014).
3.2.1 Pitch Control
Assuming decoupled system, and using (3), (8), (9),
and (11), the closed-loop system for pitch regulation
using the 3-STA approach and state estimation is
obtained as:
2
1
15
3
3
1
1
5
33
ˆ
ˆˆ
||sign() (,)
sign( )
xx
x
kxfxx
xk
θθ θ θ
θθθ
φφ
φζ






=
=− + +
=−

+



(12)
00
00
//
//
1000 00
and
0100 00
tpp p tpy p
typ y tyy y
B
DK J DK J
DK J DK J
CD
=
==





 
 
 
(
)
2
3
221 1
||sign()kz zz φ =+
001 0
000 1
/0 / 0
000 /
sp p p p
yy
A
KJ DJ
DJ
=
−
−





ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
482

with: and
If gains
1
k
θ
,
2
k
θ
and
3
k
θ
are chosen carefully and
disturbance
θθ
ζ ≤Δ
, then the controller in (12)
stabilizes the pitch subsystem in finite time.
3.2.2 Yaw Control
Following the same methodology to design the 3-
STA controller for the yaw axis, using (3), (8), (9),
and (11) the closed-loop system for yaw regulation
using the proposed approach is given by:
1
24
46
2
1
63
ˆ
||sign()
sign( )x
xx
xk x
k
ψψ ψ
ψψψ
φφ
φζ
=
=− +


=−



+





(13)
Where:
and
The proposed controller in (13) stabilizes the yaw
subsystem in finite time if the disturbance
ψ
ζ
is
bounded and gains
1
k
ψ
,
2
k
ψ
, and
3
k
ψ
are carefully
designed.
The two controllers in (12) and (13), though
designed for decoupled subsystems, will be
implemented on the real, cross-coupled system to
evaluate the robustness against cross-coupling.
4 EXPERIMENTAL RESULTS
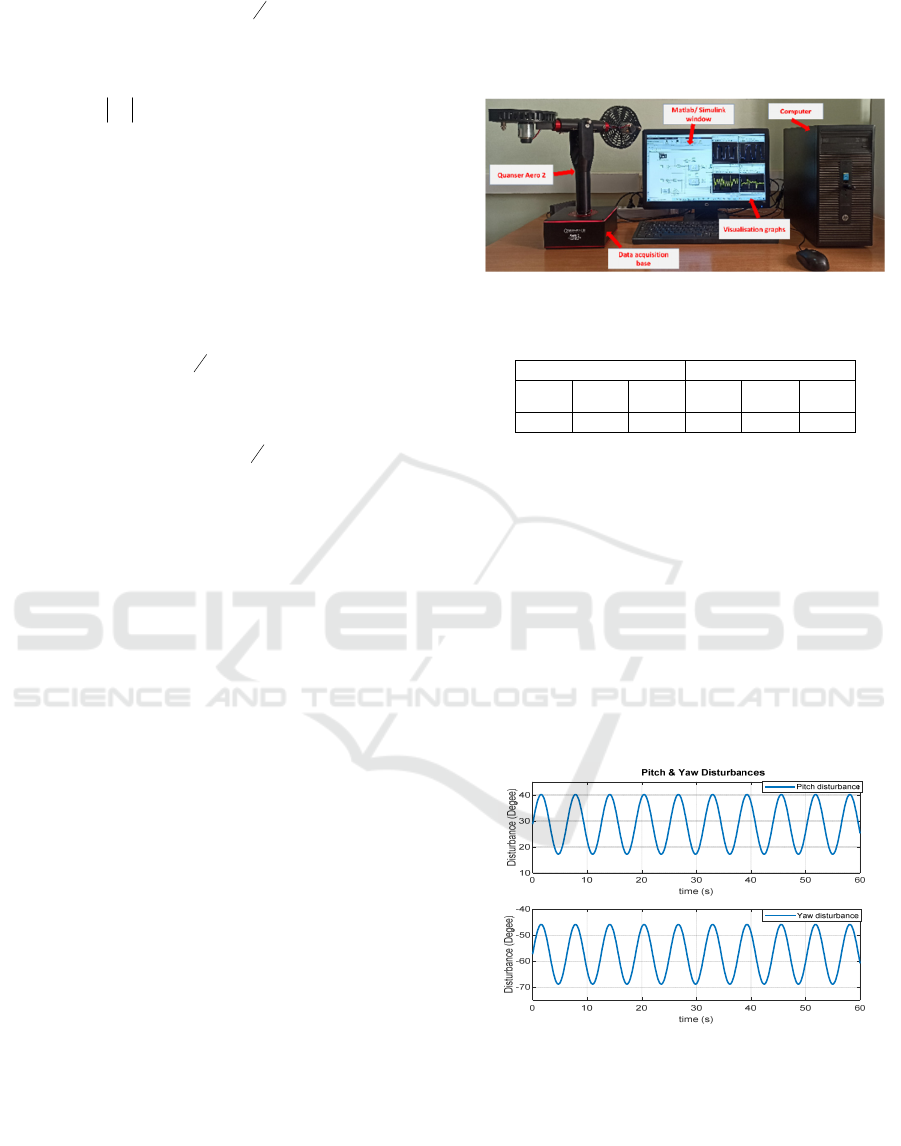
To evaluate the proposed approach, we implemented
the designed controllers using the experimental setup
illustrated in Figure 2. The Quanser Aero 2 platform
is equipped with a real-time control system (Fellag &
Belhocine, 2024b; Quanser, 2022b), namely the
QUARC Real-Time Control Software, a proprietary
solution from Quanser that is integrated within
Simulink from MathWorks Inc.
Initial conditions for the observer x
0
= 0 and
the system are considered null. Square input waves
are used as reference signals for pitch and yaw axes.
Model parameters of the Quanser Aero 2 are given in
Table 1. Some of these parameters are obtained
through identification, and others from the user
manual (Quanser, 2022b). The gains of the controllers
and the observer are adjusted through multiple
experiments and are given in Table 2. Two non-
vanishing disturbance signals are introduced to assess
the robustness of the controllers (Figure 3).
Moreover, the system is subject to uncertainties and
cross-coupling.
Figure 2: Experimental setup.
Table 2: Controllers gains.
Pitch controlle
r
Yaw controlle
r
1
k
θ
2
k
θ 3
k
θ
1
k
ψ
2
k
ψ 3
k
ψ
2 12 1 2 10 1
0.2 sin(t)+0.5
0.2 sin(t)-1
d
d
θ
ψ
=



=


(14)
The experimental results for the trajectory
tracking of the pitch and yaw axes are illustrated in
Figure 4 and Figure 5 respectively. The first plot
shows the pitch and yaw angles over time, with the
reference signals indicated by the solid lines and the
system responses by the dashed lines. The second plot
depicts the pitch and yaw velocities over time. The
final plot shows the evolution of the third states of the
closed-loop system over time.
Figure 3: Pitch and yaw disturbances.
(
)
2
3
221 1
ˆˆ
||sign()
ˆ
eeke
θθθθ θ
φ =+
153
ˆˆ
(, )
x
Pfxx
θθ
=+
(
)
22
2
3
11
ˆˆ
||sign()
ˆ
eeke
θψψψ ψ
φ =+
624
ˆˆ
(, )
x
Pfxx
ψψ
=+
Third Order Super Twisting Based Robust Tracking of 2-DOF Helicopter with State Estimation
483

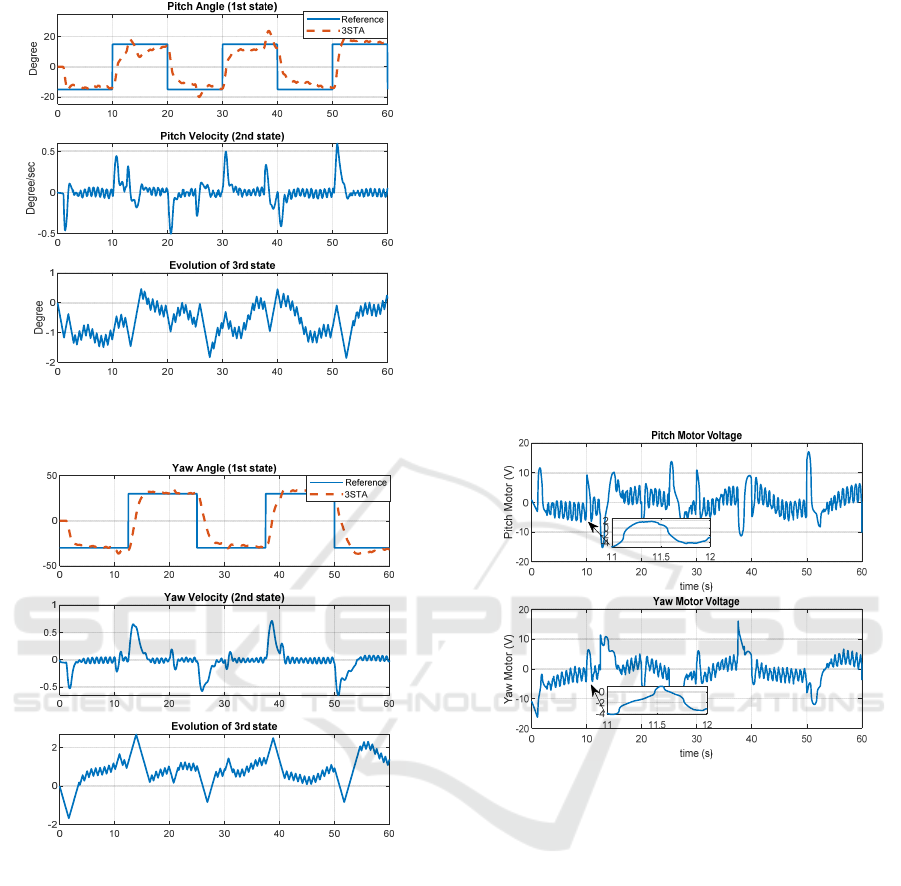
Figure 4: Pitch trajectory tracking using 3-STA and state
observer.
Figure 5: Yaw trajectory tracking using 3-STA and state
observer.
From these figures, the 3-STA controllers combined
with state observers demonstrate good tracking
performance with minimal steady-state errors and
robustness against disturbances, with the actual
angles closely following the references for both axes.
The overshoots observed in the pitch axis are caused
by the yaw axis transitions, which are a direct result
of the cross-coupling between the pitch and yaw axes.
The pitch and yaw velocity graphs show some
oscillations that are relatively small in amplitude but
present throughout the experiment. This indicates that
the system is experiencing dynamic responses to
disturbances. Some spikes occur at step changes,
indicating rapid acceleration and deceleration.
Finally, the third state curves for both pitch and yaw
axes represent the added integral states (x
5
and x
6
) for
reconstructing and cancelling bounded disturbances.
These graphs exhibit oscillatory behavior with
varying amplitudes, indicating continuous adaptation
to system dynamics, external disturbances, and cross-
coupling effects.
Figure 6 illustrates the pitch and yaw applied
motor voltages generated by the 3-STA and state
estimation controllers. These signals respect the
physical saturation of the motors. Although some
oscillations are observed, indicating rapid
adjustments in pitch and yaw voltages, the control
signal is continuous as illustrated in the zoomed
sections between 11s and 12s. This is due to the
sinusoidal nature of applied disturbances to which the
system is responding to maintain robust trajectory
tracking.
Figure 6: Pitch and yaw motor voltages.
To analyse the performance of the observer
regarding pitch and yaw state estimations, Figures 7
and 8 compare measured versus estimated angular
positions and velocities for pitch and yaw axes,
respectively. The state observer effectively reflects
the dynamics of the 2-DOF helicopter as the
estimated values closely follow the measured ones.
Occasional deviations are noticed in pitch and yaw
angular position estimation (Figure 7), due to sensor
noise, applied disturbances, or rapid changes in pitch
and yaw positions. However, the state observer
demonstrates a quick response to changes in both
pitch and yaw, which is essential for real-time
applications. Figure 8, on the other hand, indicates
that the observer effectively captures the system’s
dynamics, with estimated pitch and yaw velocities
closely following the measured values.
Degree
Degree/sec
Degree
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
484

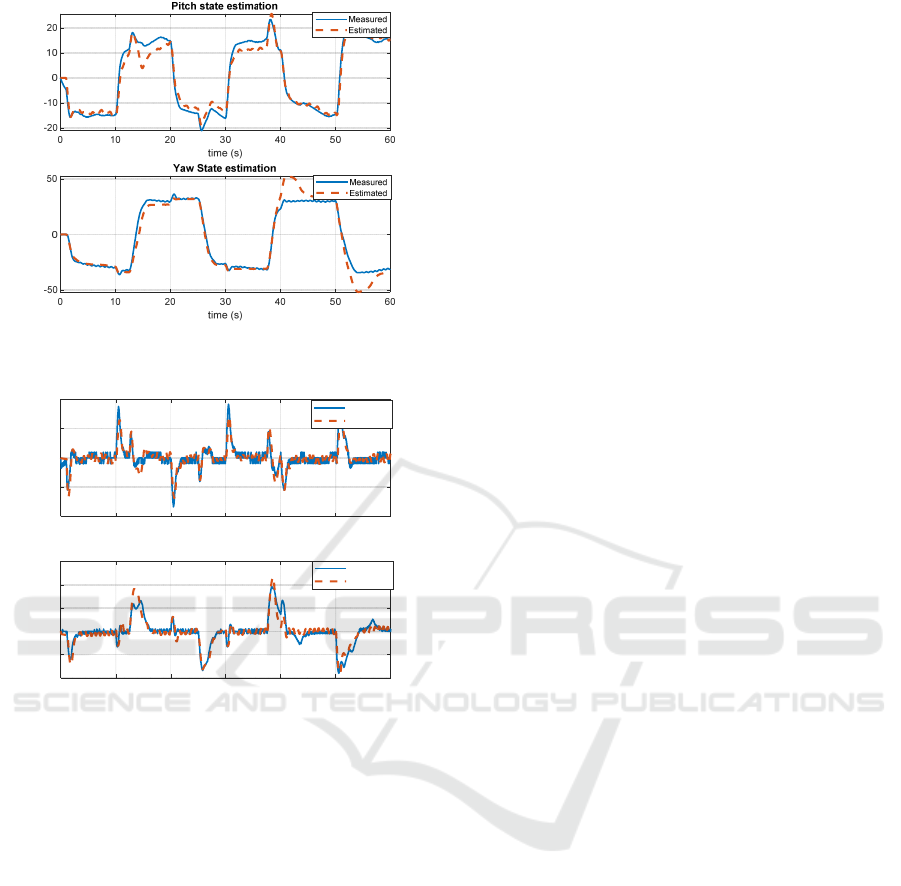
Figure 7: Pitch and yaw angular position estimation.
Figure 8: Pitch and yaw velocity estimation.
5 CONCLUSION
In this study, we investigated the analysis and
experimental validation of a 3-STA combined with a
state observer to achieve 2-DOF helicopter trajectory
tracking. The Quanser Aero 2 platform was used for
real-time hardware implementation of the proposed
approach. The obtained results demonstrate effective
and robust trajectory tracking under cross-coupling
and pitch and yaw axes continuous disturbances. The
3-STA controller relies on introducing a new state
that is the integral of a discontinuous term capable of
reconstructing the disturbances and cancelling them.
Moreover, incorporating a state observer addresses
the practical challenge of incomplete state
measurements, providing accurate estimates of the
unmeasured states. However, some oscillatory
behaviors were noticed, suggesting further fine-
tuning and the investigation of adaptive control
mechanisms to further enhance the performance of
the controller.
REFERENCES
Chalanga, A., Kamal, S., Fridman, L. M., Bandyopadhyay,
B., & Moreno, J. A. (2016). Implementation of super-
twisting control: Super-twisting and higher order
sliding-mode observer-based approaches. IEEE
Transactions on Industrial Electronics, 63(6), 3677-
3685.
Edwards, C., & Spurgeon, S. (1998). Sliding mode control:
theory and applications. Crc Press.
Fellag, R., & Belhocine, M. (2024a). 2-DOF Helicopter
Control Via State Feedback and Full/Reduced-Order
Observers. 2024 2nd International Conference on
Electrical Engineering and Automatic Control
(ICEEAC),
Fellag, R., & Belhocine, M. (2024b). Comparative analysis
of PID, fuzzy PID, and ANFIS controllers for 2-DOF
helicopter trajectory tracking: simulation and hardware
implementation. Archive of Mechanical Engineering,
vol. 71(No 3), 323-349. https://doi.org/10.24425/
ame.2024.151331
Fellag, R., Guiatni, M., Hamerlain, M., & Achour, N.
(2021). Robust continuous third-order finite time
sliding mode controllers for exoskeleton robot. Archive
of Mechanical Engineering, 68(4), 395-414.
Kamal, S., & Chalanga, A. (2014). Higher order super-
twisting algorithm. 2014 13th International Workshop
on Variable Structure Systems (VSS),
Levant, A. (1993). Sliding order and sliding accuracy in
sliding mode control. International journal of control,
58(6), 1247-1263.
Levant, A. (2007). Principles of 2-sliding mode design.
automatica, 43(4), 576-586.
Luenberger, D. (1966). Observers for multivariable
systems. IEEE Transactions on automatic control,
11(2), 190-197.
Quanser. (2022a). Aero 2 : Reconfigurable dual-rotor
aerospace experiment for controls education and
research. Retrieved 25/07/2024 from
Quanser. (2022b). Quanser Aero 2 laboratory guide.
Radisavljevic-Gajic, V. (2015). Full-and Reduced-Order
Linear Observer Implementations in Matlab\/Simulink
[Lecture Notes]. IEEE Control Systems Magazine,
35(5), 91-101.
Utkin, V. I. (2013). Sliding modes in control and
optimization. Springer Science & Business Media.
Zuo, Z., Liu, C., Han, Q.-L., & Song, J. (2022). Unmanned
aerial vehicles: Control methods and future challenges.
IEEE/CAA Journal of Automatica Sinica, 9(4), 601-
614.
Angle (Degee)Angle (Degee)
0 102030405060
time (s)
-40
-20
0
20
40
Degree/s
Pitch velocity Estimation
Measured
Estimated
0 102030405060
time (s)
-40
-20
0
20
40
60
Degree/s
Yaw velocity estimation
Measured
Estimated
Third Order Super Twisting Based Robust Tracking of 2-DOF Helicopter with State Estimation
485