LLM-Generated Class Descriptions
for Semantically Meaningful Image Classification
Simone Bertolotto
1,2 a
, Andr
´
e Panisson
2 b
and Alan Perotti
2 c
1
University of Turin, Italy
2
Centai Institute, Turin, Italy
Keywords:
Computer Vision, Image Classification, Neural Symbolic Integration, Large Language Models.
Abstract:
Neural networks have become the primary approach for tackling computer vision tasks, but their lack of trans-
parency and interpretability remains a challenge. Integrating neural networks with symbolic knowledge bases,
which could provide valuable context for visual concepts, is not yet common in the machine learning com-
munity. In image classification, class labels are often treated as independent, orthogonal concepts, resulting
in equal penalization of misclassifications regardless of the semantic similarity between the true and predicted
labels. Previous studies have attempted to address this by using ontologies to establish relationships among
classes, but such data structures are generally not available. In this paper, we use a large language model
(LLM) to generate textual descriptions for each class label, aiming to capture the visual characteristics of the
corresponding concepts. These descriptions are then encoded into embedding vectors, which are used as the
ground truth for training the image classification model. By employing a cosine distance-based loss func-
tion, our approach considers the semantic similarity between class labels, encouraging the model to learn a
more hierarchically structured internal feature representation. We evaluate our method on multiple datasets
and compare its performance with existing techniques, focusing on classification accuracy, mistake severity,
and the emergence of a hierarchical structure in the learned concept representations. The results suggest that
semantic embedding representations extracted from LLMs have the potential to enhance the performance of
image classification models and lead to more semantically meaningful misclassifications. A key advantage of
our method, compared to those that leverage explicit hierarchical information, is its broad applicability to a
wide range of datasets without requiring the presence of pre-defined hierarchical structures.
1 INTRODUCTION
Neural networks (NNs) have significantly trans-
formed the field of computer vision (CV), estab-
lishing themselves as the primary approach in tasks
such as image classification, object detection, and
more (Khan et al., 2018). Despite their widespread
success, these models often suffer from a lack of
transparency and interpretability, making it difficult
to understand their internal decision-making pro-
cesses (Buhrmester et al., 2021). This opacity poses
a significant barrier to deploying these models in sev-
eral real-world application domains.
To address these challenges, there is a growing
interest in integrating NNs with symbolic knowl-
edge (Kroshchanka et al., 2021). This integration
a
https://orcid.org/0009-0007-1960-1665
b
https://orcid.org/0000-0002-3336-0374
c
https://orcid.org/0000-0002-1690-6865
aims to enhance the contextual understanding and in-
terpretability of visual concepts, providing a more ro-
bust framework for Machine Learning (ML) models.
However, most current CV approaches still treat class
labels as unrelated entities, ignoring the semantic re-
lationships between them. Consequently, the orthog-
onal nature of the output labels does not match the
visual similarities between input images.
This approach leads to homogeneous penalization
of misclassifications, regardless of the semantic simi-
larity between the predicted and true labels.
This paper proposes a novel approach to enhance
the semantic interpretability of neural network deci-
sions in image classification tasks. We utilize a large
language model to generate textual descriptions for
each class label, capturing the inherent visual charac-
teristics of each category. These descriptions are then
transformed into embedding vectors, which serve as
the ground truth in training our models. Our goal is
50
Bertolotto, S., Panisson, A. and Perotti, A.
LLM-Generated Class Descriptions for Semantically Meaningful Image Classification.
DOI: 10.5220/0013060800003886
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 1st International Conference on Explainable AI for Neural and Symbolic Methods (EXPLAINS 2024), pages 50-61
ISBN: 978-989-758-720-7
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.

to allow the visual similarities between input images
to flow through the ML model, enabling a more struc-
tured learning of concepts, and more human-like re-
sulting classification models.
Our experiments are conducted using three dis-
tinct datasets: CIFAR-100 (Krizhevsky and Hinton,
2009), tieredImageNet (Ren et al., 2018), and iNatu-
ralist19 (Van Horn et al., 2018). For CIFAR-100, we
train our network from scratch, whereas for tieredIm-
ageNet and iNaturalist19, we fine-tune a pre-trained
EfficientNet (Tan and Le, 2019). We assess our mod-
els using several metrics, including the error rate, the
severity of misclassifications (in terms of semantic
distance), and the structure of feature space projec-
tions (through clustering metrics).
The results show that our approach not only re-
duces the error rate but also ensures that misclassifi-
cations are more semantically meaningful.
Furthermore, unlike previous similar approaches
that rely on existing explicit taxonomies/ontologies to
define a structure amongst class labels, our approach
is free from such constraints and can be applied to any
CV image classification task.
This paper is organized as follows: Section 2 pro-
vides a review of the background and related work,
exploring existing methods for neural-symbolic inte-
gration in CV, as well as highlighting their limita-
tions. Section 3 describes our methodology for en-
coding class labels using textual descriptions gener-
ated by a large language model, which are then used
to drive image classification tasks. Section 4 outlines
our experimental framework, detailing the setup, exe-
cution, and analysis of the results. Finally, Section 5
concludes the paper with a summary of our findings
and a discussion of directions for future work.
2 RELATED WORK
Neural networks have proven to be effective in solv-
ing complex image classification tasks. Convolu-
tional Neural Networks (CNNs) are the most widely
used type of neural network for image classifica-
tion (Krizhevsky et al., 2012; Simonyan and Zisser-
man, 2014; He et al., 2016). CNNs consist of mul-
tiple layers of convolutional and pooling operations
that extract features from the input image. The ex-
tracted features are then fed into fully connected lay-
ers, which output the final classification probabilities.
The image classification training process commonly
involves one-hot encoding of class labels, where each
class is represented by a binary vector with a sin-
gle non-zero entry corresponding to the class index.
While simple and effective, one-hot encoding fails to
capture the semantic relationships between classes.
The problem of hierarchical classification was ini-
tially explored in the literature (Silla and Freitas,
2011), and other research works showed how lever-
aging richer semantic information about labels can
benefit model interpretability (Dong et al., 2017), im-
age summarization (Pasini et al., 2022), and classifi-
cation itself (Bertinetto et al., 2020). However, this
approach was never incorporated into standard train-
ing pipelines. This problem can be decomposed into
two sub-components: (i) obtaining the relationships
amongst classes, and (ii) injecting this information
into the learning process.
2.1 Semantic Information
Representations
In some cases, class labels belong to an explicit,
structured knowledge representation. For instance,
CV models are often pre-trained on ImageNet (Rus-
sakovsky et al., 2014), and each Imagenet label is a
node in the WordNet (Miller, 1995) ontology. Word-
net defines relationships between words through var-
ious semantic relations, such as A is-a B and C
part-of D. Also in the benchmark dataset CIFAR-
100 (Krizhevsky and Hinton, 2009), the labels are or-
ganised in a shallow taxonomy. In a few other cases,
such as iNaturalist (Van Horn et al., 2018), classes
belong to domain-specific ontologies. However, typ-
ically, there is no predefined structure that enables
the straightforward determination of pairwise seman-
tic distance between labels.
When labels lack inherent structure, their seman-
tic information can be inferred from pre-trained lan-
guage models, represented as word embeddings (In-
citti et al., 2023). These vector representations cap-
ture semantic relationships in a continuous space,
based on raw labels or detailed descriptions from var-
ious sources. Models like CLIP (Radford et al., 2021)
have demonstrated the effectiveness of using natural
language supervision to learn visual representations,
further emphasizing the benefits of integrating seman-
tic information into image classification models.
2.2 Semantic Information Injection
In the context of image classification, an encoding
refers to a function that maps a class label, typi-
cally a word or short phrase, into a real-valued vec-
tor that can be used as ground-truth in the training
phase. The aforementioned one-hot encoding is a fa-
miliar example, although quite simplistic. The en-
coding process is crucial as it not only significantly
impacts the model’s performance and interpretability
LLM-Generated Class Descriptions for Semantically Meaningful Image Classification
51

but also allows for the representation of relationships
among class labels. Hierarchical label encodings are
designed to represent relationships inherent in a tree
structure, ensuring that similar labels have similar
encodings. Various approaches are used to achieve
this, including solving systems of equations (Barz and
Denzler, 2019), applying normalization functions to
the rows of similarity matrices, and concatenating en-
codings from different hierarchy levels (Redmon and
Farhadi, 2016). Barz and Denzler (Barz and Denzler,
2019) calculate encodings by recursively solving sys-
tems of linear equations to ensure that the dot product
of two encodings equals their similarity in the hier-
archy tree. Bertinetto et al. (Bertinetto et al., 2020)
propose an encoding that applies a row-wise softmax
function to a negative rescaling of the lowest com-
mon ancestor (LCA) heights, effectively capturing the
hierarchical relationships between classes. Perotti et
al. (Perotti et al., 2023) use a similar approach but
start from the LCA similarities matrix, clip at zeros,
normalize row-wise, and add a weighted one-hot en-
coding.
Word embeddings (Frome et al., 2013; Mikolov
et al., 2013a; Mikolov et al., 2013b) can be used as
target encoding in the context of image classifica-
tion. By using the latent representations of words,
word embeddings can capture semantic similarities
between classes without requiring an explicit hier-
archy. However, word embeddings have limitations
when dealing with out-of-vocabulary words or homo-
graphs.
Custom loss functions account for label rela-
tionships, steering the model towards hierarchi-
cally structured representations. Examples include
context-sensitive losses for nearest-neighbor classi-
fiers (Verma et al., 2012), regularization terms based
on hierarchy levels (Garg et al., 2022; Wu et al., 2016;
Bilal et al., 2018), disentangled features (Chang et al.,
2021), and factorizing probabilities along hierarchy
paths (Bertinetto et al., 2020; Chen et al., 2019a; Chen
et al., 2019c; Chen et al., 2019b).
3 LLM-GENERATED CLASS
DESCRIPTIONS
Description encodings overcome the limitations of
word embeddings by providing additional context
about each class in the form of a description. In this
paper, we propose our methodology, namely Large
Language Model (LLM) Generated Class Descrip-
tions (LGCD), to produce description encodings for
classification labels and use them to drive the learn-
ing process. LGCD can be summarized as follows:
1. Generate a description for each class label, either
manually, by scraping from the web, or using a
language model such as OpenAI’s GPT-3.5-turbo.
The descriptions should focus on the visual char-
acteristics of the class and be written in an ency-
clopedic style.
2. Embed the descriptions using a pre-trained sen-
tence embedding model, such as OpenAI’s text-
embedding-ada-002, to obtain a high-dimensional
vector representation for each class.
3. Apply a dimensionality reduction technique, such
as Principal Component Analysis (PCA), to
project the high-dimensional embeddings into a
lower-dimensional space of size D, resulting in
the final description encodings. The choice of D
is a hyperparameter that can be tuned based on the
dataset and model architecture.
4. Perform a supervised training task using the de-
scription encodings as ground truth and the Co-
sine Distance as loss function.
In our experiments, we also explored non-
linear dimensionality reduction methods such as
UMAP (Sainburg et al., 2021) and t-SNE (van der
Maaten and Hinton, 2008), but did not observe signif-
icant differences in performance compared to PCA.
Consequently, we decided to use PCA due to its sim-
plicity and computational efficiency. Alternatively,
one could consider using embedding models that pro-
duce lower-dimensional representations or employ
techniques like Matryoshka embeddings (Kusupati
et al., 2022) to reduce the embedding size.
Formally, the first three steps correspond to func-
tions: the writer mapping from the set of class labels
C to the set of descriptions W , the embedder taking
a description as input and returning a vector of R
˜
D
,
and the projector which projects the embedding to a
lower-dimensional space R
D
.
writer : C → W embedder : W → R
˜
D
projector : R
˜
D
→ R
D
So the encoder is simply the function composition
of these transformations:
encoder := projector◦ embedder◦ writer encoder : C → R
D
.
The text embeddings have
˜
D components, which
enable representing text as real vectors in a discrimi-
native way from a great variety of contexts. However,
we are using them as a way to represent descriptions
of classes and discard fine-grain information by us-
ing a dimensionality reduction algorithm (projector).
The size D of the encoding is also the output dimen-
sion of the model, so reducing from
˜
D to D lowers the
number of parameters in the last layer of the network,
enhancing its trainability.
EXPLAINS 2024 - 1st International Conference on Explainable AI for Neural and Symbolic Methods
52

3.1 Similar Approaches
Throughout the paper, we compare our approach
against standard one-hot encoding and other tech-
niques that produce encodings from hierarchical in-
formation: Table 1 collects all considered encoding-
loss combinations. In this Section, we highlight
the fundamental differences amongst these techniques
and LGCD.
Table 1: Methods for target encodings and their Encod-
ing/Loss combinations. XE stands for cross-entropy loss
and CD stands for cosine distance loss.
Name Encoding Loss Parameter Hierarchy?
XE One-hot One-hot XE None No
XE MBM Bertinetto et al. XE β Yes
XE B3P Perotti et al. XE α Yes
CD BD Barz & Denzler CD None Yes
CD LGCD (ours) Description CD D No
The first part of the naming convention in Table 1
uses the initial two letters to denote the loss (XE for
cross-entropy and CD for cosine distance) while the
second part indicates the encoding. The acronym
MBM refers to the paper by Bertinetto et al. (Bertinetto
et al., 2020), titled “Making Better Mistakes”. B3P
and BD are acronyms for the authors of the respective
papers: Perotti, Bertolotto, Pastor, Panisson (Perotti
et al., 2023), and Barz, Denzler (Barz and Denzler,
2019).
In BD (Barz and Denzler, 2019; Barz and Denzler,
2020) the authors compute encodings by requiring
that the cosine similarity of the produced encoding is
proportional to the class’s closeness in the hierarchy.
It is thus natural to employ the cosine distance as a
loss function. We also leverage the cosine distance as
loss function, but LGCD is not based on a hierarchy;
instead, it is derived from the textual description of
the class. Furthermore, LGCD allows to adapt the en-
coding size through the hyperparameter D, while BD
does not involve hyperparameters.
On the other hand, both MBM and B3P require the
tuning of a hyperparameter, and in both cases, it regu-
lates the ”amount of one-hot encoding” in these hier-
archical encodings. Both hyperparameters are defined
as ”β” in the respective papers; to avoid confusion, in
this paper, we use two different letters, selecting α for
B3P and β for MBM.
In MBM, β ranges from 0 to +∞, and we obtain
the one-hot encoding as β tends to +∞ (being the ar-
gument of an exponential function, for β > 30, en-
codings are practically indistinguishable from one-hot
encoding). In B3P α ∈ [0,1], and B3P is equivalent to
one-hot encoding for α = 1. The reason to introduce
a certain amount of one-hot encoding in a purely hier-
archical encoding is to be able to train the model for
classification tasks.
The only encodings that do not require a hierarchy
are the one-hot and LGCD, which can be applied to any
dataset. Its general applicability is the main strength
of description encodings compared to other methods
to inject semantic information leveraging pre-defined
hierarchies. For example, in figs. 1a and 1b we show
UMAP projections of BD encoding and LGCD encod-
ing respectively. Points are colored according to their
class at different levels of the hierarchy. For BD en-
coding, we expect a perfect sub-clusters structure due
to how those encodings are constructed. It’s not ob-
vious at all that the LGCD encodings structure should
resemble the one derived from hard-coded hierarchy.
Moreover, this kind of similarity seems to hold at var-
ious levels of the hierarchy.
As a final remark, we add that this kind of visual
inspection for hierarchical encoding and LGCD encod-
ing accordance is not applicable when the number of
classes increases. More classes translate to longer
encoding vectors and dimensionality reduction meth-
ods struggle to map higher-dimensional vectors to the
plane in a consistent way.
4 EXPERIMENTAL EVALUATION
In this section, we describe the experimental pipeline
we built in order to evaluate our approach, LGCD. We
remark that a distinctive feature of LGCD is that it re-
quires no explicit structured representation of labels;
however, for the sake of comparison with competing
methodologies that require such symbolic informa-
tion, we focus our experiments on datasets with ex-
plicit label hierarchies.
4.1 Datasets
To evaluate models trained with different encodings,
we use three datasets with an explicit underlying hier-
archical structure: CIFAR-100 (Krizhevsky and Hin-
ton, 2009), iNaturalist19 (Van Horn et al., 2018),
and tieredImageNet (Ren et al., 2018). As previ-
ous works about image classification on the same
datasets exploit their hierarchy to improve model per-
formance, we assume that their respective hierarchies
are a good proxy for visual distinctive characteristics.
This means that two classes which are similar from
the point of view of the hierarchy present similar vi-
sual characteristics, while elements of classes that are
distant on the hierarchy tree show different visual fea-
tures. While using description encoding, these ex-
LLM-Generated Class Descriptions for Semantically Meaningful Image Classification
53

Level 2 Level 3 Level 4
(a) BD encoding of CIFAR-100 labels.
Level 2 Level 3 Level 4
(b) LGCD encoding of CIFAR-100 labels.
Figure 1: UMAP projection of BD(a) and LGCD(b) encodings.
plicit hierarchies are not used, and this requirement
is not explicitly stated in the LLM prompt for the de-
scription generation.
CIFAR-100 is a common benchmarking dataset
for image classification tasks over 100 different
classes, which can be grouped into 20 superclasses
with 5 classes each, defining a 3-level hierarchy (ac-
counting for the root node in the hierarchy tree). We
employed the improved 6-level handcrafted hierarchy
proposed in (Garnot and Landrieu, 2020).
iNaturalist19 is a comprehensive dataset designed
for image classification tasks, focusing on the fine-
grained recognition of species within their natural
habitats. It encompasses a diverse array of 1,010 nat-
ural species classes. The dataset is structured accord-
ing to a biological taxonomy, presenting a hierarchi-
cal organization that spans 8 levels from broader cate-
gories such as kingdom and phylum down to specific
species.
Finally, tieredImageNet is a dataset tailored for hi-
erarchical image classification tasks derived from the
well-known ImageNet dataset (Russakovsky et al.,
2014), featuring 608 classes distributed across 13 hi-
erarchical levels. tieredImageNet labels belong to a
pruned version of WordNet (Miller, 1995), the hierar-
chy from which ImageNet was developed.
4.2 Class Descriptions, Label Encodings
For all class labels in CIFAR-100, iNaturalist19, and
tieredImageNet, we produced LGCD encodings as de-
scribed in Section 3. For the writer function, GPT-
3.5-turbo was prompted as follows ([class] is a
placeholder for the class name):
You are a helpful assistant that has to provide
the description of a [class].
- What a [class] is.
- What a [class] looks like (for example, color,
texture, shape, ...).
- In what context [class] is used or can be found.
Focus on the visual characteristics of a [class].
Write 7 short sentences to describe a [class] in
encyclopedic style.
The embedder step transformed each description
into a 1536-dimensional embedding for each class,
and the following PCA projected these vectors into
D-dimensional encodings. We tuned the hyperparam-
eter D independently in the three cases, and report the
selected values in Table 2. For CIFAR-100, we chose
D = 100 to ensure that the resulting model has the
same number of parameters as models trained with
other methods. For iNaturalist19 and tieredImageNet,
EXPLAINS 2024 - 1st International Conference on Explainable AI for Neural and Symbolic Methods
54

we experimented with D = 100, 200, 300, 400, 500,
seeking embeddings sufficiently large to discriminate
between classes while keeping the number of param-
eters in the last fully-connected layer low (≈ D × last
hidden layer dimension). We selected D = 300 which
yields the best results.
Table 2: Hyperparameters choice for various encodings.
The datasets names are shortened for compactness: C100
stands for CIFAR-100, iNat for iNaturalist19, and t-IMGN
for tieredImageNet.
Name Parameter C100 iNat t-IMGN
XE MBM β 5.0 15.0 15.0
XE B3P α 0.4 0.5 0.5
CD LGCD D 100 300 300
For the sake of comparison and benchmarking, we
produced competing encodings of the same labels, ac-
cording to relevant research works: MBM (Bertinetto
et al., 2020) (referred to as “Soft labels” in the paper),
B3P (Perotti et al., 2023) (referred to as “HT-AL*” in
the paper), and BD (Barz and Denzler, 2019). As for
the hyperparameter D of LGCD, we tuned B3P’s α and
MBM’s β: we report the final values in Table 2.
4.3 Models and Classification Tasks
We carried out three image classification tasks, one
for each dataset introduced above. In all cases, we re-
lied on the PyTorch implementation of EfficientNet-
B0 (Tan and Le, 2019) to build our models. For
CIFAR-100, we trained the NN from scratch, while
for iNaturalist19 and tieredImageNet, we used the
weights of a pretrained model on ImageNet1K. We
only changed the number of output neurons in the last
layer to match the number of classes in the case of
XE models and the dimension of the encoding for CD
models.
For each image classification task, we compute the
error rate and hierarchical distance metrics, detailed
below. Each training run was repeated five times with
different random seeds in order to compute the stan-
dard deviation values of the two selected metrics, and
plot error bars.
The Error rate accounts for the number of mis-
classifications (errors) when the model is evaluated on
the testing split. It is defined as the number of errors
divided by the number of samples in the test dataset.
It is equivalent to 1 − accuracy.
The Hierarchical distance of a Mistake (HDM) is
a metric introduced by Bertinetto et al. in (Bertinetto
et al., 2020). It quantifies the severity of misclassifica-
tions in a hierarchical classification context. Specifi-
cally, it measures the mean height of LCA between
the ground truth and the predicted class when the
model incorrectly predicts the class with the highest
likelihood. The HDM value of a test fold is the av-
erage HDM value of single misclassifications; we re-
mark that HDM does not depend on the number of
misclassifications.
Together, error rate and HDM can describe the
model performance in classification tasks by answer-
ing the question ”How many errors does the model
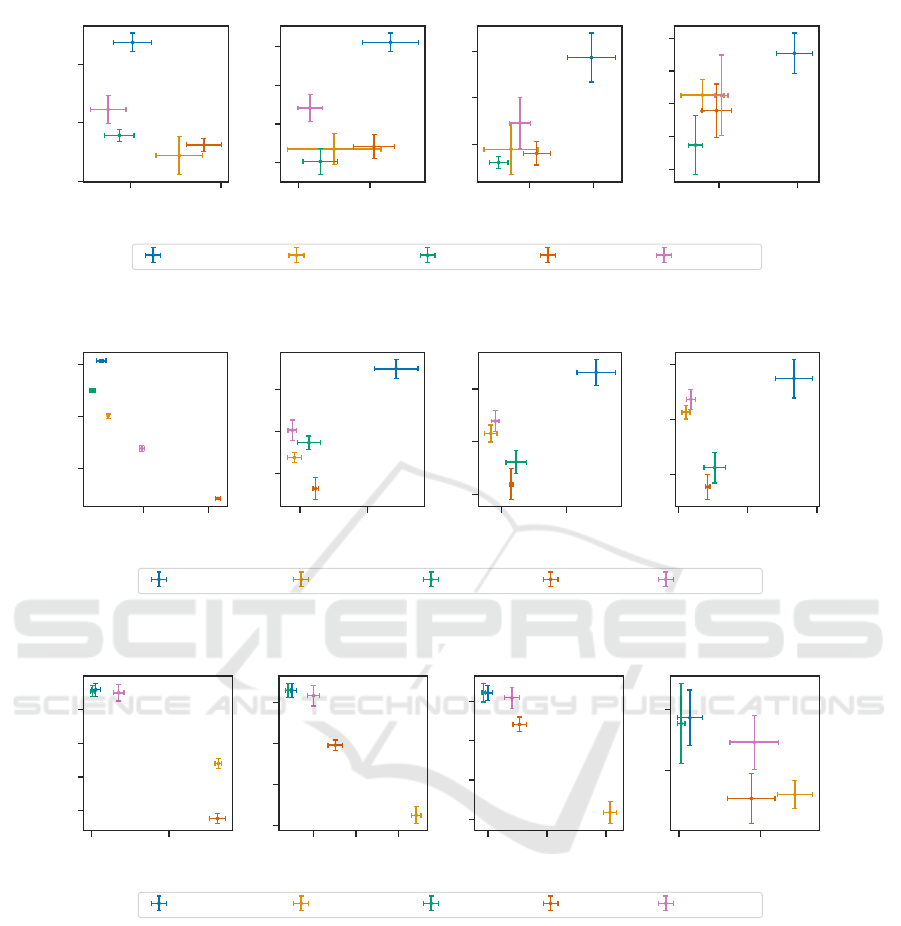
produce?” and ”How severe are those errors?”. Fig-
ures 2 to 4 depict these metric values in a scatter plot
with error rate on the x-axis and HDM on the y-axis.
In all panels, the best models lie in the lower-left
quadrant (less and milder errors) while on the oppo-
site spectrum, in the top-right corner, there are models
which produce many severe mistakes.
In all figures, the leftmost panel, titled Level 0,
corresponds to the fine-grained classification task.
When a class label hierarchy is available, as it is the
case in these experiments, the single class labels can
be progressively lumped together according to the hi-
erarchy. Two classes with LCA height equal to one
will belong to the same superclass at level 1: for in-
stance, if apple and orange (Level 0) share the com-
mon direct Level-1 ancestor fruit, all images labelled
as apple and orange at Level-0 are labelled fruit at
Level-1. We can therefore evaluate our two metrics
(error rate and HDM) at different levels of the labels’
hierarchy. Clearly, there is a relationship between er-
ror rate and HDM when considering labels at differ-
ent hierarchical levels: models which produce milder
mistakes at a lower level of the hierarchy (finer classi-
fication), will produce fewer errors when evaluating at
a higher level of the hierarchy (coarser classification).
As an example, a mild misclassification of an apple-
labelled image as orange will not be considered a mis-
classification at all at Level-1, where both the true and
predicted labels will correspond to fruit; conversely, a
(more-severe) apple/airplane misclassification would
still be a mistake at higher levels of the label hierar-
chy.
Figures 2,3 and 4 show that models trained with
one-hot encoding consistently produce more severe
errors across all granularity of classification. On the
other hand, methods that leverage an explicit hierar-
chy produce similar amounts of error, but less severe,
at the Level 0 and outperform one-hot when evaluated
at higher levels.
Models trained with CD LGCD are on par with hier-
archical methods and they seem to scale better than XE
B3P and CD BD when the number of classes increases,
i.e., Level 0 of iNaturalist19 and tieredImageNet. Ta-
bles with plot values and the metrics computed on
higher levels of the hierarchy are in Section 4.5.
LLM-Generated Class Descriptions for Semantically Meaningful Image Classification
55

0.28 0.30
Error rate
2.2
2.3
2.4
Level 0
0.17 0.18
Error rate
2.05
2.10
2.15
2.20
Level 1
0.11 0.12
Error rate
1.75
1.80
1.85
Level 2
0.05 0.06
Error rate
1.62
1.64
1.66
1.68
1.70
Hier. dist. mistake
Level 3
XE One-hot XE MBM XE B3P CD BD CD LGCD
Figure 2: CIFAR-100: Error rate vs Hierarchical distance of a Mistake.
0.4 0.5
Error rate
1.8
2.0
2.2
Level 0
0.11 0.12
Error rate
3.15
3.20
3.25
Level 1
0.10 0.11
Error rate
2.35
2.40
2.45
Level 2
0.08 0.09 0.10
Error rate
1.65
1.70
1.75
Hier. dist. mistake
Level 3
XE One-hot XE MBM XE B3P CD BD CD LGCD
Figure 3: iNaturalist19: Error rate vs Hierarchical distance of a Mistake.
0.25 0.30
Error rate
4.2
4.4
4.6
4.8
Level 0
0.225 0.250 0.275
Error rate
4.0
4.2
4.4
4.6
Level 1
0.175 0.200 0.225
Error rate
3.8
4.0
4.2
4.4
Level 2
0.13 0.14
Error rate
4.5
4.6
Hier. dist. mistake
Level 3
XE One-hot XE MBM XE B3P CD BD CD LGCD
Figure 4: tieredImageNet: Error rate vs Hierarchical distance of a Mistake.
4.4 Representation Learning
We have showed how it is possible to construct encod-
ings and train models achieving accuracy comparable
to that of cross-entropy while improving the quality of
errors. However, we are also interested in checking
how structured is the learned internal representation
of the labels-concepts within different classifiers.
Many CV models can be decomposed into two
main components: a deep feature extraction network,
converting images into feature vectors, followed by a
relatively shallow classifier, tasked with learning and
defining separation hyperplanes.
Clearly, the better the feature vectors cluster ac-
cording to ground-truth classes, the easier the task of
the classifier is. If the model has successfully built a
good internal representation during the training pro-
cess, then the feature vectors will be organized into
clusters. Ideally, the organization of feature vectors
follows a structure similar to that of the hierarchy: a
nested structure of subclusters corresponding to dif-
ferent levels of the hierarchy. This is true if the ex-
plicit hierarchies considered are constructed from vi-
sual concepts that help discriminate between different
EXPLAINS 2024 - 1st International Conference on Explainable AI for Neural and Symbolic Methods
56

CIFAR-100 iNaturalist19 tieredImageNet
0
1
2
3
4
5
Davies-Bouldin
CIFAR-100 iNaturalist19 tieredImageNet
0.0
0.2
0.4
0.6
0.8
SDBw
XE One-hot XE MBM XE B3P CD BD CD LGCD
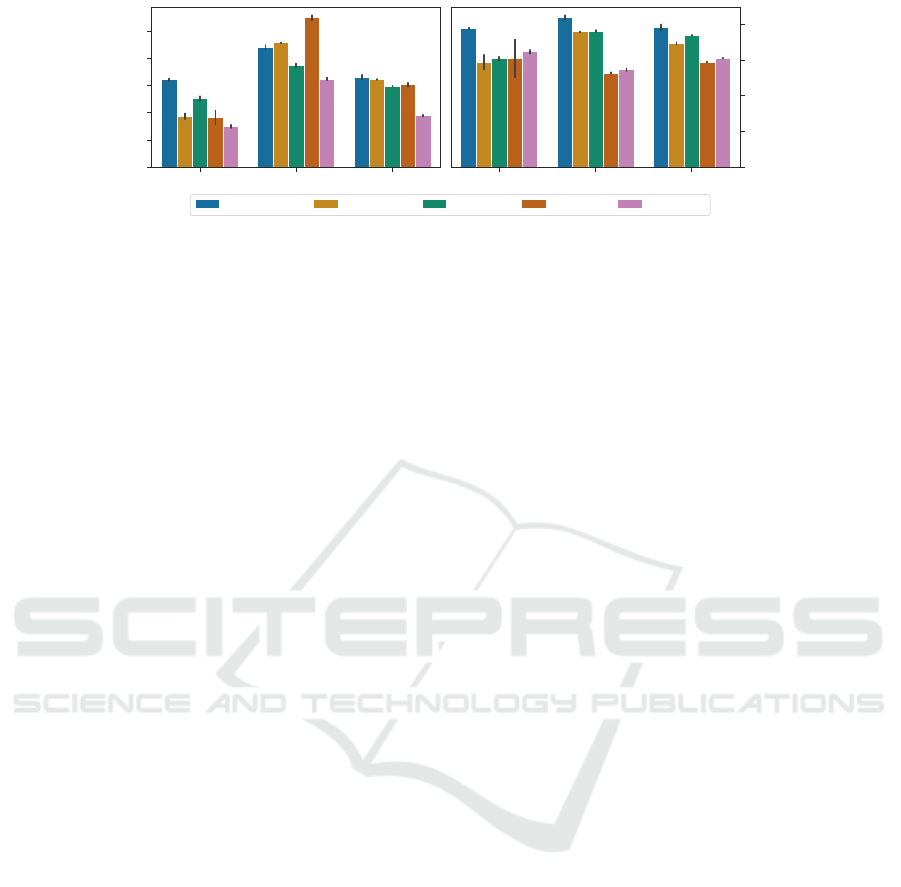
Figure 5: Davies–Bouldin index and SDBw index at level 0 of the hierarchy.
classes in a classification task.
In the case of EfficientNet, the classifier corre-
sponds to the very last layer. We have therefore an-
alyzed the output produced by the penultimate layer
of our models when applied on the test folds of the
three datasets, transforming each image into a feature
vector.
To assess the quality of these internal represen-
tations, we evaluated the clustering of feature vec-
tors using two metrics: the Davies-Bouldin index and
the SDBw index. The Davies-Bouldin Index, intro-
duced by Davies and Bouldin in (Davies and Bouldin,
1979), is a distance clustering metric based on the
ratio of within-cluster distances to between-cluster
distances. Halkidi and Vazirgiannis in (Halkidi and
Vazirgiannis, 2001) define the validity index SDBw as
the sum of two terms: intra-cluster variance and inter-
cluster density. Liu et al. in (Liu et al., 2010) con-
ducted a study on eleven clustering metrics, including
the aforementioned ones, evaluating their strengths
and weaknesses on synthetic data. They conclude
that SDBw is a metric that has proven to be reliable
against challenging data distributions. It is pertinent
to note that for both the Davies-Bouldin index and
the SDBw index, lower values are indicative of better
clustering quality, reflecting more distinct and well-
separated clusters.
In Figure 5 we show the clustering scores for
level-0; results for higher levels are reported in Sec-
tion 4.5. The figure is divided into two panels, rep-
resenting the two selected clustering quality metrics:
Davies-Bouldin and SDBw. Within each panel, re-
sults are grouped by dataset. For each dataset, we
report the clustering score of the different methodolo-
gies, along with error bars. For both metrics, lower
scores indicate better clustering quality.
First, it is worth mentioning how the results in the
two panels differ, suggesting the fact that the two met-
rics capture different aspects. The Davies-Bouldin
index varies more across datasets, with MBM and BD
performing worse than one-hot encoding on the iNat-
uralist19 dataset. SDBw seems to be more depen-
dent on the number of classes: for the datasets with
a higher number of classes (iNaturalist19 and tiered-
ImageNet), the cosine-distance-based approaches (BD
and LGCD) display better performances, whereas on
CIFAR-100 all non-standard approaches have com-
parable results, with the sole exception of B3P dis-
playing a wider error bar. Furthermore, we remark
how MBM, B3P, and BD require an explicit structured
representation of labels, thus not being applicable in
the general case. Our approach LGCD shows better
clustering quality than one-hot encoding, the only
other “hierarchy-blind” approach, across both cluster-
ing metrics and all three experimental datasets.
4.5 Extended Results
This subsection contains evaluation results across the
considered metrics. For each dataset, we first report
results for Error Rate (Tables 3, 5 and 7) and Hierar-
chical Distance of a Mistake (Tables 4, 6 and 8), and
then we present the Davies-Bouldin Index (Tables 9,
11 and 13) and SDBw Index (Tables 10, 12 and 14)
computed over the feature vectors of images.
In these tables, metric scores are reported for all
levels of the hierarchy, while Figures 2 to 5 plot the
scores for the lower levels of the hierarchies. Each
cell in the tables contains the average score across
five models trained with different random seeds (5
seeds × 5 encodings × 3 datasets = 75 models
trained). Next to the average, the standard deviation
is reported. The background color of each cell indi-
cates the model’s performance relative to others: the
greener the cell, the better the model’s performance.
The best-performing model is highlighted in bold.
As mentioned in the main section, clustering met-
rics (Davies-Bouldin and SDBw indexes) can be sen-
sitive to pathological data distributions (Liu et al.,
2010). This instability is reflected in out-of-scale
standard deviation values in some cells at hierarchy
levels greater than 0.
In conclusion, it is important to consider that
evaluating metrics at different levels of the hierar-
chy may produce results. The class aggregation al-
gorithm used to compute these metrics relies on the
LLM-Generated Class Descriptions for Semantically Meaningful Image Classification
57

Table 3: CIFAR-100: Error Rate.
level CD BD CD LGCD XE B3P XE MBM XE One-hot
0 0.296 ± 0.004 0.275 ± 0.004 0.278 ± 0.003 0.291 ± 0.005 0.281 ± 0.004
1 0.181 ± 0.003 0.172 ± 0.002 0.173 ± 0.002 0.175 ± 0.007 0.183 ± 0.004
2 0.111 ± 0.002 0.108 ± 0.002 0.105 ± 0.001 0.107 ± 0.004 0.120 ± 0.004
3 0.050 ± 0.002 0.050 ± 0.001 0.047 ± 0.001 0.048 ± 0.003 0.060 ± 0.002
Table 4: CIFAR-100: Hierarchical distance of a Mistake.
level CD BD CD LGCD XE B3P XE MBM XE One-hot
0 2.262 ± 0.011 2.323 ± 0.024 2.279 ± 0.010 2.244 ± 0.033 2.438 ± 0.016
1 2.071 ± 0.016 2.121 ± 0.018 2.052 ± 0.017 2.068 ± 0.020 2.206 ± 0.012
2 1.740 ± 0.012 1.773 ± 0.028 1.730 ± 0.006 1.744 ± 0.027 1.843 ± 0.026
3 1.656 ± 0.016 1.665 ± 0.025 1.635 ± 0.018 1.665 ± 0.010 1.691 ± 0.012
Table 5: iNaturalist19: Error Rate.
level CD BD CD LGCD XE B3P XE MBM XE One-hot
0 0.515 ± 0.004 0.398 ± 0.004 0.322 ± 0.004 0.345 ± 0.001 0.335 ± 0.007
1 0.112 ± 0.000 0.109 ± 0.001 0.111 ± 0.002 0.109 ± 0.001 0.124 ± 0.003
2 0.101 ± 0.000 0.099 ± 0.001 0.102 ± 0.002 0.098 ± 0.001 0.115 ± 0.003
3 0.084 ± 0.000 0.082 ± 0.001 0.085 ± 0.002 0.081 ± 0.001 0.097 ± 0.003
4 0.027 ± 0.001 0.029 ± 0.000 0.029 ± 0.000 0.029 ± 0.000 0.035 ± 0.001
5 0.015 ± 0.000 0.017 ± 0.000 0.015 ± 0.000 0.016 ± 0.000 0.020 ± 0.000
Table 6: iNaturalist19: Hierarchical distance of a Mistake.
level CD BD CD LGCD XE B3P XE MBM XE One-hot
0 1.683 ± 0.004 1.877 ± 0.013 2.102 ± 0.007 2.002 ± 0.008 2.214 ± 0.007
1 3.132 ± 0.013 3.202 ± 0.012 3.187 ± 0.008 3.169 ± 0.006 3.274 ± 0.011
2 2.360 ± 0.015 2.420 ± 0.010 2.381 ± 0.011 2.408 ± 0.008 2.466 ± 0.013
3 1.638 ± 0.012 1.719 ± 0.009 1.656 ± 0.014 1.707 ± 0.006 1.737 ± 0.018
4 1.993 ± 0.013 2.006 ± 0.007 1.937 ± 0.022 2.011 ± 0.016 2.015 ± 0.029
5 1.777 ± 0.016 1.754 ± 0.004 1.775 ± 0.006 1.774 ± 0.017 1.775 ± 0.011
Table 7: tieredImageNet: Error Rate.
level CD BD CD Desc. XE B3P XE MBM XE One-hot
0 0.331 ± 0.005 0.268 ± 0.003 0.251 ± 0.002 0.332 ± 0.002 0.253 ± 0.003
1 0.238 ± 0.004 0.225 ± 0.003 0.210 ± 0.001 0.285 ± 0.003 0.212 ± 0.003
2 0.188 ± 0.003 0.185 ± 0.003 0.173 ± 0.001 0.227 ± 0.003 0.175 ± 0.002
3 0.139 ± 0.003 0.139 ± 0.003 0.130 ± 0.000 0.144 ± 0.002 0.131 ± 0.002
4 0.122 ± 0.002 0.123 ± 0.003 0.115 ± 0.001 0.124 ± 0.002 0.116 ± 0.001
5 0.108 ± 0.002 0.109 ± 0.003 0.102 ± 0.001 0.109 ± 0.001 0.103 ± 0.001
6 0.099 ± 0.002 0.101 ± 0.003 0.094 ± 0.001 0.101 ± 0.001 0.096 ± 0.001
7 0.072 ± 0.002 0.073 ± 0.002 0.069 ± 0.001 0.074 ± 0.001 0.071 ± 0.002
8 0.027 ± 0.001 0.030 ± 0.001 0.028 ± 0.001 0.030 ± 0.001 0.029 ± 0.001
9 0.026 ± 0.001 0.029 ± 0.001 0.027 ± 0.001 0.030 ± 0.001 0.028 ± 0.001
10 0.015 ± 0.001 0.017 ± 0.001 0.018 ± 0.001 0.019 ± 0.001 0.017 ± 0.000
Table 8: tieredImageNet: Hierarchical distance of a Mistake.
level CD BD CD Desc. XE B3P XE MBM XE One-hot
0 4.152 ± 0.030 4.900 ± 0.049 4.909 ± 0.033 4.479 ± 0.029 4.918 ± 0.039
1 4.391 ± 0.025 4.633 ± 0.051 4.659 ± 0.035 4.048 ± 0.041 4.659 ± 0.035
2 4.282 ± 0.038 4.418 ± 0.054 4.444 ± 0.048 3.836 ± 0.057 4.443 ± 0.038
3
4.454 ± 0.041 4.546 ± 0.044 4.577 ± 0.066 4.460 ± 0.023 4.586 ± 0.046
4 3.930 ± 0.036 4.019 ± 0.026 4.038 ± 0.046 4.024 ± 0.023 4.054 ± 0.030
5 3.298 ± 0.038 3.387 ± 0.023 3.436 ± 0.037 3.440 ± 0.027 3.432 ± 0.026
6 2.516 ± 0.043 2.593 ± 0.034 2.653 ± 0.040 2.642 ± 0.024 2.628 ± 0.020
7 2.098 ± 0.040 2.201 ± 0.040 2.233 ± 0.043 2.244 ± 0.018 2.199 ± 0.014
8 2.890 ± 0.030 2.941 ± 0.037 3.007 ± 0.021 3.011 ± 0.041 2.947 ± 0.022
9 1.970 ± 0.033 2.029 ± 0.035 2.083 ± 0.017 2.069 ± 0.037 2.013 ± 0.022
10 1.643 ± 0.016 1.694 ± 0.015 1.692 ± 0.012 1.692 ± 0.022 1.681 ± 0.016
EXPLAINS 2024 - 1st International Conference on Explainable AI for Neural and Symbolic Methods
58

Table 9: CIFAR-100: Davies-Bouldin Index.
level CD BD CD Desc. d 100 XE B3P β0.4 XE MBM β 5.0 XE One-hot
0 1.83 ± 0.02 1.50 ± 0.03 2.52 ± 0.01 1.87 ± 0.04 3.23 ± 0.00
1 2.80 ± 43.04 3.17 ± 12.43 3.97 ± 9.03 2.86 ± 29.92 4.24 ± 1.07
2 3.90 ± 0.26 4.66 ± 0.06 4.17 ± 0.09 4.03 ± 0.11 3.97 ± 0.04
3 4.90 ± 0.10 5.75 ± 0.01 3.37 ± 0.01 5.06 ± 0.04 4.21 ± 0.00
Table 10: CIFAR-100: SDBw Index.
level CD BD CD LGCD XE B3P XE MBM XE One-hot
0 0.609 ± 0.021 0.646 ± 0.027 0.608 ± 0.009 0.589 ± 0.036 0.779 ± 0.002
1 0.825 ± 43.045 0.916 ± 12.430 0.722 ± 9.029 0.790 ± 29.919 0.893 ± 1.072
2 0.906 ± 0.256 0.978 ± 0.058 0.745 ± 0.089 0.838 ± 0.107 0.921 ± 0.045
3 0.994 ± 0.105 1.018 ± 0.010 0.743 ± 0.010 1.013 ± 0.041 0.925 ± 0.002
Table 11: iNaturalist19: Davies-Bouldin Index.
level CD BD CD LGCD XE B3P XE MBM XE One-hot
0 5.51 ± 0.01 3.26 ± 0.01 3.75 ± 0.01 4.59 ± 0.00 4.43 ± 0.00
1 1.52 ± 1.04 2.86 ± 0.93 3.90 ± 1.14 2.94 ± 0.33 4.50 ± 1.86
2 1.86 ± 0.09 3.22 ± 0.05 4.14 ± 0.07 2.96 ± 0.01 4.74 ± 0.07
3 2.43 ± 0.00 4.11 ± 0.01 4.85 ± 0.01 3.28 ± 0.00 5.53 ± 0.01
4 3.65 ± 0.01 5.24 ± 0.02 4.61 ± 0.00 3.28 ± 0.00 6.87 ± 0.00
5 5.12 ± 18.89 7.03 ± 8.07 3.51 ± 9.31 3.38 ± 2.63 8.74 ± 12.71
Table 12: iNaturalist19: SDBw Index.
level CD BD CD LGCD XE B3P XE MBM XE One-hot
0 0.528 ± 0.012 0.545 ± 0.005 0.763 ± 0.006 0.758 ± 0.001 0.837 ± 0.001
1 0.721 ± 1.036 0.884 ± 0.929 0.861 ± 1.145 0.828 ± 0.333 0.926 ± 1.860
2 0.741 ± 0.091 0.896 ± 0.047 0.867 ± 0.070 0.844 ± 0.009 0.930 ± 0.071
3 0.822 ± 0.004 0.929 ± 0.008 0.890 ± 0.005 0.877 ± 0.002 0.960 ± 0.013
4 0.780 ± 0.010 0.877 ± 0.022 0.885 ± 0.003 0.930 ± 0.001 0.913 ± 0.001
5 0.817 ± 18.889 0.841 ± 8.071 0.926 ± 9.309 0.924 ± 2.626 0.894 ± 12.708
Table 13: tieredImageNet: Davies-Bouldin Index.
level CD BD CD LGCD XE B3P XE MBM XE One-hot
0 3.04 ± 0.02 1.90 ± 0.00 2.99 ± 0.00 3.24 ± 0.00 3.32 ± 0.01
1 2.06 ± 0.68 2.07 ± 0.48 3.14 ± 0.22 3.13 ± 0.89 3.44 ± 1.53
2 2.09 ± 0.07 2.50 ± 0.03 3.55 ± 0.01 3.18 ± 0.01 3.84 ± 0.09
3 2.31 ± 0.00 3.30 ± 0.00 4.14 ± 0.00 3.09 ± 0.01 4.64 ± 0.02
4 2.87 ± 0.01 4.23 ± 0.01 5.00 ± 0.00 3.29 ± 0.00 5.70 ± 0.01
5 3.26 ± 1.01 4.59 ± 0.21 5.25 ± 0.21 3.30 ± 1.26 6.09 ± 1.65
6 3.86 ± 0.06 5.11 ± 0.02 5.32 ± 0.01 3.47 ± 0.01 6.40 ± 0.10
7 4.47 ± 0.00 5.82 ± 0.00 5.39 ± 0.00 3.64 ± 0.01 7.12 ± 0.01
8 5.32 ± 0.01 6.22 ± 0.02 4.36 ± 0.00 3.75 ± 0.00 7.35 ± 0.01
9 5.79 ± 2.01 6.58 ± 0.66 4.41 ± 0.37 4.02 ± 2.11 7.82 ± 1.95
10 5.46 ± 0.08 5.90 ± 0.03 3.86 ± 0.02 3.77 ± 0.03 6.17 ± 0.13
Table 14: tieredImageNet: SDBw Index.
level CD BD CD LGCD XE B3P XE MBM XE One-hot
0 0.589 ± 0.015 0.611 ± 0.004 0.739 ± 0.001 0.693 ± 0.001 0.783 ± 0.008
1 0.638 ± 0.680 0.675 ± 0.483 0.771 ± 0.216 0.718 ± 0.890 0.812 ± 1.531
2 0.701 ± 0.070 0.736 ± 0.030 0.810 ± 0.011 0.758 ± 0.015 0.846 ± 0.088
3
0.769 ± 0.002 0.822 ± 0.002 0.872 ± 0.002 0.813 ± 0.007 0.900 ± 0.015
4 0.852 ± 0.011 0.898 ± 0.006 0.922 ± 0.001 0.862 ± 0.001 0.937 ± 0.008
5 0.897 ± 1.007 0.933 ± 0.209 0.938 ± 0.211 0.893 ± 1.257 0.960 ± 1.650
6 0.898 ± 0.064 0.941 ± 0.020 0.921 ± 0.011 0.890 ± 0.012 0.957 ± 0.104
7 0.912 ± 0.004 0.960 ± 0.002 0.922 ± 0.002 0.894 ± 0.006 0.952 ± 0.014
8 0.874 ± 0.014 0.946 ± 0.020 0.932 ± 0.001 0.903 ± 0.002 0.940 ± 0.006
9 0.860 ± 2.013 0.932 ± 0.661 0.960 ± 0.366 0.942 ± 2.111 0.954 ± 1.952
10 0.779 ± 0.083 0.890 ± 0.028 1.002 ± 0.018 0.952 ± 0.032 0.937 ± 0.131
LLM-Generated Class Descriptions for Semantically Meaningful Image Classification
59

hierarchy itself, giving an inherent advantage to mod-
els trained explicitly on this hierarchy. Conversely,
hierarchy-agnostic models, specifically XE One-hot
and CD LGCD, might achieve higher accuracy and de-
velop a more structured internal representation. How-
ever, they may score lower in the tables if their ”hier-
archical world representation” deviates from the one
defined by the hard-coded hierarchy.
5 DISCUSSION AND
CONCLUSIONS
Although neural networks are widely used in com-
puter vision tasks, they typically ignore the contextual
semantics of class labels. Image classification models
generally map input images (with a hierarchy of vi-
sual features) to orthogonal, meaningless labels. Ad-
dressing this limitation presents a strategic opportu-
nity to improve the interpretability of these “black-
box” models. In this paper, we introduced LLM-
Generated Class Descriptions (LGCD), a simple ap-
proach that produces detailed visual descriptions of
class labels, enhancing semantic interpretability in
image classification. These descriptions are subse-
quently transformed into embedding vectors, which
serve as a refined form of ground truth by encapsu-
lating semantic relationships between classes. The
resulting encodings, together with a cosine distance
loss, are then used to guide the learning process. Our
approach outperforms traditional one-hot encoding
methods and cross-entropy loss by systematically re-
ducing the semantic severity of misclassifications and
producing a more structured feature space.
LGCD approach introduces minimal overhead in
the training process. The class embeddings are gen-
erated once before training, with a negligible compu-
tational cost associated with generating the class de-
scriptions and computing their embeddings. This pre-
processing step does not impact the efficiency of the
model training phase, making our method practical
and scalable for large datasets. Furthermore, unlike
previous approaches that rely on explicit hierarchical
taxonomies, our approach’s flexibility allows it to be
applied to any image classification task, regardless of
the underlying structured representation of labels.
For future work, we plan to assess how robust
our method is to variations in the prompt instructions
used for generating class descriptions. Furthermore,
we aim to explore additional ways to refine the ex-
traction and use of semantic information from large
language models, potentially incorporating more dy-
namic forms of learning and interaction between the
symbolic and neural components of our methodology.
Finally, we aim to examine how our approach af-
fects robustness to adversarial attacks. We hypothe-
size that a more hierarchically organized feature space
would reduce the formation of ”pockets” between se-
mantically distant classes, making it harder to perturb
an image to be misclassified under a different label.
REFERENCES
Barz, B. and Denzler, J. (2019). Hierarchy-based image em-
beddings for semantic image retrieval. In 2019 IEEE
Winter Conference on Applications of Computer Vi-
sion (WACV), pages 638–647.
Barz, B. and Denzler, J. (2020). Deep learning on small
datasets without pre-training using cosine loss. In
2020 IEEE Winter Conference on Applications of
Computer Vision (WACV), pages 1360–1369.
Bertinetto, L., Mueller, R., Tertikas, K., Samangooei, S.,
and Lord, N. A. (2020). Making better mistakes:
Leveraging class hierarchies with deep networks. In
2020 IEEE/CVF Conference on Computer Vision and
Pattern Recognition (CVPR), pages 12503–12512.
Bilal, A., Jourabloo, A., Ye, M., Liu, X., and Ren, L. (2018).
Do convolutional neural networks learn class hierar-
chy? IEEE Transactions on Visualization and Com-
puter Graphics, 24(1):152–162.
Buhrmester, V., M
¨
unch, D., and Arens, M. (2021). Analysis
of explainers of black box deep neural networks for
computer vision: A survey. Machine Learning and
Knowledge Extraction, 3(4):966–989.
Chang, D., Pang, K., Zheng, Y., Ma, Z., Song, Y.-Z., and
Guo, J. (2021). Your “flamingo” is my “bird”: Fine-
grained, or not. In 2021 IEEE/CVF Conference on
Computer Vision and Pattern Recognition (CVPR),
pages 11471–11480.
Chen, H.-Y., Liang, J.-H., Chang, S.-C., Pan, J.-Y., Chen,
Y.-T., Wei, W., and Juan, D.-C. (2019a). Improv-
ing adversarial robustness via guided complement en-
tropy. In 2019 IEEE/CVF International Conference
on Computer Vision (ICCV), pages 4880–4888.
Chen, H.-Y., Tsai, L.-H., Chang, S.-C., Pan, J.-Y., Chen,
Y.-T., Wei, W., and Juan, D.-C. (2019b). Learn-
ing with hierarchical complement objective. ArXiv,
abs/1911.07257.
Chen, H.-Y., Wang, P.-H., Liu, C.-H., Chang, S.-C., Pan, J.-
Y., Chen, Y., Wei, W., and Juan, D.-C. (2019c). Com-
plement objective training. ArXiv, abs/1903.01182.
Davies, D. L. and Bouldin, D. W. (1979). A cluster separa-
tion measure. IEEE Transactions on Pattern Analysis
and Machine Intelligence, PAMI-1:224–227.
Dong, Y., Su, H., Zhu, J., and Zhang, B. (2017). Improving
interpretability of deep neural networks with semantic
information. In 2017 IEEE Conference on Computer
Vision and Pattern Recognition, pages 975–983.
Frome, A., Corrado, G. S., Shlens, J., Bengio, S., Dean, J.,
Ranzato, M., and Mikolov, T. (2013). Devise: A deep
visual-semantic embedding model. In Proceedings of
EXPLAINS 2024 - 1st International Conference on Explainable AI for Neural and Symbolic Methods
60

the 26th International Conference on Neural Informa-
tion Processing Systems - Volume 2, page 2121–2129.
Garg, A., Sani, D., and Anand, S. (2022). Learning hierar-
chy aware features for reducing mistake severity. In
Avidan, S., Brostow, G., Ciss
´
e, M., Farinella, G. M.,
and Hassner, T., editors, Computer Vision – ECCV
2022, pages 252–267, Cham. Springer Nature.
Garnot, V. S. F. and Landrieu, L. (2020). Leveraging class
hierarchies with metric-guided prototype learning. In
British Machine Vision Conference.
Halkidi, M. and Vazirgiannis, M. (2001). Clustering validity
assessment: finding the optimal partitioning of a data
set. In 2001 IEEE International Conference on Data
Mining. IEEE Comput. Soc.
He, K., Zhang, X., Ren, S., and Sun, J. (2016). Deep
residual learning for image recognition. In Proc. of
the IEEE conference on computer vision and pattern
recognition.
Incitti, F., Urli, F., and Snidaro, L. (2023). Beyond word
embeddings: A survey. Information Fusion, 89:418–
436.
Khan, S., Rahmani, H., Shah, S. A. A., Bennamoun, M.,
Medioni, G., and Dickinson, S. (2018). A guide to
convolutional neural networks for computer vision.
Springer.
Krizhevsky, A. and Hinton, G. (2009). Learning multiple
layers of features from tiny images. Technical report,
University of Toronto.
Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). Im-
agenet classification with deep convolutional neural
networks. In Advances in neural information process-
ing systems, pages 1097–1105.
Kroshchanka, A., Golovko, V., Mikhno, E., Kovalev, M.,
Zahariev, V., and Zagorskij, A. (2021). A neural-
symbolic approach to computer vision. In Interna-
tional Conference on Open Semantic Technologies for
Intelligent Systems, pages 282–309. Springer.
Kusupati, A., Bhatt, G., Rege, A., Wallingford, M., Sinha,
A., Ramanujan, V., Howard-Snyder, W., Chen, K.,
Kakade, S., Jain, P., and Farhadi, A. (2022). Ma-
tryoshka representation learning. In Advances in Neu-
ral Information Processing Systems, volume 35, pages
30233–30249. Curran Associates, Inc.
Liu, Y., Li, Z., Xiong, H., Gao, X., and Wu, J. (2010). Un-
derstanding of internal clustering validation measures.
In 2010 IEEE 10th International Conference on Data
Mining (ICDM). IEEE.
Mikolov, T., Chen, K., Corrado, G. S., and Dean, J. (2013a).
Efficient estimation of word representations in vector
space. In International Conference on Learning Rep-
resentations.
Mikolov, T., Sutskever, I., Chen, K., Corrado, G. S., and
Dean, J. (2013b). Distributed representations of words
and phrases and their compositionality. In Neural In-
formation Processing Systems.
Miller, G. A. (1995). Wordnet: a lexical database for en-
glish. Communications of the ACM, page 39–41.
Pasini, A., Giobergia, F., Pastor, E., and Baralis, E. (2022).
Semantic image collection summarization with fre-
quent subgraph mining. IEEE Access, 10:131747–
131764.
Perotti, A., Bertolotto, S., Pastor, E., and Panisson, A.
(2023). Beyond one-hot-encoding: Injecting seman-
tics to drive image classifiers. In World Conference
on Explainable Artificial Intelligence, pages 525–548.
Springer.
Radford, A., Kim, J. W., Hallacy, C., Ramesh, A., Goh, G.,
Agarwal, S., Sastry, G., Askell, A., Mishkin, P., Clark,
J., et al. (2021). Learning transferable visual models
from natural language supervision. In International
conference on machine learning, pages 8748–8763.
PMLR.
Redmon, J. and Farhadi, A. (2016). Yolo9000: Better,
faster, stronger. 2017 IEEE Conference on Computer
Vision and Pattern Recognition, pages 6517–6525.
Ren, M., Triantafillou, E., Ravi, S., Snell, J., Swersky, K.,
Tenenbaum, J. B., Larochelle, H., and Zemel, R. S.
(2018). Meta-learning for semi-supervised few-shot
classification. In Proceedings of 6th International
Conference on Learning Representations, ICLR.
Russakovsky, O., Deng, J., Su, H., Krause, J., Satheesh, S.,
Ma, S., Huang, Z., Karpathy, A., Khosla, A., Bern-
stein, M. S., Berg, A. C., and Fei-Fei, L. (2014). Im-
agenet large scale visual recognition challenge. Inter-
national Journal of Computer Vision, 115:211 – 252.
Sainburg, T., McInnes, L., and Gentner, T. Q. (2021).
Parametric umap embeddings for representation and
semisupervised learning. Neural Computation,
33(11):2881–2907.
Silla, C. N. and Freitas, A. A. (2011). A survey of hierarchi-
cal classification across different application domains.
Data Mining and Knowledge Discovery, 22:31–72.
Simonyan, K. and Zisserman, A. (2014). Very deep con-
volutional networks for large-scale image recognition.
CoRR, abs/1409.1556.
Tan, M. and Le, Q. (2019). EfficientNet: Rethinking model
scaling for convolutional neural networks. In Pro-
ceedings of the 36th International Conference on Ma-
chine Learning, volume 97 of Proceedings of Machine
Learning Research, pages 6105–6114. PMLR.
van der Maaten, L. and Hinton, G. (2008). Visualizing data
using t-sne. Journal of Machine Learning Research,
9(86):2579–2605.
Van Horn, G., Mac Aodha, O., Song, Y., Cui, Y., Sun,
C., Shepard, A., Adam, H., Perona, P., and Belongie,
S. (2018). The inaturalist species classification and
detection dataset. In 2018 IEEE/CVF Conference
on Computer Vision and Pattern Recognition, pages
8769–8778.
Verma, N., Mahajan, D., Sellamanickam, S., and Nair, V.
(2012). Learning hierarchical similarity metrics. In
2012 IEEE Conference on Computer Vision and Pat-
tern Recognition (CVPR). IEEE.
Wu, H., Merler, M., Uceda-Sosa, R., and Smith, J. R.
(2016). Learning to make better mistakes: Semantics-
aware visual food recognition. In Proceedings of the
24th ACM International Conference on Multimedia,
page 172–176.
LLM-Generated Class Descriptions for Semantically Meaningful Image Classification
61