A Novel Reliable Leader-Following Consensus for Continuous-Time
Multi-Agent Systems Under Nonhomogeneous and Asynchronous
Markov Network Topology
Ngoc Hoai An Nguyen
a
and Sung Hyun Kim
⋆ b
Department of Electrical, Electronic and Computer Engineering, University of Ulsan, Ulsan City, Korea
Keywords:
Reliable Control, Multi-Agent Systems, Leader-Following Consensus, Actuator Faults, Markov Network
Topology, Asynchronous Network Topology, Nonhomogeneous Process.
Abstract:
This paper tackles the challenge of achieving robust leader-following consensus in multi-agent systems fac-
ing actuator faults and asynchronous network-dependent controllers. Specifically, it establishes sufficient
conditions for ensuring reliable consensus, including: i) integration of actuator faults and network topology
asynchronism into the control synthesis for each follower, ii) solutions to convex problems arising from the
multiplication between time-varying transition rates and conditional probabilities, and iii) development of an
innovative relaxation technique that reformulates H
∞
stabilization conditions into linear matrix inequalities.
1 INTRODUCTION
In recent years, multi-agent systems (MASs) have
drawn attention in various applications such as
unmanned vehicles, rendezvous, distributed sensor
networks, formation control, flocking control, and
swarming control. The most interesting issue in
the control problem of MASs is consensus control,
which empowers a team of agents to achieve a uni-
fied agreement. Consensus control is typically clas-
sified into two categories: leader-following consen-
sus and leaderless consensus. The main advantage of
the leader-following consensus control is that it en-
hances communication efficiency, conserves energy,
and reduces control costs. In leader-following con-
sensus, the leader functions independently of other
agents, while the remaining agents track the leader’s
state trajectories. However, the network topology of
MASs in practical network environments can be in-
fluenced and continuously fluctuating over time due
to various factors such as connectivity disturbances,
bandwidth limitations, and random packet dropout.
To alleviate the concerns raised by the drawback of
fixed network topology of MASs, the concept of time-
varying network topology has been recently focused.
Especially, Markov process has been emerged as an
a
https://orcid.org/0000-0001-7651-2537
b
https://orcid.org/0000-0003-2495-7117
⋆
Corresponding author
effective modeling approach for representing the ran-
dom abrupt variation of variables in controlled sys-
tems. Therefore, one of the effective way to cap-
ture the sudden random shifts in network topology in
MASs is embedding the framework of Markov pro-
cess in the considered MASs. In particular, to deter-
mine the network topology in MASs under Markov
network topology, it is essential to obtain the values of
transition rates. However, measuring the exact value
of transition rates is challenging due to high equip-
ment costs, complexities in sensor interface, and lim-
ited sensor precision. Therefore, the concept of a non-
homogeneous Markov process is ideal for represent-
ing network topology in leader-following consensus
of MASs, where the transition rates are either partially
known or entirely unknown.
Concurrently, the phenomenon of actuator faults
can occur in many control systems due to various rea-
sons, including the inherent physical limitations of
actuators, electrical or mechanical failures, and en-
vironmental factors. In this context, reliable control
has become an inevitable trend in the state-of-the-art
control engineering, aiming to ensure that control sys-
tems operate satisfactorily even in the presence of ac-
tuator faults. At the same time, packet dropout and
time delay can frequently happen during the analysis
of network topology modes and the transmission of
that information to each follower’s controller. Thus,
this makes it challenging for the controller to identify
486
Nguyen, N. and Kim, S.
A Novel Reliable Leader-Following Consensus for Continuous-Time Multi-Agent Systems Under Nonhomogeneous and Asynchronous Markov Network Topology.
DOI: 10.5220/0013063800003822
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 21st International Conference on Informatics in Control, Automation and Robotics (ICINCO 2024) - Volume 1, pages 486-493
ISBN: 978-989-758-717-7; ISSN: 2184-2809
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.

control topology that stays in synchronization with
the dynamic network topology. Based on these ob-
servations, it is comprehensively necessary to investi-
gate the impact of asynchronous control and actuator
faults on the leader-following consensus of MASs un-
der nonhomogeneous Markov network topology. The
concept of Markov switching network topologies for
MASs has been firstly applied in (Li et al., 2015);
however, the network topologies were assumed to be
completely fixed and constant. Later, (Sakthivel et al.,
2018) studied the leader-following exponential con-
sensus of MASs by investigating a set of Lyapunov
function candidates containing integral terms. How-
ever, the network topology was also assumed to be
characterized by a constant Markov network topol-
ogy. Most recently, (Yang et al., 2023) addressed
the leader-following consensus control problem for
discrete-time MASs with actuator faults. To han-
dle the uncertain semi-Markov network topology, the
transition rates in (Yang et al., 2023) were assumed to
be bounded and confined to a polytope. Based on the
above discussion, the leader-following consensus for
MASs, considering actuator faults and asynchronous
control topology, should be given greater focus, espe-
cially when analyzing the transitions in the nonhomo-
geneous Markov network topology.
This paper tackles the challenge of achieving re-
liable asynchronous leader-following consensus for
MASs under a nonhomogeneous Markov network
topology with H
∞
performance. The main contribu-
tion of this paper can be summarized as follows:
• Unlike (Li et al., 2015; Sakthivel et al., 2018;
Wang et al., 2019), the network topology is char-
acterized by a nonhomogeneous Markov process,
which includes a more general and practical for-
mulation of transition rates. Since obtaining
transition rates that provide valuable information
about the network topology in real-time is chal-
lenging, considering partially known or entirely
unknown transition rates can result in a less con-
servative stabilization condition.
• As mentioned above, the controller at each fol-
lower must detect the network topology to de-
termine important network-dependent matrices,
such as the Laplacian matrices and the leader ad-
jacency matrices, and use them to construct the
control signals. However, it is practically difficult
to detect the exact network topology and fully uti-
lize these matrices at each follower’s control side.
As a result, asynchronous reliable controllers with
actuator faults have been designed using an asyn-
chronous control-topology-dependent Lyapunov
function and a linear matrix inequalities (LMIs)
approach.
• To manage the parameterized linear matrix in-
equalities (PLMIs) influenced by both time-
varying transition rates and conditional probabili-
ties, the relaxation technique is necessary to con-
vert PLMIs-based stabilization conditions in solv-
able ones. Compared to (Yang et al., 2023), the
continuous-time nonhomogeneous Markov net-
work topology we are considering is more com-
plex due to the presence of both negative and pos-
itive transition rates, whereas only positive rates
are considered in the discrete-time case in (Yang
et al., 2023). The differing signs of transition rates
are crucial in relaxation techniques, as they make
the relaxation technique more intricate. Further-
more, unlike (Nguyen and Kim, 2019; Nguyen
and Kim, 2021), the relaxation technique is based
on an augmented matrix formed from both the
partly known transition rates and the entirely un-
known transition rates, allowing the inclusion of a
broader scope of transition rates in the relaxation
technique.
Notations. The term (∗) is utilized to express sym-
metrical terms in symmetric matrices; E{·} represents
for the mathematical expectation; He{Q } = Q + Q
T
where Q
T
is the transpose matrix of Q ; ⊗ denotes
the Kronecker product. Moreover, for scalar or vector
a
i
, col(a
1
,a
2
,··· ,a
n
) = [a
T
1
a
T
2
··· a
T
n
]
T
and diag(·)
is a diagonal matrix. Correspondingly, some useful
augmented matrices are utilized as follows: For A =
{a
1
,a
2
,··· ,a
n
},

Q
a
i

a
i
∈A
= col(Q
a
1
,Q
a
2
,··· ,Q
a
n
)
and

Q
a
i

d
a
i
∈A
= diag(Q
a
1
,Q
a
2
,··· ,Q
a
n
), where Q
a
i
denotes real sub-matrices with appropriate dimen-
sions.
2 PROBLEM STATEMENT
2.1 Markov Network Topology
Multi-agent systems under the network topology are
established as time-varying directed graph G
φ
t
=

S,E
φ
t
,A
φ
t

, where S = {n
i
} denotes the nodes set
or agents set where i ∈ N = {1, 2, . . . , N}; φ
t
∈
N
φ
= {1, 2, · · · , n
φ
} denotes the network topology
mode; E
φ
t
⊆ {(n
j
,n
i
) | n
i
,n
j
∈ S, j ̸= i} denotes
the edge set with the ordered pairs (n
j
,n
i
) mean-
ing the information flow from node n
j
to node n
i
;
and A
φ
t
=

a
i j,φ
t

i, j∈N
denotes the adjacency ma-
trix with a
i j,φ
t
= 0 if and only if the pair (n
j
,n
i
) /∈
E
φ
t
and a
i j,φ
t
> 0, otherwise. The leader depends
on an extended directed graph G
0
φ
t
= (S
0
,E
0
φ
t
) with
S
0
= S
S
{n
0
} and E
0
φ
t
⊆ {(n
0
,n
i
) | n
i
∈ S}. In addi-
A Novel Reliable Leader-Following Consensus for Continuous-Time Multi-Agent Systems Under Nonhomogeneous and Asynchronous
Markov Network Topology
487

tion, the network-topology-dependent Laplacian ma-
trix of G
φ
t
is constructed by L
φ
t
=

l
i j,φ
t

i, j∈N
= D
φ
t
−
A
φ
t
, where D
φ
t
=

d
i,φ
t

d
i∈N
and d
i,φ
t
=
∑
j∈N
a
i j,φ
t
.
Furthermore, the network-topology-dependent leader
adjacency matrix of G
0
φ
t
is established by M
φ
t
=

m
i,φ
t

d
i∈N
, where m
i,φ
t
> 0 if and only if the leader n
0
transmits information to the follower n
i
and m
i,φ
t
= 0,
otherwise.
Notably, the network topology is defined by a
continuous-time nonhomogeneous Markov process
{φ
t
,t ≥ 0} subject to the following time-varying tran-
sition probabilities:
Pr

φ
t+θ
= h


φ
t
= g

=

π
gh
(t)θ + o(θ) if h ̸= g
1 + π
gg
(t)θ + o(θ) if h = g
where θ > 0, lim
θ→0
(o(θ)/θ) = 0; and π
gh
(t) stands
for the transition rates (TRs) from topology mode g at
time t to topology mode h at time t + θ, satisfying
π
gh
(t) ≥ 0 and π
gg
(t) = −
∑
h∈N
φ
\{g}
π
gh
(t). (1)
Moreover, based on the precision and availability of
π
gh
(t), the network topology mode set can be com-
posed of three subsets such that N
φ
= N
⋆
φ
+
e
N
φ
+ N
×
φ
N
⋆
φ
=

h | π
gh
is known and constant

e
N
φ
=

h | π
gh
(t) is time-varying and bounded by
π
gh
(t) ∈ [π
gh
,π
gh
]

N
×
φ
=

h | π
gh
(t) is entirely unknown

. (2)
From the characteristics of each topology set (2), one
can conclude the two main formulations related to the
transition rates π
gh
(t):
• π
gh
(t) ∈ [π
gh
,π
gh
] for h ∈
e
N
φ
(3)
• 0 = π
gg
+
∑
h∈N
⋆
φ
\{g}
π
gh
+
∑
h∈
e
N
φ
\{g}
π
gh
(t) +
∑
h∈N
×
φ
\{g}
π
gh
(t), if g ∈ N
⋆
φ
. (4)
2.2 Multi-Agent Systems
Let us consider the following continuous-time dy-
namics of the ith follower and the leader with non-
homogeneous Markov network topology:





˙x
i
t
= Ax
i
t
+ BΓ
t
u
i
t
+ D f (x
i
t
) + Ew
i
t
˙x
0
t
= Ax
0
t
+ D f (x
0
t
)
z
i
t
= C

x
i
t
− x
0
t

(5)
where x
i
t
∈ R
n
x
, u
i
t
∈ R
n
u
, w
i
t
∈ R
n
w
, f (x
i
t
) ∈ R
n
f
, x
0
t
∈
R
n
x
, f (x
0
t
) ∈ R
n
f
, and z
i
t
∈ R
n
z
denote the state of the
ith follower, the control input of the ith follower, the
external disturbance of the ith follower satisfying w
i
t
∈
L
2
[0,∞), the nonlinear function of the ith follower,
the state of the leader, the nonlinear function of the
leader, and the performance output of the ith follower,
respectively. Furthermore, Γ
t
=

Γ
ℓ
t

d
ℓ∈{1,2,...,n
u
}
is
employed to represent the actuator fault model, where
the ℓth element Γ
ℓ
t
satisfies 0 < Γ
ℓ
≤ Γ
ℓ
t
≤ Γ
ℓ
≤
1. Thus, Γ
t
can be represented by Γ
t
= R + ∆
t
S,
where R =

(Γ
ℓ
+ Γ
ℓ
)/2

d
ℓ∈{1,2,...,n
u
}
, S =

(Γ
ℓ
−
Γ
ℓ
)/2

d
ℓ∈{1,2,...,n
u
}
, ∆
t
=

∆
ℓ
t

d
ℓ∈{1,2,...,n
u
}
with |∆
ℓ
t
| ≤
1.
Continuously, let us consider the following con-
trol protocol with asynchronous network topology:
u
i
t
= F
ρ
t

˜x
i
t
+ m
i,φ
t

x
i
t
− x
0
t

(6)
where ˜x
i
t
=
∑
j∈N
l
i j,φ
t

x
j
t
− x
0
t

. In (6), ρ
t
∈ N
ρ
=
{1,2,··· ,n
ρ
} represents the control network topol-
ogy, which is asynchronous to the multi-agent sys-
tem’s network topology described in (5). Here, ˜x
i
t
denotes the synthesized signal, and F
ρ
t
refers to the
asynchronous control gain that will be designed later.
Especially, to demonstrate the relationship between
the nonhomogeneous Markov network topology and
asynchronous control network topology, we construct
the condition probability as follows:
Pr

ρ
t
= p


φ
t
= g

= ϖ
gp
(7)
where
ϖ
gp
∈ [0,1] and
∑
p∈N
ρ
ϖ
gp
= 1. (8)
In the next step, the error between the leader and
the ith follower are introduced by
¯x
i
t
= x
i
t
− x
0
t
and
¯
f
i
t
= f (x
i
t
) − f (x
0
t
).
Based on the brief representation of O
g
= O(φ
t
= g)
and O
p
= O(ρ
t
= p), the dynamics of the ith error
system can be formulated by:
˙
¯x
i
t
= A ¯x
i
t
+ BΓ
t
F
p
∑
j∈N
l
i j,g
¯x
j
t
+ m
i,g
¯x
i
t
!
+ D
¯
f
i
t
+ Ew
i
t
. (9)
Subsequently, let us introduce some following aug-
mented vectors: ¯x
t
=

¯x
i
t

i∈N
,
¯
f
t
=

¯
f
i
t

i∈N
, w
t
=

w
i
t

i∈N
, and z
t
=

z
i
t

i∈N
. The resultant closed-loop
system is given by:





˙
¯x
t
=

(I
N
⊗ A) + (L
g
+ M
g
) ⊗ BΓ
t
F
p

¯x
t
+ (I
N
⊗ D)
¯
f
t
+ (I
N
⊗ E)w
t
z
t
= (I
N
⊗C)¯x
t
.
(10)
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
488

The following assumption and mathematical lem-
mas serve benefit platform for our future derivation:
Assumption 1. (Valentine, 1945) Given a constant
ε > 0, the nonlinear function f (x
0
t
) and f (x
i
t
) satisfy
the following Lipschitz condition:




f (x
i
t
) − f (x
0
t
)




≤ ε




x
i
t
− x
0
t




. (11)
Lemma 2.1. (Xie and de Souza, 1990) For any matri-
ces S ∈ R
n×m
, T ∈ R
n×m
, and 0 < P = P
T
∈ R
n×n
,
the following inequality holds:
He

S
T
T

≤ S
T
P S + T
T
P
−1
T . (12)
Lemma 2.2. (Takaba, 1998) Let Ξ, R
1
, ∆
t
, and R
2
be real matrices with proper dimensions such that
∆
T
t
∆
t
≤ I and there exits a positive scalar α. Then,
the following condition holds 0 > Z + He

R
1
∆
t
R
2

,
if the following condition is ensured:
0 >

Z + αR
1
R
T
1
(∗)
R
2
− αI

.
The target of this paper is to design a reliable asyn-
chronous controller such that the closed-loop system
(10) of the continuous-time multi-agent system (5) is
stochastically stable with H
∞
performance level.
3 MAIN RESULTS
Let us choose the Lyapunov function candidate de-
pendent on the asynchronous control network topol-
ogy mode ρ
t
= p:
V (t,ρ
t
) = ¯x
T
t

I
N
⊗ P
p

¯x
t
(13)
where 0 < P
p
= P
T
p
∈ R
n
x
×n
x
and I
N
⊗ P
p
=
diag(P
p
,P
p
,··· ,P
p
| {z }
N
). Then, the weak infinitesimal op-
erator of V (t,ρ
t
) is provided by
∇V (t, ρ
t
)
= lim
θ→0
1
θ
E
n
V (t + θ,ρ
t+θ
= q|φ
t
= g)
−V (t, ρ
t
= p|φ
t
= g)
o
= ¯x
T
t
He
n
(I
N
⊗
e
P
g
)

(I
N
⊗ A) +(L
g
+ M
g
) ⊗ BΓ
t
F
p

o
¯x
t
+ He
n
¯x
T
t
(I
N
⊗
e
P
g
D)
¯
f
t
o
+ ¯x
T
t

I
N
⊗ P
×
g

¯x
t
+ He
n
¯x
T
t
(I
N
⊗
e
P
g
E)w
t
o
(14)
where
e
P
g
=
∑
p∈N
ρ
ϖ
gp
P
p
, P
×
g
=
∑
h∈N
φ
∑
q∈N
ρ
π
gh
(t)ϖ
hq
P
q
.
In parallel, it follows from Assumption 1 that ||
¯
f
i
t
|| ≤
ε|| ¯x
i
t
||, which leads to
¯
f
T
t
¯
f
t
≤ ¯x
T
t
(I
N
⊗ ε
2
I
n
x
) ¯x
t
. (15)
Then (15) and Lemma 2.1 allow
He
n
¯x
T
t
(I
N
⊗
e
P
g
D)
¯
f
t
o
≤ ¯x
T
t

I
N
⊗
e
P
g
DD
T
e
P
g

¯x
t
+
¯
f
T
t
¯
f
t
≤ ¯x
T
t

I
N
⊗
e
P
g
DD
T
e
P
g

¯x
t
+ ¯x
T
t
(I
N
⊗ ε
2
I
n
x
) ¯x
t
= ¯x
T
t

I
N
⊗
∑
p∈N
ρ
ϖ
gp
P
p
DD
T
P
p

¯x
t
+ ¯x
T
t
(I
N
⊗ ε
2
I
n
x
) ¯x
t
.
Next, let us define η
T
t
=

¯x
T
t
| w
T
t

, the H
∞
leader-
following consensus condition of (10) is constructed
by
||z
t
||
2
− γ
2
||w
t
||
2
+ ∇V (t, ρ
t
)
≤ η
T
t
Ξη
t
< 0 (16)
where
Ξ =

Ξ
11
(∗)
(I
N
⊗ E
T
e
P
g
) −γ
2
I
N·n
w

Ξ
11
= He
n
I
N
⊗
e
P
g
A
o
+

I
N
⊗ P
×
g

+

I
N
⊗ ε
2
I
n
x

+ He
n
(I
N
⊗
e
P
g
)

(L
g
+ M
g
) ⊗ BΓ
t
F
p

o
+ (I
N
⊗C
T
C)
+ I
N
⊗
∑
p∈N
ρ
ϖ
gp
P
p
DD
T
P
p
!
.
To deal with the non-convexity of time-varying
transition rates π
gh
(t) in parameterized linear ma-
trix inequalities (PLMIs), the following theorem pro-
vides the relaxed reliable H
∞
control synthesis condi-
tions, formulated in terms of linear matrix inequalities
(LMIs). 5
Theorem 3.1. For given scalars ε and β, there ex-
ists 0 <
¯
P
p
=
¯
P
T
p
∈ R
n
x
×n
x
, Q
pq
= Q
T
pq
∈ R
n
x
×n
x
,
¯
F
p
∈ R
n
u
×n
x
, T
gh
= T
T
gh
∈ R
n
x
×n
x
, X
g
∈ R
n
x
×n
x
, scalars
0 < γ, and 0 < α
g
, such that the following conditions
hold: for g ∈ N
φ
and p ∈ R
ρ
0 >


Ω
(1)
+ T
(1)
+ X
(1)
(∗) (∗)
Ω
(2)
+ T
(2)
+ X
(2)
T
(3)
0
Ω
(3)
+ X
(3)
0 0


(17)
0 ≤

Q
pq
(∗)
¯
P
p
¯
P
q

, ∀q ∈ N
ρ
(18)
where
A Novel Reliable Leader-Following Consensus for Continuous-Time Multi-Agent Systems Under Nonhomogeneous and Asynchronous
Markov Network Topology
489

Ω
(1)
=





Ω
⋆
11
(∗) (∗) (∗) (∗)
(I
N
⊗ E
T
) −γ
2
I
N·n
w
0 0 0
(I
N
⊗ ε
¯
P
p
) 0 −I
N·n
x
0 0
(I
N
⊗C
¯
P
p
) 0 0 −I
N·n
z
0
(I
N
⊗ S
¯
F
p
) 0 0 0 −α
g
I
N·n
u





Q
q
(β) =
∑
q∈N
ρ
ϖ
hq
Q
pq
+
∑
q∈N
ρ
ϖ
gq
β
2
¯
P
q
− 2β
¯
P
p
Ω
⋆
11
= I
N
⊗

He{A
¯
P
p
} + DD
T

+ He{(L
g
+ M
g
) ⊗ BR
¯
F
p
}
+ α
g
((L
g
+ M
g
) ⊗ B)((L
g
+ M
g
) ⊗ B)
T
+


I
N
⊗
∑
h∈N
⋆
g
\{g}
π
gh
Q
q
(β)


Ω
(2)
=

I
N
⊗
1
2
Q
q
(β)

χ

h∈
e
N
g
\{g}
Ω
(3)
=

I
N
⊗
1
2
Q
q
(β)

χ

h∈N
×
g
\{g}
T
(1)
= χ
T


I
N
⊗
∑
h∈
e
N
g
\{g}
π
gh
π
gh
T
gh


χ
T
(2)
=

I
N
⊗
1
2
(−π
gh
− π
gh
)T
gh

χ

h∈
e
N
g
\{g}
T
(3)
= [(I
N
⊗ T
gh
)]
d
h∈
e
N
g
\{g}
X
(1)
=
(
χ
T

I
N
⊗ He
n
∑
h∈N
⋆
g
π
gh
X
g
o
χ, if g ∈ N
⋆
g
0, otherwise
X
(2)
=
(
[(I
N
⊗ X
g
)χ]
h∈
e
N
g
\{g}
, if g ∈ N
⋆
g
0, otherwise
X
(3)
=
(
[(I
N
⊗ X
g
)χ]
h∈N
×
g
\{g}
, if g ∈ N
⋆
g
0, otherwise
χ =

I
N·n
x
0 0 0 0

∈ R
N·n
x
×N·n
χ
n
χ
= 2n
x
+ n
w
+ n
z
+ n
u
.
Proof: From the property of (8) that
∑
p∈N
ρ
ϖ
gp
=
1, it can be referred (16) to the following control-
topology-dependent H
∞
leader-following consensus:
0 > Ξ =
∑
p∈N
ρ
ϖ
gp
Ξ
p
(19)
where
Ξ
p
=






He
{
I
N
⊗ P
p
A
}
+

I
N
⊗ P
×
g

+ He
{
(L
g
+ M
g
) ⊗ P
p
BΓ
t
F
p
}
+

I
N
⊗ P
p
DD
T
P
p

+

I
N
⊗ ε
2
I
n
x

+ (I
N
⊗C
T
C)
(∗)
(I
N
⊗ E
T
P
p
) −γ
2
I
N·n
w






.
In addition, from the property of (8) that ϖ
gp
∈
[0,1], it can be referred (19) to the following control-
topology-dependent H
∞
leader-following consensus:
0 > Ξ
p
(20)
where its Schur complement can be represented by
Ξ
p
=




Ξ
11,p
(∗) (∗) (∗)
(I
N
⊗ E
T
P
p
) −γ
2
I
N·n
w
0 0
(I
N
⊗ εI
n
x
) 0 −I
N·n
x
0
(I
N
⊗C) 0 0 −I
N·n
z




Ξ
11,p
= I
N
⊗

He{P
p
A} + P
p
DD
T
P
p

+

I
N
⊗ P
×
g

+ He
{
(L
g
+ M
g
) ⊗ P
p
BΓ
t
F
p
}
.
Next, let us perform the congruence transformation
on (20) by diag(I
N
⊗
¯
P
p
,I
N·n
w
,I
N·n
x
,I
N·n
z
) and its
transpose, which leads to
0 >




¯
Ξ
11,p
(∗) (∗) (∗)
(I
N
⊗ E
T
) −γ
2
I
N·n
w
0 0
(I
N
⊗ ε
¯
P
p
) 0 −I
N·n
x
0
(I
N
⊗C
¯
P
p
) 0 0 −I
N·n
z




(21)
where
¯
Ξ
11,p
= I
N
⊗

He{A
¯
P
p
} + DD
T

+

I
N
⊗
¯
P
p
P
×
g
¯
P
p

+ He
{
(L
g
+ M
g
) ⊗ BΓ
t
¯
F
p
}
¯
P
p
= P
−1
p
,
¯
F
p
= F
p
¯
P
p
.
Especially, to deal with the non-convexity emerged
from the multiplication time-varying transition rates
and topology-dependent conditional probability,
based on (1), the following equality is definitely
necessary
¯
P
p
P
×
g
¯
P
p
=
∑
h∈N
φ
\{g}
π
gh
(t)
∑
q∈N
ρ
ϖ
hq
¯
P
p
P
q
¯
P
p
−
∑
q∈N
ρ
ϖ
gq
¯
P
p
P
q
¯
P
p
!
. (22)
Moreover, Lemma 2.1 allows that
−
¯
P
p
P
q
¯
P
p
≤ β
2
P
−1
q
− 2β
¯
P
p
. (23)
Based on (23) and (18) ensuring
¯
P
p
P
q
¯
P
p
≤ Q
pq
, (22)
can be bounded by
I
N
⊗
¯
P
p
P
×
g
¯
P
p
≤
∑
h∈N
φ
\{g}
π
gh
(t)(I
N
⊗ Q
q
(β)) (24)
where
Q
q
(β) =
∑
q∈N
ρ
ϖ
hq
Q
pq
+
∑
q∈N
ρ
ϖ
gq
β
2
¯
P
q
− 2β
¯
P
p
.
Thus, by combining (24) and recalling Γ
t
= R + ∆
t
S,
(21) can be ensured by
0 >




Ω
11,∆
(∗) (∗) (∗)
(I
N
⊗ E
T
) −γ
2
I
N·n
w
0 0
(I
N
⊗ ε
¯
P
p
) 0 −I
N·n
x
0
(I
N
⊗C
¯
P
p
) 0 0 −I
N·n
z




(25)
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
490

where
Ω
11,∆
= I
N
⊗

He{A
¯
P
p
} + DD
T

+ He{(L
g
+ M
g
) ⊗ BR
¯
F
p
}
+ He{(L
g
+ M
g
) ⊗ B∆
t
S
¯
F
p
}
+


∑
h∈N
φ
\{g}
π
gh
(t)(I
N
⊗ Q
q
(β))


.
Under the help of Lemma 2.2 and the usage of χ =

I
N·n
x
0 0 0 0

, (25) is equivalent to
0 > Ω + χ
T


∑
h∈N
φ
\{g}
π
gh
(t)(I
N
⊗ Q
q
(β))


χ (26)
where
Ω =





Ω
11
(∗) (∗) (∗) (∗)
(I
N
⊗ E
T
) −γ
2
I
N·n
w
0 0 0
(I
N
⊗ ε
¯
P
p
) 0 −I
N·n
x
0 0
(I
N
⊗C
¯
P
p
) 0 0 −I
N·n
z
0
(I
N
⊗ S
¯
F
p
) 0 0 0 −α
g
I
N·n
u





Ω
11
= I
N
⊗

He{A
¯
P
p
} + DD
T

+ He{(L
g
+ M
g
) ⊗ BR
¯
F
p
}
+ α
g
((L
g
+ M
g
) ⊗ B)((L
g
+ M
g
) ⊗ B)
T
.
Next, let us denote some useful matrices as follows:
ζ
1
(t) =

π
gh
(t)

h∈
e
N
g
\{g}
, ζ
2
(t) =

π
gh
(t)

h∈N
×
g
\{g}
Φ
T
(t) =

I |

ζ
1
(t) ⊗ χ

T
|

ζ
2
(t) ⊗ χ

T

.
Based on N
φ
= N
⋆
g
+
e
N
g
+ N
×
g
, (26) is rewritten by
0 > Ω + χ
T


∑
h∈N
⋆
g
\{g}
π
gh
(I
N
⊗ Q
q
(β))
+
∑
h∈
e
N
g
S
N
×
g
\{g}
π
gh
(t)(I
N
⊗ Q
q
(β))


χ
= Ω
(1)
+ He
n

ζ
1
(t) ⊗ χ

T
Ω
(2)
o
+ He
n

ζ
2
(t) ⊗ χ

T
Ω
(3)
o
. (27)
Further, it can be referred from (26) that 0 > T
(3)
en-
suring 0 > T
gh
for all h ∈
e
N
g
\ {g}. Then, it follows
from (3) that
0 ≤
∑
h∈
e
N
g
\{g}
(π
gh
(t) − π
gh
)(π
gh
(t) − π
gh
)χ
T

I
N
⊗ T
gh

χ
= T
(1)
+ He
n

ζ
1
(t) ⊗ χ

T
T
(2)
o
+

ζ
1
(t) ⊗ χ

T
T
(3)

ζ
1
(t) ⊗ χ

. (28)
Especially, if g ∈ N
⋆
g
, (4) leads to
0 =


∑
h∈N
⋆
g
π
gh
+
∑
h∈
e
N
g
\{g}
π
gh
(t) +
∑
h∈
e
N
+
g
\{g}
π
gh
(t)


× χ
T
He

I
N
⊗ X
g

χ
= X
(1)
+ He
n

ζ
1
(t) ⊗ χ

T
X
(2)
o
+ He
n

ζ
2
(t) ⊗ χ

T
X
(3)
o
. (29)
Hence, according to the S-procedure and the defini-
tion of Φ(t), combining (27) with (28) and (29) re-
sults in
0 > Φ
T
(t)


Ω
(1)
+ T
(1)
+ X
(1)
(∗) (∗)
Ω
(2)
+ T
(2)
+ X
(2)
T
(3)
0
Ω
(3)
+ X
(3)
0 0


Φ(t)
which directly leads to (17).
4 NUMERICAL EXAMPLE
Let us consider the multi-agent system featuring three
followers and one leader, as discussed in (He et al.,
2020):
A =


−3 0 1
0 0 0
0 0 −1


, B =


0
1
0


, E =


1.0
0.1
1.0


C =

0.2 0.8 1.0

, D =


0.2 0
0.1 0.1
0.1 0


. (30)
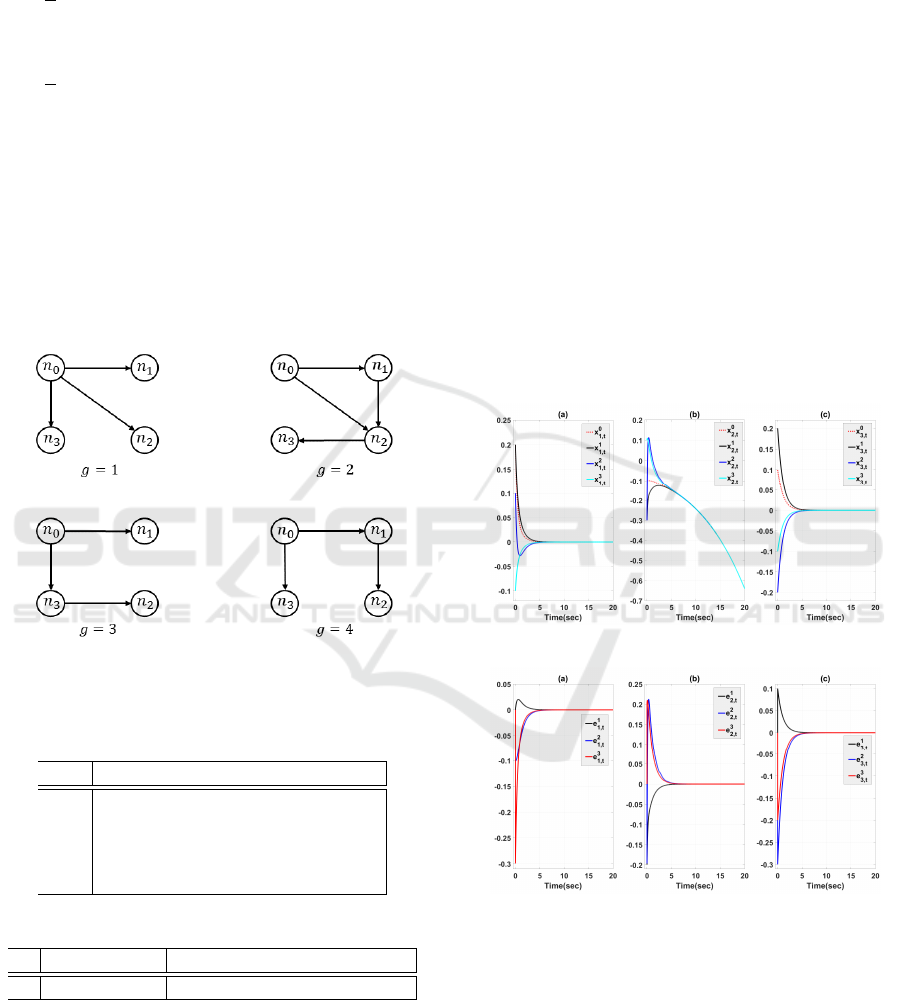
Fig. 1 shows the directed graph of the multi-agent
system (30) with the nonhomogeneous Markov net-
work topology. As shown in Fig. 1, one can es-
tablish the network-topology-dependent leader ad-
jacency matrices M
φ
t
and the network-topology-
dependent Laplacian matrices L
φ
t
as follows, for
N
φ
= {1,2,3,4}:
M
1
= diag(1,1, 1), M
2
= diag(1,1, 0)
M
3
= diag(1,0, 1), M
4
= diag(1,0, 1)
L
1
=


0 0 0
0 0 0
0 0 0


, L
2
=


0 0 0
−1 1 0
0 −1 1


L
3
=


0 0 0
0 1 −1
0 0 0


, L
4
=


0 0 0
−1 1 0
0 0 0


.
The actuator fault level is given by (Γ
1
,Γ
1
=
(0.8,1.0). Further, the bounds of π
gh
(t) ∈ [π
gh
,π
gh
]
A Novel Reliable Leader-Following Consensus for Continuous-Time Multi-Agent Systems Under Nonhomogeneous and Asynchronous
Markov Network Topology
491

and condition probability ϖ
gp
are:

π
gh

g,h∈N
φ
=



−2.0 0.1 × ×
× × 0.1 0.1
0.2 × −2.0 ×
0.1 × × ×




π
gh

g,h∈N
φ
=



−1.0 0.5 × ×
× × 0.6 0.8
0.9 × −1.0 ×
0.8 × × ×




ϖ
gp

g∈N
φ
,p∈N
ρ
=



0.5 0.2 0.1 0.2
0.2 0.5 0.1 0.2
0.1 0.2 0.5 0.2
0.2 0.2 0.1 0.5



where “×” denotes the entirely unknown transition
rate. Based one the availability of transition rates
π
gh
(t), one can obtain the following network topol-
ogy sets in Table 1. By applying Theorem 3.1, Ta-
Figure 1: Network-topology-dependent digraphs for g ∈
N
φ
= {1, 2,3, 4}.
Table 1: Network topology mode subsets for each network
topology mode g.
g Network topology mode subsets
1 N
⋆
1
=
/
0,
e
N
1
= {1,2}, N
×
1
= {3,4}
2 N
⋆
2
=
/
0,
e
N
2
= {3,4}, N
×
2
= {1,2}
3 N
⋆
3
=
/
0,
e
N
3
= {1,3}, N
×
3
= {2,4}
4 N
⋆
4
=
/
0,
e
N
4
= {1}, N
×
4
= {2,3,4}
Table 2: Comparison of H
∞
performance levels.
Theorem 3.1 (He et al., 2020, Theorem 2)
γ 1.4068 1.5139
ble 2 displays the comparison between the minimum
H
∞
performance level γ obtained by (He et al., 2020,
Theorem 2) and Theorem 1. As shown in Table 2,
the reliable H
∞
control synthesis condition outlined
in Theorem 3.1 attains better performance compared
to (He et al., 2020, Theorem 2). Especially, differ-
ent from (He et al., 2020, Theorem 2), Theorem 3.1
even opens up the possibility to deal with the appear-
ance of actuator faults. Then, for β = 1.0 and ε = 0.5,
the asynchronous control gains are determined as fol-
lows:
F
1
=

−2.1250 −12.2710 −11.0770

F
2
=

−2.1250 −11.7660 −10.5670

F
3
=

−2.0630 −11.4580 −10.2930

F
4
=

−2.2540 −12.8940 −11.6260

(31)
where f (x
i
t
) =

sin(x
i
1,t
) sin(x
i
2,t
)

T
. Based on (31),
Figs. 2-(a), (b), and (c) demonstrate the state re-
sponses of (30) with w
t
≡ 0, where x
0
0
= [0.2 −
0.1 0.1]
T
, x
1
0
= [0.2 − 0.3 0.2]
T
, x
2
0
= [0.1 −
0.3 − 0.2]
T
, and x
3
0
= [−0.1 0.1 − 0.1]
T
. More-
over, Figs. 3-(a), (b), and (c) display the error system
of three followers. Thus, as illustrated in Fig. 2 and
Fig. 3, the leader-following consensus is successfully
achieved, even in the presence of asynchronous con-
trol topologies and actuator faults. In addition, for
Figure 2: State response of (30) with w
t
≡ 0.
Figure 3: Error tracking of (30) with w
t
≡ 0.
x
0
0
= x
1
0
= x
2
0
= x
3
0
= 0, Figs. 4-(a), (b), and (c) demon-
strate the error responses ¯x
i
t
= x
i
t
− x
0
t
of (30) with
w
1
t
= 1,w
2
t
= −1,w
3
t
= 2, for t ∈ [0,3); w
1
t
= −1,w
2
t
=
1,w
3
t
= −2, for t ∈ [3, 6); and w
1
t
= w
2
t
= w
3
t
= 0,
otherwise. Fig. 4 illustrates the state trajectories
of each agent, highlighting their achievement of ro-
bust H
∞
leader-following consensus. Furthermore,
Figs. 5-(a), (b), and (c) display the error system of
three followers in this case, Fig. 5-(d) demonstrates
the control input applied to each follower, Fig. 5-(e)
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
492

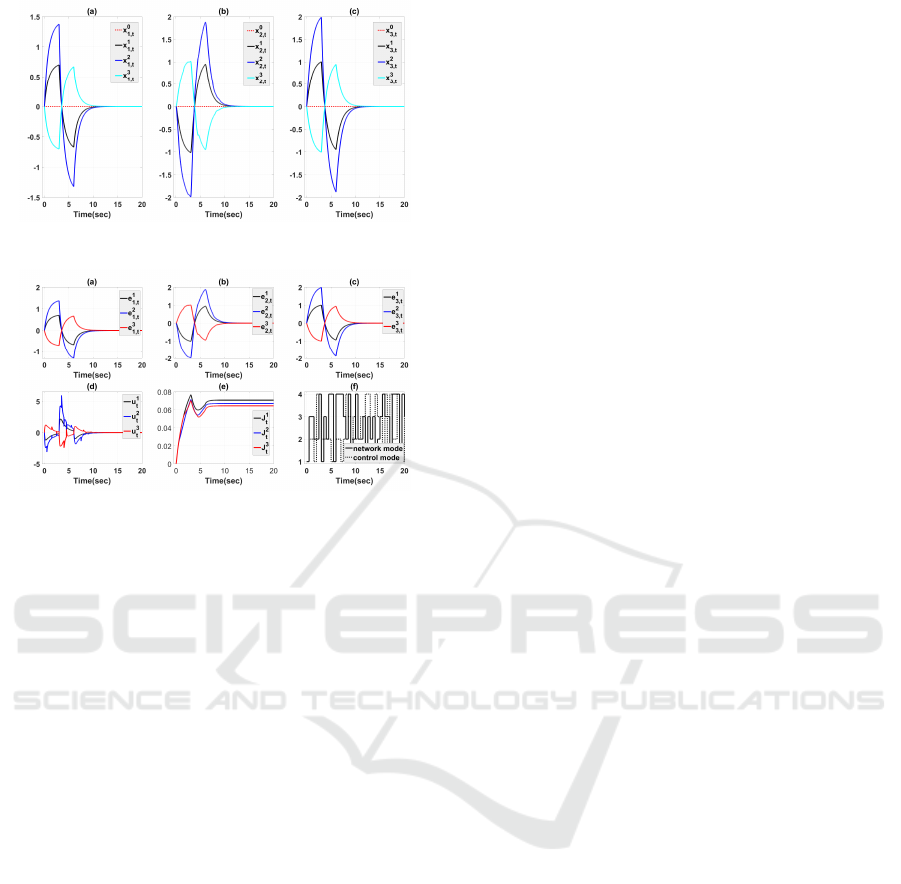
Figure 4: State response of (30) with w
t
̸= 0.
Figure 5: (a), (b), (c): Error tracking of (30) with w
t
̸=
0; (d): the control input of (30); (e): the real value of
J
i
t
=
R
t
0
∥z
i
τ
∥
2
dτ/
R
t
0
∥w
i
τ
∥
2
dτ; (f): mode evolution of net-
work topology and control topology.
shows the value of J
i
t
=
R
t
0
∥z
i
τ
∥
2
dτ/
R
t
0
∥w
i
τ
∥
2
dτ for
each follower, and Fig. 5-(f) displays the evolution
of the generated topologies for both the system net-
work and control input. As depicted in Fig. 5, the
error responses of a group of agents are approaching
to zero despite the occurrence of asynchronous con-
trol topologies, actuator faults, and non-zero distur-
bances. Additionally, Fig. 5-(e) reveals that the actual
H
∞
performance levels are lower than those derived
using Theorem 3.1.
5 CONCLUDING REMARKS
This paper tackles the challenge of ensuring re-
liable and asynchronous leader-following consen-
sus in multi-agent systems with nonhomogeneous
Markov network topologies. To simplifies transition
rate-dependent and conditional probability-dependent
consensus conditions into a finite set of solvable lin-
ear matrix inequalities, the proposed method i) intro-
duces an asynchronous control-topology-dependent
Lyapunov function, ii) develops an innovative relax-
ation technique distinct from exiting ones, which is
based on entirely unknown transition rates, and iii)
addresses the non-convexity arising from multiple
varying-time parameters. Looking ahead, our future
research will explore control strategies for leaderless
consensus in nonlinear multi-agent systems, particu-
larly in the context of denial-of-service attacks.
ACKNOWLEDGEMENTS
This work was sponsored by the National Research
Foundation of Korea Grant funded by the Korean
Government (NRF-2023R1A2C1002635).
REFERENCES
He, M., Mu, J., and Mu, X. (2020). H
∞
leader-following
consensus of nonlinear multi-agent systems under
semi-Markovian switching topologies with partially
unknown transition rates. Information Sciences,
513:168–179.
Li, W., Xie, L., and Zhang, J. (2015). Containment control
of leader-following multi-agent systems with marko-
vian switching network topologies and measurement
noises. Automatica, 51:263–267.
Nguyen, N. and Kim, S. (2019). Relaxed robust stabiliza-
tion conditions for nonhomogeneous Markovian jump
systems with actuator saturation and general switch-
ing policies. International Journal of Control, Au-
tomation and Systems, 17(3):586–596.
Nguyen, N. and Kim, S. (2021). Asynchronous H
∞
observer-based control synthesis of nonhomogeneous
Markovian jump systems with generalized incomplete
transition rates. Applied Mathematics and Computa-
tion, 411:126532.
Sakthivel, R., Sakthivel, R., Kaviarasan, B., and Alzahrani,
F. (2018). Leader-following exponential consensus
of input saturated stochastic multi-agent systems with
Markov jump parameters. Neurocomputing, 287:84–
92.
Takaba, K. (1998). Robust H
2
control of descriptor system
with time-varying uncertainty. International Journal
of Control, 71(4):559–579.
Valentine, F. (1945). A lipschitz condition preserving ex-
tension for a vector function. American Journal of
Mathematics, 67(1):83–93.
Wang, Y., Xia, J., Wang, Z., Zhou, J., and Shen, H.
(2019). Reliable consensus control for semi-Markov
jump multi-agent systems: A leader-following strat-
egy. Journal of the Franklin Institute, 356(6):3612–
3627.
Xie, L. and de Souza, C. (1990). Robust H
∞
control for lin-
ear time-invariant systems with norm-bounded uncer-
tainty in the input matrix. Systems & Control Letters,
14(5):389–396.
Yang, H., Zhang, H., Wang, Z., and Yan, H. (2023).
Reliable leader-following consensus of discrete-time
semi-Markovian jump multi-agent systems. IEEE
Transactions on Network Science and Engineering,
10(6):3505–3518.
A Novel Reliable Leader-Following Consensus for Continuous-Time Multi-Agent Systems Under Nonhomogeneous and Asynchronous
Markov Network Topology
493