Uncertainty-Aware DNN for Multi-Modal Camera Localization

M. Vaghi

1 a

, A. L. Ballardini

2 b

, S. Fontana

1 c

and D. G. Sorrenti

1 d

Universit

a degli Studi di Milano - Bicocca, Milan, Italy

Universidad de Alcal

a, Alcal

a de Henares, Spain

Keywords:

Camera Localization, Deep Learning, Uncertainty Estimation.

Abstract:

Camera localization, i.e., camera pose regression, represents an important task in computer vision with many

practical applications such as in the context of intelligent vehicles and their localization. Having reliable es-

timates of the regression uncertainties is also important, as it would allow us to catch dangerous localization

failures. In the literature, uncertainty estimation in Deep Neural Networks (DNNs) is often performed through

sampling methods, such as Monte Carlo Dropout (MCD) and Deep Ensemble (DE), at the expense of un-

desirable execution time or an increase in hardware resources. In this work, we considered an uncertainty

estimation approach named Deep Evidential Regression (DER) that avoids any sampling technique, providing

direct uncertainty estimates. Our goal is to provide a systematic approach to intercept localization failures

of camera localization systems based on DNNs architectures, by analyzing the generated uncertainties. We

propose to exploit CMRNet, a DNN approach for multi-modal image to LiDAR map registration, by mod-

ifying its internal conﬁguration to allow for extensive experimental activity on two different datasets. The

experimental section highlights CMRNet’s major ﬂaws and proves that our proposal does not compromise the

original localization performances, but also provides the necessary introspection measures that would allow

end-users to act accordingly.

1 INTRODUCTION

Although DNN-based techniques achieve outstanding

results in camera localization (Radwan et al., 2018;

Sarlin et al., 2021), a main challenge is still unsolved:

to determine when such models are providing a re-

liable localization output since inaccurate estimates

could endanger other road users. Therefore, being

able to assign a reliable degree of uncertainty to the

model predictions allows us to decide whether the

outputs can be safely used for navigation (McAllister

et al., 2017).

The uncertainty associated with the model output

can be of two different types: aleatoric and epistemic.

“Aleatoric uncertainty represents the effect on the out-

put given by variability of the input data that can-

not be modeled: this uncertainty cannot be reduced

even if more data were to be collected. Epistemic

uncertainty, on the other hand, quantiﬁes the lack of

knowledge of a model, which arises from the limited

https://orcid.org/0000-0003-1093-7270

https://orcid.org/0000-0001-6688-5081

https://orcid.org/0000-0001-7823-8973

https://orcid.org/0000-0002-4734-7330

Figure 1: We compare three approaches for estimating un-

certainty in DNNs for camera localization by integrating

them in a camera-to-LiDAR map registration model. We

assess uncertainty quality by measuring calibration, show-

ing that we obtain competitive results with a DER-based

approach.

amount of data used for tuning its parameters. This

uncertainty can be mitigated with the usage of more

data.” Adapted from (Kendall and Gal, 2017).

DNN-based camera localization proposals that

also estimate uncertainty already exist in the litera-

ture, e.g., (Kendall and Cipolla, 2016; Deng et al.,

Vaghi, M., Ballardini, A., Fontana, S. and Sorrenti, D.

Uncertainty-Aware DNN for Multi-Modal Camera Localization.

DOI: 10.5220/0013064600003822

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 21st International Conference on Informatics in Control, Automation and Robotics (ICINCO 2024) - Volume 2, pages 80-90

ISBN: 978-989-758-717-7; ISSN: 2184-2809

2022). However, only partial comparisons with the

consolidated approaches are available, e.g., (Kendall

and Cipolla, 2016) just deals with MCD. In ad-

dition, since those techniques deal only with image

data, their effectiveness with multi-modal approaches

should be explored.

Given the importance of uncertainty estimation

for DNN-based camera localization, in this work we

propose an application of DER for epistemic uncer-

tainty estimation in Convolutional Neural Networks

(CNNs) within a multi-modal camera localization ap-

proach, and show that the proposed approach achieves

competitive results compared to other sampling-based

techniques (Gal and Ghahramani, 2016; Lakshmi-

narayanan et al., 2017) in terms of localization ac-

curacy, uncertainty calibration, and failures detection

(Figure 1). We chose CMRNet (Cattaneo et al., 2019),

an approach for camera localization using a camera

image and an available 3D map, typically built from

LiDAR data. The reason for this is the ability of such

a model to provide accurate localisation estimates at

high frequencies allowing it to be used in a more re-

alistic scenario. Moreover, we consider it signiﬁcant

to have developed a version of a camera localization

DNN model that is able to estimate uncertainty by us-

ing DER.

2 RELATED WORK

In the last decade, many DNN-based approaches for

camera localization emerged. In general, we can

divide existing methods into two categories: cam-

era pose regression (Kendall et al., 2015; Kendall

and Cipolla, 2017; Radwan et al., 2018; Yin and

Shi, 2018; Sarlin et al., 2021) and place recognition

(Arandjelovic et al., 2016; Zhu et al., 2018; Hausler

et al., 2021) techniques.

Using an image, the former category predicts

the pose of a camera, while the latter ﬁnds a cor-

respondence with a previously visited location, de-

picted in another image. Multi-modal approaches,

which employ image and Light Detection And Rang-

ing (LiDAR) data, propose to jointly exploit visual in-

formation and the 3D geometry of a scene to achieve

higher localization accuracy (Wolcott and Eustice,

2014; Caselitz et al., 2016; Neubert et al., 2017). Re-

cently, DNN-based methods emerged also for image-

to-LiDAR-map registration. An example is CMRNet

(Cattaneo et al., 2019), which performs direct re-

gression of the camera pose by implicitly matching

RGB images with the corresponding synthetic LiDAR

image generated using a LiDAR map and a rough

camera pose estimate. Its ultimate goal is to re-

ﬁne common GPS localization measures. CMRNet

is map-agnostic. Feng et al. (Feng et al., 2019) pro-

posed another multi-modal approach, where a DNN is

trained to extract descriptors from 2D and 3D patches

by deﬁning a shared feature space between hetero-

geneous data. Localization is then performed by

exploiting points for which 2D-3D correspondences

have been found. Similarly, Cattaneo et al. (Cat-

taneo et al., 2020) proposed a DNN-based method

for learning a common feature space between images

and LiDAR maps to produce global descriptors, used

for place recognition. Although the previous multi-

modal pose regression techniques achieve outstanding

results, none of them estimate the epistemic uncer-

tainty of their predictions. This is a severe limitation,

especially considering the ﬁnal goal: to deploy them

in critical scenarios, where it is important to detect

when the model is likely to fail.

Epistemic uncertainty estimation in Neural Net-

works (NNs) is a known problem. In the last years,

different methods have been proposed to sample from

the model posterior (Kingma et al., 2015; Lakshmi-

narayanan et al., 2017) and, more recently, to pro-

vide a direct uncertainty estimate through eviden-

tial deep learning (Sensoy et al., 2018; Amini et al.,

2020; Meinert and Lavin, 2021). NNs uncertainty es-

timation gained popularity also in the computer vi-

sion ﬁeld (Kendall and Gal, 2017; Kendall et al.,

2018), and different uncertainty-aware camera-based

localization approaches have been proposed. For in-

stance, Kendall et al. (Kendall and Cipolla, 2016)

introduced Bayesian PoseNet, a DNN that estimates

the camera pose parameters and uncertainty by ap-

proximating the model posterior employing dropout

sampling (Gal and Ghahramani, 2016). Deng et al.

(Deng et al., 2022) proposed another uncertainty-

aware model, which relies on Bingham mixture mod-

els for estimating a 6DoF pose from an image. Re-

cently, Petek et al. (Petek et al., 2022) proposed an

approach to camera localization that exploits an ob-

ject detection module, which is used to enable local-

ization within sparse HD maps. In particular, their

method estimates the vehicle pose using the uncer-

tainty of the objects in the HD map using a DER

approach (Amini et al., 2020). Another interesting

approach is HydraNet (Peretroukhin et al., 2019),

which is a neural network for estimating uncertainty

on quaternions. All the mentioned techniques deal

with the problem of camera localization using only

images, they learn to localize a camera in the envi-

ronment represented in the training set. In contrast,

CMRNet is map-agnostic, i.e., by being able to take in

input a LiDAR-map, it can perform localization also

in previously unseen environments. Furthermore, to

Uncertainty-Aware DNN for Multi-Modal Camera Localization

Figure 2: In this picture the CMRNet + DER approach is shown. The last FC-layers (red) are modiﬁed according to the method

proposed by Amini et al. (Amini et al., 2020) for estimating the parameters m

= (γ

, ν

, α

, β

) of different Normal Inverse

Gamma (NIG) distributions. During training, L

(green) and L

evd

(grey) loss functions are computed both for translation and

rotation components.

the best of our knowledge, this is the ﬁrst work to

implement a DER-based approach for direct camera

localization.

3 METHOD

In this section, we present the methodology used to

integrate DER (Amini et al., 2020) and the popular

sampling techniques of MCD (Gal and Ghahramani,

2016) and DE (Lakshminarayanan et al., 2017) into a

camera localization model. Although they all assume

that epistemic uncertainty can be described by a nor-

mal distribution, they are different techniques and re-

quire different interventions on the network to which

they are applied. Therefore, in this section, we ﬁrst in-

troduce and then describe the modiﬁcations required

in CMRNet to estimate uncertainty using each of the

three different methods.

3.1 Introduction to CMRNet

CMRNet is a regression Convolutional Neural Net-

work (CNN) used to estimate the 6DoF pose of a cam-

era mounted on-board a vehicle navigating within a

LiDAR map (Cattaneo et al., 2019). In particular, this

model takes two different images as input: an RGB

image and a LiDAR image obtained by synthesizing

the map as viewed from an initial rough camera pose

estimate H

init

. CMRNet performs localization by im-

plicitly matching features extracted from both images,

and estimates the misalignment H

out

between the ini-

tial and the camera pose. In this case, H represents a

generic rototranslation matrix:

H =



(3,3)

(3,1)

(1,3)



∈ SE(3) (1)

where R

(3,3)

and T

(3,1)

are a rotation matrix and a

translation vector respectively. In particular, H

out

computed as: tr

(1,3)

= (x, y, z) for translations, and

unit quaternion q

(1,4)

= (q

, q

) for rotations.

We propose to estimate its epistemic uncertainty by

providing a reliability value for each pose component.

The estimation of possible cross-correlations between

the pose components has not been considered in this

paper.

3.2 Uncertainty-Aware CMRNet

We deﬁne an input camera image with I

, an input

LiDAR image as I

, a set of trained weights with W

and an Uncertainty Aware (UA) version of CMRNet

as a function f (I

, I

, W).

Monte Carlo Dropout: The idea behind MCD is to

sample from a posterior distribution by providing dif-

ferent output estimates given a single input, which

are later used for computing the mean and variance

of a Gaussian distribution. This sampling is per-

formed by randomly deactivating the weights of the

fully-connected layers using a random dropout func-

tion d(W, p) multiple times during model inference,

where p represents the dropout probability. There-

fore, for MCD there is no modiﬁcation of the network

architecture. We applied the dropout to the regres-

sion part of the original CMRNet architecture. When

many correlations between RGB and LiDAR features

are found, we expect to obtain similar samples, de-

spite the dropout application, that is, we expect our

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

model to be more conﬁdent with respect to its predic-

tions. For each pose parameter µ

, we compute the

predicted value and the corresponding epistemic un-

certainty as follows:

E [µ

] =

∑

f (I

, I

, d

regr

(W, p)),

Var[µ

] =

∑

( f (I

, I

, d

regr

(W, p)) − E [µ

])

(2)

where n is the number of samples drawn for a given

input. Please note that E [µ

] and Var[µ

], for the ori-

entation, are computed after the conversion from unit

quaternion to Euler angles.

Deep Ensemble: DE-based approaches perform pos-

terior sampling by exploiting different models trained

using different initialization of the weights, but shar-

ing the same architecture.

Using different parameterizations of the same

model leads to the recognition of a wider range of

data-patterns, and to an increment of the overall ac-

curacy (Fort et al., 2019). On the other hand, when

receiving in input patterns not well-represented in the

training set, all the Neural Network (NN)s in the en-

semble would give out low-quality results, so leading

to an increment of variance. In our case, we expect to

obtain large epistemic uncertainty when each model

identiﬁes a different set of correspondences between

RGB and LiDAR features, leading to signiﬁcant dif-

ferent pose estimates. By training CMRNet n times

with different random initializations, we obtain a set

of weights W

set

= {W

, ..., W

}, which describe dif-

ferent local minima of the model function f (·). For

each pose parameter µ

we compute the predicted ex-

pected value and the corresponding epistemic uncer-

tainty as follows:

E [µ

] =

∑

j=1

f (I

, I

, W

Var[µ

] =

∑

j=1

( f (I

, I

, W

) − E [µ

])

(3)

where n represents the number of models of the en-

semble. In this case too, E [µ

] and Var[µ

] of rotations

are computed after the conversion from unit quater-

nion to Euler angles.

Deep Evidential Regression: While adapting to

MCD and DE methods does not require particular

modiﬁcations of CMRNet, the technique proposed by

Amini et al. (Amini et al., 2020) requires substantial

changes both in the training procedure and in the ﬁnal

part of the architecture.

In Deep Evidential Regression, the main goal

is to estimate the parameters of a Normal Inverse

Gamma distribution NIG(γ, ν, α, β). A neural net-

work is trained to estimate the NIG parameters, which

are then used to compute the expected value and the

corresponding epistemic uncertainty, for each pose

parameter:

E [µ] = γ, Var[µ] =

ν(α − 1)

(4)

To train the model, the authors propose to exploit

the Negative Log Likelihood L

NLL

and the Regular-

ization L

loss functions to maximize and regularize

evidence:

L(W) = L

NLL

(W) + λ · L

(W) (5)

NLL

= −log p(y|m) L

= Φ · |y − γ| (6)

where Φ = 2ν + α is the amount of evidence, see

(Amini et al., 2020) for details, and λ represents a

manually-set parameter that affects the scale of un-

certainty, p(y|m) represents the likelihood of the NIG.

Note that, p(y|m) is a pdf that follows a t-Student dis-

tribution St(γ,

β(1+ν)

να

, 2α) evaluated with respect to a

target y.

One of the main advantages of DER is to provide a

direct estimate of epistemic uncertainty and to employ

less resources than sampling-based methods. For a

complete description of loss functions and theoretical

aspects of DER, please refer to the work of Amini et

al. (Amini et al., 2020).

To integrate DER within CMRNet, we need to

deal with the following issues: how to apply DER

for regressing multiple parameters, how to manage

rotations, and how to aggregate the results when com-

puting the ﬁnal loss. We changed the last FC-layers,

which predict the rotation q

(1,4)

= (q

, q

) and

translation tr

(1,3)

= (x, y, z) components, in order to

estimate the NIG distributions associated to each pose

parameter. As it can be seen in Figure 2, we modiﬁed

CMRNet to regress Euler angles instead of quater-

nions, then we changed the FC-layers to produce

the matrices eul

(4,3)

and tr

(4,3)

, where each column

|γ

, ν

, α

, β

′

represents a speciﬁc NIG (Amini et al.,

2020).

Since the original CMRNet model represents rota-

tions using unit quaternions q

(1,4)

, we cannot compute

the L

NLL

and L

loss functions directly, as addition

and multiplication have different behavior on the S

manifold. As mentioned above, we modiﬁed the last

FC-layer of CMRNet to directly estimate Euler angles

eul

(1,3)

= (r, p, y). We also substitute the quaternion

distance-based loss used in (Cattaneo et al., 2019)

with the smooth L

loss (Girshick, 2015), which will

Uncertainty-Aware DNN for Multi-Modal Camera Localization

be later used also in L

and L

, by also consider-

ing the discontinuities of Euler angles. Although the

Euler angles representation is not optimal (Schneider

et al., 2017), it allows for easier management of the

training procedure and enables a direct comprehen-

sion of uncertainty for rotational components. As we

will demonstrate in Sec. 4, this change does not pro-

duce a decrease in accuracy.

Since CMRNet performs multiple regressions, it

is necessary to establish an aggregation rule for the

NLL

and L

loss functions, which are computed for

each predicted pose parameter. With the application

of the original loss as in (Amini et al., 2020) we expe-

rienced unsatisfactory results. We are under the im-

pression that, in our task, L

NLL

presents an undesir-

able behavior: since the negative logarithm function

is calculated over a probability density, it is not lower

bound, as the density gets near to be a delta.

We propose to overcome the previous issues by

avoiding the computation of the logarithm and con-

sidering a distance function that is directly based on

the probability density p(y|m), that is the pdf of the

t-Student distribution. Therefore, we replaced L

NLL

with the following loss L

and we also reformulate

∑

i=1

d(p(y

)

−1

, 0)

∑

i=1

d(y

, γ

) · Φ

(7)

Similarly to L

NLL

, the idea behind L

is to pe-

nalize predictions according to the conﬁdence level

output by our model with respect to the deviation be-

tween a target and an estimated values. However,

since this loss function admits a lower bound and is

deﬁned in the positive interval, it allows direct com-

putation of a distance metric d(·) on the vector of in-

verse densities. To ensure a better numerical stability,

we clip p(y

) when it returns too low density val-

ues, i.e., < 0.04. Regarding L

, we simply scale the

distance error on each pose component with the re-

spective evidence. We the compute the mean error by

managing rotations and translations separately. The

ﬁnal evidence loss is computed as follows:

evd

= L

+ λL

(8)

We noticed that the localization accuracy was de-

creasing when employing only L

evd

during training.

Therefore, we opted to also employ the original ge-

ometric loss function L

used in (Cattaneo et al.,

2019), and to employ the smooth L1 loss on rotations

as geometric loss L

rot

The overall loss is therefore computed as follows:

rot

= L

rot

+ s

evd

rot

· L

evd

rot

= L

+ s

evd

· L

evd

(9)

f inal

= s

rot

· L

rot

+ s

· L

(10)

where the s hyper-parameters represent scaling fac-

tors.

3.3 Training Details

For all three methods (i.e., MCD, DE, DER), we fol-

lowed a similar training procedure as in (Cattaneo

et al., 2019). We trained all models from scratch for a

total of 400 epochs, by ﬁxing a learning rate of 1e

−4

by using the ADAM optimizer and a batch size of 24

on a single NVidia GTX1080ti. The code was imple-

mented with the PyTorch library (Paszke et al., 2019).

Concerning the DE models, random weights ini-

tialization was performed by deﬁning a random

seed before each training. For DER we ini-

tially ﬁxed the scaling parameters (s

rot

, s

, λ

rot

) =

(1., 1., 0.01, 0.1) and (s

evd

rot

, s

evd

) = (0.1, 0.1). How-

ever, we experienced an increment of L

evd

after ap-

proximately 150 epochs. Therefore, we decided to

stop the training, change (s

evd

rot

, s

evd

) = (5e

−3

, 5e

−3

and then proceed with the training. This modiﬁca-

tion mitigated overﬁtting. Deactivating L

evd

during

the second training step led to uncalibrated uncertain-

ties.

4 EXPERIMENTAL RESULTS

The experimental activity described in the follow-

ing section has a dual purpose. On the one hand, it

proves that the localization performances of the pro-

posed models achieve comparable results concerning

the original CMRNet implementation, providing at

the same time reliable uncertainty estimates. On the

other hand, we propose one possible application of the

estimated uncertainties through a rejection scheme for

the vehicle localization problem.

4.1 Dataset

We used the KITTI odometry (Geiger et al., 2012)

and KITTI360 (Liao et al., 2022) datasets to train and

validate our models, implying that for each proposed

method we have two distinct training procedures, i.e.,

one for each dataset.

For the KITTI dataset, we followed the exper-

imental setting proposed in (Cattaneo et al., 2019)

and used images and LiDAR data from KITTI se-

quences 03 to 09, and sequence 00 for the assessment

of the estimated-uncertainty quality. Run 00 presents

a negligible overlap of approximately 4% compared

to the other sequences, i.e., resulting in a fair valida-

tion containing a different environment never seen by

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

Table 1: Localization Results.

KITTI KITTI360

Method

Translation Error (m) Rotation Error (deg) Translation Error (m) Rotation Error (deg)

median mean/std median mean/std median mean/std median mean/std

Rough Initial Pose 1.88 1.82 ± 0.56 9.8 9.6 ± 2.8 1.87 1.82 ± 0.56 9.8 9.6 ± 2.8

CMRNet (no iter) 0.52 0.65 ± 0.45 1.3 1.6 ± 1.2 0.40 0.48 ± 0.35 1.2 1.3 ± 0.8

CMRNet + MCD 0.58 0.69 ± 0.44 1.8 2.1 ± 1.3 0.44 0.52 ± 0.34 1.8 1.9 ± 1.0

CMRNet + DE 0.47 0.57 ± 0.39 1.2 1.5 ± 1.1 0.33 0.40 ± 0.29 1.0 1.2 ± 0.7

CMRNet + DER 0.54 0.65 ± 0.46 1.8 2.1 ± 1.4 0.39 0.48 ± 0.35 1.6 1.8 ± 1.0

Localization results of different CMRNet versions. We present the results of the original model without any iterative reﬁne-

ment (no iter), but the same strategy proposed in (Cattaneo et al., 2019) could be applied to all the other methods. Note that,

we do not alter CMRNet accuracy without DER-based approach.

CMRNet at training time. We exploited the ground

truth poses provided by (Behley et al., 2019) to cre-

ate accurate LiDAR maps. To simulate the initial

rough pose estimate, we added uniformly distributed

noise both on translation [−2m; +2m] and rotation

components [−10

◦

;+10

◦

]. To mimic real-life usage

and differently from (Cattaneo et al., 2019), we re-

moved all dynamic objects (e.g., cars and pedestrians)

from within the LiDAR maps, allowing some mis-

matches between the RGB image and the LiDAR im-

age. This aspect makes the task more difﬁcult since

now CMRNet has also to implicitly learn how to dis-

card incorrect matches.

We followed the previous procedure with the

KITTI360 dataset and we used sequences from 03 to

10 (∼ 40k samples) for training, run 02 (∼ 10.5k sam-

ples) for testing and sequence 00 (∼ 11.5k samples)

for validation.

4.2 Evaluation Metrics

We evaluated the proposed methods by comparing

both localization estimates and uncertainty calibration

accuracies. In particular, we assessed the localization

by measuring the euclidean and quaternion distances

between the ground truth and the estimated transla-

tion/rotation components. When considering DER,

we compute the quaternion distance by initially per-

forming a conversion from euler angles to unit quater-

nion.

Note that, differently from (Cattaneo et al., 2019),

our main goal is not to minimize the localization er-

ror. Instead, we aim to provide a reliability estimate

by means of epistemic uncertainty estimation without

undermining CMRNet performance. In particular, we

veriﬁed the accuracy of the estimated uncertainty us-

ing the calibration curves proposed by Kuleshov et

al. (Kuleshov et al., 2018). This procedure allows

us to reveal whether the trained model produces in-

ﬂated or underestimated uncertainties, by comparing

the observed and the ideal conﬁdence level.

4.3 Localization Assessment

Our experimental activities encompass the evaluation

of the localization performances using all the methods

presented in section 3.2, with respect to the original

CMRNet proposal.

Concerning CMRNet + MCD, we applied the

dropout to the FC layers with a probability of 0.3 and

obtained the approximated epistemic uncertainty by

exploiting 30 samples. Our extensive experimental

activity proves this setting provides the best trade-off

between accuracy, uncertainty calibration, and com-

putational time.

We implemented a similar approach to identify the

suitable number of networks as regards the CMRNet

+ DE approach. Here we identiﬁed the best perfor-

mances in using 5 networks, not noticing any perfor-

mance gain by adding more models to the ensemble.

Table 1 shows the obtained localization results, to-

gether with the statistics of the initial rough pose dis-

tribution and, in general, we observe the same trend

for each method across the KITTI and KITTI360

datasets. In particular, MCD decreases the perfor-

mances of the original CMRNet, resulting in the worst

method among those evaluated. On the other hand,

CMRNet + DE achieves the best results in terms of

accuracy, at the expense of having to train and exe-

cute n different networks. This method reduces the er-

rors’ standard deviation, as expected from ensemble-

based methods. Lastly, CMRNet + DER achieves re-

sults comparable to the original CMRNet implemen-

tation, proving that our modiﬁcations had any nega-

tive effect in terms of accuracy. Some applications

would appreciate the beneﬁts that such an approach

provides: a direct estimate of epistemic uncertainty,

i.e., a reduced computational time and space required

for inference, because of the absence of sampling. Ta-

ble 2 reports a brief ablation study performed on the

KITTI dataset to ﬁnd the optimal training parameter-

ization from which we obtained the best DER-based

model (last row). As shown in the previous localiza-

Uncertainty-Aware DNN for Multi-Modal Camera Localization

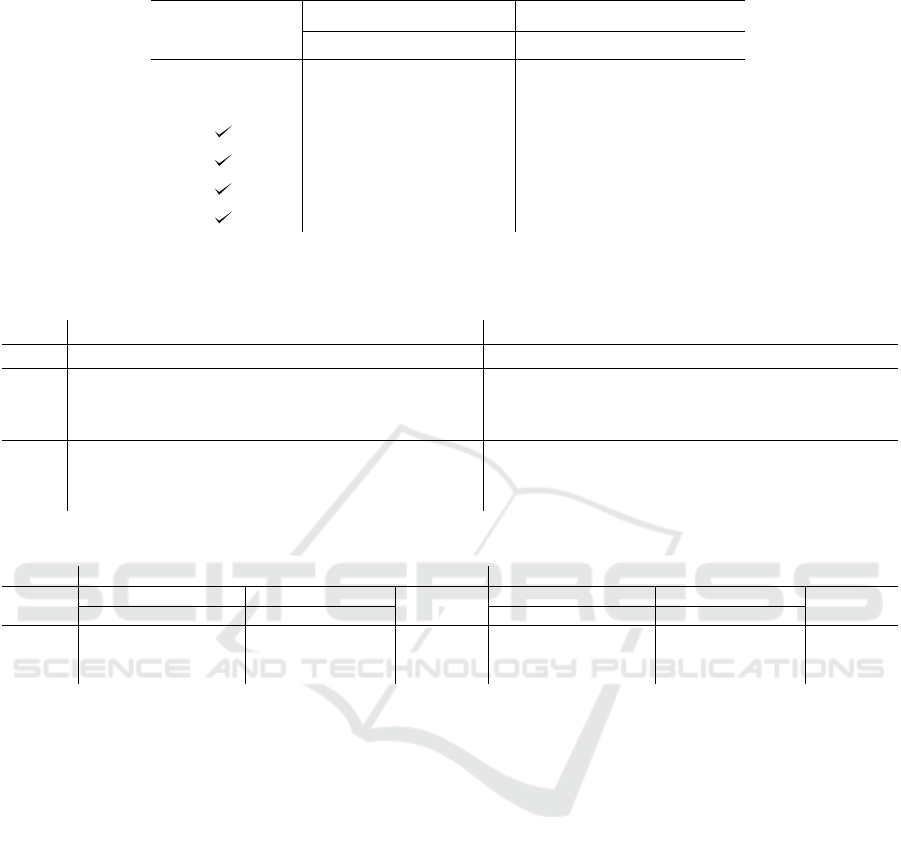
Table 2: Ablation study CMRNet + DER - KITTI dataset.

evd

Loc. Error (mean/std) Calib. Error (mean/std)

Tr. (m) Rot. (°) Tr. Rot.

NLL

- 1. 1.23 ± 0.57 2.0 ± 1.7 .080 ± .069 .135 ± .082

- 1. 0.91 ± 0.53 2.6 ± 1.5 .041 ± .041 .080 ± .074

NLL

−1

0.90 ± 0.56 1.8 ± 1.4 .090 ± .056 .172 ± .120

−1

074 ± 0.49 2.5 ± 1.4 .035 ± .027 .093 ± .079

NLL

−3

† 0.68 ± 0.49 1.7 ± 1.3 .107 ± .073 .150 ± .010

−3

† 0.65 ± 0.46 2.1 ± 1.4 .063 ± .040 .076 ± .060

† is the two training steps procedure described in section 3C.

Table 3: Mean Calibration Errors.

KITTI KITTI360

Axis MCD DE DER MCD DE DER

x 0.045 ± 0.025 0.077 ± 0.040 0.042 ± 0.023 0.054 ± 0.044 0.064 ± 0.040 0.018 ± 0.010

y 0.066 ± 0.032 0.093 ± 0.056 0.081 ± 0.052 0.042 ± 0.028 0.092 ± 0.061 0.026 ± 0.013

z 0.148 ± 0.082 0.062 ± 0.036 0.067 ± 0.027 0.171 ± 0.098 0.045 ± 0.022 0.080 ± 0.056

roll 0.126 ± 0.069 0.068 ± 0.033 0.080 ± 0.043 0.157 ± 0.092 0.149 ± 0.088 0.098 ± 0.054

pitch 0.162 ± 0.092 0.050 ± 0.041 0.106 ± 0.063 0.162 ± 0.091 0.123 ± 0.069 0.108 ± 0.069

yaw 0.069 ± 0.049 0.089 ± 0.057 0.042 ± 0.035 0.076 ± 0.042 0.067 ± 0.038 0.092 ± 0.052

Table 4: Localization Results - Discarded Predictions.

KITTI KITTI360

Method

Transl. Error (m) Rot. Error (deg) Discarded

Pred.

Transl. Error (m) Rot. Error (deg) Discarded

Pred.median mean/std median mean/std median mean/std median mean/std

MCD 0.58 0.68 ± 0.43 1.7 2.0 ± 1.2 27.2% 0.51 0.52 ± 0.34 1.7 1.8 ± 1.0 27.5 %

DE 0.42 0.50 ± 0.32 1.1 1.3 ± 0.8 24.7% 0.29 0.34 ± 0.22 1.0 1.1 ± 0.6 24.9 %

DER 0.49 0.58 ± 0.38 1.6 1.9 ± 1.1 22.0% 0.35 0.41 ± 0.26 1.5 1.6 ± 0.8 23.8%

tion accuracy experiments, such a parameterization

also gives optimal results on the KITTI360 datasets.

We observe the same trend in the uncertainty quality

assessment presented in the following sections.

4.4 Uncertainty Calibration

The quality of the uncertainty estimates, i.e., the mean

calibration errors for the translation and rotation com-

ponents, are reported in Table 3. The errors repre-

sent the mean distances between the ideal (i.e., y = x)

and the observed calibration, for each conﬁdence in-

terval. Furthermore, in Figure 3 we show the cali-

bration curves of the most relevant pose parameters.

All three methods obtain good uncertainty calibra-

tion, i.e., they provide realistic quantities. However,

CMRNet + DER shows a better performance in terms

of mean calibration errors, considering the most im-

portant pose parameters for a ground vehicle (x, y, and

yaw). We observe such a trend on both the datasets

considered during the experimental activity. Having a

well-calibrated uncertainty-aware model with normal

distributions has a major advantage, as its realistic un-

certainty estimates can be employed within error ﬁl-

tering algorithms, such as Kalman ﬁlters.

4.5 Inaccurate Predictions Detection

By measuring the calibration we test the ability of an

uncertainty estimator to produce realistic uncertain-

ties. However, we still need to prove a direct propor-

tion between the DNN prediction error and the corre-

sponding uncertainty degree. Besides offering realis-

tic uncertainty estimates, an uncertainty-aware model

should assign a large uncertainty to an inaccurate pre-

diction (Amini et al., 2020). For instance, a higher

level algorithm could exploit a CMRNet estimate ac-

cording to its associated uncertainty, e.g., by deciding

whether to rely only on the measure provided by a

Global Navigation Satellite System (GNSS) or even

the subsequent correction performed by the CNN.

To assess that our model provides large uncertainties

in presence of very inaccurate predictions, we intro-

duce the following threshold-based strategy. For both

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

Calibration Plots

KITTI

KITTI360

(a) Monte Carlo Dropout (b) Deep Ensemble (c) Deep Evidential Regression

Figure 3: Calibration curves computed on KITTI and KITTI360 validation sets. On the x axis the expected conﬁdence

level, on the y axis the observed conﬁdence level. All the approaches show a good calibration with respect to the components

considered. However, CMRNet + DER achieves those results with a single shot prediction and avoids any expensive sampling

of uncertainty. For the sake of clarity, we report only the three most important pose parameters, for a ground vehicle, x, y, and

yaw.

translation and rotation, we compute the trace of the

covariance matrix and compare them to a threshold

that allows us to discard predictions with large un-

certainty. Rather than deciding an arbitrary value for

the thresholds, we use the value at the top 15% of

the traces of the entire validation set, respectively for

translation and rotation. The prediction is therefore

discarded when both the trace of the covariance of

the translation and of the covariance of the rotation

are larger than their threshold. In Table 4 we report

the translation and rotation errors, together with the

percentage of discarded predictions by testing the dif-

ferent models on each 00 run of both the KITTI and

KITTI360 datasets. As can be seen, with CMRNet

+ DE we are able to detect inaccurate estimates and

improve the overall accuracy. With CMRNet + DER

we obtain a large localization improvement, outper-

forming the original model. Furthermore, CMRNet +

DER discards fewer predictions than the other meth-

ods on both the KITTI and KITTI360 datasets, which

means that it is able to produce more consistent un-

certainties with respect to the different pose compo-

nents. Although CMRNet + MCD provides good un-

certainty calibration, this model is not able to produce

uncertainty estimates that increase with the predic-

tion accuracy. In fact, we obtain the same localiza-

tion results reported in Table 1 even though such a

method discards the largest amount of samples. In

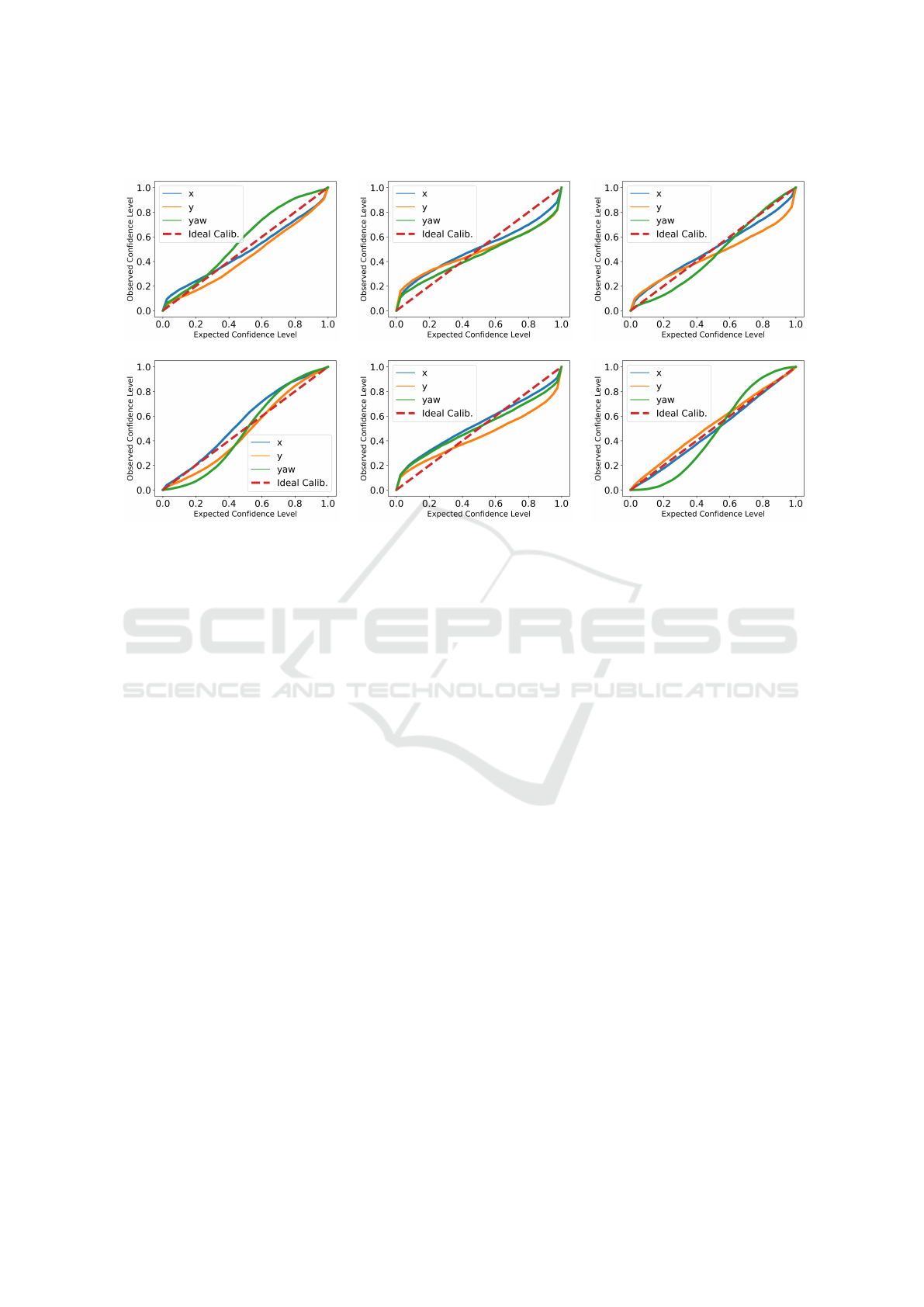
Figure 4, we report the localization accuracy of each

proposed method by varying the top% threshold used

for discarding predictions. As can be seen, except

for CMRNet + MCD, when the model conﬁdence in-

creases (low uncertainty), its accuracy increases as

well. As can be seen, CMRNet + DER shows a sim-

ilar trend compared to CMRNet + DE, but without

leveraging on expensive sampling techniques. An-

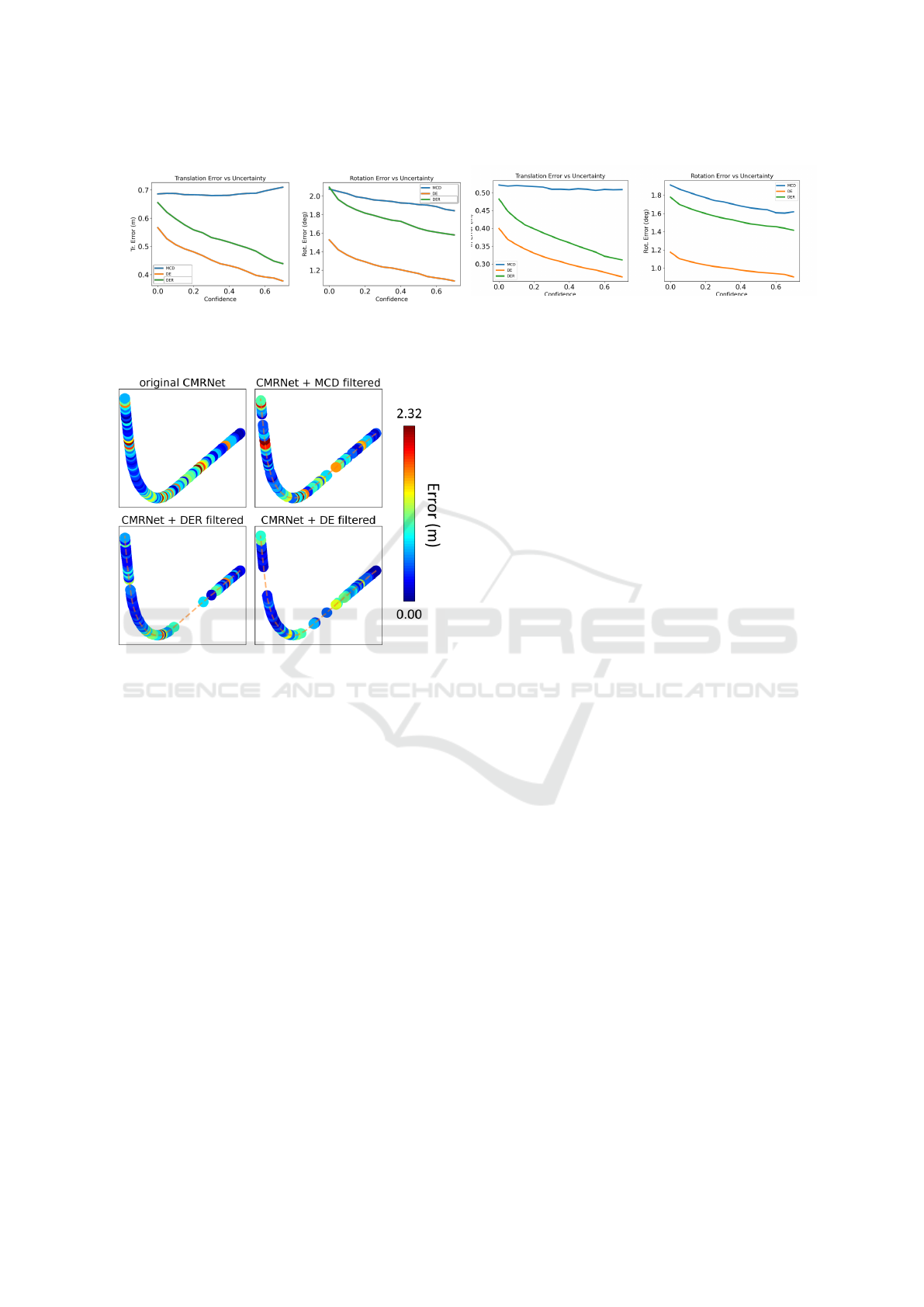
other advantage of CMRNet + DE and CMRNet +

DER is shown in Figure 5. Each plot represents the

same piece of the path (125 frames) of the KITTI 00

run; in this curve, all methods show large localiza-

tion errors. However, by exploiting DE and DER we

are able to detect most localization failures. This is

an interesting property since both DE and DER can

also be exploited as a tool to discover in which scenes

CMRNet is likely to fail, even for datasets without an

accurate pose ground truth.

5 CONCLUSIONS

We proposed an application of state-of-the-art meth-

ods for uncertainty estimation in a multi-modal DNN

for camera localization. In particular, we consid-

ered a direct uncertainty estimation approach named

Uncertainty-Aware DNN for Multi-Modal Camera Localization

KITTI KITTI360

Figure 4: Prediction errors vs CMRNet conﬁdence level. High conﬁdence coincides with small uncertainty (except for

MCD). Blue color corresponds to MCD, orange to DE, and green to DER. With DE and DER we can assign large uncertainty

to inaccurate predictions.

Figure 5: Qualitative comparison between original

CMRNet and our uncertainty aware models on a slice of

the kitti 00 run. While the original CMRNet provides in-

accurate estimates in the proximity of the depicted curve,

CMRNet + DE and CMRNet + DER are able to identify lo-

calization failures and ﬁnally to discard them.

DER (Amini et al., 2020) that we compared to other

two popular sampling-base methods, i.e., MCD and

DE (Gal and Ghahramani, 2016; Lakshminarayanan

et al., 2017). To evaluate these methods, we pro-

posed to integrate them within CMRNet (Cattaneo

et al., 2019), which performs map-agnostic camera

localization by matching a camera observation with

a LiDAR map. As shown in this work, the integra-

tion of DER required several changes in the model

architecture and training procedure. The experiments

performed on the KITTI and KITTI360 datasets eval-

uate localization accuracy and uncertainty calibration,

also assessing the direct proportion between the in-

crease in accuracy and the decrease in the estimated

uncertainty. Although CMRNet + MCD showed good

localization accuracy and uncertainty calibration, it

cannot guarantee that in presence of large uncertainty,

we also obtain large errors. Although this behaviour

was instead observed with CMRNet + DE, together

with an increase in the overall localisation accuracy

and a decrease in the variance of the error distribu-

tion, it should be considered that such a method relies

on multiple model instances by increasing the com-

putational resources required. Finally, without under-

mining its original localization accuracy, we applied

a DER-based approach to CMRNet showing the abil-

ity to provide well-calibrated uncertainties that can be

also employed to detect localization failures using a

one-shot estimation scheme. To the best of our knowl-

edge, this is the ﬁrst work that integrates a DER-based

approach in a DNN for camera pose regression.

ACKNOWLEDGMENTS

The work of Augusto Luis Ballardini has been funded

by the Mar

ıa Zambrano Grants for the attraction of

international talent in Spain.

REFERENCES

Amini, A., Schwarting, W., Soleimany, A., and Rus, D.

(2020). Deep evidential regression. In Larochelle,

H., Ranzato, M., Hadsell, R., Balcan, M., and Lin,

H., editors, Advances in Neural Information Process-

ing Systems, volume 33, pages 14927–14937. Curran

Associates, Inc.

Arandjelovic, R., Gronat, P., Torii, A., Pajdla, T., and Sivic,

J. (2016). Netvlad: Cnn architecture for weakly super-

vised place recognition. In Proceedings of the IEEE

Conference on Computer Vision and Pattern Recogni-

tion (CVPR).

Behley, J., Garbade, M., Milioto, A., Quenzel, J., Behnke,

S., Stachniss, C., and Gall, J. (2019). SemanticKITTI:

A Dataset for Semantic Scene Understanding of Li-

DAR Sequences. In Proc. of the IEEE/CVF Interna-

tional Conf. on Computer Vision (ICCV).

Caselitz, T., Steder, B., Ruhnke, M., and Burgard, W.

(2016). Monocular camera localization in 3d lidar

maps. In 2016 IEEE/RSJ International Conference on

Intelligent Robots and Systems (IROS), pages 1926–

1931.

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

Cattaneo, D., Vaghi, M., Ballardini, A. L., Fontana, S.,

Sorrenti, D. G., and Burgard, W. (2019). Cmrnet:

Camera to lidar-map registration. In 2019 IEEE In-

telligent Transportation Systems Conference (ITSC),

pages 1283–1289.

Cattaneo, D., Vaghi, M., Fontana, S., Ballardini, A. L., and

Sorrenti, D. G. (2020). Global visual localization in

lidar-maps through shared 2d-3d embedding space. In

2020 IEEE International Conference on Robotics and

Automation (ICRA), pages 4365–4371.

Deng, H., Bui, M., Navab, N., Guibas, L., Ilic, S., and

Birdal, T. (2022). Deep bingham networks: Dealing

with uncertainty and ambiguity in pose estimation. In-

ternational Journal of Computer Vision, pages 1–28.

Feng, M., Hu, S., Ang, M. H., and Lee, G. H. (2019). 2d3d-

matchnet: Learning to match keypoints across 2d im-

age and 3d point cloud. In 2019 International Con-

ference on Robotics and Automation (ICRA), pages

4790–4796.

Fort, S., Hu, H., and Lakshminarayanan, B. (2019). Deep

ensembles: A loss landscape perspective. arXiv

preprint arXiv:1912.02757.

Gal, Y. and Ghahramani, Z. (2016). Dropout as a bayesian

approximation: Representing model uncertainty in

deep learning. In Balcan, M. F. and Weinberger,

K. Q., editors, Proceedings of The 33rd International

Conference on Machine Learning, volume 48 of Pro-

ceedings of Machine Learning Research, pages 1050–

1059, New York, New York, USA. PMLR.

Geiger, A., Lenz, P., and Urtasun, R. (2012). Are we ready

for autonomous driving? the kitti vision benchmark

suite. In Conference on Computer Vision and Pattern

Recognition (CVPR).

Girshick, R. (2015). Fast r-cnn. In Proceedings of the IEEE

International Conference on Computer Vision (ICCV).

Hausler, S., Garg, S., Xu, M., Milford, M., and Fischer, T.

(2021). Patch-netvlad: Multi-scale fusion of locally-

global descriptors for place recognition. In Proceed-

ings of the IEEE/CVF Conference on Computer Vi-

sion and Pattern Recognition (CVPR), pages 14141–

14152.

Kendall, A. and Cipolla, R. (2016). Modelling uncertainty

in deep learning for camera relocalization. In 2016

IEEE International Conference on Robotics and Au-

tomation (ICRA), pages 4762–4769.

Kendall, A. and Cipolla, R. (2017). Geometric loss func-

tions for camera pose regression with deep learning.

In Proceedings of the IEEE Conference on Computer

Vision and Pattern Recognition (CVPR).

Kendall, A. and Gal, Y. (2017). What uncertainties do we

need in bayesian deep learning for computer vision?

In Guyon, I., Luxburg, U. V., Bengio, S., Wallach, H.,

Fergus, R., Vishwanathan, S., and Garnett, R., editors,

Advances in Neural Information Processing Systems,

volume 30. Curran Associates, Inc.

Kendall, A., Gal, Y., and Cipolla, R. (2018). Multi-task

learning using uncertainty to weigh losses for scene

geometry and semantics. In Proceedings of the IEEE

Conference on Computer Vision and Pattern Recogni-

tion (CVPR).

Kendall, A., Grimes, M., and Cipolla, R. (2015). Posenet: A

convolutional network for real-time 6-dof camera re-

localization. In Proceedings of the IEEE International

Conference on Computer Vision (ICCV).

Kingma, D. P., Salimans, T., and Welling, M. (2015). Vari-

ational dropout and the local reparameterization trick.

In Cortes, C., Lawrence, N., Lee, D., Sugiyama, M.,

and Garnett, R., editors, Advances in Neural Infor-

mation Processing Systems, volume 28. Curran Asso-

ciates, Inc.

Kuleshov, V., Fenner, N., and Ermon, S. (2018). Accurate

uncertainties for deep learning using calibrated regres-

sion. In Dy, J. and Krause, A., editors, Proceedings of

the 35th International Conference on Machine Learn-

ing, volume 80 of Proceedings of Machine Learning

Research, pages 2796–2804. PMLR.

Lakshminarayanan, B., Pritzel, A., and Blundell, C. (2017).

Simple and scalable predictive uncertainty estimation

using deep ensembles. In Guyon, I., Luxburg, U. V.,

Bengio, S., Wallach, H., Fergus, R., Vishwanathan,

S., and Garnett, R., editors, Advances in Neural Infor-

mation Processing Systems, volume 30. Curran Asso-

ciates, Inc.

Liao, Y., Xie, J., and Geiger, A. (2022). KITTI-360: A

novel dataset and benchmarks for urban scene under-

standing in 2d and 3d. Pattern Analysis and Machine

Intelligence (PAMI).

McAllister, R., Gal, Y., Kendall, A., Van Der Wilk, M.,

Shah, A., Cipolla, R., and Weller, A. (2017). Con-

crete problems for autonomous vehicle safety: Ad-

vantages of bayesian deep learning. In Proceedings

of the 26th International Joint Conference on Artiﬁ-

cial Intelligence, IJCAI’17, page 4745–4753. AAAI

Press.

Meinert, N. and Lavin, A. (2021). Multivariate deep evi-

dential regression. CoRR, abs/2104.06135.

Neubert, P., Schubert, S., and Protzel, P. (2017). Sampling-

based methods for visual navigation in 3d maps by

synthesizing depth images. In 2017 IEEE/RSJ Inter-

national Conference on Intelligent Robots and Sys-

tems (IROS), pages 2492–2498.

Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J.,

Chanan, G., Killeen, T., Lin, Z., Gimelshein, N.,

Antiga, L., Desmaison, A., Kopf, A., Yang, E., De-

Vito, Z., Raison, M., Tejani, A., Chilamkurthy, S.,

Steiner, B., Fang, L., Bai, J., and Chintala, S. (2019).

Pytorch: An imperative style, high-performance deep

learning library. In Wallach, H., Larochelle, H.,

Beygelzimer, A., d'Alch

e-Buc, F., Fox, E., and Gar-

nett, R., editors, Advances in Neural Information Pro-

cessing Systems 32, pages 8024–8035. Curran Asso-

ciates, Inc.

Peretroukhin, V., Wagstaff, B., Giamou, M., and Kelly,

J. (2019). Probabilistic regression of rotations using

quaternion averaging and a deep multi-headed net-

work. CoRR, abs/1904.03182.

Petek, K., Sirohi, K., B

uscher, D., and Burgard, W. (2022).

Robust monocular localization in sparse hd maps

leveraging multi-task uncertainty estimation. In 2022

International Conference on Robotics and Automation

(ICRA), pages 4163–4169.

Uncertainty-Aware DNN for Multi-Modal Camera Localization

Radwan, N., Valada, A., and Burgard, W. (2018). Vloc-

net++: Deep multitask learning for semantic visual

localization and odometry. IEEE Robotics and Au-

tomation Letters, 3(4):4407–4414.

Sarlin, P.-E., Unagar, A., Larsson, M., Germain, H., Toft,

C., Larsson, V., Pollefeys, M., Lepetit, V., Ham-

marstrand, L., Kahl, F., and Sattler, T. (2021). Back to

the feature: Learning robust camera localization from

pixels to pose. In Proceedings of the IEEE/CVF Con-

ference on Computer Vision and Pattern Recognition

(CVPR), pages 3247–3257.

Schneider, N., Piewak, F., Stiller, C., and Franke, U. (2017).

Regnet: Multimodal sensor registration using deep

neural networks. In 2017 IEEE Intelligent Vehicles

Symposium (IV), pages 1803–1810.

Sensoy, M., Kaplan, L., and Kandemir, M. (2018). Evi-

dential deep learning to quantify classiﬁcation uncer-

tainty. In Bengio, S., Wallach, H., Larochelle, H.,

Grauman, K., Cesa-Bianchi, N., and Garnett, R., edi-

tors, Advances in Neural Information Processing Sys-

tems, volume 31. Curran Associates, Inc.

Wolcott, R. W. and Eustice, R. M. (2014). Visual local-

ization within lidar maps for automated urban driving.

In 2014 IEEE/RSJ International Conference on Intel-

ligent Robots and Systems, pages 176–183.

Yin, Z. and Shi, J. (2018). Geonet: Unsupervised learning

of dense depth, optical ﬂow and camera pose. In Pro-

ceedings of the IEEE Conference on Computer Vision

and Pattern Recognition (CVPR).

Zhu, Y., Wang, J., Xie, L., and Zheng, L. (2018). Attention-

based pyramid aggregation network for visual place

recognition. In Proceedings of the 26th ACM Inter-

national Conference on Multimedia, MM ’18, page

99–107, New York, NY, USA. Association for Com-

puting Machinery.

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics