TX-Gen: Multi-Objective Optimization for Sparse Counterfactual
Explanations for Time-Series Classification
Qi Huang
a
, Sofoklis Kitharidis
b
, Thomas B
¨
ack
c
and Niki van Stein
d
Institute of Advanced Computer Science, Leiden University, Einsteinweg 55, Leiden, The Netherlands
Keywords:
Explainable Artificial Intelligence, Counterfactuals, Time-Series Classification, Evolutionary Computation.
Abstract:
In time-series classification, understanding model decisions is crucial for their application in high-stakes do-
mains such as healthcare and finance. Counterfactual explanations, which provide insights by presenting
alternative inputs that change model predictions, offer a promising solution. However, existing methods
for generating counterfactual explanations for time-series data often struggle with balancing key objectives
like proximity, sparsity, and validity. In this paper, we introduce TX-Gen, a novel algorithm for generating
counterfactual explanations based on the Non-dominated Sorting Genetic Algorithm II (NSGA-II). TX-Gen
leverages evolutionary multi-objective optimization to find a diverse set of counterfactuals that are both sparse
and valid, while maintaining minimal dissimilarity to the original time series. By incorporating a flexible
reference-guided mechanism, our method improves the plausibility and interpretability of the counterfactuals
without relying on predefined assumptions. Extensive experiments on benchmark datasets demonstrate that
TX-Gen outperforms existing methods in generating high-quality counterfactuals, making time-series models
more transparent and interpretable.
1 INTRODUCTION
The increasing adoption of machine learning mod-
els for time-series classification (TSC) in critical do-
mains such as healthcare (Morid et al., 2023) and fi-
nance (Chen et al., 2016) has raised the demand for
interpretable and transparent decision-making pro-
cesses. However, the black-box nature of many high-
performing classifiers, such as neural networks or en-
semble models, limits their interpretability, making it
difficult for practitioners to understand why a partic-
ular decision is made. In this context, counterfactual
explanations have emerged as a valuable approach in
Explainable AI (XAI) (Theissler et al., 2022), pro-
viding instance-specific insights by identifying alter-
native inputs that lead to different classification out-
comes. Despite the growing body of work in this area,
generating meaningful counterfactuals for time-series
data presents unique challenges due to its sequential
nature, dependency on temporal structure, and multi-
dimensional complexity.
a
https://orcid.org/0009-0007-4989-135X
b
https://orcid.org/0009-0005-8404-0724
c
https://orcid.org/0000-0001-6768-1478
d
https://orcid.org/0000-0002-0013-7969
While counterfactual generation has been exten-
sively explored for tabular and image data, methods
tailored to time-series classification remain scarce and
underdeveloped. The few existing methods often fail
to balance key properties such as proximity, spar-
sity, and validity. Moreover, most approaches require
high computational resources or rely on rigid heuris-
tics, limiting their applicability in real-world scenar-
ios. This gap motivates the development of an ef-
ficient, model-agnostic method capable of generat-
ing high-quality counterfactual explanations for time-
series classifiers.
In this paper, we propose TX-Gen, a novel al-
gorithm for generating counterfactual explanations in
time-series classification tasks using a modified Non-
dominated Sorting Genetic Algorithm II (NSGA-II).
Unlike previous approaches that combine evolution-
ary computing with explainable AI (Zhou et al.,
2024), TX-Gen leverages the power of evolutionary
multi-objective optimization to find a diverse set of
Pareto-optimal counterfactual solutions that simulta-
neously minimize multiple objectives, such as dis-
similarity to the original time-series and sparsity of
changes, while ensuring the classifier’s decision is al-
tered. Additionally, our approach incorporates a flex-
ible reference-based mechanism, which guides the
62
Huang, Q., Kitharidis, S., Bäck, T. and van Stein, N.
TX-Gen: Multi-Objective Optimization for Sparse Counterfactual Explanations for Time-Series Classification.
DOI: 10.5220/0013066400003886
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 1st International Conference on Explainable AI for Neural and Symbolic Methods (EXPLAINS 2024), pages 62-74
ISBN: 978-989-758-720-7
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.

counterfactual generation process without relying on
restrictive assumptions or predefined shapelets.
Contributions. The key contributions of this work
are as follows:
• We introduce TX-Gen, a novel framework for
generating counterfactual explanations specifi-
cally tailored to time-series classification, which
efficiently balances proximity, sparsity, and valid-
ity through multi-objective optimization.
• Our method employs a reference-guided approach
to select informative subsequences, improving the
plausibility and interpretability of counterfactuals.
• We demonstrate the effectiveness of TX-Gen
across multiple benchmark datasets, showing that
our approach outperforms existing methods in
terms of sparsity, validity and proximity of the
counterfactual examples.
In the following sections, we detail the method-
ology behind TX-Gen, present our experimental re-
sults, and discuss the implications of our findings for
advancing explainability in time-series classification.
1.1 Problem Statement
We begin our problem formulation by first introduc-
ing the context of this research.
Given a collection (set) of univariate time se-
ries, denoted as S = {T
1
,T
2
,...,T
n
}, where each T =
{t
i
∈ R}
m
i=1
consists of observations orderly recorded
across m timestamps. In the context of a time series
classification (TSC) task, each time series T is asso-
ciated with a true descriptive label L ∈ {L
1
,...,L
k
}
from k unique categories. The objective of TSC is to
develop an algorithmic predictor f (·) that can maxi-
mize the probability P( f (T ) = L) for T ∈ S and also
any unseen T /∈ S (provided that the true label of such
a T /∈ S also equals L). Here, we presume the classifier
provides probabilistic or logit outputs. Moreover, as-
sume a function g : R
m
→ R
m
that can element-wise
perturb or transform any given time series T into a
new in-distribution time series instance
ˆ
T . We then
say that
ˆ
T is a counterfactual of T regarding a TSC
predictor f if f (
ˆ
T ) ̸= f (T ) while the dissimilarity be-
tween T and
ˆ
T is minimized (Wachter et al., 2017; De-
laney et al., 2021). It is noteworthy that counterfactual
explanations are fundamentally instance-based expla-
nations aimed at interpreting the predictions of the
classifier being explained, rather than the true labels,
regardless of whether the real labels are known or not.
Goal. Considering a robust time series classifica-
tion predictor f trained on the dataset S, and a time
series instance T
e
to be explained, this work proposes
an explainable AI method, i.e., the aforementioned
function g, which can identify the counterfactual of
T
e
concerning f . Notably, T
e
may be either part of the
dataset S or external to it.
2 BACKGROUND
2.1 Evaluation Metrics
The evaluation criteria for our counterfactual genera-
tion method are articulated through several key met-
rics, each addressing specific aspects of counterfac-
tual quality and effectiveness:
• Proximity. Measures the element-wise similarity
between the counterfactual instance and the target
time series, typically by using the L
p
metrics.
• Validity. Assesses whether the counterfactuals
successfully alter the original class label, thereby
reflecting their effectiveness.
• Diversity. Measures the variety in the generated
counterfactual solutions for each to-be-explained
time series instance.
• Sparsity. Quantifies the simplicity of the counter-
factual by counting the number of element-wise
differences between the generated counterfactual
and the original series.
These metrics, widely recognized in explainable
AI for time series, provide a robust framework for
evaluating counterfactual explanations, emphasizing
minimalism, diversity, validity, and closeness to orig-
inal instances. Our selection of metrics follows the
methodologies of key studies in the field, including
(Delaney et al., 2021); (Li et al., 2022); (Li et al.,
2023); (H
¨
ollig et al., 2022) and (Refoyo and Luengo,
2024).
2.2 Related Work
The evolution of explainable artificial intelligence
(XAI) for generating counterfactuals for time se-
ries has been marked by significant advances in
methods that provide clear, actionable insights into
model decisions. This line of research has been
initiated by (Wachter et al., 2017), introducing an
optimization-based approach that focuses on mini-
mizing a loss function to modify decision outcomes
while maintaining minimal Manhattan distance from
the original input. This foundational method encour-
aged further development of algorithms that enhance
TX-Gen: Multi-Objective Optimization for Sparse Counterfactual Explanations for Time-Series Classification
63

the quality and effectiveness of counterfactual expla-
nations through additional modifications to the loss
function.
Building upon the concept of influencing specific
features within time series data, the introduction of
local tweaking via a Random Shapelet Forest clas-
sifier (Karlsson et al., 2020) targets specific, influ-
ential shapelets for localized transformations within
time series data. In contrast, global tweaking (Karls-
son et al., 2018) uses a k-nearest neighbor classifier to
guide broader transformations ensuring minimal yet
meaningful alterations to change class outcomes.
Advancing these concepts, (Delaney et al., 2021)
developed the Native Guide Counterfactual Explana-
tion (NG-CF) which utilizes the Dynamic Barycen-
ter Averaging with the nearest unlike neighbor. Sub-
sequently, (Li et al., 2022) introduced the Shapelet-
Guided Counterfactual Explanation (SG-CF), exploit-
ing time series subsequences that are maximally
representative of a class to guide the perturbations
needed for generating counterfactual explanations.
This method was further elaborated upon with the
introduction of the Attention-Based Counterfactual
Explanation for Multivariate Time Series (AB-CF)
by (Li et al., 2023) which incorporates attention
mechanisms to further refine the selection of shapelets
and optimize the perturbations.
Moreover, TSEvo by (H
¨
ollig et al., 2022) utilizes
the Non-Dominated Sorting Genetic Algorithm to
strategically balance multiple explanation objectives
such as proximity, sparsity, and plausibility while in-
corporating three distinct mutations. Most recently,
Sub-SpaCE (Refoyo and Luengo, 2024) employs ge-
netic algorithms too, with customized mutation and
initialization processes, promoting changes in only
a select few subsequences. This method focuses on
generating counterfactual explanations that are both
sparse and plausible without extensive alterations.
Despite the progress in generating counterfactual
explanations for time-series classification, these ex-
isting approaches still face several significant lim-
itations. Many methods, such as optimization-
based (Refoyo and Luengo, 2024) or shapelet-guided
(Karlsson et al., 2018; Karlsson et al., 2020; Li et al.,
2022) approaches, rely heavily on predefined assump-
tions about the data, such as the importance of specific
subsequences or the necessity for local perturbations.
These assumptions often reduce the generalizability
of the methods across diverse datasets and classifiers.
Furthermore, most methods struggle to balance the
trade-offs between proximity, sparsity, and diversity
of the generated counterfactuals, often prioritizing
one metric at the expense of others (Delaney et al.,
2021). This can lead to counterfactuals that are ei-
ther too similar to the original instance to be mean-
ingful or excessively altered, making them unrealistic
or hard to interpret. Additionally, many existing ap-
proaches lack scalability, becoming computationally
expensive when applied to larger or more complex
time-series data (H
¨
ollig et al., 2022). In contrast,
our proposed method, TX-Gen, addresses these lim-
itations by leveraging the flexibility of evolutionary
multi-objective optimization to dynamically explore
the solution space and by guiding the search using
reference samples from the training data. This allows
TX-Gen to generate diverse, sparse, and valid coun-
terfactuals, making it more applicable to real-world
time-series classification tasks.
Among the discussed works, TSEvo (H
¨
ollig et al.,
2022), Sub-SpaCE (Refoyo and Luengo, 2024), and
our proposed TX-Gen all generate candidate coun-
terfactual instances by applying evolutionary heuris-
tics to optimize objective functions based on the cri-
teria outlined in Section 2.1. However, while both
TSEvo and Sub-SpaCE focus on heuristically and di-
rectly manipulating the variables of the instance be-
ing explained to generate counterfactuals, our method
instead models the differences between the desired
counterfactual instances and the original instance.
This represents a fundamental deviation from the
other two strategies, despite their similarities in form.
3 METHODOLOGY
The Framework. Our proposed method, TX-Gen,
aims to jointly locate the subsequence of interest in
a to-be-explained time series T while also transform-
ing T into its counterfactual. This is achieved by mu-
tually minimizing two objective functions under the
guidance of reference samples, using a customized
iterative optimization heuristic based on the Non-
Dominated Sorting Genetic Algorithm II (NSGA-
II) (Deb et al., 2002). A high-level pseudocode of
our algorithm is given in Algorithm 1 assuming the
respect readers are familiar with the concepts of evo-
lutionary algorithms (Back et al., 1997; B
¨
ack et al.,
2023) Following the self-explainable high-level pseu-
docode, the key components proposed in our algo-
rithm are further explained.
3.1 Model-Based Selection of
References
In TSC, consider a time series instance T that belongs
to category C. A counterfactual-based explainer can
be viewed as a reference-guided method if it lever-
ages example instances—originating from the same
EXPLAINS 2024 - 1st International Conference on Explainable AI for Neural and Symbolic Methods
64

Algorithm 1: High-level pseudocode for our coun-
terfactual discovery algorithm TX-Gen .
Data: Population size N; crossover probability p
c
;
mutation probability p
m
, number of
generations G; to-be-explained time series
T ; classifier f ; a set of references S; number
of final reference instances K
Result: Set of non-dominated counterfactual
candidate solutions
1 Initialize population P
0
of size N as described in
section 3.3.1
▷ Selection of references using Algorithm 2
2 ψ ← SelectReference(T, S, f ,K)
3 Generate the counterfactual candidate sets
Θ
0
=
S
N
i=1
{
ˆ
T
i
} for all individuals in P
0
using the
Generate function from Algorithm 5.
4 Evaluate the fitness of each individual in P
0
(Θ
0
)
using two objective functions (see section 3.2)
5 for t = 1 to G do
6 Generate offspring Q
t
from P
t−1
by:
7 - Select the parents for mating using binary
tournament selection
8 - Crossover the parents (with probability p
c
)
to obtain Q
′
t
using Algorithm 3
9 - Mutate the individuals in Q
′
t
in place (with
probability p
m
) using Algorithm 4
10 - Enumeratively expand each
−→
X
i
∈ Q
′
t
into K
chromosomes and merge them into a new set
Q
t
=
2N
[
i=1
K
[
j=1
−→
X
i, j
,
where each
−→
X
i, j
= (x
i,1
,x
i,2
, j)
11 Obtain the counterfactual candidates Θ
t
for all
samples in Q
t
using Generate function
12 Evaluate the fitness of each candidate in Θ
t
and assign the resulting values to respective
individuals in Q
t
13 Combine parent population P
t−1
and offspring
population Q
t
into a combined population R
t
of size (2K + 1)N
14 Perform non-dominated sorting on R
t
and
assign crowding distances to individuals
within each front
15 Select individuals for the next population P
t
based on rank and crowding distance,
ensuring the population size is N
16 end
17 Return the non-dominated individuals as well as
their corresponding counterfactual candidates
from the final population P
G
task but known to belong to categories other than C
—to assist in transforming T into its counterfactual.
Existing literature on reference-guided methods pri-
marily identifies the reference instances by selecting
those with low shape-based or distance-based simi-
larities to the given instance to be explained, e.g., the
nearest unlike neighbors as seen in (Delaney et al.,
2021; H
¨
ollig et al., 2022). In contrast, our work pro-
poses selecting reference samples solely based on the
classifier’s outputs.
Following the settings in Section 1.1, let f (·) be
a probabilistic classifier for a TSC task Ω with k
classes. That is, instead of predicting the exact label,
f predicts the probability distribution over all candi-
date class labels for any given target time series T.
Definition 1 (Distance in the Classifier). For any
pairs of time series (T
i
,T
j
) of the TSC task Ω, we de-
fine their Distance in the Classifier f as the Jensen-
Shannon distance between f (T
i
) and f (T
j
):
D
f
(T
i
,T
j
) =
r
KL( f (T
i
) | P
m
) + KL( f (T
j
) | P
m
)
2
,
(1)
where P
m
is the element-wise mean of f (T
i
) and
f (T
j
), and KL denotes the well-known Kullback-
Leibler (KL) divergence (Endres and Schindelin,
2003). Apart from the properties that a valid metric
holds, this distance is also bounded, D
f
(T
i
,T
j
) ∈ [0,1]
if we use 2 as the logarithm base in KL divergence.
With this definition, as described in Algorithm 2,
we can retrieve reference instances for a to-be-
explained time series T from a candidate set that con-
tains samples that both are predicted to belong to dif-
ferent categories than T and are close to T with re-
spect to the distance in the classifier.
Algorithm 2: Select References for a Time Series.
Input: Target time series T ; the classifier f ; refer-
ence set S; number of reference samples K
Output: A set of reference samples ψ ⊆ S..
1 Function SelectReference(T , S, f , K):
2 foreach T
i
∈ S do
3 if f (T
i
) ̸= f (T ) then
4 Compute D
f
(T,T
i
) as in Definition 1
5 else
6 Set D
f
(T,T
i
) ← 1.01
7 end
8 end
9 Get the set: ψ ← arg min
T
i
∈S
|ψ|=K
D
f
(T,T
i
)
10 return ψ
3.2 The Objective Functions
To address the idea (see section 1.1) that a decent
counterfactual
ˆ
T = {
ˆ
t
i
∈ R}
m
i=1
shall closely resemble
the target time series T = {t
i
∈ R}
m
i=1
while flipping
the prediction of a given classifier f , we propose to
determine feasible candidates
ˆ
T
∗
by jointly minimiz-
ing two real-valued objectives as follow:
• The minimum Distance in Classifier between a
counterfactual candidate
ˆ
T
∗
and the samples in
TX-Gen: Multi-Objective Optimization for Sparse Counterfactual Explanations for Time-Series Classification
65

the reference set ψ:
F
1
(
ˆ
T
∗
,ψ) =
(
minD
f
(
ˆ
T
∗
,T
i
), ∀T
i
∈ ψ if f (
ˆ
T
∗
) ̸= f (T ),
1.01 if f (
ˆ
T
∗
) = f (T ).
The second condition is to penalize the case where
ˆ
T
∗
fails to flip the prediction of the classifier.
• Joint sparsity and proximity between
ˆ
T
∗
and T :
F
2,1
(
ˆ
T
∗
,T ) =
∑
i=[1,...,m]
1
ˆ
t
i
̸=t
i
m
,
F
2,2
(
ˆ
T
∗
,T ) =
|
ˆ
T
∗
− T |
2
|
ˆ
T
∗
|
2
+ |T |
2
,
F
2
(
ˆ
T
∗
,T ) =
1
2
(F
2,1
(
ˆ
T
∗
,T ) + F
2,2
(
ˆ
T
∗
,T ))
Here we normalize and combine the two indica-
tors into one objective (F
2
), where the sparsity
(F
2,1
) measures the degree of element-wise per-
turbation, and the second indicator F
2,2
aims to
quantify the scale change between
ˆ
T
∗
and T .
In summary, the two objective functions can jointly
ensure the found counterfactual solutions are valid
and minimized. What is more, the proposed two ob-
jective functions are both bounded, saying F
1
∈ [0, 1]
and F
2
∈ [0, 1].
3.3 Locating the Sequences of Interest
3.3.1 Chromosome Representation
Previous works that utilize evolutionary computation
predominantly adopt a unified chromosome represen-
tation that encodes the entire counterfactual instance.
In other words, the number of variables in each solu-
tion is at least as large as the number of timestamps in
the target time series. Furthermore, these approaches
typically apply crossover, mutation, and other evo-
lutionary operators directly to the chromosomes to
generate the next set of feasible candidates in one-
go (H
¨
ollig et al., 2022; Refoyo and Luengo, 2024).
One advantage of encoding the entire time series into
the individual is that it can find multiple Segment or
Subsequence of Interest (SoI) at the same time.
In contrast, our approach reduces the complex-
ity of candidate solutions by representing each one
with only three mutable integer variables, i.e., X =
[x
1
,x
2
,x
3
], regardless of the number of timestamps in
the target time series. Specifically, x
1
and x
2
denote
the starting and ending indices of the single subse-
quence of interest considered in this individual, re-
spectively. Meanwhile, x
3
represents the index of the
reference sample in the set ψ, which is used to guide
the discovery of potential counterfactual observations
for the SoI (see section 3.4).
Similar to previous approaches, our method can
also identify multiple SoI for each target time series
by generating various counterfactual solutions. Fur-
thermore, by leveraging the concept of Pareto effi-
ciency in multi-objective optimization, our approach
ensures that the diverse SoI discovered are all equally
significant.
Initialization. Several existing works explicitly in-
corporate low-level XAI strategies to identify the SoI
in the target instance, thereby facilitating the counter-
factual search process. These strategies include fea-
ture attribution methods, such as the GradCAM fam-
ily (Selvaraju et al., 2017), which are employed in
works like (Delaney et al., 2021; Refoyo and Luengo,
2024). Additionally, subsequence mining methods,
such as Shapelet extraction (Ye and Keogh, 2009), are
utilized in studies like (Li et al., 2022; Huang et al.,
2024). Unlike other XAI techniques, we do not use
this (possibly biased) initialization, instead the first
population in our search algorithm is randomly sam-
pled. Given a to-be-explained time series T = {t
i
∈
R}
m
i=1
and its reference sample set ψ of size K, the
variables in a individual solution
−→
X
j
= [x
j,1
,x
j,2
,x
j,3
]
are step-by-step uniformly randomly sampled as:
x
j,1
∼ U(1, m − 1)
x
j,2
∼ U(x
j,1
,m)
x
j,3
∼ U(1, K)
3.3.2 Crossover
Crossover is a crucial operator in evolutionary algo-
rithms, designed to create new offspring by combin-
ing decision variables from parent solutions. This
process helps the algorithm exploit the search space
within the current population. The parent solutions
are chosen through a selection mechanism. In this
work, we employ the well-known tournament selec-
tion method to select mated parents, and we refer in-
terested readers to the literature (Goldberg and Deb,
1991) for more details.
Bearing in mind the idea behind crossover, our
customized crossover operator is dedicated to fulfill-
ing two additional criteria: (i) minimizing the inter-
section between the SoI of offspring. (ii) minimizing
the total lengths of the SoI tracked by offspring.
The proposed crossover is demonstrated in Algo-
rithm 3. The crossover operation by default produces
two offspring. The function GetUnique returns the
unique, non-duplicate values of its inputs in an array,
sorted in ascending order. Notably, in line 22 of the
EXPLAINS 2024 - 1st International Conference on Explainable AI for Neural and Symbolic Methods
66

Algorithm 3: The Crossover Operator.
Input: The parent individuals
−→
X
1
= (x
1,1
,x
1,2
,x
1,3
)
and
−→
X
2
= (x
2,1
,x
2,2
,x
2,3
); crossover probability P
cx
.
Output: The two offspring
−→
Y
1
= (y
1,1
,y
1,2
,y
1,3
)
and
−→
Y
2
= (y
2,1
,y
2,2
,y
2,3
). .
1 Function GetUnique(a
1
,a
2
,a
3
,a
4
):
2 b
1
,b
2
,b
3
,b
4
← AscendingSort(a
1
,a
2
,a
3
,a
4
)
3
−→
β ← (b
1
)
4 if b2 ̸= b1 then
5
−→
β ←
−→
β ∥(b
2
) ▷ Concatenate b
2
to
−→
β
6 end
7 if b3 ̸= b2 then
8
−→
β ←
−→
β ∥(b
3
)
9 end
10 if b4 ̸= b3 then
11
−→
β ←
−→
β ∥(b
4
)
12 end
13 return
−→
β
14 Function Crossover(
−→
X
1
,
−→
X
2
,P
cx
):
15 p
c
∼ U(0,1)
16
−→
α ← GetUnique(x
1,1
,x
1,2
,x
2,1
,x
2,2
)
17
−→
Y
1
,
−→
Y
2
←
−→
X
1
,
−→
X
2
18 if p
c
≤ P
cx
then
19 if |
−→
α | = 4 then
20 A ← |x
1,1
− x
2,1
| + |x
1,2
− x
2,2
|
21 B ← |x
1,1
− x
2,2
| + |x
1,2
− x
2,1
|
22 if A ≤ B then
23 y
1,1
← min(x
1,1
,x
2,1
)
24 y
1,2
← max(x
1,1
,x
2,1
)
25 y
2,1
← min(x
1,2
,x
2,2
)
26 y
2,2
← max(x
1,2
,x
2,2
)
27 else
28 y
1,1
← min(x
1,1
,x
2,2
)
29 y
1,2
← max(x
1,1
,x
2,2
)
30 y
2,1
← min(x
1,2
,x
2,1
)
31 y
2,2
← max(x
1,2
,x
2,1
)
32 end
33 else if |
−→
α | = 3 then
34 y
1,1
,y
1,2
← α
1
,α
2
35 y
2,1
,y
2,2
← α
2
,α
3
36 else
37 y
1,1
,y
2,2
← α
1
,α
2
38 y
1,2
∼ U(α
1
,α
2
)
39 y
2,1
← y
1,2
40 end
41 end
42 return (
−→
Y
1
,
−→
Y
2
)
pseudocode, we compare the total lengths of the SoI
under two feasible crossover options and intentionally
set the relational operator to ≤ instead of <. This en-
sures that, in cases where the SoIs of two parents do
not overlap, their offspring will have minimal inter-
sections. Between lines 33 and 40, we address the
corner cases where the indices recorded in the parents
are partially or entirely the same.
3.3.3 Mutation
In general, the mutation operators help to explore un-
foreseen areas of the solution space and prevent pre-
mature convergence. Unlike the crossover operator
that mixes the SoIs from different parent solutions,
the mutation operator proposed in this work aims to
adjust the length of the SoI tracked by each individual
selected for mutation. The pseudocode of our muta-
tion strategy is provided in Algorithm 4.
Algorithm 4: The Mutation Operator.
Input: The individual
−→
X = (x
1
,x
2
,x
3
); mutation
probability P
mu
; tolerable SoI length ratio τ; M, the
number of timestamps (length) of the target time
series T .
Output: The offspring
−→
Y = (y
1
,y
2
,y
3
) after muta-
tion. .
1 Function Mutate(
−→
X ,P
mu
,τ, M):
2
−→
Y ←
−→
X
3 p
u
∼ U(0,1)
▷ Configure the p of a Bin(n, p)
4 if p
u
≤ P
mu
then
5 if τ ∈ (0,1) then
6 σ ←
log(0.5)
τ
·
x
2
−x
1
M
7 p
b
← e
σ
8 else
9 p
b
← 0.5
10 end
▷ Determine the direction to scale
p
s
∼ U(0,1)
▷ Sample the new SoI length
l ∼ Bin(2(x
2
− x
1
), p
b
)
11 if p
s
≤ 0.5 then
12 y
2
← min(max(y
1
+ l, y
1
+ 1),M)
13 else
14 y
1
← max(min(y
2
− l, y
2
− 1),1)
15 end
16 end
17 return
−→
Y
The strategy employs a dynamic scaling of the
SoI length for the new instance
−→
Y based on the SoI
length of the previous instance
−→
X . The new length
is randomly sampled from a binomial distribution
Bin(n, p), where the number of trials n is twice the
length of the SoI in
−→
X . This approach allows the
SoI length to potentially increase almost exponen-
tially between adjacent generations during optimiza-
tion, effectively simulating the idea of a binary search.
Another vital parameter to specify a binomial distri-
bution is p, the success rate of trials, which can be
interpreted as the probability of extending (p > 0.5)
or shrinking (p < 0.5) the SoI in this context. In lines
TX-Gen: Multi-Objective Optimization for Sparse Counterfactual Explanations for Time-Series Classification
67

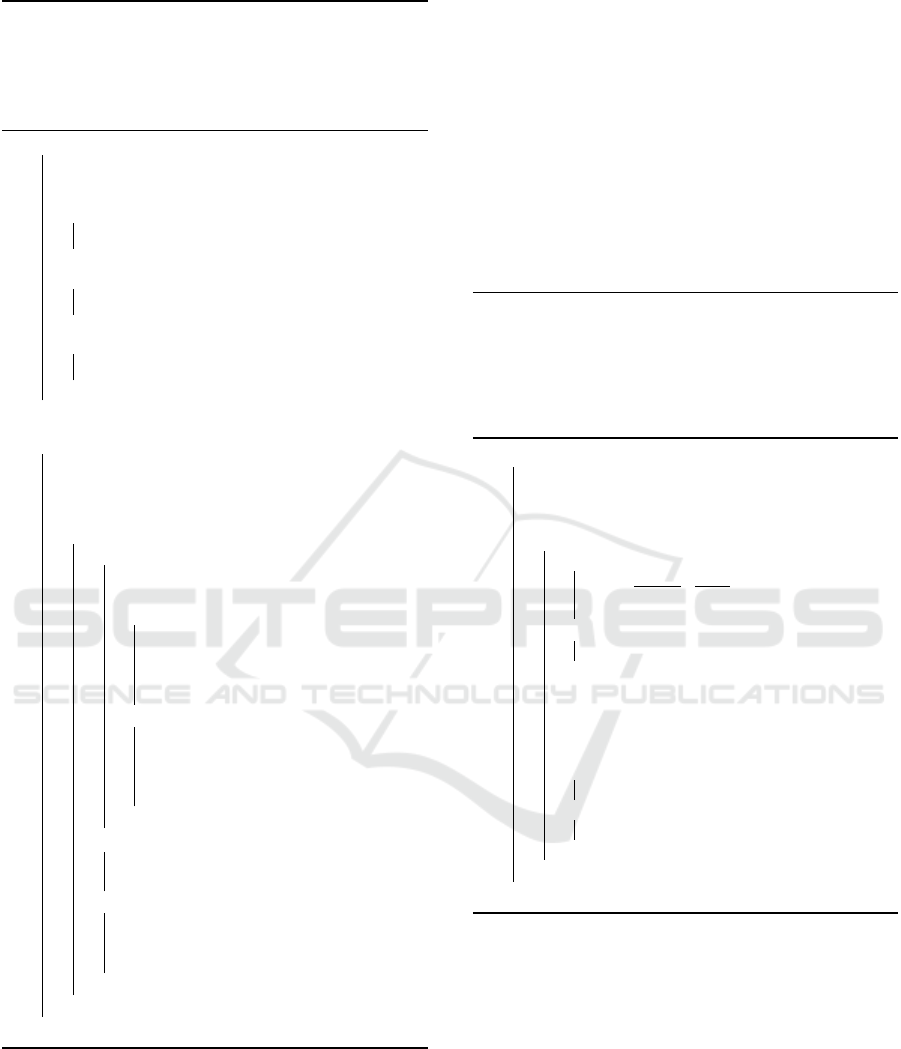
5 to 10 of Algorithm 4, given τ, a tolerable (or ideal)
ratio of the SoI length to the length of the time se-
ries, the value p is determined such that the peak of
the probability mass function of the binomial distribu-
tion is close to ⌊M · τ⌋. Empirical illustrations of this
concept are provided in Figure 1. As shown in Fig-
ure 1a, under the same τ, the success rate decreases
(increases) as the SoI length increases (decreases).
Additionally, for the same SoI length, an increase (de-
crease) in τ leads to a corresponding increase (de-
crease) in the likelihood of extending the SoI. Fur-
thermore, Figure 1b demonstrates that the probability
of sampling a new length close to the tolerable length
is increased, enabling the adaptive adjustment of the
SoI length, particularly discouraging excessively long
SoIs. This can be observed as the peak of n = 80 (SoI
length 40) is shifted further left of the tolerable length
compared to that of n = 40 (SoI length 20).
(a) An empirical plot of multiple success rates p
b
versus the
length of SoI in to-be-mutated individuals X under various
tolerable SoI length ratios τ.
(b) An example Probability Mass Function (PMF) of a bi-
nomial distribution under our configuration. The tolerable
SoI length ratio is set to τ = 0.4, which results in a tolerable
length of 16. And the five displayed PMFs are calculated
based on SoI lengths 5, 10, 20, 30, and 40, respectively.
Figure 1: In both figures, the length of the to-be-explained
time series is M = 40.
3.4 Modeling of the New SoI
It is noteworthy that several previous works also sep-
arate counterfactual generation into two stages: the
discovery of SoIs (or other forms of sensitivity anal-
ysis) and the subsequent generation or search for the
actual values. While the crossover and mutation op-
erators described above facilitate the search for op-
timal SoIs within the time series, the specific values
corresponding to these subsequences must still be de-
termined to find true counterfactual explanations. Ex-
isting approaches to determining the values for SoIs
can be broadly categorized into three types: 1. heuris-
tic methods, which iteratively optimize specific crite-
ria (Wachter et al., 2017; H
¨
ollig et al., 2022); 2. di-
rect use of (sub)sequences from reference data, typ-
ically selected from the training set (Delaney et al.,
2021; Li et al., 2022); 3. generation of values using
machine learning models, such as generative mod-
els (Lang et al., 2023; Huang et al., 2024). Interest-
ingly, the second strategy essentially complements the
last. By combining these two approaches, it becomes
feasible to obtain an SoI efficiently without being re-
stricted to values from the reference data, which is the
foundation of our proposed approach.
The proposed method relies on two assumptions.
Given a univariate time series T of length m and one
of its counterfactual candidate
ˆ
T . Suppose the located
subsequence of interest is between timestamps i and j
where i < j, then the first assumption is as follows:
Assumption 1. The time series T = {t
k
∈ R}
m
k=1
and
its counterfactual
ˆ
T = {
ˆ
t
k
∈ R}
m
k=1
differ only in the
subsequence of interest, i.e., t
k
=
ˆ
t
k
, ∀k /∈ [i, j].
While this assumption aims to ensure the true im-
portance of the found SoI, the second assumption is
developed to further restrict the values of SoI to a sim-
plified form for efficient modeling and generation.
Assumption 2. The difference between the SoI of the
counterfactual candidate
ˆ
T = {
ˆ
t
k
∈ R}
m
k=1
and that
of the target time series T = {t
k
∈ R}
m
k=1
, denoted as
Z = {
ˆ
t
k
−t
k
}
j
k=i
, is a stationary process where the cur-
rent values are linearly dependent on its past values.
Consequently, Z can be modeled by an autoregressive
model of order p (AR-p) with a Gaussian error term.
This assumption is straightforward and aims to de-
fine the nature of the difference between the SoIs.
To the best of our knowledge, in contrast to previ-
ous approaches that directly obtain the observations
(values) of counterfactuals, we are the first to model
the difference between the counterfactual and the to-
be-explained time series instance. Moreover, in sec-
tion 3.1, it is mentioned that this method is reference-
guided. By utilizing the reference instances found
EXPLAINS 2024 - 1st International Conference on Explainable AI for Neural and Symbolic Methods
68

using Algorithm 2 and the chromosome representa-
tions, we now describe the methodology of generat-
ing counterfactual instances in Algorithm 5. Given
Algorithm 5: Generation of the SoI of counterfac-
tual candidate
Input: The target time series T = {t
k
∈ R}
m
k=1
;
the individual
−→
X = (x
1
,x
2
,x
3
); a reference sample
e
T = {
˜
t
k
∈ R}
m
k=1
; the order (lags) of the autoregres-
sive model p.
Output: The counterfactual candidate
ˆ
T .
1 Function Generate(T,
−→
X ,ψ, p,m):
2
ˆ
T ← T
3 l ← x
2
− x
1
4 i, j ← max(x
1
− p,1), min(x
2
+ p,m)
5 ζ ← {
˜
t
k
−t
k
}
j
k=i
6 Fit an autoregressive model AR(p) on ζ
7 Predict ζ ← {t
k
}
j−i+1
k=1
using the AR(p)
8 i
∗
← min(x
1
, p)
9 j
∗
← i
∗
+ l
10
ˆ
T [x
1
: x
2
] ← ζ[i
∗
: j
∗
] + T [x
1
: x
2
]
11 return
ˆ
T
a target time series T and a chromosome representa-
tion of the SoI
−→
X , the algorithm generates a counter-
factual candidate based on a chosen instance
ˆ
T from
the reference set. In lines 4 and 5, the element-wise
differences between the reference and the target are
computed as a new time series ζ. Further, from lines
6 to 10, an autoregressive model of order p is fitted to
learn the distribution of ζ through conditional max-
imum likelihood estimation. The in-sample predic-
tions are then added to the SoI values of T to form the
counterfactual SoI. In this context, the autoregressive
model essentially acts as a process of denoising and
smoothing.
4 EXPERIMENTAL SETUP
The experiments are performed using a diverse selec-
tion of time-series classification benchmarks and two
popular time-series classifiers.
The UCR datasets (Bagnall et al., 2017) from the
time-series classification archive (Chen et al., 2015)
chosen in this study represent a diverse array of ap-
plication domains in time-series classification, all of
which are one-dimensional. Furthermore, they are
categorized in Table 1 based on their domain speci-
ficity and characteristics, providing a comprehensive
assessment of the proposed method’s robustness and
adaptability across varied types of time series data.
For the classification tasks within our framework,
Table 1: The summary of the datasets along with the accu-
racy of the trained classifiers used in the experiments.
Dataset Length Train + Test Size Balanced Classes Catch22 STSF
ECG200 96 100 + 100 No 2 0.83 0.87
GunPoint 150 50 + 150 Yes 2 0.94 0.94
Coffee 286 28 + 28 Yes 2 1.00 0.964
CBF 128 30 + 900 Yes 3 0.96 0.98
Beef 470 30 + 30 Yes 5 0.60 0.66
Lightning7 319 70 + 73 No 7 0.69 0.75
ACSF1 1460 100 + 100 Yes 10 0.87 0.82
each dataset was trained and tested using two spe-
cific classifiers: the Catch22 classifier (C22) (Lubba
et al., 2019) and the Supervised Time Series Forest
(TSF) (Cabello et al., 2020). These classifiers were
meticulously chosen not only for their computational
efficiency and ease of implementation but also for
their ability to produce probabilistic outputs. The
generation of probabilistic outputs, rather than mere
binary labels, is crucial for our methodology. It al-
lows for the nuanced detection of subtle variations in
the probability distributions across different classes.
This feature is integral to our approach as it supports
the generation of counterfactual explanations that are
highly sensitive to minor but significant shifts in the
data.
4.1 Hyperparameters Setup
The customized NSGA-II algorithm central to our ap-
proach is designed with several hyperparameters that
can influence its operation and performance. The
standard NSGA-II hyper-parameters (and their set-
ting between brackets), population size (50), number
of generations (50), the probability of crossover (0.7)
and probability of mutation (0.7), are very common
in evolutionary optimization algorithms, and are set
based on the results of a few trials. A new hyper-
parameter, Number of Reference Instances, is set
to 4 in this work. This parameter specifies both the
number of reference cases used to evaluate the per-
formance of a candidate solution and the number
of teachers employed to guide the search for find-
ing counterfactual examples. These hyper-parameters
could be further optimized in future work.
4.2 Metrics and Baselines
As introduced in section 4.2, five criteria can be used
to assess the effectiveness of the counterfactual ex-
planation algorithms. Given a to-be-explained time
series T = {t
i
∈ R}
m
i=1
, a set of n counterfactuals can-
didates Θ = {
ˆ
T
j
= {
ˆ
t
i
∈ R}
m
i=1
}
N
j=1
, and the classifier
f , we define the five evaluation metrics as follow:
1. L1-Proximity(T,
ˆ
T ) =
|
ˆ
T −T |
|
ˆ
T |+|T |
TX-Gen: Multi-Objective Optimization for Sparse Counterfactual Explanations for Time-Series Classification
69

2. L2-Proximity(T,
ˆ
T ) =
|
ˆ
T −T |
2
|
ˆ
T |
2
+|T |
2
3. Validity(T,
ˆ
T | f ) = 1
f (T )̸= f (
ˆ
T )
4. Sparsity(T,
ˆ
T ) =
∑
i=[1,...,m]
1
ˆ
t
i
̸=t
i
m
5. Diversity(T,Θ | f ) =
N−1
∑
i=1
(
N
∏
j=i+1
1
ˆ
T
i
̸=
ˆ
T
j
) · 1
f (T )̸= f (
ˆ
T
i
)
,
ˆ
T
i
,
ˆ
T
j
∈ Θ
Among the five metrics, the first four are pairwise
metrics. In contrast, Diversity is focused on mea-
suring the number of unique and valid counterfac-
tuals generated by the explainer for each target time
series in a single run. In this work, we evalu-
ate the performance of TX-Gen against four well-
established algorithms which can be separated into
two groups: w-CF (Wachter et al., 2017) and Native-
Guide (Delaney et al., 2021), the hall-of-fame base-
lines; TSEvo (H
¨
ollig et al., 2022) and AB-CF (Li
et al., 2023), the state-of-the-art counterfactual ex-
plainers.
Table 2: The Validity metric for each counterfactual XAI
method on two different classifiers (TSF and C22) and
seven different benchmark datasets.
Explainer
ECG200 Coffee GunPoint CBF Lightning7 ACSF1 Beef
Validity Validity Validity Validity Validity Validity Validity
NG (C22) 0.56 0.46 0.43 0.59 – – 0.83
w-CF (C22) 0.03 – 0.01 0.01 – 0.11 0.13
AB-CF (C22) 0.93 1.00 1.00 0.99 0.99 1.00 1.00
TSEvo (C22) 0.39 0.54 0.45 0.50 0.56 0.51 0.07
TX-Gen (C22) 1.00 1.00 1.00 1.00 1.00 1.00 1.00
NG (TSF) 0.35 0.50 0.50 – – – 0.10
w-CF (TSF) – – – 0.01 0.11 0.17
AB-CF (TSF) 0.74 1.00 1.00 1.00 0.99 0.99 0.97
TSEvo (TSF) 0.35 0.50 0.50 0.35 0.44 0.22 0.20
TX-Gen (TSF) 1.00 1.00 1.00 1.00 1.00 1.00 1.00
5 RESULTS AND DISCUSSIONS
Our experimental results clearly demonstrate that
TX-Gen consistently outperforms competing meth-
ods across several key metrics, as shown in Tables
2-5. In terms of validity, TX-Gen achieves a 100%
success rate in generating valid counterfactuals across
all datasets, regardless of the classifier used (Table 2).
This significantly outperforms baseline methods like
w-CF, which struggles with generating valid counter-
factuals, achieving a mere 1% ∼ 17% validity across
different datasets and classifiers. TSEvo, while better
than w-CF, also lags behind TX-Gen in validity, par-
ticularly when using the Catch22 classifier. AB-CF
is in terms of validity only marginally worse than our
proposed solution.
Sparsity is a key strength of TX-Gen, as demon-
strated in Table 3. While methods like TSEvo also
optimize for sparsity, TX-Gen achieves lower sparsity
values across most datasets. In terms of proximity,
Tables 4 and 5 show that TX-Gen performs compet-
itively with state-of-the-art methods such as AB-CF
and TSEvo, which also optimize for proximity. How-
ever, TX-Gen’s use of multi-objective optimization
allows it to maintain a strong proximity score while
simultaneously achieving higher validity and diver-
sity. The L1-Proximity and L2-Proximity results re-
flect that TX-Gen generates counterfactuals that are
closer to the original time series, ensuring more inter-
pretable and actionable insights.
As shown in the examples of Figure 2 and also in
Table 6, our method generates a diverse set of Pareto-
optimal solutions allowing for a wide range of plau-
sible counterfactuals. All other methods only provide
one counterfactual example per instance. This is par-
ticularly important in real-world applications, where
generating multiple plausible alternatives can provide
more comprehensive insights for end-users. The num-
ber of sub-sequences of the counterfactual examples
by TX-Gen is always 1, while for TSEvo this is on av-
erage 13.8 sub-sequences, Native-Guide provides 1.8,
w-CF 1.7 and AB-CF 1.8 sub-sequences on average
over all datasets. In general, less sub-sequences are
more informative for counterfactual examples. How-
ever, it could be a limitation that the proposed method
only provides 1 sub-sequence, however, TX-Gen pro-
vides multiple examples per instance, one could com-
bine the sub-sequences from these examples to allevi-
ate this limitation. All results and source code can be
found in our Zenodo repository
1
.
In summary, TX-Gen’s use of evolutionary multi-
objective optimization and its reference-guided mech-
anism make it more effective than existing methods
across key metrics. The method not only generates
more valid and sparse counterfactuals but does so
with a high degree of proximity and diversity, offering
a remarkable advancement in generating explainable
counterfactuals for time-series classification.
6 CONCLUSIONS
In this paper, we presented TX-Gen, a novel frame-
work for generating counterfactual explanations for
time-series classification tasks using evolutionary
multi-objective optimization. Through extensive ex-
perimentation, we demonstrated that TX-Gen consis-
tently outperforms state-of-the-art methods in terms
of validity, sparsity, proximity, and diversity across
multiple benchmark datasets. By leveraging the flex-
1
https://doi.org/10.5281/zenodo.13711886
EXPLAINS 2024 - 1st International Conference on Explainable AI for Neural and Symbolic Methods
70

Table 3: The Sparsity metric for each counterfactual XAI method on two different classifiers (TSF and C22) and seven
different benchmark datasets.
Explainer
ECG200 Coffee GunPoint CBF Lightning7 ACSF1 Beef
Mean Std. Mean Std. Mean Std. Mean Std. Mean Std. Mean Std. Mean Std.
NG (C22) 0.403 0.310 0.962 0.131 0.052 0.065 0.989 0.067 – – – – 1.000 0.000
w-CF (C22) 0.010 0.000 – – 0.007 0.000 0.669 0.468 – – 0.092 0.287 0.252 0.432
AB-CF (C22) 0.430 0.254 0.437 0.106 0.525 0.296 0.461 0.276 0.350 0.269 0.534 0.334 0.467 0.267
TSEvo (C22) 0.408 0.154 0.280 0.189 0.237 0.197 0.485 0.213 0.347 0.271 0.558 0.291 0.698 0.302
TX-Gen (C22) 0.113 0.137 0.016 0.016 0.121 0.161 0.043 0.052 0.044 0.056 0.041 0.086 0.040 0.091
NG (TSF) 0.967 0.096 0.932 0.169 0.963 0.061 – – – – – – 0.667 0.470
w-CF (TSF) – – – – – – – – 0.006 0.000 0.818 0.385 0.207 0.397
AB-CF (TSF) 0.589 0.218 0.871 0.030 0.307 0.063 0.410 0.284 0.580 0.298 0.589 0.265 0.528 0.324
TSEvo (TSF) 0.154 0.105 0.180 0.072 0.170 0.084 0.194 0.076 0.140 0.072 0.512 0.338 0.128 0.040
TX-Gen (TSF) 0.113 0.131 0.054 0.037 0.051 0.046 0.049 0.029 0.030 0.027 0.053 0.081 0.033 0.044
Table 4: The L1-Proximity metric for each counterfactual XAI method on two different classifiers (TSF and C22) and seven
different benchmark datasets.
Explainer
ECG200 Coffee GunPoint CBF Lightning7 ACSF1 Beef
Mean Std. Mean Std. Mean Std. Mean Std. Mean Std. Mean Std. Mean Std.
NG (C22) 0.121 0.086 0.098 0.260 0.010 0.011 0.383 0.220 – – – – 1.000 0.000
w-CF (C22) 0.001 0.000 – – 0.001 0.000 0.001 0.001 – – 0.00003 0.00002 0.00003 0.0002
AB-CF (C22) 0.132 0.081 0.024 0.007 0.069 0.059 0.236 0.144 0.222 0.114 0.060 0.084 0.103 0.195
TSEvo (C22) 0.311 0.161 0.021 0.011 0.036 0.023 0.275 0.097 0.240 0.139 0.090 0.075 0.036 0.023
TX-Gen (C22) 0.062 0.076 0.002 0.002 0.039 0.067 0.032 0.037 0.045 0.062 0.008 0.017 0.047 0.133
NG (TSF) 0.164 0.118 0.026 0.011 0.062 0.029 – – – – – – 0.515 0.365
w-CF (TSF) – – – – – – – – 0.0001 0.0000 0.035 0.061 0.0003 0.0001
AB-CF (TSF) 0.161 0.067 0.045 0.009 0.043 0.037 0.168 0.110 0.251 0.169 0.065 0.073 0.092 0.150
TSEvo (TSF) 0.067 0.054 0.016 0.005 0.015 0.012 0.073 0.029 0.083 0.041 0.067 0.074 0.143 0.110
TX-Gen (TSF) 0.056 0.060 0.007 0.004 0.012 0.019 0.030 0.020 0.039 0.062 0.012 0.020 0.020 0.036
Table 5: The L2-Proximity metric for each counterfactual XAI method on two different classifiers (TSF and C22) and seven
different benchmark datasets.
Explainer
ECG200 Coffee GunPoint CBF Lightning7 ACSF1 Beef
Mean Std. Mean Std. Mean Std. Mean Std. Mean Std. Mean Std. Mean Std.
NG (C22) 0.182 0.068 0.105 0.259 0.046 0.034 0.478 0.216 – – – – 1.000 0.000
w-CF (C22) 0.006 0.001 – – 0.008 0.000 0.007 0.005 – – 0.001 0.000 0.004 0.002
AB-CF (C22) 0.193 0.086 0.041 0.008 0.118 0.083 0.349 0.130 0.376 0.127 0.145 0.167 0.132 0.228
TSEvo (C22) 0.440 0.145 0.045 0.011 0.096 0.047 0.430 0.067 0.430 0.161 0.200 0.155 0.045 0.031
TX-Gen (C22) 0.134 0.105 0.017 0.008 0.076 0.098 0.121 0.076 0.117 0.127 0.036 0.061 0.084 0.207
NG (TSF) 0.175 0.113 0.036 0.016 0.091 0.046 – – – – – – 0.561 0.395
w-CF (TSF) – – – – – – 0.001 0.000 0.058 0.128 0.058 0.128 0.002 0.000
AB-CF (TSF) 0.209 0.068 0.055 0.010 0.101 0.090 0.283 0.094 0.332 0.160 0.137 0.149 0.111 0.172
TSEvo (TSF) 0.169 0.094 0.043 0.007 0.051 0.038 0.181 0.046 0.210 0.113 0.125 0.105 0.357 0.255
TX-Gen (TSF) 0.133 0.107 0.027 0.011 0.047 0.057 0.112 0.062 0.100 0.102 0.045 0.060 0.060 0.104
Table 6: The Diversity metric for each counterfactual XAI method on two different classifiers (TSF and C22) and seven
different benchmark datasets. (For all other methods this is always 1.00).
Explainer
ECG200 Coffee GunPoint CBF Lightning7 ACSF1 Beef
Mean Std. Mean Std. Mean Std. Mean Std. Mean Std. Mean Std. Mean Std.
TX-Gen (C22) 6.95 2.73 7.46 3.52 10.70 4.08 14.45 4.39 25.07 8.93 24.86 8.49 20.80 6.60
TX-Gen (TSF) 4.89 0.92 4.79 0.82 4.12 1.26 5.27 1.00 5.89 1.67 6.58 2.28 6.13 1.28
TX-Gen: Multi-Objective Optimization for Sparse Counterfactual Explanations for Time-Series Classification
71

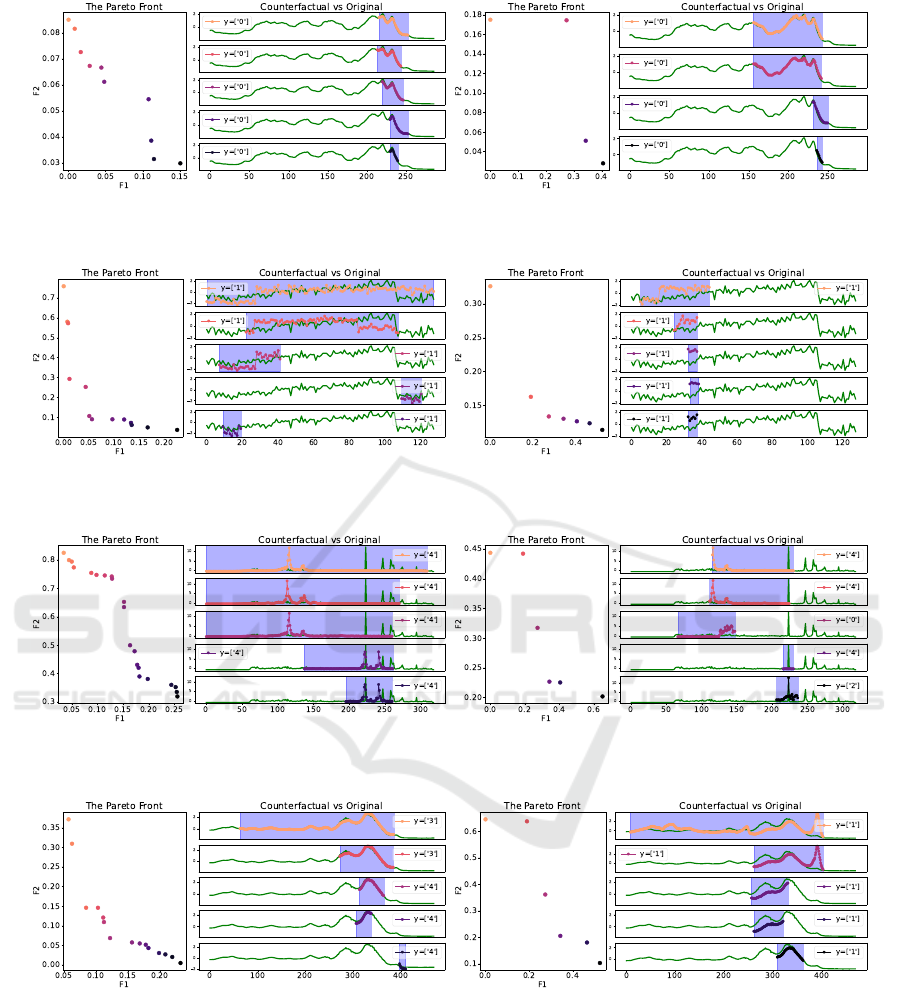
(a) An example of the Pareto-efficient counterfactuals for the test sample (20) of a binary classification task Coffee
using Catch22 (left) and Supervised Time-series Forest (right).
(b) An example of the Pareto-efficient counterfactuals for the test sample (10) of a binary classification task CBF using
Catch22 (left) and Supervised Time-series Forest (right).
(c) An example of the Pareto-efficient counterfactuals for the test sample (35) of a multi-class classification task Light-
ning7 using Catch22 (left) and Supervised Time-series Forest (right).
(d) An example of the Pareto-efficient counterfactuals for the test sample (10) of a multi-class classification task Beef
using Catch22 (left) and Supervised Time-series Forest (right).
Figure 2: Selection of examples of TX-Gen on different datasets and using different classifiers. In each subfigure, the left part
shows the distribution of objective values (F
1
on the x axis and F
2
on the y axis) of the Pareto front. The right part of each
figure displays the counterfactual examples and corresponding labels. The time series being explained is highlighted in green,
while the counterfactual subsequence of interest (SoIs) are color-coded according to their position on the Pareto front.
ibility of the NSGA-II algorithm and incorporat-
ing a reference-guided mechanism, our approach en-
sures that the generated counterfactuals are both in-
terpretable and computationally efficient.
The good performance of TX-Gen particularly in
achieving 100% validity and maintaining high diver-
sity while optimizing for proximity and sparsity, high-
lights its potential for real-world applications where
EXPLAINS 2024 - 1st International Conference on Explainable AI for Neural and Symbolic Methods
72

model transparency is critical. Our proposed method
strikes an effective balance between multiple conflict-
ing objectives, offering a robust solution for generat-
ing meaningful counterfactuals in time-series classifi-
cation.
Future work can explore several promising direc-
tions. First, further tuning of the hyper-parameters,
particularly the number of reference instances, could
lead to even greater improvements in performance.
Additionally, extending TX-Gen to handle multivari-
ate time-series data and real-time counterfactual gen-
eration could broaden its applicability to more com-
plex, real-world scenarios.
ACKNOWLEDGEMENT
This publication is part of the project XAIPre (with
project number 19455) of the research program Smart
Industry 2020 which is (partly) financed by the Dutch
Research Council (NWO).
REFERENCES
Back, T., Fogel, D. B., and Michalewicz, Z. (1997). Hand-
book of Evolutionary Computation. IOP Publishing
Ltd., GBR, 1st edition.
B
¨
ack, T. H., Kononova, A. V., van Stein, B., Wang, H.,
Antonov, K. A., Kalkreuth, R. T., de Nobel, J., Ver-
metten, D., de Winter, R., and Ye, F. (2023). Evolu-
tionary algorithms for parameter optimization—thirty
years later. Evolutionary Computation, 31(2):81–122.
Bagnall, A., Lines, J., Bostrom, A., Large, J., and Keogh,
E. (2017). The great time series classification bake
off: A review and experimental evaluation of recent
algorithmic advances. Data Mining and Knowledge
Discovery, 31(3):606–660.
Cabello, N., Naghizade, E., Qi, J., and Kulik, L. (2020).
Fast and accurate time series classification through su-
pervised interval search. In 2020 IEEE International
Conference on Data Mining (ICDM), pages 948–953.
IEEE.
Chen, J.-F., Chen, W.-L., Huang, C.-P., Huang, S.-H., and
Chen, A.-P. (2016). Financial time-series data analysis
using deep convolutional neural networks. In 2016 7th
International conference on cloud computing and big
data (CCBD), pages 87–92. IEEE.
Chen, Y., Keogh, E., Hu, B., Begum, N., Bagnall, A.,
Mueen, A., and Batista, G. (2015). The ucr time se-
ries classification archive. www.cs.ucr.edu/
∼
eamonn/
time series data/.
Deb, K., Pratap, A., Agarwal, S., and Meyarivan, T. (2002).
A fast and elitist multiobjective genetic algorithm:
NSGA-II. IEEE Transactions on Evolutionary Com-
putation, 6(2):182–197.
Delaney, E., Greene, D., and Keane, M. T. (2021). Instance-
Based Counterfactual Explanations for Time Series
Classification. In S
´
anchez-Ruiz, A. A. and Floyd,
M. W., editors, Case-Based Reasoning Research and
Development, pages 32–47, Cham. Springer Interna-
tional Publishing.
Endres, D. and Schindelin, J. (2003). A new metric for
probability distributions. IEEE Transactions on Infor-
mation Theory, 49(7):1858–1860.
Goldberg, D. E. and Deb, K. (1991). A Comparative Analy-
sis of Selection Schemes Used in Genetic Algorithms.
In Rawlins, G. J. E., editor, Foundations of Genetic
Algorithms, volume 1, pages 69–93. Elsevier.
H
¨
ollig, J., Kulbach, C., and Thoma, S. (2022). TSEvo: Evo-
lutionary Counterfactual Explanations for Time Se-
ries Classification. In 2022 21st IEEE International
Conference on Machine Learning and Applications
(ICMLA), pages 29–36.
Huang, Q., Chen, W., B
¨
ack, T., and van Stein, N. (2024).
Shapelet-based Model-agnostic Counterfactual Local
Explanations for Time Series Classification. Presented
at the AAAI 2024 Workshop on Explainable Machine
Learning for Sciences (XAI4Sci).
Karlsson, I., Rebane, J., Papapetrou, P., and Gionis, A.
(2018). Explainable time series tweaking via irre-
versible and reversible temporal transformations.
Karlsson, I., Rebane, J., Papapetrou, P., and Gionis, A.
(2020). Locally and globally explainable time se-
ries tweaking. Knowledge and Information Systems,
62(5):1671–1700.
Lang, J., Giese, M. A., Ilg, W., and Otte, S. (2023). Generat-
ing Sparse Counterfactual Explanations for Multivari-
ate Time Series. In Iliadis, L., Papaleonidas, A., An-
gelov, P., and Jayne, C., editors, Artificial Neural Net-
works and Machine Learning – ICANN 2023, pages
180–193, Cham. Springer Nature Switzerland.
Li, P., Bahri, O., Boubrahimi, S. F., and Hamdi, S. M.
(2022). SG-CF: Shapelet-Guided Counterfactual Ex-
planation for Time Series Classification. In 2022 IEEE
International Conference on Big Data (Big Data),
pages 1564–1569.
Li, P., Bahri, O., Boubrahimi, S. F., and Hamdi, S. M.
(2023). Attention-Based Counterfactual Explanation
for Multivariate Time Series. In Wrembel, R., Gam-
per, J., Kotsis, G., Tjoa, A. M., and Khalil, I., editors,
Big Data Analytics and Knowledge Discovery, pages
287–293, Cham. Springer Nature Switzerland.
Lubba, C. H., Sethi, S. S., Knaute, P., Schultz, S. R.,
Fulcher, B. D., and Jones, N. S. (2019). catch22:
CAnonical time-series CHaracteristics: Selected
through highly comparative time-series analysis. Data
Mining and Knowledge Discovery, 33(6):1821–1852.
Morid, M. A., Sheng, O. R. L., and Dunbar, J. (2023).
Time series prediction using deep learning methods
in healthcare. ACM Transactions on Management In-
formation Systems, 14(1):1–29.
Refoyo, M. and Luengo, D. (2024). Sub-SpaCE:
Subsequence-Based Sparse Counterfactual Explana-
tions for Time Series Classification Problems. In
Longo, L., Lapuschkin, S., and Seifert, C., editors,
TX-Gen: Multi-Objective Optimization for Sparse Counterfactual Explanations for Time-Series Classification
73

Explainable Artificial Intelligence, pages 3–17, Cham.
Springer Nature Switzerland.
Selvaraju, R. R., Cogswell, M., Das, A., Vedantam, R.,
Parikh, D., and Batra, D. (2017). Grad-CAM: Vi-
sual Explanations from Deep Networks via Gradient-
Based Localization. In 2017 IEEE International Con-
ference on Computer Vision (ICCV), pages 618–626.
Theissler, A., Spinnato, F., Schlegel, U., and Guidotti, R.
(2022). Explainable ai for time series classification:
a review, taxonomy and research directions. Ieee Ac-
cess, 10:100700–100724.
Wachter, S., Mittelstadt, B., and Russell, C. (2017). Coun-
terfactual explanations without opening the black box:
Automated decisions and the GDPR. SSRN Electronic
Journal.
Ye, L. and Keogh, E. (2009). Time series shapelets: A new
primitive for data mining. In Proceedings of the 15th
ACM SIGKDD International Conference on Knowl-
edge Discovery and Data Mining, KDD ’09, pages
947–956, New York, NY, USA. Association for Com-
puting Machinery.
Zhou, R., Bacardit, J., Brownlee, A., Cagnoni, S., Fyvie,
M., Iacca, G., McCall, J., van Stein, N., Walker, D.,
and Hu, T. (2024). Evolutionary computation and ex-
plainable ai: A roadmap to transparent intelligent sys-
tems.
EXPLAINS 2024 - 1st International Conference on Explainable AI for Neural and Symbolic Methods
74