Control of Fixed-Wing Tethered Aircraft in Circular Take-Off and

Landing Maneuvers

ergio Vinha

, Gabriel M. Fernandes

, Manuel C. R. M. Fernandes

Huu Thien Nguyen

and Fernando A. C. C. Fontes

SYSTEC-ISR-ARISE, Department of Electrical and Computer Engineering,

Faculty of Engineering, University of Porto, Rua Dr. Roberto Frias, 4200-465 Porto, Portugal

Keywords:

Airplane Control, Tethered Aircraft, Automatic Take-off and Landing, Circular Take-off and Landing,

Unmanned Aerial Vehicles (UAVs), Airborne Wind Energy.

Abstract:

This article addresses the control of tethered aircraft with ﬁxed wings during take-off and landing maneuvers

with a circular motion, particularly focusing on controlling the aircraft’s roll attitude. The tether forces acting

on the aircraft make the roll control, in some operating regions, particularly challenging or even impossible

when just ailerons are used. We describe a novel bridle system to actuate on the roll angle, the development

of a controller for such a device, and its integration in the overall take-off and landing control architecture.

Simulation results are reported, showing the adequacy of the approach. Further analysis identiﬁes operational

regions where it is possible to have a tethered ﬂight or a coordinated turn ﬂight as a function of the tether

length and of the aircraft’s height.

1 INTRODUCTION

In the last few years, we have been witnessing a rapid

increase in tethered aircraft applications and in the

literature on this subject. A recent survey (Marques

et al., 2023) identiﬁed a broad range of applications,

namely inspection/monitoring, security/surveillance,

military, agricultural spraying, communications, ve-

hicle towing and the generation of electrical power.

The latter application, known as Airborne Wind En-

ergy (AWE), has seen a particularly active research

(Schmehl, 2018; Directorate-General for Research

and Innovation (European Commission) and Ecorys,

2018).

Airborne Wind Energy Systems (AWES) are

mechanisms that convert wind energy into electricity

using autonomous aircraft attached to the ground by

a tether. These mechanisms can harvest wind energy

at high altitudes, where the wind is stronger and less

intermittent, being able to generate electricity from

a yet unexplored renewable energy resource. This

https://orcid.org/0000-0002-6364-6736

https://orcid.org/0009-0005-6321-8677

https://orcid.org/0000-0003-2322-8182

https://orcid.org/0000-0002-2266-9560

https://orcid.org/0000-0003-3516-5094

makes AWE a promising renewable energy player.

However, developing AWES into a competitive and

commercially viable renewable energy technology is

challenging. One of the main challenges is the abil-

ity to operate safely, reliably, and autonomously for

long periods of time in various weather and environ-

mental conditions (see e.g., the European Commis-

sion report (Directorate-General for Research and In-

novation (European Commission) and Ecorys, 2018)

and a study for Airborne Wind Europe (Blanch et al.,

2022)). Despite the progress made in this ﬁeld, most

existing technology demonstrators still require super-

vised operation, particularly in the take-off and land-

ing phases, and thus, are not fully autonomous. To

achieve full autonomous operation it is essential to de-

velop reliable automatic Take-Off and Landing (TOL)

schemes for tethered aircraft.

The control of tethered aircraft, in particular for

AWE, is a demanding problem, but one for which

a signiﬁcant number of contributions has been pro-

duced (see e.g.(Vermillion et al., 2021) and the many

references therein). Different Automatic Take-Off

and Landing (ATOL) approaches for tethered aircraft

have been tried (Fagiano and Schnez, 2017). Among

those, we can distinguish three techniques for ﬁxed-

wing aircraft: linear, vertical and circular TOL tech-

niques. In vertical TOL, the technology is vastly stud-

Vinha, S., Fernandes, G., Fernandes, M., Nguyen, H. and Fontes, F.

Control of Fixed-Wing Tethered Aircraft in Circular Take-Off and Landing Maneuvers.

DOI: 10.5220/0013067000003822

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 21st International Conference on Informatics in Control, Automation and Robotics (ICINCO 2024) - Volume 2, pages 319-326

ISBN: 978-989-758-717-7; ISSN: 2184-2809

319

ied in the multicopter area. The same happens in the

linear TOL with the common airplanes. However, cir-

cular TOL has a much lower possibility of reusing

existing similar technology and thus is the least in-

vestigated technique of the three. The Circular Take-

off and Landing (CTOL) is the technique studied in

this article and it has several advantages: the facil-

ity to re-launch due to the inﬁnite runway (the air-

craft can do as many turns as needed) and the low

peak power and additional mass required for climb-

ing (Vinha et al., 2024a). There are two variants of

the CTOL technique. One of such variants, the most

investigated one, uses a rotating platform or rigid arm

to generate enough airspeed (Sieberling et al., 2011;

Zanon et al., 2013; Geebelen et al., 2013; Rieck et al.,

2017). Other variants use a tethered aircraft equipped

with landing gear and propellers to produce the cir-

cular motion during the take-off and landing phases,

similarly to the scheme studied here and in (Cherubini

et al., 2017; Cherubini, 2017; Fernandes, 2023; Vinha

et al., 2024b). It is also noteworthy that Miles Loyd,

a pioneer of Airborne Wind Energy, describes in its

seminal patent (Loyd, 1981) a mechanism based on a

circular launch system.

A control system for automatic circular take-off

and landing and transition to ﬂight has been pro-

posed, which can be adopted by a ﬁxed-wing, self-

motorized, tethered aircraft. The main application

foreseen for the proposed technology is to include it

in an Airborne Wind Energy System. It used a hierar-

chical control architecture. In the top layer, a supervi-

sory controller is responsible for governing the transi-

tion between ﬂight phases, for path-planning, and for

setting the references to the lower-level controllers at

each phase of operation. At the lower level, the con-

trollers that were designed for each phase range from

simple PID, controlling on a single variable, to multi-

variable optimal regulators for the locally linearized

systems. This control architecture was detailed in

(Vinha et al., 2024b) and is summarized here for com-

pleteness.

In this paper, we introduce a novel bridle actuator

to control the angle between the wings and the tether

and thereby control the roll angle of the tethered air-

craft. We also develop a dynamic model and control

system for the aircraft’s roll angle, integrated into the

overall control architecture.

The control of the roll angle in tethered aircraft

can be demanding in some situations due to the ten-

dency of the tether tension to impose a speciﬁc wings-

tether angle. The take-off, landing, and transition to

normal tethered ﬂight are some of such demanding

situations for which it is crucial to have a roll angle

control authority. Here, we explore in the examples

the roll control during the phase immediately after the

take-off, in loiter with levelled wings, and in coordi-

nated turn situations. The developed controllers have

been tested in simulations. The results show the vi-

ability of the approach to take-off and transition to

other tethered ﬂight modes. In the analysis of the re-

sults, we identify viable operational regions accord-

ing to tether length and height for different roll angle

intervals.

The document is organized as follows. In Section

2, we derive the model used to represent the motion of

a tethered aircraft and introduce the control architec-

ture used. Next, in Section 3 we detail the parameters

and results from simulations designed to test the pro-

posed control system. Finally, in Section 4, we dis-

cuss the results and implications of the simulations,

including a discussion of the conditions in which co-

ordinated turn ﬂight is possible.

2 TETHERED AIRCRAFT

MODEL

The motion of a tethered aircraft, when the tether is

taut, is constrained to the surface of a sphere with

a radius equal to the tether length. Therefore, it is

convenient to use spherical coordinates centred at the

tether anchorage point. The aircraft’s location is rep-

resented by (r,ϕ,β), where r is the radial distance, ϕ

is the azimuth angle, and β the elevation angle (mea-

sured from the horizontal plane). The coordinate ba-

sis is denoted by (e

). See nomenclature in Ta-

ble 1. In spherical coordinates, the position, velocity,

and acceleration vectors are (Riley et al., 2006):

p =









p =





˙r

r cos β





, and (1)

p =





¨r

r cos β











−r

− r

cos

2˙r

ϕcos β − 2r

βsin β

2˙r

β + r

cosβ sin β







. (2)

The aircraft’s velocity vector is also denoted by V

(V =

p) and the airspeed vector is given by V

V − V

where V

is the wind speed vector (assumed

zero in this work). The last term in

p is due to the use

of a rotating frame and is equal to −F

/m, where F

represents the inertial force,

= m







+ r

cos

−2˙r

ϕcos β + 2r

βsin β

−2˙r

β − r

cosβ sin β







. (3)

It is also convenient to consider the body coordi-

nate frame with basis (e

), where e

is the air-

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

320

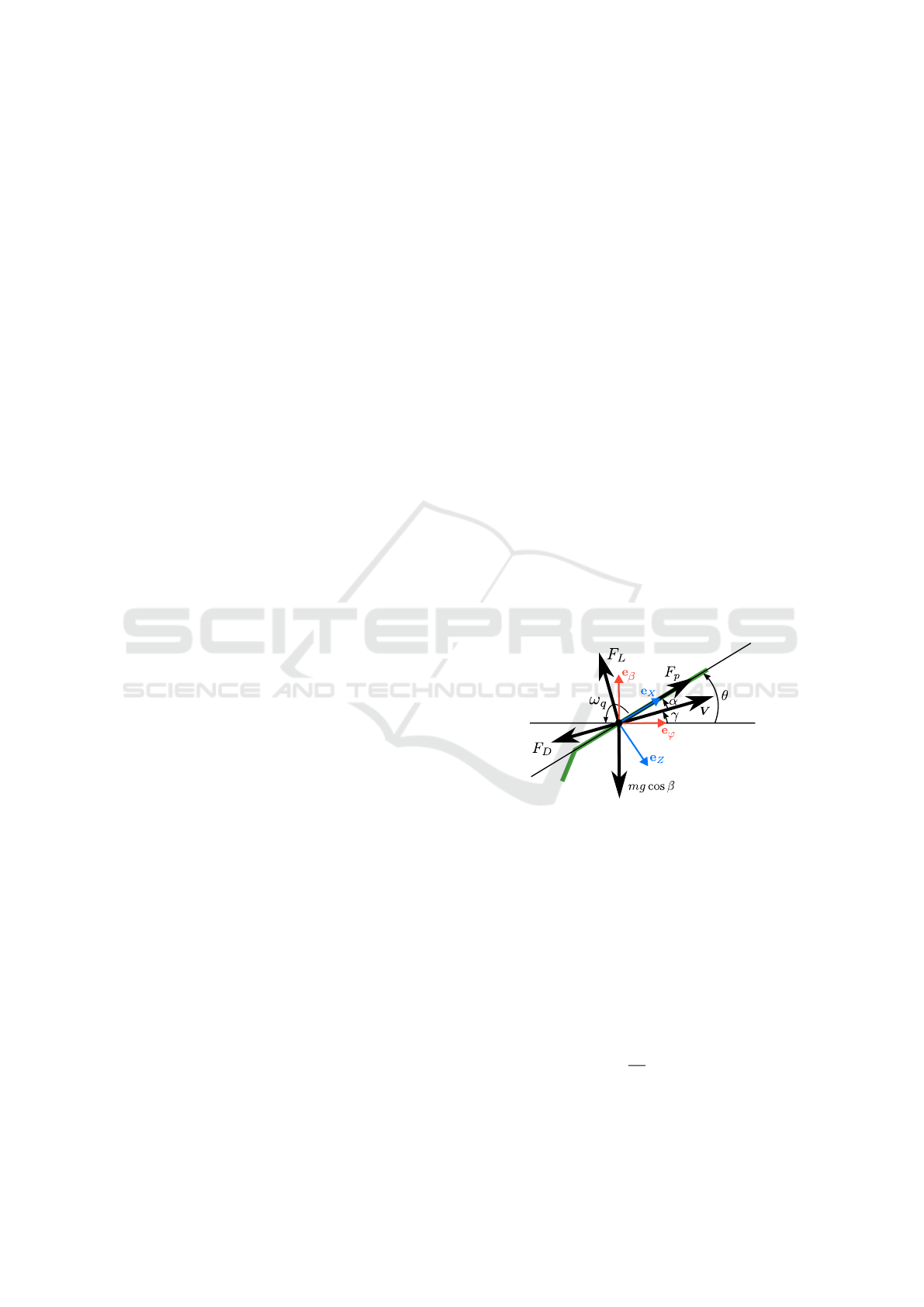
Table 1: Nomenclature.

A wing area

b wingspan [m]

aerodynamic drag and lift coefﬁcients

aerodynamic drag vector and magnitude [N]

aerodynamic lift vector and magnitude [N]

propeller thrust vector and magnitude [N]

inertial force vector and magnitude in a rotating frame [N]

tether force vector and magnitude [N]

g gravitational acceleration

−2

m mass [kg]

ρ air density

kgm

−3

h height [m]

p kite position

V,V kite velocity vector and magnitude

−1

kite airspeed vector and magnitude

−1

wind velocity vector and magnitude

−1

X,U state and control vectors

r,ϕ, β spherical coordinates [m],[

◦

,rad],[

◦

,rad]

α,γ angle-of-attack and ﬂight-path angle [

◦

,rad]

φ,θ, ψ roll, pitch and yaw angles [

◦

,rad]

ζ wings-tether angle [

◦

,rad]

,ω

roll, pitch and yaw rates

◦

−1

,rad s

−1

craft’s longitudinal axis pointing to its nose, e

is the

transversal axis pointing out of the right wing, and e

is the aircraft’s vertical axis pointing down from its

belly.

We deﬁne also a set of angles that characterize the

aircraft’s attitude. The pitch angle, denoted by θ, is

the angle between the direction of the aircraft’s longi-

tudinal axis e

and the horizontal plane. The ﬂight-

path angle, denoted by γ, is the angle between the hor-

izontal plane and the aircraft’s velocity vector V. The

aircraft’s angle-of-attack, denoted by α, is the angle

between the aircraft’s longitudinal axis and its veloc-

ity vector (when both the sideslip angle and the wind

speed are considered to be zero, as is the case in this

work). These three angles are represented in Fig. 1

and are related by the equation θ = γ + α . The roll

angle, denoted by φ, is the angle between the hori-

zontal plane and the aircraft’s transversal axis e

. We

deﬁne also the wings-tether angle ζ to be the angle be-

tween the aircraft’s transversal axis e

and the tether

direction e

. These angles are related by the equation

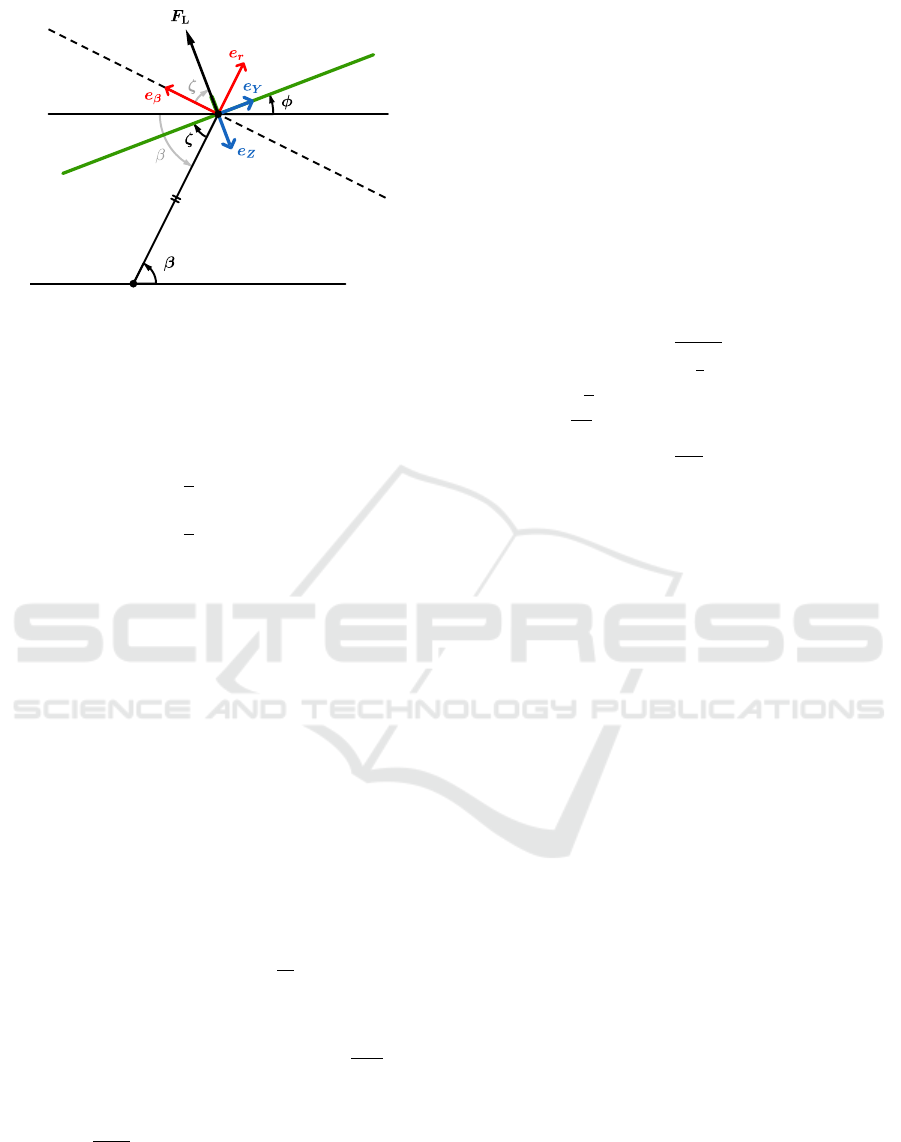
β = φ + ζ and are represented in Fig. 2.

In the spherical coordinate frame, the kinematic

horizontal line

longitudinal axis

Figure 1: Airplane longitudinal model for circular tethered

ﬂight (aircraft longitudinal shape colored green).

model of the aircraft is

r cos β

ϕ =V cos γ,

β =V sin γ,

θ = ω

(4)

where ω

is the pitch rate. Taking the derivative of the

kinematics (4), when r is assumed constant, we have

β =sin γ

V +V cos γ

γ,

r cos β

ϕ =cos γ

V − V sin γ

tanβ cos γ sinγ .

(5)

The aircraft is subject to the following forces: the pro-

peller thrust F

= F

, the weight F

with magnitude

Control of Fixed-Wing Tethered Aircraft in Circular Take-Off and Landing Maneuvers

321

-1.5-1.5 -1-1 -0.5-0.5 0.50.5 11 1.51.5 22 2.52.5 33 3.53.5 44 4.54.5 55 5.55.5 66 6.56.5 77 7.57.5 88 8.58.5 99

1.51.5

2.52.5

3.53.5

4.54.5

5.55.5

6.56.5

horizontal plane

Figure 2: Tethered aircraft with wings-tether angle ζ possi-

bly nonzero (aircraft lateral axis colored green).

mg pointing down, the aerodynamic lift F

= −F

the aerodynamic drag F

= −F

, the tether pull

= −F

, and also the inertial forces F

when a ro-

tating frame are considered. In this setting,

ρAV

(α) (6)

ρAV

(α) (7)

where V

is the magnitude of the airspeed vector V

Considering the total force in spherical coordi-

nates m

p = [F

]

= F

we obtain for each component

sinζ − F

− mg sinβ

+ mr

cos

β,

= − F

sinγ cos ζ − F

cosγ + F

cosθ

− 2m˙r

ϕcos β + 2mr

βsin β, (8)

cosγ cos ζ − F

sinγ + F

sinθ − mg cosβ

− mr

cosβ sin β − 2m˙r

β.

Combining the last two equations with (5) and solving

for (

V ,

γ), we have



sinγ V cosγ

cosγ −V sin γ





/m −

tanβ cos γ sin γ

which results in the dynamic equations for V and γ:

V = − F

+ F

cosα − mg cosβ sin γ −

2V ˙r

γ =F

cos(β − φ) + F

sinα − mg cosβ cos γ

−

tanβ cos γ.

(9)

These latter equations combine with the kinematics

(4) to deﬁne the longitudinal motion model of the

tethered aircraft. The resulting model is analogous

to the well-known longitudinal model of a ﬁxed-wing

plane (see (Nguyen et al., 2023; Beard and McLain,

2012) and Fig. 1) when applied to the case of circular

tethered ﬂight.

We deﬁne the control variables to be the thrust

force F

, the pitch rate ω

, and the wings-tether an-

gle ζ.

The resulting state and control vectors consid-

ered are, respectively, X =



ϕ,β,V, γ,θ



⊤

, U =



,ω

,ζ



⊤

, and the state-space model is given by

X = f (X,U), (10)

where the dynamic function f is obtained by combin-

ing equations (4) and (9), yielding



















r cos(β)

V cos γ

V sin γ



−F

+ F

cosα − mg cosβ sin γ





cosζ + F

sinα − mg cosβ cos γ

−





tanβ cos γ









2.1 Supervisory Controller

The control of a tethered airplane during the different

stages of take-off, tethered ﬂight and landing has var-

ious control requirements, needing different control

references and even methodologies. As such, we have

developed a hierarchical control architecture where,

in the top layer, we have designed a supervisory con-

troller that is responsible for overseeing phase transi-

tions, path planning, and establishing references for

lower-level controllers throughout each operational

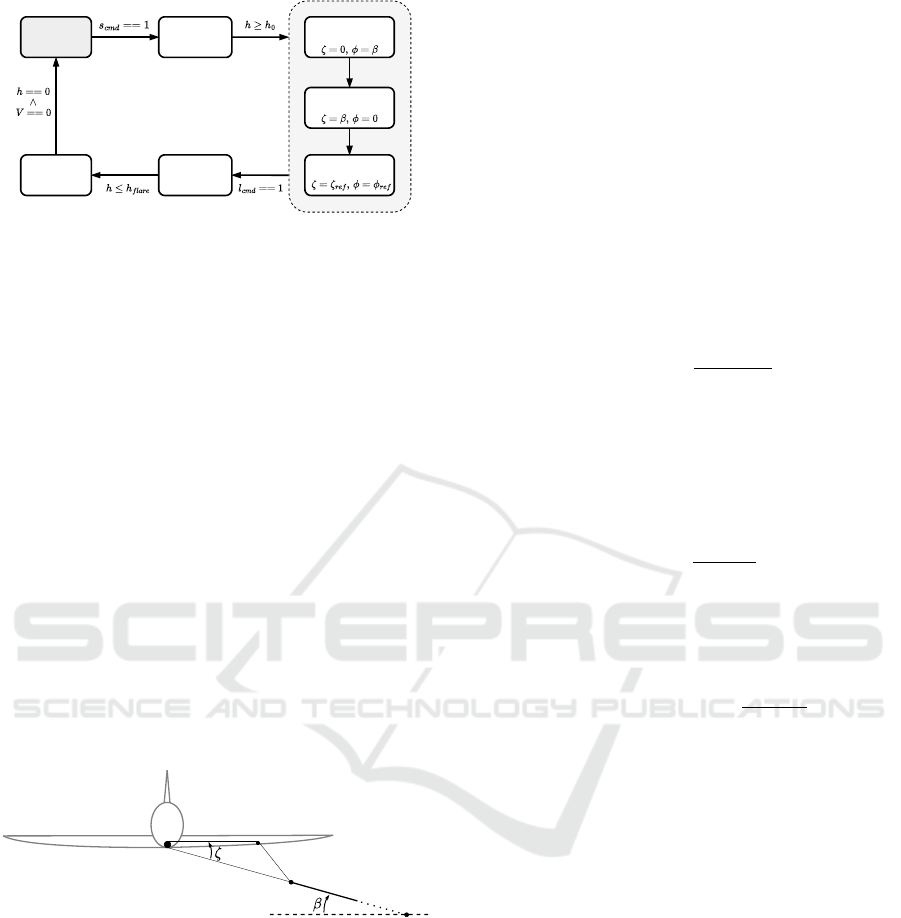
phase. Figure 3 delineates the operational phases con-

sidered. The operational phase follows closely the

work (Vinha et al., 2024b), where further details can

be found. In the current work, we will focus on the

loiter phases and roll control (see Fig. 3, dashed and

shadowed loiter phase). As explained below, we study

three different loiter phases with distinct roll angles:

(i) loiter with zero wings-tether angle, (ii) loiter with

zero roll angle, and ﬁnally (iii) loiter with zero lateral

acceleration in coordinated turn ﬂight.

2.2 Roll Control and Wings-Tether

Angle Actuation

In tethered aircraft, the tether tension tends to set the

roll angle into a speciﬁc position, being very hard to

drive to any other position just using the ailerons as

in standard untethered airplanes. This is because the

tether is restricting the motion and centrifugal forces

play a major role in this situation. Therefore the air-

craft’s center of mass tends to align with the tether

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

322

Take-off

ApproachLanding

Rest

Loiter

with

Loiter

with

Coordinated

Turn

Figure 3: The different operational phases of a tethered air-

craft during take-off and landing and three loiter maneuvers

with three different roll angles φ (and the corresponding dif-

ferent wings-tether angles ζ).

direction. The roll position is φ = β if the tether at-

tachment point is at the wing tip, or is φ = β − π/2

if the attachment point is on the fuselage surface, on

the vertical symmetry plane (see Fig. 2). In the for-

mer situation, the wings align with the tether direc-

tion, making the wings-tether angle ζ equal to zero. In

the latter, it is the aircraft’s vertical axis e

that aligns

with the tether direction, making the wings-tether an-

gle ζ equal to 90 degrees. To overcome such a limita-

tion, we have devised a bridle system with attachment

points in both the wing and the fuselage surface, with

a winch inside the aircraft (see Fig. 4). The actuation

on the winch enables the bridle geometry, and thereby

the wings-tether angle and roll angle, to be controlled.

This control can be done for a wide range of values:

for the wings-tether angle ζ between 0 and π/2 rad,

corresponding to a roll angle φ between β − π/2 and

β. This bridle system was developed in (Fontes et al.,

2023) and we refer to it for further details.

Figure 4: Bridle system with attachment points on both the

wing and on the fuselage surface, with a winch inside the

aircraft to change the bridle geometry and the wings-tether

angle (in this ﬁgure, φ = 0).

2.3 Coordinated Turn

The coordinated turn is a crucial ﬂight condition in

manned ﬂight operations primarily for enhancing pas-

senger comfort. It involves executing turns without

experiencing lateral acceleration in the aircraft’s body

frame, resulting in a smoother ﬂight experience. In

our work, this technique allows the aircraft to exe-

cute turns instead of skidding laterally, thus reducing

or even cancelling out the tension in the tether that

is connected to the aircraft. If there is a situation in

which the tether has to be released during the ATOL,

this coordinated turn can be performed so that the

aircraft can still perform the turn, without the tether.

Otherwise, the instant release of the tether could re-

sult in instability or even a crash.

During a coordinated turn, the roll angle φ is set

so that there is no net side force acting on the aircraft.

For this condition, the centrifugal force acting is

equal and opposite to the horizontal component of the

lift force. Moreover, in equilibrium, the vertical com-

ponent of the lift force is equal and opposite to the

vertical component of the gravity force. Summing the

forces in the horizontal and vertical direction we have

sinφ = m

(V cos γ)

, (11)

cosφ = mg cosγ , (12)

where R is the curvature radius, the horizontal pro-

jection of the tether length r in the horizontal plane

R = r cos β. Dividing both equations we obtain the

roll angle required for this maneuver

tanφ

ref

cosγ

. (13)

Since the wings-tether angle ζ is the variable that

can be actuated directly via the bridle mechanism, we

have

ref

= β − φ

ref

= β − arctan

cosγ

gr cos β

. (14)

2.4 Roll Controller

The roll control itself is an easy task since it is an im-

mediate consequence of an actuated variable (recall

φ = β− ζ). However by changing the roll, the vertical

and horizontal components of the lift are modiﬁed,

with consequences on the equilibrium of forces that

the tethered aircraft is subject to. The challenge is

then to maintain the equilibrium when changing the

roll. Thus, we use a multivariable control method

and as is usual in airplane control methodology, we

devise a set of equilibrium points, compute a lin-

earized model around those points, and design a Lin-

ear Quadractic Regulator (LQR) as the controller.

For the required values of β, α, γ and φ, we deter-

mine the equilibrium points with a speed V satisfying

(

β,

V ,

γ,

θ) = (0, 0,0, 0). In section 3, in Table 3, we

report the values for the reference states used. The

state considered to design the LQR does not include

the azimuth angle ϕ. Since in CTOL we have an end-

less runway, there is no need to control the azimuth

position ϕ. Moreover, the evolution of β, V

, γ, and θ

Control of Fixed-Wing Tethered Aircraft in Circular Take-Off and Landing Maneuvers

323

described by the dynamic equations is not dependent

on ϕ. As such, we can safely omit ϕ from the state-

space considered for control purposes, just using it to

draw the kite trajectories during the simulation.

In LQR, we start by deﬁning the error state

x =

X − x

re f

, and the error control

u = U − u

re f

. The lin-

earized model around the equilibrium point (

u) =

(0,0) is expressed as

x = A

x + B

u, where A and B

are the Jacobian matrices computed at the equilibrium

point.

The objective function

∞



x +



dt, in-

cludes two matrices, Q and R, which are initially set

to be diagonal and satifying the Bryson and Ho rule

(Bryson and Ho, 1975). These matrices are then man-

ually adjusted to achieve the desired response. Table

3 reports the values of the matrices used in the simu-

lation for each phase.

In order to test the roll controllers, we devise an

experiment with three loiter phases with different roll

values (see Fig. 3).

In the ﬁrst loiter phase, we maintain the wings-

tether equal to zero (corresponding to roll angle equal

to β). In the second loiter phase, we seek another sim-

ple control objective which is to attain zero roll, cor-

responding to leveled wings. In this case , we want

that φ

ref

= 0 and ζ

ref

= β These variables can be mea-

sured and controlled directly by the aircraft sensors

and actuators (in our case using a small winch). In

the third loiter phase, the control objective is to attain

a coordinated turn. The variable to regulate is, as we

have seen, the lateral acceleration a

. As the last case,

this variable can be measured directly by the aircraft

sensors.

The transitions between phases can be done by

an operator command or after a speciﬁed time pe-

riod. In this simulation, we deﬁned as t

loiter1

∈

[0,10]s, t

loiter2

∈ [10,30]s and t

loiterCT

∈ [30,60]s to be

the time in each loiter phase, respectively.

3 SIMULATION RESULTS

The simulation parameters were established consid-

ering a small-scale aircraft, facilitating the compari-

son of simulation results with future experiments data.

The aircraft and simulation parameters are given in

Table 2.

Table 2: Aircraft and Simulation Parameters.

A = 0.0720m

, m = 0.350kg

b = 0.60m, r = 30b = 18m

∈ [−20;20]

◦

−1

, F

∈ [0;1.5] N, ζ ∈ [0;90]

◦

ρ = 1.225kg m

−3

, g = 9.8m s

−2

, V

= 0m s

−1

Table 3 provides a summary of the reference

values and gains for the controllers tested for each

phase. The controllers were implemented using Mat-

lab/Simulink and the results of the simulation are dis-

played in Fig. 5.

Table 3: Controller references, gains, and objectives for

each loiter phase.

Loiter with φ = β

(β,V,γ, θ)

re f

= (20.00,8.95, 0,0)

Q = diag([63.68 0.085 5.62e3 33.19])

R = diag([2.61 8.21])

Loiter with φ = 0

(β,V,γ, θ)

re f

= (35.00,10.57, 0,0)

Q = diag([14.59 0.39 8.21 8.21])

R = diag([0.44 8.21 2.68])

Coordinated Turn

(β,V,γ, θ)

re f

= (50,9.71, 0,0)

Q = diag([14.59 0.39 8.21 8.21])

R = diag([0.44 8.21 2.68])

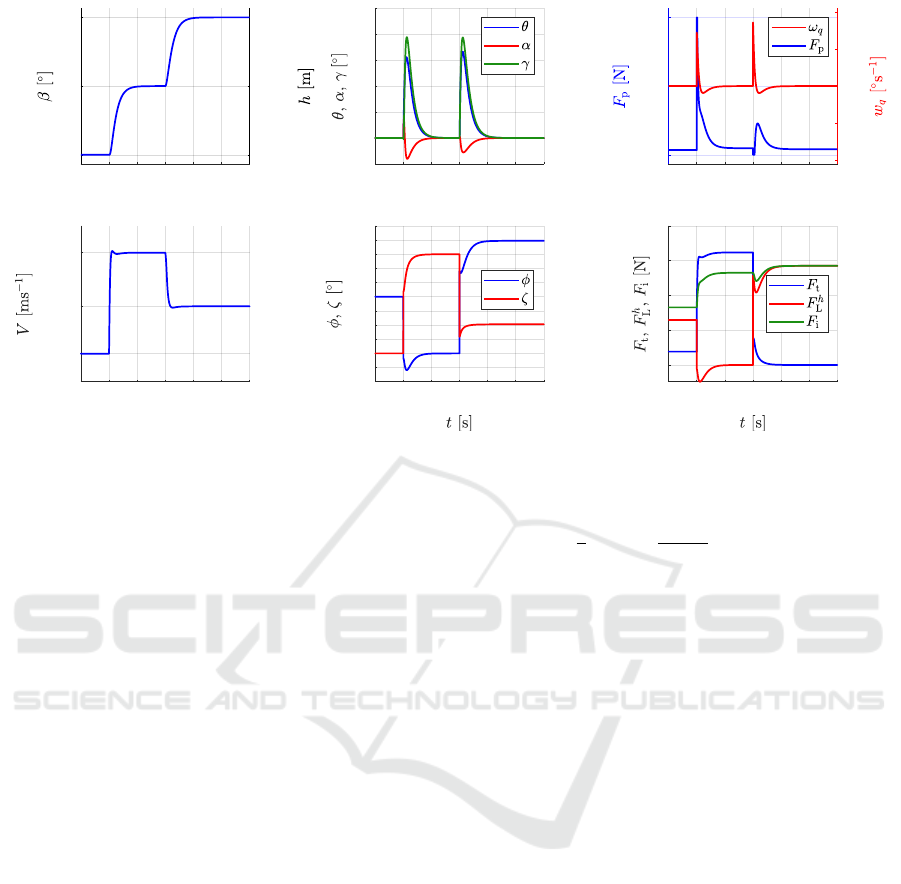
In the left column of the ﬁgure, we can see the el-

evation angle of the kite on the left axis and the height

on the right axis, on top of the velocity V of the air-

craft. In the second column, we can see the pitch,

angle-of-attack and ﬂight-path angles on the top, and

on the bottom the control variables: propeller thrust

force and pitch rate (with different axes on the oppo-

site side, respectively). Finally, in the right column,

we can see the roll and wings-tether angles above the

forces graph: tether force, the horizontal component

of the lift force (F

) and the inertial force magnitude.

We can observe that the trajectories follow closely

the references determined previously. Starting with

the ﬁrst loiter, where ζ is zero, the aircraft maintains

its attitude and altitude/elevation for 10s without any

changes. Then, in the second loiter phase, the roll

angle is set to zero and the elevation angle to 35

◦

This makes the aircraft pitch up and accelerate until it

reaches the new speed required for this new equilib-

rium point. As predicted, ζ goes to 35

◦

, which equals

the new elevation angle. Note that in this phase, the

horizontal component of the lift force is zero, that is

true when the roll is zero. Finally, after 20s in this

second phase, the aircraft performs a coordinated turn

ﬂight with an elevation angle chosen as 50

◦

. Here, the

kite goes to a new equilibrium point where the wings-

tether angle goes to the predeﬁned value computed

using equation (14), which is 10

◦

. The new speed ref-

erence is also followed. We can also point out that

in the coordinated turn phase, the tether force is zero,

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

324

6.16

10.32

13.79

8.95

9.71

10.57

-2

0.75

1.5

-20

-10

-5

Figure 5: Simulation results during the 3 types of loiter.

which proves that if the tether needs to be released,

the aircraft will still be able to perform the turn with-

out it. Also, as predicted, the inertial force magnitude

is equal to the horizontal component of the lift force

acting on the aircraft.

4 DISCUSSION AND

CONCLUSIONS

It was shown that the aircraft is able to successfully

control its roll angle during each of the three phases

described here. This paper, together with (Vinha

et al., 2024b), reveals that the implementation of a

circular take-off and landing approach, particularly

for tethered aircraft like those employed in Airborne

Wind Energy Systems, is viable and allows the au-

tomation required by this industry.

In the overall control architecture, we switch be-

tween different controllers. We are aware that such an

approach might lead to instability issues. The simula-

tion results do not show any unstable behavior. Nev-

ertheless, the stability properties of the overall archi-

tecture should be studied in future work.

The tethered ﬂight is here further explored by im-

plementing a coordinated turn ﬂight which grants the

aircraft the capability to be released from its tether

and remain stably airborne. However, a coordinated

turn ﬂight can only be performed within certain con-

ditions. If we combine F

from equations (11) and

(7), and assuming that we are in a situation with

= 0, both V

terms can be cancelled. Also, if we

assume that we are in the 1st loiter phase where ζ = 0

and β = φ, we can solve for β, obtaining:

∗

= φ

∗

arcsin



rρAc



, β ∈ [0, 45]

◦

. (15)

This equation identiﬁes, for the aircraft dimen-

sions deﬁned previously, the regions where it is possi-

ble to perform a coordinated turn ﬂight for a speciﬁc

tether length in this loiter phase. In Fig. 6, β

∗

is plot-

ted for several tether lengths (dark line). This line cor-

responds to a situation in which the coordinated turn

ﬂight is performed with ζ = 0 and the tether force is

zero. A coordinated turn ﬂight would be impossible

to achieve for the ﬂight conditions with the elevation

and tether length in the red region (left and below the

dark line). In this situation, the tether tension would

be negative which is an impossible condition since the

tether is not rigid.

Finally, the green area, above the dark line, is the

region where any tethered ﬂight can be achieved using

a positive wings-tether angle. Here, the tether force is

positive, partially canceling the centrifugal forces act-

ing on the aircraft in this ﬂight condition. Note that, in

this region, the aircraft can also perform a coordinated

turn ﬂight, if the roll angle is set adequately. However,

the use of a bridle device is essential to achieve such

roll with a positive wings-tether angle, as was simu-

lated in the third loiter case.

We can also conclude that the length of the tether

serves as a crucial design parameter, signiﬁcantly de-

termining the maximum altitude achievable through

a circular take-off and landing strategy, but also the

conditions for which is possible to perform coordi-

nated turn ﬂights.

Control of Fixed-Wing Tethered Aircraft in Circular Take-Off and Landing Maneuvers

325

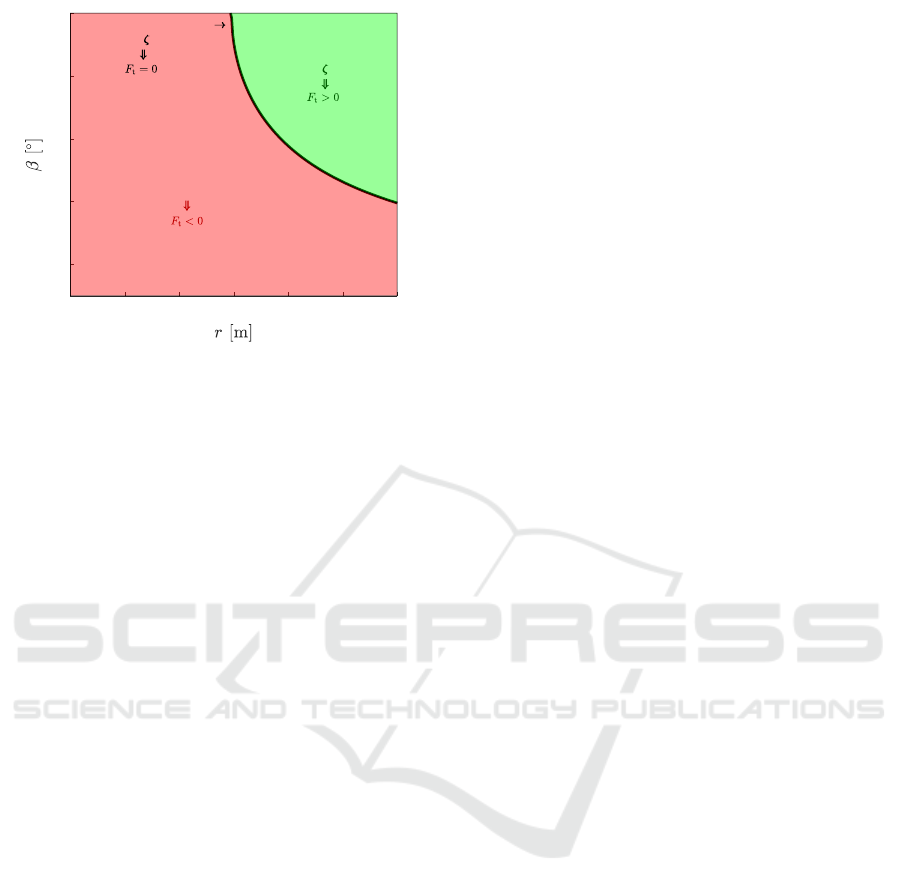
0 5 10 15 20 25 30

Coordinated turn flight

with = 0

Any tethered flight

(coordinated turn or not)

with > 0

Coordinated turn flight

impossible

Figure 6: Plot of β

∗

for various tether lengths, using the

aircraft parameters from the simulation.

ACKNOWLEDGEMENTS

This research is supported by FCT/MCTES

(PIDDAC), through projects 2022.02320.PTDC-

KEFCODE, and 2022.02801.PTDC-UPWIND-

ATOL (https://doi.org/10.54499/2022.02801.PTDC),

and grants 2021.06313.BD, and 2021.07346.BD.

REFERENCES

Beard, R. W. and McLain, T. W. (2012). Small Unmanned

Aircraft. Princeton.

Blanch, M., Makris, A., and Valpy, B. (2022). Getting air-

borne – the need to realise the beneﬁts of airborne

wind energy for net zero. Technical report, Zenodo.

Bryson, A. E. and Ho, Y.-C. (1975). Applied Optimal Con-

trol: Optimization, Estimation, and Control. Taylor &

Francis.

Cherubini, A. (2017). Advances in airborne wind en-

ergy and wind drones. PhD thesis, Scuola Superiore

Sant’Anna.

Cherubini, A., Szalai, B., Schmehl, R., and Fontana, M.

(2017). Preliminary Test on Automatic Take-Off and

Landing of a Multi-Drone Low-Drag Airborne Wind

Energy System. In 7th Airborne Wind Energy Confer-

ence (AWEC 2017).

Directorate-General for Research and Innovation (European

Commission) and Ecorys (2018). Study on challenges

in the commercialisation of airborne wind energy sys-

tems. Publications Ofﬁce of the European Union, LU.

Fagiano, L. and Schnez, S. (2017). On the take-off of air-

borne wind energy systems based on rigid wings. Re-

newable Energy, 107:473–488.

Fernandes, G. M. (2023). Take-off and Landing of Au-

tonomous Flying Wings in Airborne Wind Energy

Systems. Master’s thesis, Universidade do Porto,

Porto, Portugal.

Fontes, F. A. C. C., Paiva, L. T., Fernandes, M. C. R. M., and

Vinha, S. (2023). A tethered aircraft bridle system,

method of operating the same and use thereof. Internal

Report, SYSTEC, University of Porto.

Geebelen, K., Vukov, M., Zanon, M., Gros, S., Wagner, A.,

Diehl, M., Vandepitte, D., Swevers, J., and Ahmad,

H. (2013). An Experimental Test Setup for Advanced

Estimation and Control of an Airborne Wind Energy

System. In Ahrens, U., Diehl, M., and Schmehl,

R., editors, Airborne Wind Energy, Green Energy and

Technology, pages 459–471. Springer, Berlin, Heidel-

berg.

Loyd, M. L. (1981). Wind driven apparatus for power gen-

eration.

Marques, M. N., Magalh

aes, S. A., Dos Santos, F. N., and

Mendonc¸a, H. S. (2023). Tethered Unmanned Aerial

Vehicles—A Systematic Review. Robotics, 12(4):117.

Number: 4 Publisher: Multidisciplinary Digital Pub-

lishing Institute.

Nguyen, H. T., Prodan, I., and Fontes, F. A. C. C. (2023).

Trajectory Optimization and NMPC Tracking for a

Fixed–Wing UAV in Deep Stall with Perch Landing.

In 2023 European Control Conference (ECC), pages

1–7.

Rieck, B., Ranneberg, M., Candade, A., Bormann, A., and

Skutnik, S. (2017). Comparison of Launching and

Landing Approaches. In 7th Airborne Wind Energy

Conference (AWEC 2017).

Riley, K., Hobson, M., and Bence, S. (2006). Mathemati-

cal Methods for Physics and Engineering. Cambridge

University Press.

Schmehl, R., editor (2018). Airborne Wind Energy: Ad-

vances in Technology Development and Research.

Green Energy and Technology. Springer, Singapore.

Sieberling, S., Ruiterkamp, R., de Bie, R., and Bontekoe,

E. (2011). Discussion of a rotating platform for take-

off and landing of a tethered aircraft. In 4th Airborne

Wind Energy Conference (AWEC 2011).

Vermillion, C., Cobb, M., Fagiano, L., Leuthold, R., Diehl,

M., Smith, R. S., Wood, T. A., Rapp, S., Schmehl,

R., Olinger, D., and Demetriou, M. (2021). Electric-

ity in the air: Insights from two decades of advanced

control research and experimental ﬂight testing of air-

borne wind energy systems. Annual Reviews in Con-

trol, 52:330–357.

Vinha, S., Fernandes, G. M., and Fontes, F. A. C. C.

(2024a). A Discussion on Automatic Take-off and

Landing Approaches for Airborne Wind Energy Sys-

tems. In Book of Abstracts of the International Air-

borne Wind Energy Conference 2024, Madrid, Spain.

Vinha, S., Fernandes, G. M., Nguyen, H. T., Fernandes,

M. C., and Fontes, F. A. (2024b). Automatic Circular

Take-off and Landing of Motorized Tethered Aircraft.

In 2024 European Control Conference (ECC), pages

681–686.

Zanon, M., Gros, S., and Diehl, M. (2013). Rotational start-

up of tethered airplanes based on nonlinear MPC and

MHE. In 2013 European Control Conference (ECC),

pages 1023–1028.

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

326