Optimal Segmentation of LPV Systems for Control Applications via

Genetic Algorithms

Zolt

an T

eczely

and B

alint Kiss

Budapest University of Technology and Economics, Department of Control Engineering and Information Technology,

uegyetem rkp. 3, H-1111 Budapest, Hungary

Keywords:

LPV, Polytopic, Conservatism, LMI, Genetic Algorithms, Global Optimization.

Abstract:

The paper presents an automatic method for subdividing parameter regions in a Linear Parameter-Varying

(LPV) controlled system based on global optimization. A known limitation of the LPV framework is the

conservatism originating from excessive parameter regions. This conservatism can be relaxed if the controller

design is performed in a collection of subregions of the parameter bounding box wherein local controllers are

synthesized yielding an increased performance level. The choice of subregion boundaries, however, is usually

based on heuristics. This, combined with the recurring issue of scheduling variable selection motivates an

automated LPV parameter space description. The paper suggests genetic algorithms to automate parameter

space subdivision where the problem is posed in terms of global optimization, considering closed-loop per-

formance, computational complexity and parameter-dependent performance constraints. The beneﬁts of the

proposed approach are demonstrated on a pitch-axis missile autopilot, which is formulated as a quasi-LPV

model but generally does not admit the polytopic framework. Hence, the necessary simpliﬁcations and selec-

tion criteria are introduced to effectively employ polytopic LPV methods in the vertical acceleration control

for such a missile.

1 INTRODUCTION

Nonlinear mechatronic systems are often mod-

elled and controlled based on the polytopic Linear

Parameter-Varying framework. Numerically efﬁcient

controller synthesis is usually formulated as a set of

linear matrix inequality (LMI) problems largely built

around the works of (Gahinet and Apkarian, 1994)

and (Apkarian and Gahinet, 1995). Arguably the most

important limitation characterizing LPV control is the

conservatism introduced by the deﬁnition of the pa-

rameter region which might be a result of inadequate

knowledge of the system operating range or geomet-

ric and computational complexity. Traditionally, in

the overwhelming majority of research efforts, a large

emphasis has been put on parameter dimension re-

duction, e.g. (Kwiatkowski and Werner, 2008) or the

notion of parameter-dependent Lyapunov functions

(PDLFs) (Gahinet et al., 1996). The celebrated paper

(Scherer, 2001) introduced the idea of subdivision of

the parameter space stating that, performance can be

increased arbitrarily, while (Kruszewski et al., 2009)

https://orcid.org/0009-0005-7592-9038

https://orcid.org/0000-0002-5532-3435

uses a fuzzy approach. Regarding the transition be-

tween two sets of polytope regions, several famous

articles have been presented including (Lu and Wu,

2004) and (Yan and

Ozbay, 2007) stating the theoret-

ical problem whilst more recent advancements tend

to be more application-oriented e.g. (Jiang et al.,

2015) and (Huang et al., 2021) and (Robert et al.,

2007). Most of these articles are concerned with mul-

tiple Lyapunov functions assigned to neighbouring

systems resulting in the problem of switching LPV

systems. Although these methods form the basis of

current developments in LPV control, a more sophis-

ticated mathematical effort prevents them from being

used day-to-day in engineering practices. Although

polytope segmentation is nothing new, an automated

framework for scheduling variable selection and deal-

ing with more complicated nonlinear matters is still

lacking. On the other hand, computational complex-

ity issues and along with them, associated solutions

typically originate from either high-complexity struc-

tures or inherently numerically demanding models

like ﬂows (Das and Heiland, 2023).

The primary contribution of this paper, therefore,

is a systematic method for designing segmented poly-

Téczely, Z. and Kiss, B.

Optimal Segmentation of LPV Systems for Control Applications via Genetic Algorithms.

DOI: 10.5220/0013067200003822

In Proceedings of the 21st International Conference on Informatics in Control, Automation and Robotics (ICINCO 2024) - Volume 1, pages 503-510

ISBN: 978-989-758-717-7; ISSN: 2184-2809

503

topic LPV controllers. The proposed method uses a

common Lyapunov function as the basis of the solu-

tion and partitions the parameter space into multiple

smaller sub-polytopes according to a cost function in-

volving a joint metric describing the performance gain

and additional complexity. A secondary contribution

is a case study on a missile, wherein the key hardships

and limitations are also highlighted along with open

questions and improvement possibilities. The general

missile model is a well-known example of quasi-LPV

modelling and subsequent control but the polytopic

approach is not particularly suited for it unless the

necessary design consideration steps are taken.

The remainder of the paper is structured as fol-

lows: the following section introduces the necessary

background for LPV controller synthesis and pro-

poses the segmented polytopic description. Section

3 presents a genetic algorithm-based optimization for

such a system and Section 4 introduces the missile

model in a polytopic LPV formulation. Finally, Sec-

tions 5 and 6 include validation results performed in

a simulation environment and conclusive remarks re-

spectively.

2 BACKGROUND

2.1 LPV Models and Robust Controller

Synthesis

A polytopic LPV model can be generated from gen-

eral LPV models with the sector nonlinearity ap-

proach (Ohtake et al., 2001), even if the parameters

enter the matrices nonlinearly. Consider a polytopic

LPV model in the form

˙x =

∑

i=1

(θ)(A

x + B

u + B

y =

∑

i=1

(θ)(C

(1)

where µ

are weighting functions belonging to the

simplex



µ(θ) ∈ R

∑

i=1

(θ) = 1

(θ) ≥ 0



(2)

and the scheduling parameter vector θ and its deriva-

tive ρ are available in real-time and lie inside the hy-

percube deﬁned by



(θ

...θ

)

∈ (θ

min

max

)





(ρ

...ρ

)

∈ (ρ

min

max

)



(3)

with N = 2

Based on these parameter boxes, vectors can be

formed by taking all possible permutations of the

bounds of the parameters. These vectors will, in turn,

accommodate the polytopic LPV form. If the depen-

dence of the state space matrices in (1) on the schedul-

ing variables θ is afﬁne, all the possible models will be

located inside the polytope of models whose vertices

are the images of the vertices, ω

, that is, the param-

eter vector belongs to the convex hull formed by the

vertices

P(θ) ∈ Co







∑

i=1

(θ)M

(θ) ≥ 0,

∑

i=1

(θ) = 1



(4)

Controller synthesis for an LPV system with H

∞

objective can be built on the well-known Bounded-

Real Lemma (BRL) (Apkarian et al., 1995). For the

closed-loop, it states that the LPV system of the form

(1) has quadratic performance γ if and only if there

exists a single matrix X ≻ 0 such that





(θ)X +XA

(θ) * *

(θ)X −γI *

(θ) D

(θ) −γI





≺ 0 (5)

is feasible for any values of the parameter vector.

Based on convex geometric considerations, the above

theorem holds if and only if it holds at the vertices.

This result holds for the situation, where the matri-

ces are afﬁne functions of the scheduling parameters

(Apkarian et al., 1995). For the static state feedback

u(t) = K(θ(t))x(t) (6)

we need the controller, that is parameterized by the

scheduling parameters

K(θ(t)) =

∑

i=1

(θ)K

, µ

(t) ≥ 0,

∑

i=1

(t) = 1 (7)

where the controller corresponding to the vertex is de-

signed with respect to a common Lyapunov function.

The resulting controller can be scheduled in real-time

based on (7) by the weighting functions µ.

2.2 Segmentation Strategy

Now let us consider the following scenario: the oper-

ating region is assumed to fully cover the parameter

space S

and an H

∞

LPV controller is designed for P

with γ performance. Let us now deﬁne P

⊂ P and

⊂ P such that P

∩ P

0 and corresponding H

∞

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

504

controllers are designed with better (γ

< γ and γ

< γ)

performances such that (P

∪P

) = P . In general, it is

always assured, that whichever subregion the system

resides in, corresponds to a less conservative perfor-

mance level, that is, γ

< γ and γ

< γ. For now, we

do not care about the relation between γ

and γ

Starting from (1) with a slight reformulation, let

us consider i number of convex hulls and P

. These

sets of systems lie within these polytopes

(θ

) =





A(θ) B

(θ) B

(θ)

(θ) D

(θ)

(θ) D

(θ)





∈ P

(8)

that is, the model sets are parameterised by i sets of

scheduling variables that describe the same quantities

but have different bounds.

For each of these sets of models, we require the

closed-loop BRL (5) to hold, moreover, the semideﬁ-

nite programming task should be performed simulta-

neously corresponding to a common Lyapunov matrix

X. The resulting optimization problem is then formu-

lated as

min

(9)

subject to

X ≻ 0







cl,i

(θ)X +XA

cl,i

(θ) * *

cl,i

(θ)X −γ

I *

cl,i

(θ) D

cl,i

(θ) −γ







≺ 0

(10)

where i denotes the number of subsegments. Based

on these minimization problems, dynamic or static

feedback controllers can be designed and the result-

ing sub-controllers can be easily switched in real time

according to the instantaneous state of the system.

Remark 1. The closed-loop is quadratically stable

and has H

∞

performance with γ

performance limit for

the separate subsections as long as all regions corre-

spond to a common Lyapunov function.

3 AUTOMATIC SEGMENTATION

Polytope segmentation and, in fact, the selection of

the scheduling variables especially if there is nonlin-

ear coupling in the system is usually a heuristic pro-

cess, in many cases, leading to suboptimal choices.

Therefore, to depart from this nature, a systematic

procedure is proposed to reﬁne the number of sub-

polytopes and their respective boundaries. This leads

to an optimization task, which prescribes a maximiza-

tion of overall closed-loop performance over the en-

tire parameter range with additional penalty terms

for computational complexity and operating point-

dependent weighting in the loss function. Since these

constraints often counteract each other, a multiobjec-

tive optimization framework is adopted in the form

of genetic algorithms. The next two sections present

an overview of genetic algorithms and multiobjec-

tive global optimization. The described methods are

directly applicable to the internal LMI optimization

loop with a user-deﬁned loss function involving a

number of conﬁgurable performance and robustness

metrics, out of which a key element is the closed-loop

∞

norm γ.

3.1 Genetic Algorithms

Genetic algorithms are based on the natural selec-

tion scheme initializing with a random population

evolving through the genetic operations selection,

crossover and mutation into a subsequent population.

First, the survival of the ﬁttest individuals is ensured

by the selection process, then the crossover and mu-

tation operations will generate the following popula-

tion. The optimization is continued until the optimiza-

tion objectives or any exit criteria (e.g. number of

generations) are reached. For the interested reader,

an overview of genetic algorithms can be found in

(Kramer, 2017).

3.2 Multiobjective Optimization

Genetic algorithms are suitable options for multiob-

jective optimization problems described by

min

x∈C

F(x) =







(x)







(11)

where n is the number of optimization objectives. Of

course, especially if these objectives are conﬂicting,

the existence of a x

∗

solution is not guaranteed. The

usual solution to this is through the notion of Pareto-

sets (Marler and Arora, 2004). In this paper, the

weighted sum method is applied, which converts mul-

tiple objectives to a single objective via the convex

combinations of the individual objectives (Do et al.,

2011) resulting in

min J =

∑

i=1

(x), x ∈ C (12)

where

∑

i=1

= 1.

Optimal Segmentation of LPV Systems for Control Applications via Genetic Algorithms

505

3.3 Optimization of LPV Segment

Boundaries for H

∞

Control

Let us denote the vector of the optimization variable

with η. Then, the general augmented LPV system is





˙x









A(θ,η) B

(θ,η) B

(θ,η)

(θ,η) D

(θ,η)

(θ,η) D

(θ,η)













(13)

where x ∈ R

is the state vector, w ∈ R

is the input

vector of disturbances, u ∈ R

is the vector of control

inputs, z ∈ R

are the performance outputs and y ∈ R

are the measured outputs.

For any vertex model, all parameter boundaries

- or the extreme values of scheduling variables - are

part of the optimization vector, that is, θ ⊂ η. Hence,

the dependence (η, θ) will be shortened to (η) More-

over, η may contain terms corresponding to the con-

troller (tuning parameters) and meta-information re-

garding the number of sub-polytopes formulated by

the ’closeness’ of the parameter boundaries.

The dynamic LPV controller is deﬁned as



˙x





(θ) B

(θ)

(θ) D

(θ)





(14)

with A

∈ R

n×n

, B

∈ R

n×n

, C

∈ R

×n

and D

∈

×n

The standard way of closed-loop controller syn-

thesis is to start from (10) and develop controllers

with a single Lyapunov matrix for all vertices. The

number of vertices for a single polytope is exact but

for a segmented polytope, the number of subsegments

(i) needs to be deﬁned in advance. Therefore our

strategy is to declare a maximum number of segments

on each dimension and set the boundaries according

to the optimization outcome, which in the extremes

may mean that either no segmentation takes place (all

boundaries are optimized to be the same) or the max-

imum number of subsegments are generated.

Let us now introduce the shorthand notations with

separated performance outputs z = [z

]

and dis-

turbance inputs for reference and actual disturbance

parts w = [w

]

A(η)

= A(η) − B

(η)C

(η)

A(η)

= A(η) − B

(η)C

(η)

= [B

(η) B

(η)]

(η)

= [C

(η) C

(η)]

where the dependence on (η) suggests that each ma-

trix corresponds to an individual in the genetic algo-

rithm population.

Based on (Wu et al., 1995) the general formulation

of (10) is augmented with the optimization variables

leading to the set of synthesis LMIs





AY − B

* *

Y I

ne1

−1

0 −I





≺ 0





X +X

A −C

* *

X I

nd1

−1

0 −I





≺ 0



X γ

−1



⪰ 0

(15)

with

A =

A(η),

A =

A(η), B

⋆

= B

⋆

(η), C

⋆

= C

⋆

(η)

and γ = γ(i) dependence omitted for conciseness. This

semideﬁnite programming task will have to be solved

for all possible edge models for all individuals in the

population.

Once the optimization is performed, the controller

can be recovered based on (Wu et al., 1995).

3.4 Recombination and Mutation

Deﬁnition

Mutation in the genetic algorithm for the nested LMI

optimization task can be described by

child

= η

parent

rand[0,

parent

max

] (16)

Recombination in the genetic algorithm for the

nested LMI optimization task is performed as de-

scribed in (Deep et al., 2009) by the Laplace crossover

logic as

child,1

= η

parent,1

+ λ



(η

parent,1

–η

parent,2

)



child,2

= η

parent,2

+ λ



(η

parent,1

–η

parent,2

)



(17)

where λ is an integer randomly chosen from a Laplace

distribution.

3.5 Objective Function

The decision vector will include the optimizing vari-

ables η, the closed-loop performance γ

for each sub-

segment and an added computational complexity met-

ric (Cc). With each term, a weighting α will be asso-

ciated. Moreover, a kernel function is introduced with

the objective of weighting the relevant parameter sub-

space.

Since the scheduling parameter space might cover

combinations that are physically not reachable (this

can happen e.g. when there is a coupling between

multiple scheduling variables) an extra weighting

function is introduced to remove the importance of

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

506

unreachable subregions. This is formulated via a ker-

nel function denoted with K

and the corresponding

weights are given as the convolution of K

and the

closed-loop H

∞

norm γ by the equation

w(1,. ..,i) = K

∗ ∥F

(P(η),

K(θ))∥

H∞

(18)

with the controller

K(θ) =

∑

i=1

(θ)K

(19)

where θ = [θ

.. .θ

] is the scheduling parameter

vector, r is the number of scheduling parameters,

w(η

,. .., η

) is the weight of the actual subsegment

and F

represents the lower linear fractional transfor-

mation operation. The optimization term correspond-

ing to subsegment weighting then reads

w(i)∥F

(P(η),

K(θ))∥

H∞

η (20)

Note, that in (20) the integral is a multiple integral

depending on the dimension of θ. An example result

of the subsection weighting is presented in Figure 1.

Figure 1: Edge models encompassing parameter subsec-

tions with corresponding weights represented by colours.

Moreover, computational complexity is formu-

lated as a polynomial function of the number of sub-

polytopes to reﬂect the number of LMIs to be solved,

that is,

Cc = r

(21)

The combination of the subsegment performance

terms will be predeﬁned according to the system con-

straints and performance criteria. With that, the ob-

jective function reads

J(η,γ,Cc,w) = α

+ α

w(i)∥F

(P(η),

K(θ))∥

H∞

(22)

3.6 Genetic Algorithm Program for

Optimised LMI Synthesis

3.6.1 Algorithm

The program for the nested genetic algorithm - LMI

optimization task is presented in the following algo-

rithm.

Data: η,γ,Cc

Result: Optimal boundaries of polytopes

Initialize with η = η

and γ = γ

and

Cc = Cc

;

Set frozen w weighting to each subsegment;

while exit criteria do

Solve synthesis LMIs (15) to acquire γ;

Calculate computational complexity

value (Cc);

Compute the loss function J(η,γ,Cc,w)

for the current generation;

Select the individuals;

Apply crossover and mutation to generate

child

;

end

Algorithm 1: Polytopic segmentation based on closed-loop

gain optimization.

3.6.2 Computational Complexity

As per the synthesis process, for r number of schedul-

ing variables the number of LMIs to be solved is

(3r + 2) to make sure X and Y in (15) are positive

deﬁnite. That is, for a single polytopic LPV region.

Assuming equal segmentation in all dimensions, the

growth can be described by (3r +2)r

. This results in

O(n

) which means the problem is tractable and can

be solved in polynomial time.

4 PITCH-AXIS CONTROL OF A

MISSILE

For the validation of the automatic segmentation

method, the well-known example of a generic missile

is presented based on (Shamma and Cloutiert, 1993)

and (Tan et al., 2000) with the single purpose of ver-

tical acceleration control. The main design steps and

modelling ideas are taken over from (Wu et al., 1995),

while the fundamental difference of using a polytopic

formulation is also introduced. The notations are col-

lected in table 1. The plant variables are tail deﬂection

(δ[deg]), angle of attack (α[deg]), pitch rate (q[

deg

]),

requested and measured normal acceleration (A

z,req

[g]

and A

[g]) respectively and the Mach number (M).

Optimal Segmentation of LPV Systems for Control Applications via Genetic Algorithms

507

Table 1: Parameters of the missile model.

Notation Value Description

4748

Static pressure at

6000 m

S 0.04 m

Surface area

m 204 kg Mass

315

Speed of sound

d 0.2286 m Diameter

0.7 Pitch-axis inertia

7 scale(P

S/mv

)

7 scale(P

Sd/I

)

3.5 scale(P

S/m)

-0.3 Drag coefﬁcient

0.000103f deg

−3

-0.00945f deg

−2

-0.1696f deg

−1

-0.034f deg

−1

0.000215f deg

−3

-0.0195f deg

−2

0.051f deg

−1

-0.206f deg

−1

where f is the power-dependent deg to rad conversion

operator.

4.1 Quasi-LPV Model of a Missile

The nonlinear model of the missile reads

α = K

(α,δ, M)cos(α) + q

˙q = K

(α,δ, M)

(23)

with the aerodynamic coefﬁcients

(α,δ, M) = α(a

+ b

+ c

(2 −

))

+ d

(α,δ, M) = α(a

+ b

+ c

(−7 +

))

+ d

(24)

and the measurement equation is

= K

(α,δ, M) (25)

One common way to recover an LPV model from

the missile is to select the scheduling variables θ =

(α,M). However, the scheduling variables do not

enter the state space matrices linearly preventing the

adoption of polytopic LPV techniques. The usual way

therefore is to create a grid in the parameter space and

design controllers at those speciﬁc operating points.

On the other hand, polytopic LPV allows for desir-

able qualities, like asymptotic stability over the en-

tire polytope region as long as the edge closed-loop

models are stable (Apkarian and Gahinet, 1995). We

may therefore choose the new scheduling variables as

θ = (α

) and use the approximation cos(α) ≈ 1

for small angles. Moreover, the dependence on M

may remain frozen at a single value and the same

design procedure can be performed over a grid over

the feasible parameter range. In real-time, traditional

gain scheduling can be adopted, leading to the quasi-

LPV model



˙q





M p















0 1









(26)

with the shorthands

= a

+ b

+ c

(2 −

)

= a

+ b

+ c

(−7 +

)

(27)

Note, that for the current paper, actuator dynamics

character is not considered, but a general saturation

for the ﬁn deﬂection is set at ±40 deg.

Remark 2. The new scheduling variables bear the

burden of conservative parameter layout design due

to the coupling between them. In other words, to hide

the nonlinear character of the missile model, we have

to add an extra dimension to the variable vector (Fig-

ure 1). To offset this, the proposed method helps to

reduce the weight of the infeasible parameter region.

Remark 3. Since the state α is not available as a

measured variable, we have to estimate it. For the

sake of this paper, estimation was modelled with a

second-order lowpass ﬁlter.

Figure 2 presents the extended model structure

with weights.

Figure 2: Augmented closed-loop control structure with

synthesis weights.

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

508

There is a good case to be made for the inclusion

of these weights in the optimization vector η but for

demonstrative purposes, they were kept frozen at

re f

200(−0.05s + 1)

0.7s

+ 19.2s + 200

, Act = 1,

0.01s + 10

10(s + 1)

8s + 0.1

, W

= W

= 0.001.

(28)

4.2 Optimizing Missile Polytope

Parameters

Parameter boundaries were preset as θ

= [0 0.09]

rad

and θ

= [0 0.3] rad. For ease, the maximum

number of subsegments was set at 9. The optimiza-

tion process was terminated after 15 generations and

the optimized scheduling variable boundaries were

found to be

= [0 0.016 0.063 0.09]

= [0 0.11 0.21 0.3]

The objective function (22) was slightly modiﬁed for

better tunability by the addition of a constant in the

optimization vector η on the individual edge con-

trollers. These can then be set optimally so that the

tuning weights can be kept frozen throughout the en-

tire process. It is to be noted though, that a more com-

prehensive solution would be to include actuator input

and error weight transfer function terms in the vec-

tor η. Controller design based on (15) was nested in

the genetic algorithm framework. The resulting LPV

controllers are then selected and subsequently gain-

scheduled based on the scheduling variable vector in

real time.

5 SIMULATIONS

Every step of the calculations was implemented in

Matlab/Simulink with a sampling time of 1 ms. The

actuator effort was set to an equal average power in all

cases. Vertical acceleration control is demonstrated

on a step manoeuvre. For reference, a standard PID

controller and a regular polytopic LPV controller are

given.

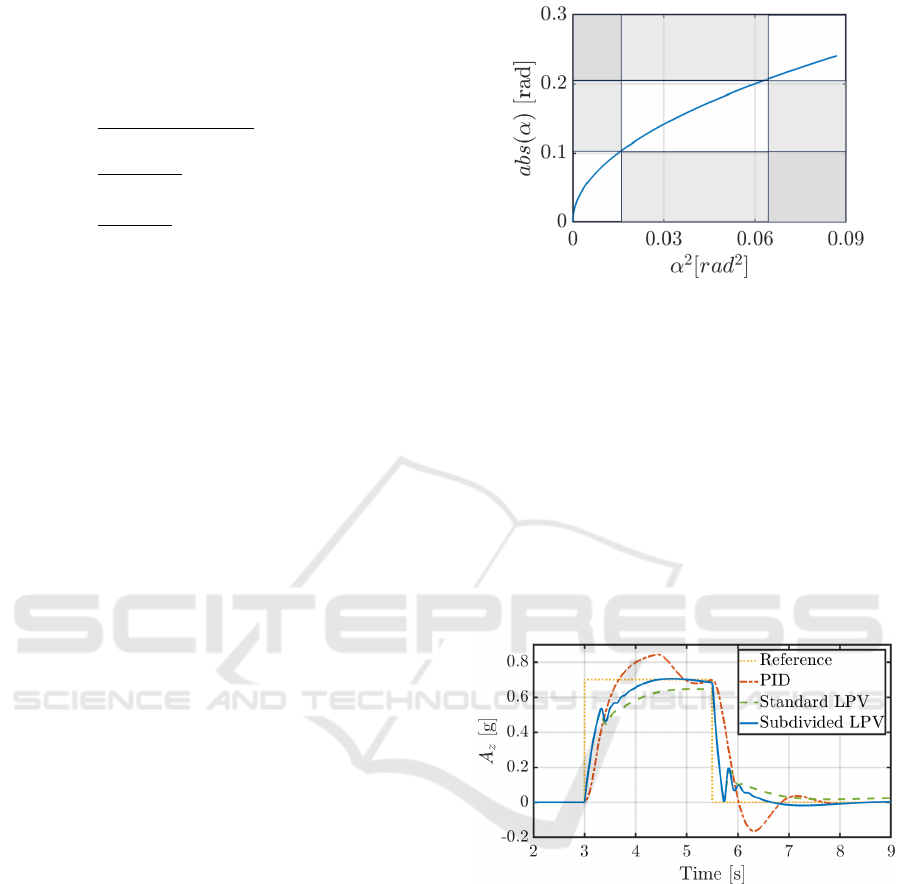
Figure 3 gives a visual representation of the op-

timized parameter boundaries for 9 regions and the

corresponding parameter trajectories.

Figure 3: Optimized polytopic subsegments with actual

scheduling variable trajectory. The colours denote the

weighting of each subsegment (darker - less weight)).

It is easy to see that the darker areas are outside

of interest with respect to the parameter trajectory.

A standard LPV controller weights the overall edge

controllers without consideration of the actual values

of the parameter vector while the proposed method

can efﬁciently exclude those controllers and automat-

ically deploy the controllers more closely related to

the actual operating point.

Figure 4 presents a comparison between standard

LPV and the proposed approach for a typical vertical

acceleration reference series.

Figure 4: Comparison of controllers in a series of step input

reference tracking task.

Since the PID is a linear controller and the missile

is nonlinear, it is no wonder, that the PID has con-

siderably lesser performance. The standard LPV on

the other hand shows much better behaviour but the

proposed partitioned controller can surpass its perfor-

mance due to the reduced conservatism.

In Figure 5 the vertical acceleration in relation to

the angle of attack is presented for a series of step

inputs in different directions.

Optimal Segmentation of LPV Systems for Control Applications via Genetic Algorithms

509

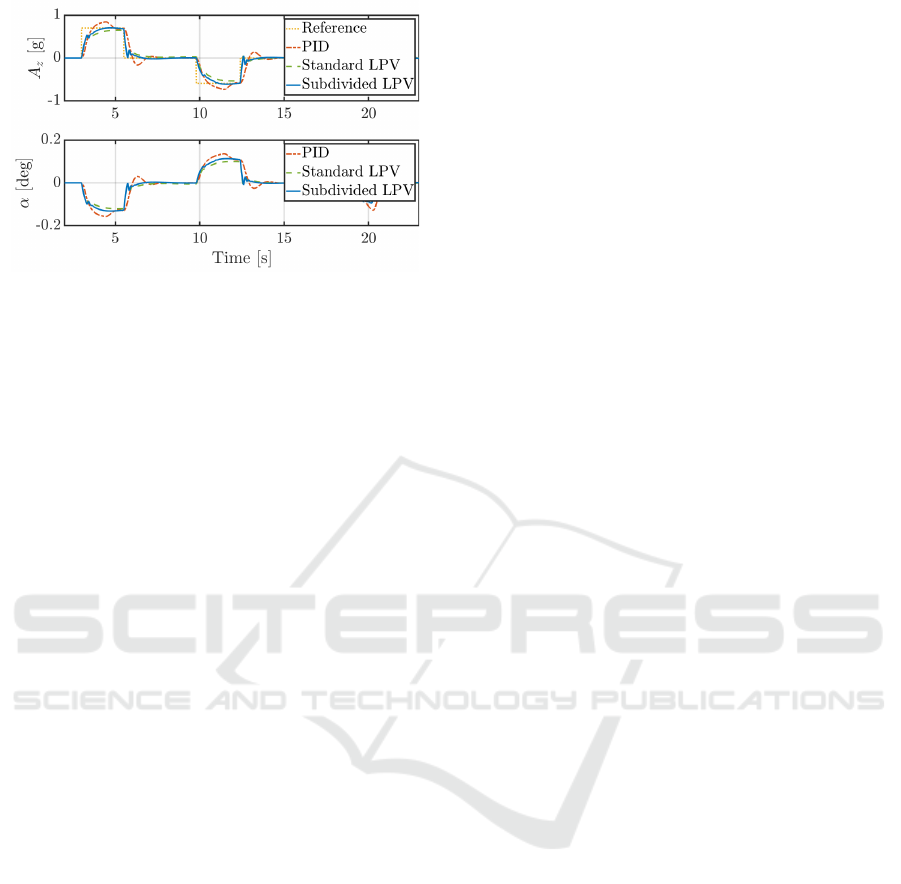
Figure 5: Vertical acceleration and corresponding angle of

attack.

6 CONCLUSIONS

The proposed method demonstrates an automatic de-

cision method for polytopic LPV parameter range

subdivision. The results of the paper showed that con-

troller performance can be signiﬁcantly improved by

reducing the allowable operating region. Moreover,

an example was given for a missile control problem

otherwise not well-suited for the polytopic control

framework. As a future ﬁeld of study, further investi-

gation into the optimization process might be worth-

while and also, a deeper inspection of several nonlin-

ear models is needed to map the possible modiﬁcation

requisites and potential improvement options related

to individual classes of systems.

REFERENCES

Apkarian, P. and Gahinet, P. (1995). A convex characteriza-

tion of gain-scheduled h∞ controllers. Automatic Con-

trol, IEEE Transactions on Automatic Control, 40:853

– 864.

Apkarian, P., Gahinet, P., and Becker, G. (1995). Self-

scheduled h∞ control of linear parameter-varying sys-

tems: a design example. Automatica, 31(9):1251–

1261.

Das, A. and Heiland, J. (2023). Low-order linear param-

eter varying approximations for nonlinear controller

design for ﬂows.

Deep, K., Singh, K. P., Kansal, M., and Mohan, C. (2009).

A real coded genetic algorithm for solving integer and

mixed integer optimization problems. Applied Math-

ematics and Computation, 212(2):505–518.

Do, A., Sename, O., Dugard, L., and Soualmi, B. (2011).

Multi-objective optimization by genetic algorithms

in h

∞

/lpv control of semi-active suspension. IFAC

Proceedings Volumes, 44(1):7162–7167. 18th IFAC

World Congress.

Gahinet, P. and Apkarian, P. (1994). A linear matrix in-

equality approach to h∞ control. International Jour-

nal of Robust and Nonlinear Control, 4(4):421–448.

Gahinet, P., Apkarian, P., and Chilali, M. (1996). Afﬁne

parameter-dependent lyapunov functions and real

parametric uncertainty. IEEE Transactions on Auto-

matic Control, 41:436 – 442.

Huang, B., Lu, B., Li, Q., and Tong, Y. (2021). Average

dwell time based smooth switching linear parameter-

varying proportional-integral-derivative control for an

f-16 aircraft. IEEE Access, 9:30979–30992.

Jiang, W., Dong, C., and Wang, Q. (2015). A systematic

method of smooth switching lpv controllers design for

a morphing aircraft. Chinese Journal of Aeronautics,

28(6):1640–1649.

Kramer, O. (2017). Genetic Algorithm Essentials.

Kruszewski, A., Sala, A., Guerra, T. M., and Ari

No, C.

(2009). A triangulation approach to asymptotically

exact conditions for fuzzy summations. IEEE Trans-

actions on Fuzzy Systems, 17(5):985–994.

Kwiatkowski, A. and Werner, H. (2008). Pca-based parame-

ter set mappings for lpv models with fewer parameters

and less overbounding. Control Systems Technology,

IEEE Transactions on, 16:781 – 788.

Lu, B. and Wu, F. (2004). Control design of switched

lpv systems using multiple parameter-dependent lya-

punov functions. In Proceedings of the 2004 Ameri-

can Control Conference, volume 4, pages 3875–3880

vol.4.

Marler, R. and Arora, J. (2004). Survey of multi-objective

optimization methods for engineering. Structural and

Multidisciplinary Optimization, 26:369–395.

Ohtake, H., Tanaka, K., and Wang, H. (2001). Fuzzy mod-

eling via sector nonlinearity concept. In Proceed-

ings Joint 9th IFSA World Congress and 20th NAFIPS

International Conference (Cat. No. 01TH8569), vol-

ume 1, pages 127–132.

Robert, D., Sename, O., and Simon, D. (2007). A reduced

polytopic lpv synthesis for a sampling varying con-

troller: Experimentation with a t inverted pendulum.

In 2007 European Control Conference (ECC), pages

4316–4323.

Scherer, C. (2001). Lpv control and full block multipliers.

Automatica, 37(3):361–375.

Shamma, J. and Cloutiert, J. (1993). Gain-scheduled missile

autopilot design using linear parameter varying trans-

formation. Journal of Guidance Control and Dynam-

ics - J GUID CONTROL DYNAM, 16:256–263.

Tan, W., Packard, A., and Balas, G. (2000). Quasi-lpv mod-

eling and lpv control of a generic missile. In Proceed-

ings of the 2000 American Control Conference. ACC

(IEEE Cat. No.00CH36334), volume 5, pages 3692–

3696 vol.5.

Wu, F., Packard, A., and Balas, G. (1995). Lpv control de-

sign for pitch-axis missile autopilots. In Proceedings

of 1995 34th IEEE Conference on Decision and Con-

trol, volume 1, pages 188–193 vol.1.

Yan, P. and

Ozbay, H. (2007). On switching h

∞

controllers

for a class of linear parameter varying systems. Sys-

tems & Control Letters, 56(7):504–511.

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

510