Unsupervised Feature Selection Using Extreme Learning Machine

Mamadou Kanout

, Edith Grall-Ma

es and Pierre Beauseroy

Computer Science and Digital Society Laboratory (LIST3N), Universit

e de Technologie de Troyes, Troyes, France

Keywords:

Neural Network, Sparse Learning, Nonlinear Method, Unsupervised Feature Selection.

Abstract:

In machine learning, feature selection is an important step in building an inference model with good general-

ization capacity when the number of variables is large. It can be supervised when the goal is to select features

with respect to one or several target variables or unsupervised where no target variable is considered and the

goal is to reduce the number of variables by removing redundant variables or noise. In this paper, we propose

an unsupervised feature selection approach based on a model that uses a neural network with a single hidden

layer in which a regularization term is incorporated to deal with nonlinear feature selection for multi-target

regression problems. Experiments on synthetic and real-world data and comparisons with some methods in

the literature show the effectiveness of this approach in the unsupervised framework.

1 INTRODUCTION

Nowadays with technological advances (storage and

capturing systems), data can be collected in different

ways in which variables can be numerous and of dif-

ferent types (continuous or categorical). These vari-

ables can be used to infer some results or explain cer-

tain relationships or trends. However, some of them

can be not informative or redundant and must be re-

moved to reduce the cost of data storage or create less

complex and interpretable models. Variable selection

is a machine learning technique that determines a sub-

set of relevant variables from an original set. The se-

lection can be supervised or unsupervised. The su-

pervised framework allows the selection of relevant

variables with respect to one or several target vari-

ables. The unsupervised framework that concerns our

work allows to perform the selection without target

variables; the aim is to reduce the redundancy within

the variables or to select them while preserving the

geometric structure of the data. Many methods have

been proposed for variable selection in the unsuper-

vised setting and can be categorized into 3 classes

(Solorio-Fern

andez et al., 2020).

• Filter methods use statistical measures between

variables to select important variables based on

intrinsic properties of the data such as (He et al.,

2005) where the Laplacian score is used as a sta-

tistical measure to determine important variables.

• Wrapper methods are methods based on the per-

formance of a learning algorithm. Many of these

https://orcid.org/0009-0009-6225-2880

methods in the unsupervised setting are based on

clustering algorithms and the relevance of the se-

lected variables depends on their contribution to

the results of the clustering . In (Cai et al., 2010),

authors propose Multi-Cluster Feature Selection

(MCFS) which performs ﬁrstly spectral clustering

to get cluster labels and then makes the supervised

feature selection with respect to the determined

cluster labels.

• Embedded methods include a regularization term

to the unsupervised learning problem. In (Wang

et al., 2015) authors propose an embedded fea-

ture selection framework that incorporates sparse

learning in the clustering problem to select fea-

tures with respect to the cluster labels.

Recently, new unsupervised variable selection meth-

ods have emerged, allowing to reduce redundancy

in data without label information. These methods

are based on the principle of self-representation (Zhu

et al., 2015), artiﬁcial neural networks (Han et al.,

2018), . . .

In this work, we are interested in problems of un-

supervised nonlinear variable selection problems for

continuous variables. Using our former work FS-

ELM (Kanout

e et al., 2023) based on neural networks

and proposed to deal with nonlinear feature selection

for multi-target regression problems, our contribution

is to propose an extension of this approach to the case

of unsupervised feature selection problem. Applica-

tions to remove noise and redundant variables from

the original set of variables on both synthetic and real-

world datasets will be introduced to analyze the per-

formances of this new method.

Kanouté, M., Grall-Maës, E. and Beauseroy, P.

Unsupervised Feature Selection Using Extreme Learning Machine.

DOI: 10.5220/0013067500003837

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Joint Conference on Computational Intelligence (IJCCI 2024), pages 621-628

ISBN: 978-989-758-721-4; ISSN: 2184-3236

621

The core part of the paper is organized as fol-

lows: in section 2, notations are introduced and re-

lated works are detailed. In section 3, the method

extended in the unsupervised framework is exposed.

Experimental results are given and discussed in sec-

tion 4. Finally, in section 5, conclusions are drawn.

2 NOTATIONS AND RELATED

WORKS

2.1 Notations

Considering the problem of unsupervised feature se-

lection, the following notations are used:

• S is the set of variables.

• X is the matrix of n observations whose variables

are in S . It is supposed that X is normalized, that

is to say, that for each variable of X, the mean is 0

and the variance is 1.

• For any matrix M, the vectors M

and M

are the

row and j

column of M respectively.

• For any matrix M ∈R

n×d

(matrix of n rows and d

columns), the Frobenius norm (Noble and Daniel,

1997) is deﬁned as follows:

||M||

tr(M

M) =

∑

1≤i≤n

∑

1≤j≤d

i j

(1)

• For any matrix M ∈ R

n×d

, the l

2,1

norm (Ding

et al., 2006) is deﬁned as follows:

||M||

2,1

∑

i=1

∑

j=1

i j

(2)

The ||.||

2,1

norm ﬁrst applies the l

norm to each

row of the matrix and then applies the l

norm to

the computed norm. This norm, therefore, makes

it possible to impose sparsity on the rows.

• For two matrices M ∈ R

n×d

and

M ∈ R

n×d

, the

Mean Squared Error (MSE) is deﬁned as follows:

MSE(M,

M) =

∑

j=1

∑

i=1

i j

−

i j

)

||M −

M||

(3)

2.2 Related Works

In this section, some unsupervised feature selection

methods related to this work are described. In (Zhu

et al., 2015) the authors propose a regularized self-

representation (RSR) model for unsupervised fea-

ture selection. It is based on the principle of self-

representation (where each feature can be represented

as the linear combination of its relevant features) and

2,1

-norm regularization. RSR makes it possible to re-

move redundancy in S by selecting important features

that participate in the representation of most of the

other features. The representation coefﬁcients matrix

noted W

(1)

is determined by minimizing the follow-

ing expression:

(W) = ||X −XW

(1)

2,1

+C||W

(1)

2,1

, (4)

C is the regularization parameter for sparsity. The

larger is C the sparser is W

(1)

. This parameter tunes

the trade-off between the reconstruction loss and the

number of selected variables. Once C

∗

the opti-

mal value has been determined according to a crite-

rion, the importance of each variable is determined

by calculating the Euclidean norm of its correspond-

ing row in W

(1)

, and variables with low weight can

be removed. Only the linear relationships between

the variables are exploited by this approach. In

(Han et al., 2018), the authors propose AutoEncoder-

inspired unsupervised Feature Selection (AEFS), a

nonlinear approach based on a single hidden layer

auto-encoder and a l

2,1

-norm regularization term on

the weight matrix of the hidden layer to select rele-

vant features while reconstructing the network inputs.

The expression to be optimized is:

(Θ) =

||X −

X||

+C||W

(1)

2,1

∑

i=1

||W

(i)

(5)

where

• n is the number of observations for training.

• Θ = {W

(1)

(2)

} is the set of neural network pa-

rameters to be optimized, where W

(1)

and W

(2)

are respectively the weight matrices of the hidden

layer and the output layer.

•

X = σ(XW

(1)

(2)

where σ is an activation func-

tion.

• C is a regularization parameter for sparsity (as de-

ﬁned in Equation 4).

• λ is a regularization parameter allowing stability

and promoting convergence.

Once the optimal couple (C

∗

, λ

∗

) has been deter-

mined according to a criterion, the importance of each

variable i is determined by calculating the Euclidean

norm of its corresponding row in W

(1)

i.e. ||W

(1)

Although AEFS exploits nonlinear relationships un-

like RSR, one of its limitations is due to the simplic-

ity of the model. Indeed, AEFS is composed of a sin-

gle hidden layer with a number of neurons smaller

than the number of input variables, which could not

capture the complex nonlinear relationships between

NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications

622

features. In (Mirzaei et al., 2020) the authors pro-

pose Unsupervised Teacher-Student Feature Selection

(U-TSFS) an approach based on knowledge distil-

lation. Two models called teacher and student net-

works are considered. The teacher model is a complex

nonlinear method such as deep auto-encoder or man-

ifold learning techniques (PCA (Hotelling, 1933),

TSNE (Van der Maaten and Hinton, 2008), ISOMAP

(Tenenbaum et al., 2000)) which tries to obtain the

best low dimensional representation of the data de-

noted L ∈R

n×l

with l << d deﬁned as follows:

L = F(X) (6)

where F is the complex nonlinear function model

such as a deep autoencoder or manifold learning

techniques.

The student model is a simple single-layer neural

network in which a l

2,1

-norm regularization term is

added to the weight matrix of the hidden layer to

select relevant features while trying to mimic the

low dimensional L. Hence the feature selection is

done with a simple hidden layer so that the error can

be easily back-propagated and the relevant features

selected efﬁciently. For better training in the student

model, the low representation L has been normalized

between 0 and 1 as follows (L

)

i j

−min(L

)

max(L

)−min(L

)

for 1 ≤ i ≤ n and 1 ≤ j ≤ l. The expression to be

minimized in the student network is:

||L

−

+C||W

(1)

2,1

(7)

where

= Relu(XW

(1)

+ b

(1)

(2)

+ b

(2)

The importance of each variable i is determined by

calculating the Euclidean norm of its corresponding

row in W

(1)

i.e. ||W

(1)

RSR, NFSN, and U-TSFS are methods that allow

unsupervised variable selection. RSR exploits only

linear relationships between variables while AEFS

and U-TSFS exploit nonlinear relationships between

variables. In these approaches, the importance of vari-

ables is determined by taking the Euclidean norm over

the rows of a weight matrix and ranking the variables

according to these calculated norms.

3 PROPOSED APPROACH

In this part, the formulation of FS-ELM method pro-

posed to deal with multi-target feature selection prob-

lems is introduced ﬁrst and its extension to the un-

supervised case is then developed. In section 4, the

proposed extension is assessed.

3.1 Feature Selection Using Extreme

Learning Machine (FS-ELM)

Feature Selection Using Extreme Learning Machine

(FS-ELM) (Kanout

e et al., 2023) is an approach

that determines relevant features based on nonlinear

multi-output regression. The feature selection is done

by training a regression model using Extreme Learn-

ing Machine (ELM) (Schmidt et al., 1992) which is

a type of neural network with one hidden layer with

randomly generated weights W

(1)

, and an output layer

in which the weights W

(2)

are updated. The feature

selection idea consists of associating to each feature

i a weight α

∈ [0, 1] to be tuned during the training

of ELM. This model has been proposed ﬁrst in (Chal-

lita et al., 2016) for a two-class classiﬁcation problem.

Figure 1 illustrates the architecture of this model.

Let n be the sample size and p the number of vari-

ables.

Let Nneur be the number of neurons in the hidden

layer.

Let X = [a

, ··· , a

] ∈ R

N×p

where a

∈ R

is the re-

alisation of feature i for all observations and Y ∈R

N×c

a matrix containing the target variables (c > 1).

The selection of features is done by minimizing with

respect to Θ, the following expression:

λ,C

(Θ) = ||Y −Y

+ λ||W

(2)

∑

i=1

(8)

where

• Θ = (W

(2)

, α = (α

, . . . , α

)) are the parameters

to be optimized.

• Y

= S

(2)

∈ R

N×c

is the network output.

– W

(2)

∈R

Nneur×c

is the weight matrix of the net-

work output also including a bias.

– S

= σ[X

(1)

] where

σ is an activation function.

(1)

∈ R

(p+1)×Nneur

is the weight matrix of

the hidden layer that includes a bias coefﬁ-

cient. It is a random matrix.

= X

′

is a N ×(p + 1) matrix where

· X

′





is N ×(p + 1) matrix with 1

a vector of R

containing only 1.

· D

∈ R

(p+1)×(p+1)

is a diagonal matrix con-

taining the weight associated to each vari-

able such that (D

)

i,i

= α

with α

∈ [0, 1]

the weight associated to each variable i for

i = 1, ··· , p and α

p+1

is the weight associ-

ated to the ﬁxed input (bias) arbitrarily set to

1 i.e. α

p+1

= 1.

Unsupervised Feature Selection Using Extreme Learning Machine

623

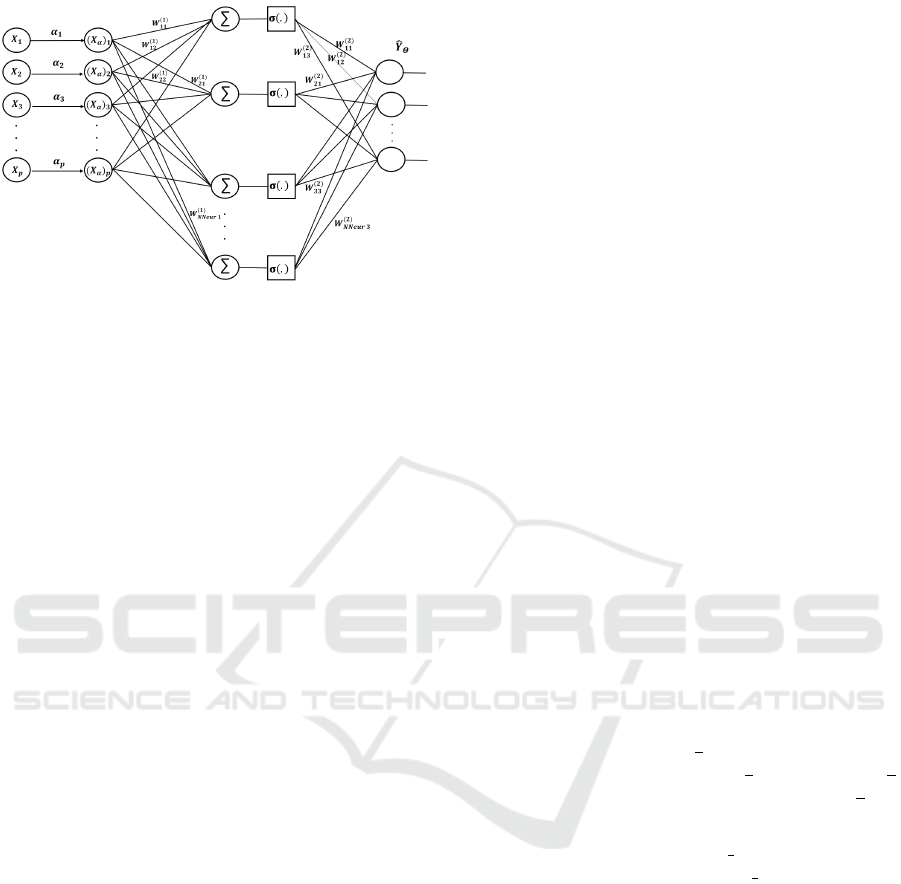
Figure 1: Architecture of the used approach.

• C is the regularization parameter for sparsity that

allows setting some α

to 0.

• λ is the regularization parameter allowing im-

provement of stability and promoting conver-

gence.

3.2 Determination of Parameters

To select features for estimating the target variables,

the optimal values of Θ = (W

(2)

, α) are determined

using an optimization strategy that consists of updat-

ing them alternately and iteratively. That is, W

(2)

updated with ﬁxed D

and vice versa.

For a given value α, W

(2)

is updated by calculating the

derivative of Equation 8 with respect to W

(2)

, which

leads to the simple closed form solution:

(2)

= (S

+ λI)

−1

Y (9)

For ﬁxed W

(2)

, α = (α

, . . . , α

) is updated such that

∈ [0, 1]. In our former work, the partial derivative

of Equation 8 with respect to α

is approximated using

numerical methods. The optimization problem can be

reformulated as:

minimize

λ,C

(Θ)

subject to α

∈ [0, 1] for i = 1, . . . , p.

(10)

3.3 Unsupervised Feature Selection

Using Extreme Learning Machine

(U-FS-ELM)

The effectiveness of FS-ELM for multi-target vari-

able selection has been shown on synthetic and real

data. The proposed approach called U-FS-ELM

meaning Unsupervised Feature Selection Using Ex-

treme Learning Machine is an extension of our for-

mer work in the unsupervised case by taking Y = X.

Unsupervised feature selection in U-FS-ELM is per-

formed by minimizing with respect to Θ the following

expression:

λ,C

(Θ) = ||X −X

+ λ||W

(2)

∑

i=1

(11)

Unlike the nonlinear approaches mentioned above

(AEFS, U-TSFS) which determine the important fea-

tures from a low-dimensional representation, this ap-

proach has the advantage of being feedforward in

addition to associating weights between 0 and 1 to

each feature according to their importance in the

data (linear or non-linear relationship with other vari-

ables). Thus by choosing a very large number of neu-

rons Nneur, the input variables can be correctly esti-

mated as stated in the universal approximation theo-

rem (Hornik, 1991) and the addition of sparsity regu-

larisation allows variable selection.

4 EXPERIMENTS

In this part, the original set S of the features is as-

sumed to be deﬁned. The determination of a subset

of relevant variables S

′

⊂S by U-FS-ELM for the re-

construction of the variables of S is assessed.

The subsections 4.1 and 4.2 concern respectively the

evaluation of U-FS-ELM on synthetic data and real-

world data. U-FS-ELM with Nneur = 400 is com-

pared with the following approaches:

• RSR

• AEFS with Nneur ∈ {⌊

⌋+ 1, p −1} where p is

the number of variables and ⌊

⌋ is the ﬂoor of

i.e. the greatest integer less than or equal to

• U-TSFS where the teacher model F is T SNE with

the number of components n

comp ∈{2, 3}and in

the student network Nneur = n comp ×10.

To assess the proposed method and compare it with

other methods, the relevance of the selected features

for each approach is assessed. To avoid the bias prob-

lem during the assessment, the original dataset D has

been split into two subsets D

train

(67% of D) and D

test

(33% of D). Optimal values of hyperparameters have

been determined according to a criterion on the MSE

by 5-fold cross-validation on D

train

as follows:

• for C ∈ I

= {10

−4

, 10

−3

, . . . , 10

, 10

} and for

λ ∈ I

= {10

−4

, 10

−3

, . . . , 10

, 10

Compute

(λ,C)

the estimate of Y associated with

C and λ and MSE(Y,

(λ,C)

• Choose (C

∗

, λ

∗

) ∈ I

×I

such that

∗

, λ

∗

) = argmin

(C,λ)∈I

×I

MSE(Y,

(λ,C)

) < 0.1 (12)

NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications

624

obtained by 5 fold cross-validation on D

train

For RSR and U-TSFS the procedure is similar to

the one above but only C

∗

is determined.

Once the optimal hyperparameters have been chosen,

the feature weights have been determined by running

the feature selection approach on all observations of

train

using the optimal hyperparameters. Then the

importance of each feature has been determined using

its representation in the feature weights as follows:

• for RSR, AEFS, and U-TSFS, rank the variables

as deﬁned in section 2.2.

• for U-FS-ELM, rank the variables according to

the scaling factors α

Once features have been ranked, the pertinence has

been assessed by building p models on D

train

and

evaluating them on D

test

by keeping from 1 to p vari-

ables corresponding to the highest rank for recon-

structing all variables of S. The model used for eval-

uation is a one-hidden-layer neural network with 500

neurons. The activation function is sigmoid and the

optimizer is adam. The metric used for the assess-

ment of the model is the MSE.

The observations of all variables have been normal-

ized (removing the mean and scaling to unit variance)

to avoid scaling problems.

4.1 Synthetic Dataset

This section describes the results with two generated

datasets called synth1 and synth2. In synth1, there

are only linear relationships (coefﬁcients have been

randomly determined according to a continuous uni-

form distribution between -1 and 1) between features

while in synth2 there are nonlinear relationships

between features. In synth1 (resp. synth2), 7 (resp.

8) features were ﬁrstly deﬁned then 5 (resp. 7)

random features that depend on these 7 (resp. 8)

features with linear (resp. nonlinear) relationships

were deﬁned. Finally, in synth1, 3 redundant features

were created from the 7 features ﬁrst deﬁned. Thus

2000 observations have been generated from these 15

features for each dataset. In synth1, the variables are

deﬁned as follows :

, f

, . . . , f

∼ N (0, 1)

= −0.56 f

+ 0.22 f

− 0.84 f

− 0.46 f

+ 0.2 f

−

0.72 f

−0.96 f

+ ε

= 0.74 f

+ 0.54 f

+ 0.48 f

− 0.18 f

− 0.46 f

−

0.66 f

−0.6 f

+ ε

= −0.58 f

+ 0.04 f

− 0.12 f

− 0.4 f

− 0.44 f

0.92 f

+ 0.4 f

+ ε

= 0.84 f

−0.4 f

−0.68 f

+0.26 f

−0.5 f

+0.92 f

0.56 f

+ ε

= −0.02 f

− 0.62 f

+ 0.76 f

+ 0.16 f

− 0.34 f

−

0.62 f

−0.96 f

+ ε

= f

+ ε

, f

= f

+ ε

, f

= f

+ ε

, ε

∼N (0, 0.05) and ε

, ε

∼N (0, 1).

For synth2, the variables are deﬁned as follows:

∼ N (1, 0.5) ; f

∼ N (0.7, 1); f

∼ N (3, 1);

∼ N (0, 0.5); f

∼ N (0.3, 1) ; f

∼ N (2, 0.7) ;

∼ U(−1, 1) ; f

∼ U(−3, 1)

= f

sin( f

) + ε

where ε

∼ N (0, 0.08)

= f

+ 2 f

+ e

−f

−cos( f

− f

+ f

) + ε

where

∼ N (0, 0.08)

= e

−f

+ ε

where ε

∼ N (0, 0.1)

+ f

+ ε

where ε

∼ N (0, 0.04)

= e

cos( f

) + ε

∼ N (0, 0.02)

= arctanh( f

) + ε

where ε

∼ N (0, 0.08)

= ln(3 − f

− 2 f

) + arctan(

√

3 − f

) + ε

where

∼ N (0, 0.08)

For the two datasets, the goal was to determine

the subset S

′

⊂ S such that the reconstruction loss

between the variables of S and their estimate from

the variables of S

′

is minimized. The optimal values

for the hyperparameters have been determined by 5-

fold cross-validation for each approach as described

above. The chosen parameters on each dataset for

each approach are given in Table 1. After the choice

of regularization parameters on synth1 and synth2,

variables have been ranked according to their impor-

tance for each approach, and the list is given in Ta-

ble 2. It may be noticed that U-FS-ELM manages to

better select independent features compared to RSR,

AEFS, and U-TSFS, in particular on synth1 it set all

coefﬁcients to zero after the 7th most important vari-

able. Figure 2 shows the estimated value of the mean

of MSE between X and its estimated value

X versus

the number of most important variables used to build

the model.

Table 1: Chosen parameters on each synthetic dataset for

each approach.

synth1 synth2

Methods λ C λ C

U-FS-ELM (Nneur = 400) 1 10

−1

RSR - 10

- 10

AEFS (Nneur = 8) 10

−3

−2

−4

−2

AEFS (Nneur = 14) 10

−4

−1

−3

−2

U-TSFS (n comp = 2) - 10

−3

- 10

−3

U-TSFS (n comp = 3) - 10

−3

- 10

−3

Unsupervised Feature Selection Using Extreme Learning Machine

625

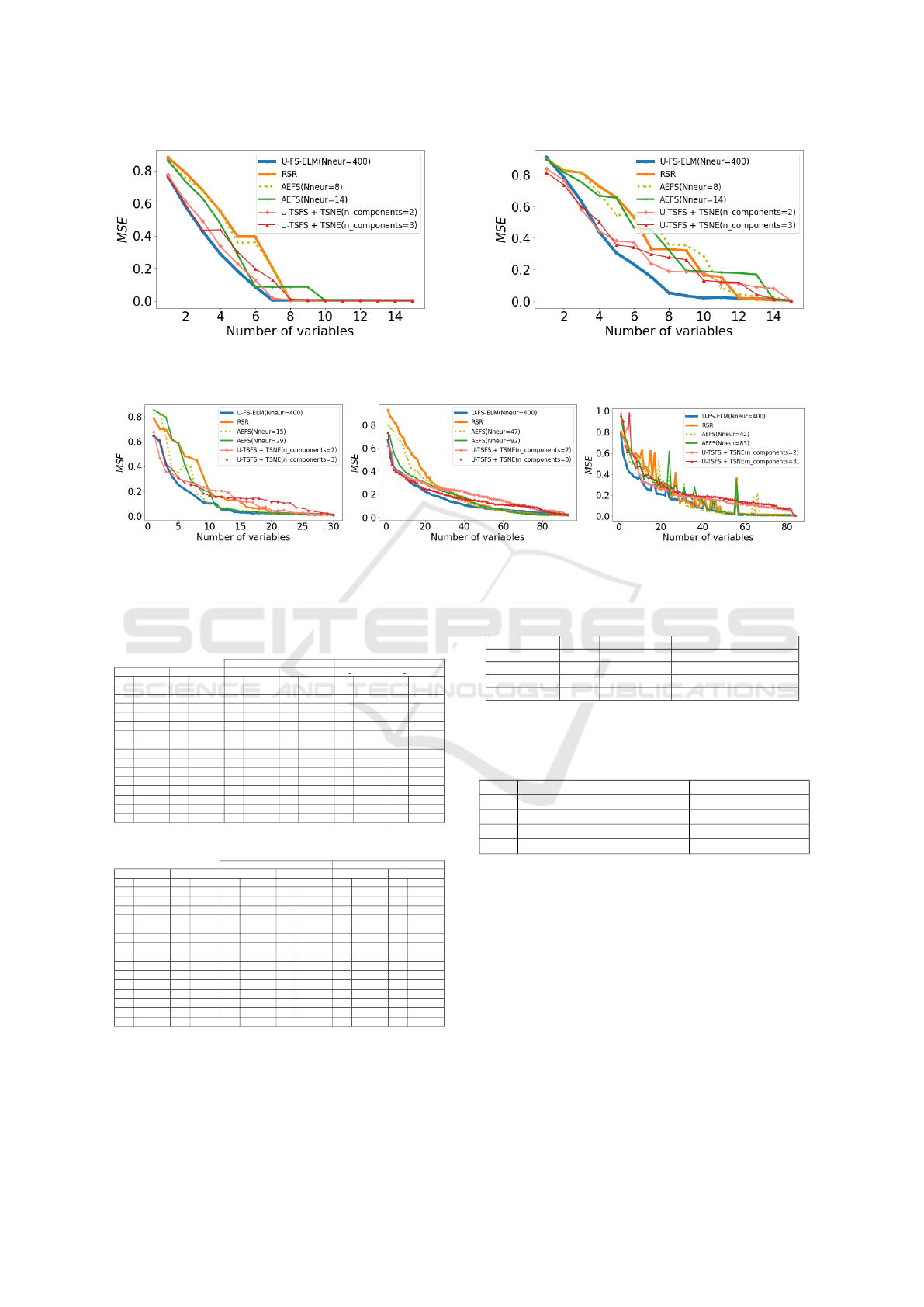
(a) synth1 (b) synth2

Figure 2: MSE versus the number of most important variables on synthetic data.

(a) Breast cancer data set (b) Ansur data II (c) US crimes dataset

Figure 3: MSE versus the number of most important variables on real-world datasets.

Table 2: List of ranked variables for each approach.

(a) synth1 dataset

AEFS U-TSFS+TSNE

U-FS-ELM RSR Nneur = 8 Nneur = 14 n comp = 2 n comp = 3

var weight var weight var weight var weight var weight var weight

5, 5.10

−2

7, 5.10

−1

2, 5.10

−1

4, 5.10

−4

4, 9.10

−1

2, 5.10

−1

5, 3.10

−2

6, 3.10

−1

1, 9.10

−1

2, 9.10

−4

3, 4.10

−1

2.10

−1

5.10

−2

3, 9.10

−1

1, 6.10

−1

2, 4.10

−4

2, 6.10

−1

1, 6.10

−1

4, 8.10

−2

2, 9.10

−1

1, 6.10

−1

−4

2, 4.10

−1

1, 3.10

−1

4, 7.10

−2

1, 6.10

−1

6.10

−2

8, 9.10

−5

2, 3.10

−1

1, 3.10

−1

4, 6.10

−2

1, 4.10

−1

4.10

−2

6, 9.10

−5

2, 2.10

−1

1, 2.10

−1

3, 9.10

−2

1, 3.10

−1

3, 2.10

−2

5, 3.10

−5

1, 4.10

−1

1, 1.10

−1

0 f

1, 2.10

−1

3.10

−2

3, 8.10

−5

1, 2.10

−1

9, 2.10

−2

0 f

9, 4.10

−2

3.10

−2

2, 2.10

−5

1, 1.10

−1

8, 4.10

−2

0 f

7, 8.10

−2

1, 8.10

−2

2, 2.10

−5

1, 1.10

−1

7, 3.10

−2

0 f

8, 8.10

−3

2, 1.10

−3

1, 9.10

−5

−1

6, 4.10

−2

0 f

7, 6.10

−3

1, 6.10

−3

8, 4.10

−6

8, 2.10

−2

5, 8.10

−2

0 f

6, 8.10

−3

1, 4.10

−3

1, 5.10

−6

6, 3.10

−2

5, 8.10

−2

0 f

5, 8.10

−3

9, 1.10

−4

1, 5.10

−6

2, 1.10

−2

3, 8.10

−2

0 f

4, 1.10

−3

5, 4.10

−4

6.10

−8

1, 9.10

−2

2, 9.10

−2

(b) synth2 dataset

AEFS U-TSFS + TSNE

U-FS-ELM RSR Nneur = 8 Nneur = 14 n comp = 2 n comp = 3

var weight var weight var weight var weight var weight var weight

1, 2.10

−1

1 f

2, 5.10

−2

3, 1.10

−1

4, 9.10

−1

2, 4.10

−1

7, 9.10

−2

1 f

2, 3.10

−2

2.10

−1

2, 9.10

−1

1, 8.10

−1

6, 6.10

−2

1 f

1, 4.10

−2

1, 7.10

−1

2, 2.10

−1

1, 4.10

−1

2, 5.10

−2

1 f

4.10

−3

1, 4.10

−1

1, 3.10

−1

1, 3.10

−1

2, 2.10

−2

1 f

2, 7.10

−3

1, 1.10

−1

1, 2.10

−1

1, 3.10

−1

1, 8.10

−2

1 f

2, 6.10

−3

3, 8.10

−2

1, 1.10

−1

1, 1.10

−1

1, 8.10

−2

1 f

2, 4.10

−3

3, 4.10

−2

8, 8.10

−2

9, 9.10

−2

1, 8.10

−2

1 f

2, 2.10

−3

2, 9.10

−2

8, 7.10

−2

8, 8.10

−2

1, 8.10

−2

1 f

1, 8.10

−3

2, 9.10

−2

8, 5.10

−2

8, 8.10

−2

1, 7.10

−2

1 f

1, 7.10

−3

2, 6.10

−2

7.10

−2

8.10

−2

0 f

1 f

1, 3.10

−3

2, 5.10

−2

4, 6.10

−2

6, 6.10

−2

0 f

1 f

9, 7.10

−4

2, 1.10

−2

3, 4.10

−2

2, 6.10

−2

0 f

1 f

6, 9.10

−4

2.10

−2

3.10

−2

2, 5.10

−2

0 f

1 f

5, 9.10

−4

1, 6.10

−2

2, 1.10

−2

2, 1.10

−2

0 f

1 f

2, 2.10

−4

1, 5.10

−2

1, 5.10

−3

1, 4.10

−2

4.2 Real-World Datasets

This part presents the results on real-world datasets.

Table 3 contains the list of real-world data used as

Table 3: Real-world data sets.

Name Size Features Source

Breast Cancer 569 30 (Zwitter and Soklic, 1988)

Ansur data 2 6068 93 (Paquette et al., 2009)

US crimes 2215 125 (Redmond, 2009)

Mnist 10000 784 (28 ×28) (Deng, 2012)

Table 4: Number of variables with weights greater than 0

and percentage of selected variables among the 784 vari-

ables for different values of C with λ = 10

−2

C Number of variables with α

> 0 % of selected features

−2

457 58.29 %

−1

365 46.56 %

1 208 26.53 %

106 13.52 %

well as the number of variables, and the number of

samples. Some information about these datasets as

well as the pre-processing done are described below:

• Breast cancer

The breast cancer dataset contains 569 observations

of features extracted from a digitized image of a ﬁne

needle aspirate (FNA) of a breast mass. They de-

scribe the characteristics of the cell nuclei present in

the image. The goal is to determine if breast can-

cer is cancerous or non-cancerous based on extracted

features. This dataset is often used to explore fea-

ture selection techniques. In this paper, the nominal

variable containing the classes is removed. U-FS-

ELM and other unsupervised feature selection tech-

NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications

626

Figure 4: Mnist dataset image reconstruction using 200 im-

ages as the training dataset. The ﬁrst row contains the re-

tained pixels (ﬁrst column) and some original images (sec-

ond column to last column). The following 4 rows con-

tain respectively the retained pixels by U-FS-ELM (ﬁrst

column) and the reconstruction results (second column to

last column) using the retained pixels for C = 10

−2

,C =

−1

,C = 1,C = 10

with λ = 10

−2

niques have been applied to the normalized obser-

vations of 29 variables to select important features

and remove the redundant variables. The dataset

can be downloaded on the UCI website at this URL:

https://archive.ics.uci.edu/datasets.

• Ansur data II

The Anthropometric Survey of US Army Personnel

(ANSUR 2 or ANSUR II) is a database with mea-

surements of American military personnel done in

2012 and made public in 2017. This database con-

tains 6000 observations (4082 men and 1986 women)

of 93 numerical anthropometric measurements that

describe the size and shape of the human. The

feature selection methods have been applied to the

1145 observations of females whose age is between

20 and 30. The dataset is available at this URL:

https://www.openlab.psu.edu/ansur2/.

• Communities and Crime

It is a dataset on crime in communities in the United

States. The data combines socio-economic data from

the 1990 US Census, law enforcement data, and crime

data with a target variable and 127 other variables.

Among the 127 remaining variables, 5 variables are

considered as non-predictive in the description of the

dataset. After removing the variables with missing

values and non-predictive variables, the feature selec-

tion approaches have been applied to 84 continuous

variables to select important features allowing the re-

construction of all of them. The data set is available

on the UCI website.

• Mnist (Mixed National Institute of Standards and

Technology)

This dataset is composed of 10000 black and white

handwritten digits images used for training neural net-

work in computer visions. It contains ten classes cor-

responding to the 10 numerical digits. For each hand-

written digit, there are 28 × 28 pixels between 0 and

255. To apply our approach, the dataset has been

normalized by the min-max feature scaling method

which brings all values between 0 and 1 and is deﬁned

for each variable as x

′

x −min(x)

max(x) −min(x)

where x

contains observations of a variable of S. To deter-

mine the feature weights, only 200 observations have

been considered as training dataset and another 200

observations as the test dataset.

After the choice of the regularization parameters

and the ranking of the features for each approach, X

has been reconstructed by building p models from 1

to p variables corresponding to the highest rank. The

number of important variables taken successively is

{1, 2, . . . , 30} on Breast cancer data set, {1, 2, . . . , 93}

on Ansur data II set, {1, 2, . . . , 84} on Communities

and Crime data set. Figure 3 shows the MSE between

X and its estimated value

X versus the number of im-

portant variables taken successively on these datasets

and it can be noticed that U-FS-ELM performs well

compared to AEFS and U-TSFS, precisely on Breast

cancer dataset between 1 and 10 ﬁrst important vari-

ables, on Ansur data II dataset between the ﬁrst 15 and

the ﬁrst 40 important variables, and on Communities

and Crime dataset U-FS-ELM has the lowest MSE for

any number of variables taken.

The proposed method successfully reduces the ini-

tial number of variables in structured continuous data

by keeping relevant variables that can estimate prop-

erly other related variables. It can also be noticed that

generally, U-FS-ELM selects important variables bet-

ter than AEFS and U-TSFS. Indeed, if the number of

variables p is not very large, AEFS is a simple au-

toencoder that may not capture complex relationships

between features, and in the U-TSFS approach the

teacher model must be chosen according to the data

to obtain a better representation of the data in order to

avoid propagating the estimation errors in the student

model and this latter also requires the choice of the

right activation function, the number of neurons, the

choice of the optimal parameter C

∗

, . . .

U-FS-ELM has been also applied to image data,

the mnist dataset. The goal was to determine rel-

evant variables among 784 (28 ×28) variables cor-

responding to pixels on each handwritten digit. U-

FS-ELM with λ = 10

−2

and C ∈{10

−2

, 10

−1

, 1, 10

}

was trained on 200 images (20 images per class)

Unsupervised Feature Selection Using Extreme Learning Machine

627

randomly chosen and the number of variables with

weights greater than 0 and percentage of selected vari-

ables among the 784 variables for each value of C is

given in Table 4.

The reconstruction results using these hyperpa-

rameter values for some images in the test dataset are

shown in Figure 4 and it can be noticed that U-FS-

ELM has reduced the number of features while keep-

ing useful information. It should be noted that this

approach is different from reduction methods which

determine a representation of the data in a subspace

while here a selection of important variables is done.

5 CONCLUSIONS

In this paper, an approach is proposed to deal with un-

supervised feature selection problems exploiting non-

linear relationships between variables. It consists of

assigning to each feature i a weight α

∈[0, 1] updated

during the reconstruction of the input variables and of

determining hyperparameters λ and C which are re-

spectively parameters for stability and sparsity. By

tuning these hyperparameters according to MSE, the

weights α

associated to the features make it possi-

ble to determine important features while minimizing

the reconstruction error. Many experiments have been

done on two synthetic data, three structured continu-

ous real-world data, and one image data and the re-

sults have been compared with other methods. They

show the effectiveness of the proposed approach.

REFERENCES

Cai, D., Zhang, C., and He, X. (2010). Unsupervised fea-

ture selection for multi-cluster data. In Proceedings

of the 16th ACM SIGKDD international conference

on Knowledge discovery and data mining, pages 333–

342.

Challita, N., Khalil, M., and Beauseroy, P. (2016). New

feature selection method based on neural network and

machine learning.

Deng, L. (2012). The mnist database of handwritten digit

images for machine learning research. IEEE Signal

Processing Magazine, 29(6):141–142.

Ding, C., Zhou, D., He, X., and Zha, H. (2006). R 1-

pca: Rotational invariant l 1-norm principal compo-

nent analysis for robust subspace factorization. In

ICML 2006 - Proceedings of the 23rd International

Conference on Machine Learning.

Han, K., Wang, Y., Zhang, C., Li, C., and Xu, C. (2018).

Autoencoder inspired unsupervised feature selection.

In 2018 IEEE international conference on acoustics,

speech and signal processing (ICASSP), pages 2941–

2945. IEEE.

He, X., Cai, D., and Niyogi, P. (2005). Laplacian score for

feature selection.

Hornik, K. (1991). Approximation capabilities of mul-

tilayer feedforward networks. Neural networks,

4(2):251–257.

Hotelling, H. (1933). Analysis of a complex of statistical

variables into principal components. Journal of edu-

cational psychology, 24(6):417.

Kanout

e, M., Grall-Ma

es, E., and Beauseroy, P. (2023).

Neural network-based approach for supervised non-

linear feature selection. In Proceedings of the 15th In-

ternational Joint Conference on Computational Intel-

ligence - Volume 1: NCTA, pages 431–439. INSTICC,

SciTePress.

Mirzaei, A., Pourahmadi, V., Soltani, M., and Sheikhzadeh,

H. (2020). Deep feature selection using a teacher-

student network. Neurocomputing, 383:396–408.

Noble, B. and Daniel, J. W. (1997). Applied linear algebra.

2nd ed.

Paquette, S., Gordon, C. C., and Bradtmiller, B. (2009). An-

thropometric survey (ansur) ii pilot study: Methods

and summary statistics.

Redmond, M. (2009). Communities and Crime.

UCI Machine Learning Repository. DOI:

https://doi.org/10.24432/C53W3X.

Schmidt, W., Kraaijveld, M., and Duin, R. (1992). Feed-

forward neural networks with random weights. In

Proceedings., 11th IAPR International Conference on

Pattern Recognition. Vol.II. Conference B: Pattern

Recognition Methodology and Systems, pages 1–4.

Solorio-Fern

andez, S., Carrasco-Ochoa, J. A., and

Mart

ınez-Trinidad, J. F. (2020). A review of unsuper-

vised feature selection methods. Artiﬁcial Intelligence

Review, 53(2):907–948.

Tenenbaum, J. B., Silva, V. d., and Langford, J. C. (2000).

A global geometric framework for nonlinear dimen-

sionality reduction. science, 290(5500):2319–2323.

Van der Maaten, L. and Hinton, G. (2008). Visualizing data

using t-sne. Journal of machine learning research,

9(11).

Wang, S., Tang, J., and Liu, H. (2015). Embedded unsuper-

vised feature selection. In Proceedings of the AAAI

conference on artiﬁcial intelligence, volume 29.

Zhu, P., Zuo, W., Zhang, L., Hu, Q., and Shiu, S. C. (2015).

Unsupervised feature selection by regularized self-

representation. Pattern Recognition, 48(2):438–446.

Zwitter, M. and Soklic, M. (1988). Breast Can-

cer. UCI Machine Learning Repository. DOI:

https://doi.org/10.24432/C51P4M.

NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications

628