A Comparison of Adaptive PID, Adaptive Dual-PID and Adaptive
Fractional PID Controllers for a Nonlinear System with Variable
Parameters
Sebastian Vega
a
, Mateo Vasquez-Guevara
b
and Oscar Camacho
c
Colegio de Ciencias e Ingenier
´
ıas “El Polit
´
ecnico”, Universidad San Francisco de Quito USF, Quito, Ecuador
Keywords:
Adaptive PID , Dual-Adaptive PID, Adaptive Gain FO-PID , Nonlinear Processes, Variable Parameters.
Abstract:
This paper presents a comparative analysis of three control strategies: Adaptive PID, Dual-Adaptive PID,
and Adaptive Gain FO-PID controllers. These controllers were evaluated on nonlinear dynamic systems with
varying parameters, considering set point variations, disturbances, and measurement noise. Performance was
quantified using key metrics such as settling time, overshoot, Integral of Squared Error (ISE), and Integral of
Squared Control Output (ISCO). The results demonstrate that the Adaptive Gain FO-PID consistently outper-
forms the other methods, highlighting its superior ability to manage the complexities of nonlinear systems.
1 INTRODUCTION
Industrial processes are often characterized by a high
level of complexity arising from various factors such
as nonlinear behavior, uncertainties in system pa-
rameters, and unmodeled dynamics, all of which
can complicate the design and implementation of
effective control strategies(Liptak, 2018). In addi-
tion to these challenges, many industrial systems ex-
hibit poorly understood or difficult-to-characterized
plant properties, further increasing the difficulty of
accurately modeling the process(Smith and Corripio,
2005). Furthermore, time delays are a common fea-
ture in industrial processes, which can severely limit
the performance and stability of traditional control
techniques, requiring the development of more ad-
vanced and robust control methods to address these
multifaceted challenges (Mejia et al., 2022).
PID control remains the benchmark algorithm
for addressing a vast majority of control challenges
across industry, academia, and everyday applications.
Even today, it dominates industrial control, account-
ing for more than 90% of solutions, while also serv-
ing as the foundational model for teaching feedback
control principles in universities and technical institu-
tions. Furthermore, it is widely adopted as a standard
automated solution in numerous household devices
a
https://orcid.org/0009-0001-3840-8189
b
https://orcid.org/0009-0001-3333-8142
c
https://orcid.org/0000-0001-8827-5938
and utilities, including smartphones, cruise control
systems in cars, ovens, microwaves, drones, air con-
ditioning units, heating systems, electric bikes, Seg-
ways, hoverboards and elevators (Borase et al., 2021;
H
¨
agglund and Guzm
´
an, 2024).
The classical PID controller is typically tuned by
trial and error or based on the model parameters near
a specific operating point (O’dwyer, 2009). However,
in highly non-linear systems, PID control may strug-
gle to maintain a stable response, resulting in poor
tracking and disturbance rejection performance (An-
chitipan and Camacho, 2021). As noted in (Yurke-
vich, 2011), the effectiveness of PID control is often
correlated with the dynamic characteristics of the sys-
tem, and many industrial processes can be adequately
represented by simplified first- or second-order dy-
namic models (O’dwyer, 2009).
Given the popularity of the PID controller, some
improvements have been made that incorporate some
modifications to the original algorithm. These
methodologies, specifically developed to address the
complexities of dynamic processes, can potentially
enhance the performance of PID controllers beyond
traditional outcomes. There are various modifications
such as non-linear PID (Han, 2009), two-degree-of-
freedom PID (Taguchi and Araki, 2000), Fractional
Order PID (Podlubny, 1994; Podlubny, 1999b), and
Dual-Adaptive PID (Chotikunnan and Chotikunnan,
2023; Obando et al., 2023).
Despite their widespread use and success in var-
166
Vega, S., Vasquez-Guevara, M. and Camacho, O.
A Comparison of Adaptive PID, Adaptive Dual-PID and Adaptive Fractional PID Controllers for a Nonlinear System with Variable Parameters.
DOI: 10.5220/0013068100003822
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 21st International Conference on Informatics in Control, Automation and Robotics (ICINCO 2024) - Volume 1, pages 166-177
ISBN: 978-989-758-717-7; ISSN: 2184-2809
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.

ious industrial applications, both conventional PID
controllers and PID with modifications enhancement
face limitations, particularly in adapting to evolving
process conditions (Samad, 2017). These challenges
have motivated ongoing research into improved PID
controller designs using adaptive control techniques
and self-tuning methods to improve process control
performance(
˚
Astr
¨
om and Wittenmark, 2008).
Adaptive control aims to manage uncertain dy-
namic systems in real time using adaptation and learn-
ing mechanisms (Annaswamy and Fradkov, 2021).
Adaptive PID control techniques have gained signifi-
cant traction, with numerous studies exploring param-
eter adaptation, model reference adaptive control, and
self-tuning methods to enhance system performance
(Isermann and Isermann, 1991; Cha
´
ınho et al., 2005;
Annaswamy and Fradkov, 2021; Liu et al., 2021).
These approaches deliver improved dynamic behavior
and precise regulation, which makes them highly suit-
able for industrial applications. Adaptive controllers
can be realized on platforms like Microchip Technol-
ogy’s microcontrollers, specifically dsPIC microcon-
trollers, which integrate the capabilities of a Digital
Signal Processor (DSP) and a Programmable Intelli-
gent Computer (PIC). These dsPIC microcontrollers
provide a computationally efficient and effective so-
lution for process control. Furthermore, self-tuning
Adaptive PID controllers, which continuously update
parameters during closed-loop operation, further im-
prove control performance in systems with variable
dynamics (Huang et al., 2002). Adaptive controllers
scheduled for gains, designed to adjust gains in re-
sponse to changes in system parameters, have also
demonstrated superior stability and control accuracy
compared to classical PID controllers, ensuring ro-
bust performance under diverse operating conditions
(Vesel
`
y and Ilka, 2013).
Adaptive PID controllers have been extended to
various industrial applications. For example, (Zhao
et al., 2012) developed an Adaptive PID controller
that automatically adjusts the parameters to accom-
modate changing environments, simplifying the inter-
face between processes and control systems. Sim-
ilarly, (Razmi et al., 2022) used Lyapunov-based
adaptive rules to enhance load frequency control
(LFC), while (Wase et al., 2023) applied a fuzzy gain
scheduling PID controller to a CSTR, achieving ro-
bust disturbance rejection and improved performance.
This research focuses on comparing three Adap-
tive PID control strategies: PID, Dual-Adaptive PID,
and fractional one. They are applied to a non-linear
process with variable parameters. A performance
evaluation is done using ISE and ISCO indices.
The remainder of this paper is organized as fol-
lows. Section 2 describes the fundamentals. Section
3 outlines the results and Section 4 conclusions.
2 FUNDAMENTALS
This section is dedicated to describing the three adap-
tive schemes used. First, a PID gain scheduling is pre-
sented, then a Dual-Adaptative and an Adaptive Gain
FO-PID .
2.1 Gain Scheduling
Gain scheduling is a widely used technique in the
design of controllers for nonlinear systems, particu-
larly those with time-varying parameters. It involves
dynamically adjusting the controller gains based on
measurable parameters, ensuring stability and optimal
performance across a wide range of operating condi-
tions. This approach is frequently applied in PID con-
trollers, offering enhanced robustness and efficiency
in systems where dynamic changes necessitate con-
tinuous adjustments to the controller. By adapting
to varying system dynamics, gain scheduling ensures
consistent and reliable control (Milhim et al., 2010).
2.2 Adaptive PID
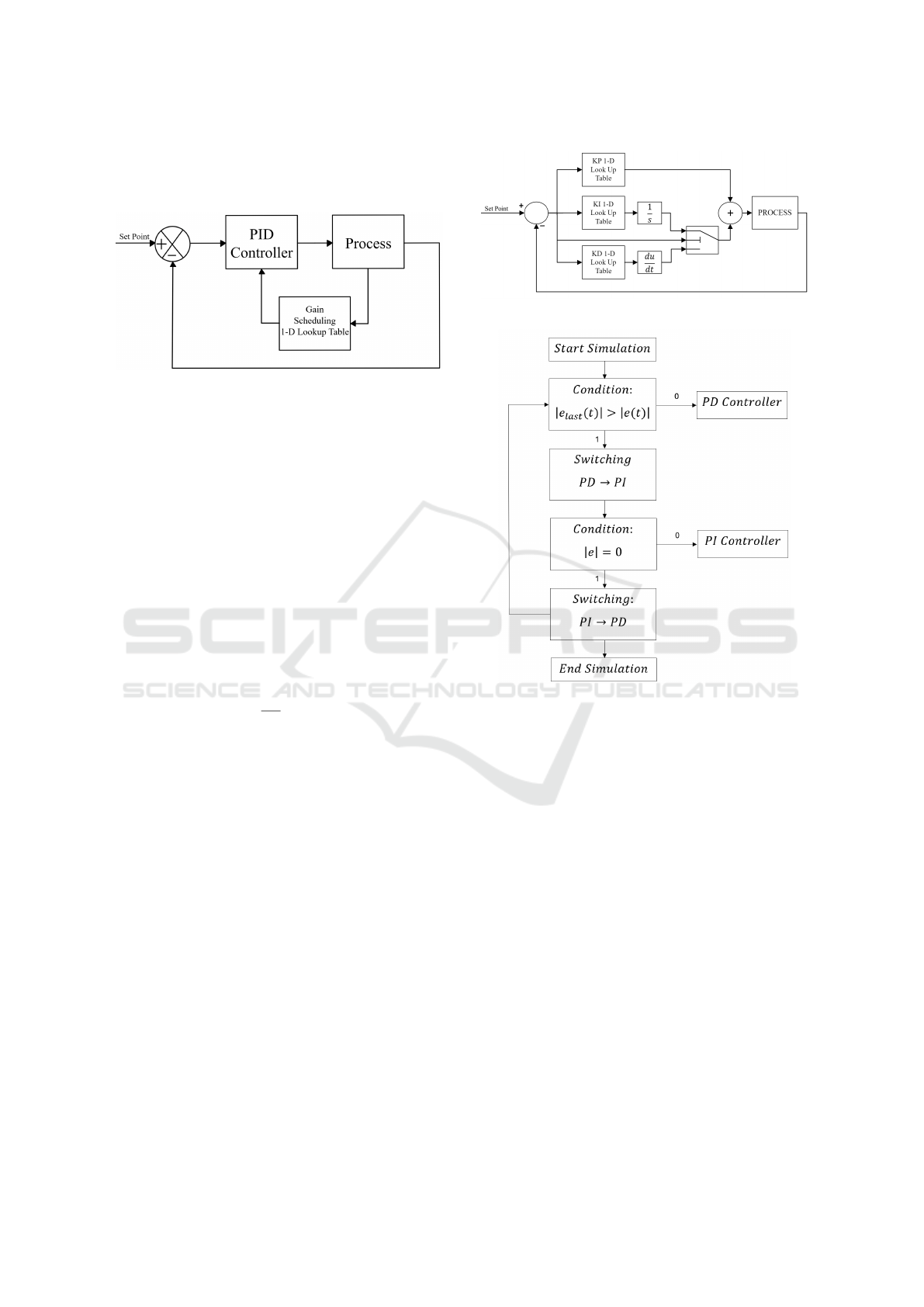
The architecture of the controller is depicted in Fig-
ure 1. A gain scheduling strategy is employed, where
the controller gains are adjusted dynamically based
on the system’s current state. This is achieved using
a Lookup Table that provides optimal gain values for
different operating conditions, ensuring that the con-
troller adapts in real-time to variations in the system’s
behavior (Huang and Shah, 1999).
The general form of a Adaptive PID controller
with gain scheduling is expressed as:
u(t) = K
p
(x)e(t) + K
i
(x)
R
t
0
e(t)dt + K
d
(x)
de(t)
dt
. (1)
In this formulation, K
p
(x), K
i
(x), and K
d
(x) rep-
resent the proportional, integral, and derivative gains,
respectively. These gains are not fixed; instead, they
vary as functions of the measurable parameter x,
which is typically derived from the system’s output,
such as a sensor or transmitter reading (Smith and
Corripio, 2005). By adjusting the gains according
to the parameter x, the controller can respond more
effectively to changes in the system dynamics, im-
proving stability and performance across a range of
operating conditions. This gain scheduling approach
ensures that the controller maintains optimal perfor-
mance even when the system is subject to significant
disturbances or when operating across a wide range of
A Comparison of Adaptive PID, Adaptive Dual-PID and Adaptive Fractional PID Controllers for a Nonlinear System with Variable
Parameters
167

setpoints. Such adaptability makes it particularly use-
ful in processes where system dynamics are nonlinear
or time-varying.
Figure 1: Adaptive PID Controller Design.
2.3 Dual-Adaptive PID
The controller scheme is depicted in Figure 2. This
system implements a Dual-Adaptive PID control
strategy that switches between a PD and a PI con-
troller depending on the magnitude of the system er-
ror. The adaptive mechanism of this Dual-Adaptive
PID follows a similar gain scheduling approach as de-
scribed in the previous Adaptive PID controller. In
this configuration, both PI and PD with Look up Table
controllers are employed, with the ability to dynami-
cally switch between them based on the error condi-
tions during the simulation. The flowchart detailing
the switching logic is shown in Figure 3.
The control law for the Dual-Adaptive PID is de-
fined as:
u(t) =
(
K
p
(x)e(t) + K
d
(x)
de(t)
dt
, if |e
last
(t)| ≥ |e(t)|,
K
p
(x)e(t) + K
i
(x)
R
t
0
e(t)dt, if |e
last
(t)| < |e(t)|.
(2)
In this expression, the proportional gain K
p
(x),
the integral gain K
i
(x), and the derivative gain K
d
(x)
are functions of the measurable system parameter x.
The switching condition is determined by comparing
the current error e(t) with the previous error e
last
(t).
When the error decreases over time, the PD controller
is active, and when the error is 0, the system switches
to the PI controller. This dynamic switching mecha-
nism allows the controller to balance responsiveness
and stability, making it suitable for systems with vary-
ing dynamics and disturbances. By alternating be-
tween the PD and PI modes, the Dual-Adaptive PID
controller provides a more flexible and efficient ap-
proach to maintaining desired performance across a
range of operating conditions.
2.4 Adaptive Gain Fractional-Order
PID
The design of the controller scheme is illustrated in
Figure 4. This figure shows how Lookup Tables are
Figure 2: Dual-Adaptive PID Controller Design.
Figure 3: Switching condition flowchart.
utilized to determine the PID controller constants,
with the added feature of fractional-order components
by incorporating the optimal values of λ and µ (Pod-
lubny, 1994). The control law for an Adaptive Gain
Fractional-Order PID (FO-PID) controller can be ex-
pressed as follows:
u(t) = K
p
(x)e(t)+K
i
(x)D
−λ
t
e(t)+K
d
(x)D
µ
t
e(t). (3)
In this equation, D
−λ
t
and D
µ
t
represent the frac-
tional integral and derivative operators, respectively.
These fractional orders introduce additional flexibil-
ity to control dynamics, enhancing performance. The
values of λ and µ were determined through trial and
error to optimize the robustness and responsiveness of
the system (Petr
´
a
ˇ
s, 2011), (Podlubny, 1999a).
The adaptive gain scheduling mechanism lever-
ages Lookup Tables to dynamically adjust controller
parameters K
p
(x), K
i
(x), and K
d
(x) based on the oper-
ating conditions of the system. This adaptability en-
sures that the Adaptive Gain FO-PID controller can
maintain superior control performance across a range
of dynamic environments and disturbances.
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
168

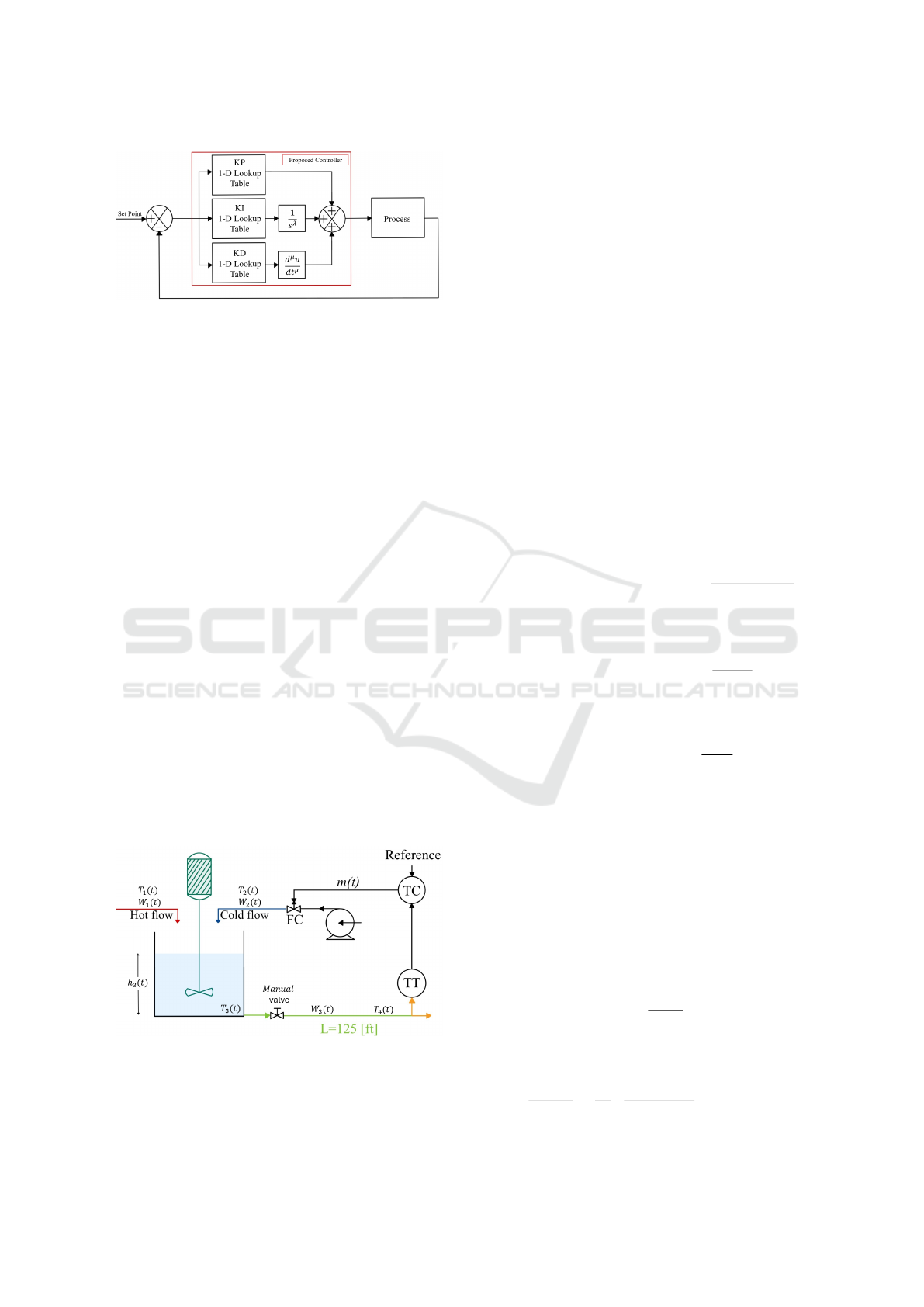
Figure 4: Adaptive Gain FO-PID Controller Design.
The FOMCON toolbox (Tepljakov et al., 2019)
was used together with Simulink to implement the
Adaptive Gain FO-PID controller.
3 NONLINEAR PROCESS UNDER
STUDY
This section presents results and discussion regarding
the application of adaptive approaches to a nonlinear
process. Based on (Iglesias et al., 2007), a brief initial
description of nonlinear systems is provided. This is
followed by an explanation of the empirical modeling
procedure and the tuning process. .
3.1 Nonlinear Process Model
The variable height mixing tank process illustrated
in Figure 5 consists of three flows: an input of hot
fluid W
1
(t) at temperature T
1
(t), an input of cold fluid
W
2
(t) at temperature T
2
(t) controlled by the FC valve,
and an output flow W
3
(t) at temperature T
3
(t) arising
from the combination of the input streams. Specif-
ically, the FC actuator regulates the cold stream to
maintain T
3
(t). The temperature T
4
(t) is obtained by a
transmitter positioned 125 feet downstream from the
tank, with a range of 100 to 200
◦
F.
Figure 5: Mixing Tank Process.
The variable height mixing tank model is a modi-
fied version of the process described in (Camacho and
Smith, 2000), adapted in (Iglesias et al., 2007), and
later discussed in (Morales et al., 2021; Prado et al.,
2022; V
´
asquez et al., 2023).
The control objective in this process lies in main-
taining the mixing temperature T3(t) against external
disturbances of hot flow W 1(t) through the control
output U(t) at the FC valve position FC.
For this work, the following assumptions were
made:
• The tank content and the pipeline are entirely iso-
lated.
• The tank is fully mixed with a uniform internal
temperature.
• The liquid volume varies but does not overflow.
• The main disturbance of the tank is the hot flow
W
1
(t).
The system’s mathematical model is obtained by uti-
lizing the fundamental principles of energy and mass
balance conservation laws, as detailed below.
Energy Balance:
W
1
(t)C
p
1
T
1
(t) +W
2
(t)C
p
2
T
2
(t) −W
3
(t)C
p
3
T
3
(t) =
A
3
ρC
v
3
d(h
3
(t)T
3
(t))
dt
.
(4)
Mass balance:
W
1
(t) +W
2
(t) −W
3
(t) = A
3
ρ
dh
3
(t)
dt
. (5)
The mixing output flow can be expressed as a function
of level h
3
(t) in the following manner:
W
3
(t) = 11.8685C
V L3
p
h
3
(t). (6)
The temperature T
4
(t) of the mixture, after being
transferred from the mixing tank to the transmitter’s
site, is defined by:
T
4
(t) = T
3
(t − t
0
(t)). (7)
where t
0
represents the time delay for the product
mixture with temperature T
3
(t) to arrive at the end-
point of the pipeline, with a temperature of T
4
(t). This
delay is influenced by the length of the pipe and its
cross section A. Thus, the time delay can be quanti-
fied by:
t
0
(t) =
LAρ
W
3
(t)
. (8)
Dynamics of the temperature transmitter can be de-
scribed as follows:
dT 0(t)
dt
=
1
τ
T

T
4
(t) − 100
100
− T 0(t)

. (9)
A Comparison of Adaptive PID, Adaptive Dual-PID and Adaptive Fractional PID Controllers for a Nonlinear System with Variable
Parameters
169

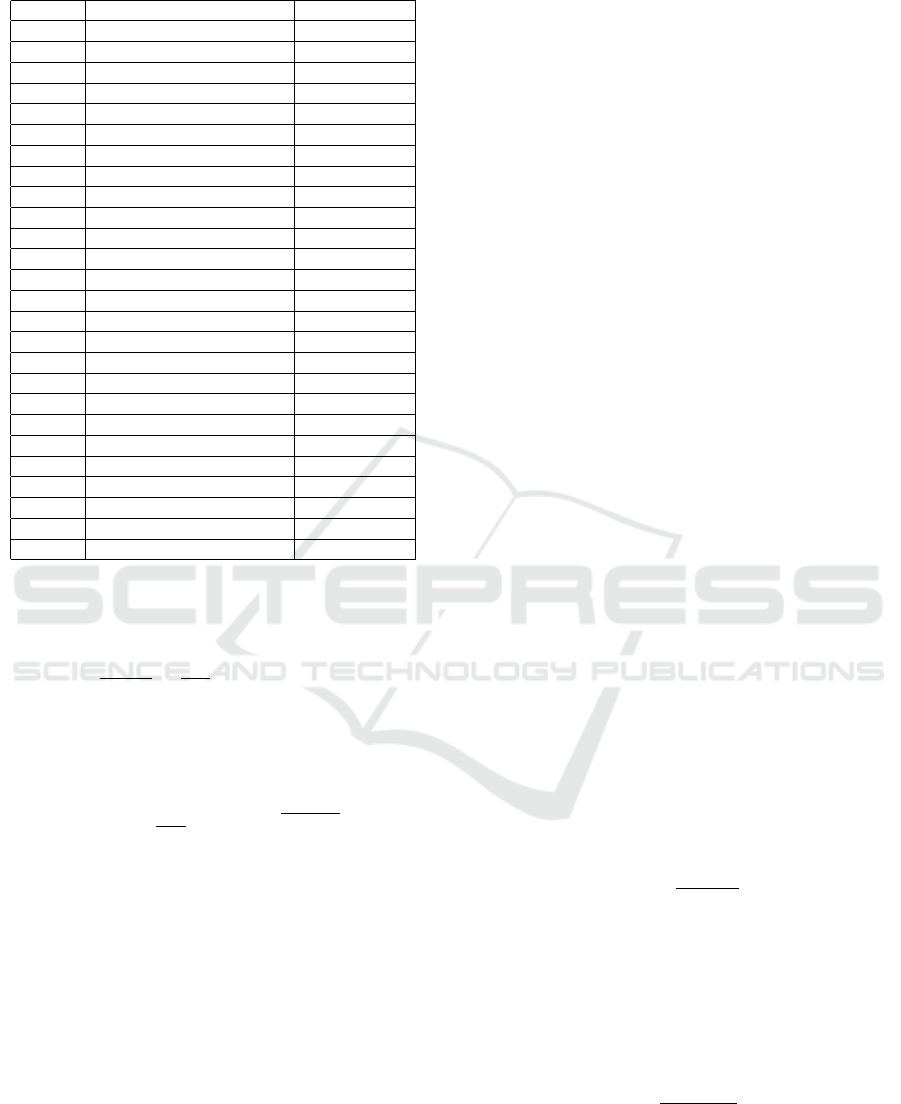
Table 1: Variables and stationary state values of the process.
Variable Description Stationary value
W
1
Hot current mass flow 250 lb/min
W
2
Cold current mass flow 191.17 lb/min
W
3
Output current mass flow 441.17 lb/min
C
p1
Heat capacity (hot flow side) 0.8 Btu/lb-
◦
F
C
p2
Heat capacity (cold flow side) 1.0 Btu/lb-
◦
F
C
p3,v3
Heat capacity at constant volume 0.9 Btu/lb-
◦
F
Ref. Reference (Temperature) 150
◦
F
T
1
Hot flow temperature 250
◦
F
T
2
Cold flow temperature 50
◦
F
T
3
Product temperature 150
◦
F
T
4
Temp. considering time delay –
ρ Content density 62.4 lb/ft
3
A
3
Mixing tank section 3.51692 ft
2
h
3
Liquid level 4.26509 ft
C
CVL3
Manual valve flow coeff. 18 gpm/ ft
1/2
C
CVL
Control valve flow coeff. 12 gpm/ psi
1/2
TO Transmitter output signal 0.5 p.u
V
p
Valve position 0.478
m Controller output 0.478 p.u
G
f
Specific gravity 1
δP
v
Pressure loss 16 psi
τ
T
Sensor time constant 0.5 min
τ
V
p
Valve time constant 0.4 min
t
o
Time delay –
A Pipeline cross-section 0.2006 ft
2
L Pipeline length 125ft
where τ
T
denotes the constant time of the temperature
sensor. The servo-valve positioning is driven by the
controller according to the following equation:
dV
p
(t)
dt
=
1
τ
V P
[m(t) −V
p
(t)]. (10)
where m(t) is the controller output of the process to
be controlled. Based on the servo-valve position, the
input cold flow can be calculated as follows:
W
2
(t) =
500
60
C
V L
V
p
(t)
p
G
F
∆P
V
. (11)
The variables of the non-linear model and the sta-
tionary state values with their respective units are
summarized in Table 1.
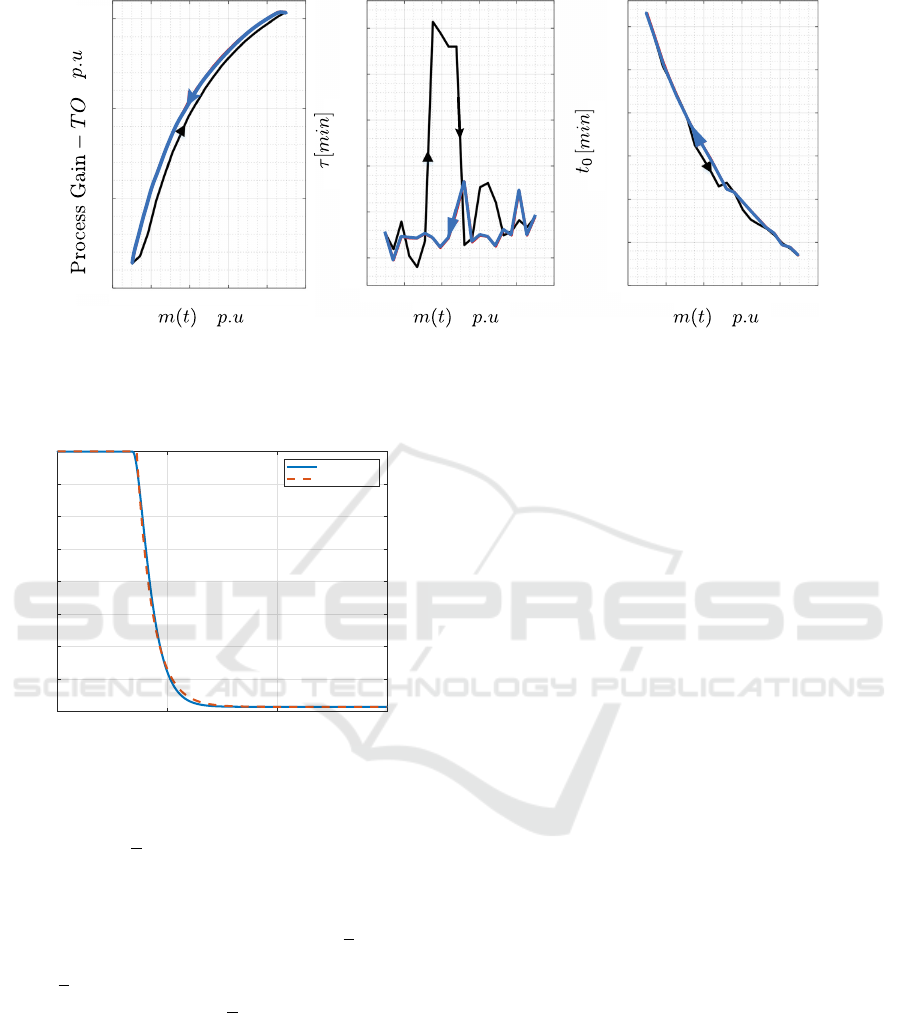
3.2 Process Nonlinear Behavior
To evaluate the non-linear properties of the system,
it is recommended to examine the variations in the
parameters K, τ, and t
0
as the input signal m(t) to the
valve undergoes a sequence of small step changes. It
is crucial to consider that the attributes of the mixing
tank are influenced by the operating conditions.
Therefore, the parameters of the First-Order Plus
Dead-Time (FOPDT) model will alter at various op-
erating points. Figure 6 illustrates the changes in the
mixing tank process parameters in response to varia-
tions in the input signal. As the signal increases from
0.1 to 0.898 per unit with increments of +10%, the
parameters trace the black curves. In contrast, the pa-
rameters trace the blue curves as the signal drops from
0.898 to 0.1 per unit with decrements of −10%. It is
noted that both K and t
0
show an almost linear growth
pattern, while the time constant (τ) does not show a
clear correlation with the plant input signal m(t).
The ambiguity in τ, combined with the hysteresis-
like behavior in K and t
0
, undermines the ef-
fectiveness of the traditional Proportional-Integral-
Derivative (PID) controller.
3.3 Empirical Modeling Procedure
Given the system’s highly nonlinear behavior, one ap-
proach to implementing adaptive control schemes is
by constructing the scheduling process using a col-
lection of simple reduced-order models. The reaction
curve method described in (Smith and Corripio, 2005;
Liptak, 2018) is utilized to obtain these models. The
derived reduced-order models are utilized to develop
the gain scheduling scheme. It is important to remem-
ber that gain scheduling adaptive control is a method
to dynamically adjust the controller’s parameters in
real-time based on variations in operating conditions
or system dynamics. As the system moves from one
operating region to another, the controller adjusts its
gains by selecting the pre-determined set of gains as-
sociated with the current operating condition.
This approach is especially beneficial for manag-
ing nonlinear or time-varying systems, where the con-
troller gains are contingent on the system’s present
state or environment.
The approximate or reduced FOPDT model of the
process is derived using the reaction curve method
(Smith and Corripio, 2005) and can be expressed as:
G(s)=
Ke
−t
0
(τs + 1)
. (12)
Where: (K) Process Gain, (τ) Time Constant, and (t
0
)
Delay, which are obtained directly from the proce-
dure.
For example, if we consider that the controller out-
put is 0.5 the resulting FOPDT model is presented in
Equation (13).
G
p
1
(s) =
−0.8217
0.73 s + 1
e
−3.6 s
. (13)
Figure 7 illustrates the actual response of the non-
linear mixing tank model along with the FOPDT
model. It can be seen that the results closely match the
operating point, validating the accuracy of the model,
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
170

s
( )
( )
( )
-0.5
-1.0
-1.5
-2.0
0 0.2 0.4 0.6 0.8 1.0
0.95
0.90
0.85
0.80
0.75
0.70
0 0.2 0.4 0.6 0.8 1.0
5.5
5.0
4.5
4.0
3.5
3.0
2.5
0 0.2 0.4 0.6 0.8 1.0
( )
Figure 6: Nonlinear behavior of the characteristic parameters of the mixing tank process, (Iglesias et al., 2007).
but it changes depending on the controller output, as
is seen in Figure 6.
0 5 10 15
Time [s]
0.46
0.465
0.47
0.475
0.48
0.485
0.49
0.495
0.5
TO [p.u]
NON-LINEAR
LINEAR
Figure 7: Comparative responses of the approximated
FOPDT model and real system. The model output was de-
picted using a reaction curve test around the operation point.
In addition,
t
0
τ
= 4.9, called the controllability ra-
tio, indicates the difficulty of controlling a process
(Obando et al., 2023; Mejia et al., 2022). Also known
as normalized dead time or normalized time delay
(
˚
Astr
¨
om et al., 2006), smaller values of
t
0
τ
indicate
processes that are easier to control, while larger val-
ues of
t
0
τ
represent systems that are harder to control.
A value greater than one for
t
0
τ
signifies a difficult pro-
cess with a dominant time delay.
4 CONTROLLERS EVALUATIONS
The controllers are then assessed for their response
to change in setpoints and disturbance variations, and
performance metrics are used to facilitate their com-
parative analysis.
4.1 Controller Tunings
The Dahlin equations were applied to tune the PID
parameters, leveraging the values obtained from the
Open-Loop Tuning method (
˚
Astr
¨
om and H
¨
agglund,
2006). The required PID gains, K
P
, K
I
, and K
D
,
were calculated by developing 20 approximations of
FOPDT models, 10 for an increase of 10% and 10
for a decrease of 10% in system parameters. These
models enabled the design of three 1-D Lookup Ta-
ble blocks in Simulink, each corresponding to PID
gains. The breakpoints in the Lookup Tables were
configured to adapt to both reference changes and dis-
turbances, allowing the system to dynamically select
the optimal gain values. Furthermore, adjustments to
fractional parameters λ and µ were fine-tuned through
trial and error to balance performance improvements
with robustness.
4.2 Control Performance Indices
Process controller performance is often evaluated by
comparing control quality with a standard or desired
value (Liptak, 2018; Smith and Corripio, 2005). We
are using here the integral of squared error (ISE), the
integral of the squared variation of the control signal
(ISCO), maximum overshoot, and settling time (Ts)
to assess the proposed approach against PID and SMC
controllers.
Integral of the Squared Error (ISE). Quantifies
the system performance by integrating the squared er-
ror over a set time interval(Smith and Corripio, 2005;
Liptak, 2018).
ISE =
Z
∞
0
e(t)
2
dt. (14)
Integral of the Squared Variation of the Control
Signal (ISCO). This reflects the effort exerted by the
A Comparison of Adaptive PID, Adaptive Dual-PID and Adaptive Fractional PID Controllers for a Nonlinear System with Variable
Parameters
171

control signal. It can be calculated using the follow-
ing formula:
ISCO =
Z
u(t)
2
dt. (15)
Overshoot (M
p
). It is defined as the deviation of the
response at the time when a maximum peak appears
with respect to the final or desired value of the re-
sponse. It also called the maximum overshoot, is the
amount of the output system that exceeds its target
value as a percentage (%) (Smith and Corripio, 2005).
Settling Time (t
s
). The time required for the response
to reach a steady state and remain within the specified
tolerance bands around the final value. The normally
used tolerance bands are 2% and 5% (Smith and Cor-
ripio, 2005).
4.3 Comparison of Controllers to
Reference Change
Given the non-linearity of the mixing tank process
and the varying non-linearity and hysteresis of the
FOPDT model at different operating points, it is cru-
cial to improve the conventional PID controller to ad-
dress these issues. This research proposes develop-
ing some adaptive controllers as potential solutions.
The following section details the use of these differ-
ent controller configurations.
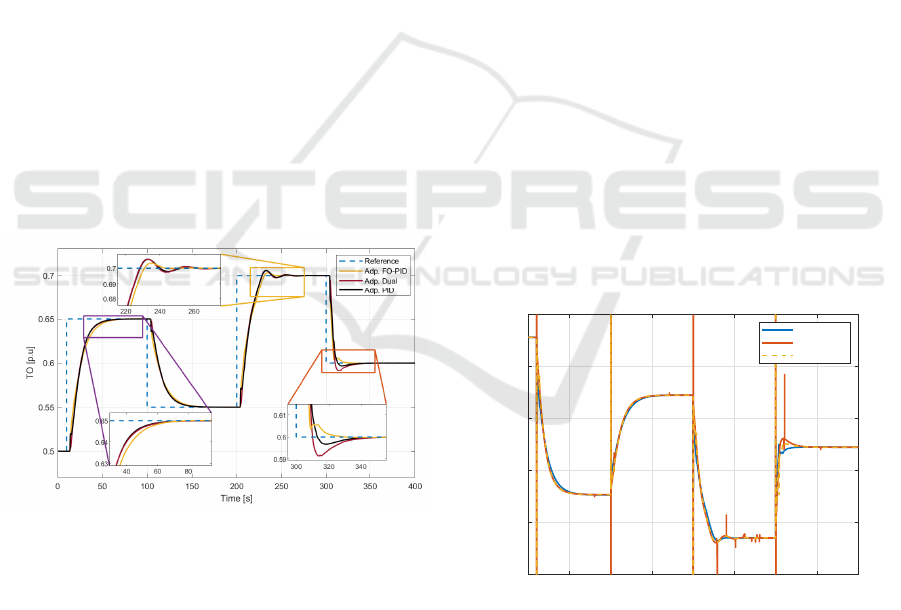
Figure 8: System response to Reference Changes.
Figure 8 illustrates the process response of a mix-
ing tank under the application of Adaptive Gains FO-
PID , Dual-Adaptive PID, and Adaptive PID con-
trollers. While all controllers effectively guide the
system toward the reference values, a more detailed
analysis reveals significant differences in their perfor-
mance.
The Adaptive PID controller performs similarly
to the Dual-Adaptive PID controller during the refer-
ence shifts at 10 and 200 seconds. However, the most
notable difference is observed during the 300-second
reference shift, where the Adaptive PID demonstrates
excellent reference tracking capability with minimal
overshoot. Additionally, a detailed examination of the
final reference shift reveals that the Adaptive PID con-
troller maintains a stable response with less overshoot
compared to the Dual-Adaptive PID.
The Dual-Adaptive PID controller exhibits
slightly slower response times compared to the
Adaptive PID controller. However, the most signif-
icant difference is observed during the 300-second
reference shift, where the Adaptive PID controller
demonstrates superior reference tracking capability.
At this point, the Dual-Adaptive PID begins to
outperform the Adaptive PID, switching during the
overshoot to achieve faster response times. When
the final reference change occurs, the Dual-Adaptive
PID becomes even faster, transitioning from PD to PI
during the overshoot to quickly reach the reference.
On the other hand, the Adaptive Gain FO-PID
controller strikes a balance between settling time and
overshoot, avoiding excessive stabilization times or
high overshoot percentages. It is observed that, in re-
sponse to a reference change, this controller demon-
strates an immediate response compared to the other
controllers, reducing its speed as it approaches the
reference. These observations highlight the inherent
trade-offs among the different adaptive control strate-
gies concerning response time and overshoot. Under-
standing these trade-offs is crucial for optimizing con-
trol performance in mixing tank processes, ensuring
that controllers are selected based on the specific per-
formance criteria required for the application.
0 50 100 150 200 250 300 350 400
Time [s]
0.25
0.3
0.35
0.4
0.45
0.5
CO [p.u]
Adp. FO-PID
Adp. Dual
Adp. PID
Figure 9: Control Action of Change Reference.
Figure 9 illustrates the response of various con-
trollers to reference changes, specifically comparing
the performance of the Adaptive Controllers with dif-
ferent control laws: Adaptive PID, Dual-Adaptive
PID, and Adaptive Gain FO-PID.
The Adaptive PID controller provides intermedi-
ate behavior between the other two controllers. While
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
172

it offers a balance between smoothness and response
speed, it exhibits minor oscillations in the controller
output.
The Dual-Adaptative PID controller exhibits a
more abrupt response to reference changes due to the
switching of controllers when the response deviates
from the reference. This behavior can be disadvan-
tageous in systems that are sensitive to rapid fluctua-
tions.
In contrast, the Adaptive Gain FO-PID controller
demonstrates the smoothest response to reference
changes, making it advantageous for applications that
require precise control and finely-tuned stability.
These observations highlight the distinct charac-
teristics of each controller, emphasizing that each has
its own advantages and limitations based on the spe-
cific requirements of the control application, such as
in the case of a mixing tank with variable parameters.
Table 2: Comparison of Performance parameters for the last
reference changes.
Controllers ISE ISCO t
s
[s] M
p
[%]
Adap. FO-PID 0.54 66.27 25.12 0.00
Adap. Dual 0.59 66.41 33.84 0.82
Adap. PID 0.58 66.40 35.91 0.30
Table 2 compares the performance of three control
strategies Adaptive FO-PID, Dual-Adaptive PID, and
Adaptive PID. The table evaluates critical metrics, in-
cluding ISE, ISCO, t
s
, and M
p
, which collectively in-
dicate the controllers’ accuracy, control effort, speed
of response, and stability when subjected to distur-
bances.
The Adaptive FO-PID stands out by achieving the
fastest settling time with no overshoot, reflecting its
ability to maintain precise and stable control under
changing conditions. This makes it ideal for applica-
tions requiring minimal error and smooth transitions.
The Dual-Adaptive PID, although slightly slower
in settling time, leverages its dynamic switching be-
tween control modes (PD and PI) to optimize its re-
sponse, particularly by balancing speed and control
accuracy. It does exhibit a minor overshoot, which is
acceptable in scenarios prioritizing quick responses.
On the other hand, The Adaptive PID exhibits the
longest settling time among the three controllers but
compensates with low overshoot and consistent con-
trol. This balance between smoothness and stabil-
ity makes it suitable for applications where gradual
convergence to the reference is preferred over rapid
changes. Overall, the table highlights the distinct
strengths and trade-offs of each controller, showcas-
ing the adaptability and control efficiency required for
different system dynamics.
4.4 Comparison of Controllers Under
Disturbances
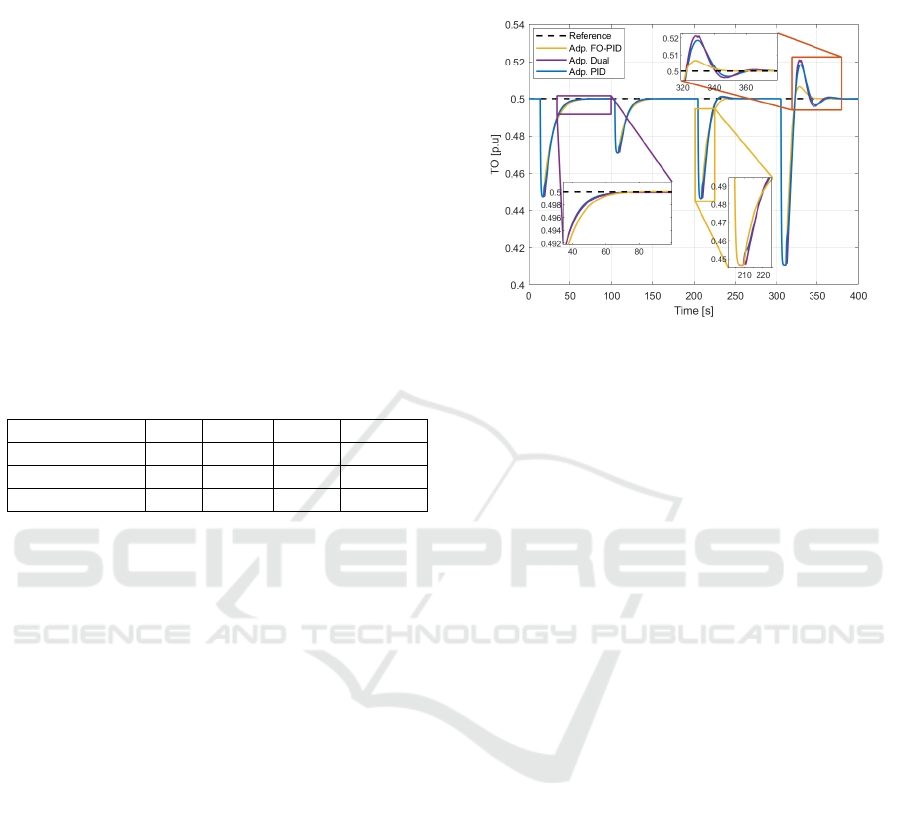
Figure 10: Comparison of disturbance rejection in the hot
water.
Figure 10 illustrates the system’s response to four dis-
turbances in hot water introduction, applied at various
values and times. This analysis evaluates the perfor-
mance of three controllers: Adaptive Gain FO-PID,
Dual-Adaptive PID, and Adaptive PID.
In the first disturbance, the Adaptive PID con-
troller is shown to be much faster than the other con-
trollers, while the Adaptive Gain FO-PID is the quick-
est to start rejecting the disturbance but is the slowest
overall. This is due to its balance between perfor-
mance and robustness.
In the second disturbance, all controllers exhibit a
similar response, causing the parameters to continue
varying. However, in the third disturbance, the con-
trollers begin to differentiate. The Dual-Adaptive PID
becomes faster than the Adaptive PID, also showing
the overshoot of both controllers, while the Adaptive
Gain FO-PID demonstrates robustness against this
disturbance. The zoomed-in view of this disturbance
better illustrates the controllers’ behavior: the switch-
ing of the Dual-Adaptive PID, the peak of the deriva-
tive part of the Adaptive PID, and the quick response
of the Adaptive Gain FO-PID.
Finally, with the variability of the parameters
and the magnitude of the disturbance, the controllers
face greater demands. The Adaptive PID and Dual-
Adaptive PID show an increase in overshoot, with the
Dual-Adaptive PID having the highest due to its faster
passage through the reference point. At the maximum
overshoot point, it performs a new switch to com-
pensate and attempt to stabilize more quickly at the
reference than the Adaptive PID. On the other hand,
the Adaptive Gain FO-PID shows much greater ro-
bustness, with a much lower overshoot than the other
controllers and stabilizing without oscillations more
A Comparison of Adaptive PID, Adaptive Dual-PID and Adaptive Fractional PID Controllers for a Nonlinear System with Variable
Parameters
173

quickly. This characteristic of robustness is crucial
for rejecting large magnitude disturbances and high
variability in nonlinear systems.
0 50 100 150 200 250 300 350 400
Time [s]
0.25
0.3
0.35
0.4
0.45
0.5
CO [p.u]
Adp. FO-PID
Adp. Dual
Adp. PID
Figure 11: Comparison of control action in disturbances re-
jection in the hot water.
Figure 11 illustrates the control actions for each
scenario. The Adaptive Gain FO-PID controller
demonstrates the smoothest response to disturbances,
making it particularly advantageous in applications
where minimizing controller activity and power con-
sumption is critical. This smooth response is due to
its balanced approach to performance and robustness.
In contrast, the Dual-Adaptive PID controller ex-
hibits a more abrupt response to disturbances. This
is because it switches abruptly between controllers,
as shown in the flowchart in Figure 3. Addition-
ally, other impulses can be observed, which are the
switches that occur when a new maximum error is de-
tected. These abrupt changes can lead to higher power
consumption and more wear on the system compo-
nents.
The Adaptive PID controller displays an interme-
diate behavior, balancing smoothness and response
speed. However, as the speed increases, it also in-
troduces oscillations in the control output. This can
be beneficial in scenarios where a quick response is
needed, but it may also lead to instability if not prop-
erly managed.
These findings underscore the varying adaptive
characteristics of the controllers. Each control strat-
egy offers unique benefits and drawbacks depending
on the specific demands of the application.
Table 3: Comparison of Performance Parameters for the
Last Disturbance.
Controllers ISE ISCO t
s
[s] M
p
[%]
Adap. FO-PID 0.12 62.40 42.18 0.65
Adap. Dual 0.14 62.44 54.75 2.12
Adap. PID 0.13 66.41 56.95 1.86
Table 3 provides a comprehensive comparison of
the performance parameters for disturbance rejection
across three adaptive controllers.
The Adaptive FO-PID controller exhibits the best
overall performance, achieving the lowest error, min-
imal control effort, and a short settling time. Its low
overshoot makes it particularly effective in maintain-
ing system stability during disturbance rejection, en-
suring smooth and rapid recovery without significant
oscillations. This controller is ideal for systems re-
quiring high precision, fast stabilization, and minimal
energy consumption.
The Dual-Adaptive PID controller, while demon-
strating strong responsiveness, shows a slight increase
in control effort and settling time compared to the
FO-PID. Its dynamic nature, characterized by switch-
ing between control modes, results in faster correc-
tive actions but introduces a higher overshoot. This
makes the Dual-Adaptive PID a good choice in sce-
narios where fast disturbance rejection is more critical
than maintaining minimal fluctuations, though it may
lead to less stable recovery.
In contrast, the Adaptive PID controller offers
a more moderate balance across the parameters. It
achieves reasonable error minimization and control
effort but lags behind the FO-PID in terms of settling
time and exhibits more pronounced oscillations, re-
flected in a higher overshoot. While it can perform ad-
equately in many applications, its slower response and
higher energy consumption make it less efficient for
systems requiring optimal disturbance rejection per-
formance.
4.5 Comparison of Controllers with
White Noise
0 50 100 150 200 250 300 350 400
Time [s]
0.5
0.6
0.7
TO [p.u]
Reference
Adp. FO-PID
0 50 100 150 200 250 300 350 400
Time [s]
0.5
0.6
0.7
TO [p.u]
Reference
Adp. Dual
0 50 100 150 200 250 300 350 400
Time [s]
0.5
0.6
0.7
TO [p.u]
Reference
Adp. PID
Figure 12: System Response to Reference Changes in
Noisy Conditions.
Figure 12 illustrates the response of the mixing tank
under noisy conditions, controlled by Adaptive Gain
FO-PID , Dual-Adaptive PID, and Adaptative PID
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
174

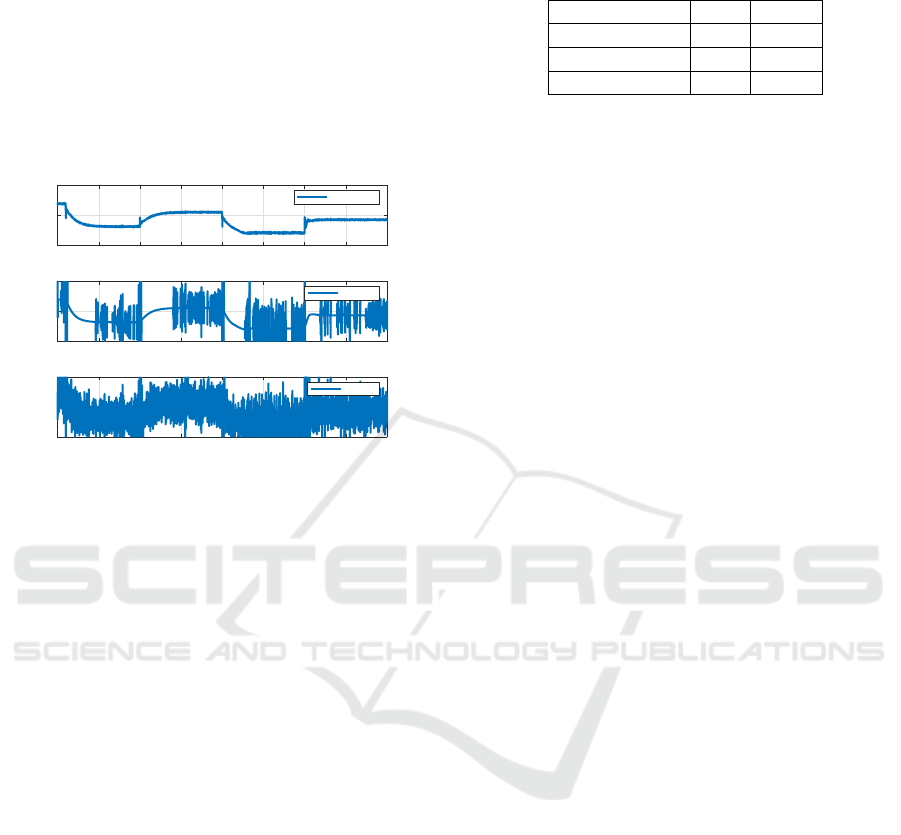
controllers. All controllers successfully guide the sys-
tem to the reference values. However, the presence of
noise does not result in significant differences in the
system’s response to the reference changes across the
controllers. The most notable variations are observed
in the control actions, where the controllers exhibit
markedly different behaviors. Analyzing the control
action is crucial, as significant variations are observed
depending on the controller used.
0 50 100 150 200 250 300 350 400
Time [s]
0.2
0.4
0.6
CO [p.u]
Adp. FO-PID
0 50 100 150 200 250 300 350 400
Time [s]
0.2
0.4
0.6
CO [p.u]
Adp. Dual
0 50 100 150 200 250 300 350 400
Time [s]
0.2
0.4
0.6
CO [p.u]
Adp. PID
Figure 13: Control Actions in Response to Reference
Changes Under Noisy Conditions.
Figure 13 compares the control actions of the
Adaptive FO-PID, Dual-Adaptive PID, and Adaptive
PID controllers under noisy conditions in response to
reference changes.
The Adaptive FO-PID exhibits the smoothest and
most stable control output, effectively rejecting noise
and adapting to reference changes with minimal fluc-
tuations. This performance is attributed to the frac-
tional parameters in the integral and derivative gains,
making this controller the best option in noisy envi-
ronments.
In contrast, the Dual-Adaptive PID demonstrates
how switching occurs when the error is not zero. This
type of dual controller has an advantage in noisy con-
ditions because it can reduce noise due to the PD con-
troller’s lack of an integral parameter, which other-
wise increases noise. Additionally, when operating as
a PI controller, the absence of a derivative gain fur-
ther amplifies noise. These characteristics are evident
in the control actions, showcasing the Dual-Adaptive
PID’s ability to handle noisy conditions effectively.
Lastly, the Adaptive PID controller displays the
highest sensitivity to noise, with significant oscilla-
tions throughout the response period, indicating less
stability compared to the other controllers.
This figure highlights the superior robustness of
the FO-PID, the responsiveness but increased vari-
ability of the Dual-Adaptive PID, and the instability
of the Adaptive PID under noisy conditions.
Table 4: Comparison of performance parameters for refer-
ence shifting under noise conditions.
Controllers ISE ISCO
Adap. FO-PID 0.55 66.28
Adap. Dual 0.61 66.43
Adap. PID 0.58 66.55
Table 4 provides a comparative analysis of the per-
formance indices for three adaptive controllers Adap-
tive Gain FO-PID, Dual-Adaptive PID, and Adaptive
PID based on two critical performance metrics: ISE
, which quantifies the controller’s ability to minimize
tracking errors, and ISCO, which measures the con-
trol effort or energy consumption required to achieve
the desired performance, particularly in noisy envi-
ronments.
The Adaptive Gain FO-PID controller stands out
with superior performance in both categories. It
demonstrates exceptional error minimization, which
indicates its high accuracy in maintaining the sys-
tem’s reference signal despite noise. Additionally,
this controller achieves the highest energy efficiency,
making it a balanced choice for applications where
both precision and energy conservation are crucial. Its
ability to optimize these two factors simultaneously
makes it the most effective solution among the three
controllers.
The Dual-Adaptive PID controller, while not as
precise as the FO-PID in terms of error minimiza-
tion, still delivers strong energy efficiency. Its slight
increase in error is compensated by its low energy
consumption, making it a viable alternative in cases
where conserving control effort is prioritized over ab-
solute accuracy. This balance between control pre-
cision and energy usage positions the Dual-Adaptive
PID as a competitive option when compared to the
FO-PID, especially in scenarios where performance
trade-offs are acceptable.
On the other hand, the Adaptive PID controller,
though capable of providing moderate error min-
imization, shows the highest energy consumption
among the three controllers. This suggests that while
it may be effective in reducing errors to a reason-
able extent, its efficiency is compromised, leading to
higher operational costs in terms of control effort. As
a result, the Adaptive PID is less suited for applica-
tions that demand both high accuracy and energy ef-
ficiency, although it could still be a feasible choice in
less demanding situations where energy consumption
is not a critical concern.
A Comparison of Adaptive PID, Adaptive Dual-PID and Adaptive Fractional PID Controllers for a Nonlinear System with Variable
Parameters
175

5 CONCLUSIONS
This study provides insight into the performance of
three adaptive control strategies under various condi-
tions when applied to a nonlinear process with vari-
able parameters and dominating delay. The tested
controllers used were Adaptive PID, Dual-Adaptive
PID, and Adaptive Gain FO-PID . The Adaptive Gain
FO-PID consistently minimized the ISE and main-
tained a low ISCO, contributing to the life of the fi-
nal control element with precise control and energy
efficiency.
Adaptive Gain FO-PID achieved rapid stabiliza-
tion with minimal overshoot and smooth disturbance
response, making it suitable for tight control and ro-
bustness. Conversely, the Dual-Adaptive PID con-
troller responded more aggressively to disturbances,
resulting in higher ISE and ISCO values, which can
be suitable for environments prioritizing quick adap-
tation but non-efficiency in energy. The Adaptive PID
controller balanced error minimization and control ef-
fort, making it suitable for moderate error reduction,
although its oscillations may limit effectiveness in dy-
namic or noise-sensitive environments.
These findings stress the importance of select-
ing the appropriate adaptive control strategy based
on application requirements, balancing error mini-
mization, energy efficiency, response time, and distur-
bance robustness. Therefore, the Adaptive Gain FO-
PID presents the best for precision and performance,
the Dual-Adaptive PID for rapid adaptation, and the
Adaptive PID for a balanced approach.
Despite their advantages in performance for iden-
tification and control, fractional-order controllers re-
quire further development for practical implementa-
tions. Implementing Adaptive Gain FO-PID con-
trollers involves fractional calculus, making them
challenging since transitioning to fractional order re-
quires advanced numerical methods, adding complex-
ity and computational overhead. The gap between
theory and practice should be reduced, and improve-
ments in the knowledge of fractional calculus should
be made so that plant operators can prove the advan-
tages over conventional PID solutions.
ACKNOWLEDGEMENTS
SV and MV thank the Advanced Control Systems Re-
search Group at USFQ for a research internship.
The Universidad San Francisco de Quito sup-
ported this work through the Poli-Grants Program un-
der Grant 24280.
REFERENCES
Anchitipan, E. and Camacho, O. (2021). Processes with
variable parameters and dominant time delay: a fuzzy
adaptive control approaches comparison. In Recent
Advances in Electrical Engineering, Electronics and
Energy: Proceedings of the CIT 2020 Volume 1, pages
181–195. Springer.
Annaswamy, A. M. and Fradkov, A. L. (2021). A historical
perspective of adaptive control and learning. Annual
Reviews in Control, 52:18–41.
˚
Astr
¨
om, K. J. and H
¨
agglund, T. (2006). Pid control. IEEE
Control Systems Magazine, 1066.
˚
Astr
¨
om, K. J., H
¨
agglund, T., and Astrom, K. J. (2006). Ad-
vanced PID control, volume 461. ISA-The Instrumen-
tation, Systems, and Automation Society Research
Triangle Park.
˚
Astr
¨
om, K. J. and Wittenmark, B. (2008). Adaptive control.
Courier Corporation.
Borase, R. P., Maghade, D., Sondkar, S., and Pawar, S.
(2021). A review of pid control, tuning methods and
applications. International Journal of Dynamics and
Control, 9:818–827.
Camacho, O. and Smith, C. A. (2000). Sliding mode con-
trol: an approach to regulate nonlinear chemical pro-
cesses. ISA transactions, 39(2):205–218.
Cha
´
ınho, J., Pereira, P., Rafael, S., and Pires, A. (2005).
A simple pid controller with adaptive parameter in
a dspic; case of study. In Proceedings of the 9th
Spanish-Portuguese Congress on Electrical Engineer-
ing.
Chotikunnan, P. and Chotikunnan, R. (2023). Dual de-
sign pid controller for robotic manipulator applica-
tion. Journal of Robotics and Control (JRC), 4(1):23–
34.
H
¨
agglund, T. and Guzm
´
an, J. L. (2024). Give us pid
controllers and we can control the world. IFAC-
PapersOnLine, 58(7):103–108.
Han, J. (2009). From pid to active disturbance rejection
control. IEEE transactions on Industrial Electronics,
56(3):900–906.
Huang, B. and Shah, S. L. (1999). Performance Assessment
of Control Loops: Theory and Applications. Springer.
Huang, H.-P., Roan, M.-L., and Jeng, J.-C. (2002). On-line
adaptive tuning for pid controllers. IEE Proceedings-
Control Theory and Applications, 149(1):60–67.
Iglesias, E., Garc
´
ıa, Y., Sanjuan, M., Camacho, O., and
Smith, C. (2007). Fuzzy surface-based sliding mode
control. ISA transactions, 46(1):73–83.
Isermann, R. and Isermann, R. (1991). Adaptive control
systems (a short review). Digital Control Systems:
Volume 2: Stochastic Control, Multivariable Control,
Adaptive Control, Applications, pages 127–140.
Liptak, B. G. (2018). Instrument engineers’ handbook, vol-
ume two: Process control and optimization. CRC
press.
Liu, Z.-G., Xue, L., and Zhang, W. (2021). Universal adap-
tive control strategies for stochastic nonlinear time-
delay systems with odd rational powers. Automatica,
125:109419.
ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics
176

Mejia, C., Salazar, E., and Camacho, O. (2022). A compar-
ative experimental evaluation of various smith predic-
tor approaches for a thermal process with large dead
time. Alexandria Engineering Journal, 61(12):9377–
9394.
Milhim, A., Zhang, Y., and Rabbath, C.-A. (2010). Gain
scheduling based pid controller for fault tolerant con-
trol of quad-rotor uav. In AIAA infotech@ aerospace
2010, page 3530.
Morales, L., Aguilar, J., Camacho, O., and Rosales, A.
(2021). An intelligent sliding mode controller based
on lamda for a class of siso uncertain systems. Infor-
mation Sciences, 567:75–99.
Obando, C., Rojas, R., Ulloa, F., and Camacho, O.
(2023). Dual-mode based sliding mode control ap-
proach for nonlinear chemical processes. ACS omega,
8(10):9511–9525.
O’dwyer, A. (2009). Handbook of PI and PID controller
tuning rules. World Scientific.
Petr
´
a
ˇ
s, I. (2011). Fractional-order feedback control of a dc
motor. Journal of Electrical Engineering, 62(1):1–9.
Podlubny, I. (1994). Fractional-order systems and
fractional-order controllers. Institute of Experimen-
tal Physics, Slovak Academy of Sciences, Kosice,
12(3):1–18.
Podlubny, I. (1999a). Fractional Differential Equations.
Academic Press.
Podlubny, I. (1999b). Fractional-order systems and
pi/sup/spl lambda//d/sup/spl mu//-controllers. IEEE
Transactions on automatic control, 44(1):208–214.
Prado, A. J., Herrera, M., Dominguez, X., Torres, J., and
Camacho, O. (2022). Integral windup resetting en-
hancement for sliding mode control of chemical pro-
cesses with longtime delay. Electronics, 11(24):4220.
Razmi, P., Rahimi, T., Sabahi, K., Gheisarnejad, M., and
Khooban, M.-H. (2022). Adaptive fuzzy gain schedul-
ing pid controller for frequency regulation in modern
power system. IET Renewable Power Generation.
Samad, T. (2017). A survey on industry impact and chal-
lenges thereof [technical activities]. IEEE Control
Systems Magazine, 37(1):17–18.
Smith, C. A. and Corripio, A. B. (2005). Principles and
practices of automatic process control. John wiley &
sons.
Taguchi, H. and Araki, M. (2000). Two-degree-of-freedom
pid controllers—their functions and optimal tuning.
IFAC Proceedings Volumes, 33(4):91–96.
Tepljakov, A., Petlenkov, E., Belikov, J., and Petr
´
a
ˇ
s, I.
(2019). Fomcon toolbox for modeling, design and im-
plementation of fractional-order control systems. Ap-
plications in control, 6:211–236.
V
´
asquez, M., Yanascual, J., Herrera, M., Prado, A., and
Camacho, O. (2023). A hybrid sliding mode control
based on a nonlinear pid surface for nonlinear chem-
ical processes. Engineering Science and Technology,
an International Journal, 40:101361.
Vesel
`
y, V. and Ilka, A. (2013). Gain-scheduled pid con-
troller design. Journal of process control, 23(8):1141–
1148.
Wase, M. G., Gebrekirstos, R. F., Jin, G.-G., and So, G.-
B. (2023). Fuzzy gain scheduling of the fractional-
order pid controller for a continuous stirred-tank reac-
tor process. Processes, 11(12):3275.
Yurkevich, V. D. (2011). Advances in PID control. BoD–
Books on Demand.
Zhao, P., Chen, J., Song, Y., Tao, X., Xu, T., and Mei, T.
(2012). Design of a control system for an autonomous
vehicle based on adaptive-pid. International Journal
of Advanced Robotic Systems, 9(2):44.
A Comparison of Adaptive PID, Adaptive Dual-PID and Adaptive Fractional PID Controllers for a Nonlinear System with Variable
Parameters
177