A New Observer-Based Fault Tolerant Shared Control for SbW Systems

with Actuator Fault for Driver Assistance

Mohammed Boudaoud

1,2

, Chouki Sentouh

1,3

, Cindy Cappelle

, Maan El Badaoui El Najjar

and Jean-Christophe Popieul

1,3

LAMIH UMR CNRS 8201, Universit

e Polytechnique Hauts-de-France, Valenciennes, France

Univ. Lille, CNRS, Centrale Lille, UMR 9189 CRIStAL, F-59000 Lille, France

INSA Hauts-de-France, Valenciennes, France

Keywords:

SbW System, Fault-Tolerant Control, Fault Estimation, Observer, Shared Control, Lane Keeping Systems,

T-S Fuzzy Models, LPV System.

Abstract:

This paper addresses the problem of fault tolerant shared control (FTSC) of Steer-by-Wire (SbW) systems

with actuator fault for driver lane keeping assistance system. The main contribution of this work is to propose

a novel co-design of a robust adaptive simultaneous estimation of system state and actuator faults associated

with an adaptive control law for the stability purposes and also to ensure lane keeping performance even

in faulty situations by limiting the inﬂuence of actuator faults on the vehicle trajectory. An LPV observer

architecture is proposed to estimate the vehicle state and unknown actuator faults considering real-time un-

measurable variations in longitudinal and lateral velocities, represented within a polytope with ﬁnite vertices.

Subsequently, a robust and adaptive state feedback active fault-tolerant controller is proposed using the Takagi-

Sugeno (T-S) approach. An optimization problem is formulated in terms of linear matrix inequalities (LMI)

to guarantee system stability and the asymptotic convergence of state and fault estimation errors. Lyapunov

stability arguments are used to allow more relaxation and additional robustness against immeasurable nonlin-

earities. Hardware validation carried out with the SHERPA dynamic car simulator in real driving situations

demonstrated the performance and the effectiveness of the proposed FTSC scheme.

1 INTRODUCTION

The integration of computers and electronics into

modern vehicles has paved the way for innovations

such as electric vehicles (EVs) equipped with Steer-

by-Wire (SbW) systems. These systems present

unique advantages over traditional mechanical steer-

ing systems by eliminating the mechanical linkage be-

tween the steering wheel and the front wheels. In-

stead, SbW systems use two motors and an electronic

control unit (ECU) to generate feedback torque and

steering angle, coupled with sensors that measure the

driver’s steering input and the front wheel angle. The

ECU processes the electronic signals from these sen-

sors and translates them into mechanical motion (Al-

tby and Majdanzic, 2014). Before the commercial-

ization of SbW systems can proceed, two of the most

pressing issues that must be resolved are maintain-

ing reliability and fault-tolerance capabilities. Sensor

faults in autonomous vehicles can result in a partial or

complete loss of critical information needed to per-

form driving tasks. In contrast, actuator failures can

cause a total loss of vehicle control, leading to inef-

fective or unstable maneuvers with potentially catas-

trophic consequences (Sentouh et al., 2024).

When an actuator motor suddenly fails, it becomes

difﬁcult for the driver to maintain the same steering

behavior as before, potentially causing the vehicle to

deviate from its intended lane. In such situations, the

driver must exert considerable effort to keep the vehi-

cle on course and ensure its stability through manual

steering operations. This research aims to support the

driver’s steering actions and enhance the performance

and fault-tolerance capabilities of the SbW system,

especially during actuator failures. Hence, actuator

faults detection and compensation schemes ensuring

that the system remains operational even when fail-

ures occur, play an important role in achieving the re-

liability of SbW system. In the literature, many stud-

ies have been reported on fault detection and isolation

(FDI), fault diagnosis (FD), and fault-tolerant con-

trol (FTC) to address these concerns (Zinoune et al.,

Boudaoud, M., Sentouh, C., Cappelle, C., El Najjar, M. and Popieul, J.

A New Observer-Based Fault Tolerant Shared Control for SbW Systems with Actuator Fault for Driver Assistance.

DOI: 10.5220/0013069800003822

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 21st International Conference on Informatics in Control, Automation and Robotics (ICINCO 2024) - Volume 1, pages 189-197

ISBN: 978-989-758-717-7; ISSN: 2184-2809

189

2015) (Kommuri et al., 2016) (Xiong et al., 2019)

(Khelladi et al., 2020) (Abbaspour et al., 2020).

Substantial research has been conducted on fault-

tolerant control (FTC) of SbW systems with actuator

or sensor failures. FTC systems can be categorized

into active FTC systems (AFTCS) and passive FTC

systems (PFTCS). Active FTC systems react to fail-

ures through a reconﬁguration mechanism, adapting

the control system based on real-time fault informa-

tion from an FDI scheme. In contrast, passive FTC

systems assume a predeﬁned set of potential malfunc-

tions known a priori and do not require an FDI scheme

or controller reconﬁguration. The goal of a passive

FTC design is to synthesize a single ﬁxed controller

that makes the closed-loop system as insensitive as

possible to these predeﬁned faults. Reliable passive

FTC of an autonomous electric vehicle affected by

front wheel steering actuator faults was proposed in

(Chen et al., 2019) for path following. A robust H

∞

fault-tolerant observer-based PID path tracking con-

trol strategies have been developed to integrate both

actuator and sensor faults as well as control saturation

is proposed in (Chen et al., 2024).

Despite these advances, passive FTC systems of-

ten struggle to achieve optimal performance under

varying fault conditions compared to active FTC sys-

tems. Most work on SbW FTC systems has fo-

cused on active approaches, where FDI plays a vi-

tal role in providing information about faults, en-

abling corresponding actions to eliminate or mini-

mize their effects and maintain overall system per-

formance. FDI aims to monitor the system, identify

faults as they occur, and pinpoint their type and loca-

tion. Two fundamental analytical redundancy-based

approaches for FDI are residual-based FDI and fault

estimation-based FDI. Residual-based FDI methods

generate residuals, the difference between measured

and calculated variables, which have a nominal zero

mean value under normal conditions. Common resid-

ual generation methods for SbW systems include un-

known input observers (dos Santos et al., 2016), slid-

ing mode observers (Anwar and Niu, 2014), Kalman

ﬁlters (Gadda, 2009), and interval observers (Ifqir

et al., 2019). However, residual methods do not pro-

vide direct information about the fault itself. In con-

trast, observer-based fault estimation techniques use

observers to estimate faults directly, providing infor-

mation on their size, severity, and nature. By using

the fault estimation dynamics, the controller can be

designed to compensate for the effect of the fault.

Two stage Kalman ﬁlter is presented in (Huang et al.,

2021) to estimate state and efﬁciency loss factor sim-

ulaniously in the presence of front wheel actuator

fault and based on the fault information the MPC-

based reconﬁgurable controller replaces the old fault-

free model with a new faulty model to maintain ve-

hicle stability and steering tracking performance. In

(Zhao et al., 2020), through the forgetting factor re-

cursive least squares (FFRLS) algorithm, the state

and the partial damage degree of the motor are trans-

ferred to ECU then they propose an individual aux-

iliary and fault-tolerant control considering different

drivers steering characteristics in the case of actua-

tor fault. An interval observer is used to estimate

the actuator fault as though as if it were another (un-

measurable) state of the system in (Lamouchi et al.,

2022). Adaptive fault diagnosis observer (AFDO) ap-

proaches have also gained attention for their ability to

estimate both the state vector and actuator fault vector

simultaneously (Jiang et al., 2006)(Wang and Daley,

1996)(Zhang et al., 2008). A fuzzy fast adaptive fault

estimation (FAFE) algorithm for T-S fuzzy nonlinear

systems is proposed in (Zhang et al., 2009)(Zhang

et al., 2008).

The aforementioned works offer valuable insights

and solutions, primarily focus on the quadratic ap-

proach to study the asymptotic convergence of the

system and the observer separately. However, they

do not address the robust co-design needed to achieve

simultaneously an adaptive fault estimation (FE) and

FTC strategy.

In this paper, we focus on the front wheel subsys-

tem of the SbW system to assist the driver in faulty

situation. The main objective is to utilize the steering

command to reduce the physical steering workload of

the driver during faulty steering actuator situations.

One of the main challenges we address is providing a

natural and a smoother transition mode by offering

fault-tolerant shared control between the controller

and the driver, especially in cases where the actuators

fail. When the steering actuator suddenly fails, it is

difﬁcult for the driver to maintain the steering behav-

ior, which can lead to a vehicle lateral deviation from

its desired lane. The driver then must exert consider-

able effort to keep the vehicle in the lane and ensure

the vehicle stability through steering operations.

Under these conditions of steering motor failure,

the purpose of this work is to propose a novel co-

design to achieve both adaptive fault estimation (FE)

and fault-tolerant control (FTC) strategy. For that, a

robust adaptive observer for simultaneous state and

actuator fault estimation is combined with an adap-

tive feedback control to guarantee the observer-based

fault-tolerant system stability while ensuring the lane

keeping performance by restricting the impact of ac-

tuators’ faults on the vehicle trajectory.

The remainder of the paper is structured as fol-

lows. The vehicle system modeling is given in

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

190

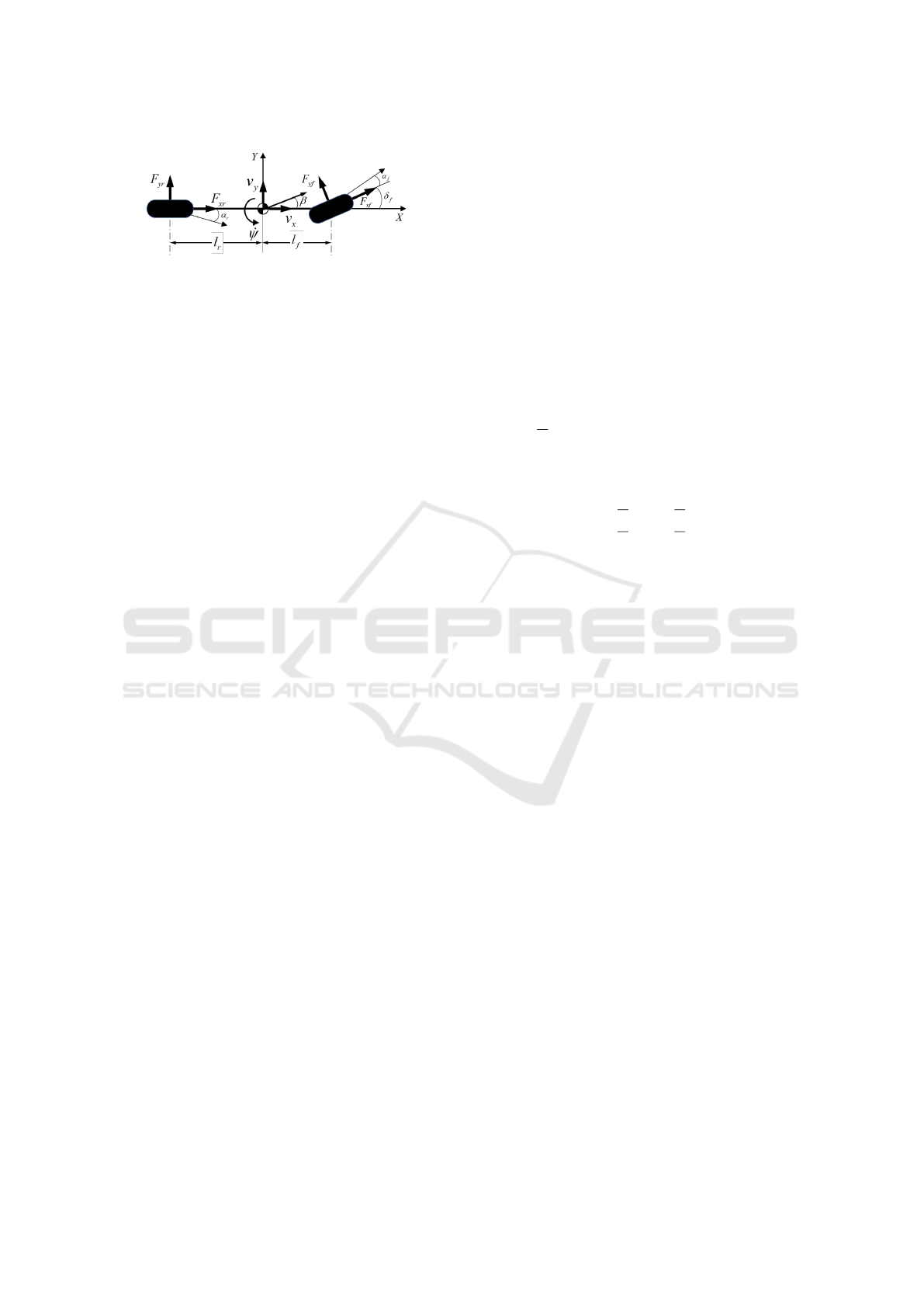
Figure 1: Bicycle model for lateral dynamics.

Sec.2. Sec.3 presents the representation of this model

through the T-S fuzzy model. Then, the adaptive ob-

server design is given in Sec. 4 while Sec.5 presents

the proposed fault-tolerant shared control and the

closed-loop stability. Finally, the experimental vali-

dation are discussed in Ses.6.

2 VEHICLE SYSTEM MODELING

NOMENCLATURE

m Mass of vehicle [kg]

Yaw inertia



kg.m



Lateral and longitudinal velocity [m/s]

y f

Front/rear wheels lateral tire forces [N]

Lateral aerodynamic drag coefﬁcient[Kg/m]

x f

Front wheels longitudinal tire forces [N]

Steering wheel angle [rad]

Crosswinds force [N]

Heading error [rad]

Lateral position error [m]

Road curvature [m

−1

]

Front/rear cornering stiffness [N/rad]

,α

Front/rear side slip angle [rad]

ψ Yaw rate [rad/s]

Distance from COG to front and rear axles [m]

2.1 Lateral Dynamic Model

In this section, we explore the modeling of vehicle

lateral motion by considering the non-linear dynam-

ics of a bicycle model. The vehicle is modeled as a

symmetric single-track bicycle in a ﬁxed frame with

six degrees of freedom (6 DoF). Neglecting roll and

pitch motions, the left and right wheels at each axle

are combined into a single equivalent tire as described

by (Rajamani, 2011) and illustrated in Fig.1. The lat-

eral dynamics of the vehicle, characterized by vari-

ations in lateral speed v

and yaw rate

ψ, are repre-

sented by the following equations:







m ˙v

= F

x f

sin(δ

) + F

y f

cos(δ

) + F

− mv

ψ −C

ψ = l

y f

cos(δ

) − l

+ l

x f

sin(δ

) + l

(1)

2.2 Tire Force Dynamics

Most tire models used in the literature primarily con-

sider a small values of the slip ratio λ and the slip

angle α and maintain the tire behavior within the lin-

ear zone (Rajamani, 2011). Thus, the longitudinal and

lateral forces of the front and rear tires are expressed

as:



f ,r

= C

f ,r

= C

f ,r

(2)

Although this model describes static behavior, the

elastic deformation of tires introduces a transient be-

havior. To account for this transient behavior, some

literature incorporates a ﬁrst-order low-pass ﬁlter dy-

namics (

), as described in (Vantsevich and Gray,

2015) and (Rajamani, 2011) where σ

is the time con-

stant. So, the tire-ground forces are then dynamically

modeled as:

(

f ,r

= −

f ,r

= −

f ,r

(3)

2.3 Lateral Positioning

To ensure effective lane keeping when control is

shared between the driver and the system, it is es-

sential to minimize the lateral position error y

and

the heading error ψ

at a lookahead distance l

. The

dynamics of these two errors are given by (Sentouh

et al., 2018):

ψ − ρ

˙y

= v

+ l

ψ + ψ

(4)

3 T-S FUZZY MODELING OF

VEHICLE DYNAMICS

3.1 Actuator Faults

Actuator faults in the vehicular system can be addi-

tive or multiplicative, as shown in Tab.1. The faulty

control input to the system can be deﬁned as f

(t) =

− ρ

)u(t) for given feedback control u(t). This

fault can be easily rewritten as an external additive

signal (u(t) + f

(t)) where f

(t) = −ρ

u(t).

3.2 T-S Model Formulation in the

Presence of Actuator Faults

Note that the system nonlinearity is caused by the

variation of longitudinal and lateral velocities. These

A New Observer-Based Fault Tolerant Shared Control for SbW Systems with Actuator Fault for Driver Assistance

191

Table 1: Actuator faults.

Fault Kind Conditions Fault Name

Additive if f

constant Bias

(t)+ f

(t) if f

= λ

t, Drift

0 < λ ≪ 1

Multiplicative if ρ

= 1 Totally effective

(t) if ρ

= 0 Totally loss

if 0 < ρ

(t) ≤ 1 Loss of

for all t effectiveness

variations are treated as premise parameters (q = 2)

and transformed into T-S representation by the upper

and lower bounds using the sector nonlinearity con-

cept (Tanaka and Wang, 2004) with r = 2

= 4 sub-

models weighted by membership functions η

(θ). By

assuming a small variation of the steering angle under

normal driving conditions, a continuous LPV road-

vehicle system with actuator faults can be described

from Eq.(1)(3)(4) by the following state-space equa-

tions:



˙x(t) = A(θ)x(t) + B(θ)u(t) + d(θ)w(t) + E(θ) f

(t)

y(t) = Cx(t)

(5)

where x =



ψ F

y f



⊤

the state space vector, u =





⊤

is the control in-

put for the SbW system, y =



ψ a



⊤

the output vector. Whereas w =





⊤

is the

disturbance vector. f

(t) represent the actuator faults.

Since we consider only the steering angle as a control

input then E(θ) = B(θ) and the state space equation

(5) can be written as:



˙x(t) = A(θ)x(t) + B(θ)(u(t) + f

(t)) + d(θ)w(t)

y(t) = Cx(t)

(6)

Note that the system matrices A(θ), B(θ), d(θ)

and E(θ) in (5) explicitly depend on the premise

variables vector θ given as:

θ = {v

, v

}, q = 2 (7)

It is assumed that θ is bounded and also included in a

convex polytopic domain of vertices such that:

Θ = {θ(t) ∈ R

| v

∈ [v

min

, v

max

]; v

∈ [v

min

, v

max

]}

(8)

Where v

min

and v

max

(respectively v

min

and v

max

) are

known lower and upper bounds on longitudinal and

lateral speeds. Considering the time-varying matrices

S ∈ {A, B, d, E} in (5), and using the sector nonlin-

earity approach in (Tanaka and Wang, 2004), we can

derive the following polytopic LPV representation of

model (5) with :

S =

∑

i=0

(θ)S

(9)

Where S

∈ {A

, B

, d

, E

} are constant for all i ∈

[0,...,r]. The variable r = 2

represents the number

of local sub-models, with the q non-linearities related

to θ ∈ Θ captured via membership weighting func-

tions η

(θ). The membership functions adhere to the

convex-sum property within the compact set of the

state space:



∑

i=0

(θ) = 1,

∑

i=0

(θ) = 0, η

∈ [0 1]

∀i = {1, 2,..., r}

(10)

4 ADAPTIVE LPV-TS OBSERVER

FOR STATE AND FAULT

ESTIMATION

In this section, we are interested to propose an adap-

tive LPV-TS observer to estimate the system state and

detect the actuator fault at the same time. For this

purpose, the following assumptions must be veriﬁed

Assumption 1. The triples (A,B,C) are controllable

and observable to guarantee the LMI solution.

Assumption 2. The matching condition for the faults

hold

rank(CB

) = rank(B

) (11)

Assumption 3. The faults f

(t) are assumed to be a

time varying signal, and have a norm-bounded ﬁrst-

time derivative.

∥

(t) ∥≤ f

max

, 0 ≤ f

max

≤ ∞

(12)

Motivated by the adaptive observer proposed in

(Zhang et al., 2009) and (Sentouh et al., 2024), an

adaptive Luenberger nonlinear observer for a vehi-

cle equipped with SbW system considering actuator

faults (5) is proposed as:











ˆx(t) = A(θ) ˆx(t) + B(θ)(u(t) +

(t)) + d(θ)w(t)

+ L( ˆy(t) − y(t))

ˆy(t) = C ˆx(t)

(t) = ΓH(˙e

− σe

)

(13)

Where ˆx ∈ R

is the observer state vector, ˆy ∈ R

is the observer output vector, L ∈ R

n×m

and H ∈ R

f ×m

are the observer gain matrices, and

f ∈ R

is the esti-

mated fault vector which depends on the output error

vector e

and its derivative. Note that the observer’s

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

192

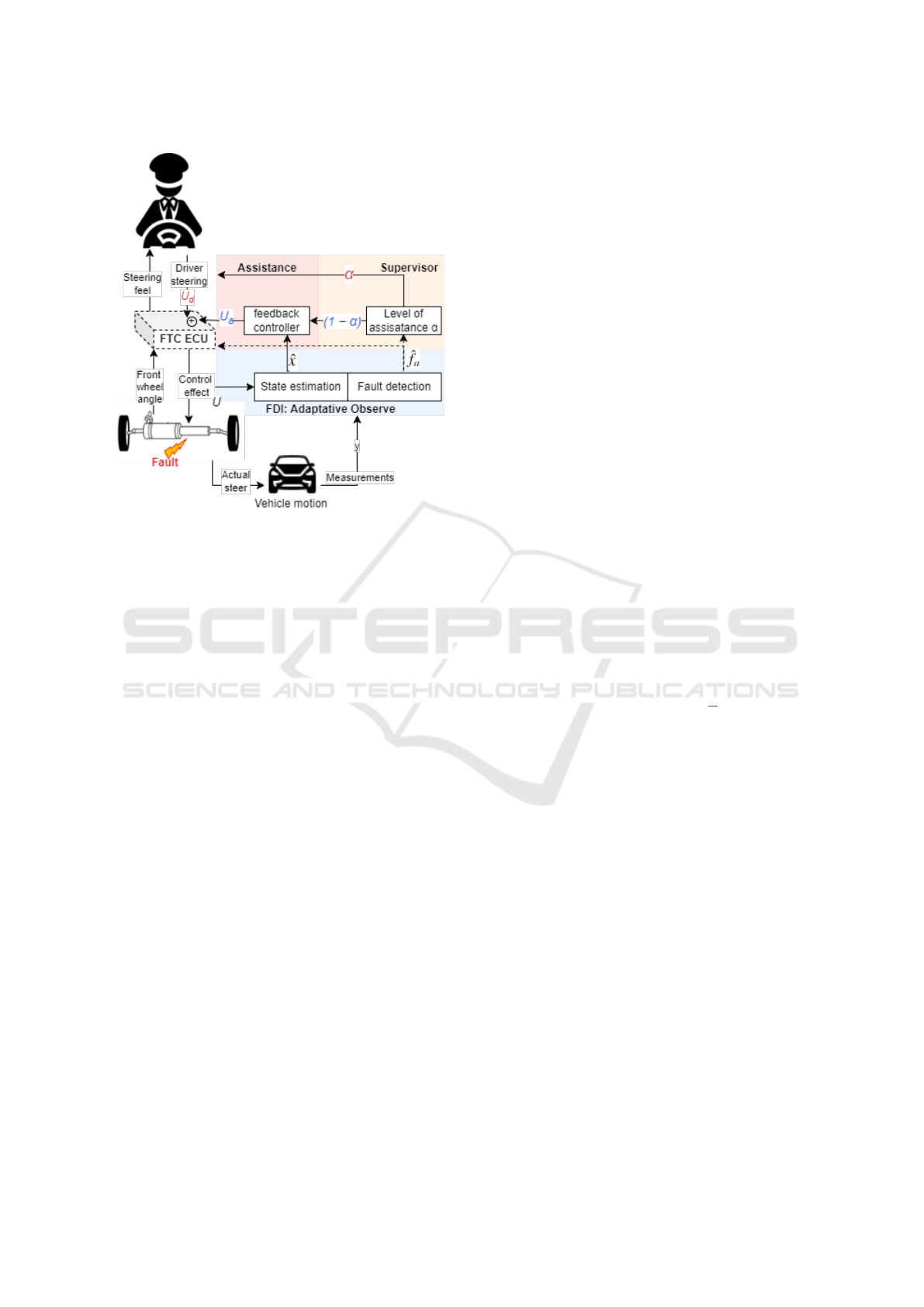
Figure 2: Driver assistance in SbW system with actuator

fault.

matrices L and H are parameter varying with the same

LPV form (9) and given by:

L =

∑

i=0

(θ)L

, H =

∑

i=0

(θ)H

(14)

This adaptive fault estimation algorithm can guar-

antee lim

t→∞

(t) = 0 and lim

t→∞

(t) = 0 where e

is the state estimation error and e

is the fault esti-

mation error, Γ ∈ R

f × f

is the learning rate and σ is a

tuning parameter.

5 FTC SHARED CONTROL FOR

ACUATOR FAULT

COMPENSATION

In this work, the objective is to compute a new shared

control law u(t) in order to compensate the effect of

the actuators’ faults and minimize the driver physical

steering workload as shown in the architecture Fig. 2.

for that, the FTC shared controller is given by:

u = αu

+ (1 − α)u

−

(15)

Where u

is the driver steering angle and u

is the

feedback controller given by:

= −K ˆx (16)

Where the controller gain k is parameter varying with

the same LPV form (9) and given by

K =

∑

i=0

(θ)K

(17)

The purpose of the feedback controller u

is to as-

sist the driver in keeping the vehicle on the lane, espe-

cially when the actuator fails. To take into account the

lane-keeping performance, we deﬁne the performance

output of system (6) as:

y =



ψ a



⊤

(18)

We deﬁne the following cost function:

J =

∞

⊤

Qy + u

⊤

dt (19)

Where Q and R are two symmetric positive def-

inite matrices and are referred as the weighting ma-

trices. The automatic system can takes over the con-

trol of the vehicle (α = 0) when the actuator becomes

faulty. The SbW control reconﬁgures the fault toler-

ant controller for a good steering performance.

In the following, we present the robust co-design

conditions of adaptive fault estimation and FTSC

strategy expressed as an LMIs optimization problem.

The design process is based on a Lyapunov function,

which takes into account both the observer and the

system stability, as well as the lane keeping perfor-

mance and robustness against actuator faults and dis-

turbances. Considering the following polytopic Lya-

punov function deﬁned by:

V (t) = x

⊤

(t)Px(t) + e

⊤

(t)P

(t) +

⊤

(t)Γ

−1

(t)

(20)

Where P ∈ R

n×n

and P

∈ R

n×n

are symmetric positive

deﬁnite matrices.

In order to stabilize the vehicle system (6), as well

as the observer (13) and to guarantee an upper-bound

for the cost function (19) under zero-initial condition

we apply the following condition:

V (t) + x

⊤

(t)Qx(t) + u

⊤

(t)Ru(t) ≤ γ f

⊤

+ γw

⊤

(21)

Where

V (t) is the time-derivative of the Lyapunov

function (20) along the trajectory of (6).

Lemma 1. For every positive deﬁnite matrix G > 0

the following property holds (Fouka et al., 2021)

⊤

−1

≤ e

⊤

G +

−1

(22)

Using successively Schur complement lemma

(Boyd et al., 1994) and Lemma.1 with X = P

−1

M = KX and N = P

L it follows that we can obtain

the LMI optimization problem after some algebraic

A New Observer-Based Fault Tolerant Shared Control for SbW Systems with Actuator Fault for Driver Assistance

193







(AX −BM) X

⊤

0 B D 0 0 I

⊤

∗ −Q

−1

0 0 0 0 0 0 0 0

∗ ∗ −R

−1

0 0 0 0 0 0 0

∗ ∗ ∗ H

A − NC) −

⊤

B −C

⊤

B − P

B) 0 P

D P

0 0

∗ ∗ ∗ ∗

G 0

−B

⊤

−B

⊤

0 0

∗ ∗ ∗ ∗ ∗ −γ 0 0 0 0

∗ ∗ ∗ ∗ ∗ ∗ −εI

0 0 0

∗ ∗ ∗ ∗ ∗ ∗ ∗ −εI

0 0

∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ −εI

∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ −γ + R







< 0

(23)

manipulations as shown in the matrix at the top of

the next page (see Equation 23), with I

∈ R

n×n

and

∈ R

ω×ω

are identity matrix. γ, ε are positive scalars,

and the operator H

(A) = A

⊤

A . When the above con-

dition hold, the observer gain matrix is given by:

L = P

−1

N (24)

And the controller gain matrix is given by:

K = MX

−1

(25)

On the other hand, if the assumption rank(CB) =

rank(B) holds, it is possible to obtain matrices H such

that (see (Corless and Tu, 1998)):

HC = B

⊤

(26)

The control and observer co-design conditions ex-

pressed in terms of LMIs (23) are solved with

YALMIP toolbox and SeDuMi solver (Lofberg,

2004).

6 EXPERIMENTAL VALIDATION

The experimental validation involves the implemen-

tation in a SHERPA-LAMIH road vehicle dynamic

simulator as shown in Fig.3. Note that in this work,

the steering wheel feedback motor is controlled by a

PD regulator of the tracking error between the actual

steering wheel angle and front wheel angle to provide

the driver with the true feeling of the steering effort.

In this section, we explain our main results

through two use cases. The ﬁrst one (Fig. 4 and Fig.

5), the human driver takes over the control authority

and undergoes a lane-keeping maneuver. During this

maneuver, time-varying fault signals for the steering

are generated to represent a varying degree of efﬁ-

ciency loss in the actuator, as discussed in Section

3.1. These fault signals simulate real-world scenar-

ios where the steering system might not operate opti-

mally due to various reasons. Figure 4 illustrates the

observer performance, showing that the proposed ob-

server provides an accurate estimation of both the sys-

tem states and actuator faults accurately. This demon-

strates the robustness and reliability of the proposed

fault estimation approach.

The performance of the actuator fault compensa-

tion system are depicted in Figure 5, where the ve-

hicle dynamics behavior with and without the fault

compensation are compared to that of the normal driv-

ing condition (without faults). This ﬁgure highlights

the effectiveness of our compensation strategy in min-

imizing the impact of actuator faults during manual

driving. However, even though a driver can manipu-

late the steering wheel angle and correct the deviation

path through the compensation of the steering wheel

angle, he/she does not have a good understanding of

the driving situation and can deviate from the desired

lane.

In the second use case, we are interested by the

purpose of further assisting the steering behavior of

the driver especially during an actuator faults. Figures

6 and 7 show the main results of the FTC shared con-

trol. We performed a test by injecting an actuator fault

at time t = 30s as shown in Fig. 6. When the fault is

detected, the control is shared between the driver and

the system. Hence, driver authority decreases, and the

need for assistance increases by activating the weight-

ing decision parameter α for shared control to guar-

antee a smooth control transition between the driver

and the lane keeping assist system. We can observe

from Fig. 7 the good performance of the proposed

fault-tolerant shared control to maintain a lower vehi-

cle lateral deviation after the appearance of the actu-

ator fault. After activating the driving assistance dur-

ing the actuator fault compensation, the lateral posi-

tion error becomes smaller compared to the manual

driving mode with actuator fault compensation, en-

suring that the vehicle maintains its desired trajectory

and stability more efﬁciently even in the presence of

faults. The observed results clearly indicate that our

fault compensation mechanism can effectively restore

the vehicle’s positioning performance as the nominal

driving situation, thereby enhancing safety and relia-

bility.

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

194

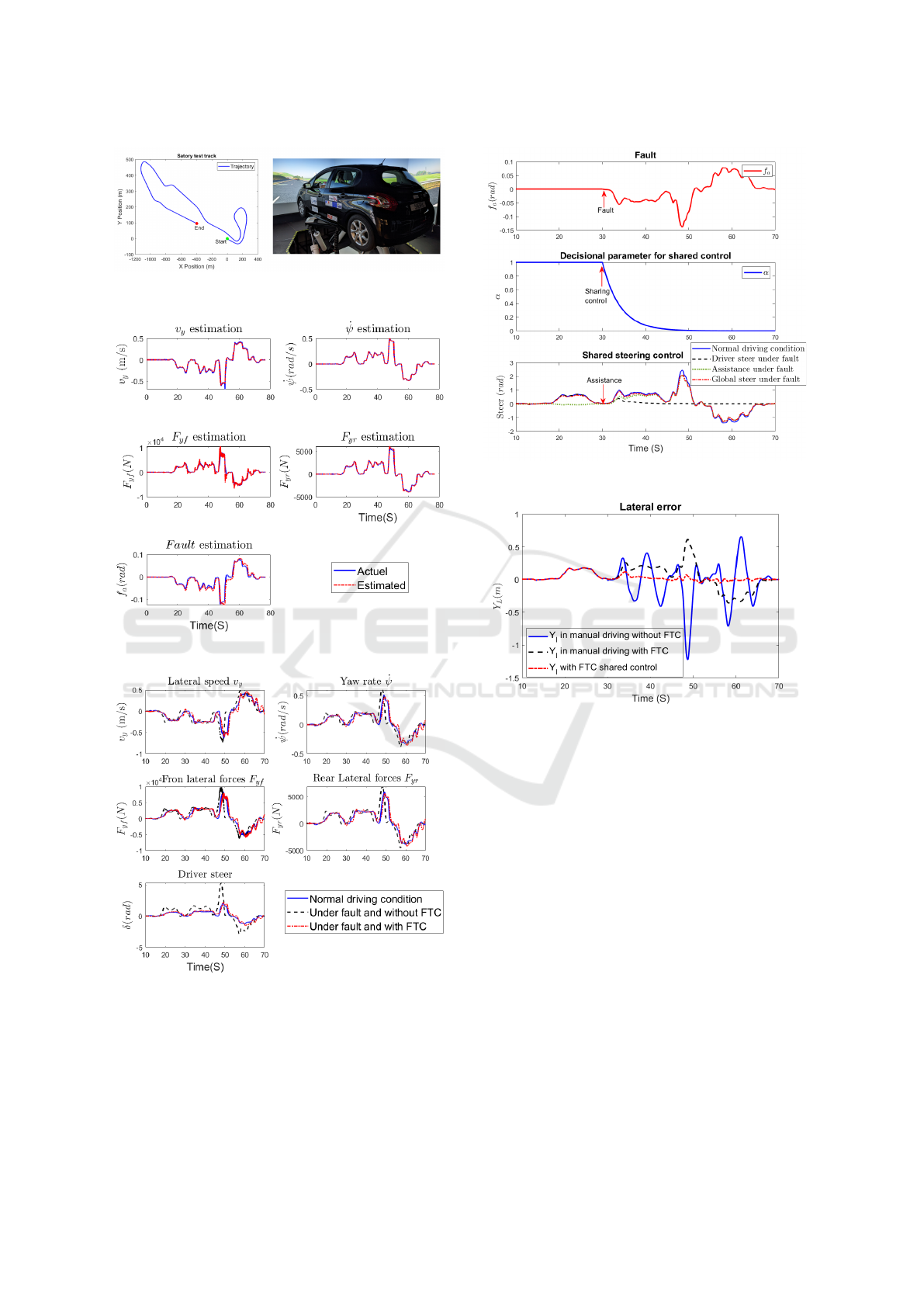
Figure 3: SHERPA dynamic driving simulator on the Satoty

test.

Figure 4: Observer performance: state and fault estimation.

Figure 5: FTC performance: Actuator Fault Compensation

in manual driving.

7 CONCLUSIONS

This paper proposed a new co-design of the observer-

based fault-tolerant shared control strategy of Steer-

Figure 6: FTC shared control.

Figure 7: FTC shared control performance: lateral error in

manual and assistance driving during actuator fault.

by-Wire (SbW) systems with actuator fault for driver

lane keeping assistance system. An LPV observer ar-

chitecture was proposed to estimate simultaneously

the vehicle state and unknown actuator faults con-

sidering real-time unmeasurable variations in longi-

tudinal and lateral velocities based on T-S represen-

tation with polytopic approach. Based on the Lya-

punov stability arguments, the system stability and

the asymptotic convergence of state and fault estima-

tion errors has been proved. The control and observer

co-design conditions have been obtained through an

optimization problem which is formulated in terms of

linear matrix inequalities (LMI). Experimental valida-

tion was performed using the LAMIH-SHERPA dy-

namic car simulator in real driving situations. The

experimental results showed that the LPV observer

provides an accurate estimation of both the vehicle

state and actuator faults. On the other hand, the fault-

tolerant controller effectively minimizes the impact of

such faults, where the shared control mechanism al-

A New Observer-Based Fault Tolerant Shared Control for SbW Systems with Actuator Fault for Driver Assistance

195

lows to guarantee a smooth control transition between

the driver and the lane keeping assist system, which

enhance safety and system reliability. The obtained

results demonstrated the performance and the effec-

tiveness of the proposed FTSC strategy.

8 FUTURE WORK

In this work, we addressed the issue of loss of actuator

effectiveness as a fault. Our control system strategy is

effective in cases of additive or multiplicative faults

with a loss of actuator efﬁciency of up to 90%. How-

ever, we did not consider scenarios where the nature

of the fault changes or there is a total loss of the actu-

ator. Investigating these scenarios will be the focus of

our future work.

REFERENCES

Abbaspour, A., Mokhtari, S., Sargolzaei, A., and Yen, K. K.

(2020). A survey on active fault-tolerant control sys-

tems. Electronics, 9(9):1513.

Altby, A. and Majdanzic, D. (2014). Design and implemen-

tation of a fault-tolerant drive-by-wire system.

Anwar, S. and Niu, W. (2014). A nonlinear observer based

analytical redundancy for predictive fault tolerant con-

trol of a steer-by-wire system. Asian Journal of Con-

trol, 16(2):321–334.

Boyd, S., El Ghaoui, L., Feron, E., and Balakrishnan, V.

(1994). Linear matrix inequalities in system and con-

trol theory. SIAM.

Chen, B.-S., Liu, H.-T., and Wu, R.-S. (2024). Robust $

h \infty $ fault-tolerant observer-based pid path track-

ing control of autonomous ground vehicle with control

saturation. IEEE Open Journal of Vehicular Technol-

ogy.

Chen, T., Chen, L., Xu, X., Cai, Y., Jiang, H., and Sun, X.

(2019). Passive fault-tolerant path following control

of autonomous distributed drive electric vehicle con-

sidering steering system fault. Mechanical Systems

and Signal Processing, 123:298–315.

Corless, M. and Tu, J. (1998). State and input estimation for

a class of uncertain systems. Automatica, 34(6):757–

764.

dos Santos, B., Lopes, A., and Ara

ujo, R. E. (2016). Fault

detection scheme for a road vehicle with four indepen-

dent single-wheel electric motors and steer-by-wire

system. In Advanced Vehicle Control, pages 417–422.

CRC Press.

Fouka, M., Nehaoua, L., and Arioui, H. (2021). Motorcy-

cle state estimation and tire cornering stiffness identi-

ﬁcation applied to road safety: Using observer-based

identiﬁers. IEEE Transactions on Intelligent Trans-

portation Systems, 23(7):7017–7027.

Gadda, C. D. (2009). Optimal fault-detection ﬁlter design

for steer-by-wire vehicles. Stanford University.

Huang, C., Huang, H., Naghdy, F., Du, H., and Ma,

D. (2021). Actuator fault tolerant control for steer-

by-wire systems. International Journal of Control,

94(11):3123–3134.

Ifqir, S., Dalil, I., Na

ıma, A.-O., and Sa

ıd, M. (2019). Adap-

tive threshold generation for vehicle fault detection

using switched t–s interval observers. IEEE Trans-

actions on Industrial Electronics, 67(6):5030–5040.

Jiang, B., Staroswiecki, M., and Cocquempot, V. (2006).

Fault accommodation for nonlinear dynamic sys-

tems. IEEE Transactions on automatic Control,

51(9):1578–1583.

Khelladi, F., Boudali, M., Orjuela, R., Cassaro, M., Bas-

set, M., and Roos, C. (2020). An emergency hierar-

chical guidance control strategy for autonomous vehi-

cles. IEEE Transactions on Intelligent Transportation

Systems, 23(5):4319–4330.

Kommuri, S. K., Defoort, M., Karimi, H. R., and Veluvolu,

K. C. (2016). A robust observer-based sensor fault-

tolerant control for pmsm in electric vehicles. IEEE

Transactions on Industrial Electronics, 63(12):7671–

7681.

Lamouchi, R., Raissi, T., Amairi, M., and Aoun, M. (2022).

On interval observer design for active fault tolerant

control of linear parameter-varying systems. Systems

& Control Letters, 164:105218.

Lofberg, J. (2004). Yalmip: A toolbox for modeling and op-

timization in matlab. In 2004 IEEE international con-

ference on robotics and automation (IEEE Cat. No.

04CH37508), pages 284–289. IEEE.

Rajamani, R. (2011). Vehicle dynamics and control.

Springer Science & Business Media.

Sentouh, C., Fouka, M., Rath, J. J., and Popieul, J.-C.

(2024). Adaptive observer-based output feedback ftc

for nonlinear interconnected vehicle dynamics with

unknown actuator faults. IEEE Transactions on In-

telligent Vehicles, pages 1–11.

Sentouh, C., Nguyen, A.-T., Benloucif, M. A., and Popieul,

J.-C. (2018). Driver-automation cooperation oriented

approach for shared control of lane keeping assist sys-

tems. IEEE Transactions on Control Systems Technol-

ogy, 27(5):1962–1978.

Tanaka, K. and Wang, H. O. (2004). Fuzzy control sys-

tems design and analysis: a linear matrix inequality

approach. John Wiley & Sons.

Vantsevich, V. V. and Gray, J. P. (2015). Relaxation length

review and time constant analysis for agile tire dy-

namics control. In International design engineering

technical conferences and computers and informa-

tion in engineering conference, volume 57106, page

V003T01A038. American Society of Mechanical En-

gineers.

Wang, H. and Daley, S. (1996). Actuator fault diagnosis: an

adaptive observer-based technique. IEEE transactions

on Automatic Control, 41(7):1073–1078.

Xiong, J., Cheong, J. W., Xiong, Z., Dempster, A. G., Tian,

S., and Wang, R. (2019). Integrity for multi-sensor

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

196

cooperative positioning. IEEE Transactions on Intel-

ligent Transportation Systems, 22(2):792–807.

Zhang, K., Jiang, B., and Cocquempot, V. (2008). Adap-

tive observer-based fast fault estimation. Interna-

tional Journal of Control, Automation, and Systems,

6(3):320–326.

Zhang, K., Jiang, B., and Shi, P. (2009). A new approach

to observer-based fault-tolerant controller design for

takagi-sugeno fuzzy systems with state delay. Cir-

cuits, Systems & Signal Processing, 28(5):679–697.

Zhao, W., Wang, A., Zou, S., and Zhang, H. (2020). In-

dividual auxiliary and fault-tolerant control of steer-

by-wire system considering different drivers steering

characteristics. IEEE/ASME Transactions on Mecha-

tronics, 26(3):1558–1569.

Zinoune, C., Bonnifait, P., and Iba

nez-Guzm

an, J. (2015).

Sequential fdia for autonomous integrity monitor-

ing of navigation maps on board vehicles. IEEE

Transactions on Intelligent Transportation Systems,

17(1):143–155.

A New Observer-Based Fault Tolerant Shared Control for SbW Systems with Actuator Fault for Driver Assistance

197