End-to-End Steering for Autonomous Vehicles via Conditional Imitation

Co-Learning

Mahmoud M. Kishky

, Hesham M. Eraqi

2,∗

and Khaled M. F. Elsayed

Faculty of Engineering, Cairo University, Egypt

Amazon, Last Mile, U.S.A.

Keywords:

Autonomous Driving, End-to-End, Conditional Imitation Learning, Co-Learning Matrix, Co-Existence

Probability Matrix, Steering Model, CARLA.

Abstract:

Autonomous driving involves complex tasks such as data fusion, object and lane detection, behavior predic-

tion, and path planning. As opposed to the modular approach which dedicates individual subsystems to tackle

each of those tasks, the end-to-end approach treats the problem as a single learnable task using deep neural net-

works, reducing system complexity and minimizing dependency on heuristics. Conditional imitation learning

(CIL) trains the end-to-end model to mimic a human expert considering the navigational commands guiding

the vehicle to reach its destination, CIL adopts specialist network branches dedicated to learn the driving task

for each navigational command. Nevertheless, the CIL model lacked generalization when deployed to unseen

environments. This work introduces the conditional imitation co-learning (CIC) approach to address this is-

sue by enabling the model to learn the relationships between CIL specialist branches via a co-learning matrix

generated by gated hyperbolic tangent units (GTUs). Additionally, we propose posing the steering regression

problem as classiﬁcation, we use a classiﬁcation-regression hybrid loss to bridge the gap between regression

and classiﬁcation, we also propose using co-existence probability to consider the spatial tendency between the

steering classes. Our model is demonstrated to improve autonomous driving success rate in unseen environ-

ment by 62% on average compared to the CIL method.

1 INTRODUCTION

An autonomous system is capable of understanding

the surrounding environment and operating indepen-

dently without any human intervention (Bekey, 2005),

in the context of autonomous vehicles, the objective is

to mimic the behaviour of a human driver. To mimic

a human driver’s behaviour, the system is expected to

take actions similar to those taken by a human driver

in the same situation, the driver’s action can be de-

ﬁned as a set of vehicle’s controls such as steering,

throttle, brake and gear.

Autonomous driving systems can follow ei-

ther the modular approach, or the end-to-end ap-

proach(Yurtsever et al., 2019). In the modular ap-

proach, the system’s pipeline is split into several com-

ponents, each component has its own subtask, then

the information provided by each component is com-

bined to help the system understand the surround-

ing environment (Dammen, 2019) so the system can

eventually generate different actions. On the other

hand, the end-to-end approach replaces the entire task

∗

This work was conducted prior to Hesham M. Eraqi

joining Amazon.

of autonomous driving with a neural network, where

the network is fed observations (the inputs from the

different sensors) and produces the predicted actions

(steering, throttle, brake, gear), the objective is to

train the network to learn the mapping between the

observations and the actions.

The end-to-end approach was ﬁrst introduced in

(Bojarski et al., 2016), a convolutional neural net-

work (CNN) was trained to map the raw pixels from

a front-facing camera directly to steering commands.

Later, the end-to-end approach was adopted widely

in research such as in (Prakash et al., 2021), (Cui

et al., 2022), (Codevilla et al., 2018), (Hawke et al.,

2019),(Liang et al., 2018) and (Eraqi et al., 2022)

due to the simplicity of the process of development

and deployment. Also, the model is free learn any

implicit sources of information and the researcher

is only concerned with developing a network that

receives the raw data and delivers the ﬁnal output

(Dammen, 2019), unlike the modular approach, there

are no human-deﬁned information bottlenecks (Tam-

puu et al., 2020).

(Codevilla et al., 2018) proposed using a branched

network architecture as shown in Figure 1, where the

Kishky, M., Eraqi, H. and Elsayed, K.

End-to-End Steering for Autonomous Vehicles via Conditional Imitation Co-Learning.

DOI: 10.5220/0013069900003837

In Proceedings of the 16th International Joint Conference on Computational Intelligence (IJCCI 2024), pages 629-636

ISBN: 978-989-758-721-4; ISSN: 2184-3236

629

network is fed the navigational commands (go left,

go right, go straight, follow lane) from a route plan-

ner representing the driver’s intention, each special-

ist branch is dedicated to learn the mapping between

the observations and the vehicle’s actions indepen-

dently. At test time, the navigational command acts

as a switch to select the ﬁnal action taken by the net-

work. The major issue with the proposed model by

(Codevilla et al., 2018) was its lack of generalization

and the poor performance when deployed to unseen

environment.

In this work, we propose two contributions to

improve the CIL end-to-end steering. In the ﬁrst

contribution, we introduce the conditional imitation

co-learning (CIC) approach which involves modify-

ing the CIL network architecture in (Codevilla et al.,

2018). (Codevilla et al., 2018) assumed total inde-

pendence between the specialist branches while train-

ing, each branch was only trained on a subset of the

training scenarios, for instance, the specialist branch

dedicated to learn the right turns was only exposed

to right turns scenarios during training. If the train-

ing data was not big enough to cover all the scenar-

ios for all the branches, it could lead to unbalanced

learning, which means that the model may perform

properly in right turns and perform poorly in left turns

or vice verse (Dammen, 2019). We claim that one

branch can make use of the features extracted by an-

other. So, a branch dedicated to learn right turns can

learn from observations collected in left turns and vice

verse which enhances the model’s generalization and

increases its robustness in unseen environments.

The second contribution is posing regression

problem as classiﬁcation, posing regression prob-

lem as deep classiﬁcation problem was introduced in

(Rothe et al., 2015), classiﬁcation showed improve-

ment in age prediction from a single image compared

to regression. In our work, we adopt posing regres-

sion problem as classiﬁcation as introduced in (Rothe

et al., 2015), the classes were obtained by steering

discretization. However, using this approach assume

full independence between the steering classes ignor-

ing their spatial tendency. So, we propose two im-

provements to the classiﬁcation approach, the ﬁrst

improvement uses a combination of the categorical

cross-entropy and the mean squared error losses to

bridge the gap between classiﬁcation and regression.

The second improvement proposes considering

the spatial relationship between the steering classes

at the output layer using co-existence probability ma-

trix, we claim that considering the spatial relationship

between the classes will help to improve the overall

performance of the model since the network will tend

to predict the spatially close classes together.

2 RELATED WORK

2.1 Conditional Imitation Learning

End-to-end Imitation learning aims to train the model

to mimic an expert, the model with parameters w is

fed a set of observations and actions (o, a) pairs ob-

tained from the expert. The model is optimized to

learn the mapping function between the observations

and actions F(o, w). In the context of autonomous

driving, the observations are the data collected from

different sensors (Cameras, Radars, LiDARs, ..), the

actions are the vehicles controls such as steering,

throttle and brake. The model is trained to mimic the

actions taken by the expert to perform the task of au-

tonomous driving.

The problem with the imitation learning approach

is that the same observation could lead to different

actions, based on the intention of the expert. Hence,

the model cannot be trained to ﬁnd a mapping func-

tion between the observations and the actions since

it contradicts with the mathematical deﬁnition of the

function itself, a function f : O → A shall only map

observation instance o to a single action a. In other

words, the driver’s intention must be taken into con-

sideration to make it mathematically possible to have

a mapping function between the observations and the

actions. So, at time step i, the predicted action be-

comes a function of the driver’s intention h

as well

as the observation a

= F(o

, h

), the network uses

the navigational command c

at intersections coming

from a route planner to represent the driver’s inten-

tion.

(Codevilla et al., 2018) proposed conditional

imitation learning (CIL) approach by adopting a

branched architecture as shown in Figure 1. After the

feature extraction phase, the model is split into spe-

cialist branches each branch is dedicated to learn the

mapping function between the observations and the

actions given the navigational command (go left, go

right, go straight, follow lane). Hence, the network

produces the predicted action F at time step t given

navigational command c

F(o

, c

) = A

)

where A

is the predicted action by the specialist

branch dedicated for command c

, which means that

at testing, the navigational command is used as a

switch to select the proper action to be taken by the

model.

2.2 Regression as Classiﬁcation

In (Rothe et al., 2015), the regression problem of age

prediction from images was posed as classiﬁcation,

NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications

630

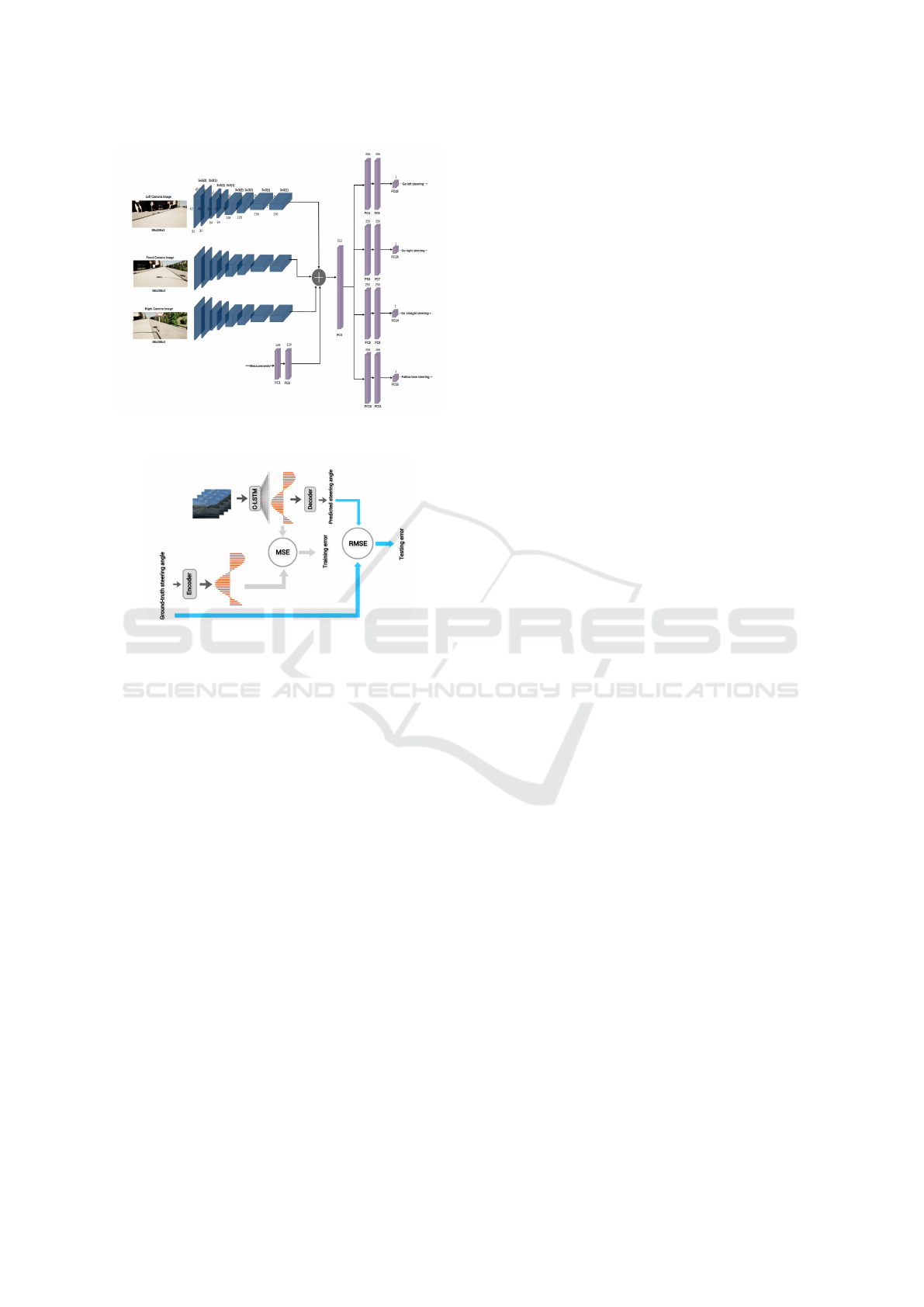
Figure 1: Network Architecture proposed by (Codevilla

et al., 2018).

Figure 2: Training and deployment paths in the work in (Er-

aqi et al., 2017).

the continuous age value was discretized to obtain the

classiﬁcation labels. Considering only the age val-

ues from 0 to 100, the network was trained to predict

the true age of the human face in the input image.

(Eraqi et al., 2017) followed the same approach to

solve autonomous vehicle steering problem. Inspired

by (Moustafa, 2005) and (Rothe et al., 2015), (Eraqi

et al., 2017) proposed posing steering angle prediction

for autonomous vehicles regression problem as clas-

siﬁcation, the model was trained and validated using

comma.ai dataset (Rasmus et al., 2016). (Eraqi et al.,

2017) also proposed considering the spatial relation-

ship between the steering angle classes using arbitrary

function encoding, the encoding function was chosen

to be a sine wave and the steering angle to be its phase

shift. According to (Eraqi et al., 2017), this choice of

sinusoidal encoding led to gradual change in the val-

ues of the activations at the output layer. As shown

in Figure 2, least squares error regression was used

to optimize the model to generate a predicted wave-

form similar to the actual one from the steering angle

encoding.

The motive behind the need to consider the spatial

relationship between the steering classes is the fact

that the crossentropy loss only penalizes the model if

the input is mislabeled neglecting all the scores corre-

sponding to the other labels, which means that in case

of mislabeling, the network will be penalized with

the same amount no matter how big the difference

between the predicted steering angle and the ground

truth steering angle is. Since classiﬁcation is only

used to mimic regression, it is important to insure that

the model still gives predictions close to the actual

steering even in case of mislabeling.

3 METHODOLOGY

3.1 Data Collection

The dataset was collected with the help of CARLA

simulator (Dosovitskiy et al., 2017), CARLA pro-

vides a set of pre-built maps vary in size and complex-

ity called towns as well as predeﬁned weather con-

ditions to facilitate the development of autonomous

driving systems. In our work, we adopted the same

three camera model proposed in (Codevilla et al.,

2018). Thus, three cameras were attached (front cam-

era, right camera, left camera) to the ego-vehicle with

resolution 200 x 88 pixels each. During data collec-

tion, we relied on CARLA simulator’s autopilot fea-

ture, this feature allows the ego-vehicle to follow the

lane and take random turns (left, right, straight) at in-

tersections based on the navigational commands com-

ing from the ego-vehicle’s navigation agent, we ran

100 data collection episodes with the vehicle on au-

topilot mode with episode predeﬁned period of ten

minutes.

Besides the cameras’ captures, we recorded the

vehicle’s steering and measurements (location and ro-

tation) as well as the navigational commands from the

ego-vehicle’s navigation agent, the data was collected

in Town01 with ClearNoon and ClearSunset weather

conditions and sampled every 0.1 second, the camera

captures were passed thought a randomized sequence

of augmentation methods such as additive Gaussian

noise, change of brightness and image cropping. As

mentioned in (Codevilla et al., 2018), noise was in-

jected into the steering during data collection, the in-

jected noise simulates the ego-vehicle’s drifting and

recovery to provide the network with examples of re-

covery from disturbances and allow the model to re-

cover after making wrong predictions during testing.

Although simulation environments fail to capture

the real world complexities, it provides a fast and safe

way to develop and test autonomous driving mod-

els, Sim-to-Real is also a way to bridge the gap be-

tween simulation and real-world data by transferring

End-to-End Steering for Autonomous Vehicles via Conditional Imitation Co-Learning

631

the learned policies from simulated data into the phys-

ical world (Bewley et al., 2019), (Muller et al., 2018).

3.2 Specialist Branches Co-Learning

As discussed in Sec.I, the CIL model introduced

in (Codevilla et al., 2018) assumed independence

between the specialist branches, each branch was

trained on a subset of the training data to learn the

mapping between the observations and actions given

the navigational command coming form the route

planner, the problem with this assumption is that it

might lead to unbalanced learning, the dataset might

contain enough scenarios for some branches to ﬁt a

mapping function and does not for the others. In our

work, we propose considering dependencies between

the specialist branches which allows the branches to

co-learn by sharing their extracted features with each

other.

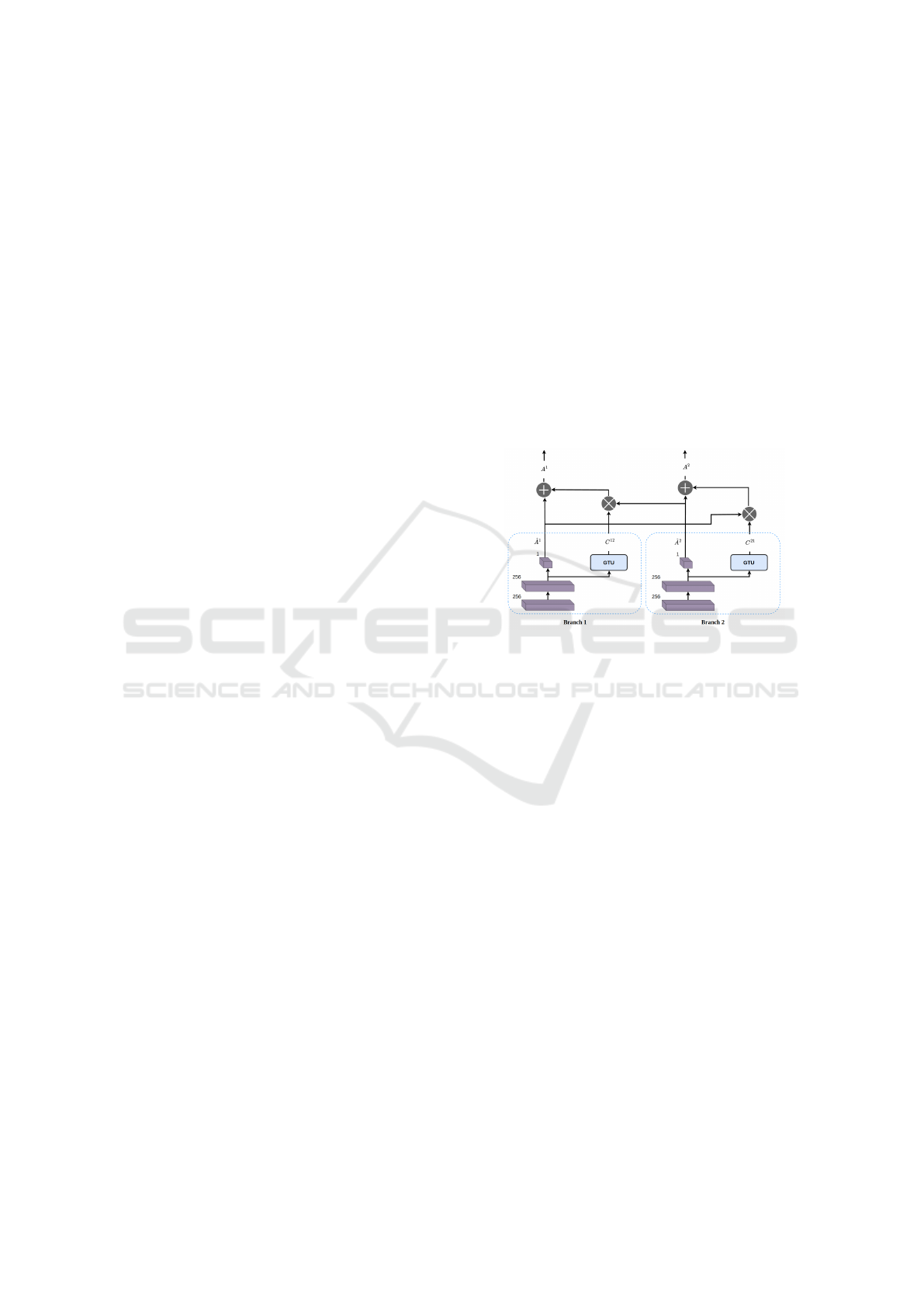
As shown in Figure 3, assuming we have an N x 1

vector

representing the extracted features from the

specialist branches at any time stamp t, where N in

the number of specialist branches, given an N x N co-

learning matrix C

, for action prediction, we propose

the following formula:

= C

(1)

For four breaches dedicated for the navigational com-

mands (go left, go right, go straight, follow lane) to

which we will refer as l, r, s, f respectively:







1 c

l f

1 c

r f

1 c

s f

f l

f r

f s













+ c

l f

+ c

r f

+ c

s f

+ c

f l

+ c

f r

+ c

f s







, each matrix coefﬁcient c

i j

represents the the re-

lationship between the extracted features

and

coming from branches i and j respectively.

In our work, we explored two approaches to gen-

erate co-learning coefﬁcients. In the ﬁrst approach,

we break down the co-learning matrix as follows:

= R · E

(2)

where R is a hyperparameter binary matrix indicat-

ing the presence or absence of relationships between

the specialist branches, the relationship matrix R is

ﬁne tuned and set manually before training. To pro-

duce matrix E, we added a dedicated neural network

to generate the co-learning coefﬁcients corresponding

to each branch, we chose tanh activation at the output

layer to allow the co-learning matrix coefﬁcients to

vary between -1 and 1, the ﬁnal predictions are then

produced using Equation 1 as shown in Figure 3.

The second approach involves generating the co-

learning coefﬁcients directly from gated tanh units

(GTUs) (Dauphin et al., 2017) allowing the net-

work to implicitly learn the relationship matrix R.

Gated units provide more control to the generated

co-learning coefﬁcients, the network is able to dy-

namically turn on/off the connections between the

branches based on the driving scenario. The idea of

the CIC approach can be extended to other applica-

tions especially those relying on foundational mod-

els, allowing the modules performing related tasks to

share useful information.

Figure 3: Co-learning between branch 1 and branch 2.

Other approaches addressed the improvement of

multi-task learning (MTL) performance, such as mix-

ture of experts (MoEs) (Jacobs et al., 1991), soft pa-

rameter sharing, cross-stitch networks (Misra et al.,

2016) and sluice networks (Ruder et al., 2019). MoEs

involves adding a gated mixture of experts layer be-

fore splitting the network into specialist branches, al-

lowing the branches to dynamically learn from a com-

bination of experts instead of single shared network,

each expert learns its own features from the input,

then a gating network is used to decide which experts

will be activated.

On the other hand, soft parameter sharing allows

each task to have its own branch with its own param-

eters, then the model is regularized by L2 distance

to encourage the parameters to be similar instead of

learning from a shared network (hard parameter shar-

ing). Unlike mixture of experts and soft parameter

sharing approaches, (Misra et al., 2016) and (Ruder

et al., 2019) allow parameter sharing between special-

ist branches via learnable parameters.

(Misra et al., 2016) introduced using cross-stitch

units to learn the linear combinations of the activa-

tions coming from the different tasks at each layer

of the network. In contrast, (Ruder et al., 2019) fo-

NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications

632

cused on determining which features should be shared

between loosely coupled tasks, the hidden layers are

split into two orthogonal subspaces, one for shared

features and the other for task-speciﬁc features, the

network learns to dynamically decide which features

to be shared via learnable parameters.

As opposed to other MTL approaches, our CIC

model is output-oriented, we focus on learning the re-

lationships between the outputs. In addition, we study

the presence or absence of these relationships using

GTUs, rather than trying to learn the relationships be-

tween hidden layer parameters. Our approach is moti-

vated by the nature of our driving problem, where the

overlapping between the branches’ subsets is minimal

and occurs only in a few speciﬁc driving scenarios,

which reduces the network ability to learn the map-

ping between the parameters in the hidden layers and

makes it less effective.

3.3 Classiﬁcation-Regression Hybrid

Loss

(Kourbane and Genc, 2021) proposed splitting the

process of object pose prediction into two stages,

coarse and reﬁnement. The coarse stage involves a

rough prediction of the pose using classiﬁcation fol-

lowed by offset prediction using regression, the net-

work was spilt into two modules after feature extrac-

tion, one module for pose classiﬁcation and the other

for offset estimation. Given that the network had two

types of outputs (softmax scores and offsets), (Kour-

bane and Genc, 2021) optimized the network using

a combination of cross-entropy loss for classiﬁcation

and Huber loss (Huber, 1992) for regression.

In our work, we adopt a similar approach to

(Kourbane and Genc, 2021), for fair comparison be-

tween classiﬁcation and regression, we only convert

the regression output layer to a softmax layer rather

than having two types of outputs in (Kourbane and

Genc, 2021). To bridge the gap between classiﬁcation

and regression, we used a combination of categorical

cross-entropy (CCE) and mean squared error (MSE)

losses for model optimization, the CCE loss imposes

high penalty to the model is case of mislabeling al-

lowing the network to produce coarse estimations to

the steering, then MSE loss tunes the output activa-

tions for more accurate predictions.

Given O Nx1 the softmax output scores, y the true

continuous steering, y Nx1 the one hot representation

of the discretized steering, m Nx1 steering midpoints

corresponding to each class, N is the number of steer-

ing classes and the hyperparameter W .

l = −

∑

i=1

log(O

) +W (y − ˆy)

(3)

where

ˆy = E(O) =

∑

i=1

3.4 Co-Existence Probability Based

Loss

Inspired by (Rothe et al., 2015) and (Eraqi et al.,

2017), this work poses vehicle steering regression

problem as classiﬁcation considering the spatial re-

lationship between the steering classes. As illustrated

in Sec.I, it’s important to insure that the model gives

desirable predictions even in the case of mislabel-

ing. Unlike (Eraqi et al., 2017), we used co-existence

probability matrix instead of sine wave encoding to

represent this relationship, using co-existence proba-

bility matrix was introduced in (Bengio et al., 2013) to

improve multi-class image categorization, this work

used the same concept to force the scores at the output

layer to follow a desired distribution which represents

the spatial relationship between the discrete steering

classes.

The co-existence probability matrix was used in

(Bengio et al., 2013) to represent the statistical ten-

dency of visual object to co-exist in images. In our

steering problem, the objective of forcing the model

to learn the output distribution is to make sure that in

the case of misprediction, the model is always able to

make acceptable predictions allowing the vehicle to

recover from disturbances.

The co-existence probability matrix µ is an N x N

matrix, where N is the number of classes, the element

i j

represents the co-existence probability between la-

bels i and j, given that the output scores O ∈ R

and

µ ∈ R

NXN

, the model shall try to ﬁnd the output vector

O that minimizes the following cost function accord-

ing to (Bengio et al., 2013):

l = −(1 − W )

∑

i=1

log(O

) − W O

µO (4)

the ﬁrst term is the crossentropy loss, the second term

describes how much the output scores vector O fol-

lows the desired distribution deﬁned by µ, and W is

a hyperparameter between 0 and 1 describing how

much we care about forcing the desired distribution.

Thus, the value O

shall be pulled up or pulled down

by O

based on how high or low the value µ

i, j

is (Ben-

gio et al., 2013), the advantage of this approach is the

ﬂexibility it provides to the researcher to deﬁne the

distribution most ﬁtted for each class. In this work,

we use Gaussian distribution with σ

= 1.

End-to-End Steering for Autonomous Vehicles via Conditional Imitation Co-Learning

633

Figure 4: Spatial relationship between the steering classes.

4 TRAINING AND EXPERIMENT

We split the dataset into training and validation sets,

70% of the dataset for training and the remaining

30% for validation, the models were trained using

Adam optimizer (Kingma and Ba, 2014) with β

0.70, β

= 0.85 and learning rate of 0.0002, we

used mini-batches of 120 samples each, the mini-

batches contained equal number of samples corre-

sponding to each navigational command, the models

were trained on the dataset collected as illustrated in

Sec.III. The steering values coming from the dataset

samples ranges between -1 and 1, where -1 means a

full turn to left and 1 means a full turn to the right,

the actual value of steering depends on the vehicle

used (Dosovitskiy et al., 2017). While training, the

samples with steering between -0.8 and 0.8 were only

considered. For classiﬁcation models, we discretized

the steering to 9 classes with 0.2 discreteization step.

The models were tested using CARLA simula-

tor, we adopted a modiﬁed CoRL 2017 benchmark

(Dosovitskiy et al., 2017) where we considered only

single turn task for performance evaluation, the task

of the ego-vehicle is to successfully navigate from a

start point and reach a destination point given pre-

deﬁned navigational commands forcing the vehicle

to perform one single turn on its way. The vehicle

was tested in in Town01 (training town) and Town02

(new town), in four different weather conditions, two

training conditions (ClearNoon and ClearSunset) and

two new conditions (midRainyNoon and wetCloudy-

Sunset), the new town and weather conditions are

fully unseen to the steering models during training.

We deﬁned 38 pairs of start and destination points in

Town01 and 40 pairs in Town02 associated with pre-

deﬁned navigational commands to cover all the inter-

sections in both towns, which gives us 312 testing sce-

narios. On testing, we got the shown results in Tables

I, II, III and IV.

Table 1: Driving Reach Destination Success Rate for Co-

learning Model.

Model

Reach destination success rate

Training town New town

Training weathers New weathers Training weathers New weathers

Regression (CIL) 94.74 86.84 52.50 46.25

GTU 100.00 93.42 81.25 75.00

Fine Tuning 97.37 92.11 78.75 78.75

Table 2: Driving Reach Destination Success Rate for

Classiﬁcation-Regression Hybrid Loss.

Model

Reach destination success rate

Training town New town

Training weathers New weathers Training weathers New weathers

Classiﬁcation 72.37 43.42 41.25 32.50

W = 5 71.05 67.11 42.50 41.25

W = 10 97.37 85.53 64.25 56.25

W = 15 86.84 50.52 50.00 41.25

Table 3: Driving Reach Destination Success Rate for Clas-

siﬁcation with Co-existence Probability Based Loss Model.

Model

Reach destination success rate

Training town New town

Training weathers New weathers Training weathers New weathers

Classiﬁcation 72.37 43.42 41.25 32.50

W = 0.4 71.05 65.79 45.00 36.25

W = 0.6 76.32 68.42 63.75 48.75

W = 0.8 69.74 61.84 50.00 41.25

Table 4: Driving Reach Destination Success Rate (All Mod-

els).

Model

Reach destination success rate

Training town New town

Training weathers New weathers Training weathers New weathers

Regression (CIL) 94.74 86.84 52.50 46.25

Co-learning (GTU) 100.00 93.42 81.25 75.00

Parameter soft sharing 96.05 84.21 67.50 60.00

Mixutre of experts 97.37 81.58 72.50 67.50

Sluice network 100.00 89.47 70.00 61.25

Classiﬁcation 72.37 43.42 41.25 32.50

Co-existence based loss 76.32 68.42 63.75 48.75

CCE + MSE 97.37 85.53 64.25 56.25

Sine wave encoding 97.37 86.84 57.50 48.75

As discussed in Sec.II, the CIL model (Codevilla

et al., 2018) lacked generalization when tested in un-

seen environments. On the other hand, our proposed

CIC model tackled this issue, we could see improve-

ment in the reach destination success rate in unseen

environment (unseen town, unseen weather) by 62%.

Classiﬁcation model failed to improve the CIL perfor-

mance which conforms to the results in (Rothe et al.,

2015) where classiﬁcation could only outperform re-

gression for some datasets. Using the hybrid loss

in Equation 3 showed 21% improvement compared

NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications

634

to the CIL model. Nevertheless, the co-existence

based loss in Equation 4 only showed improvement

compared to the basic classiﬁcation model but failed

to outperform the CIL regression model. MTL ap-

proaches such as MoEs (Jacobs et al., 1991), soft

parameter sharing and sluice networks (Ruder et al.,

2019) showed improvement to the CIL model espe-

cially in new town, but failed to outperform our CIC

model while stitch network (Misra et al., 2016) failed

to learn the driving task, sine wave encoding (Eraqi

et al., 2017) also showed slight improvement com-

pared to the CIL model.

5 CONCLUSION

In this work, we propose two contributions to the end-

to-end steering problem tackled by the conditional

imitation learning (CIL) model, the CIL model suf-

fered from lack of generalization and poor perfor-

mance when tested in unseen environment, the ﬁrst

contribution of this work is conditional imitation co-

learning (CIC), the introduced approach proposes a

modiﬁed network architecture that allows the special-

ist branches in the CIL model to co-learn to overcome

the generalization issue and increase the model’s ro-

bustness in unseen environment, the other contribu-

tion is posing the steering regression problem as clas-

siﬁcation by using a combination of CCE and MSE

losses. The CIC model showed a signiﬁcant improve-

ment to performance in unseen environment by 62%

while posing regression as classiﬁcation showed only

improvement by 21%.

REFERENCES

Bekey, G. A. (2005). Autonomous robots: from biological

inspiration to implementation and control. The MIT

Press.

Bengio, S., Dean, J., Erhan, D., Ie, E., Le, Q., Rabinovich,

A., Shlens, J., and Singer, Y. (2013). Using web co-

occurrence statistics for improving image categoriza-

tion. ArXiv preprint, arXiv:1312.5697.

Bewley, A., Rigley, J., Liu, Y., Hawke, J., Shen, R., Lam,

V.-D., and Kendall, A. (2019). Learning to drive from

simulation without real world labels. In 2019 In-

ternational Conference on Robotics and Automation

(ICRA), pages 4817–4823. IEEE.

Bojarski, M., Testa, D. D., Dworakowski, D., Firner,

B., Flepp, B., Goyal, P., Jackel, L. D., Monfort,

M., Muller, U., Zhang, J., et al. (2016). End to

end learning for self-driving cars. arXiv preprint,

arXiv:1604.07316.

Codevilla, F., Miiller, M., Lopez, A., Koltun, V., and Doso-

vitskiy, A. (2018). End-to-end driving via conditional

imitation learning. In Proceedings of the 2018 IEEE

International Conference on Robotics and Automation

(ICRA), pages 1–9.

Cui, J., Qiu, H., Chen, D., Stone, P., and Zhu, Y. (2022).

Coopernaut: End-to-end driving with cooperative per-

ception for networked vehicles. In Proceedings of the

IEEE/CVF Conference on Computer Vision and Pat-

tern Recognition (CVPR), pages 17252–17262.

Dammen, J. (2019). End-to-end deep learning for au-

tonomous driving. Master’s thesis, Norwegian Uni-

versity of Science and Technology.

Dauphin, Y. N., Fan, A., Auli, M., and Grangier, D.

(2017). Language modeling with gated convolutional

networks. In Proceedings of the 34th International

Conference on Machine Learning (ICML), pages 933–

941. PMLR.

Dosovitskiy, A., Ros, G., Codevilla, F., L

opez, A., and

Koltun, V. (2017). Carla: An open urban driving sim-

ulator. In Proceedings of the Conference on Robot

Learning (CoRL).

Eraqi, H., Moustafa, M., and Honer, J. (2017). End-

to-end deep learning for steering autonomous ve-

hicles considering temporal dependencies. CoRR,

abs/1710.03804.

Eraqi, H. M., Moustafa, M. N., and Honer, J. (2022). Dy-

namic conditional imitation learning for autonomous

driving. IEEE Transactions on Intelligent Transporta-

tion Systems.

Hawke, J., Shen, R., Gurau, C., Sharma, S., Reda, D.,

Nikolov, N., Mazur, P., Micklethwaite, S., Grif-

ﬁths, N., Shah, A., et al. (2019). Urban driving

with conditional imitation learning. arXiv preprint,

arXiv:1912.00177.

Huber, P. J. (1992). Robust estimation of a location param-

eter. In Breakthroughs in statistics, pages 492–518.

Springer, New York.

Jacobs, R. A., Jordan, M. I., Nowlan, S. J., and Hinton, G. E.

(1991). Adaptive mixtures of local experts. Neural

Computation, 3(1):79–87.

Kingma, D. and Ba, J. (2014). Adam: A method

for stochastic optimization. arXiv preprint,

arXiv:1412.6980.

Kourbane, I. and Genc, Y. (2021). A hybrid classiﬁcation-

regression approach for 3d hand pose estimation us-

ing graph convolutional networks. arXiv preprint,

arXiv:2105.10902.

Liang, X., Wang, T., Yang, L., and Xing, E. (2018).

Cirl: Controllable imitative reinforcement learning for

vision-based self-driving. In Proceedings of the Euro-

pean Conference on Computer Vision (ECCV), pages

584–599.

Misra, I., Shrivastava, A., Gupta, A., and Hebert, M. (2016).

Cross-stitch networks for multi-task learning. In Pro-

ceedings of the IEEE Conference on Computer Vision

and Pattern Recognition (CVPR), pages 3994–4003.

Moustafa, M. N. (2005). System and method for pose-angle

estimation.

Muller, M., Dosovitskiy, A., Ghanem, B., and Koltun, V.

(2018). Driving policy transfer via modularity and ab-

End-to-End Steering for Autonomous Vehicles via Conditional Imitation Co-Learning

635

straction. In Conference on Robot Learning (CoRL),

pages 1–14.

Prakash, A., Chitta, K., and Geiger, A. (2021). Multimodal

fusion transformer for end-to-end autonomous driv-

ing. In Proceedings of the Conference on Computer

Vision and Pattern Recognition (CVPR).

Rasmus, A., Valpola, H., Honkala, M., Berglund, M.,

Raiko, T., Santana, E., and Hotz, G. (2016). Learn-

ing a driving simulator. CoRR.

Rothe, R., Timofte, R., and Gool, L. V. (2015). Dex: Deep

expectation of apparent age from a single image. In

Proceedings of the IEEE International Conference on

Computer Vision Workshops (ICCV), pages 10–15.

Ruder, S., Bingel, J., Augenstein, I., and Søgaard, A.

(2019). Latent multi-task architecture learning. Pro-

ceedings of the AAAI Conference on Artiﬁcial Intelli-

gence, 33(01):4822–4829.

Tampuu, A., Matiisen, T., Semikin, M., Fishman, D., and

Muhammad, N. (2020). A survey of end-to-end driv-

ing: Architectures and training methods. IEEE Trans-

actions on Neural Networks and Learning Systems.

Yurtsever, E., Lambert, J., Carballo, A., and Takeda, K.

(2019). A survey of autonomous driving: Common

practices and emerging technologies. arXiv preprint,

arXiv:1906.05113.

NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications

636