SPACED: A Novel Deep Learning Method for Community Detection in
Social Networks
Mohammed Tirichine
1 a
, Nassim Ameur
1 b
, Younes Boukacem
1 c
, Hatem M. Abdelmoumen
1 d
,
Hodhaifa Benouaklil
1 e
, Samy Ghebache
1
, Boualem Hamroune
1
, Malika Bessedik
1,2 f
,
Fatima Benbouzid-Si Tayeb
1,2 g
and Riyadh Baghdadi
3 h
1
Ecole Nationale Sup
´
erieure d’Informatique (ESI), BP 68M - 16270 Oued Smar, Algiers, Algeria
2
Laboratoire des M
´
ethodes de Conception de Syst
`
emes (LMCS), Algeria
3
New York University Abu Dhabi, Abu Dhabi, U.A.E.
{km tirichine, kn ameur, ky boukacem, kh abdelmoumen, kh benouaklil, ks ghebache, kb hamroune, m bessedik,
Keywords:
Social Network, Community Detection, Node Embedding, Community Embedding, Deep Learning.
Abstract:
Community detection is a landmark problem in social network analysis. To address this challenge, we pro-
pose SPACED: Spaced Positional Autoencoder for Community Embedding Detection, a deep learning-based
approach designed to effectively tackle the complexities of community detection in social networks. SPACED
generates neighborhood-aware embeddings of network nodes using an autoencoder architecture. These em-
beddings are then refined through a mixed learning strategy with generated community centers, making them
more community-aware. This approach helps unravel network communities through an appropriate cluster-
ing strategy. Experimental evaluations across synthetic and real-world networks, as well as comparisons with
state-of-the-art methods, demonstrate the high competitiveness and often superiority of SPACED for commu-
nity detection while maintaining reasonable time complexities.
1 INTRODUCTION
Social networks, connecting vast numbers of indi-
viduals and entities, have become pivotal in shaping
communication, information dissemination, and so-
cial interactions, making the study of their structures
and dynamics increasingly crucial. One of the most
important social structures that characterizes these
networks is their community structure. Although a
formal definition of a community in network analy-
sis does not exist, a widely accepted definition de-
scribes a community as a subset of social agents, typ-
ically represented as graph nodes, between which in-
teractions, typically represented as graph edges, oc-
cur more ”densely” than with the rest of the net-
a
https://orcid.org/0009-0003-9205-6158
b
https://orcid.org/0009-0009-1120-6286
c
https://orcid.org/0009-0001-5896-3227
d
https://orcid.org/0009-0006-1459-2723
e
https://orcid.org/0009-0002-1239-2606
f
https://orcid.org/0000-0002-1007-9096
g
https://orcid.org/0000-0001-7032-8544
h
https://orcid.org/0000-0002-9350-3998
work. This dense intra-community connectivity in-
dicates that members within the community are more
closely related or interact more frequently with each
other than with nodes outside the community. As a re-
sult, such clusters naturally form identifiable groups,
known as communities, within the network structure
(Figure 1). It immediately appears from this defini-
tion that discovering communities inside a network,
which is commonly referred to as the community de-
tection problem, has important applications such as
targeted advertising, functional group identification,
or even terrorist threat prevention (Karatas¸ and S¸ahin,
2018).
The last decades have witnessed an increase in the
use of machine learning (ML) and deep learning (DL)
based methods to tackle this problem due to their abil-
ity to handle efficiently high dimensional data spaces
such as graphs and uncover intricate patterns on them
such as community structures. One of the mainstream
approaches in the class of DL methods is to embed the
graph nodes into a vectorial space in such a way as to
reflect their community proximities, i.e. nodes more
likely to be in the same community according to the
Tirichine, M., Ameur, N., Boukacem, Y., Abdelmoumen, H., Benouaklil, H., Ghebache, S., Hamroune, B., Bessedik, M., Tayeb, F. and Baghdadi, R.
SPACED: A Novel Deep Learning Method for Community Detection in Social Networks.
DOI: 10.5220/0013070100003825
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 20th International Conference on Web Information Systems and Technologies (WEBIST 2024), pages 141-152
ISBN: 978-989-758-718-4; ISSN: 2184-3252
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
141

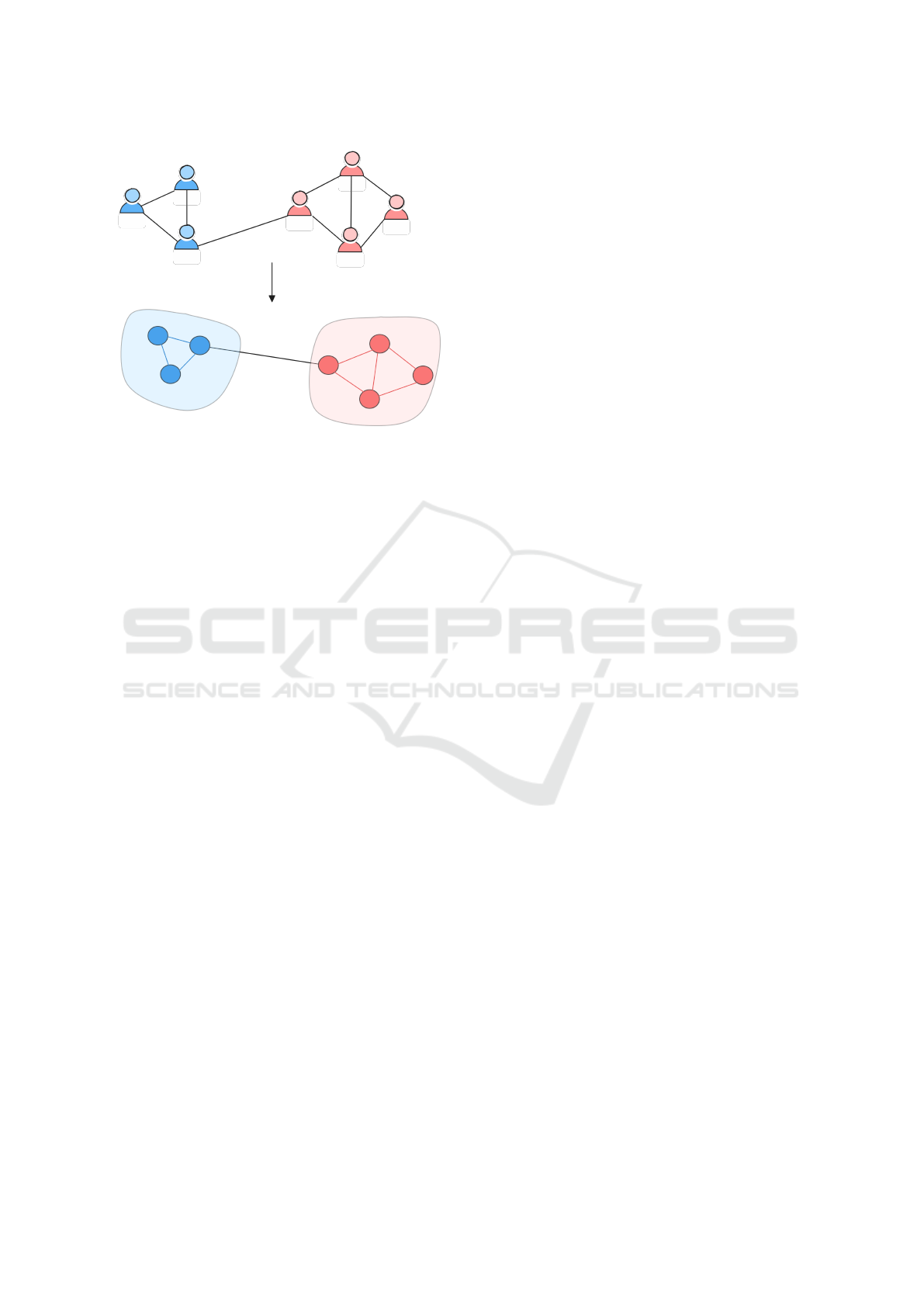
Figure 1: An undirected graph representation of a social
network used for community detection.
network data are associated with nearby embeddings
in the vectorial space, thus transforming the commu-
nity detection problem on the network into a cluster-
ing problem on the vectorial space representation.
Aligning with this class of methods, in this pa-
per, we propose SPACED, a model that aims at gen-
erating meaningful node embeddings and community
centers that uncover the community structure of so-
cial networks based solely on their topologies, i.e. the
undirected connections between the network agents.
It performs this by generating initial encodings of
the nodes based on their neighbourhoods, embedding
them using an auto-encoder architecture and generat-
ing initial community centre embeddings which will
help improve the node embeddings.
The rest of this paper is organized as follows. Sec-
tion 2 presents the related works outlining the differ-
ent sources that SPACED inspires from. Then, section
3 details the proposed solution. Section 4 presents the
obtained results on the selected benchmarks and their
significance. Lastly, section 5 concludes the paper,
summarizing our findings and suggesting directions
for future research.
2 RELATED WORKS
Various sequence-based node embedding techniques
such as Line (Tang et al., 2015), Node2Vec (Grover
and Leskovec, 2016) or DeepWalk (Perozzi et al.,
2014) base their construction of node embeddings on
the ”proximity” of the nodes inferred by their co-
occurrence on various sampling methods on the net-
work such as truncated random walks, second-order
random walks etc., reflecting on the idea that nodes
of the same community are more likely to appear
simultaneously in small sub-regions of the network.
The embeddings generated by this class of techniques
have been applied for community detection with com-
petitive results as shown in (Tandon et al., 2021).
Also, the SkipGram model (Mikolov et al., 2013)
which inspired some of the methods in this class have
in the same way motivated parts of SPACED archite-
cure.
Using auto-encoders in community detection has
gained significant attention recently. Reference(Xie
et al., 2019) introduced CDDTA, which employs
a deep auto-encoder for nonlinear feature extrac-
tion in networks and incorporates unsupervised trans-
fer learning to refine representations. Reference
(Tian et al., 2014) proposed the GraphEncoder
method, which uses graph neural networks alongside
auto-encoders to encode structural information into
low-dimensional embeddings, preserving topological
properties and enhancing clustering accuracy in large-
scale networks. Reference (Bhatia and Rani, 2019)
proposed DeCom, which integrates modularity-based
community detection with ensemble clustering, com-
bining multiple clustering results into a consensus so-
lution to enhance robustness and stability in commu-
nity detection.
For the works that consider performing node em-
bedding in conjunction with community embedding
with the goal to create better community aware node
embeddings, (Rozemberczki et al., 2019) proposed
GEMSEC, which aims to mutually enhance both node
and community embedding processes. GEMSEC em-
ploys sequence-based node embedding techniques,
where nodes occurring closely in random walks are
embedded close to each other. The optimization ob-
jective combines the negative log-likelihood of ob-
served neighbourhood samples with a clustering cost
and is solved using a variant of mini-batch gradient
descent. Another line of work in this category are
comE (Cavallari et al., 2017) and its improved ver-
sion comeE+ (Cavallari et al., 2019) which automat-
ically detects the number of communities. They con-
sider that community embeddings should reflect the
member nodes distribution in the feature space and
thus propose embedding the communities as probabil-
ity distributions by fitting them to a Gaussian mixture
model. The results obtained by comE/comE+ proved
the benefit of considering community-aware proxim-
ities in the embeddings construction process.
WEBIST 2024 - 20th International Conference on Web Information Systems and Technologies
142

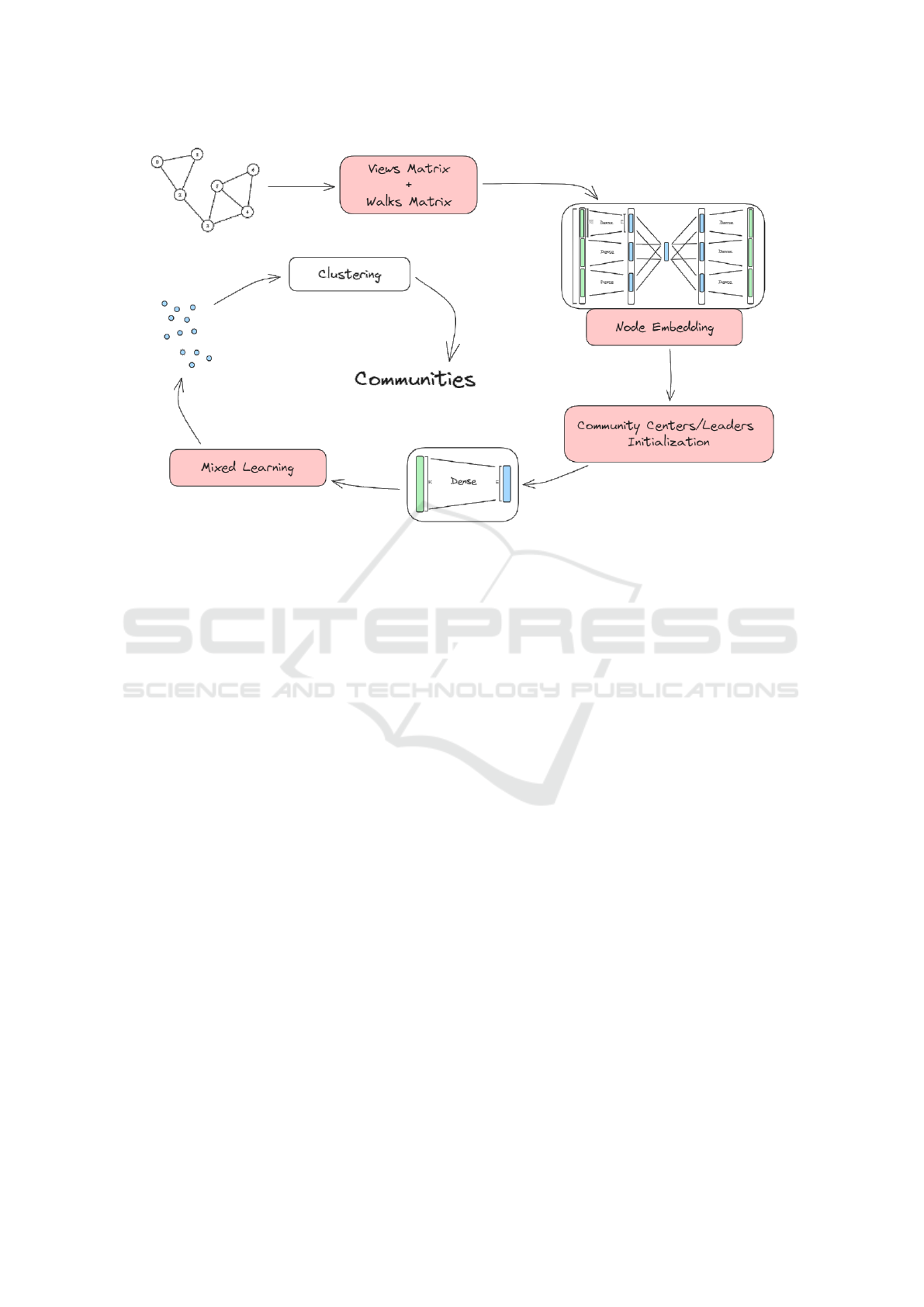
Figure 2: SPACED general architecture.
3 PROPOSED SOLVING
APPROACH
A social network can be modelled by a graph G =
(V,E) where V is the set of nodes representing in-
dividuals and E is the set of edges indicating inter-
actions between individuals. The goal is to find the
community structure within this graph which is a par-
tition C = {C
1
,C
2
,. . . ,C
K
} of K communities on the
node set V .
As stated in the introduction, our method attempts
to solve this problem by finding a node embedding
that better represents the community structure. A
node embedding is a mapping f : V → R
e
of nodes to
an embedding space of dimension e. A successful em-
bedding can then turn the problem into a straightfor-
ward point cloud clustering. The SPACED approach
follows a four-phase pipeline to achieve this as shown
in figure 2:
• Phase 1. Graph Processing to generate initial
high-dimensional encodings for graph nodes.
• Phase 2. Node embedding to obtain an initial
low-dimensional node embedding using an au-
toencoder architecture.
• Phase 3. Community centers/leaders initializa-
tion aiming to create embeddings for community
centers/leaders, in the same space as the nodes,
positioning them at the best possible position in-
side the point cloud formed by the node embed-
ding.
• Phase 4. Mixed learning where the model si-
multaneously improves node embedding while
bringing them and the community centers/leaders
closer to each other, thus, producing a more
community-aware node embedding with more
condensed clusters eventually (Rozemberczki
et al., 2019).
The following sections will thoroughly explore these
phases, along with their different variants.
3.1 Graph Processing
The first problem encountered in all community de-
tection methods is how to read the graph and explore
its topological structure most optimally, here we tried
to use a data structure that can better represent the
neighbourhood levels of a node while emphasizing
the differences between these levels. So, in this pa-
per, we propose two data structures called the Views
Matrix and Walks Matrix.
3.1.1 Views Matrix
To produce this structure, the graph is seen as a
Markov chain model, where each node is a state and
the probability of moving from a node to one of its
neighbours is uniform between all neighbours N(i)
(since the graph is unweighted). So, P is an N × N
SPACED: A Novel Deep Learning Method for Community Detection in Social Networks
143

matrix (Eq. 1) representing the probability of moving
from node i to node j.
P
i j
=
(
1
|N(i)|
if j ∈ N(i)
0 otherwise
(1)
So the matrix P can represent first-order proxim-
ity in a probabilistic format. To obtain other levels
of neighbourhood we can easily use the property of
Markov chains where P
2
represents the probability of
going from node i to j in two steps and so on. So, for
a max depth d and for all k ∈ [1, d] we would obtain:
P
(k)
= P
k
(2)
But you can notice here that the return probabil-
ity is always considered, for this we propose another
variant where we use this formula instead:
P
(k)
i j
=





0 if k = −1 or (k = 0 and i ̸= j) or P
(k−2)
i j
̸= 0
1 if k = 0 and i = j
(P
(k−1)
× P)
i j
otherwise
(3)
Now, we need to differentiate between the differ-
ent levels of neighborhood, so we add some weights
to each level matrix P
(k)
. We use two approaches:
(1) Arithmetic approach where we weighted the lev-
els by subtracting one for each level {d − 0, d − 1, ...,
d −(d −1)}; (2) Harmonic approach where we divide
by an incrementing number each level {
d
1
,
d
2
, ...,
d
d
}.
Finally these resulting matrices P
(k)
are concate-
nated along their columns resulting in a |V |×(d ∗|V|)
matrix as follows:
M =

P
(1)
w
1
P
(2)
w
2
·· · P
(d)
w
d

(4)
3.1.2 The Walks Matrix
In an attempt to imitate random walks without per-
forming them, we exploited the already constructed
views matrix by combining them with a weighted
mean using the same weights used earlier. This cre-
ates for each node i a distribution resembling the por-
tion of a node appearance in different random walks
of varying lengths started from the node i, which cre-
ates some sort of context around each node.
W =
∑
d
k=1
P
(k)
w
k
∑
d
k=1
w
k
(5)
3.2 Node Embedding
We proposed an autoencoder architecture that tries to
lower each level of neighbourhood to the embedding
space of size e individually and then learn the relation
between them. To achieve this, we created a neural
network with 3 hidden layers and an input and out-
put. For the input we use the views matrix, where
each row represents a sample (which is a node of the
graph), thus, a node is represented by a vector of size
d ∗ |V |. The first hidden layer, called the Level em-
bedding layer, lowers each level independently to an
embedding of size e so the output of this layer is a
vector of size d ∗ e. The second layer combines the
embedding of each level to a final embedding, here we
densely link each dimension from the different levels
to their respective dimension in the final embedding,
thus, learning for each dimension a weights vector of
size |V| for a total of d ∗ |V | weights for all the dimen-
sions. The last layer is a symmetric layer identical
to the Level embedding layer. Followed by an out-
put layer symmetric to that of the input layer. This
architecture is demonstrated in figure 3
3.3 Communities Centers / Leaders
Initialization
This phase aims to position community cen-
ters/leaders as optimally as possible inside the point
cloud of nodes. Community centers initialization
means putting independent points that sit at the center
of the communities. In this category, we propose two
methods: A neural network architecture, called Com-
munity Embedder, which uses a custom loss func-
tion (11) for the above-mentioned purpose, and the
KMeans method.
Community leaders initialization on the other
hand focuses on choosing a node as the leader of
its community. Here we crafted two other methods:
Leaders SA which is a simulated annealing for choos-
ing the optimal combination of nodes that minimizes
the same loss function used earlier (11), and a method
named Walk Leaders that exploits the Walks matrix
and uses a heuristic we defined to determine the lead-
ers.
3.3.1 Community Embedder
It’s a simple neural network containing only densely
connected input and output layers. The input layer
receives a one-hot encoded vector denoting the com-
munity to embed (so the size of this layer is K) and
lowers it to the embedding space represented by the
output layer (evidently of size e). To define the loss
function for this model we needed to put some theo-
ries that describe an optimal position of a community
center, we came up with four, each having a loss term
and then combined them into one loss function as fol-
lows:
First, we naively suppose that a good partitioning
WEBIST 2024 - 20th International Conference on Web Information Systems and Technologies
144

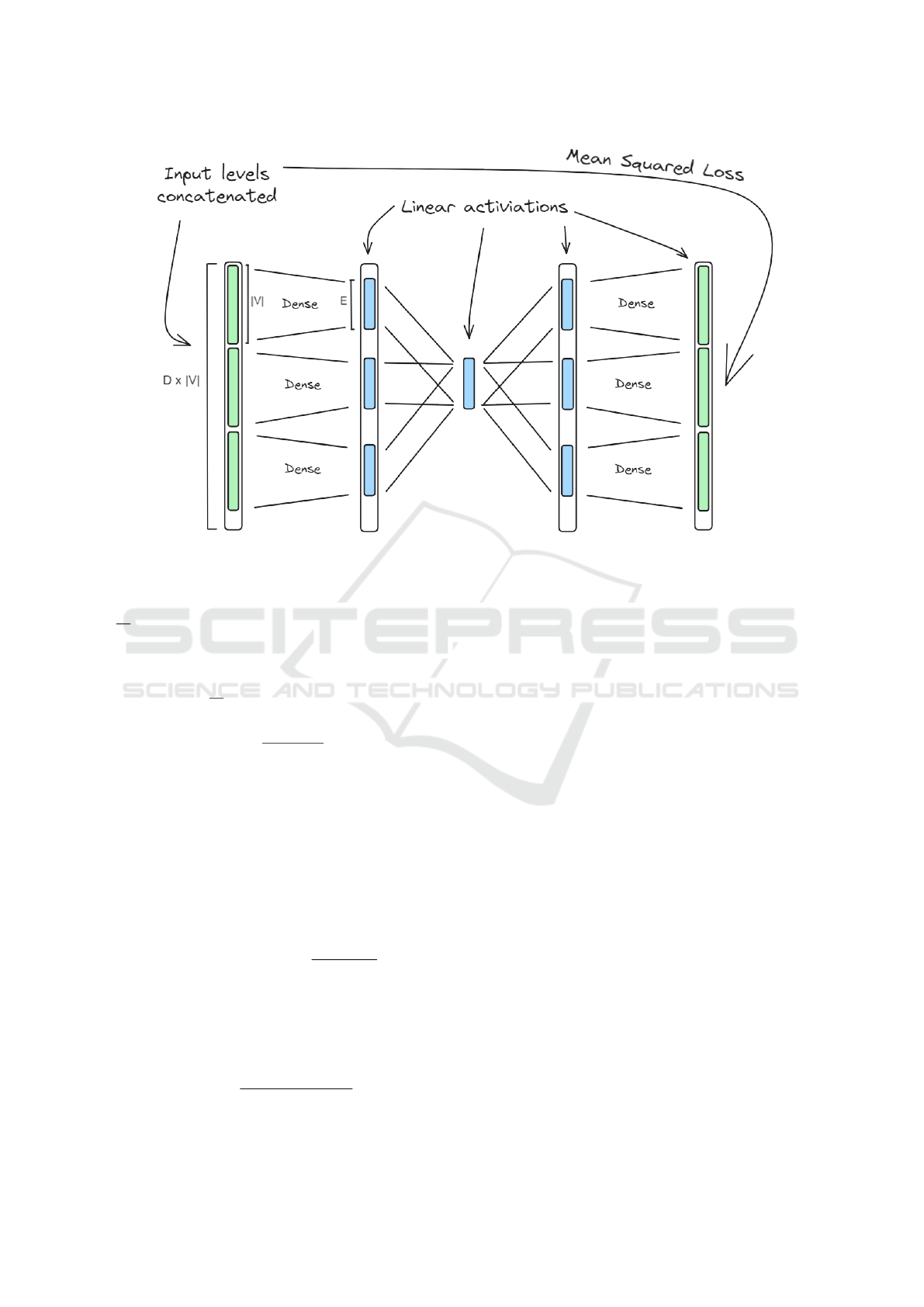
Figure 3: The autoencoder architecture.
of a point cloud gives each community an equal share
of nodes so each community in this case would get
|V |
K
nodes. So, if we call I
c
the number of nodes that
chose community center c we can have a loss function
that increases as I
c
gets higher (Dominance) or lower
(Subdominance) and approaches 0 if the number is
approximately
|V |
K
, which we can achieve with (6).
L
1
=

I
c
∗ K − N
N(K − 1)

2
(6)
For calculating I
c
we need to ensure that the func-
tion that calculates I
c
is differentiable. To do this we
use the Boltzmann Operator for a SmoothMin func-
tion (7) (α should be negative and large in absolute
value), which can help determine the minimum dis-
tance for each node to all the other centers producing
an almost-one-hot matrix specifying for each node the
community it chose. This matrix can then easily be
used to get an approximate I
c
.
SmoothMin({x
i
}) =
∑
n
i=1
x
i
e
αx
i
∑
n
i=1
e
αx
i
(7)
Second, inspired by the Modularity metric we
want to ensure that the distance between internal
nodes is much lower compared to the distance be-
tween internal nodes and external nodes:
L
2
=
∑
i, j∈c
∥ f
i
− f
j
∥
2
∑
i∈c, j /∈c
∥ f
i
− f
j
∥
2
(8)
Third, to easily approach the nodes to their com-
munity center we first need to bring the community
center closer to them, so we add another term that pe-
nalizes the distance between a community center and
the nodes of its community:
L
3
= 1 − e
−
∑
i∈c
(∥µ
c
− f
i
∥
2
)
(9)
Fourth, we assume that community centers are
generally positioned far from each other, so we pe-
nalize their closeness:
L
4
= e
−
∑
c
′
∈K,c
′
̸=c
(∥µ
c
′
−µ
c
∥
2
)
(10)
The loss function is then a weighted sum of the
previous losses:
Loss = αL1 + βL2 + γL3 + δL4 (11)
Where α, β, γ and δ are weights that sum up to 1
and denote the importance of each term.
3.3.2 Leaders SA
This method uses the Simulated Annealing meta-
heuristic (Kirkpatrick et al., 1983) to minimize as best
as possible the loss function (11). It’s important to
note that here we don’t need the derivative of the loss
function so we can use the exact way to calculate it
by directly using argmin instead of using SmoothMin.
We start by creating an initial random set of leader
nodes S. We get a neighbor of a solution S by choos-
ing a random node from it which we’ll be replaced
by a randomly chosen node from V − S. This way
SPACED: A Novel Deep Learning Method for Community Detection in Social Networks
145

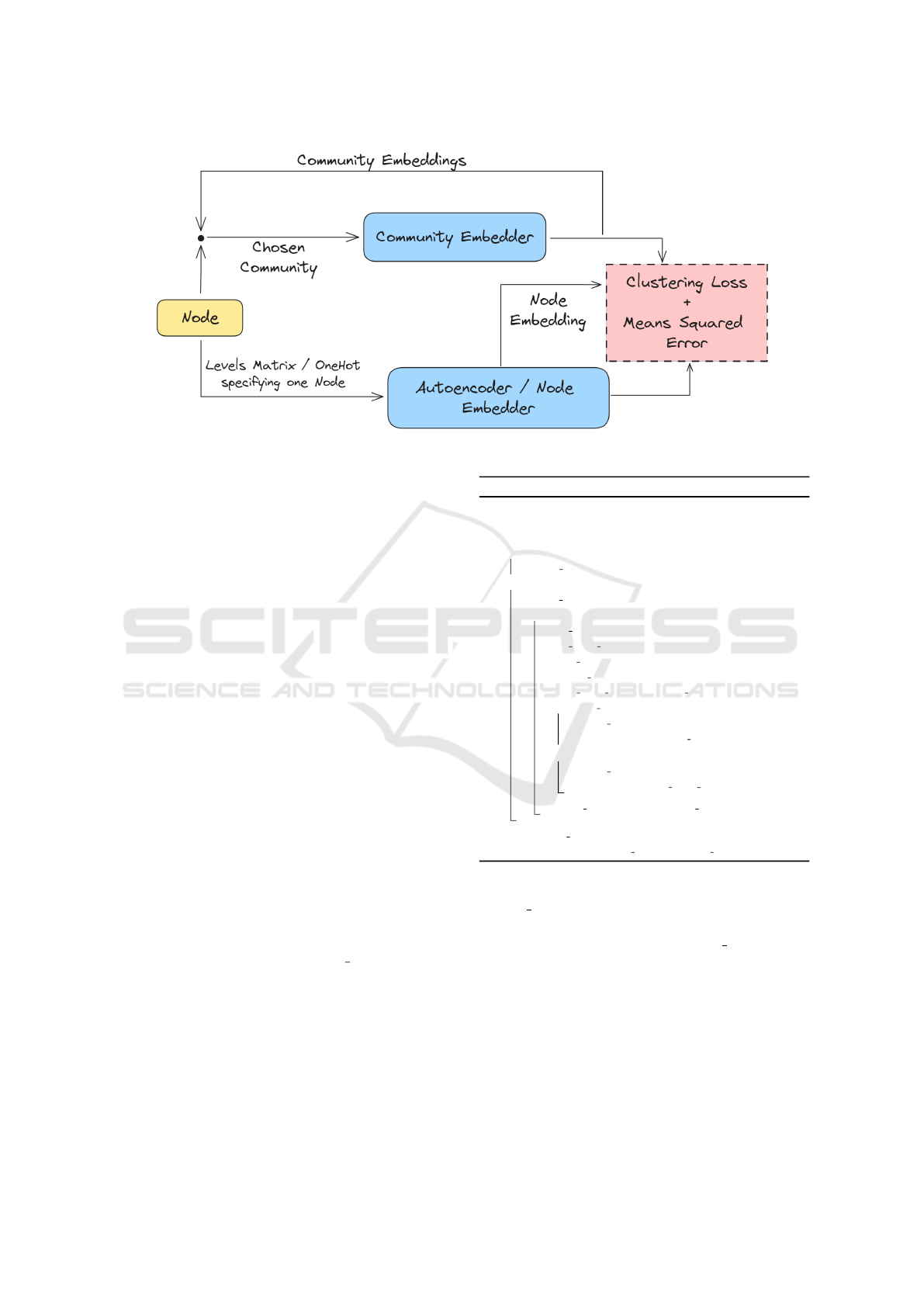
Figure 4: Mixed learning architecture.
we can execute Simulated Annealing to progressively
improve the initial solution.
3.3.3 Walk Leaders
We propose a heuristic (Algorithm 1) to extract com-
munity leaders and automatically detect the number
of communities K.
Since the walks matrix closely represents the dis-
tribution of nodes in hypothetical varying random
walks starting from each node (we call such a distri-
bution the context of the node), we can assume that the
leader of a node i is more likely to be among the nodes
with the most appearances in the context of i, so we
start by picking for each node the l leading nodes in
its context (we call them potential leaders, see line 1).
The goal here is to choose the minimal set of nodes
that contains at least one potential leader of each
node. So, for selecting the leader of each node we
first start with the potential leaders having the max-
imum number of appearances (see line 8), and then
we only take the first one that is already chosen by a
previous node (denoting the popularity of the leader
among previous nodes, see line 11), in case no max
count leader is already chosen by a previous node we
choose the one with more appearances in the context
of the node (see line 13). After iterating through all
the nodes we end up with a current leaders vector,
but this vector can still have some leader nodes that
don’t choose themselves as leaders which isn’t co-
herent. So, we used the Refinement of the idx vector
method proposed by (Taheri and Bouyer, 2020a) to
fix this conflict (see line 15).
Algorithm 1: Walk Leaders.
Input: walks matrix W , leaders window l
Output: number of leaders K, walk leaders WL
1 PL ← PotentialLeaders(W, l);
2 if l == 1 then
3 current leaders ← PL;
4 else
5 current leaders ← ∅;
6 for each node do
7 max count ← max({PLCount(p) | p ∈ PL[node]});
8 max count leaders ← {p ∈ PL[node] | PLCount(p) =
max count};
9 popular leaders ←
max count leaders ∩ current leaders;
10 if popular leaders ̸= ∅ then
11 current leader ←
first element of popular leaders;
12 else
13 current leader ←
first element of max count leaders;
14 current leaders[node] ← current leader;
15 Refine current leaders vector;
16 return UniqueCount(current leaders), current leaders;
The result of this method is a vector
current leaders assigning for each node i a leader
node, so to get the number of communities we count
the number of unique values in current leaders.
3.4 Mixed Learning
The aim of this phase is to enhance node embeddings
to represent community-aware high-order proximities
between nodes, i.e. nodes that are in the same com-
munity will have embeddings that are close to each
other. In this work, such an aim is achieved by im-
proving both node embeddings and community cen-
WEBIST 2024 - 20th International Conference on Web Information Systems and Technologies
146

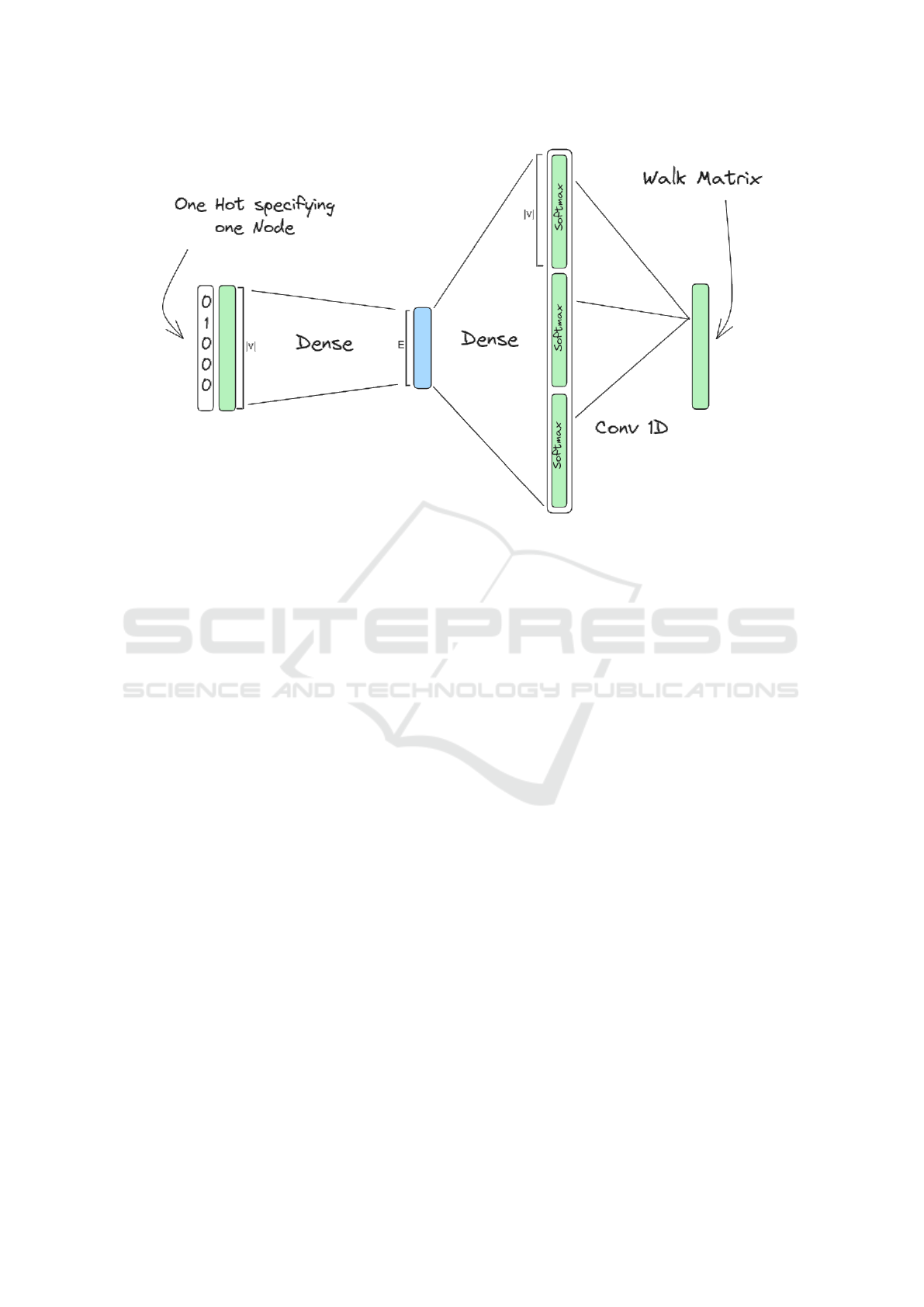
Figure 5: Node embedder architecture.
ters/leaders in one learning process by bringing them
closer to each other, which will form eventually accu-
rate clusters. In both approaches that we’ll present in
the next sub-sections, the community embedder will
either start from the weights it learned if used to ini-
tialize the centers, or will receive the centers/leaders
embedding coordinates as initial weights.
3.4.1 Autoencoder-Based
One first approach to implement the learning process
is to use the same autoencoder that was used to learn
initial node embeddings. The autoencoder weights at
the end of the initial node embedding phase are used
as initial weights in this phase. The autoencoder and
the Community Embedder are now trained at the same
time. For a given node, the input to the autoencoder is
its row in the level matrix while the input to the Com-
munity Embedder is the chosen community for that
node as a one-hot vector. The training loss is a com-
bined loss between the clustering loss (11) (using the
output from the Community Embedder and the em-
beddings from the autoencoder) and the reconstruc-
tion error of the autoencoder as shown in figure 4.
3.4.2 Node Embedder-Based
Another approach proposed in this work is to use a
new architecture to enhance node embeddings which
we named ”Node Embedder”. This architecture in-
spired by Skip-gram (Mikolov et al., 2013) has four
layers: an input layer, embedding layer, context layer,
and output layer. A node encoded as a one-hot vec-
tor of size |V | is passed to the input layer which is
connected densely to the embedding layer of size e.
The embedding layer is densely connected to the con-
text layer. The context layer contains c vectors of size
|V| (so its size is c ∗ |V|). c represents the context
size. Each vector is activated with a Softmax func-
tion. This layer represents eventually the nodes that
are in the context of the current node as one-hot vec-
tors. Then the context layer is connected to the output
layer via a one-dimensional convolutional kernel such
that the i
th
node of each vector in the context layer is
connected to the i
th
node in the output layer. Figure 5
summarizes this architecture.
The Node Embedder and Community Embedder
are trained at the same time. The input for the Node
Embedder is a one-hot vector representing the node,
and in the same way as the autoencoder-based ap-
proach, the input for the Community Embedder is the
chosen community for that node as a one-hot vector.
The training loss is a combination of the clustering
loss (11) (using the output of the Community Em-
bedder and the embeddings from the Node Embed-
der) and a mean squared error between the output of
the Node Embedder and the corresponsding row from
the walk matrix. Figure 4 details the architecture ex-
plained in this paragraph.
SPACED: A Novel Deep Learning Method for Community Detection in Social Networks
147

3.5 Clustering
For community detection, one can use any clustering
algorithm on the final node embeddings. Extracted
clusters represent the detected communities. In this
work, community centers/leaders can be used to de-
tect communities by assigning each node to the clos-
est community center. The results were also tested
with Kmeans and Affinity Propagation.
4 COMPUTATIONAL RESULTS
AND DISCUSSION
This section presents the results of computational ex-
periments assessing the performance and effective-
ness of SPACED for community detection in social
networks. All algorithms and tests were developed
in Python using TensorFlow and executed on a com-
puter running Windows 11 Pro, equipped with 16 GB
of RAM, an Intel(R) Core(TM) i5-10310U CPU at
1.70GHz, and an integrated Intel(R) UHD Graphics.
Our experiments cover both synthetic and real-
world networks. The real-world datasets included:
Table 1: Characteristics of the tested real-world bench-
marks.
Dataset
Comm-
unities
Nodes Edges
Karate
(Zachary, 1977)
2 34 78
Dolphins
(Lusseau et al., 2003)
2 62 159
Polbooks
[V. Krebs, unpublished]
3 105 441
Football
(Girvan and Newman, 2002)
12 115 613
Email
(Leskovec et al., 2007)
42 1005 25571
For the synthetic networks we used the
Lancichinetti-Fortunato-Radicchi (LFR) bench-
mark. The LFR datasets are characterized by the
mixing parameter µ which controls the level of
(a) Dolphins. (b) Polbooks. (c) Email.
(d) Football. (e) Karate.
Figure 6: NMI performance on real-world datasets.
WEBIST 2024 - 20th International Conference on Web Information Systems and Technologies
148

community overlap and noise (the higher the µ value
the more the noise). The LFR datasets comprised 128
nodes and 1024 edges, for the mixing parameter we
tested on the values : 0.00, 0.25, 0.40, 0.45, and 0.50.
To evaluate the effectiveness of our solution, we
employed the Normalized Mutual Information (NMI)
metric which is a widely used measure in literature.
NMI measures the similarity between the true com-
munity structure and the detected community struc-
ture, providing a score between 0 and 1, where 1 in-
dicates perfect matching.
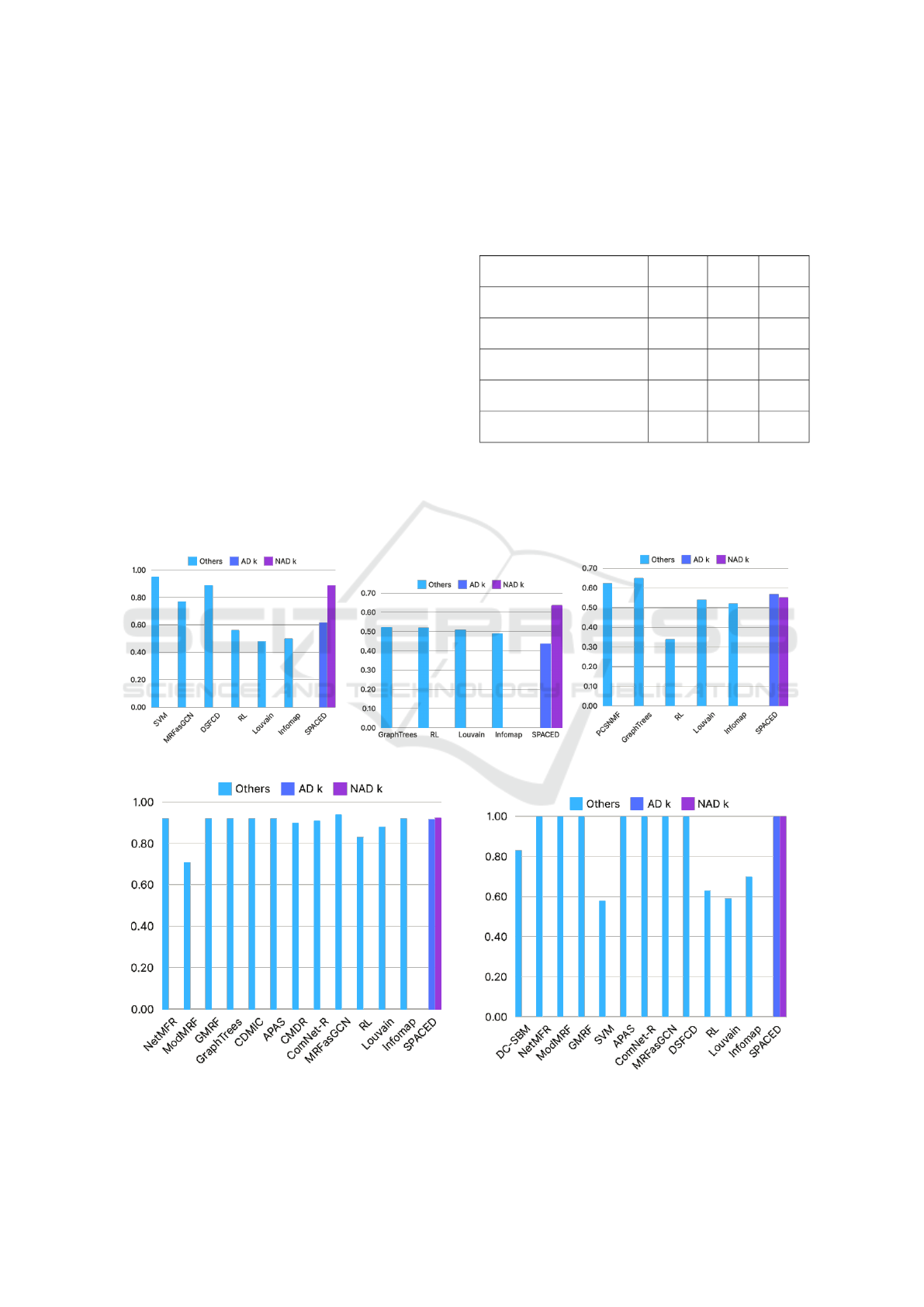
4.1 SPACED Performance Analysis on
Real-World Datasets
The performance of our method on real-world
datasets was assessed under both approaches, AD k
(Automatic Detection of the number of communities
”k”) and NAD k (No-Automatic Detection, ”k” is pre-
defined). As shown in Table 2, our results demon-
strated good accuracy in detecting the number of com-
munities which is a significant advantage over many
traditional methods that require this parameter to be
known a priori. Also as summarized in figure 7,
the community assignments produced by SPACED
showed good NMI results both for the AD k and the
NAD k modes. For instance, on the Karate network,
our method achieved an NMI of 1.0, perfectly match-
ing the ground truth.
Figure 7: AD k vs. NAD k.
Figures 6a to 6e illustrate the performance in
terms of NMI for the Karate, Dolphins, Polbooks,
Football, and Email networks respectively, compared
against several well-known community detection al-
gorithms, including Louvain (Blondel et al., 2008b),
Table 2: Real-world datasets: detected vs. ground truth
number of communities.
Dataset Ground Truth k Detected k
Karate 2 2
Dolphins 2 4
Polbooks 3 5
Football 12 15
Email 42 39
Infomap (Rosvall and Bergstrom, 2012), GraphTrees
(Dalleau et al., 2020a), and others (see Appendix).
Our method, particularly the NAD k variant, consis-
tently performed well across different datasets.
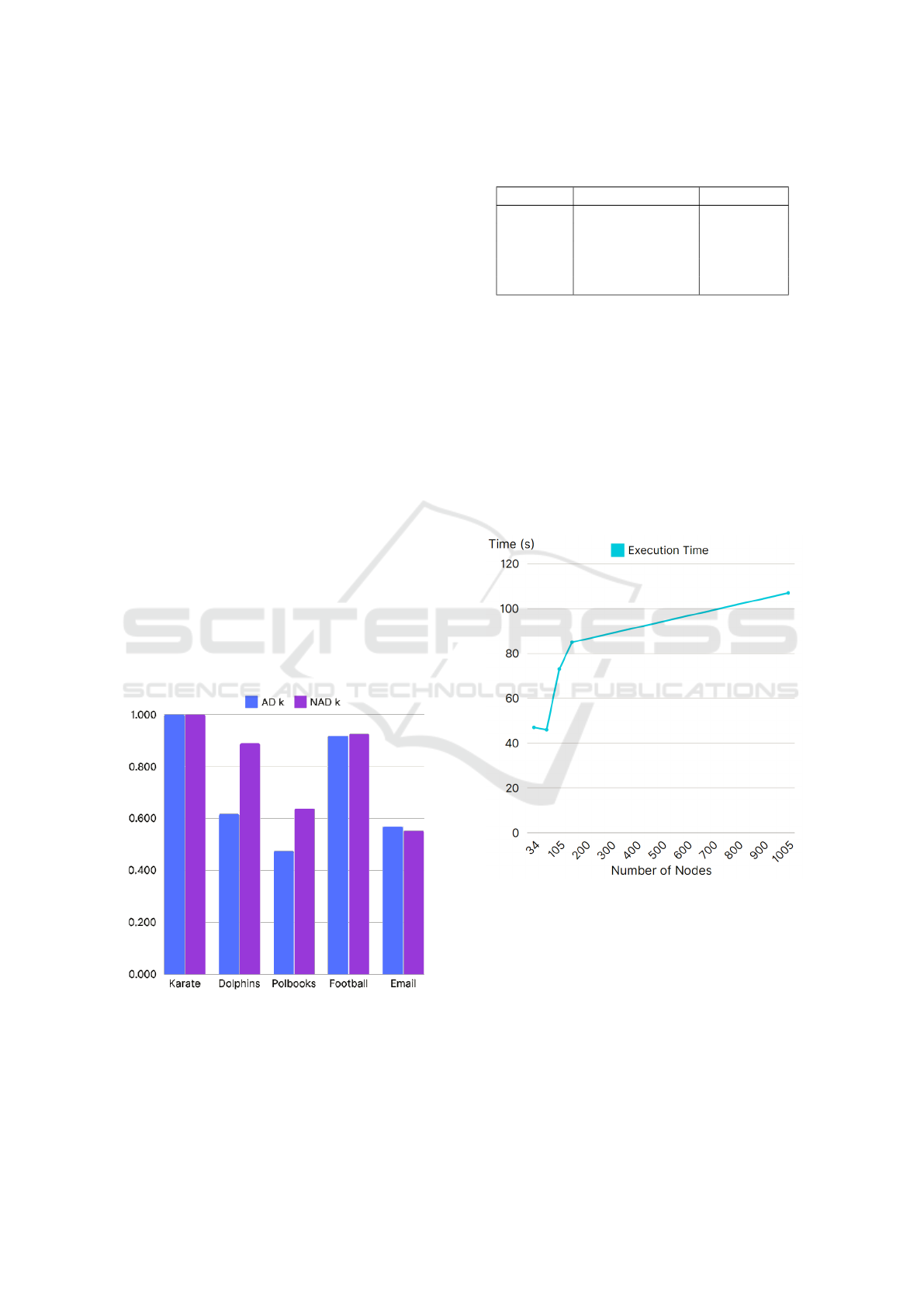
Also, SPACED has demonstrated reasonable exe-
cution times, with a direct correlation to network size.
Figure 8 presents a comparative analysis of execution
times (in seconds) across various real-world datasets,
further illustrating that the rate of increase slows as
network size grows. This demonstrates SPACED’s
strong potential for efficient scalability to larger net-
works.
Figure 8: Execution times in seconds for real-world
datasets.
However, the method faces certain limitations in
memory usage, primarily due to its reliance on the ad-
jacency matrix, which becomes impractical for large-
scale networks and may lead to excessive memory
consumption. This issue can be mitigated through
technical optimizations, such as storing only non-zero
values, as adjacency matrices in large-scale networks
are typically sparse. Additionally, techniques like
graph partitioning and distributed processing can be
explored to further optimize the performance on large
SPACED: A Novel Deep Learning Method for Community Detection in Social Networks
149

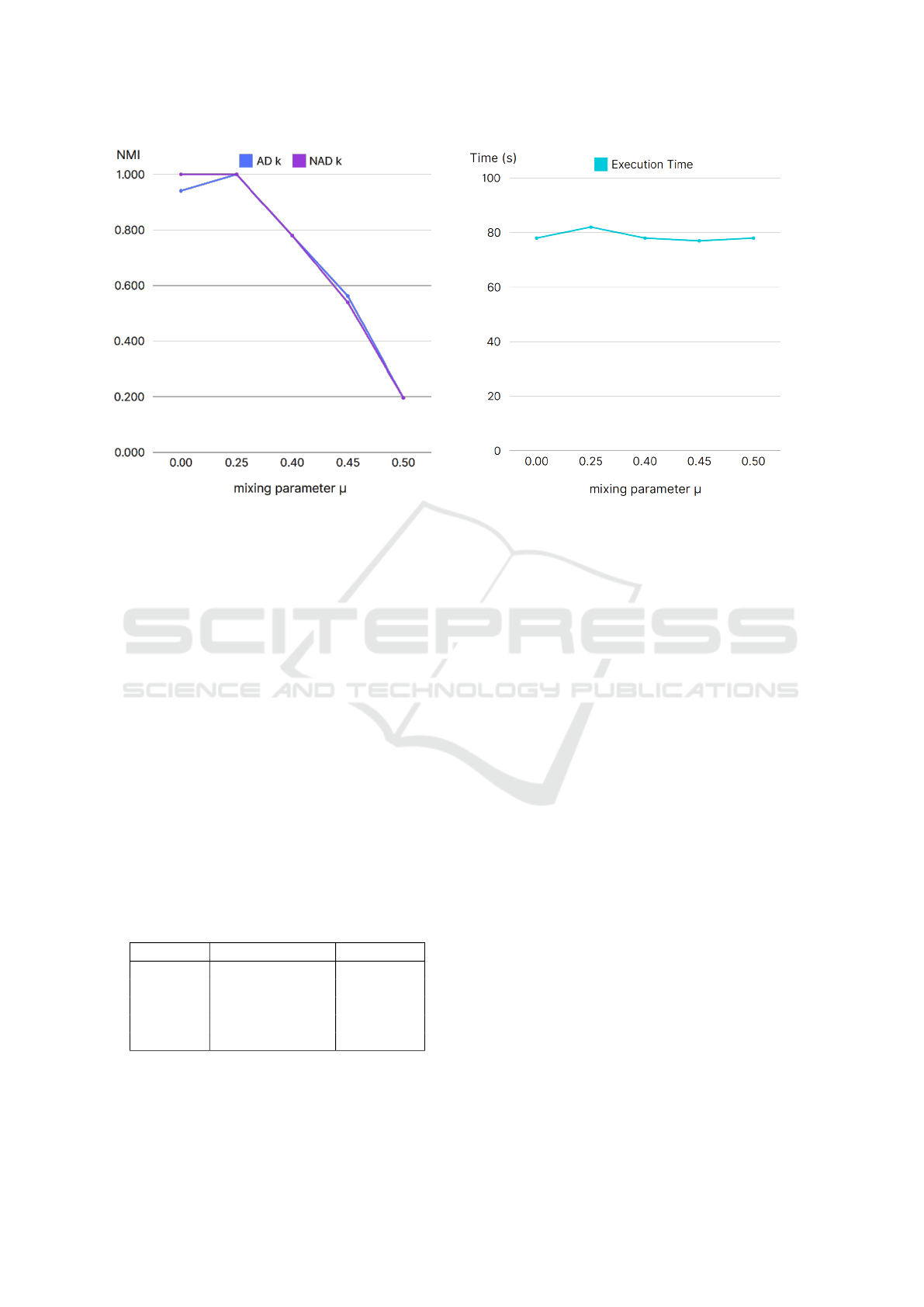
(a) NMI performance. (b) Execution times in seconds.
Figure 9: SPACED results on synthetic datasets.
networks without compromising accuracy.
4.2 SPACED Performance Analysis on
Synthetic Datasets
The synthetic datasets were generated using the LFR
benchmark with varying levels of mixing parameters.
Figure 9a illustrates the comparative performance of
our method between the AD k and NAD k variants on
the synthetic datasets for increasing values of the mix-
ing parameter, and Table 3 shows the detected number
of communities within the LFR networks. The rela-
tively high NMI values indicate the good performance
and robustness of our model, with an expected NMI
value decrease as the mixing parameter increases due
to the induced community noise. Also our method
demonstrated its strength in correctly identifying the
number of communities.
Table 3: Synthetic datasets: detected vs. ground truth num-
ber of communities.
Dataset Ground Truth k Detected k
LFR-0.00 4 5
LFR-0.25 4 4
LFR-0.40 4 4
LFR-0.45 4 3
LFR-0.50 4 4
Our method showed stable execution times inde-
pendently from the graph complexity, making it also
usable for graphs with a complex structure. The line
chart in figure 9b shows a comparative study of the
execution times in seconds for every synthetic dataset
in an increasing order of complexity.
5 CONCLUSION
In this paper, we introduced SPACED, a deep learning
model designed to uncover the community structure
of networks solely from their topology by generating
community-aware node embeddings. We evaluated
its performance on several widely recognized bench-
marks and compared it to other established methods,
showcasing its competitiveness in the field.
Future enhancements for SPACED include explor-
ing and refining the various pipeline variants to iden-
tify the optimal configuration. Additionally, while
SPACED has shown strong stability and effectiveness
on small to medium-sized datasets, it has not yet been
tested on extremely large datasets. Thus, future work
will need to address challenges in memory usage and
execution time to ensure scalability.
REFERENCES
Bhatia, V. and Rani, R. (2019). A distributed overlapping
community detection model for large graphs using
autoencoder. Future Generation Computer Systems,
94:16–26.
Blondel, V. D., Guillaume, J.-L., Lambiotte, R., and Lefeb-
WEBIST 2024 - 20th International Conference on Web Information Systems and Technologies
150

vre, E. (2008a). Fast unfolding of communities in
large networks. Journal of Statistical Mechanics:
Theory and Experiment, 2008(10):P10008.
Blondel, V. D., Guillaume, J.-L., Lambiotte, R., and
Lefebvre, E. (2008b). Louvain algorithm. Jour-
nal of Statistical Mechanics: Theory and Experiment,
2008(10):P10008.
Cai, B., Wang, Y., Zeng, L., Hu, Y., and Li, H. (2020).
Edge classification based on convolutional neural net-
works for community detection in complex network.
Physica A: statistical mechanics and its applications,
556:124826.
Cavallari, S., Cambria, E., Cai, H., Chang, K. C.-C., and
Zheng, V. W. (2019). Embedding both finite and infi-
nite communities on graphs [application notes]. IEEE
computational intelligence magazine, 14(3):39–50.
Cavallari, S., Zheng, V. W., Cai, H., Chang, K. C.-C., and
Cambria, E. (2017). Learning community embed-
ding with community detection and node embedding
on graphs. In Proceedings of the 2017 ACM on Con-
ference on Information and Knowledge Management,
pages 377–386.
Dalleau, K., Couceiro, M., and Smail-Tabbone, M. (2020a).
Computing vertex-vertex dissimilarities using random
trees: Application to clustering in graphs. In Ad-
vances in Intelligent Data Analysis XVIII, pages 132–
144, Berlin, Heidelberg. Springer-Verlag.
Dalleau, K., Couceiro, M., and Smail-Tabbone, M. (2020b).
Computing vertex-vertex dissimilarities using random
trees: Application to clustering in graphs. In Advances
in Intelligent Data Analysis XVIII, pages 132–144.
Girvan, M. and Newman, M. E. (2002). Community struc-
ture in social and biological networks. Proceedings of
the national academy of sciences, 99(12):7821–7826.
Gong, M., Liu, J., Ma, L., Cai, Q., and Jiao, L. (2014).
Novel heuristic density-based method for community
detection in networks. Physica A: Statistical Mechan-
ics and its Applications, 403:71–84.
Grover, A. and Leskovec, J. (2016). node2vec: Scal-
able feature learning for networks. In Proceedings
of the 22nd ACM SIGKDD international conference
on Knowledge discovery and data mining, pages 855–
864.
Guo, W.-F. and Zhang, S.-W. (2016). A general method of
community detection by identifying community cen-
ters with affinity propagation. Physica A: Statistical
Mechanics and its Applications, 447:508–519.
He, D., You, X., Feng, Z., Jin, D., Yang, X., and Zhang,
W. (2018). A network-specific markov random field
approach to community detection. In Proceedings of
the AAAI Conference on Artificial Intelligence, vol-
ume 32.
Jin, D., Liu, Z., Li, W., He, D., and Zhang, W. (2019a).
Graph convolutional networks meet markov random
fields: Semi-supervised community detection in at-
tribute networks. In Proceedings of the AAAI confer-
ence on artificial intelligence, volume 33, pages 152–
159.
Jin, D., You, X., Li, W., He, D., Cui, P., Fogelman-
Souli
´
e, F., and Chakraborty, T. (2019b). Incorpo-
rating network embedding into markov random field
for better community detection. In Proceedings of
the AAAI Conference on Artificial Intelligence, vol-
ume 33, pages 160–167.
Jin, D., Zhang, B., Song, Y., He, D., Feng, Z., Chen, S., Li,
W., and Musial, K. (2020). Modmrf: A modularity-
based markov random field method for community de-
tection. Neurocomputing, 405:218–228.
Karatas¸, A. and S¸ahin, S. (2018). Application areas of com-
munity detection: A review. In 2018 International
congress on big data, deep learning and fighting cy-
ber terrorism (IBIGDELFT), pages 65–70. IEEE.
Karrer, B. and Newman, M. E. (2011). Stochastic block-
models and community structure in networks. Physi-
cal review E, 83(1):016107.
Kirkpatrick, S., Gelatt Jr, C. D., and Vecchi, M. P.
(1983). Optimization by simulated annealing. science,
220(4598):671–680.
Leskovec, J., Kleinberg, J., and Faloutsos, C. (2007).
Graph evolution: Densification and shrinking diame-
ters. ACM transactions on Knowledge Discovery from
Data (TKDD), 1(1):2–es.
Lusseau, D., Schneider, K., Boisseau, O. J., Haase, P.,
Slooten, E., and Dawson, S. M. (2003). The bot-
tlenose dolphin community of doubtful sound features
a large proportion of long-lasting associations. Behav-
ioral Ecology and Sociobiology, 54(4):396–405.
Mikolov, T., Chen, K., Corrado, G., and Dean, J. (2013).
Efficient estimation of word representations in vector
space. arXiv preprint arXiv:1301.3781.
Paim, E. C., Bazzan, A. L. C., and Chira, C. (2020). De-
tecting communities in networks: a decentralized ap-
proach based on multiagent reinforcement learning. In
2020 IEEE Symposium Series on Computational Intel-
ligence (SSCI), pages 2225–2232.
Perozzi, B., Al-Rfou, R., and Skiena, S. (2014). Deepwalk:
Online learning of social representations. In Proceed-
ings of the 20th ACM SIGKDD international confer-
ence on Knowledge discovery and data mining, pages
701–710.
Rosvall, M. and Bergstrom, C. T. (2012). Infomap algo-
rithm. Physical Review E, 86(1):016108.
Rozemberczki, B., Davies, R., Sarkar, R., and Sutton, C.
(2019). Gemsec: Graph embedding with self clus-
tering. In Proceedings of the 2019 IEEE/ACM inter-
national conference on advances in social networks
analysis and mining, pages 65–72.
Shi, X., Lu, H., He, Y., and He, S. (2015). Community de-
tection in social network with pairwisely constrained
symmetric non-negative matrix factorization. In Pro-
ceedings of the 2015 IEEE/ACM International Con-
ference on Advances in Social Networks Analysis and
Mining 2015, pages 541–546.
Sui, S.-K., Li, J.-P., Zhang, J.-G., and Sui, S.-J. (2016).
The community detection based on SVM algorithm.
In 2016 13th International Computer Conference on
Wavelet Active Media Technology and Information
Processing (ICCWAMTIP).
Taheri, S. and Bouyer, A. (2020a). Community detection in
SPACED: A Novel Deep Learning Method for Community Detection in Social Networks
151

social networks using affinity propagation with adap-
tive similarity matrix. Big data, 8(3):189–202.
Taheri, S. and Bouyer, A. (2020b). Community detec-
tion in social networks using affinity propagation with
adaptive similarity matrix. Big Data, 8(3):189–202.
PMID: 32397731.
Tandon, A., Albeshri, A., Thayananthan, V., Alhalabi, W.,
Radicchi, F., and Fortunato, S. (2021). Community
detection in networks using graph embeddings. Phys-
ical Review E, 103(2):022316.
Tang, J., Qu, M., Wang, M., Zhang, M., Yan, J., and Mei,
Q. (2015). Line: Large-scale information network em-
bedding. In Proceedings of the 24th international con-
ference on world wide web, pages 1067–1077.
Tian, F., Gao, B., Cui, Q., Chen, E., and Liu, T.-Y. (2014).
Learning deep representations for graph clustering. In
Proceedings of the AAAI Conference on Artificial In-
telligence, volume 28.
Xie, Y., Gong, M., Wang, S., and Yu, B. (2018). Commu-
nity discovery in networks with deep sparse filtering.
Pattern Recognition, 81:50–59.
Xie, Y., Wang, X., Jiang, D., and Xu, R. (2019). High-
performance community detection in social networks
using a deep transitive autoencoder. Elsevier. Article
history: Received 18 December 2018; Revised 8 April
2019; Accepted 10 April 2019; Available online 17
April 2019.
Zachary, W. W. (1977). An information flow model for con-
flict and fission in small groups. Journal of anthropo-
logical research, pages 452–473.
APPENDIX
References for the Compared Against
Methods
DC-SBM (Karrer and Newman, 2011)
NetMRF(He et al., 2018)
ModMRF(Jin et al., 2020)
GMRF (Jin et al., 2019b)
SVM (Sui et al., 2016)
APAS (Taheri and Bouyer, 2020b)
ComNet-R(Cai et al., 2020)
MRFasGCN(Jin et al., 2019a)
DSFCD(Xie et al., 2018)
RL (Paim et al., 2020)
Louvain (Blondel et al., 2008a)
Infomap (Rosvall and Bergstrom, 2012)
GraphTrees (Dalleau et al., 2020b)
CDMIC (Guo and Zhang, 2016)
CMDR (Gong et al., 2014)
PCSNMF(Shi et al., 2015).
WEBIST 2024 - 20th International Conference on Web Information Systems and Technologies
152