Computing Bounds for the Synchronization Errors of Nonidentical

Nonlinear Oscillators with Time-Varying Diffusive Coupling

Tabea Trummel, Zonglin Liu

and Olaf Stursberg

Control and System Theory, EECS Dept., University of Kassel, Germany

{t.trummel, z.Liu, stursberg}@uni-kassel.de

Keywords:

Oscillators, Synchronization, Networked Systems, Reachable Sets, Limit Cycles.

Abstract:

The paper studies bounds of the synchronization error for networks of diffusively coupled and nonidentical

nonlinear oscillators. In contrast to preceding work, which only analyzes the synchronization error in the limit

and for constant coupling, a method based on over-approximating reachable sets of the synchronization error

is proposed. The method allows the evaluation of different and time-varying gains along the limit cycles.

Instead of using st rong coupling gains to preserve synchronization, it is proposed to vary the coupling gains

over time, while the synchronization error determined via reachable set does not exceed a speciﬁed bound.

Evaluation results for the proposed method are provided for different types of coupled oscillators.

1 INTRODUCTION

The synchronization of sets of oscillators has been in-

vestigated in context of several applications, such as

high-precision motion contro l (Xiao and Zhu, 2006),

power grids (Wang et al., 2 016), or in biological sys-

tems (Kim et al., 2019).

An essential point is to investigate in how far the

coupling strengths among the oscillators as well as the

interaction topology affects the synchronization error

over time. This error encodes (temporary or perma-

nent) deviation of the amplitudes (or phases) of the

oscillators. While for coupled identical linear oscilla-

tors, the dynam ic s of the synchronization error can be

expressed explicitly (Scardovi and Sepulchre, 2008),

the situation for sets of nonlin ear oscillators is more

involved, since the dynamics of the syn chronization

error cannot be co mputed in closed form. Existing

work can roughly be categorized in appro aches that

aim to seek sufﬁciently large static gains of diffusive

coupling to obtain convergen ce of the errors to zero

in th e limit, a nd to those where the coupling strength

is varied over time – this paper is focused on the latter

case.

Among th e existing approaches for this case,

(Zhao et al., 2012) determine time-varying coupling

gains by treating the error of nonidentical nonlin-

ear systems with Lyapunov-like functions. Although

https://orcid.org/0000-0002-0196-9476

https://orcid.org/0000-0002-9600-457X

bounded synchronization is guaranteed by the cou -

pling gains, the network structure is restricted to an

undirected form and the error is only considered in

the limit, potentially leading to conservatively large

gains. In the work by (Wang et al., 2011), the p roce-

dure is similar but o nly identical nonlin ear systems in

discrete time are consider ed. Also, (Zhu et al., 2020)

and (Panteley and Lor´ıa, 2017) u se the construction of

Lyapunov- like functions to synthe size coupling gains

bounding the error. The disadvantage of these ap-

proach e s is, apart from using possibly larger gains

than necessary for synchronizatio n, the lack of the

possibility to compute the evolution of the synchro-

nization error over time.

A different approach for bounded synch ronization

uses funnel control (Lee et al., 2022), where the syn-

chroniza tion error of nonidentical nonlinear systems

is forced to a speciﬁc bo und by different time-varying

coupling gains. However, the evolution of the error

over time is restricted by the funnel shape, i.e., it is

not possible to allow a larger synchronization error

for certain times if an application requires this. It is

not possible to check which e rror bounds arise fr om

given coupling gain s.

In contrast to the aforementioned approaches, the

method proposed in this paper offers the possibility to

(i) analyze if the synchronization error stays beyond

a certain threshold for given coupling gains, and ( ii)

to synthesize time-varying coupling gain s (possibly

different for any coupling of the network topology)

while maintaining a chosen error bound. The syn-

612

Tr ummel, T., Liu, Z. and Stursberg, O.

Computing Bounds for the Synchronization Errors of Nonidentical Nonlinear Oscillators with Time-Varying Diffusive Coupling.

DOI: 10.5220/0013071100003822

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 21st International Conference on Informatics in Control, Automation and Robotics (ICINCO 2024) - Volume 1, pages 612-622

ISBN: 978-989-758-717-7; ISSN: 2184-2809

thesis of gains is particularly useful if a compromise

between the synch ronization error and th e synchro -

nization effort (through large couplin g gains) has to

be determined. A recent pa per by (Trummel e t al.,

2023) has suggested to solve this task by numeric op -

timization, however, the computation of error bounds

was not included there.

In order to establish the schemes f or analysis and

synthesis, the paper on hand uses the techn ique of

computing over-approximatio ns of reachable sets for

nonlinear systems, see e.g. (Stursberg and Krogh,

2003), (Girard, 2005), (Rungger and Zama ni, 2018)

and adopts it to analyze the evolution of the synchro-

nization error. According to the knowledge of the

authors, this is the ﬁrst exposition on using reach-

able sets to explicitly compute upper bounds of syn-

chroniza tion errors for coupled nonlinear oscillators,

while the only similar work by (Sang and Zhao, 2020)

limits the focus to linear time-delayed local dynamics.

After introdu cing into the proble m setting in

Sec. 2, the main part (Sec. 3) introduces the procedure

for computing over-approxima tions of reachable sets

for synch ronization errors for given coupling gains,

including an analysis of the c omplexity of the compu-

tation. The section includes also a modiﬁcation o f the

proced ure, in which the coupling gains are iteratively

changed on certain time intervals in order to limit the

upper bounds of the synchro nization errors on the re-

spective inte rvals. The effectiveness of the techniqu e s

is illustrated by numerical examples in Sec. 4, before

a conclusion and an outlook on future work is pro-

vided in Sec. 5.

2 PROBLEM DESCRIPTION

With an index set N = {1, . . . , n}, consider a set of

nonlinear dynamics:

˙x

(t) = f

(t)), i ∈ N (1)

with state vector x

∈ R

, tim e variable t ∈ R, and

ﬂow function f

: R

→ R

Assumption 1. Let f

(t)) be c ontinuous in time,

continuously differentiable with respect to x

(t), as

well as bounded on ea ch c ompact subset of R

. For

the solution of (1), let furthermore a unique limit cy-

cle

exist, and let x

(t) converge to the limit c y cle for

any initialization.

With this assumption, we refer to the set o f dy-

namics according to (1) as nonidentical nonline ar os-

cillators. Obviously, one can expect different limit

For a deﬁnition of limit cycles, see e.g. the book by

(Ye and Cai, 1986).

cycles for any i in th e general case. Now con sider an

extension of (1) by a diffusive coupling law to:

˙x

(t) = f

(t)) +

∑

j∈N

i j

(t)(x

(t) −x

(t)) ∈ R

(2)

with the subset of N

⊆ N of indices referring to

the o scillators cou pled directly to oscillator i, and

i j

(t) ∈ R

≥0

denotes different time-varying cou pling

gains. Any k

i j

(t) models the individual gain by which

the state difference of j and i affects the oscillator i.

Assume that k

i j

(t) 6= k

(t) is possible and that th e

coupling network is directed and strongly co nnected.

From (Lee and Shim, 2022) it is known that the

solutions of diffusively coupled nonidentical nonlin-

ear systems

converge for a sufﬁciently large k

i j

(t) =

k = const.∀i, j ∈ N to the solution s(t) ∈ R

of the

averaged dynamics:

˙s(t) =

∑

i∈N

(s(t)), s(t

) =

∑

i∈N

). (3)

It is shown by (Lee and Shim, 2022) that for any syn-

chroniza tion acc uracy ε > 0 , a threshold κ of the co u-

pling gain k exists for which:

limsup

t→∞

k x

(t) −s(t) k≤ ε, ∀i ∈ N (4)

for any k ≥ κ ∈ R

≥0

. Since Eq. (3) represents the av-

eraged dynamics of all oscillators and encodes itself a

nonlinear oscillator, the averaged trajectory s(t) also

converges to a lim it cycle for t → ∞.

In the following, the existence of the averaged dy-

namics is exploited to determine the error dynamics,

whereas the requirement of a large gain is omitted,

(e.g., in order to establish tradeoffs between synchro-

nization errors and efforts). In particular, the quan-

titative determination of gains, or upper bounds of

the synchronization errors are addre ssed along the fol-

lowing lines:

Problem 1. For a given κ or given time-dependent

proﬁles o f the coupling g ains k

i j

(t), determine the nu-

meric value o f the up per bound σ > 0 of the synchro-

nization error.

Problem 2. For speciﬁed time-varyin g upper bounds

of the synchronization error, determine values k

i j

(t)

which ensure that error bound s a re never exceeded.

Both problems will be addressed based on the

computation of over-approximations of the sets of

reachable synchronization errors. When ca lc ulating

the reachable sets, both the local d ynamics and the

(Lee and Shim, 2022) refer to the case that the network

is undirected and connected, which corresponds to the case

of a directed and strongly connected network.

Computing Bounds for the Synchronization Errors of Nonidentical Nonlinear Oscillators with Time-Varying Diffusive Coupling

613

network structu re are taken into account in order to re-

duce the conser vatism of the over-approximation. For

the case of Problem 1, the question may arise where

from the course of the k

i j

(t) would b e known. A pos-

sible option is the use of the method by (Trummel

et al., 2023), which uses a scheme of numeric op-

timization to compu te the tim e-varying gains, how-

ever, without guaranteeing synchronization for these

gains. The procedure proposed below to solve Prob-

lem 1 aims at providing this g uarantee. The scheme

to be developed as solution to Prob le m 2 iterates over

candidates for the gain proﬁles in order to eventually

satisfy the speciﬁed bounds on the synchronization er-

ror.

3 ENCLOSURE OF

SYNCHRONIZATION ERRORS

3.1 Conservative Linearization of the

Coupled Dynamics

Since it is, in the general case, not possible to compute

the dynamics of the synchronization error in closed

form, the concept followed here is to (1.) conser-

vatively linearize the nonlinear oscillator dynamics,

i.e., to resor t to a local differential inclusions of afﬁne

structure (which is guaranteed to include the nonlin-

ear dynamics), and (2.) to use the differential inclu-

sions to determine upper bounds for the synchroniza-

tion error.

Assume for the moment that all coupling gain s

i j

(t) would be known and c onstant at any time, such

that a limit cycle of the averaged dynamics s(t) will

be obtained. It is then reasonable to select a suitable

number of suppo rting points along this limit cycle in

order to obtain th e local conservative linearizations.

Assume further tha t the oscillators have initial states

) = x

i,0

close to a point s(t

) that belongs to the

solution of the averaged dynamic s (i.e., an initial syn-

chroniza tion er ror is possible).

Choosing a ﬁrst linearization po int x

i,0

and an ele-

ment of the set:

i,0



x ∈ R



|x −x

i,0

| ≤

√



(5)

for all i ∈ N , where 1

∈ R

denotes a vector of

ones and ε is a g iven desired accuracy according to

(4). Additional linearization points x

i,1

, x

i,2

, . . . , x

i,p

are distributed along the limit cycle s(t) for sample

times t

, thus leading to partitioning of the period of

the limit cycle into time intervals [t

q+1

] with t

q+1

+ δt

and q ∈ {0, 1, . . ., p −1}. δt

> 0 can change

from time step to time step, and is suitably chosen

based on the curvature of s(t), i.e., based on the value

of the second derivative of (3).

Assumption 2. Assume from now on that the cou-

pling gains k

i j

(t) are piecewise constant on [t

q+1

]

and thus denoted by k

i j,q

The linearization points result from the step-by-

step computation of the solutions x

(t)∀t ∈ [t

q+1

where the set X

i,q

of the current linearization point

is the initial set for the next computation. The set-

based com putation of the solutions is carried out us-

ing the procedure previously proposed in (Althoff

et al., 2008), which uses Lagrangian remainders to

conservatively encode the right-hand sides of (2).

When denoting the Lagrangian remainders by L

i,q,r

the conservative linearization of (2) around x

i,q

for all

i ∈ N and q ∈ {0, 1, . . . , p −1} is:

˙x

i,r

(t) = f

i,r

) +

∂ f

i,r

(t))

∂x

(t)



(t)=x

i,q

(t) −x

i,q

)

∑

j∈N

i j,q

j,r

(t) −x

i,r

(t)) + L

i,q,r

(6)

for each dimension r ∈ {1, . . . , n

} of x

(t) with t ∈

q+1

]. L

i,q,r

is evaluated on a set X

i,q

which is pa-

rameterized according to (5) using x

i,q

, leading to the

bound:

i,q,r

| ≤w

max,i,q,r

(7)

with:

max,i,q,r

:= max

0≤α≤1,x

∈X

i,q



−x

i,q

)

∂

i,r

)

∂x



=ξ

−x

i,q

)



and ξ := x

i,q

+ α(x

−x

i,q

). The values w

max,i,r

form a

vector w

max,i

∈ R

and are used to establish:

max,i,q

:= {w

∈ R



| ≤ w

max,i,q

Now, the nonlinear dynamics (2) is over-

approximated by the linearized inclusions:

˙x

(t) ∈(A

i,q

(t) + b

i,q

∑

j∈N

i j,q

(t) −x

(t))) ⊕W

max,i

(8)

for t ∈ [t

q+1

], where:

i,q

∂ f

)

∂x



i,q

and b

i,q

:= f

i,q

) −A

i,q

holds, and the symbol ⊕ denotes Minkowski addi-

tion. In order to ensure the tightness of the over-

approximations, it is important to determine or select

appropriate δt

, as already mentioned.

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

614

Furthermore, the quantities of the local lineariza-

tions are c ollected in A

:= diag(A

1,q

, . . . , A

n,q

), b

1,q

. . . b

n,q

]

, w

m,q

:= [w

max,1,q

. . . w

max,n,q

]

, and

in the weighted Laplacian matrix:







. . . m







∈R

n×n

. (9)

In here, m

∑

j∈N

i j,q

and m

i j

= −k

i j,q

applies if a

coupling from oscillator j to i exists, while m

i j

= 0

otherwise. By deﬁn ing W

m,q

:= {w ∈ R



|w| ≤

m,q

}, the dynamics of the global vector x(t) =

(t) . . . x

(t)]

satisﬁes:

˙x(t) ∈ ((A

−(K

⊗I

))x(t) + b

) ⊕W

m,q

(10)

for t ∈[t

q+1

], where ⊗ denotes the Kronecker pr od-

uct an d I

is the n

×n

identity matrix.

3.2 Dynamics of the Synchronization

Error

The synch ronization error e(t) ∈ R

(n−1)

for t ≥t

deﬁned as the difference between x

(t) and any other

(t), j ∈ {2, 3, . . . , n}, i.e.:

e(t) =







(t) −x

(t)

(t) −x

(t)

(t) −x

(t)







= (







−1 1 0 0 . . . 0

−1 0 1 0 . . . 0

−1 0 . . . 0 1 0

−1 0 . . . 0 0 1







⊗I

)

{z }

:=L

x(t).

By use of (10), the over-approximation of the reach-

able state set can be computed by propagating the set

at time t

forward over the time interval [t

q+1

]. An

over-approximation of reachable synchronization er-

rors e(t) can be de termined by using the extreme val-

ues of each loc al state x

(t), i ∈ N in each dimension

r ∈{1, . . . , n

}. The result may, however, be conserva-

tive, i.e., the set of feasible e(t) may be considerably

over-approximated. To address this p roblem, the con-

servatively linearized dynamics of e(t) is determined

accordin g to (10): First, a new matrix:



×n

(n−1)

]



∈ R

n×n

(11)

is deﬁned based on L

, and L

is always invertible.

Since the relations:



(t)

e(t)



= L

x(t),



˙x

(t)

˙e(t)



= L

˙x(t) (12)

hold, the dynamic s of the vector [x

(t) e

(t)]

for t ∈

q+1

] is given by:



˙x

(t)

˙e(t)



∈ (L

−(K

⊗I

))L

−1

)



(t)

e(t)



+ L

) ⊕W

d,q

(13)

accordin g to (10) with:

d,q



w ∈ R



−|L

m,q

≤ w ≤ |L

m,q



When deﬁning d(t) := [x

(t) e

(t)]

for simplicity of

notation, the initial set E(t

) of d(t

) can be written

as:

E(t

) :=











d ∈ R



|d −







1,0







| ≤







max

















(14)

with x

max

√

accordin g to (5). Starting

from E(t

), a method to compute a tight over-

approximation of the reachable set of d(t) (and thus

of the synchronization er ror e(t)) for the time interval

] is introduced, which is based on the results by

(Girard, 2005).

3.3 Reachable Set of the

Synchronization Error

As (10) and (13) only hold for the time interval

q+1

], the reachable set of d(t) is iteratively c om-

puted for each q ∈ {0, 1, . . . p − 1}. As the reach-

able set of d(t) may be small at the sampling time

, while being large otherwise, the reac hable set of

d(t) is computed for each interval, instead of only at

the sampling times.

For the interval [t

q+1

], it is known from (13) that

the relation:

d(t) ∈e

d,q

δt

E(t

)

⊕

q+1

−τ)A

d,q

⊕W

d,q

)dτ (15)

holds with A

d,q

:= L

− (K

⊗ I

))L

−1

. The

set on the right-hand side of (15) thus con-

tains the true reachable set of d(t) in this in-

terval. To (efﬁciently) determine this set, the

Computing Bounds for the Synchronization Errors of Nonidentical Nonlinear Oscillators with Time-Varying Diffusive Coupling

615

integral

q+1

−τ)A

d,q

⊕ W

d,q

)dτ is over-

approximated by a hypercube C

⊆ R

centered in

the origin 0

, and all sides have a com mon length

∈R

determined by:

:= 2

q+1

−τ)kA

d,q

∞

k L

+ |L

m,q

∞

dτ

2(e

δt

d,q

∞

−1)

k A

d,q

∞

k L

+ |L

m,q

∞

. (16)

Let R

q+1

]

(E(t

)) denote the true reachable set

of d(t) for the interval [t

q+1

]. The relation:

q+1

]

⊆







[

t∈[t

q+1

]

d,q

E(t

)







⊕C

(17)

thus applies according to ( 15) and (16), where

t∈[t

q+1

]

d,q

E(t

) is the union of e

d,q

E(t

) for all

t ∈ [t

q+1

]. Following the method in (Girar d, 2005)

to determine the union, the reachable set of d(t) at

time t

q+1

is ﬁrst over-approximated by:

E(t

q+1

) := e

d,q

q+1

E(t

) ⊕C

(18)

accordin g to (17). Based on E(t

) and

E(t

q+1

the union

t∈[t

q+1

]

d,q

E(t

) is then over-

approximated by a zonotope. The general form of a

zonotope is:

Z := {z ∈ R

| z = c +

∑

h=1

, |z| ≤ 1} (19)

with the center c ∈ R

and the generators g

∈

, h ∈ {1, . . . , o} of Z. Note that the initial set

E(t

) in (14) also represents a zo notope Z

with

the center c

:= [x

1,q

1×n

(n−1)

]

and a number of

n generators g

h,t

∈ R

with: [g

1,t

, . . . , g

n,t

] :=

diag(x

max

, 2x

max

, . . . , 2x

max

). Based on Z

, a

new zonotope Z

q+1

]

with the center:

q+1

]

:= 0.5(e

d,q

+ e

d,q

q+1

)d(t

) (20)

and a numb er of 2n

n + 1 generators g

h,[t

q+1

]

∈R

h ∈{1, . . . , 2n

n + 1}can be determined. The ﬁrst n

generato rs are ob tained to:

h,[t

q+1

]

:= 0.5(e

d,q

+ e

d,q

q+1

h,t

(21)

for all h ∈ {1, . . . , n

n}, while for the last n

n genera-

tors:

h,[t

q+1

]

:= 0.5(e

d,q

−e

d,q

q+1

h−(n

n+1),t

(22)

applies for all h ∈ {n

n + 2, . . . , 2n

n + 1}. The re-

maining (n

n + 1)-th generator assumes the value:

n+1,[t

q+1

]

:= 0.5(e

d,q

−e

d,q

q+1

)d(t

). (23)

In this way, the zonotope Z

q+1

]

is ensured to con-

tain the initial set E(t

) and th e end set

E(t

q+1

Then, a new hypercube C

is deﬁned with a center

at 0

and with all sides having a common length

∈ R

:= (e

q+1

d,q

∞

−t

q+1

k A

d,q

∞

−1) sup

d∈{e

d,q

E(t

)}

k d k

∞

. (24)

In accordance with a result in (Girard, 2005), the

relation:

[

t∈[t

q+1

]

d,q

E(t

) ⊆ Z

q+1

]

⊕C

(25)

holds. To this end, the reachable set R

q+1

]

(E(t

))

is over-approxim ated by a new set:

q+1

]

(E(t

)) := Z

q+1

]

⊕C

(26)

accordin g to (17), see also Fig. 1.

Remark 1. The described procedure to compute the

set

q+1

]

(E(t

)) is tractable even for a large num-

ber of oscillators, which is important for the applica-

tion to larger networks. This holds true since l

and

of the two hypercubes can b e directly computed

according to (16) and (24), while for the zonotope

q+1

]

, the numbe r of generators to be computed

increases only linearly with the number n of oscilla-

tors.

By iteratively determining the over-approximated

reachable sets of Eq. (26), an over-approximated

reachable set can be determined for the whole period

] of the limit cycle consisting of p intervals:

]

(E(t

)) :=

p−1

[

q=0

q+1

]

(

E(t

q+1

)) (27)

with

E(t

) := E(t

). As only the part e(t) of the vec-

tor d(t) := [x

(t) e

(t)]

refers to th e synchronization

3 4

(t)

Figure 1: Consider the ﬁrst reachable set for compo-

nent three and four of d(t): Starting from E

3,4

which is also the zonotope Z

,3,4

, the sets

3,4

) and

]3,4

3,4

)) can be determined, and both are zono-

topes.

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

616

error, on e can project

q+1

]

(

E(t

q+1

)) o nto the cor-

respond ing subspac e in order to obtain the reachable

set of e(t). Now let σ := k

]

(E(t

))k

max

, such

that the so ught u pper bound of the synchronization

error is obtaine d.

3.4 Determination of Coupling Gains

Based on Reachable Sets

While the last section aimed at computing an upper

bound o n the size of the over-approximated set of syn-

chroniza tion errors, the perspective is now r everted,

i.e., given a bounding set fo r the erro r, the objective is

to obtain adm issible time-varying coupling gains.

First of all, a possibly time-varying bounding set

max

(t) ⊆ R

of the maximally allowable synchro-

nization errors is chosen for any x

(t) − x

(t), j ∈

{2, . . . , n}. Corre sponding to Assumption 2, it makes

sense to c hoose aga in a piecewise constant bounding

set E

max

(t) = E

max,q

for t ∈[t

q+1

]. The objective is

now to synthesize the coupling gains k

i j,q

such that

the reachable set of x

(t) −x

(t) within one period

never leaves E

max,q

. An option to o btain k

i j,q

is to

start from an initial value and then to iterate it until

the size of the over-approximation of the set of reach-

able synchroniza tion errors is limited to E

max,q

To do so, ﬁrst determine the period T of the limit

cycle of (3) and set t

equal to T while t

= 0 . The pe-

riod is divided into p inter vals, whereby it should be

noted that although the k

i j,q

are assumed to be dif-

ferent for each time interval [t

q+1

], the coupling

gains can also be constant for a series of time inter-

vals [t

q+1

], . . . , [t

q+v

q+1+v

] with v ∈ N, v < p.

Starting from initial values x

i,0

close to a poin t

of the limit cycle of the averaged dynamics, an ini-

tial set E(0) results as in (14), and the reachable

set

[0,T ]

(E(0)) can thus be determined. By allow-

ing the coupling gains to be adjusted in each inter val

q+1+r

], the reachable set

q+l

q+1+l

]

(

E(t

p+l

)),

l ∈ {0, . . . , v + 1} can be su ccessively constructed.

The synthesis ta sk, accordingly, is to ﬁnd suitable

gains k

i j,q

for ea c h interval (e.g. the smallest on es

which are just sufﬁcient to keep the error within the

selected bound).

Theorem 1. Let the projectio ns of

q+l

q+1+l

]

(

E(t

p+l

)), l ∈ {0, . . . , v + 1} onto each

subspace of e

( j,1)

(t) := x

(t) −x

(t), j ∈ {2, . . . , n}

be denoted by

q+l

q+1+l

]r,r+1

r,r+1

)) with the

dimensions r ∈ {1, . . . , n

n −1}. If:

a.) the projected sets

q+l

q+1+l

]r,r+1

r,r+1

))

with the dimensions r ∈ {1, . . . , n

n −1} are co n-

tained in E

max,q

for all coordinates r and all q,

and if

b.)

E(T ) is contained in the initial set E(t

) at the

end of the last interval,

then the synchronization error e

( j,1)

(t), j ∈{2, . . . , n},

never exceeds E

max,q

for the whole phase of preserv-

ing syn chroniza tion.

Proof. Starting from the ﬁrst interval of the limit cy-

cle, the if-cond ition under a.) ensures that the syn-

chroniza tion error starting from E(0) at t = 0 is al-

ways bounded by the E

max,q

within the ﬁrst period.

At the time t = T , which is the end of the ﬁrst pe-

riod as well as the beginning of the second period,

the second if-condition b.) ensures that the initial set

E(T ) of the second period is a subset of E(0). Thus,

the synchron iz ation er ror within the second period is

further bounded by the E

max,q

and containe d in E(0)

at the end. Recursive application guarantees that the

error is bounded by the E

max,q

for all t > 0.

By using this scheme, Problem 2 of synth esizing

the couplin g gains k

i j,q

is solved. Note that the set

q+l

q+1+l

]

(

E(t

p+l

)), l ∈ {0, . . . , v + 1 } for each in-

terval dep ends explicitly on the linearization (10) and

the Laplacian matrix L.

4 NUMERICAL EXAMPLES

In the following, two settings with two different

classes of nonlinear limit cycle oscillato rs are consid-

ered. For the ﬁrst setting, a constant gain k

i j

(t) = k

is used, while a tim e-variable k(t) is synthesized for

the r e spective oscillator ne twork in the second setting.

For the sake of sim plicity, the gains for all coupling

links are selected to be the same, a uniform step size

δt

= δt > 0 is selected, and E

max

(t) is chosen to be

constantly E

max

for all times.

4.1 Coupled van-der-Pol Oscillators

In the ﬁrst te st, the synchronization problem for an

example of n = 10 nonidentical van-der-Pol o scilla-

tors:



˙x

i,1

(t)

˙x

i,2

(t)





i,2

(t)

−x

i,1

(t)+ µ

(1−x

i,1

(t)

i,2

(t)



(28)

with signiﬁcantly different parameter µ

> 0 and i ∈

N is considered, see e.g. (Trummel et al., 2023). The

value of µ

decides the form of each loc a l limit cycle.

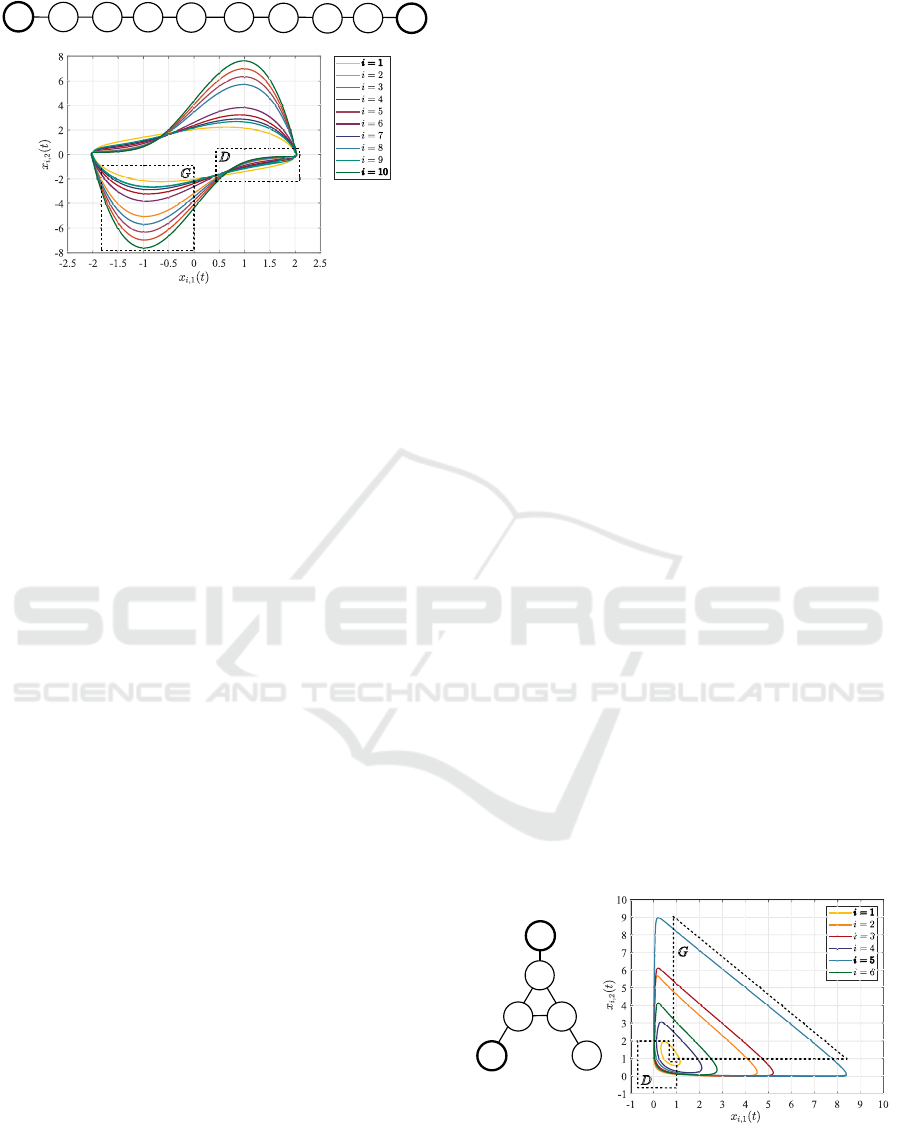
It can be noticed fr om their limit cycles in Fig. 2

that even without coupling, the lim it cycles are close

to each other in the region marked as D, while far

to each in the region G. Hence, one can infer that a

Computing Bounds for the Synchronization Errors of Nonidentical Nonlinear Oscillators with Time-Varying Diffusive Coupling

617

Figure 2: The considered 10 oscillators are assumed

to be connected by undirected edges in chain structure,

while their parameters are selected to: µ

= 0.5, µ

3, µ

= 4.5, µ

= 1.5, µ

= 4, µ

= 2, µ

= 1.2, µ

= 3.5, µ

1, µ

= 5. Their uncoupled limit cycles are quite different

in the region G, while being quite similar in the region D.

larger coupling gain would be required to preserve the

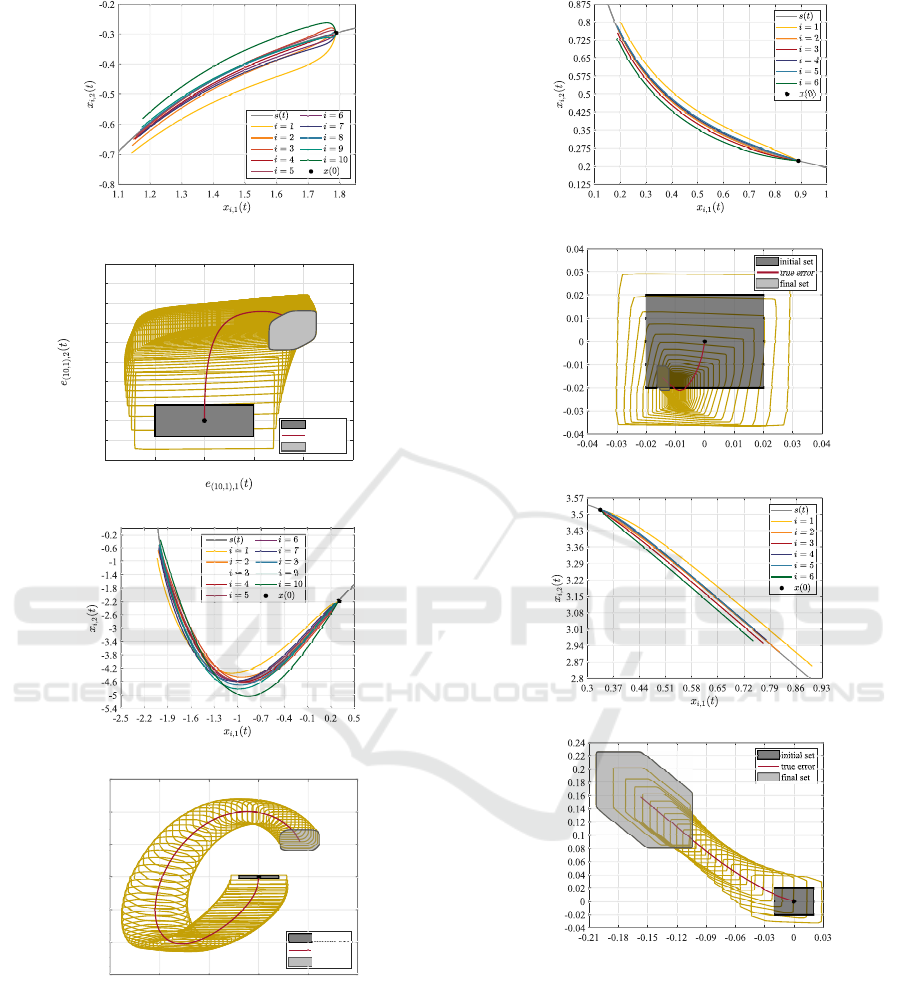
synchro nization in G than in D. To examine this, the

reachable set

[0,t

]

(E(t

)) of the synchronization er-

ror is computed for using a gain k = 20 – once for an

initial set in the region G (on the limit cycle of the

averaged dynamics (3)), and once with an initial set

in D, see Fig. 4. Note that the obtained reachable set

[0,t

]

(E(t

)) is projected onto the subspace of the

error e

10,1

(t) for illustration rea sons. This pair of os-

cillators is chosen since the parameters µ

= 0.5 and

= 5 differ the most over all oscillators. By com-

paring the reachable sets in Fig . 4b and Fig. 4d, one

can notice that th e reac hable set starting from the re-

gion D in the former plot is m uch smaller than the

one starting from G even for a la rger time interval

= 1.5 versus t

= 0.75). This shows that, in or-

der to keep the synchronization e rror below a certain

bound, a coupling gain sm a ller than k = 20 can be ap-

plied for the region D, while a larger on e is required

for the region G.

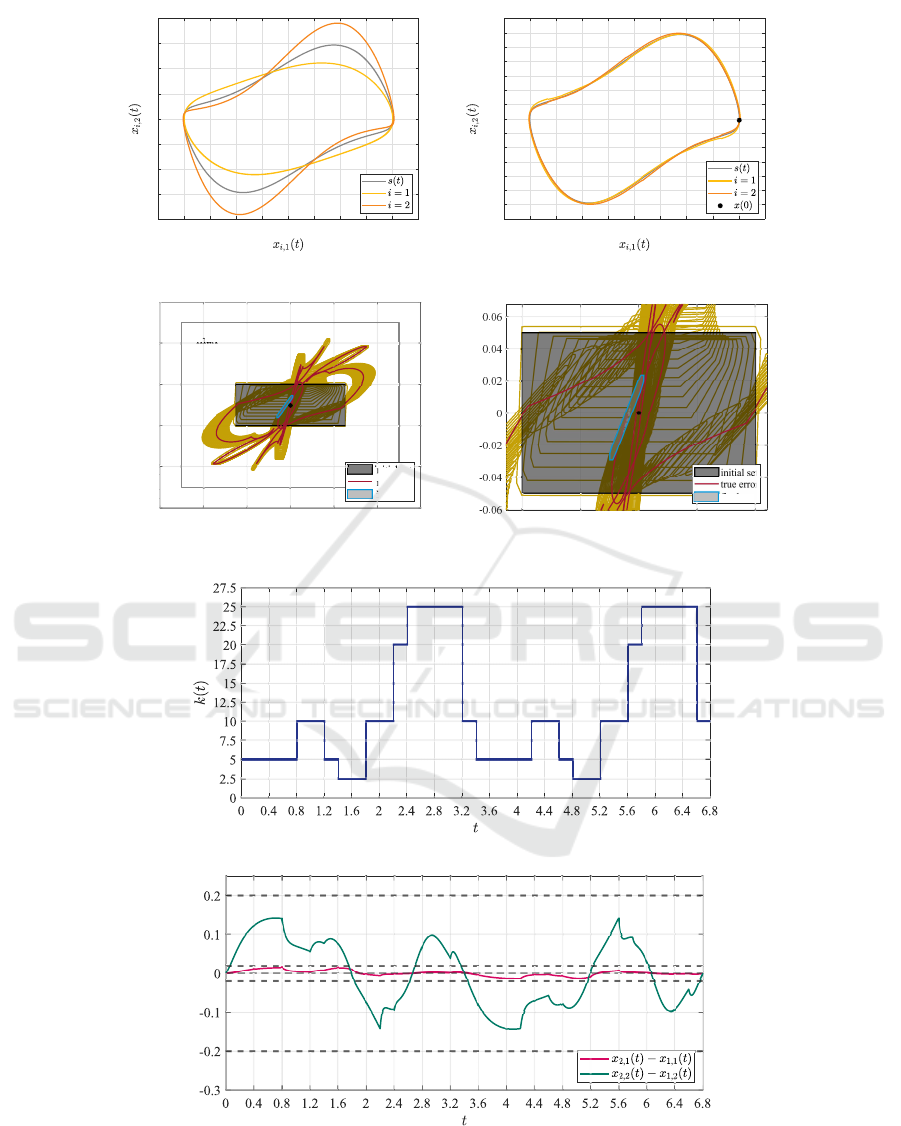
Then, the coupling gain k for two diffusively cou-

pled van-der-Pol oscillators with µ

= 0.5 and µ

= 2

is synthesized based on the reachable set (see the limit

cycles of the two oscillators and the one of the aver-

aged dynamics (3) in Fig. 6a). A given set E

max

of a

maximally permitted synchronization er ror is shown

in Fig. 6c. It is shown that by using the time -varying

coupling ga in in Fig. 6e, the reachable sets of the syn-

chroniza tion error are always contained in E

max

. At

the same time, the reachable set

E(T ) at the end of a

period with T = 6.8 and v = 34 is also contained in

the initial set E(0), see Fig. 6d.

4.2 Coupled Merkin–Needham–Scott

Oscillators

In the second test, a number of six diffusively coupled

Merkin–N eedham–Scott oscillators (Saha and Gan-

gopad hyay, 2017) in the form of:



˙x

i,1

(t)

˙x

i,2

(t)





−x

i,1

(t) + (η

+ x

i,1

(t)

i,2

(t)

−(η

+ x

i,1

(t)

i,2

(t)



with non identical parameters η

≥ 0, β

∈ R, and

i ∈ N are consid e red, see Fig. 3. The regions D and

G are deﬁned equivalently to the previous example,

and again the oscillators with the largest difference

between their limit cycles are taken into account. It

can be noticed that the reachable error sets starting

from regio n D are much smaller than the one initializ-

ing from area G. T herefore, a gain much smaller tha n

5 can be applied to obtain a synchronization which is

similar to the one for k = 5. For the area G, the re-

verse case is observed: the gain has to be increased to

reduce the size of the reachable sets. This observation

can once more be exam ined b y computing the reach-

able set of the synchronization error for usin g a gain

k = 5, and similar as the ﬁrst test, once starting from

the region G a nd once from the region D. The result-

ing reachable sets are demonstrated in Fig. 5, which

conﬁrmed the ob servation.

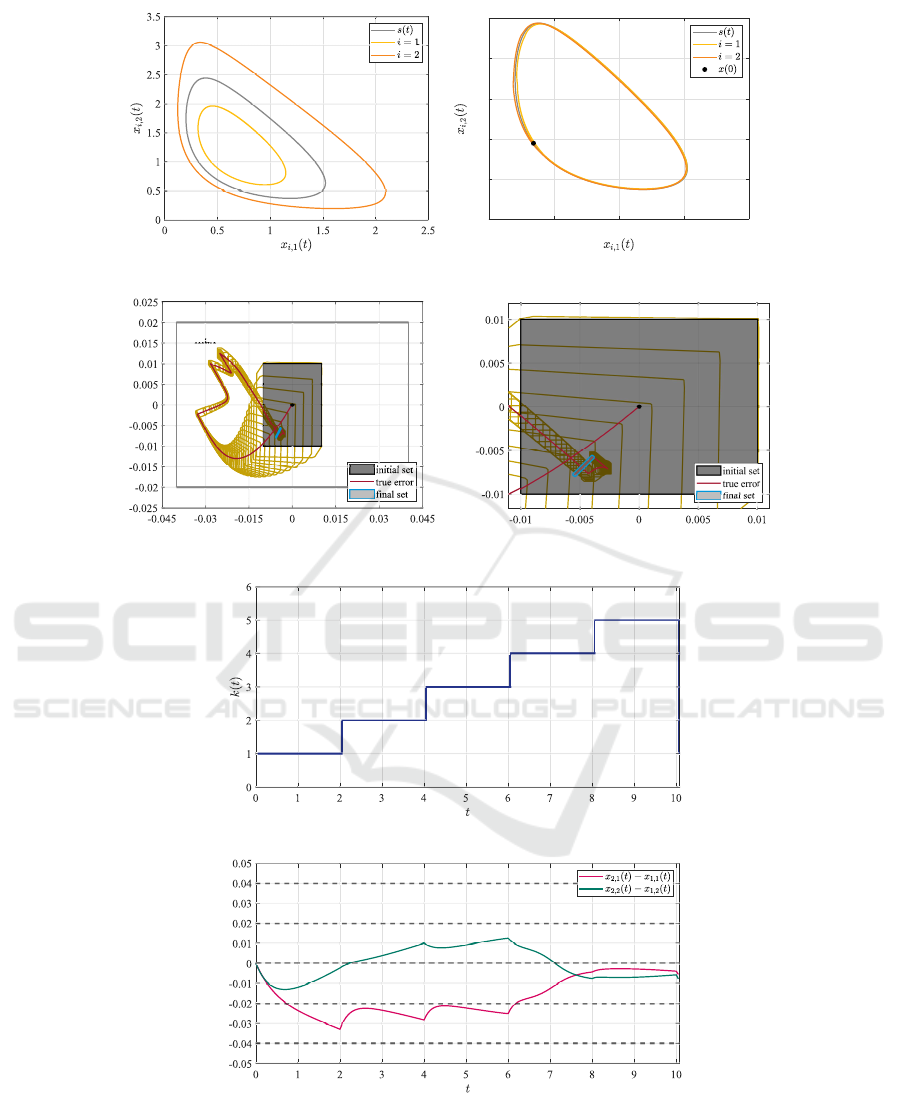
Finally, the coupling gains for two coupled

Merkin–N eedham–Scott oscillators (see Fig. 7a) with

parameters η

= 0.1, β

= 0.6, η

= 0.05, and β

0.5 are synthesized for the phase of preserving syn-

chroniza tion. The application of the procedure ex-

plained in Sec. 3.4 results in the time-varying cou-

pling gains shown in Fig. 7e, and satisfying E

max

in Fig. 7c. Obviously, E

max

contains

E(T ) at the end

of a period with T = 10.05 and v = 201, see Fig. 7d.

Thus, the time-varying coupling gain satisﬁes the

two conditio ns in Sec. 3.4, making it a good choice

for preserving synchronization.

Figure 3: Network of 6 Merkin–Needham–Scott limit cy-

cle oscillators with parameters: η

= 0.1, η

= 0.01, η

0.01, η

= 0.05, η

= 0.005, η

= 0.02, and β

= 0.6, β

0.2, β

= 0.3, β

= 0.5, β

= 0.4, β

= 0.25. Similar to the

van-der-Pol oscillator example, the trajectories in region D

are more similar than the ones in area G.

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

618

(a)

-0.04 -0.02 0 0.02 0.04 0.06

-0.05

-0.025

0.025

0.05

0.075

0.1

0.125

0.15

0.175

0.2

initial set

true error

final set

(b)

(c)

-0.15 -0.1 -0.05 0 0.05 0.1

-1.5

-1

-0.5

0.5

1.5

initial set

true error

final set

(10,1),1

(t)

(10,1),2

(t)

(d)

Figure 4: By using a coupling gain k = 20, the reachable set

of e

(10,1)

(t) is computed once starting from the region D and

once from the region G in Fig. 2. The gray limi t cycle seg-

ments in (a) and (c) are the one from the averaged dynamics

(3). The zonotopes in yellow in (b) and (d) are the interme-

diate reachable sets

q+1

]

(

E(t

q+1

)) projected onto the

space of e

(10,1)

(t) with δt = 0.005. The union of those inter-

mediate reachable sets is thus the reachable set of the whole

interval [0, 1.5] for (b) and [0, 0.75] for (d).

(a)

(5,1),1

(t)

(5,1),2

(t)

(b)

(c)

(5,1),1

(t)

(5,1),2

(t)

(d)

Figure 5: Reachable sets of e

(5,1)

(t) determined for k = 5,

once starting from the region D and once from G in Fig.

3. The parts (a) and (c) show the gray limit cycle seg-

ments from the averaged dynamics (3). The yellow colored

zonotopes in (b) and (d) are the intermediate reachable sets

q+1

]

(

E(t

q+1

)) projected onto the space of e

(5,1)

(t) with

δt = 0.05. The union of these reachable sets is the reachable

set for the whole interval [0, 2] for (b) and [0, 1] for (d).

Computing Bounds for the Synchronization Errors of Nonidentical Nonlinear Oscillators with Time-Varying Diffusive Coupling

619

-2.5 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 2.5

-4

-3

-2

-1

(a)

-2.5 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 2.5

-3.5

-3

-2.5

-2

-1.5

-1

-0.5

0.5

1.5

2.5

3.5

(b)

-0.024 -0.016 -0.008 0 0.008 0.016 0.024

-0.25

-0.15

-0.05

0.05

0.15

0.25

initial set

true error

final set

(2,1),1

(t)

(2,1),2

(t)

max

(c)

-0.01 -0.005 0 0.005 0.01

final set

(2,1),1

(t)

(2,1),2

(t)

(d)

(e)

(f)

Figure 6: By using the time-varying coupling gains in (e), the reachable sets of the synchronization error in (c) are always

contained in E

max

for the whole period, while

E(T ) at the end of a period is also contained in E(0), see (d). A possible

evolution of the synchronization error e

(2,1)

(t) in (f) of the synchronizing states in (b) conﬁrms the result.

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

620

(a)

0 0.5 1 1.5 2

0.5

1.5

2.5

(b)

(2,1),1

(t)

(2,1),2

(t)

max

(c)

(2,1),1

(t)

(2,1),2

(t)

(d)

(e)

(f)

Figure 7: The application of the time-varying coupling gains in (e) leads to the reachable sets of the synchronization error in

(c), while they are always contained in E

max

for the whole period.

E(T ) at t he end of a period is also contained in E(0), see

(d). In (f), the evolution of the synchronization error e

(2,1)

(t) is illustrated for the synchronizing states in (b).

Computing Bounds for the Synchronization Errors of Nonidentical Nonlinear Oscillators with Time-Varying Diffusive Coupling

621

5 CONCLUSIONS

The pap e r has provid ed techniques to analyze and

synthesize bounds of the synchronization error f or a

network of diffusively coupled nonidentical nonlin-

ear limit cycle oscillators. Since the synchronization

error cannot be derived as analytic expression due to

the non linear dynamics of the local oscillators, over-

approximating reachable sets of the error are deter-

mined for evaluation over time. Based on the obtained

reachable set, a suitable coupling gain to preserve

the sync hronizatio n can be synthesized with a guar-

anteed bound on the maximal synchronization e rror.

Effectiveness of this method is con ﬁrmed in differ-

ent simulations with respect to both, the reachable set

computations and the synthesis of the cou pling gain.

The method s can be applied to any possible coupling

topology of the oscillator network.

Future work aims at applying the method to other

types of n onlinear oscillators, and to the consideration

of exogenous signals imposed on the oscillators.

ACKNOWLEDGMENTS

Partial funding from the German Research Founda-

tion (DFG) as part of the Research Training Group

’Biological Clocks o n Mu ltiple Time Scales’ is grate-

fully acknowledged.

REFERENCES

Althoff, M., Stursberg, O., and Buss, M. (2008). Reach-

ability analysis of nonlinear systems with uncertain

parameters using conservative linearization. In IEEE

Conf. on Decision and Control, pages 4042–4048.

Girard, A. (2005). Reachability of uncertain linear systems

using zonotopes. In Int. Workshop on Hybrid Systems:

Computation and Control, pages 291–305. Springer.

Kim, P., Oster, H., Lehnert, H., Schmid, S. M., Sala-

mat, N., Barclay, J. L., Maronde, E ., Inder, W. , and

Rawashdeh, O. (2019). Coupling the circadian clock

to homeostasis: The role of period in timing physiol-

ogy. Endocrine reviews, 40(1):66–95.

Lee, J. G. and Shim, H. (2022). Design of heteroge-

neous multi-agent system for distri buted computation.

Trends in Nonlinear and Adaptive Control: A Tribute

to Laurent Praly for his 65th Birthday, pages 83–108.

Lee, J. G., Trenn, S., and Shim, H. (2022). Synchro-

nization with prescribed transient behavior: Hetero-

geneous multi-agent systems under f unnel coupling.

Automatica, 141:110276.

Panteley, E. and Lor´ıa, A. (2017). Synchronization and

dynamic consensus of heterogeneous networked sys-

tems. IEEE Trans. on Automatic Control, 62(8):3758–

3773.

Rungger, M. and Zamani, M. (2018). Accurate reachability

analysis of uncertain nonlinear systems. In Int. Conf.

on Hybrid Systems: Comp. and Control, pages 61–70.

Saha, S. and Gangopadhyay, G. (2017). Isochronicity and

limit cycle oscillation in chemical systems. Journal of

Mathematical Chemistry, 55:887–910.

Sang, H . and Zhao, J. (2020). Event-driven synchronization

of switched complex networks: A reachable-set-based

design. IEEE Trans. on Neural Networks and Learn-

ing Systems, 32(10):4761–4768.

Scardovi, L. and Sepulchre, R. (2008). Synchronization in

networks of identical linear systems. In IEEE Conf.

on Decision and Control, pages 546–551.

Stursberg, O. and Kr ogh, B. H . (2003). Efﬁcient representa-

tion and computation of reachable sets for hybrid sys-

tems. In Hybrid Systems: Comp. and Control, pages

482–497. Springer.

Trummel, T., Liu, Z., and Stursberg, O. (2023). On optimal

synchronization of diffusively coupled heterogeneous

van-der-Pol oscillators. Proc. of the 22nd IFAC World

Congress, pages 9475––9480.

Wang, B., Suzuki, H., and Aihara, K. (2016). Enhancing

synchronization stability in a multi-area power grid.

Scientiﬁc reports, 6(1):26596.

Wang, Y.-W., Xiao, J.-W., Wen, C., and Guan, Z.-H. (2011).

Synchronization of continuous dynamical networks

with discrete-time communications. IEEE Trans. on

neural networks, 22(12):1979–1986.

Xiao, Y. and Zhu, K. (2006). Optimal synchronization con-

trol of high-precision motion systems. IEEE Trans. on

Industrial Electronics, 53(4):1160–1169.

Ye, Y. and Cai, S.-l. (1986). Theory of limit cycles, vol-

ume 66. American Mathematical Soc.

Zhao, J., Hill, D. J., and Liu, T. (2012). Global bounded

synchronization of general dynamical networks with

nonidentical nodes. IEEE Trans. on Automatic Con-

trol, 57(10):2656–2662.

Zhu, S., Zhou, J. , Yu, X., and Lu, J. (2020). Bounded

synchronization of heterogeneous complex dynamical

networks: A uniﬁed approach. IEEE Trans. on Auto-

matic Control, 66:1756–1762.

ICINCO 2024 - 21st International Conference on Informatics in Control, Automation and Robotics

622