A Graph-Based Deep Learning Model for the Anti-Money Laundering

Task of Transaction Monitoring

Nazanin Bakhshinejad

, Uyen Trang Nguyen

, Shahram Ghahremani

and Reza Soltani

Department of Electrical Engineering and Computer Science, York University, 4700 Keele St, Toronto,

M3J 1P3, ON, Canada

{nbakhshi, unguyen, shg}@yorku.ca, rts@cse.yorku.ca

Keywords:

Anti-Money Laundering, Transaction Monitoring, Machine Learning, Deep Learning, Graph Convolutional

Networks, Class Imbalance.

Abstract:

Anti-money laundering (AML) refers to a comprehensive framework of laws, regulations, and procedures

to prevent bad actors from disguising illegally obtained funds as legitimate income. The AML framework

encompasses customer identity veriﬁcation and risk assessment, monitoring transactions to detect suspicious

money laundering activities, and reporting suspicious transactions to regulators. In this paper, we focus on the

transaction monitoring task of the AML framework. We propose a graph convolutional networks (GCN) model

to classify transactions as legitimate or suspicious of money laundering. We tested and evaluated the model on

a publicly available large dataset to promote reproducibility. The proposed model was trained and evaluated

using the classiﬁcation objectives for AML transaction monitoring per industry standard. We describe in detail

our solutions to the class imbalance problem typical of AML datasets. We present comprehensive experiments

to demonstrate and justify how the important parameters of the model were optimized and selected. This helps

to support reproducibility and comparison with future work.

1 INTRODUCTION

Money laundering (ML) is the process of converting

illicit funds, often referred to as “dirty” money, into

assets that appear legitimate. This process typically

involves proceeds from a wide range of criminal ac-

tivities, including but not limited to tax evasion, hu-

man trafﬁcking, illegal gambling, terrorism, and theft.

Money laundering is a global threat to economy and

security, ranking as the third-largest industry within

the realm of criminal enterprises. It contributes to ap-

proximately 2% to 5% of the global gross domestic

product (GDP) (UNODC, 2022). This translates to

a staggering $800 billion to $2 trillion in current US

dollars.

1.1 Background and Motivations

To combat money laundering (anti-money launder-

ing), ﬁnancial institutions are legally required to im-

plement measures aimed at identifying and preventing

https://orcid.org/0009-0003-7386-7844

https://orcid.org/0000-0002-4860-3551

https://orcid.org/0000-0001-9905-7530

https://orcid.org/0000-0001-7146-9920

such illicit activities. These measures include strin-

gent customer identity veriﬁcation, risk assessment of

customers, monitoring of their accounts and ﬁnancial

transactions, and reporting of any suspicious activity

to the corresponding national regulator (e.g., FinCEN

in the United States and FINTRAC in Canada). Fail-

ures to report AML cases or comply with AML regu-

lations have resulted in huge ﬁnes for many ﬁnancial

institutions (Husain, 2024). In this article, we limit the

scope of AML to transaction monitoring and use the

term “AML” to refer to the task of monitoring transac-

tions to detect suspicious money laundering activities.

In the current systems for monitoring transactions,

alerts are typically triggered by a rule-based algo-

rithm (Ross and Hannan, 2007) when customer trans-

actions violate certain rules, e.g., when a customer

in the U.S. or Canada deposits a cheque of $10,000

or more and withdraws cash immediately after that.

These alerts then progress through three stages: alert

stage, case stage, and reporting stage (Jullum et al.,

2020). During the alert stage, investigators quickly

assess and classify alerts as either “false positives” or

“suspicious”. Those ﬂagged as suspicious advance

to the second stage (case stage) for an in-depth re-

view and validation. Investigators perform thorough

496

Bakhshinejad, N., Nguyen, U., Ghahremani, S. and Soltani, R.

A Graph-Based Deep Learning Model for the Anti-Money Laundering Task of Transaction Monitoring.

DOI: 10.5220/0013071700003837

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Joint Conference on Computational Intelligence (IJCCI 2024), pages 496-507

ISBN: 978-989-758-721-4; ISSN: 2184-3236

and detailed examinations to determine the nature

of the suspicious transactions (e.g., unusual activity,

high-risk transfer), and verify whether the transac-

tions are indeed part of money laundering activity.

If so, these cases are forwarded to the third stage,

(reporting stage). Stage-3 investigators further re-

view the cases forwarded and validate the ﬁndings of

stage-2 investigations. If deemed accurate and com-

pliant, these cases are reported to the Money Laun-

dering Reporting Ofﬁcer (MLRO) of the ﬁnancial in-

stitution with a recommendation for ﬁling suspicious

activity/transaction reports to the regulators.

Note that the thresholds for the alert generation

logic are set to highly conservative values to catch

the maximum possible number of money laundering

transactions, but also lead to high numbers of false

positives (legitimate transactions labeled as money

laundering). The false alert rate (FAR), deﬁned as the

number of false positives divided by the total number

of alerts generated, is typically 95% - 98%. Investi-

gators must thoroughly examine all alerts to dismiss

false positives. This process is very costly due to high

FAR and manual investigations.

Machine learning can signiﬁcantly reduce the

FAR while accurately detecting money launder-

ing (Jullum et al., 2020; Raiter, 2021). Also, machine

learning can detect emerging patterns absent in a rule-

based system and learn new patterns quickly via re-

training with new data. On the other hand, develop-

ing machine learning models for AML face several

challenges, more so than most other applications of

machine learning.

1.2 Challenges in Developing Machine

Learning Models for AML and Our

Methodology

We identify the three most challenging issues: 1) lack

of real-world datasets; 2) extremely imbalanced class

distributions in AML datasets; and 3) improper use of

metrics to evaluate AML machine learning models.

1.2.1 Lack of Real-World Datasets

This results from stringent data protection regulations

to protect the privacy and conﬁdentiality of customer

data. Real-world datasets used in prior research are

usually very small, or do not have real money laun-

dering transactions (Bakhshinejad, 2023).

Given the severe scarcity of real-world datasets,

synthetic data have been used to enable the ﬁrst

step towards developing machine learning models for

AML. Such models can be ﬁne-tuned when real-

world data are made available. In this article, we use a

synthetic dataset named PaySim (Lopez-Rojas et al.,

2016) and adapt it to the requirements of the AML

transaction monitoring task.

1.2.2 Extremely Imbalanced Class Distributions

Financial transaction data for AML are inherently and

extremely imbalanced, with the positive to negative

(P/N) sample ratio in the range of 1/100 to 1/1,000.

Given a large number of negative samples (legiti-

mate transactions) versus very few positive samples

(money laundering transactions), the training model

will learn from negative samples most of the time and

not enough from positive samples. This will lead to

a high number of misclassiﬁcations, especially in the

minority class. In AML, failing to catch money laun-

dering transactions may result in ﬁnes in the range

of millions of dollars (Rae, 2024; AUSTRAC, 2024),

imposed by regulators on the offending institutions.

A prior survey (Bakhshinejad, 2023) noted that many

papers on AML did not discuss the problem of data

imbalance or solutions to the problem in their data.

We suspect that many did not even resolve or miti-

gate the problem. In the development of our proposed

AML model, we resolve the data imbalance prob-

lem using SMOTE (Synthetic Minority Oversampling

Technique) (Chawla et al., 2002) and near-miss un-

dersampling (Mani and Zhang, 2003) discussed in

Section 4.1.

1.2.3 Improper Use of Metrics to Evaluate AML

Machine Learning Models

A prior survey (Bakhshinejad, 2023) noted that many

papers on AML use accuracy and F1 score to evaluate

their models against some baseline. Given a test set

with a positive to negative sample ratio of 1/1,000, a

ıve algorithm that returns false (i.e., negative label)

for every input sample would result in an accuracy of

99.99%!

F1 score favors a balance of recall and preci-

sion. In AML, the ultimate goal is to reach a recall

of 100% (not missing any money laundering trans-

actions), even at the expense of precision (which is

equal to one minus the false alarm rate). In fact, false

alert rates in current rule-based transaction monitor-

ing systems are about 95% to 98% (equivalent to pre-

cision values of 5% to 2%, respectively). For this

reason, F1 score is not suitable for evaluating AML

machine learning models.

The survey (Bakhshinejad, 2023) noted that many

papers on AML used accuracy and F1 score as the

only metrics to evaluate their models, which cannot

tell us about the effectiveness and performance of a

model for AML transaction monitoring. Table 1 pro-

A Graph-Based Deep Learning Model for the Anti-Money Laundering Task of Transaction Monitoring

497

vides examples of earlier models that used the PaySim

dataset (Lopez-Rojas et al., 2016) and their classiﬁca-

tion performance as reported in the respective papers.

The accuracy of these models ranges from 81.25%

to 99%, while the class distribution of the PaySim

dataset is approximately 1/1000. The above na

ıve al-

gorithm with an accuracy of 99.99% would have out-

performed all the models in Table 1 in terms of accu-

racy

Table 1: Performance metrics in existing works that use the

PaySim dataset (FPR: false positive rate, FNR: false nega-

tive rate).

Model Accuracy F1 Score FPR FNR

(Raiter, 2021) 99.00 36.00 - -

(Tundis et al., 2021) 95.44 95.89 6.70 2.70

(Pambudi et al., 2019) 88.00 90.00 – –

(Kumar et al., 2020) 81.25 – – –

In this paper, we use two main metrics to eval-

uate our proposed model: recall and false alert rate

(equivalent to 1− precision). All metrics used will be

discussed in detail in Section 4.2.

1.3 Contributions and Methodology

In this article, we propose a model based on graph

convolutional networks (GCN) to classify transac-

tions as legitimate or suspicious of money laun-

dering. We use the node embedding algorithm

node2vec (Grover and Leskovec, 2016) to capture es-

sential structural information about nodes and their

relationships to enhance the classiﬁcation perfor-

mance of the GCN model. Equally important, we pro-

vide detailed solutions to the class imbalance problem

of AML data and use appropriate metrics for evalu-

ating machine learning models for AML transaction

monitoring. Following are the contributions of this

paper:

• We propose a GCN classiﬁer named N2V-GCN to

detect suspicious money laundering transactions,

which outperforms traditional machine learning

techniques such as random forests, logistic re-

gression, and SVM. N2V-GCN is among the ﬁrst

GCN models developed speciﬁcally for AML

transaction monitoring.

• We provide experimental results that show that

node embeddings (using node2vec) noticeably en-

It is not clear if the authors of the above papers had

applied any resampling techniques to get a positive to nega-

tive sample ratio higher than that of the PaySim dataset for

evaluating their models. The papers did not discuss how the

problem of imbalanced data was handled.

hances the classiﬁcation performance of the GCN

classiﬁer.

• Different from most existing work, our proposed

model was ﬁne tuned using the following objec-

tives. The primary objective is to maximize the

recall (true positive rate), ideally reaching 100%,

even at the expense of the false alert rate (or pre-

cision). This objective is consistent with the cur-

rent industry practice, with false alert rates rang-

ing from 95% - 98%. The reason is that the cost

of a false negative is much higher than the cost of

a false positive. Failures to report money launder-

ing cases or to comply with AML regulations have

resulted in ﬁnes in the range of millions to billions

of US dollars (Husain, 2024). Given the same re-

call value, the secondary objective is to reduce the

false alert rate (or to increase the precision, which

is equal to one minus the false alert rate).

• Different from existing work, our work shows

how class imbalance negatively affects the clas-

siﬁcation performance via experimental results.

We applied resampling to obtain a more balanced

dataset to train our model, resulting in higher clas-

siﬁcation performance.

The remainder of this article is structured as fol-

lows. Section 2 reviews existing work on machine

learning for AML. In Section 3, we describe our pro-

posed graph-based deep learning model designed for

AML transaction monitoring. Section 4 presents ex-

perimental results of various scenarios: class distri-

butions, ﬁne tuning of model thresholds, ﬁne tuning

node embedding parameters, ablation study of node

embeddings, and performance comparison with tradi-

tional machine learning techniques. Section 6 sum-

marizes key ﬁndings and outlines potential issues for

future research.

2 RELATED WORK

We brieﬂy review related work on machine learning

for AML, including traditional machine learning tech-

niques, deep learning, graph-based learning and un-

supervised learning. In-depth surveys and reviews on

machine learning for AML can be found in (Thom-

mandru et al., 2023; Youssef et al., 2023; Kute et al.,

2021; Chen et al., 2018a; Bakhshinejad, 2023; Chen

et al., 2018b; Labib et al., 2020; Alsuwailem and

Saudagar, 2020).

NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications

498

2.1 Traditional Machine Learning

Most research on money laundering detection lever-

ages supervised machine learning. Early AML super-

vised models used Bayesian networks (Kumar et al.,

2020), decision trees (Jullum et al., 2020; Jayas-

ree and Balan, 2017), logistic regression (Tertychnyi

et al., 2020), scan statistics (Liu and Zhang, 2010),

neural networks (Chen et al., 2021), SVM (Raiter,

2021; Tang and Yin, 2005; Keyan and Tingting,

2011; Lopez-Rojas and Axelsson, 2012), and ran-

dom forests (Lopez-Rojas and Axelsson, 2012; Ke-

tenci et al., 2021).

2.2 Deep Learning

Deep learning models have recently been developed

for the task of fraud detection. Autoencoders have

been applied to detect anomalies by learning to re-

construct inputs and identifying those that cannot be

accurately reconstructed as suspicious (Paula et al.,

2016; Kumar et al., 2022). Generative Adversarial

Networks (GANs) have also shown promise in AML

by generating synthetic data to train models for bet-

ter fraud detection (Pereira et al., 2023; Pandey et al.,

2022). Other deep learning approaches, such as Long

Short-Term Memory (LSTM) networks, have been

employed to capture temporal dependencies in trans-

action sequences, improving detection accuracy (Jur-

govsky et al., 2018; Roy et al., 2018). Transformers,

which have revolutionized natural language process-

ing, have been adapted for AML tasks to model com-

plex dependencies in transactional data (Tatulli et al.,

2023).

2.3 Graph-Based Machine Learning

Graph analytics is particularly effective for AML due

to its ability to analyze complex connections among

customers, accounts, and transactions (Soltani et al.,

2016). Recently, several models based on GCN have

been proposed for anti-ﬁnancial crime tasks. (Marasi

and Ferretti, 2024), (Ning et al., 2024), (Wan and Li,

2024) and (Guo et al., 2023) propose and/or evalu-

ated GCN models to detect illicit cryptocurrency ac-

tivities using the Elliptic dataset (Weber et al., 2019a).

This dataset contains a large set of Bitcoin transac-

tions which are labeled as licit or illicit. Illicit trans-

actions are those associated with illicit websites or

sources. The patterns of illicit Bitcoin transactions are

different from those of bank transactions due to the

anonymity of Bitcoin transactions. Thus the ﬁndings

from the above works may not be applicable to bank

transaction monitoring. (Silva et al., 2023) compare

the performance of GCN, Skip-GCN (Weber et al.,

2019b), and NENN architecture (Yang and Li, 2020)

for detecting money laundering transactions. The pa-

per focuses on achieving a balance of recall and pre-

cision as represented by the F1 score. On the other

hand, the main focus of detecting money laundering

should be to maximize recall to catch the maximum

possible number of money laundering transactions.

2.4 Unsupervised Learning

Compared to supervised learning, there is a limited

number of works using unsupervised learning. The

most commonly used algorithm is k-means clustering

(Chen et al., 2014; Dre

zewski et al., 2015). Other

clustering algorithms that have been used for AML

include expectation maximization (Chen et al., 2014),

CLOPE (Cao and Do, 2012), and minimum spanning

trees (Wang and Dong, 2009).

In addition to clustering, unsupervised anomaly

detection techniques have been used to detect suspi-

cious cases of fraud or money laundering (Pham and

Lee, 2016). Unlike clustering techniques that sepa-

rate data points into different groups, anomaly detec-

tion models aim to ﬁnd data points that deviate from

the normal behavior of the majority of data points in

the dataset.

3 THE PROPOSED MODEL

Figure 1 presents an overview of the proposed model,

which we name N2V-GCN. This model integrates the

node2vec (N2V) graph embedding technique with a

graph convolutional network (GCN).

To train the model, we aimed to have a training

set more balanced than the original class distribu-

tion of the PaySim dataset (Lopez-Rojas et al., 2016).

To achieve this, we applied the following resampling

techniques:

• oversampling the minority class (money launder-

ing transactions) using SMOTE (Synthetic Mi-

nority Over-sampling Technique)(Chawla et al.,

2002).

• undersampling the majority class (legitimate

transactions) using near-miss undersampling.

The resampled training dataset is then converted into

a graph, in which vertices represent customer ac-

counts and edges represent transactions between cus-

tomer accounts, one edge per transaction. The ver-

tices and edges of the graph are then transformed into

vector representations using node2vec embeddings,

A Graph-Based Deep Learning Model for the Anti-Money Laundering Task of Transaction Monitoring

499

which are then input into the GCN model. The model

is trained using the vectors output by node2vec.

The testing and evaluation process is similar to the

above procedure, except that the test data is not re-

sampled but keeps the natural distribution, which is

1/1,000 on the PaySim dataset.

3.1 Generating Node Embeddings with

node2vec

We employed node2vec (Grover and Leskovec,

2016), a node embedding technique based on Deep-

Walk, to generate embedding vectors for transaction

graphs. DeepWalk explores a graph through random

walks, but its randomness limits representation qual-

ity. Node2vec improves this by using a biased random

walk with two key parameters:

• In-out parameter q: Controls exploration depth,

balancing between exploring far nodes (BFS-like)

or staying local (DFS-like).

• Return parameter p: Adjusts the probability of

revisiting nodes, promoting either local or broad

exploration.

These parameters guide walk paths and control the

balance between local and global exploration. Node

sequences generated by node2vec are processed with

the skip-gram algorithm to create embedding vectors,

which are then used as input for the graph convolu-

tional network (Mikolov et al., 2013).

3.2 Learning Algorithm Using a Graph

Convolution Network

We use the graph convolution network (GCN) al-

gorithm proposed by Kipf and Welling (Kipf and

Welling, 2016), to classify transactions as legitimate

or suspicious. The GCN algorithm consists of three

main layers: input layer, convolution (or hidden)

layer, and output layer. At the input layer, the GCN

algorithm takes two inputs: embedding vectors gener-

ated using the node2vec algorithm and the adjacency

matrix representing the graph.

In our model, the embedding vectors generated by

the node2vec algorithm are used as a feature set to

classify transactions. These embedding vectors form

a matrix of numerical values, where each row repre-

sents the embedding vector for a speciﬁc node in the

graph. This matrix is depicted in Figure 2.

At each layer of neighborhood aggregation, an

embedding vector is generated for each node. As a

result, nodes have different embeddings at each layer.

For instance, in the input layer, node embeddings are

essentially the input matrix X that represents the ini-

tial features of the node network.

In each layer, the neural network performs the

propagation step while learning a set of weights for

the input data. This process repeats for all layers

in GCN, increasing the size of the local neighbor-

hood used to calculate embedding for each node.

This type of computation is a ﬁrst-order approxima-

tion of the local spectral ﬁlters on the graph, which

improves computational efﬁciency (Palamuttam and

Chen, 2017).

Following the convolution layer, a fully connected

layer combines the information from all nodes in the

graph to make a ﬁnal prediction or decision. We apply

two neurons in the output layer, each of which repre-

sents one of the two classes: legitimate or suspicious

transaction. The softmax activation function converts

a raw output into the probability that the correspond-

ing input belongs to a particular class. This probabil-

ity is in the range of (0, 1] and provides an intuitive

interpretation of the output, e.g., “there is a 75% prob-

ability that this transaction is money laundering” or

“there is a 90% probability that this transaction is le-

gitimate.” The two-neuron conﬁguration allows us to

obtain prediction probabilities directly for each class

(instead of relying on a threshold probability value

separating the two classes in the one-neuron conﬁg-

uration, e.g., 60% or higher indicating money laun-

dering, and under 60% indicating legitimate trans-

actions). The more intuitive and user-friendly pre-

diction probabilities can assist investigators in prior-

itizing cases for investigation and quickly dismissing

false alerts to improve productivity.

4 EXPERIMENT SETTINGS AND

MODEL PARAMETERS

In this section, we describe the dataset used, data pre-

processing, solutions to the class imbalance problem,

performance metrics, and node2vec and GCN param-

eters.

4.1 Dataset and Data Processing

We use a synthetic dataset named PaySim (Lopez-

Rojas et al., 2016) publicly available on Kaggle.

PaySim consists of 1,142 illegitimate transactions and

1,047,433 legitimate transactions, giving a minor-

ity/majority sample ratio of approximately 1/1,000.

Each transaction in the PaySim dataset is composed

of several features and a classiﬁcation label indicat-

ing if the transaction is licit or illicit. The features in-

clude the type of transaction, amount, sender account

NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications

500

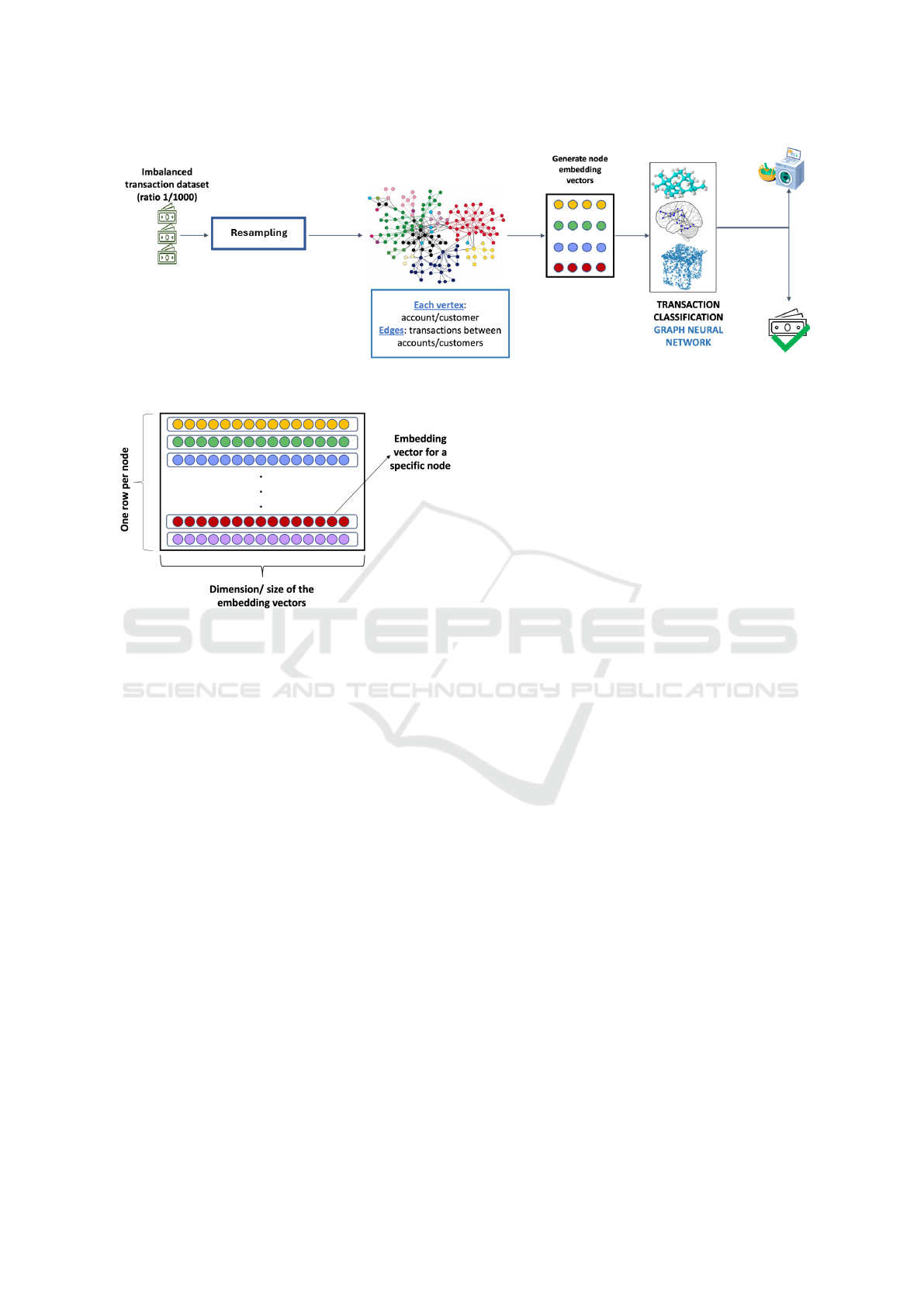
Figure 1: An overview of N2V-GCN.

Figure 2: Resulting matrix from node embeddings by

node2vec.

number, receiver account number, sender account bal-

ances before and after the transaction, and receiver

account balances before and after the transaction.

We partitioned the dataset into three subsets for

training (60%), validation (20%) and testing (20%).

The partition maintained the original class distribu-

tion of 1/1000 in all three sets.

Using SMOTE and near-miss undersampling, we

generated nine different class distributions, in addi-

tion to the natural distribution of PaySim, to obtain

the following 10 distributions: 1/1000, 1/500, 1/200,

1/100, 1/50, 1/20, 1/10, 1/5, 1/2, 1/1. These class dis-

tributions were implemented only in the training sets

to evaluate the impact of various class distributions

on the learning algorithm’s performance. The test set

keeps the natural distribution 1/1,000 of PaySim, as

imbalanced data is typical in real-world AML sce-

narios. Experimental results that demonstrate the im-

pact of class distributions on the classiﬁcation perfor-

mance are presented in Section 5.2.

We then converted the tabular data into graph data

structures using the NetworkX library in Python.

4.2 Performance Evaluation Metrics

We use two main metrics for classiﬁcation perfor-

mance: recall (true positive rate) and false alert rate

(FAR, which equals 1− precision). The objective of

the classiﬁer is to maximize the recall, ideally reach-

ing 100%. Given the same recall value, the secondary

objective is to minimize the false alert rate.

To facilitate the discussions, we will also show the

following metrics in the results, which are related to

the recall and false alert rate:

• number of false negatives (money laundering

transactions misclassiﬁed as legitimate).

• false negative rate (FNR), which equals 1− recall.

• precision, which equals 1− FAR.

4.3 Graph Embedding node2vec

Parameters

There are ﬁve parameters to be conﬁgured when using

node2vec:

• Return Parameter p: It controls the likelihood of

the random walk returning to the previous node

in the walk. A higher p value discourages back-

tracking to the previous node, encouraging explo-

ration of new nodes and capturing a more global

structure. A value of 1 corresponds to an unbiased

random walk.

• In-Out Parameter q: It controls the likelihood of

the random walk exploring new nodes. A higher q

value encourages the random walk to explore dis-

tant nodes, capturing a broader view of the graph.

• Number of Walks: It speciﬁes the number of walks

to start at each node. More walks from each node

help in capturing more comprehensive structural

information.

A Graph-Based Deep Learning Model for the Anti-Money Laundering Task of Transaction Monitoring

501

• Walk Length: It speciﬁes the number of nodes vis-

ited in each walk. A longer walk length helps in

exploring deeper structures of the graph.

• Size of Embedding Vectors: It speciﬁes the di-

mensionality of the resulting embedding vectors,

which represent each node in a lower-dimensional

space and can be used for various downstream

machine learning tasks.

To obtain the best possible results in our exper-

iments, we conducted tests with various sets of pa-

rameters and ultimately selected the combination that

yielded the most favourable outcomes. The grid

search method was employed to determine the opti-

mal set of hyperparameters for node2vec, as follows:

• p: 1, selected from the range of [0.25, 0.5, 1, 1.25,

1.5, 2].

• q: 2, selected from the range of [0.25, 0.5, 1, 1.25,

1.5, 2].

• Number of Walks: 15, chosen from [5, 10, 15].

The default value in node2vec is 10. We tested all

three values to arrive at the selection (see section

5.3).

• Walk Length: 32, chosen from [16, 32, 64, 80].

We tested all four values, including the default

value of 80 in node2vec (see section 5.3).

• Size of Embedding Vectors: 128, chosen from [64,

128, 256], with 128 being the default value in

node2vec.

In section 5.3, we provide a quantitative analy-

sis of the selection of the number of walks and walk

length.

4.4 Graph Convolution Network

Parameters

We evaluated multiple sets of parameters to determine

the optimal combination for achieving the best perfor-

mance in our experiments. We applied the grid search

method using the validation set. The resulting hyper-

parameters optimal for the PaySim dataset and our

classiﬁcation performance objectives are as follows:

• Network Structure: two convolutional layers that

use 16 ﬁlters and have a kernel size of 3, which de-

termines the number of neighbours to aggregate.

The ReLU activation function is applied, and a

fully connected sigmoid layer is used for the out-

put.

• Learning Rate: the model is trained using the

Adam optimizer (Zhang, 2018), while the learn-

ing rate is set to 0.01.

• Batch Size: 16.

• Number of Epochs: 20.

• Threshold: 0.32. The threshold should be chosen

to maximize the recall (true positive rate), ideally

reaching 100%, while maintaining an acceptable

false alert rate, i.e., lower than the industry stan-

dard of 95%. Experimental results with different

threshold values are presented in Section 5.1.

5 EXPERIMENTAL RESULTS

We present experimental results for various scenarios:

1. Determining the optimal classiﬁer threshold to

maximize the recall;

2. Evaluating the impact of different class distribu-

tions on the performance of N2V-GCN;

3. Determining the optimal number of walks for

node2vec;

4. Determining the optimal walk length for

node2vec;

5. Verifying the effectiveness of node embeddings

(ablation study of node2vec);

6. Comparing N2V-GCN with baseline models.

Table 2 summarizes the parameters of the experi-

ments.

5.1 Experiment #1. Determining the

Optimal Classiﬁer Threshold

The choice of the threshold depends on the objective

of classiﬁcation performance. In our case, the objec-

tive is to maximize recall (i.e., minimizing the number

of false negatives), while keeping the false alert rate

(FAR) as low as possible.

We conducted this experiment using the optimal

parameters for N2V-GCN, which are discussed in

Sections 4.3 and 4.4 and summarized in Table 2.

The optimal threshold for N2V-GCN was 0.32 and

obtained through a grid search within the range of

thresholds from 0.30 to 0.80, with the aim of min-

imizing false negatives. Table 3 displays a part of

the results obtained from threshold adjustments, pro-

viding clearer insights into how altering the threshold

might impact the count of false negatives. According

to the results, from the 0.30 to the 0.32 threshold, the

false negative rate remained constant. Therefore, we

chose 0.32 as the threshold because it produced lower

FAR than 0.30 and 0.31. Note that different dataset

may need a different threshold depending on several

NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications

502

Table 2: Parameters for each experiment.

Experiment Threshold Class Distribution for Training Number of WalksWalk Length

1 [0.30, 0.31, . . . , 0.40] 1/1 15 32

2 0.32 [1/ {1, 2, 5, 10, 20, 50, 100, 200, 500, 1000}] 15 32

3 0.32 1/1 [5, 10, 15] 32

4 0.32 1/1 15 [16, 32, 64]

5 0.32 1/1 15 32

6 0.32 1/1 15 32

Table 3: Results of the experiment that investigated the im-

pact of adjusting the threshold for a balanced dataset in

N2V-GCN. The best threshold for N2V-GCN is highlighted

in green . Thresholds that show a sudden increase in FNR

are highlighted in blue . #FN is the number of false nega-

tives.

Threshold FNR #FN FAR Recall Precision

0.30 0 0 69.10 100 30.89

0.31 0 0 66.37 100 33.63

0.32 0 0 63.70 100 36.30

0.33 0.87 2 61.76 99.12 38.24

0.34 0.87 2 60.07 99.12 39.93

0.35 1.31 3 59.31 98.68 40.69

0.36 1.75 4 57.25 98.25 42.75

0.37 1.75 4 55.73 98.25 44.27

0.38 1.75 4 54.75 98.25 45.25

0.39 1.75 4 52.74 98.25 47.26

0.40 2.19 5 51.31 97.80 48.69

factors such as the properties of the transaction graph,

transaction patterns and class distribution.

Furthermore, the data presented in Table 3 reveals

distinct peaks in threshold values (0.33, 0.35, 0.36,

and 0.40) coinciding with sudden rises in the FNR.

Notably, at a threshold of 0.32, our N2V-GCN model

achieved the detection of all money laundering trans-

actions. However, a slight elevation of the threshold

to 0.33 resulted in the misclassiﬁcation of two money

laundering transactions. Increasing the threshold to

0.40 produced a signiﬁcant increase in false nega-

tives, causing the model to misclassify ﬁve instances

of money laundering.

5.2 Experiment #2. Evaluating the

Impact of Different Class

Distributions on the Performance of

N2V-GCN

In this section, we explore how different class distri-

butions affect the performance of N2V-GCN in terms

of FNR, FAR, recall, and precision. To achieve this,

we modiﬁed the original class distribution of PaySim

(1/1000) and generated nine new class distributions

(1/1, 1/2, 1/5, 1/10, 1/20, 1/50, 1/100, 1/200, 1/500).

Table 4 shows the results of N2V-GCN performance

for each class distribution.

We observe that as the class distribution becomes

Table 4: Results of the experiment examining the effect of

various class distributions on N2V-GCN. The best result is

obtained by 1/1 class distribution, which is highlighted in

green . #FN is the number of false negatives.

Class

distributions FNR #FN FAR Recall Precision

1/1000 11.40 26 20.78 88.60 79.22

1/500 8.77 20 27.78 91.23 72.22

1/200 6.57 15 31.07 93.42 68.93

1/100 4.82 11 31.11 95.18 68.89

1/50 4.82 11 31.76 95.18 68.24

1/20 3.50 8 36.96 96.50 63.04

1/10 2.19 5 44.39 97.80 55.61

1/5 1.75 4 48.39 98.25 51.61

1/2 0.43 1 63.03 99.56 36.97

1/1 0 0 63.70 100 36.30

more balanced (going from 1/1000 to 1/1), the FNR

decreases, or equivalently, the recall increases. For

example, comparing the class distributions of 1/1000

and 1/1, we note that the FNR decreases by 11.40 per-

centage points (11.40% vs. 0). This improvement is

due to additional positive samples in the 1/1 dataset,

enabling the model to learn more about the positive

class. The class distribution 1/1 achieves the best

FNR (recall) in this experiment.

We note that as the recall increases, the precision

decreases. This is expected because we prioritize re-

call: our classiﬁcation objective is to maximize recall

(catching the maximum possible number of money

laundering transactions), even at the expense of pre-

cision. When the class distribution is 1/1, the recall,

precision and FAR are 100%, 36.30% and 63.70%, re-

spectively. While a FAR of 63.70% seems high, it is

much lower than the industry standard of 95% - 98%

(Ketenci et al., 2021), and allow us to achieve a recall

of 100%.

5.3 Determining the Optimal node2vec

Parameters

Experiment #3. Varying the Number of Walks

The purpose of this experiment is to assess how the

number of walks impacts the performance of our

AML model. We conducted an experiment by holding

all other parameters constant while varying the num-

ber of walks from 5 to 15. The results of this experi-

A Graph-Based Deep Learning Model for the Anti-Money Laundering Task of Transaction Monitoring

503

mentation are summarized in Table 5.

Table 5: Results of experiments that examined how the

number of walk parameter in node2vec affects N2V-GCN.

Number of Walks FNR FAR Recall Precision

5 1.31 76.68 98.68 23.31

10 0.43 73.20 99.56 26.80

15 0 63.70 100 36.30

It can be seen that with higher numbers of walks

(10 and 15), the model exhibits enhanced results. This

is particularly notable in terms of lowered FNR val-

ues, signifying improved classiﬁcation of positive and

negative instances, respectively. Noteworthy is the re-

duction of the model’s FNR by 1.31 percentage points

when number of walks is increased from 5 to 15. Sim-

ilarly, the recall improves as the number of walks

increases. This improvement is in line with the de-

creased FNR, as FNR = 1− recall.

Furthermore, the results show that increasing the

number of walks leads to a lower FAR. This is par-

ticularly noticeable for the highest number of walks

(15), when the FAR is lower than that in the case of

ﬁve walks (63.70% vs. 76.68%).

Finally, the precision metric shows an interesting

trend where it increases moderately from ﬁve to 10

walks (23.31% vs. 26.80%) and then increases sig-

niﬁcantly from 10 to 15 walks (23.31% vs. 36.30%).

This indicates that the model performs better at clas-

sifying legitimate transactions when the number of

walks increases.

Experiment #4: Varying the Walk Length

To explore the impact of this parameter on the per-

formance of N2V-GCN, we conducted an experiment

in which we maintained all other parameters as con-

stants and varied the length of the walks, ranging from

16 to 64. Table 6 summarizes the results of this exper-

iment using various walk lengths.

Table 6: Results of the experiments that examined how the

walk length parameter in node2vec affects N2V-GCN.

Walk Length FNR FAR Recall Precision

16 0.43 48.05 99.56 51.95

32 0 63.70 100 36.30

64 1.75 87.40 98.25 12.59

We observe that longer walk lengths tend to yield

better performance, but only up to a certain point. A

comparison between walk lengths 16 and 32 shows

a minor but important reduction in FNR (0.43 vs. 0

percentage points). Although this change is not sub-

stantial, it is considered signiﬁcant in the context of

AML because the FNR is critical. The walk length of

64 results in a slight decrease in recall and a notice-

able increase in FAR. For the graph (dataset) that we

use, a walk length of 32 is optimal.

5.4 Experiment #5: Effectiveness of

node2vec Node Embeddings

In this section, we compare the performance of our

AML model with and without node2vec. In the latter

case, the transaction graph is input directly into the

GCN model. In the former case, the transaction graph

is ﬁrst embedded by node2vec, and the output from

node2vec is input into the GCN model. In both cases,

the training data has a class distribution of 1/1. The

other parameters are listed in Table 2. The results are

summarized in Table 7.

Table 7: The performance of the AML model with and with-

out node2vec node embeddings.

FNR FAR Recall Precision

N2V-GCN 0 63.70 100 36.30

GCN 3.50 73.54 96.50 26.46

The results show that N2V-GCN outperforms the

GCN model without node2vec embeddings for all

evaluation metrics. The FAR of the N2V-GCN model

is almost 10 percentage points lower than the FAR

of the other model (63.70% vs. 73.54%). Its re-

call is also 3.50 percentage points higher (100%

vs. 96.50%). Node embedding with node2vec

learns continuous node representations by exploring

local neighborhood connections, while a GCN aggre-

gates information from neighboring nodes to capture

broader graph relationships. This combination allows

the model to effectively leverage both local and global

graph information, resulting in more accurate classi-

ﬁcation of money laundering instances.

5.5 Experiment #6: GCN vs. Other

Machine Learning Methods

In this experiment, we compared the performance

of N2V-GCN with other commonly used machine

learning techniques for AML transaction monitoring,

namely, random forest, logistic regression and sup-

port vector machine (SVM). The parameters used for

N2V-GCN are listed in Table 2. For the graph con-

volution network, we kept all the parameters at their

optimal values (as described in section 4.4), with a

threshold of 0.32 and the balanced class distribution

(1/1) for training data. For the other machine learn-

NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications

504

ing techniques, we used their default values and only

changed the classiﬁer thresholds to the optimal ones,

which are 0.35, 0.40, and 0.41 for SVM, random for-

est, and logistic regression, respectively. The results

of the experiment are given in Table 8.

Table 8: Comparison results of N2V-GCN with other clas-

siﬁcation algorithms.

Algorithm FNR FAR Recall Precision

N2V-GCN 0 63.70 100 36.30

Random forest 7.87 82.37 92.13 17.63

Logistic regression 4.37 99.66 95.63 0.33

SVM 10.49 77.21 89.50 22.79

The results show that the N2V-GCN model out-

performs the other models for all evaluation metrics.

Speciﬁcally, it has the highest recall and lowest FAR.

Among these, SVM has the lowest recall, while logis-

tic regression has the highest FAR.

We attempted to compare N2V-GCN with existing

models that also used the PaySim dataset for evalua-

tion, which are listed in Table I. However, the reported

results in (Raiter, 2021; Tundis et al., 2021; Pambudi

et al., 2019; Kumar et al., 2020) are only accuracy and

F1 scores, which do not effectively capture the perfor-

mance of an AML transaction monitoring system, as

discussed in Section 1.2.3. The paper by Tundis et

al. (Tundis et al., 2021) compared the performance of

traditional machine learning algorithms: random for-

est, decision trees, SVM, linear regression, and naive

Bayes. They relied heavily on feature engineering,

which may not meet high processing demands of mil-

lions of transactions daily.

6 CONCLUSION

The proposed N2V-GCN model outperforms tradi-

tional machine learning models (e.g., random for-

est, logistic regression, and SVM) thanks to the use

of graphs and GCN. The use of node2vec embed-

dings further improves the performance of the GCN.

We also present the process of ﬁne tuning the model

for optimal performance, depending on the available

dataset. For the dataset used in this article, the optimal

parameters are: walk length of 32, number of walks

of 15, and class distribution of 50/50 for training data.

A different dataset with different transactions patterns

and data distributions will require ﬁne tuning to get its

optimal parameters for the best performance, which

may be different from those reported in this article.

In this preliminary work, we used the PaySim

dataset, which contains transactions for mobile pay-

ments, and adapted it to the task of AML transac-

tion monitoring. We will ﬁne tune and evaluate N2V-

GCN further using other publicly available large-

scale datasets that appear recently and target AML

tasks (Altman et al., 2024; Oztas et al., 2023; Jensen

et al., 2023) . We will also incorporate explainable AI

techniques into the model to assist analysts in their

investigations by providing rationales behind the pre-

dictions output by the model.

REFERENCES

Alsuwailem, A. A. and Saudagar, A. K. (2020). Anti-money

laundering systems: a systematic literature review.

Journal of Money Laundering Control, 23(4):833–

848.

Altman, E., Blanu

sa, J., Von Niederh

ausern, L., Egressy,

B., Anghel, A., and Atasu, K. (2024). Realistic syn-

thetic ﬁnancial transactions for anti-money laundering

models. Advances in Neural Information Processing

Systems, 36.

AUSTRAC (2024). Westpac Penalty Ordered by the Fed-

eral Court of Australia. Accessed on: 2024-04-08.

Bakhshinejad, N. (2023). A Graph-Based Deep Learning

Model for Anti-Money Laundering. Master’s thesis,

York University, Toronto, Ontario.

Cao, D. K. and Do, P. (2012). Applying Data Mining

in Money Laundering Detection for the Vietnamese

Banking Industry. In Asian Conference on Intelligent

Information and Database Systems, pages 207–216.

Springer.

Chawla, N. V., Bowyer, K. W., Hall, L. O., and Kegelmeyer,

W. P. (2002). Smote: Synthetic minority over-

sampling technique. Journal of Artiﬁcial Intelligence

Research, 16:321–357.

Chen, Z., Nazir, A., Teoh, E. N., Karupiah, E. K., et al.

(2014). Exploration of the Effectiveness of Expecta-

tion Maximization Algorithm for Suspicious Transac-

tion Detection in Anti-Money Laundering. In 2014

IEEE Conference on Open Systems (ICOS), pages

145–149. IEEE.

Chen, Z., Soliman, W. M., Nazir, A., and Shorfuzzaman,

M. (2021). Variational Autoencoders and Wasser-

stein Generative Adversarial Networks for Improving

the Anti-Money Laundering Process. IEEE Access,

9:83762–83785.

Chen, Z., Van Khoa, L. D., Teoh, E. N., Nazir, A., Karup-

piah, E. K., and Lam, K. S. (2018a). Machine Learn-

ing Techniques for Anti-Money Laundering (AML)

Solutions in Suspicious Transaction Detection: A Re-

view. volume 57, pages 245–285. Springer.

Chen, Z., Van Khoa, L. D., Teoh, E. N., Nazir, S., and Thi,

H. C. (2018b). Machine learning techniques for anti-

money laundering (aml) solutions in suspicious trans-

action detection: a review. Knowledge and Informa-

tion Systems, 57(2):245–285.

Dre

zewski, R., Sepielak, J., and Filipkowski, W. (2015).

The Application of Social Network Analysis Algo-

A Graph-Based Deep Learning Model for the Anti-Money Laundering Task of Transaction Monitoring

505

rithms in a System Supporting Money Laundering De-

tection. Information Sciences, 295:18–32.

Grover, A. and Leskovec, J. (2016). node2vec: Scalable

Feature Learning for Networks. In Proceedings of

the 22nd ACM SIGKDD International Conference on

Knowledge Discovery and Data Mining, pages 855–

864.

Guo, C., Zhang, S., Zhang, P., Alkubati, M., and Song, J.

(2023). Lb-glat: Long-term bi-graph layer attention

convolutional network for anti-money laundering in

transactional blockchain. Mathematics.

Husain, O. (2024). 13 biggest aml ﬁnes ($500 million plus).

Accessed: 2024-09-05.

Jayasree, V. and Balan, R. S. (2017). Money Launder-

ing Regulatory Risk Evaluation Using Bitmap Index-

Based Decision Tree. Journal of the Association of

Arab Universities for Basic and Applied Sciences,

23:96–102.

Jensen, R. I. T., Ferwerda, J., Jørgensen, K. S., Jensen,

E. R., Borg, M., Krogh, M. P., Jensen, J. B., and Iosi-

ﬁdis, A. (2023). A Synthetic Data Set to Benchmark

Anti-Money Laundering Methods. Scientiﬁc Data,

10(1):661. Publisher: Nature Publishing Group UK

London.

Jullum, M., Løland, A., Huseby, R. B.,

Anonsen, G., and

Lorentzen, J. (2020). Detecting Money Launder-

ing Transactions with Machine Learning. Journal of

Money Laundering Control, 23(1):173–186.

Jurgovsky, J., Granitzer, M., Ziegler, K., Calabretto, S.,

Portier, P.-E., He-Guelton, L., and Caelen, O. (2018).

Sequence classiﬁcation for credit-card fraud detec-

tion. Expert Systems with Applications, 100:234–245.

Ketenci, U. G., Kurt, T.,

Onal, S., Erbil, C., Akt

urko

glu,

S., and

Ilhan, H. S¸. (2021). A Time-Frequency Based

Suspicious Activity Detection for Anti-Money Laun-

dering. IEEE Access, 9:59957–59967.

Keyan, L. and Tingting, Y. (2011). An Improved Support-

Vector Network Model for Anti-Money Laundering.

In 2011 Fifth International Conference on Manage-

ment of e-Commerce and e-Government, pages 193–

196. IEEE.

Kipf, T. N. and Welling, M. (2016). Semi-Supervised Clas-

siﬁcation with Graph Convolutional Networks. arXiv

preprint arXiv:1609.02907.

Kumar, A., Das, S., and Tyagi, V. (2020). Anti Money

Laundering Detection Using Na

ıve Bayes Classiﬁer.

In 2020 IEEE International Conference on Comput-

ing, Power and Communication Technologies (GU-

CON), pages 568–572. IEEE.

Kumar, A., Ghosh, S., and Verma, J. (2022). Guided Self-

Training Based Semi-Supervised Learning for Fraud

Detection. In Proceedings of the Third ACM Interna-

tional Conference on AI in Finance, pages 148–155,

New York, NY, USA. ACM.

Kute, D. V., Pradhan, B., Shukla, N., and Alamri, A.

(2021). Deep Learning and Explainable Artiﬁ-

cial Intelligence Techniques Applied for Detecting

Money Laundering–A Critical Review. IEEE Access,

9:82300–82317.

Labib, N. M., Rizka, M. A., and Shokry, A. E. M. (2020).

Survey of machine learning approaches of anti-money

laundering techniques to counter terrorism ﬁnance. In

Ghalwash, A. Z., El Khameesy, N., Magdi, D. A., and

Joshi, A., editors, Internet of Things—Applications

and Future, pages 73–87, Singapore. Springer Singa-

pore.

Liu, X. and Zhang, P. (2010). A Scan Statistics Based

Suspicious Transactions Detection Model for Anti-

Money Laundering (AML) in Financial Institutions.

In 2010 International Conference on Multimedia

Communications, pages 210–213. IEEE.

Lopez-Rojas, E., Elmir, A., and Axelsson, S. (2016).

PaySim: A Financial Mobile Money Simulator for

Fraud Detection. In 28th European Modeling and

Simulation Symposium, EMSS, Larnaca, pages 249–

255. Dime University of Genoa.

Lopez-Rojas, E. A. and Axelsson, S. (2012). Multi-Agent

Based Simulation (MABS) of Financial Transactions

for Anti-Money Laundering (AML). In Nordic Con-

ference on Secure IT Systems. Blekinge Institute of

Technology.

Mani, I. and Zhang, I. (2003). knn approach to unbalanced

data distributions: A case study involving information

extraction. In Proceedings of the ICML 2003 Work-

shop on Learning from Imbalanced Data Sets, pages

1–7.

Marasi, S. and Ferretti, S. (2024). Anti-money laundering

in cryptocurrencies through graph neural networks: A

comparative study. Proceedings Article.

Mikolov, T., Sutskever, I., Chen, K., Corrado, G. S., and

Dean, J. (2013). Distributed Representations of Words

and Phrases and Their Compositionality. Advances in

Neural Information Processing Systems, 26.

Ning, P., Wang, P., and Zhang, Z. (2024). An anti-

money laundering method based on spatio-temporal

graph convolutional networks. Advances in Transdis-

ciplinary Engineering.

Oztas, B., Cetinkaya, D., Adedoyin, F., Budka, M., Do-

gan, H., and Aksu, G. (2023). Enhancing Anti-Money

Laundering: Development of a Synthetic Transaction

Monitoring Dataset. In 2023 IEEE International Con-

ference on e-Business Engineering (ICEBE), pages

47–54. IEEE.

Palamuttam, R. and Chen, W. (2017). Evaluating Net-

work Embeddings: Node2Vec vs Spectral Clustering

vs GCN.

Pambudi, B. N., Hidayah, I., and Fauziati, S. (2019). Im-

proving Money Laundering Detection Using Opti-

mized Support Vector Machine. In 2019 International

Seminar on Research of Information Technology and

Intelligent Systems (ISRITI), pages 273–278. IEEE.

Pandey, A., Bhatraju, A., Markam, S., and Bhatt, D. (2022).

Adversarial Fraud Generation for Improved Detec-

tion. In Proceedings of the Third ACM International

Conference on AI in Finance, pages 123–129, New

York, NY, USA. ACM.

Paula, E. L., Ladeira, M., Carvalho, R. N., and Marza-

gao, T. (2016). Deep Learning Anomaly Detection as

Support Fraud Investigation in Brazilian Exports and

NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications

506

Anti-Money Laundering. In 2016 15th IEEE Interna-

tional Conference on Machine Learning and Applica-

tions (ICMLA), pages 954–960. IEEE.

Pereira, R. R., Bono, J., Ascens

ao, J. T., Apar

ıcio, D.,

Ribeiro, P., and Bizarro, P. (2023). The GANfa-

ther: Controllable Generation of Malicious Activity

to Improve Defence Systems. In Proceedings of the

Fourth ACM International Conference on AI in Fi-

nance, ICAIF ’23, pages 133–140, New York, NY,

USA. Association for Computing Machinery.

Pham, T. and Lee, S. (2016). Anomaly Detection in Bit-

coin Network Using Unsupervised Learning Methods.

arXiv preprint arXiv:1611.03941.

Rae, S. (2024). NEWS: Canada’s TD Bank Faces C$10M

Fine as FINTRAC Deems AML Controls Unsatisfac-

tory. Accessed: 2024-04-08.

Raiter, O. (2021). Applying Supervised Machine Learn-

ing Algorithms for Fraud Detection in Anti-Money

Laundering. Journal of Modern Issues in Business Re-

search, 1(1):14–26.

Ross, S. and Hannan, M. (2007). Money Laundering Reg-

ulation and Risk-Based Decision-Making. Journal of

Money Laundering Control, 10(1):106–115.

Roy, A., Bandyopadhyay, S. K., and Ghosh, S. K. (2018).

Automated detection of suspicious activities in large-

scale banking data using lstm-based deep learning

models. International Journal of Computer Applica-

tions, 182(30):1–8.

Silva,

I. D. G., Correia, L. H. A., and Maziero, E. G. (2023).

Graph neural networks applied to money laundering

detection in intelligent information systems. In Pro-

ceedings of the XIX Brazilian Symposium on Informa-

tion Systems, pages 252–259, New York, NY, USA.

ACM.

Soltani, R., Nguyen, U. T., Yang, Y., Faghani, M., Yagoub,

A., and An, A. (2016). A New Algorithm for Money

Laundering Detection Based on Structural Similar-

ity. In 2016 IEEE 7th Annual Ubiquitous Comput-

ing, Electronics & Mobile Communication Confer-

ence (UEMCON), pages 1–7. IEEE.

Tang, J. and Yin, J. (2005). Developing an Intelligent

Data Discriminating System of Anti-Money Launder-

ing Based on SVM. In 2005 International Conference

on Machine Learning and Cybernetics, volume 6,

pages 3453–3457. IEEE.

Tatulli, M. P., Paladini, T., D’Onghia, M., Carminati, M.,

and Zanero, S. (2023). HAMLET: A transformer

based approach for money laundering detection. In

Dolev, S., Gudes, E., and Paillier, P., editors, Cyber

Security, Cryptology, and Machine Learning, volume

13914, pages 234–250. Springer Nature Switzerland,

Cham. Series Title: Lecture Notes in Computer Sci-

ence.

Tertychnyi, P., Slobozhan, I., Ollikainen, M., and Dumas,

M. (2020). Scalable and Imbalance-Resistant Ma-

chine Learning Models for Anti-Money Laundering:

A Two-Layered Approach. In International Workshop

on Enterprise Applications, Markets and Services in

the Finance Industry, pages 43–58. Springer.

Thommandru, A., Mone, V., Mitharwal, S., and Tilwani, R.

(2023). Exploring the intersection of machine learn-

ing, money laundering, data privacy, and law. In 2023

International Conference on Innovative Data Com-

munication Technologies and Application (ICIDCA),

pages 149–155.

Tundis, A., Nemalikanti, S., and M

uhlh

auser, M. (2021).

Fighting Organized Crime by Automatically Detect-

ing Money Laundering-Related Financial Transac-

tions. In The 16th International Conference on Avail-

ability, Reliability and Security, pages 1–10.

UNODC (2022). Ofﬁcial Website of United Nations Ofﬁce

on Drugs and Crime.

Wan, F. and Li, P. (2024). A novel money laundering pre-

diction model based on a dynamic graph convolutional

neural network and long short-term memory. Symme-

try.

Wang, X. and Dong, G. (2009). Research on Money Laun-

dering Detection Based on Improved Minimum Span-

ning Tree Clustering and Its Application. In 2009 Sec-

ond International Symposium on Knowledge Acquisi-

tion and Modeling, volume 2, pages 62–64. IEEE.

Weber, M., Domeniconi, G., Chen, J., Weidele, D. K. I.,

Bellei, C., Robinson, T., and Leiserson, C. E. (2019a).

Anti-Money Laundering in Bitcoin: Experimenting

with Graph Convolutional Networks for Financial

Forensics. arXiv:1908.02591 [cs, q-ﬁn].

Weber, M., Domeniconi, G., Chen, J., Weidele, D. K. I.,

Bellei, C., Robinson, T., and Leiserson, C. E. (2019b).

Anti-Money Laundering in Bitcoin: Experimenting

with Graph Convolutional Networks for Financial

Forensics. arXiv preprint arXiv:1908.02591.

Yang, Y. and Li, D. (2020). Nenn: Incorporate node and

edge features in graph neural networks. In Proceed-

ings of The 12th Asian Conference on Machine Learn-

ing, volume 129 of Proceedings of Machine Learning

Research, pages 593–608.

Youssef, B., Bouchra, F., and Brahim, O. (2023). State of

the art literature on anti-money laundering using ma-

chine learning and deep learning techniques. In Has-

sanien, A. E., Haqiq, A., Azar, A. T., Santosh, K., Jab-

bar, M. A., Słowik, A., and Subashini, P., editors, The

3rd International Conference on Artiﬁcial Intelligence

and Computer Vision (AICV2023), March 5–7, 2023,

volume 164, pages 77–90. Springer Nature Switzer-

land, Cham. Series Title: Lecture Notes on Data En-

gineering and Communications Technologies.

Zhang, Z. (2018). Improved adam optimizer for deep neu-

ral networks. In 2018 IEEE/ACM 26th International

Symposium on Quality of Service (IWQoS), pages 1–2.

IEEE.

A Graph-Based Deep Learning Model for the Anti-Money Laundering Task of Transaction Monitoring

507