Neuron Labeling for Self-Organizing Maps Using a Novel

Example-Centric Algorithm with Weight-Centric Finalization

Willem S. van Heerden

Department of Computer Science, University of Pretoria, Pretoria, South Africa

Keywords:

Unsupervised Neural Networks, Self-Organizing Maps, Neuron Labeling, Data Science, Data Mining,

Exploratory Data Analysis.

Abstract:

A self-organizing map (SOM) is an unsupervised artiﬁcial neural network that models training data using

a map structure of neurons, which preserves the local topological structure of the training data space. An

important step in the use of SOMs for data science is the labeling of neurons, where supervised neuron labeling

is commonly used in practice. Two widely-used supervised neuron labeling methods for SOMs are example-

centric neuron labeling and weight-centric neuron labeling. Example-centric neuron labeling produces high-

quality labels, but tends to leave many neurons unlabeled, thus potentially hampering the interpretation or use

of the labeled SOM. Weight-centric neuron labeling guarantees a label for every neuron, but often produces

less accurate labels. This research proposes a novel hybrid supervised neuron labeling algorithm, which

initially performs example-centric neuron labeling, after which missing labels are ﬁlled in using a weight-

centric approach. The objective of this algorithm is to produce high-quality l abels while still guaranteeing

labels for every neuron. An empirical investigation compares the performance of the novel hybrid approach

to example-centric neuron labeling and weight-centric neuron labeling, and demonstrates the feasibility of the

proposed algorithm.

1 INTRODUCTION

Self-organizing maps (SOMs) are unsupervised learn-

ing neural networks (Kohonen, 2001), which have

been widely investigated in the literature (Kaski et al.,

1998; Oja et al., 2003; Poll ¨ a et al., 2009). SOMs ¨

have seen wid e use in da ta science, data mining, and

exploratory data ana lysis (van Heerden, 2017). Some

speciﬁc application areas include business analytics

(Bowen and Siegler, 2024), healthcare (Javed et al.,

2024), pandemic analysis (Galvan et al., 2021), as-

tronom y (Vantyghem et al., 2024), and environmental

research (Rosa et al., 2024). SOMs are discussed in

more detail within Section 2.

SOMs are made up of neurons, which to gether

model a training data set. Several SOM neu-

ron labeling techniques exist, each of which at-

taches typically text-based characterizations to a sub-

set of a SOM’s neurons. Neuron labeling often

plays an essential part in SOM-ba sed data analysis

(van Heerden and Engelbrech t, 2008). The quality of

SOM-based data science therefor e depends heavily

on the performance of the labeling algorithm that has

https://orcid.org/0000-0002-9736-7268

been chosen. Section 3 elaborates up on neuron label-

ing approaches.

Two of the most commonly used labeling meth-

ods are example-centric neuron labeling and weight-

centric neuron labe ling (Kohonen, 1989). Example-

centric neuron la beling is very accurate but leaves

some neur ons unlabeled, while weight-centric neuron

labeling lacks accuracy but guarantees a lab el for ev-

ery neuron (van Heerden, 2017).

Section 4 intro duces a novel SOM neuron labeling

algorithm , namely example-centric neuron labeling

with weight-centric ﬁnalization. This algorithm com-

bines the b est aspects of example-centric and weight-

centric neuron labeling, by guaranteeing high-quality

labels for every neuron of a SOM .

To demonstrate the advantages of the new algo-

rithm, an empirical analysis was conducted. Sec tion 5

presents the expe rimental results, which compare

the performan ce of the novel algorithm to example-

centric and weight-centric neuron labeling.

Finally, Section 6 concludes with a summary of

this work’s most important ﬁnd ings. Additionally,

several avenues are suggested for future investigations

stemming from the research presented here.

508

van Heerden, W.

Neuron Labeling for Self-Organizing Maps Using a Novel Example-Centric Algorithm with Weight-Centric Finalization.

DOI: 10.5220/0013072000003837

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Joint Conference on Computational Intelligence (IJCCI 2024), pages 508-519

ISBN: 978-989-758-721-4; ISSN: 2184-3236

yx2

yx1

yxI

. . .











Neuron yx

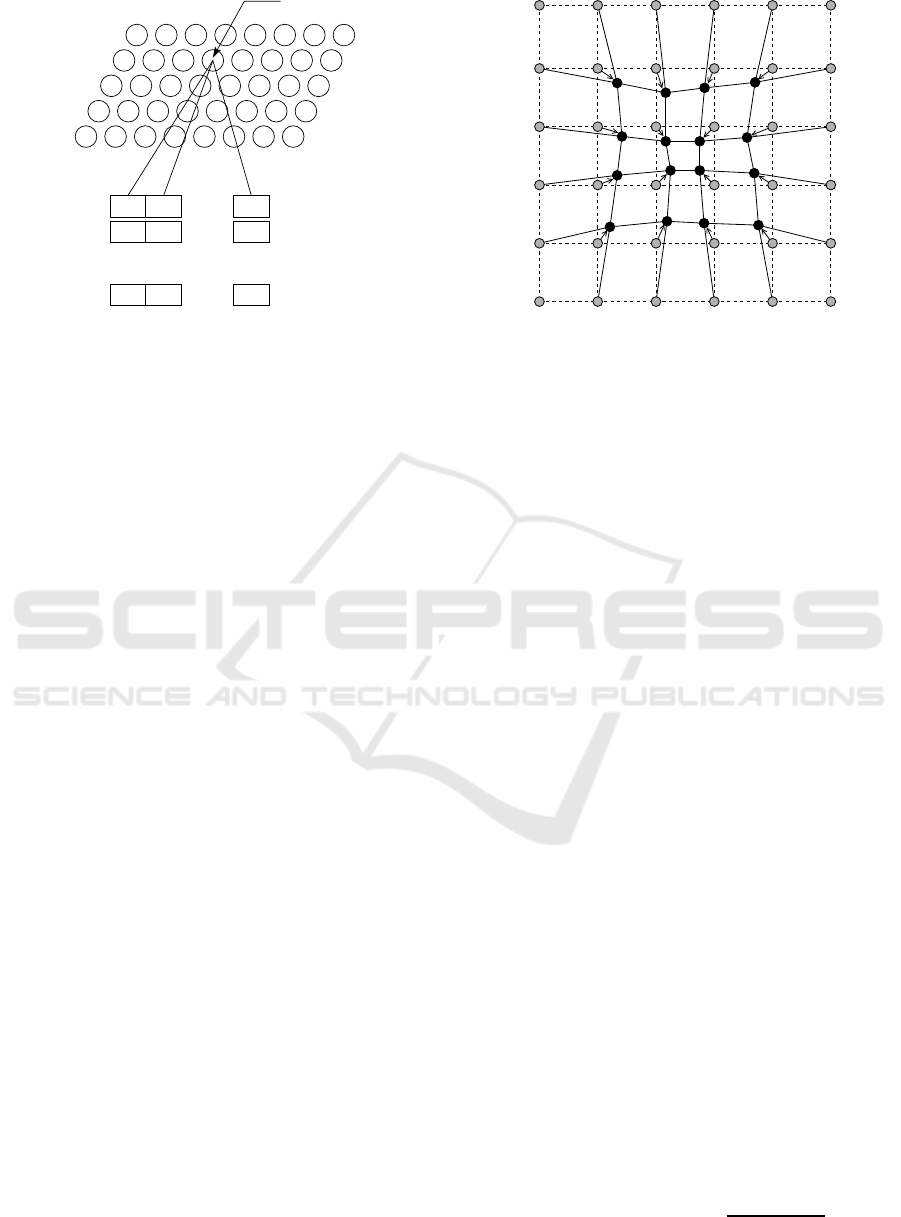
Figure 1: The architectural components making up a SOM.

2 SELF-ORGANIZING MAPS

Teuvo Kohonen intro duced the SOM , which is an un-

supervised n eural network based on th e associative

nature o f hu man cerebral cortices (Kohonen, 1982).

In contrast to supervised neural networks, the training

of a SOM does not require data classiﬁcations.

Figure 1 illustrates the architectural co mponents

of a SOM. Map training uses a training data set of

training examples, D

= {~z

,~z

,... ,~z

}. Each

training example is represented by an I-dimensional

vector of attribute values,~z

= (z

,. .. ,z

). Every

attribute value is denoted z

and is a real value.

The central map structure of a SOM consists of a

grid of neurons with Y rows and X columns. Each

neuron, denoted n

, is positioned at row y and col-

umn x of the g rid, and has a linked weight vector,

= (w

yx1

yx2

,. .. ,w

yxI

). Every real valued weight,

yxv

, corresponds to z

across every~z

in D

The objective of SOM training is to adapt every

in the map stru c ture, so that they collectively

model D

. The model is a simp liﬁed repr esentation

because D

is I-dimensional, wh ile the ma p is two-

dimensional. The map has two characteristics:

1. The map models the pr obability density function

of the data space represented by D

. Weight vec-

tors move towards denser parts of the data space

during train ing. Neurons th us model subsets o f

mutually similar da ta examples after training.

2. Data examples that are close together in the data

space are re presented by neurons that are posi-

tioned near each other in the map grid. The map

model there fore maintains the local topological

structure of th e data space represented by D

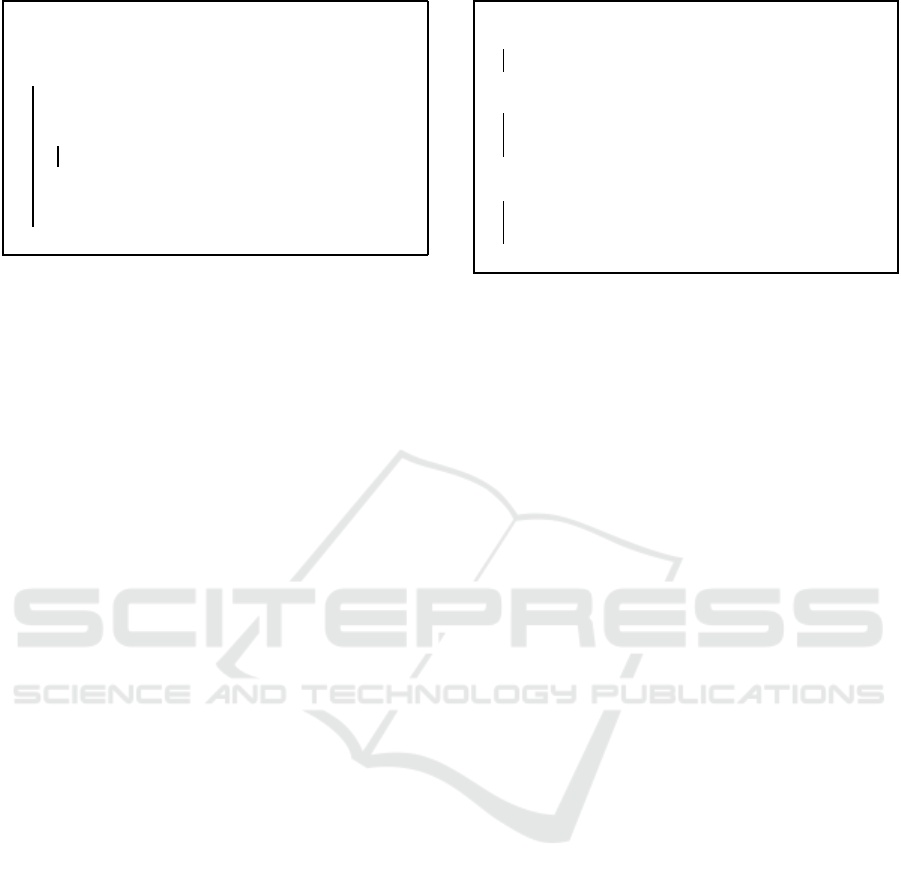
Figure 2 shows the resu lt of SOM training on syn-

thetic two-dimensional data. Gray circles represent

the original uniformly distributed positions of weight

Figure 2: SOM weight updates for two-dimensional data.

vectors in the map space, and dashed lines connect

the weig ht vectors of adjacen t neurons. Crosses show

the positions of training examples in the data space.

After training, the weight vectors shift to the loca-

tions of the black circles, where solid lines connect

the weight vectors of adjacent neurons. Characteris-

tic 1 is de monstrated by the drift of weight vectors to

the dense group of training exam ples. Training exam-

ples are also positioned close to the weight vectors of

adjacent neurons, illustrating characteristic 2.

Several SOM training algorithms exist (Engel-

brecht, 2007), which are all usable with the proposed

labeling approach. The experiments of Section 5 used

the original stochastic training procedure (Kohonen,

1982), shown in Algorithm 1, whic h is commonly

used and a good baseline for com parisons.

Stochastic training r epeatedly iterates over each

∈ D

. The best matching unit (or BMU), denoted

, with ~w

closest to~z

, is deﬁned as follows:

k~z

− ~w

= min

∀yx



k~z

− ~w



(1)

At the current training iteration, t, every ~w

on the

map is updated relative to th e BMU, as follows:

(t + 1) = ~w

(t) + ∆~w

(t) (2)

The chan ge applied to a weight vecto r is composed of

an update for each w eight, as follows:

∆~w

(t) =



∆w

yx1

(t),∆w

yx2

(t),... ,∆w

yxI

(t)



(3)

Finally, the change computed for a weight is deﬁned

accordin g to the following e quation:

∆w

yxv

(t) = h

ba,yx

(t) ·



− w

yxv

(t)



(4)

Here, h

ba,yx

(t) is the neighborhood function at itera-

tion t, which is u sually the smooth Ga ussian kernel:

ba,yx

(t) = η(t) · exp

−

− c

2 ·



σ(t)



(5)

Neuron Labeling for Self-Organizing Maps Using a Novel Example-Centric Algorithm with Weight-Centric Finalization

509

initialize map grid

set current training iteration, t = 0

randomly shufﬂe D

repeat

choose unselected~z

∈ D

use Equation (1) to ﬁnd BMU, n

, for~z

forall ~w

in the map do

update ~w

using Equation (2)

end

update current training iteration, t = t + 1

if all~z

∈ D

selected, shufﬂe D

until a stopping condition is satisﬁed

Algorithm 1: Stochastic SOM training procedure.

In this equation, η(t) is the learning rate hyperparam-

eter and σ(t) is the kernel width hyp erparame te r, both

at iteration t, while kc

− c

is th e distance be-

tween the m a p coo rdinates of n

and n

For SOM trainin g to converge, the learning rate

and kernel width must both be monoton ic ally decreas-

ing functions of t. The repo rted experiments used an

exponential decay f unction for the learning rate:

η(t) = η(0) · e

−t/τ

(6)

Here, η(0) is the initial learning rate at the start of

training, and τ

is a constant governing the decay rate.

Similarly, the kernel width decays as follows:

σ(t) = σ(0) · e

−t/τ

(7)

The initial kernel width is σ(0 ), and τ

is a constant

affecting the rate of kern el width decay.

3 SOM NEURON LABELING

Neuron labeling attaches textual descriptions

to neurons, to represent neuron characteristics.

Neuron labels are often used during SOM-

based exploratory data analy sis, and are essen-

tial to automated rule extraction from SOMs

(van Heerden and Engelbrech t, 2016). Neuron label-

ing approaches are either supervised or unsupervised

(Azcarrag a et al., 200 8).

Supervised labeling uses classiﬁed examples from

a labeling data set (either the training set or separate

data). Algorithms in this category include example-

centric neuron labeling (Kohonen, 1989), example-

centric cluster labeling (Samarasinghe, 2007), and

weight-cen tric neuron labeling (Kohonen, 1989).

Unsupervised labeling is not based on cla ssiﬁed

labeling data. In the simplest instance, a human an-

alyst manually a ssigns ne uron labels (Corradini and

Gross, 1999). Algorithmic methods also exist, which

base labe ls either on the weight vectors of the map, or

train a SOM, m ap, with Y × X neurons

forall n

in map do

deﬁne empty mapped example set, M

end

forall labeling examples~z

use Equation (1) to ﬁnd BMU, n

, for~z

add~z

to M

end

forall n

in map do

ﬁnd most common class, A

cls

, within M

label n

with A

cls

end

Algorithm 2: Example-centric neuron labeling.

the labelin g data in relation to the map neuro ns. These

unsuper vised algorithms include unique cluster label-

ing (Deboeck , 1999), unsupervised weight-based la-

beling (Serrano-Cinca, 1996; Lagus and Kaski, 1999;

van Heerden and Engelbrecht, 2012), and unsuper-

vised example -based labeling (Rauber and Merkl,

1999; Azcarraga et al., 2008).

Unsupervised labeling techniques are more ﬂexi-

ble than their supervised c ounterparts. However, un-

supervised labelings are difﬁcult to interpret objec-

tively, posing a problem for their empirical analysis.

As a consequence, most research focuses on super-

vised labeling algorithms, as this paper does.

Example-centric cluster labeling performs poorly,

particularly in the presence of heterogeneo us clusters

of weight vectors (van Heerden, 2017). This research

therefore focuses only on example-centric neuro n la-

beling and weight-centric neuron labeling, w hich are

elaborated upon in Sections 3.1 a nd 3.2.

3.1 Example-Centric Neuron Labeling

Algorithm 2 represents example-centric neuron label-

ing. An initially empty set of mapped labeling exam-

ples is associated with each neuron on the map. Each

labeling example,~z

, is then mapped to its BMU us-

ing Equatio n (1), and ~z

is added to the labeling ex-

ample set of the BMU. Finally, each neu ron is labeled

using the most common classiﬁcation appe aring in the

correspo nding labeling example set.

Example-centric neuron labeling leaves neurons

unlabeled when the associated labeling example sets

are empty. Suc h ne urons a re often referred to as inter-

polating units, and represent a large proportion of the

map in some instances (van He e rden, 2023).

Despite these u nlabeled neuro ns, example-centric

neuron la beling has been shown to outperform the

other supervised labeling methods when used as a

basis for simple classiﬁcation tasks (van Heer den,

2017). It has also been observed that the presence of

NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications

510

VIR SET

VER

VIR

VIR VER

SET SET SET SET SET

VER

VIR

VIR VIR

VIR

VER

VIR

VER

SET

VIR

VER

SET SET

SET

VIR

VER

VIR

VER

VIR

VER

VIR

VER

VIR

VER

SET

VER

SET

VER

VIR

VER

SET

VER

SET

VER

SET

VER

SET

VER

SET

VER

VIR

Figure 3: A SOM trained on the I ris data set and labeled

using example-centric neuron labeling.

unlabeled neurons is not strongly correlated to poor

label quality (van Heerden an d Engelbrecht, 2016).

While unlabeled neurons do not negatively

impact the quality of map characterization, th e

missing labels often hamper SOM-based ex-

plorator y data analysis performed by hum an experts

(van Heerden and Engelbrech t, 2016). This is

because the labeled map is broken up by u ncharacter-

ized areas, which obscur e a broader overview of the

model characteristics.

The outcomes of the labeling algorithms un-

der investigation are shown using an example SOM

that was trained on the well-known Ir is data set

(Fisher, 1936). Figure 3 shows the example SOM la-

beled using example-centric neuron labeling. T he la-

bels “SET”, “VER”, and “VIR” respectively represent

the Iris Setosa, Iris Versicolor, and Iris Virginica c la s-

siﬁcations present in the data set. The abundance of

empty circle s in this visualization clearly illustrates

the large numbe r of unlabeled neurons left by the al-

gorithm, which account for 38.8% of the map.

3.2 Weight-Centric Neuron Labeling

Weight-ce ntric neuron labeling is outlined in Algo-

rithm 3. In contrast to example-centric neuron la-

beling, weight-centric neuro n labeling maps neurons

to da ta examples from a labeling set. Eac h neuron’s

weight vecto r is mapped to the closest labeling exam-

train a SOM, map, with Y × X neurons

forall n

in map do

use Equation (8) to ﬁn d BME,~z

, for ~w

ﬁnd class, A

cls

, associated with~z

label n

with A

cls

end

Algorithm 3: Weight-centric neuron labeling.

VER VER SET SET

VER

VIR

VIR VER

VIR

VER SET SET SET SET SET

VIR VER

VIR

VIR VIR

VER

VIR

VER

VIR

VER

VIR

VER

SET

VIR

VER

SETVER SET

VER SET

VIR

VER

VIR

VER

VIR

VER

VIR

VER

VIR

VER

VIR

VER

VIR

VER

SET

VIR

VER

SET

VER

SET

VER

SET

VER

SET

VER

SET

VER

SET

VER

SET

VER

SET

VER

SET

VER

SET

Figure 4: A SOM trained on the I ris data set and labeled

using weight-centric neuron labeling.

ple,~z

, which is called the best m a tc hing example (or

BME), and is deﬁned as follows:

k~w

−~z

= min

∀s



k~w

−~z



(8)

The neuron currently under consideration is then la-

beled with the classiﬁcation of its BME.

Weight-ce ntric neuron labe ling is simpler than

example-centr ic neur on labeling, and does not require

the stor a ge and searchin g of mapped labeling exam-

ple sets. Additionally, the algor ithm gu a rantees a la-

bel for every neuron on a map, facilitating easier in-

terpretation for human data analysts.

Unfortu nately, neurons will receive poor weight-

centric labels if the BME match is not close. This re-

sults in a tendency for weight-centric neuron labeling

to produce less accurate labels than example-centric

neuron labeling (van Heerden, 2017).

Figure 4 depicts th e result of performing w e ight-

centric neuron labeling on the previously-mentioned

example SOM trained on the Iris data set. It is clear

that every neuron on th e map has received a label,

making the map more interpretable when compared

to the example-centric neuron labeling in Figure 3.

4 THE PROPOSED ALGORITHM

The proposed algorithm is referred to as example-

centric neuro n la beling with weight-centric ﬁnaliza-

tion, and hybr idizes example-centric neuron la beling

with weight-centric neuron labeling. The objective is

to generate labels that are accurate, while also guar-

anteeing labels for every ne uron o n a map.

Algorithm 4 represents the proposed technique,

which is a two-phase process. The ﬁrst phase p er-

forms a norma l example- centric neuron labeling, in

which neurons that are BMUs at least once are la-

beled. This phase will typically produce high-quality

Neuron Labeling for Self-Organizing Maps Using a Novel Example-Centric Algorithm with Weight-Centric Finalization

511

train a SOM, map, with Y × X neurons

forall n

in map do

deﬁne empty mapped example set, M

end

forall labeling examples~z

use Equation (1) to ﬁn d BMU, n

, for~z

add~z

to M

end

forall n

in map do

ﬁnd most common class, A

cls

, within M

label n

with A

cls

end

forall n

in map do

if n

has no associated label then

use Equation (8) to ﬁnd BME,~z

, for ~w

ﬁnd class, A

cls

, associated with~z

label n

with A

cls

end

Algorithm 4: Example-centric neuron labeling with weight-

centric ﬁnalization.

labels for o nly a subset of the map neurons. The

second phase then iterates over only the neurons that

have remained unlabeled, assigning a weight-centric

label to each. For e ach of these neurons, the classi-

ﬁcation of its BME becomes the neuron label. The

labels pro duced by the second phase will be of lower

quality, but will ensure a complete set of labels.

The labeling for the example Iris data set SOM,

which is p roduced by the pr oposed algorithm, is

shown in Figure 5. When comparing this labeling to

the standard weight-centric neuron labeling shown in

Figure 4, it is clear th at the labelings are very simi-

lar. The maps only differ in terms of two neuron la-

bels: the second from the left on the top row, and the

third from the right on the bottom row. By consulting

Figure 3 it is clear that these differences ar e due to

the example-centric neuron labeling performed dur-

ing the ﬁrst labeling phase. It is hypothesized that

such differences constitute more accurate labels than

those produced by example-centric neur on labeling.

5 EXPERIMENTAL RESULTS

To explore the hypothesized advantage s of example-

centric neuro n la beling with weight-cen tric ﬁnaliza-

tion, a series of experiments were con ducted. These

experiments compared the perfo rmance of the novel

algorithm against ba sic example-centric and weight-

centric neuron labeling, when the algorithms were

used in SOM-based data c la ssiﬁcation tasks.

VIR VER SET SET

VER

VIR

VIR VER

VIR

VER SET SET SET SET SET

VIR VER

VIR

VIR VIR

VER

VIR

VER

VIR

VER

VIR

VER

SET

VIR

VER

SETVER SET

VER SET

VIR

VER

VIR

VER

VIR

VER

VIR

VER

VIR

VER

VIR

VER

VIR

VER

SET

VIR

VER

SET

VER

SET

VER

SET

VER

SET

VIR

VER

SET

VER

SET

VER

SET

VER

SET

VER

SET

VER

SET

Figure 5: A SOM trained on the I ris data set and labeled

using the proposed algorithm.

The standard stochastic tra ining algorithm pro-

duced SOMs for several b enchmar k data sets. Six

data sets were drawn f rom the UCI Machine Learning

Repository, namely the Iris data set (Fisher, 1936), the

ionosphere data set (Sigillito et al., 19 89), the th ree

monk’s problems data sets (Wnek, 1993), and the

glass identiﬁcation data set (Ge rman, 1987). It should

be noted that the third monk’s problem set has 5%

classiﬁcation noise added to the training data. The

data sets were preprocessed by using one-hot encod-

ing for nominal attributes (Bishop, 2006), and scaling

all attribute values to a [0.0, 1.0] range using min-max

normalization (Han et al., 2012).

The classiﬁcation task was executed using the au-

thor’s open-source SOM an d labeling algorithm col-

lection (van Heerden, 2024), which is ba sed on Ko-

honen ’s original SOM

PAK r e ference implementa-

tion (Koho nen et al., 1996). Square maps were used

throughout, and all weight vectors we re initialized

using hyper cube initialization (Su et al., 19 99). The

SOM’s main stopping co ndition was a limit of 0.0001

on a 30-iteration moving average of the standard de-

viation compu te d fo r the map’s quantization error

(van Heerden, 2017). To ensure termination, training

was also stopped after 100 000 iterations.

Following map training, the appropriate neuron

labeling algorithm was applied. Fina lly, classiﬁca-

tions wer e performed by mapping a data example to

its BMU. The label of the BMU was then applied as

the classiﬁcation of the da ta example. Each classiﬁ-

cation was compared to the actual classes of the data

example, and a misclassiﬁcation occurred if a match

was not found. If the BMU was un la beled, the data

example re mained unclassiﬁed.

Hyperpa rameter tuning was pe rformed separately

for the three n e uron labeling algorithms a pplied to

each of the benchmark data sets. The tuning proce-

dure (van Heer den, 2017; Franken, 2009) used Sobol’

NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications

512

Table 1: Optimal hyperparameters per data set for example-centric neuron labeling.

Parameter Iris Ionosphere Monks 1 Monks 2 Monks 3 Glass

Y and X 5 7 14 15 11 6

η(0) 5.488 3.848 6.055 8.867 9.941 0.449

1 432.617 1 209.961 849.609 1 365.234 577.148 430.664

σ(0) 2.119 1.818 10.445 1.348 3.029 1.948

77.539 59.570 9.766 31.641 83.008 7.617

Table 2: Optimal hyperparameters per data set for weight-centric neuron labeling.

Parameter Iris Ionosphere Monks 1 Monks 2 Monks 3 Glass

Y and X 12 17 14 15 19 11

η(0) 4.609 0.918 6.563 8.867 9.629 0.508

574.219 594.727 46.875 1 365.234 61.523 1 236.328

σ(0) 10.781 14.045 4.813 1.348 4.639 1.904

96.094 87.305 34.375 31.641 67.383 5.859

Table 3: Optimal hyperparameters per data set for example-centric neuron labeling with weight-centric ﬁnalization.

Parameter Iris Ionosphere Monks 1 Monks 2 Monks 3 Glass

Y and X 11 15 15 16 14 13

η(0) 7.266 8.945 8.867 2.480 1.836 7.910

363.281 908.203 1 365.234 1 391. 602 1 060.547 1 163.08 6

σ(0) 6.273 1.934 1.348 0.719 5.414 1.082

16.406 58.984 31.641 2.930 55.078 75.195

sequences (Sobol’ , 1967) to generate conﬁgurations

that sample the parameter space uniformly. Ta-

bles 1 to 3 present the optimal hyperparameters for

example-centr ic neuron labeling, weig ht-centric neu-

ron labeling, and examp le-centric neuron labeling

with weight-centric ﬁnalization, respectively.

For each algorithm and data set, a 30-fold cross-

validation was performed, and perfor mance measures

were recorded. To test whether performance mea-

sure differences wer e statistically signiﬁcant, two-

tailed n on-parametric Wilcoxon signe d-rank hypoth-

esis tests (Wilcoxon, 1945) were performed with a

conﬁdence level of 0.05. A Bonferroni correction

(Miller, 1981) was applied, to counteract the multi-

ple comparisons problem. The results tables tha t fol-

low report the mean and standa rd deviation for each

performance measure, as well as a hypothesis test p-

value. When a p-value indicates a signiﬁcant p e rfor-

mance differenc e , the mean and standar d deviation of

the better-performing algor ithm are marked in bold.

Tables 4 and 5 respectively compare the overall

training set e rror perfor mance of the proposed ap-

proach against example-centric neuron labeling and

weight-cen tric neuron labeling. These errors could

be due to a combination of misclassiﬁed and unclas-

siﬁed training set data examples. The tables clearly

illustrate that the proposed algorithm o utperforms

example-centr ic neuron labeling in all instances, and

weight-cen tric neuron labeling in all but one case

(for the third monk’s problem, which included train-

ing data noise, weight-centric neuron labelin g outper-

formed the proposed algorithm). The proposed ap-

proach generally did not outperform example-centr ic

neuron labeling by a very large margin, except in the

case of the ionosphere and glass identiﬁcation data

sets. In contrast, weight-centric neuron labeling un-

derperformed by a substantial amount in the cases of

the ionosphere, glass identiﬁcation, an d the ﬁrst two

monk’s pro blems data sets.

To gain a deeper insight into whether any type of

classiﬁcation error was more prevalent, Tables 6 and 7

summarize the training set errors due only to misclas-

siﬁed data examples, when comparing the proposed

algorithm to exam ple-centric and weight-centric neu-

ron labelin g, respectively. The performance differ-

ences wer e exactly th e same as those observed for the

overall training set error, ind ic a ting that all classiﬁca-

tion errors wer e due to incorrect c lassiﬁcations.

Tables 8 and 9 respectively present the differences

in performance when comparing the novel algorithm

Neuron Labeling for Self-Organizing Maps Using a Novel Example-Centric Algorithm with Weight-Centric Finalization

513

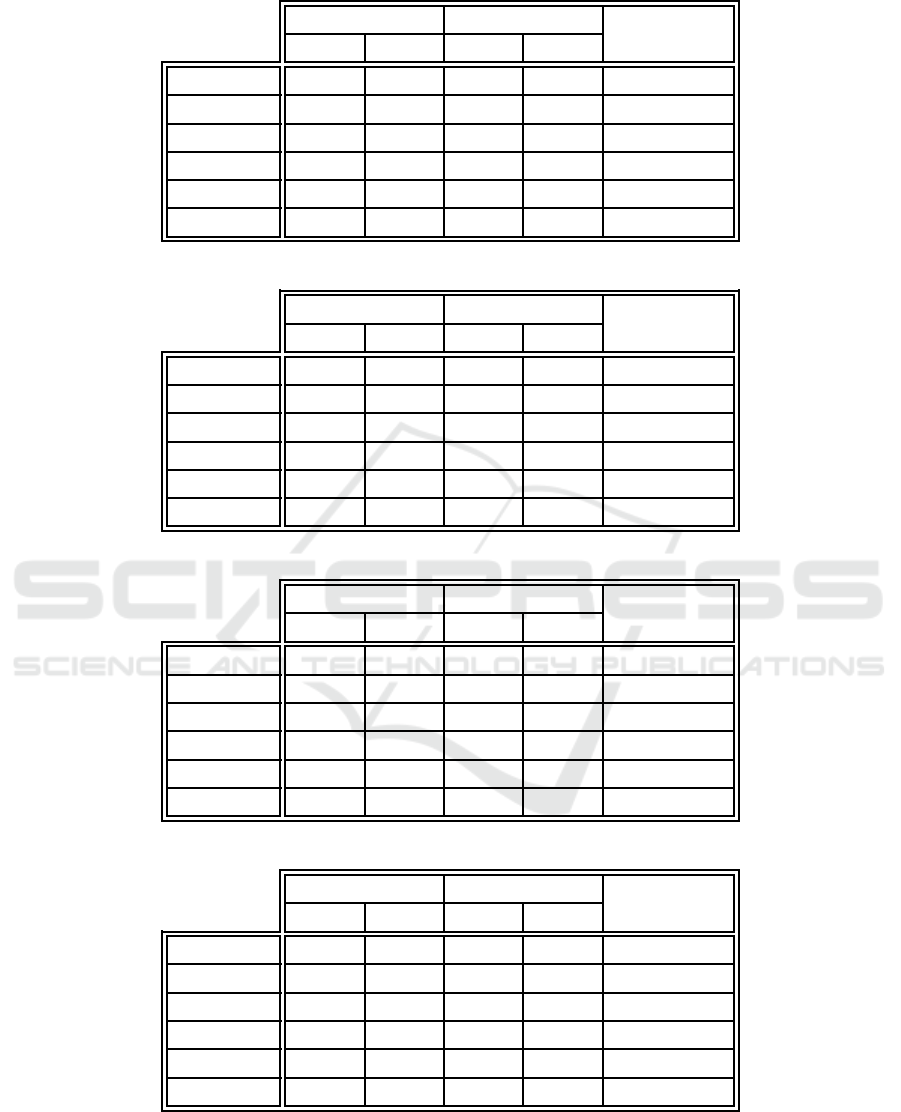
Table 4: Overall training error comparison between the proposed algorithm and example-centric neuron l abeling.

EC-WC EC

p-value

Iris 1.724 0.594 3 .655 0.705 3.725 × 10

−9

Ionosphere 3.647 0.845 10.137 1.221 1.863 × 10

−9

Monks 1 17.049 1.108 18.126 1.084 0.001

Monks 2 15.056 0.854 15.766 0.657 0.001

Monks 3 22.225 1.224 23.828 1.792 0.001

Glass 11.449 1.518 26.28 1.531 1.863 × 10

−9

Table 5: Overall training error comparison between the proposed algorithm and weight-centric neuron labeling.

EC-WC WC

p-value

Iris 1.724 0.594 2 .575 0.700 2.265 × 10

−6

Ionosphere 3.647 0.845 15.216 1.62 6 1.863 × 10

−9

Monks 1 17.049 1.108 27.974 2.416 1.863 × 10

−9

Monks 2 15.056 0.854 23.947 2.693 1.863 × 10

−9

Monks 3 22.225 1.224 19.769 1.873 5.307 × 10

−6

Glass 11.449 1.518 27.778 2.720 1.863 × 10

−9

Table 6: Training misclassiﬁed error comparison between the proposed algorithm and example-centric neuron labeling.

EC-WC EC

p-value

Iris 1.724 0.594 3 .655 0.705 3.725 × 10

−9

Ionosphere 3.647 0.845 10.137 1.22 1 1.863 × 10

−9

Monks 1 17.049 1.108 18.126 1.084 0.001

Monks 2 15.056 0.854 15.766 0.657 0.001

Monks 3 22.225 1.224 23.828 1.792 0.001

Glass 11.449 1.518 26.28 1.531 1.863 × 10

−9

Table 7: Training mi sclassiﬁed error comparison between the proposed algorithm and weight-centric neuron labeling.

EC-WC WC

p-value

Iris 1.724 0.594 2 .575 0.700 2.265 × 10

−6

Ionosphere 3.647 0.845 15.216 1.62 6 1.863 × 10

−9

Monks 1 17.049 1.108 27.974 2.416 1.863 × 10

−9

Monks 2 15.056 0.854 23.947 2.693 1.863 × 10

−9

Monks 3 22.225 1.224 19.769 1.873 5.307 × 10

−6

Glass 11.449 1.518 27.778 2.720 1.863 × 10

−9

NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications

514

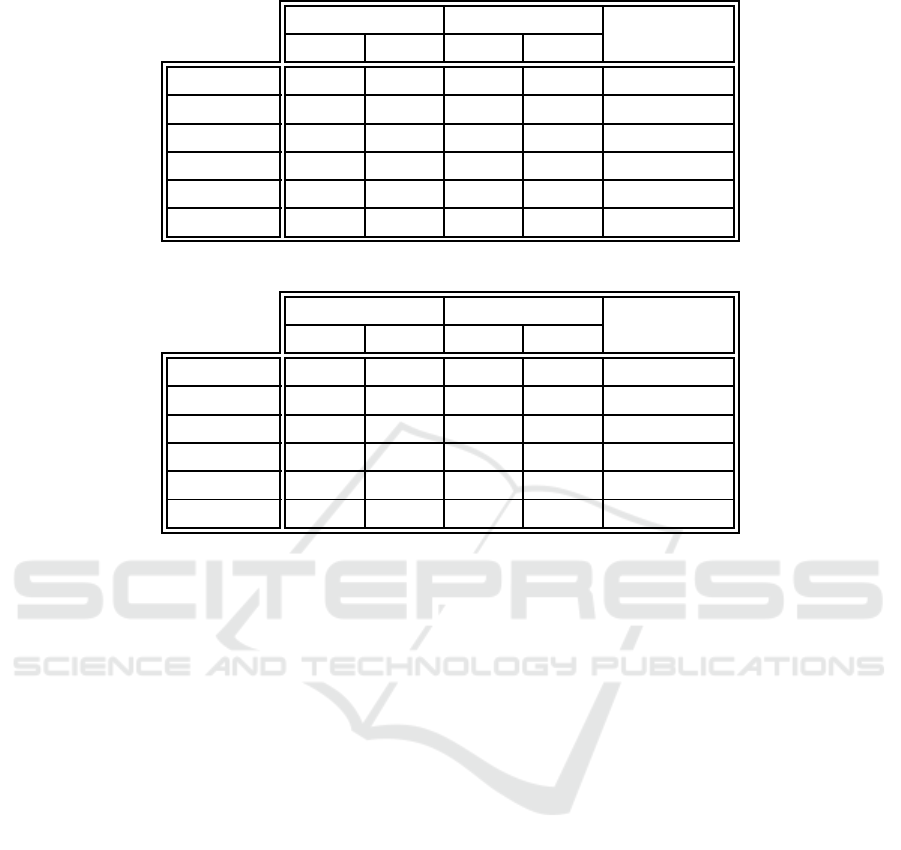
Table 8: Training unclassiﬁed error comparison between the proposed algorithm and example-centric neuron labeling.

EC-WC EC

p-value

Iris 0.000 0.000 0 .000 0.000 N/A

Ionosphere 0.000 0.000 0.000 0.000 N /A

Monks 1 0.000 0.000 0 .000 0.000 N/A

Monks 2 0.000 0.000 0 .000 0.000 N/A

Monks 3 0.000 0.000 0 .000 0.000 N/A

Glass 0.000 0.000 0.000 0.000 N/A

Table 9: Training unclassiﬁed error comparison between the proposed algorithm and weight-centric neuron labeling.

EC-WC WC

p-value

Iris 0.000 0.000 0 .000 0.000 N/A

Ionosphere 0.000 0.000 0.000 0.000 N /A

Monks 1 0.000 0.000 0 .000 0.000 N/A

Monks 2 0.000 0.000 0 .000 0.000 N/A

Monks 3 0.000 0.000 0 .000 0.000 N/A

Glass 0.000 0.000 0.000 0.000 N/A

to the standard example-centric and weigh t-centric

methods, in ter ms of the training set error due only to

unclassiﬁed data examp les. Here, it is observable that

no training examples were left unclassiﬁed by any of

the algorithms. All the labeling a pproaches therefore

fully modeled the u nderlying training data.

In terms of algorithm analysis, training set per-

formance is not a realistic representation of the real-

world behavior that can be expected from an algo-

rithm. As a result, the next three sets of comparisons

focus o n test set e rror, computed from data examples

that were not presented during SOM training.

The differences in overall test set classiﬁcation

performance, when contrasting the new algorithm

and the basic example-centric and weight-centric la-

beling techniques, are illustrated in Tables 10 and

11. No statistically signiﬁcant differences in test er-

ror performance were observed when comparing the

proposed method to example-cen tric neuron label-

ing. This implies that example-centric neuron la-

beling with weight-centric ﬁnalization classiﬁes ex-

amples as well as example-centric labeling alone.

This is expe c te d, because the ﬁrst phase of the hy-

brid technique is based on example-c entric labeling.

The weig ht-centric ﬁnalization thus does not inter-

fere with classiﬁcation accuracy. Weight-centric la-

beling performed signiﬁcantly worse than the novel

algorithm by large margins in half of the data sets

(the ionosphere and ﬁrst two mon k’s proble ms). In

the other three data sets, no signiﬁcant performance

difference was obser ved. The example-centric basis

of the hybrid method is responsible for this behavior.

Tables 12 and 13 juxtapose the test set error due

to only misclassiﬁcations. While very small perfor-

mance differences were observable when comparing

the novel approach to example-centric labeling, none

were statistically signiﬁcant. The compa rison against

weight-cen tric labeling prod uced very similar results

to those observed for th e overall test error.

The test set e rror due to unclassiﬁed examples is

compare d in Tables 14 and 15. No statistically sig-

niﬁcant differences were observed when comparing

the new algorithm against either example-centric or

weight-cen tric neuron labeling. This supports the ob-

servation that classiﬁcation errors were due mostly to

misclassiﬁcations, w hich was made when considering

the training set error performance.

Finally, Tables 16 and 17 compare the percentage

of neuron s th a t were le ft unlabeled by th e algorithms.

The example-centric method produced signiﬁcantly

more unlabeled neu rons than the proposed algorithm.

The observed d ifferences were generally large, with

example-centr ic neuron labeling leaving ne arly half

the neurons for the ﬁrst two monk’s prob le ms u nchar-

acterized. The combined approach and weight-ce ntric

labeling of course both lef t no neurons unlabeled.

When viewed holistically, example-centric label-

ing with weight-centric ﬁnalization classiﬁed data ex-

Neuron Labeling for Self-Organizing Maps Using a Novel Example-Centric Algorithm with Weight-Centric Finalization

515

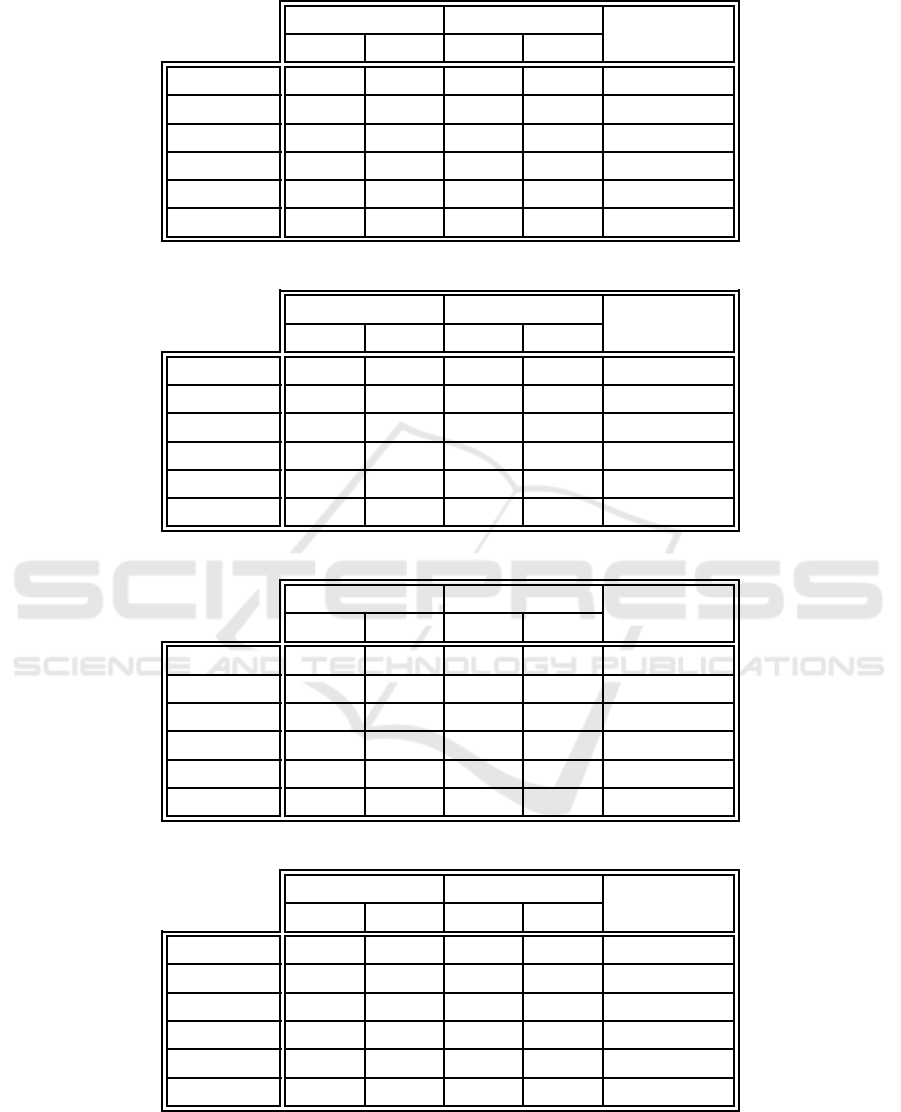
Table 10: Overall test error comparison between the proposed algorithm and example-centric neuron labeling.

EC-WC EC

p-value

Iris 2.667 6.915 4 .000 8.137 0.688

Ionosphere 8.788 9.086 11.515 10.9 23 0.124

Monks 1 19.286 12.178 20.00 0 12.358 0.532

Monks 2 19.762 10.559 20.23 8 10.116 0.866

Monks 3 26.190 9.807 26.429 12.178 0.959

Glass 25.714 14.236 31.905 18 .639 0. 187

Table 11: Overall test error comparison between the proposed algorithm and weight-centric neuron labeling.

EC-WC WC

p-value

Iris 2.667 6.915 3 .333 7.581 1.000

Ionosphere 8.788 9.086 15.152 12.0 16 0.002

Monks 1 19.286 12.178 31.66 7 11.817 2.365 × 10

−4

Monks 2 19.762 10.559 29.76 2 9.395 3.052 × 10

−5

Monks 3 26.190 9.807 27.619 12.118 0.842

Glass 25.714 14.236 33.333 17 .729 0. 024

Table 12: Test misclassiﬁed error comparison between the proposed algorithm and example-centric neuron labeling.

EC-WC EC

p-value

Iris 2.667 6.915 3 .333 7.581 1.000

Ionosphere 8.788 9.086 11.212 10.3 19 0.191

Monks 1 19.286 12.178 18.81 0 12.226 0.965

Monks 2 19.762 10.559 19.52 4 9.177 0.971

Monks 3 26.190 9.807 25.952 12.082 0.734

Glass 25.714 14.236 30.476 19 .031 0. 314

Table 13: Test misclassiﬁed error comparison between the proposed algorithm and weight-centric neuron labeling.

EC-WC WC

p-value

Iris 2.667 6.915 3 .333 7.581 1.000

Ionosphere 8.788 9.086 15.152 12.0 16 0.002

Monks 1 19.286 12.178 31.66 7 11.817 2.365 × 10

−4

Monks 2 19.762 10.559 29.76 2 9.395 3.052 × 10

−5

Monks 3 26.190 9.807 27.619 12.118 0.842

Glass 25.714 14.236 33.333 17 .729 0. 024

NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications

516

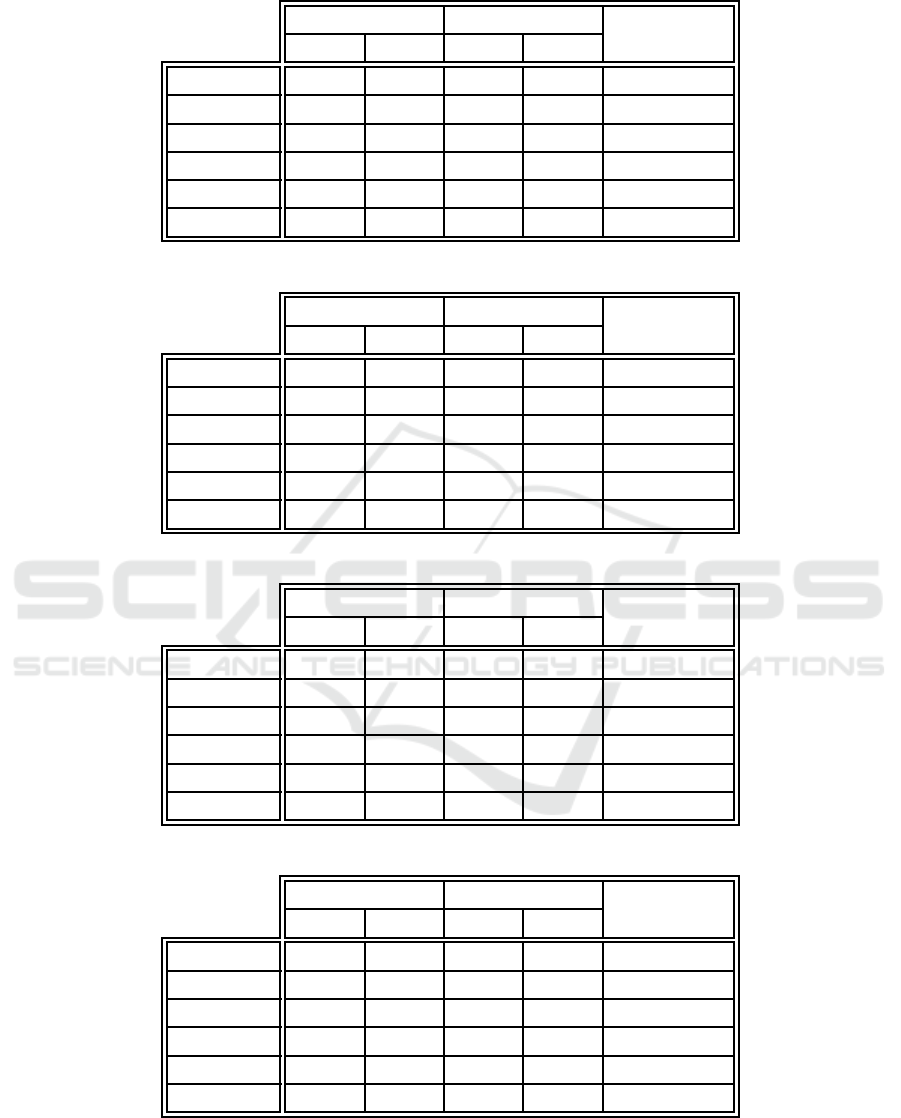
Table 14: Test unclassiﬁed error comparison between the proposed algorithm and example-centric neuron labeling.

EC-WC EC

p-value

Iris 0.000 0.000 0 .667 3.651 1.000

Ionosphere 0.000 0.000 0.303 1.660 1.000

Monks 1 0.000 0.000 1 .190 3.294 0.125

Monks 2 0.000 0.000 0 .714 2.179 0.250

Monks 3 0.000 0.000 0 .476 1.812 0.500

Glass 0.000 0.000 1.429 4.359 0.250

Table 15: Test unclassiﬁed error comparison between the proposed algorithm and weight-centric neuron labeling.

EC-WC WC

p-value

Iris 0.000 0.000 0 .000 0.000 N/A

Ionosphere 0.000 0.000 0.000 0.000 N /A

Monks 1 0.000 0.000 0 .000 0.000 N/A

Monks 2 0.000 0.000 0 .000 0.000 N/A

Monks 3 0.000 0.000 0 .000 0.000 N/A

Glass 0.000 0.000 0.000 0.000 N/A

Table 16: Unlabeled neuron percentage comparison between the proposed algorithm and example-centric neuron labeling.

EC-WC EC

p-value

Iris 0.000 0.000 19.467 3. 104 1.863 × 10

−9

Ionosphere 0.000 0.000 3.810 1.912 3.7 25 × 1 0

−9

Monks 1 0.000 0.000 43.469 3. 065 1.863 × 10

−9

Monks 2 0.000 0.000 49.807 1. 885 1.863 × 10

−9

Monks 3 0.000 0.000 32.700 4. 967 1.863 × 10

−9

Glass 0.000 0.000 8.241 3.961 7.45 1 × 10

−9

Table 17: Unlabeled neuron percentage comparison between the proposed algorithm and weight-centric neuron labeling.

EC-WC WC

p-value

Iris 0.000 0.000 0 .000 0.000 N/A

Ionosphere 0.000 0.000 0.000 0.000 N /A

Monks 1 0.000 0.000 0 .000 0.000 N/A

Monks 2 0.000 0.000 0 .000 0.000 N/A

Monks 3 0.000 0.000 0 .000 0.000 N/A

Glass 0.000 0.000 0.000 0.000 N/A

Neuron Labeling for Self-Organizing Maps Using a Novel Example-Centric Algorithm with Weight-Centric Finalization

517

amples no worse than basic example-centric label-

ing, a nd had better classiﬁcation performance than

normal weight-centric labeling. At the same time,

example-centr ic labeling with weight-centric ﬁnaliza-

tion clearly maintained a high er perc entage of labeled

neurons than example-centric neuron labeling.

The proposed algorithm underperformed in terms

of training misclassiﬁcation error on the single data

set with injec te d noise (the third monk’s problem),

when compare d to weight-ce ntric neuron labeling.

This type of performance shortfall is, however, not

clear when considering test e rror. A more thorough

investigation into the performance of the algorithms

in the presence of noise is deferred to future studies.

6 CONCLUSIONS

This paper introduces a novel supervised neuron la-

beling algorithm that succe ssfully comb ines the ad-

vantages of both example-centric and weight-centric

neuron labeling. If only label q uality is imp ortant, the

proposed technique is largely equivalent to example-

centric labeling , with the latter bein g preferable due

to a less complex algorithm. However, if humans are

to analyze a SOM’s labels, the proposed hybrid ap-

proach is preferable becau se it maintains a fully la-

beled map wh ile offering high-q uality labels.

Future work will focus on a lternative ways in

which high-quality complete SOM labelings can be

achieved. Three approaches are under consideration:

• An approa ch (Li and Eastman, 2006) that has

been brieﬂy proposed, but not experime ntally ex-

plored, characterizes each unlabeled neuron us-

ing the mean distance between the weight vector

of the unlabeled neuron and the weight vectors

of neuron groups tha t are labeled with the sam e

class. The unlabeled neuron r eceives the label of

the class with the smallest mean distance.

• The propagation of labels from characterized neu-

rons to adjacent uncharacterized neurons will be

investigated. A possible basis for this is neuron

proxim ity graphs (Herrmann and Ultsch, 2007).

• Sem i-supervised SOMs learn the distribution of

classiﬁcation attributes ac ross the map, without

biasing training (Kiviluoto and Bergius, 1997).

Labels will be based on the learned cla ssiﬁcation

attributes for each neuron.

Finally, the general perform ance characteristics of the

supervised labeling algorithms will be investigated in

greater d e pth. T he scalability of supervised labeling

algorithm s to very large datasets and maps will be of

interest. It will also be informative to analyze the per-

formance characteristics of the algorithms in the pres-

ence of classiﬁcation and attribute noise.

REFERENCES

Azcarraga, A., Hsieh, M.-H., Pan, S.-L., and Setiono, R.

(2008). Improved SOM labeling methodology for

data mining applications. In Soft Computing for

Knowledge Discovery and Data Mining, pages 45–75.

Springer. doi:10.1007/978-0-387-69935-6

Bishop, C. M. (2006). Pattern Recognition and Machine

Learning. Springer.

Bowen, F. and Siegler, J. (2024). Self-organizing maps:

A novel approach to identify and map business clus-

ters. Journal of Management Analytics, 11(2):228–

246. doi:10.1080/23270012.2024.2306628.

Corradini, A. and Gross, H .-M. (1999). A hy-

brid stochastic-connectionist architecture for gesture

recognition. In Proceedings of ICIIS, pages 336–341.

doi:10.1109/ICIIS.1999.810286.

Deboeck, G. (1999). Public domain vs. commercial tools

for creating neural self-organizing maps. PC AI,

13(1):27–33.

Engelbrecht, A. P. (2007). Computational Intelli-

gence: An Introduction. Wiley, 2nd edition.

doi:10.1002/9780470512517.

Fisher, R. A. (1936). Iris data set. UCI Machine Learning

Repository. doi:10.24432/C56C76.

Franken, N. ( 2009). Visual exploration of algorithm param-

eter space. In Proceedings of CEC, pages 389–398.

doi:10.1109/CEC.2009.4982973.

Galvan, D., Effting, L., Cremasco, H., and Conte-Junior,

C. A. (2021). The spread of the COVID-19 out-

break in Brazil: An overview by Kohonen Self-

Organizing Map networks. Medicina, 57(3):1–19.

doi:10.3390/medicina57030235.

German, B. (1987). Glass identiﬁcation data set. UCI Ma-

chine Learning Repository. doi:10.24432/C5WW2P.

Han, J., Kamber, M., and Pei, J. (2012). Data Mining: Con-

cepts and Techniques. Morgan Kaufmann, 3rd edition.

doi:10.1016/C2009-0-61819-5.

Herrmann, L. and Ultsch, A. (2007). Label prop-

agation for semi-supervised learning in Self-

Organizing Maps. In Proceedings of WSOM.

doi:10.2390/biecoll-wsom2007-113.

Javed, A., Rizzo, D. M., Lee, B. S., and Gramling, R.

(2024). S O MTimeS: S elf organizing maps for time

series clustering and its application to serious illness

conversations. Data Mining and Knowledge Discov-

ery, 38:813–839. doi:10.1007/s10618-023-00979-9.

Kaski, S., Kangas, J., and Kohonen, T. (1998). B ibliography

of Self-Organizing Map (SOM) papers: 1981–1997.

Neural Computing Surveys, 1:102–350.

Kiviluoto, K. and Bergius, P. (1997). Analyzing ﬁnancial

statements with the Self-Organizing Map. In Proceed-

ings of WSOM, pages 362–367.

NCTA 2024 - 16th International Conference on Neural Computation Theory and Applications

518

Kohonen, T. (1982). Self-organizing formation of topolog-

ically correct feature maps. Biological Cybernetics,

43(1):59–69. doi:10.1007/BF00337288.

Kohonen, T. (1989). Self-Organization and As-

sociative Memory. Springer, 3rd edition.

doi:10.1007/978-3-642-88163-3.

Kohonen, T. (2001). Self-Organizing Maps. Springer-

Verlag, 3rd edition. doi:10.1007/978-3-642-56927-2.

Kohonen, T., Hynninen, J., Kangas, J., and Laaksonen, J.

(1996). SOM

PAK: The Self-Organizing Map pro-

gram package. Technical Report A31, Helsinki Uni-

versity of Technology.

Lagus, K. and Kaski, S. (1999). Keyword selection

method for characterizing text document maps. In

Proceedings of ICANN, volume 1, pages 371–376.

doi:10.1049/cp:19991137.

Li, Z. and Eastman, J. R. (2006). The nature and clas-

siﬁcation of unlabelled neurons in t he use of Ko-

honen’s Self-Organizing Map for supervised clas-

siﬁcation. Transactions in GIS, 10(4):599–613.

doi:10.1111/j.1467-9671.2006.01014.x.

Miller, Jr, R. G. (1981). Simultaneous Statisti-

cal Inference. Springer-Verlag, 2nd edition.

doi:10.1007/978-1-4613-8122-8.

Oja, M., Kaski, S., and Kohonen, T. (2003). Bibliography

of Self-Organizing Map (SOM) papers: 1998–2001

addendum. Neural Computing Surveys, 3:1–156.

P¨oll¨a, M., Honkela, T., and Kohonen, T. (2009). Bibliog-

raphy of Self-Organizing Map (SOM) papers: 2002-

2005 addendum. Technical Report T KK -ICS-R23,

Helsinki University of Technology.

Rauber, A. and Merkl, D. (1999). The SOMLib digital li-

brary system. In Proceedings of ECDL, pages 323–

342. doi:10.1007/3-540-48155-9

21.

Rosa, A. H., Stubbings, W. A., Akinrinade, O. E., Gon-

tijo, E. S. J., and Harrad, S. (2024). Neural net-

work for evaluation of the impact of the UK COVID-

19 national lockdown on atmospheric concentrations

of PAHs and PBDEs. Environmental Pollution,

341:122794. doi:10.1016/j.envpol.2023.122794.

Samarasinghe, S. (2007). Neural Networks for Applied

Sciences and Engineering: From Fundamentals to

Complex Pattern Recognition. Auerbach Publica-

tions, B oca Raton, Florida, United States of America.

doi:10.1201/9780849333750.

Serrano-Cinca, C. (1996). Self organizing neural networks

for ﬁnancial diagnosis. Decision Support Systems,

17(3):227–238. doi:10.1016/0167-9236(95)00033-X.

Sigillito, V., Wing, S., H utt on, L ., and Baker, K. (1989).

Ionosphere data set. UCI Machine Learning Reposi-

tory. doi:10.24432/C5W01B.

Sobol’, I. M. (1967). On the distribution of points

in a cube and the approximate evaluation of

integrals. USSR Computational Mathemat-

ics and Mathematical Physics, 7(4):86–112.

doi:10.1016/0041-5553(67)90144-9.

Su, M.-C., Liu, T.-K., and Chang, H.-T. (1999). An efﬁcient

initialization scheme for the self-organizing feature

map algorithm. In Proceedings of IJCNN, volume 3,

pages 1906–1910. doi:10.1109/IJCNN.1999.832672.

van H eerden, W. S. (2017). Self-organizing feature maps for

exploratory data analysis and data mining: A practical

perspective. Master’s thesis, University of Pretoria.

van Heerden, W. S. (2023). Automatic distance-based inter-

polating unit detection and pruning in self-organizing

maps. In Proceedings of SSCI, pages 1298–1303.

doi:10.1109/SSC I52147.2023.10372025.

van Heerden, W. S. (2024). SOMLib.

https://github.com/wvheerden/SOMLib.

van Heerden, W. S. and Engelbrecht, A. P. (2008). A

comparison of map neuron labeling approaches

for unsupervised self-organizing feature maps.

In Proceedings of IJCNN, pages 2139–2146.

doi:10.1109/IJCNN.2008.4634092.

van Heerden, W. S. and Engelbrecht, A. P. (2012). Unsuper-

vised weight-based cluster labeling for self-organizing

maps. In Proceedings of WSOM, pages 45–54.

doi:10.1007/978-3-642-35230-0

van Heerden, W. S. and Engelbrecht, A. P. (2016). An

investigation into the effect of unlabeled neurons

on Self-Organizing Maps. In Proceedings of SSCI.

doi:10.1109/SSC I.2016.7849938.

Vantyghem, A. N., Galvin, T. J., Sebastian, B., O’Dea,

C., Gordon, Y. A., Boyce, M., Rudnick, L., Pol-

sterer, K., Andernach, H., Dionyssiou, M., Venkatara-

man, P., Norris, R., Baum, S., Wang, X. R., and

Huynh, M. (2024). Rotation and ﬂipping invari-

ant self-organizing maps wi th astronomical images:

A cookbook and application to the VLA Sky Sur-

vey QuickLook images. Astronomy and Computing,

47:100824. doi:10.1016/j.ascom.2024.100824.

Wilcoxon, F. (1945). Individual comparisons by rank-

ing methods. Biometrics Bulletin, 1(6):80–83.

doi:10.2307/3001968.

Wnek, J. (1993). Monk’s problems data sets. UCI Machine

Learning Repository. doi:10.24432/C5R30R.

Neuron Labeling for Self-Organizing Maps Using a Novel Example-Centric Algorithm with Weight-Centric Finalization

519