Comparative Analysis of Single and Ensemble Support Vector

Regression Methods for Software Development Effort Estimation

Mohamed Hosni

MOSI Research Team, LM2S3 Laboratory, ENSAM, Moulay Ismail Iniversity of Meknes, Meknes, Morocco

Keywords:

Support Vector Regression, Kernels, Software Effort Estimation, Ensemble Effort Estimation.

Abstract:

Providing an accurate estimation of the effort required to develop a software project is crucial for its success.

These estimates are essential for managers to allocate resources effectively and deliver the software product

on time and with the desired quality. Over the past ﬁve decades, various effort estimation techniques have

been developed, including machine learning (ML) techniques. ML methods have been applied in software

development effort estimation (SDEE) for the past three decades and have demonstrated promising levels

of accuracy. Numerous ML methods have been explored, including the Support Vector Regression (SVR)

technique, which has shown competitive performance compared to other ML techniques. However, despite the

plethora of proposed methods, no single technique has consistently outperformed the others in all situations.

Prior research suggests that generating estimations by combining multiple techniques in ensembles, rather

than relying solely on a single technique, can be more effective. Consequently, this research paper proposes

estimating SDEE using both individual ML techniques and ensemble methods based on SVR. Speciﬁcally, four

variations of the SVR technique are employed, utilizing four different kernels: polynomial, linear, radial basis

function, and sigmoid. Additionally, a homogeneous ensemble is constructed by combining these four variants

using two types of combiners. An empirical analysis is conducted on six well-known datasets, evaluating

performance using eight unbiased criteria and the Scott-Knott statistical test. The results suggest that both

single and ensemble SVR techniques exhibit similar predictive capabilities. Furthermore, the SVR variant

with the polynomial kernel is deemed the most suitable for SDEE. Regarding the combiner rule, the non-

linear combiner yields superior accuracy for the SVR ensemble.

1 INTRODUCTION

Accurately predicting the effort required to develop a

new software system during the initial phases of the

software lifecycle remains a signiﬁcant challenge in

software project management. This estimation pro-

cess, known as software development effort estima-

tion (SDEE) (Wen et al., 2012), is critical for effective

resource allocation and project planning.

Accurate estimates are critical, as errors can lead

to major challenges for software managers. Charette

(Charette, 2005) notes that inaccurate resource esti-

mates are a signiﬁcant contributor to software project

failures. To address this issue, numerous effort es-

timation methods have been proposed and studied

(de Barcelos Tronto et al., 2008), with machine

learning (ML) techniques emerging as a particularly

promising solution.

A systematic review (SLR) conducted by Wen et

https://orcid.org/0000-0001-7336-4276

al. (Wen et al., 2012) identiﬁed seven ML techniques

proposed for estimating software development effort.

The review found that these ML techniques generally

provide more accurate results than traditional non-

ML methods. Additionally, the ensemble method,

known as Ensemble Effort Estimation (EEE), has gar-

nered signiﬁcant attention within the SDEE research

community. EEE involves combining estimates from

multiple effort estimators using speciﬁc combination

rules. Studies within the SDEE literature have exten-

sively explored EEE techniques, with results suggest-

ing that they yield more accurate estimates compared

to single estimation methods.

The SLR performed a SLR focused on ensem-

ble approaches in SDEE (Idri et al., 2016). This

review analyzed 24 studies published between 2000

and 2016 and found that ensemble methods generally

outperformed single techniques, demonstrating con-

sistent performance across various datasets. The re-

view identiﬁed 16 distinct techniques used for con-

Hosni, M.

Comparative Analysis of Single and Ensemble Support Vector Regression Methods for Software Development Effort Estimation.

DOI: 10.5220/0013072300003838

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2024) - Volume 1: KDIR, pages 509-516

ISBN: 978-989-758-716-0; ISSN: 2184-3228

509

structing ensembles, with Artiﬁcial Neural Networks

(ANN) and Decision Trees (DT) being the most com-

monly employed. Additionally, it noted that 20 dif-

ferent combiners were utilized to generate ensemble

outputs, with linear combiners being the most preva-

lent. An updated review by Cabral et al. (Cabral et al.,

2023) in 2022, which covered studies from 2016 to

2021, conﬁrmed these ﬁndings.

The Support Vector Regression (SVR) technique,

introduced by Oliveira in 2006 for predicting software

development effort (Oliveira, 2006), has been the sub-

ject of extensive research. Evidence suggests that

SVR often provides more accurate results than many

other ML techniques used in SDEE (Braga et al.,

2008; Mahmood et al., 2022).

A key feature of SVR is its kernel, which maps

the input space to a higher-dimensional feature space.

Variations in SVR techniques, deﬁned by different

kernels, can lead to different estimation results.

This paper aims to assess the effectiveness of

the Ensemble Effort Estimation approach based on

SVR. The objective is to determine whether com-

bining multiple SVR techniques with various kernels

yields better performance than using a single SVR

technique.

To achieve this, the paper explores an EEE ap-

proach that integrates four SVR techniques, each

with distinct kernels and hyperparameter settings op-

timized using Particle Swarm Optimization (PSO).

The study employs several combination rules, includ-

ing three linear combiners (average, median, inverse

ranked weighted mean) and one non-linear combiner

(Multilayer Perceptron), to evaluate their impact on

estimation accuracy.To address this objective, the pa-

per investigates three key research questions (RQs):

• (RQ1). Which of the four kernel methods

used in the SVR techniques is most suitable for

SDEE datasets?

• (RQ2). Does the SVR-EEE approach consis-

tently outperform the single SVR technique,

regardless of the combiners used?

• (RQ3). Among the combiners utilized, which

one provides the highest accuracy for the pro-

posed ensemble?

The main features of this empirical work are as

follows:

1. Development of an SVR-Ensemble technique that

integrates four SVR methods with different ker-

nels and hyperparameter settings.

2. Application of Particle Swarm Optimization

(PSO) to optimize the hyperparameters of the four

SVR variants.

3. Evaluation of various combiners for generating

the ﬁnal output of the ensemble.

The structure of this paper is as follows: Sec-

tion 2 provides background information and reviews

previous research on the topic. Section 3 offers an

overview of the SVR technique. Section 4 details the

materials and methods used in the study. Section 5

presents and discusses the empirical results. Finally,

Section 6 concludes the paper and proposes directions

for future research.

2 RELATED WORK

This section begins by deﬁning Ensemble Effort Es-

timation (EEE) and then reviews the main ﬁndings

from EEE studies in the context of SDEE literature.

EEE is an approach that combines multiple indi-

vidual predictors using a speciﬁc combination rule.

The literature distinguishes between two types of en-

sembles (Hosni et al., 2019; Hosni et al., 2018a;

Hosni et al., 2021; Kocaguneli et al., 2011): homo-

geneous and heterogeneous. Homogeneous ensem-

bles consist of multiple variants of the same ML tech-

nique or a combination of a single ML technique with

meta-ensemble methods such as Bagging, Boosting,

or Random Subspace. In contrast, heterogeneous

ensembles combine at least two different ML tech-

niques. The ﬁnal output of an ensemble is obtained

by aggregating the individual estimates from its com-

ponents using a deﬁned combination rule.

To explore the application of ensemble ap-

proaches in SDEE, Idri et al. (Idri et al., 2016) con-

ducted a SLR analyzing papers published between

2000 and 2016. Their review, covering 24 papers,

yielded the following main conclusions:

• Homogeneous ensembles were the most fre-

quently studied, appearing in 17 out of the 24 pa-

pers.

• A total of 16 different effort estimation techniques

were used to construct EEE.

• Machine learning techniques were the predomi-

nant choice for ensemble components, with Arti-

ﬁcial Neural Networks (ANN) and Decision Trees

(DT) being the most frequently investigated indi-

vidual techniques.

• The Support Vector Regression (SVR) technique

was explored in ﬁve studies, primarily for con-

structing heterogeneous ensembles.

• Twenty combination rules were employed to gen-

erate the ﬁnal output of ensemble methods. These

rules were categorized into linear and non-linear

KDIR 2024 - 16th International Conference on Knowledge Discovery and Information Retrieval

510

types, with linear rules being the most extensively

investigated.

• Overall, ensemble methods demonstrated better

performance compared to single techniques.

It is also noteworthy that the SLR conducted by

Cabral et al. (Cabral et al., 2023) reached similar con-

clusions regarding the use of EEE.

3 SUPPORT VECTOR

REGRESSION: A BRIEF

DESCRIPTION

Support Vector Regression (SVR) is a supervised ML

technique tailored for regression tasks, extending the

principles of Support Vector Machines, which are

primarily employed for classiﬁcation (Vapnik et al.,

1998). The main concept behind SVR is to ﬁnd a hy-

perplane that optimally ﬁts the data while minimizing

prediction errors. SVR is capable of modeling both

linear and non-linear relationships between indepen-

dent and dependent variables by utilizing kernel func-

tions to map input features into a high-dimensional

space. Commonly used kernels include linear, poly-

nomial, radial basis function (RBF), and sigmoid.

SVR is also robust to outliers, making it highly ef-

fective across various scenarios.

SVR was ﬁrst applied to Software Develop-

ment Effort Estimation by Oliveira (Oliveira, 2006;

Oliveira et al., 2010). Subsequent studies in the SDEE

literature have shown that SVR achieves competitive

accuracy compared to other ML techniques (Braga

et al., 2008; Hosni et al., 2018b; Braga et al., 2007;

Mahmood et al., 2022; L

opez-Mart

ın, 2021).

Several parameters signiﬁcantly inﬂuence SVR

performance:

• Regularization Parameter (C): Controls the

trade-off between model complexity and error

minimization.

• Kernel Parameters: Determine the nature of the

non-linear mapping.

Careful tuning of these parameters is crucial for

optimizing SVR’s predictive performance.

4 EMPIRICAL DESIGN

This section ﬁrst introduces the performance metrics

used to evaluate the accuracy of the proposed SDEE

techniques and the statistical test employed to as-

sess their signiﬁcance. It then covers the hyperpa-

rameter optimization methods applied in the study.

The dataset utilized for developing the SDEE tech-

niques is also presented. Lastly, the section details

the methodology for constructing and evaluating the

predictive model.

4.1 Performance Measures and

Statistical Test

To evaluate the accuracy of the proposed techniques,

we employed eight commonly used performance cri-

teria in the SDEE literature. These criteria include

Mean Absolute Error (MAE), Mean Balanced Rela-

tive Error (MBRE), Mean Inverted Balanced Relative

Error (MIBRE), and their corresponding median val-

ues, Logarithmic Standard Deviation (LSD), and Pred

(25%) (Miyazaki et al., 1991; Foss et al., 2003; Hosni,

2023; Mustafa and Osman, 2024; Kumar et al., 2020).

Additionally, we used Standardized Accuracy

(SA) and Effect Size to determine whether the SDEE

techniques provided better estimates compared to ran-

dom guessing (Shepperd and MacDonell, 2012). The

mathematical formulas for these performance indica-

tors are detailed in Equations (1)–(8).

= |e

−

| (1)

Pred(0.25) =

100

∑

i=1

(

1 if

⩽ 0.25

0 otherwise

(2)

MAE =

∑

i=1

(3)

MBRE =

∑

i=1

min(e

)

(4)

MIBRE =

∑

i=1

max(e

)

(5)

LSD =

∑

i=1

(λ

)

n − 1

(6)

SA = 1 −

MAE

(7)

△ =

MAE

− MAE

(8)

where:

• The actual effort and predicted effort for the i-th

project are denoted by e

and

, respectively.

• The average Mean Absolute Error (MAE) from

multiple random guessing runs is represented as

MAE p

. This value is obtained by randomly sam-

pling (with equal probability) from the remaining

n−1 cases and setting

= e

, where r is a random

index from 1 to n, excluding i. This randomization

Comparative Analysis of Single and Ensemble Support Vector Regression Methods for Software Development Effort Estimation

511

approach is robust as it does not assume speciﬁc

distribution characteristics of the data.

• The Mean Absolute Error for prediction technique

i, denoted as MAE p

, is used as a benchmark in

comparison with the sample standard deviation of

the random guessing strategy.

• The value of λ

is calculated as the difference be-

tween the natural logarithm of e

and the natural

logarithm of

• The estimator s

is employed to estimate the resid-

ual variance associated with λ

To group the developed SDEE techniques based

on their predictive capabilities, we applied the Scott-

Knott statistical test (Hosni et al., 2018b). For valida-

tion, we utilized the Leave-One-Out Cross-Validation

(LOOCV) technique to construct and evaluate these

SDEE techniques.

4.2 Hyperparameters Optimization

Techniques

In this paper, the optimal parameters for the devel-

oped SVR techniques were determined using the Par-

ticle Swarm Optimization (PSO) technique. Table

1 details the range of hyperparameters considered by

PSO to identify the optimal settings. For the Multi-

Layer Perceptron (MLP) combination rule, used to

generate the ﬁnal prediction of the proposed ensem-

ble, hyperparameters were optimized using the Grid

Search (GS) technique. Table 1 outlines the param-

eter ranges explored by GS. Both optimization tech-

niques utilized the MAE as the ﬁtness function, with

the goal of minimizing the MAE value.

4.3 Datasets

To evaluate the performance of the proposed

techniques for estimating software development

effort, we selected six well-established datasets

from two different repositories (Kocaguneli

et al., 2011; Kumar and Srinivas, 2024). Five

datasets—Albrecht, COCOMO81, Desharnais,

Kemerer, and Miyazaki—were sourced from the

PROMISE repository. Additionally, one dataset was

obtained from the ISBSG data repository. Compre-

hensive details about these datasets, including their

size, number of attributes, and descriptive statistics of

effort (such as minimum, maximum, mean, median,

skewness, and kurtosis), are provided in Table 2.

4.4 Methodology Used

This subsection details the methodology used to ad-

dress our RQs, with the analysis performed indepen-

dently for each dataset. We developed four SVR

techniques, each employing a distinct kernel: Linear,

Polynomial, Radial Basis Function (RBF), and Sig-

moid. The homogeneous ensemble integrates these

four SVR variants. The steps of the empirical analy-

sis are outlined below:

• Step 1: Construct SVR models using Particle

Swarm Optimization (PSO) with 10-fold cross-

validation to determine the optimal hyperparam-

eters for each kernel variant.

• Step 2: Select the optimal hyperparameters iden-

tiﬁed in Step 1 for each SVR variant.

• Step 3: Rebuild the SVR models with the selected

hyperparameters using LOOCV.

• Step 4: Evaluate the performance of the SVR

models using SA and effect size, and compare

these results to the 5% quantile of random guess-

ing.

• Step 5: Evaluate the accuracy of the SVR models

using eight performance metrics: MAE, MdAE,

MIBRE, MdIBRE, MBRE, MdBRE, LSD, and

Pred (25

• Step 6: Construct SVR ensembles by combining

the four SVR variants using the following com-

bination rules: median, average, inverse-ranked

weighted mean (IRWM), and Multi-Layer Per-

ceptron (MLP).

• Step 7: Evaluate and report the performance of

the SVR ensembles using the same eight metrics.

• Step 8: Rank the single SVR models and the en-

sembles using the Borda count voting system.

• Step 9: Apply the Scott-Knott statistical test

based on Absolute Error (AE) to group the tech-

niques and identify clusters with similar predic-

tive capabilities.

For ease of reference, the following abbreviations

will be used:

• Single SVR Models: SVR followed by the kernel

type.

– SVR with Linear Kernel: SVRL

– SVR with Polynomial Kernel: SVRP

– SVR with Radial Basis Function Kernel:

SVRR

– SVR with Sigmoid Kernel: SVRS

• Ensemble SVR Models: E followed by the com-

biner type.

KDIR 2024 - 16th International Conference on Knowledge Discovery and Information Retrieval

512

Table 1: Range of Hyperparameters for PSO and GS.

SVR-Linear Kernel C{1, 100}, Epsilon {0.001, 0.5}

SVR-RBF Kernel C{1, 100}, Epsilon {0.001, 0.5}, gamma {0.001, 1}

SVR-Poly Kernel C{1, 100}, Epsilon {0.001, 0.5}, degree {1, 10}

SVR-Sigmoid Kernel C{1, 100}, Epsilon {0.001, 0.5}, Coef0 {0.001, 1}

MLP Combiner

hidden layer sizes: {(8,), (8,16), (8, 16, 32)},

activation: {’relu’, ’tanh’, ’identity’, ’logistic’},

solver: {’adam’, ’lbfgs’, ’sgd’},

learning rate: {’constant’, ’adaptive’, ’invscaling’}

Table 2: Overview of Descriptive Statistics for the Six Selected Datasets.

Dataset Size #Features Effort

Min Max Mean Median Skewness Kurtosis

Albrecht 24 7 0.5 105 21.87 11 2.30 4.7

COCOMO81 252 13 6 11400 683.44 98 4.39 20.5

Desharnais 77 12 546 23940 4833.90 3542 2.03 5.3

ISBSG 148 10 24 60270 6242.60 2461 3.05 11.3

Kemerer 15 7 23 1107 219.24 130 3.07 10.6

Miyazaki 48 8 5.6 1586 87.47 38 6.26 41.3

– Ensemble SVR with MLP as the combiner:

EMLP

– Ensemble SVR with average as the combiner:

EAVR

– Ensemble SVR with median as the combiner:

EMED

– Ensemble SVR with IRWM as the combiner:

EIRWM

5 EMPIRICAL RESULTS

In this section, we present the empirical results from

our experiments. The experiments were executed

using Python and its associated libraries, while the

Scott-Knott (SK) test was conducted using the R pro-

gramming language.

5.1 Single SVR Techniques

The initial phase of our empirical analysis involved

identifying the optimal parameters for the various

SVR techniques. To achieve this, we employed

PSO technique to ﬁne-tune the hyperparameters of

the SVR models. This optimization process was ap-

plied to the four SVR variants across the six selected

datasets, utilizing 10-fold cross-validation.

Following parameter optimization, we con-

structed the SVR models using the identiﬁed opti-

mal parameters. The performance of these models

was then compared against the 5% quantile of ran-

dom guessing, which served as our baseline estima-

tor. Speciﬁcally, we assessed whether the MAE of

the SVR variants on each dataset was lower than the

5% quantile of random guessing. This comparison

helped determine if the SVR techniques were effec-

tively making predictions.

To further validate the results, we evaluated the

effect size to assess the signiﬁcance of the improve-

ment over the baseline estimator. Table 3 presents the

SA and effect size of the constructed SVR techniques.

The results demonstrate a signiﬁcant improvement

over the baseline estimator, conﬁrming that all SVR

variants produced better predictions. Thus, we can

conﬁdently assert that the proposed SVR techniques

are effective in estimating software development ef-

fort.

The next phase of our experimental protocol in-

volves evaluating the predictive performance of the

proposed techniques using eight established perfor-

mance indicators. These indicators, recognized for

their objectivity, are crucial for assessing the accu-

racy of the techniques. To synthesize the results from

these indicators, we utilized the Borda count voting

system. The ﬁnal rankings of the single SVR tech-

niques across the selected datasets are detailed in Ta-

ble 4.

The rankings of the SVR techniques varied de-

pending on the dataset and the kernel used. Notably,

the SVR technique with a polynomial kernel (SVRP)

emerged as the most effective, achieving the highest

rank in ﬁve out of six datasets. The SVR technique

with a linear kernel (SVRL) performed well, securing

Comparative Analysis of Single and Ensemble Support Vector Regression Methods for Software Development Effort Estimation

513

Table 3: SA and Effect size values of the SVR techniques across the six datasets.

Dataset COCOMO ISBSG Miyazaki Desharnais Albrecht Kemerer

SA5% 15% 13% 34% 15% 30% 34%

Technique SA Delta SA Delta SA Delta SA Delta SA Delta SA Delta

SVRL 53% -5.41 40% -4.68 66% -2.40 42% -4.42 76% -3.83 65% -2.50

SVRR 53% -5.47 40% -4.60 63% -2.29 41% -4.31 91% -4.62 63% -2.44

SVRP 96% -9.84 55% -6.35 88% -3.17 54% -5.72 89% -4.51 89% -3.42

SVRS 39% -3.98 37% -4.32 11% -0.39 35% -3.69 33% 6.56 45% -1.75

the second position in four out of six datasets.

In contrast, the SVR technique using the sig-

moid kernel consistently ranked the lowest across all

datasets, indicating its comparatively inferior perfor-

mance.

The following summarizes the ranking of the four

SVR techniques across the six selected datasets:

• Polynomial Kernel (SVRP):

– Top Ranking: Achieved the highest ranking in

5 out of 6 datasets.

– Overall Performance: Demonstrated superior

performance in most cases.

• Linear Kernel (SVRL):

– Top Ranking: Achieved the highest ranking in

1 out of 6 datasets.

– Second Position: Secured the second position

in 4 out of 6 datasets.

– Overall Performance: Consistently per-

formed well, ranking second most frequently.

• Radial Basis Function Kernel (SVRR):

– Top Ranking: Did not achieve the highest

ranking in any dataset.

– Overall Performance: Exhibited variable per-

formance, generally not leading but still com-

petitive.

• Sigmoid Kernel (SVRS):

– Top Ranking: Did not achieve the highest

ranking in any dataset.

– Overall Performance: Consistently ranked the

lowest in all datasets, indicating the least effec-

tiveness.

Table 4: Ranking of the four SVR techniques on the se-

lected datasets.

COC. ISBSG Miyazaki Desh. Albrecht Kemerer

SVRP SVRP SVRP SVRP SVRR SVRP

SVRR SVRL SVRL SVRL SVRP SVRL

SVRL SVRR SVRR SVRR SVRL SVRR

SVRS SVRS SVRS SVRS SVRS SVRS

5.2 SVR Ensembles

The next phase of our experimental design involves

constructing a homogeneous ensemble from the four

SVR techniques. We develop four different en-

sembles, each distinguished by its combination rule.

Speciﬁcally, we use two types of combiners to gener-

ate the ﬁnal output of the proposed ensembles:

• Linear Combiners: AVG, MED, IRWM.

• Non-Linear Combiner: MLP.

The hyperparameters of the MLP combiner were

optimized using the grid search technique.

The ensemble approach combines four SVR vari-

ants, each utilizing a different kernel. These variants

have demonstrated superior performance compared

to random guessing, as shown in the previous sec-

tion. Therefore, the four ensembles constructed are

expected to outperform the baseline estimator.

To assess the performance of the proposed ensem-

bles, we utilize eight performance metrics and com-

pare them with the individual SVR techniques. The

ﬁnal rankings are determined using the Borda count

voting system, with results presented in Table 5.

The results reveal that ensemble methods achieved

the top ranking only twice. In comparison, SVRP

was ranked ﬁrst in three datasets, and SVRR secured

the top position in one dataset. It is evident that no

single ensemble approach consistently outperformed

all other techniques across every dataset. The per-

formance of the ensembles varied depending on the

dataset. However, it is noteworthy that, in the ma-

jority of cases, the ensemble methods outperformed

the SVRS technique. On the other hand, certain SVR

variants outperformed the ensemble methods in sev-

eral datasets, with the exception of the ISBSG and

Desharnais datasets, where ensembles generally sur-

passed the single SVR techniques, except for SVRP.

Consequently, there is no deﬁnitive evidence to es-

tablish the superiority of any speciﬁc technique over

others.

To statistically assess the signiﬁcant differences

between the proposed techniques, we employed the

KDIR 2024 - 16th International Conference on Knowledge Discovery and Information Retrieval

514

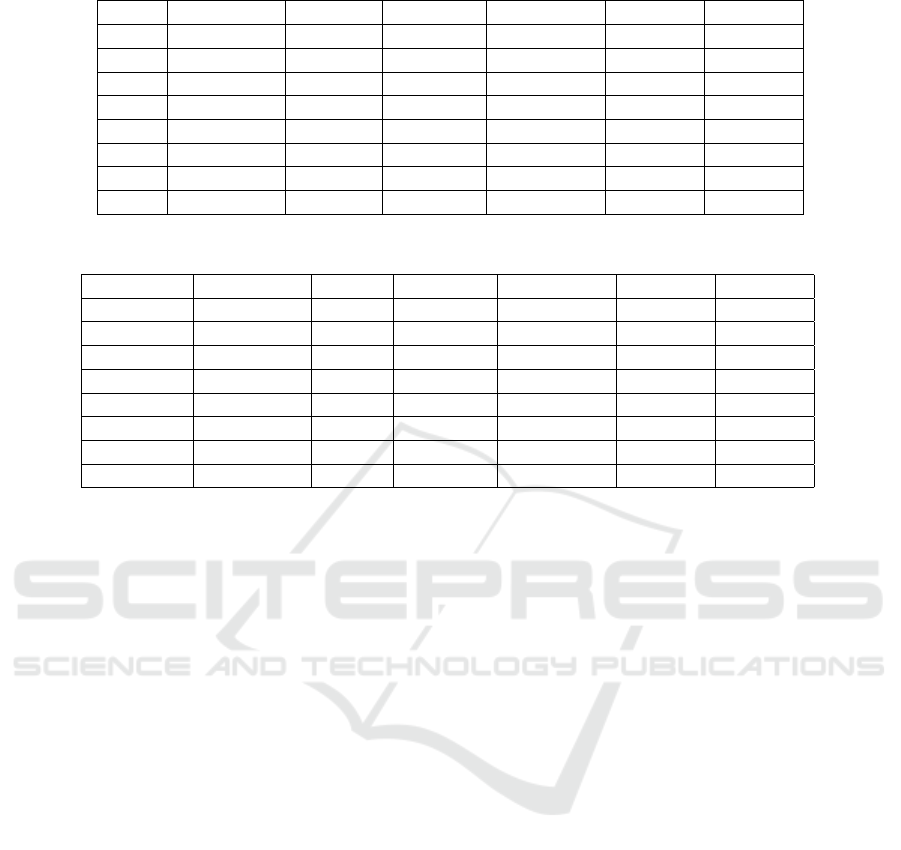
Table 5: Rank of Single and Ensemble SVR techniques over the six datasets.

Rank COCOMO ISBSG Miyazaki Desharnais Albrecht Kemerer

1 SVRP EMLP EMLP SVRP SVRR SVRP

2 EMLP SVRP SVRP EIRWM EMLP EMLP

3 SVRR EIRWM EIRWM EAVR SVRP EIRWM

4 EIRWM EAVR SVRL EMLP EMED SVRL

5 EMED EMED SVRR SVRL SVRL SVRR

6 EAVR SVRL EMED EMED EIRWM EAVR

7 SVRL SVRR SVRS SVRR SVRS EMED

8 SVRS SVRS EAVR SVRS EAVR SVRS

Table 6: Clusters identiﬁed by SK test.

Technique COCOMO ISBSG Miyazaki Desharnais Albrecht Kemerer

EAVR 2 2 3 2 5 2

EIRWM 1 2 3 1 4 2

EMED 2 2 3 2 3 2

EMLP 1 1 1 1 1 1

SVRL 2 2 3 2 3 2

SVRP 1 1 2 1 2 1

SVRR 2 2 3 2 1 2

SVRS 2 2 4 2 6 3

Scott-Knott statistical test. This test was used to iden-

tify clusters of techniques with comparable predictive

capabilities based on AE. The identiﬁed clusters for

each dataset are detailed in Table 6.

The SK test revealed two clusters in the Deshar-

nais, COCOMO, and ISBSG datasets, four clusters

in the Miyazaki dataset, and three clusters in the Ke-

merer dataset. The Albrecht dataset had the high-

est number of clusters. In the COCOMO dataset,

the SK test showed no signiﬁcant difference between

the SVRP and EMLP techniques. Similar ﬁndings

were observed for the ISBSG and Kemerer datasets.

For the Desharnais dataset, the EIRWM, EMLP, and

SVRP techniques were grouped into the same cluster,

indicating that they have similar predictive capabili-

ties. In the Albrecht dataset, the most effective cluster

included both EMLP and SVRR techniques. For the

Miyazaki dataset, the EMLP ensemble was part of the

top-performing cluster. Notably, the SVRS technique

consistently appeared in the lowest-performing clus-

ter across all datasets, while other ensemble methods,

such as those using average or median combiners, did

not fall into the worst cluster.

These results suggest that ensemble methods, par-

ticularly those incorporating non-linear rules like

MLP, show promising performance.

6 CONCLUSIONS AND FUTURE

WORK

This paper investigates the potential of Support Vector

Regression in SDEE. The study evaluates four SVR

variants tailored for SDEE and proposes a homoge-

neous ensemble of these variants, employing three

linear and one non-linear combiner. The optimiza-

tion of the SVR variants is performed using the PSO

technique. Six widely recognized datasets are used

to assess the proposed approaches, and various per-

formance indicators are applied, with the LOOCV

method utilized for validation. The research ad-

dresses three RQs, with the key ﬁndings summarized

as follows:

• (RQ1). The SVR variant using the polynomial

kernel proves to be the most suitable for SDEE.

Overall results show that this variant outperforms

others using different kernels in terms of accuracy.

• (RQ2). There is no conclusive evidence of the su-

periority of SVR ensembles over single SVR tech-

niques. Empirical results suggest that both ap-

proaches achieve similar predictive accuracy, with

no statistically signiﬁcant differences.

• (RQ3). The results indicate that the SVR ensem-

ble using the non-linear MLP rule achieves higher

performance accuracy compared to ensembles us-

ing linear rules.

Comparative Analysis of Single and Ensemble Support Vector Regression Methods for Software Development Effort Estimation

515

Ongoing work focuses on evaluating SVR tech-

niques incorporating feature selection methods and

developing a statistical framework for dynamically

selecting SVR variants as ensemble members. Fur-

ther exploration of alternative combination rules, par-

ticularly non-linear ones, is essential to validate and

extend the study’s ﬁndings.

REFERENCES

Braga, P. L., Oliveira, A. L., and Meira, S. R. (2007). Soft-

ware effort estimation using machine learning tech-

niques with robust conﬁdence intervals. In 7th inter-

national conference on hybrid intelligent systems (HIS

2007), pages 352–357. IEEE.

Braga, P. L., Oliveira, A. L., and Meira, S. R. (2008). A

ga-based feature selection and parameters optimiza-

tion for support vector regression applied to software

effort estimation. In Proceedings of the 2008 ACM

symposium on Applied computing, pages 1788–1792.

Cabral, J. T. H. d. A., Oliveira, A. L., and da Silva, F. Q.

(2023). Ensemble effort estimation: An updated and

extended systematic literature review. Journal of Sys-

tems and Software, 195:111542.

Charette, R. N. (2005). Why software fails. IEEE spectrum,

42(9):36.

de Barcelos Tronto, I. F., da Silva, J. D. S., and Sant’Anna,

N. (2008). An investigation of artiﬁcial neural net-

works based prediction systems in software project

management. Journal of Systems and Software,

81(3):356–367.

Foss, T., Stensrud, E., Kitchenham, B., and Myrtveit, I.

(2003). A simulation study of the model evaluation

criterion mmre. IEEE Transactions on software engi-

neering, 29(11):985–995.

Hosni, M. (2023). On the value of combiners in hetero-

geneous ensemble effort estimation. In KDIR, pages

153–163.

Hosni, M., Idri, A., and Abran, A. (2018a). Improved ef-

fort estimation of heterogeneous ensembles using ﬁl-

ter feature selection. In ICSOFT, pages 439–446.

Hosni, M., Idri, A., and Abran, A. (2019). Evaluating ﬁl-

ter fuzzy analogy homogenous ensembles for software

development effort estimation. Journal of Software:

Evolution and Process, 31(2):e2117.

Hosni, M., Idri, A., and Abran, A. (2021). On the value of

ﬁlter feature selection techniques in homogeneous en-

sembles effort estimation. Journal of Software: Evo-

lution and Process, 33(6):e2343.

Hosni, M., Idri, A., Abran, A., and Nassif, A. B. (2018b).

On the value of parameter tuning in heterogeneous en-

sembles effort estimation. Soft Computing, 22:5977–

6010.

Idri, A., Hosni, M., and Abran, A. (2016). Systematic liter-

ature review of ensemble effort estimation. Journal of

Systems and Software, 118:151–175.

Kocaguneli, E., Menzies, T., and Keung, J. W. (2011). On

the value of ensemble effort estimation. IEEE Trans-

actions on Software Engineering, 38(6):1403–1416.

Kumar, K. H. and Srinivas, K. (2024). An improved

analogy-rule based software effort estimation using

htrr-rnn in software project management. Expert Sys-

tems with Applications, 251:124107.

Kumar, P. S., Behera, H. S., Kumari, A., Nayak, J., and

Naik, B. (2020). Advancement from neural networks

to deep learning in software effort estimation: Per-

spective of two decades. Computer Science Review,

38:100288.

opez-Mart

ın, C. (2021). Effort prediction for the software

project construction phase. Journal of Software: Evo-

lution and Process, 33(7):e2365.

Mahmood, Y., Kama, N., Azmi, A., Khan, A. S., and Ali,

M. (2022). Software effort estimation accuracy pre-

diction of machine learning techniques: A systematic

performance evaluation. Software: Practice and ex-

perience, 52(1):39–65.

Miyazaki, Y., Takanou, A., Nozaki, H., Nakagawa, N., and

Okada, K. (1991). Method to estimate parameter val-

ues in software prediction models. Information and

Software Technology, 33(3):239–243.

Mustafa, E. I. and Osman, R. (2024). A random forest

model for early-stage software effort estimation for

the seera dataset. Information and Software Technol-

ogy, 169:107413.

Oliveira, A. L. (2006). Estimation of software project ef-

fort with support vector regression. Neurocomputing,

69(13-15):1749–1753.

Oliveira, A. L., Braga, P. L., Lima, R. M., and Corn

elio,

M. L. (2010). Ga-based method for feature selection

and parameters optimization for machine learning re-

gression applied to software effort estimation. infor-

mation and Software Technology, 52(11):1155–1166.

Shepperd, M. and MacDonell, S. (2012). Evaluating pre-

diction systems in software project estimation. Infor-

mation and Software Technology, 54(8):820–827.

Vapnik, V. N., Vapnik, V., et al. (1998). Statistical learning

theory. wiley New York.

Wen, J., Li, S., Lin, Z., Hu, Y., and Huang, C. (2012). Sys-

tematic literature review of machine learning based

software development effort estimation models. In-

formation and Software Technology, 54(1):41–59.

KDIR 2024 - 16th International Conference on Knowledge Discovery and Information Retrieval

516