Software Testing Effort Estimation Based on Machine Learning

Techniques: Single and Ensemble Methods

Mohamed Hosni

1 a

, Ibtissam Medarhri

2 b

and Juan Manuel Carrillo de Gea

3 c

MOSI Research Team, LM2S3, ENSAM, Moulay Ismail University of Meknes, Morocco

MMCS Research Team, LMAID, ENSMR-Rabat, Morocco

Department of Informatics and Systems, Faculty of Computer Science, University of Murcia, Spain

Keywords:

Software Testing, Software Testing Effort, Machine Learning, Ensemble Method, ISBSG.

Abstract:

Delivering an accurate estimation of the effort required for software system development is crucial for the

success of any software project. However, the software development lifecycle (SDLC) involves multiple ac-

tivities, such as software design, software build, and software testing, among others. Software testing (ST)

holds signiﬁcant importance in the SDLC as it directly impacts software quality. Typically, the effort required

for the testing phase is estimated as a percentage of the overall predicted SDLC effort, typically ranging be-

tween 10% and 60%. However, this approach poses risks as it hinders proper resource allocation by managers.

Despite the importance of this issue, there is limited research available on estimating ST effort. This paper

aims to address this concern by proposing four machine learning (ML) techniques and a heterogeneous ensem-

ble to predict the effort required for ST activities. The ML techniques employed include K-nearest neighbor

(KNN), Support Vector Regression, Multilayer Perceptron Neural Networks, and decision trees. The dataset

used in this study was obtained from a well-known repository. Various unbiased performance indicators were

utilized to evaluate the predictive capabilities of the proposed techniques. The overall results indicate that the

KNN technique outperforms the other ML techniques, and the proposed ensemble showed superior perfor-

mance accuracy compared to the remaining ML techniques.

1 INTRODUCTION

The software development life cycle (SDLC) encom-

passes a comprehensive range of activities that cover

multiple aspects of a software project. These activi-

ties include strategic planning, thorough requirements

speciﬁcation, meticulous analysis and design, pre-

cise programming, rigorous testing, seamless integra-

tion, smooth deployment, and various other support-

ive tasks. Together, they form a cohesive framework

for the successful development and implementation

of high-quality software systems (Radli

nski, 2023).

Ensuring precise estimation of the effort needed to

accomplish each of these activities is crucial for the

overall success of the project (Charette, 2005). De-

spite the majority of research in the literature focusing

on proposing automated techniques for accurate ef-

fort estimation in software development (Hosni et al.,

https://orcid.org/0000-0001-7336-4276

https://orcid.org/0009-0003-0052-8702

https://orcid.org/0000-0002-3320-622X

2019a; Azzeh and Nassif, 2013), there has been rela-

tively limited research conducted speciﬁcally on pre-

dicting the effort required to complete a speciﬁc ac-

tivity in the SDLC, such as testing, even though it is

a signiﬁcant and challenging area. Therefore, this re-

search work attempts to propose a software testing ef-

fort estimation technique based on machine learning

methods.

Recently, a systematic literature review (SLR) was

conducted on the use of ML in software testing (Ajor-

loo et al., 2024). This work systematically analyzes

40 studies published between 2018 and 2024, explor-

ing various ML methods, including supervised, un-

supervised, reinforcement, and hybrid approaches in

software testing. It highlights ML’s signiﬁcant role

in automating test case generation, prioritization, and

fault detection, but also identiﬁes a critical gap in the

area of software test effort prediction—an important

element for effective resource management, cost es-

timation, and project scheduling. Despite its impor-

tance, the review reveals that few studies speciﬁcally

address this area, underscoring the urgent need for

Hosni, M., Medarhri, I. and Carrillo de Gea, J.

Software Testing Effort Estimation Based on Machine Learning Techniques: Single and Ensemble Methods.

DOI: 10.5220/0013072400003838

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2024) - Volume 1: KDIR, pages 517-524

ISBN: 978-989-758-716-0; ISSN: 2184-3228

517

further research on ML-based models to improve test

effort predictions and enhance overall software test-

ing efﬁciency.

Software testing holds signiﬁcant importance in

the SDLC as it serves to identify defects, errors,

and inconsistencies within a software system (L

opez-

Mart

ın, 2022). The primary objective of this impor-

tant phase is to execute software components or sys-

tems to uncover bugs, verify adherence to speciﬁed

requirements, and ensure the overall quality of the

software product. By conducting comprehensive test-

ing, developers can detect and rectify any ﬂaws, en-

suring that the software meets the desired standards

and functions optimally (Radli

nski, 2023). The test-

ing process plays a critical role in enhancing the reli-

ability, performance, and user experience of the soft-

ware, contributing to the success of the overall devel-

opment project.

Software testing activities play a vital role in eval-

uating the functionality of software and determining

the extent to which it meets stakeholders’ expecta-

tions. Essentially, this phase ensures the software’s

desired quality. In terms of time and cost, soft-

ware testing holds signiﬁcant importance within the

SDLC. Researchers have made several efforts to esti-

mate the effort required for conducting testing activ-

ities (Radli

nski, 2023). Typically, the effort needed

to test a software system is measured in person-hours

opez-Mart

ın, 2022). During the planning phase of

a project, the overall effort required for the SDLC

is estimated, and a certain percentage is allocated

to account for software testing activities. However,

accurately predicting the effort necessary for testing

poses challenges due to the considerable variability in

the percentage allocation for testing critical software

components. This percentage can vary widely, from

10% to 60% or even higher (L

opez-Mart

ın, 2022).

Thus, accurately estimating the effort required for

testing remains a complex task.

ML techniques have been widely employed for

over three decades to estimate software development

effort with a higher degree of accuracy (Hosni and

Idri, 2018). These techniques utilize historical data

from completed projects to uncover complex relation-

ships between various software factors and the ef-

fort required to develop a software system (Ali and

Gravino, 2019; Wen et al., 2012). This enables ML

models to generate more accurate predictions, over-

coming the limitations of traditional software estima-

tion techniques, such as parametric methods. Un-

like traditional approaches, ML techniques can cap-

ture non-linear relationships between the target vari-

able (i.e., effort) and the independent variables. This

ﬂexibility makes ML models well-suited for provid-

ing reliable estimations, which in turn assist project

managers in making informed decisions regarding re-

source allocation and effectively monitoring overall

project progress.

In Software Development Effort Estimation

(SDEE), researchers have extensively explored a

novel approach known as ensemble effort estima-

tion (EEE) (Hosni et al., 2019b; Idri et al., 2016;

d. A. Cabral et al., 2023). This technique involves

combining multiple ML techniques into a single en-

semble model, utilizing a combination rule to gener-

ate predictions. The EEE approach has demonstrated

superior accuracy compared to using a single ML

technique. Extensive literature reports consistently

indicate that EEE outperforms individual ensemble

members in most cases, highlighting the effectiveness

of the ensemble approach in improving the accuracy

of SDEE.

In this paper, our objective is to explore the ap-

plication of well-established ML techniques in SDEE

speciﬁcally for estimating the effort required in soft-

ware testing activities. We have selected four widely

used ML techniques: k-nearest neighbor (KNN), Sup-

port Vector Regression (SVR), Multilayer Perceptron

(MLP) Neural Networks, and decision trees (DTs).

Additionally, we propose an ensemble model that

combines these four ML techniques. To obtain the

ﬁnal estimation from the ensemble, three combiners

are employed: average, median, and inverse ranked

weighted mean.

To conduct our study, we utilized a histori-

cal dataset obtained from the International Soft-

ware Benchmarking and Standards Group (ISBSG)

database, Release 12. In this research work, we ad-

dress three research questions (RQs):

• (RQ1). Among the four ML techniques used,

which one generates the most accurate results?

• (RQ2). Is there any evidence that the proposed

ensemble method performs better than the in-

dividual ML techniques?

• (RQ3). What are the main features that impact

software testing effort (STE) among the input

features used for the ML techniques?

The main features of this paper are as follows:

• Utilizing four well-known ML techniques for es-

timating software testing effort (STE).

• Employing an ensemble method for estimating

STE.

• Evaluating the predictive capabilities of these

STE techniques using unbiased performance mea-

sures.

KDIR 2024 - 16th International Conference on Knowledge Discovery and Information Retrieval

518

• Identifying the most signiﬁcant features that im-

pact the estimation of STE.

The organization of the remaining parts of this pa-

per is as follows: Section 2 presents a comprehensive

analysis of previous studies. Section 3 provides the

list of the ML techniques employed in this research.

Section 4 outlines the methodology implemented, in-

cluding the materials utilized. Section 5 discusses the

signiﬁcant ﬁndings derived from the study. Lastly,

the concluding section summarizes the paper and pro-

poses future research directions.

2 RELATED WORK

This section presents some related work conducted in

the literature of STE estimation and deﬁnes the EEE

approach.

opez-Mart

ın (L

opez-Mart

ın, 2022) carried out

an empirical study to explore the use of ML tech-

niques for predicting software testing effort (STE) in

the software development lifecycle (SDLC). The re-

search examined ﬁve ML models—case-based rea-

soning, artiﬁcial neural networks (ANN), support

vector regression (SVR), genetic programming, and

decision trees (DTs)—to assess their accuracy in es-

timating software development effort (SDEE). The

models were trained and evaluated using datasets

from the ISBSG, which were chosen based on fac-

tors such as data quality, development type, platform,

programming language, and resource level. The ﬁnd-

ings revealed that support vector regression (SVR)

provided the most accurate predictions, particularly

when evaluated using mean absolute error (MAE).

Labidi et al. (Labidi and Sakhrawi, 2023) con-

ducted an empirical study aimed at predicting soft-

ware testing effort (STE) using ensemble methods.

The proposed approach combined three machine

learning techniques: ANN, SVR, and DTs, with each

model optimized through grid search. The ISBSG

dataset was employed after a preprocessing step for

empirical evaluation. Results indicated that the en-

semble model outperformed the individual ML tech-

niques based on performance metrics such as root

mean square error (RMSE), R-squared, and MAE.

However, the study lacks speciﬁc details about the

dataset used for training and testing, only mentioning

that 17 features were used as inputs for the predic-

tive models. To the best of the authors’ knowledge,

this study, along with another, represents the limited

research exploring ML techniques for predicting soft-

ware testing effort.

In the last decade, there has been signiﬁcant in-

vestigation into the ensemble approach in the context

of SDEE. This approach involves predicting the ef-

fort needed to develop a software system by using

multiple estimators. Ensembles can be categorized

into two types (Azzeh et al., 2015; Elish et al., 2013):

homogeneous and heterogeneous. Homogeneous en-

sembles combine at least two variants of the same es-

timation technique or combine one estimation tech-

nique with a meta-learner such as Bagging, Boosting,

or Random Subspace. Heterogeneous ensembles, on

the other hand, involve combining at least two differ-

ent techniques. A review conducted by Idri et al. (Idri

et al., 2016) identiﬁed 16 SDEE techniques that have

been used to construct EEE techniques. The review

revealed that the homogeneous type of ensemble was

the most frequently investigated. In terms of combin-

ers, the review identiﬁed 20 different combiners that

were adopted to merge the individual estimates pro-

vided by the ensemble members. It was found that

linear rules were the most commonly used type of

combiner.

3 MACHINE LEARNING

Four ML techniques were employed in this study :

KNN (Altman, 1992), MLP (Simon, 1999), SVR (Si-

mon, 1999), and DT (Jeffery et al., 2001), besides an

heterogeneous ensemble consisting of the four ML

techniques using three combiners: average, median,

and inverse ranked weighted mean.

4 EMPIRICAL DESIGN

This section outlines the experimental design adopted

to conduct the experiments presented in this paper.

It begins by specifying the performance metrics and

statistical tests used to assess the accuracy of the

proposed predictive models. Next, it details the use

of the grid search hyperparameter optimization tech-

nique to ﬁne-tune the parameter settings of the pre-

dictive models. It then provides information on the

dataset chosen for empirical analysis. Finally, it de-

scribes the methodology employed for building the

predictive models.

4.1 Performance Metrics and Statistical

Test

To evaluate the accuracy of the proposed techniques,

we employed a set of eight widely used performance

criteria commonly found in the SDEE literature.

These criteria include Mean Absolute Error (MAE),

Software Testing Effort Estimation Based on Machine Learning Techniques: Single and Ensemble Methods

519

Mean Balanced Relative Error (MBRE), Mean In-

verted Balanced Relative Error (MIBRE), along with

their respective median values, Logarithmic Standard

Deviation (LSD), and Prediction at 25% (Pred(25))

(Miyazaki, 1991; Minku and Yao, 2013; Foss et al.,

2003).

Additionally, to determine whether the investi-

gated STEE techniques outperformed random guess-

ing, we utilized standardized accuracy (SA) and effect

size as additional evaluation measures (Shepperd and

MacDonell, 2012). The mathematical formulas for

these performance indicators are provided in Equa-

tions (1)-(8).

= |e

−

| (1)

Pred(0.25) =

100

∑

i=1

(

1 if

⩽ 0.25

0 otherwise

(2)

MAE =

∑

i=1

(3)

MBRE =

∑

i=1

min(e

)

(4)

MIBRE =

∑

i=1

max(e

)

(5)

LSD =

∑

i=1

(λ

)

n − 1

(6)

SA = 1 −

MAE

(7)

△ =

MAE

− MAE

(8)

where:

• e

and

denote the actual and predicted effort,

respectively, for the i

project.

• The average mean absolute error from numerous

random guessing trials is represented by MAE

It is computed by randomly sampling (with equal

probability) from the remaining n − 1 cases and

setting

= e

, where r is a randomly selected

value from 1 to n, excluding i. This randomiza-

tion method is robust as it does not rely on any

assumptions about the population.

• The mean of absolute errors for a given prediction

technique i, denoted as MAE

, corresponds to the

standard deviation of the sample derived from the

random guessing approach.

• λ

is determined by taking the natural logarithm

of e

and subtracting the natural logarithm of

• The term s

is used as an estimator of the residual

variance associated with λ

The predictive models were built using the Leave-

One-Out Cross-Validation (LOOCV) technique.

To assess the statistical signiﬁcance of the pro-

posed technique based on AE, the Scott-Knott (SK)

test was employed. The SK test is a statistical method

used to compare and rank different approaches or

techniques based on their performance metrics. It

helps determine whether there are signiﬁcant dif-

ferences in performance between the evaluated ap-

proaches.

4.2 Hyperparameters Optimization

Several papers in the SDEE literature have discussed

hyperparameter settings in detail (Song et al., 2013;

Hosni et al., 2018; Hosni, 2023). These studies

have highlighted the importance of optimization tech-

niques in enhancing the accuracy of predictive mod-

els. It has been observed that the performance of ML

techniques in SDEE can vary signiﬁcantly across dif-

ferent datasets. Consequently, using the same param-

eter settings for a given technique may result in an

incorrect assessment of its predictive capability. To

address this issue, we employ the grid search opti-

mization method to determine the optimal parameter

values for the selected models. Table 1 presents the

predeﬁned search space, specifying the range of opti-

mal parameter values for each ML technique.

4.3 Datasets

The predictive analysis conducted in this paper uti-

lized the dataset from the International Software

Benchmarking Standards Group (ISBSG). This com-

prehensive dataset includes over 6,000 projects and

more than 120 features covering aspects such as

project size, effort, schedule, development type, and

application environment. Prior to building the ma-

chine learning models, the dataset undergoes prepro-

cessing. This process starts with selecting software

projects with high data quality, adhering to the guide-

lines established by the ISBSG group. The selection

criteria are based on the standards outlined in (Hosni

et al., 2019a; Labidi and Sakhrawi, 2023).

Afterwards, we selected attributes that, according

to the authors’ knowledge, have a clear inﬂuence on

the STE. As a result, we selected nine numerical fea-

tures along with the target variable ’Effort Test’. The

input features used for our predictive models are listed

in Table 2. It is worth noting that any data rows with

missing values were removed from the dataset.

KDIR 2024 - 16th International Conference on Knowledge Discovery and Information Retrieval

520

Table 1: Range of parameters values for each ML technique.

Technique Search space

KNN

’n neighbors’: [1,11],

’weights’: [’uniform’, ’distance’],

’metric’: [’euclidean’, ’manhattan’, ’cityblock’, ’minkowski’]

SVR

’kernel’: [’rbf’, ’poly’],

’C’: [5, 10, 20, 30, 40, 50, 100],

’epsilon’: [0.0001, 0.001, 0.01, 0.1],

’degree’: [2, 3, 4, 5, 6],

’gamma’: [0.0001, 0.001, 0.01, 0.1]

MLP

’hidden layer sizes’: [(8,), (8,16), (8, 16, 32), (8,16,32,64)],

’activation’: [’relu’, ’tanh’, ’identity’, ’logistic’],

’solver’: [’adam’, ’lbfgs’, ’sgd’],

’learning rate’: [’constant’, ’adaptive’, ’invscaling’],

’criterion’: [’squared error’, ’friedman mse’, ’absolute error’,

’poisson’],’max depth’: [None] + [1, number of feature

space],’max features’: [None, ’sqrt’, ’log2’]

Table 2: Selected features.

Feature Importance score

Enquiry count 0.131424

File count 0.12467

Output count 0.121829

Adjusted function points 0.12108

Input count 0.120946

Max team size 0.120207

Interface count 0.103466

Value adjustment factor 0.083748

User base - locations 0.07263

Effort test -

4.4 Evaluation Methodology

This subsection outlines the experimental design em-

ployed to develop and evaluate the proposed STE

techniques in this paper.

• Step 1: Four ML algorithms: KNN, SVR, MLP

and DT, were trained and optimized using grid

search with 10-fold cross-validation to identify

the best hyperparameters.

• Step 2: Optimal hyperparameter values were se-

lected for each model based on the lowest Mean

Absolute Error (MAE).

• Step 3: The models were then retrained using the

identiﬁed optimal parameters and evaluated using

LOOCV.

• Step 4: The validity of the optimized mod-

els was assessed through Standardized Accuracy

(SA) and effect size analysis, comparing their

performance against the 5% quantile of random

guessing.

• Step 5: Performance was measured using a com-

prehensive set of indicators: Mean Absolute Error

(MAE), Median Absolute Error (MdAE), Mean

Inverted Balanced Relative Error (MIBRE), Me-

dian Inverted Balanced Relative Error (MdIBRE),

Mean Balanced Relative Error (MBRE), Median

Balanced Relative Error (MdBRE), Logarithmic

Standard Deviation (LSD), and Prediction at 25%

(Pred(25)).

• Step 6: A heterogeneous ensemble was created

by integrating the four models using three combi-

nation methods: average (AVR), median (MED),

and inverse rank-weighted mean (IRWM).

• Step 7: The ensemble’s performance was evalu-

ated using the same metrics outlined in Step 5.

• Step 8: The software effort estimation methods

were ranked using the Borda count voting system,

considering all eight performance metrics.

• Step 9: The Scott-Knott statistical test was ap-

plied to group the estimation techniques into sta-

tistically similar categories based on AE, iden-

tifying those with comparable predictive perfor-

mance.

5 EMPIRICAL RESULTS

This section presents the empirical ﬁndings derived

from the experiment conducted in this paper. The

experiments were executed using various tools, with

Python and its associated libraries being used to run

the experiments. Additionally, the R programming

language was utilized to perform the SK test.

Software Testing Effort Estimation Based on Machine Learning Techniques: Single and Ensemble Methods

521

5.1 Single Techniques Assessment

In this phase, the ﬁrst step involves identifying the

optimal parameters that yield improved estimates for

each individual technique. To achieve this, multiple

rounds of preliminary experiments were conducted

using the grid search optimization technique. The

hyperparameters were varied within the range val-

ues speciﬁed in Table 1 for the four selected ML

techniques: KNN, SVR, MLP, and DT. The evalua-

tion was performed using the 10-fold cross-validation

technique. The objective function targeted for mini-

mization was the MAE criterion. The rationale behind

selecting MAE is its unbiased nature as a performance

measure.

Subsequently, we constructed our predictive mod-

els using the optimal parameters identiﬁed in the pre-

vious step, employing the LOOCV technique for val-

idation. This approach was selected for its ability to

provide low bias and high variance estimates, enhanc-

ing the replicability of the study.

We then evaluated the reasonability of our STE

techniques by comparing them to a baseline estima-

tor suggested by Shepperd and MacDonell (Shepperd

and MacDonell, 2012), which constructs an estimator

through multiple runs of random guessing.

The evaluation was carried out using the Stan-

dardized Accuracy (SA) metric and effect size (∆),

as proposed by the authors. As shown in Table 3,

all four ML techniques signiﬁcantly outperformed

random guessing, showing substantial improvement

with effect sizes greater than 0.8 (∆ > 0.8). Notably,

all techniques exceeded the 5% quantile of random

guessing. Among the techniques, KNN ranked high-

est in both SA and effect size improvement, while

SVR ranked lowest.

Table 3: SA and effect size value of the constructed tech-

niques.

Technique SA Delta

= 0.2061

KNN 0.981245 -7.134

SVR 0.384077 -2.79237

MLP 0.548538 -3.98806

DT 0.554524 -4.03159

We then assessed the accuracy of the four ML

techniques using the eight chosen performance met-

rics. The evaluation results are summarized in Ta-

ble 4.

The KNN technique demonstrated the highest ac-

curacy among the four ML techniques used in this

study, consistently ranking ﬁrst across all eight per-

formance metrics. DT and MLP followed, frequently

alternating between second and third positions across

several indicators. SVR consistently ranked lowest

across all performance measures.

These results suggest that the proposed approach

provides satisfactory accuracy, with KNN standing

out as the most effective technique for estimating STE

among those evaluated.

5.2 Ensemble Methods

This step involves constructing the proposed hetero-

geneous ensemble using the four ML techniques.

The ensemble produces the ﬁnal estimation through

three combiners: AVR, MED, and IRWM based

on the MAE. This approach is grounded in SDEE

literature, which indicates that ensembles typically

achieve higher accuracy than individual estimation

techniques.

Performance metrics of the constructed ensemble,

based on the eight selected indicators, are presented

in Table 5. The ensemble with the IRWM combiner

(EIRWM) consistently outperformed the others, rank-

ing ﬁrst across all performance metrics. The ensem-

bles with AVR (EAVR) and MED (EMED) combiners

ranked second and third, respectively. The consistent

rankings of the ensemble techniques across all perfor-

mance indicators demonstrate their reliable and stable

accuracy.

5.3 STE Techniques Comparison

In this step, we ranked all the proposed techniques

using the eight accuracy measures. The ﬁnal rank-

ing was determined through the Borda count voting

system, which considers all eight performance met-

rics. This approach was chosen because the accu-

racy of a technique can depend on the selected per-

formance indicators, potentially leading to conﬂicting

results as different metrics may produce varying rank-

ings for each technique (Myrtveit et al., 2005; Mittas

and Angelis, 2013). Table 6 presents the ﬁnal rank-

ings obtained through the Borda count system. As

shown, the KNN technique achieved the top position,

followed by the three heterogeneous ensembles, with

SVR ranked last.

To validate these results, we conducted the SK

statistical test to identify techniques with statistically

similar predictive capabilities. The SK test was per-

formed based on the AE of the proposed techniques.

Table 6 shows the content of clusters identiﬁed by the

SK test.

The ﬁrst cluster contained only the KNN tech-

nique, while the second cluster included the proposed

ensemble methods. The last cluster was comprised

KDIR 2024 - 16th International Conference on Knowledge Discovery and Information Retrieval

522

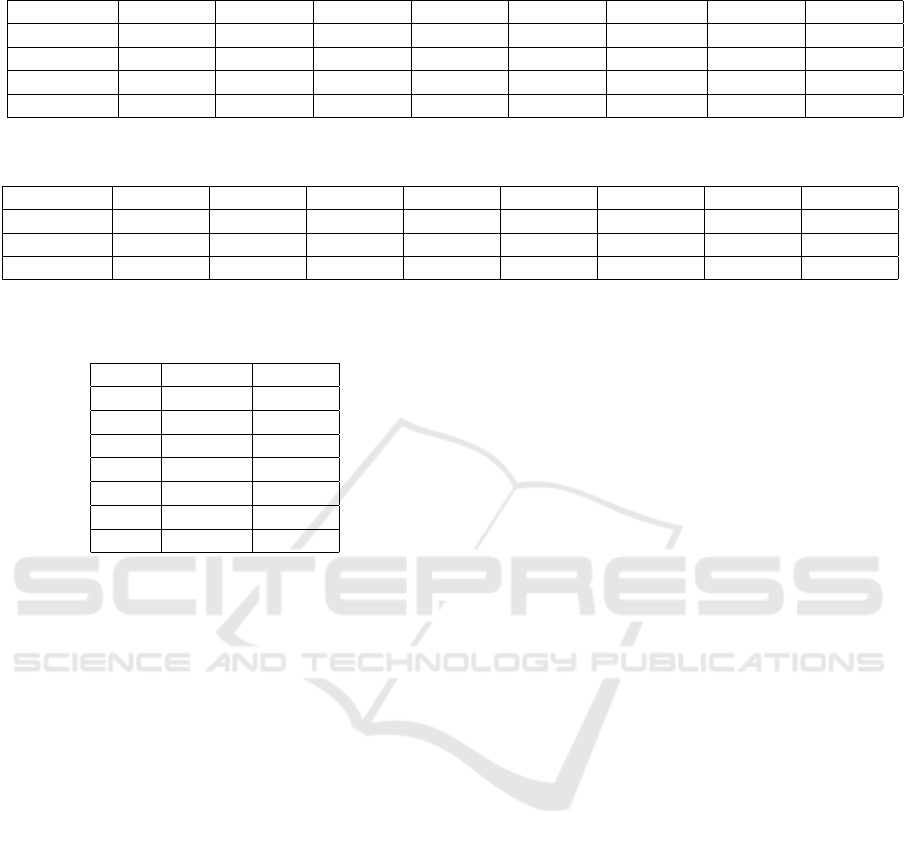
Table 4: Performance metrics for the four ML techniques.

Technique MAE MdAE MBRE MdBRE MIBRE MdIBRE PRED LSD

KNN 17.66399 0 0.168228 0 0.019629 0 95.55556 0.320259

SVR 580.0858 336.8311 112995.8 1.602058 0.523648 0.615689 17.77778 3.649184

MLP 425.1941 313.952 106435.1 0.753829 0.456234 0.429819 24.44444 3.235486

DT 419.5556 225 75112.29 0.836956 0.453273 0.455621 24.44444 3.418981

Table 5: Accuracy performance of the ensemble methods.

Technique MAE MdAE MBRE MdBRE MIBRE MdIBRE PRED LSD

EAVR 306.2841 190.1564 73635.61 0.555469 0.374774 0.3571069 35.55556 3.103686

EMED 333.5098 207.3907 90773.51 0.710584 0.394308 0.4154042 35.55556 3.236895

EIRWM 244.7196 156.9293 55120.18 0.439571 0.327887 0.3053485 42.22222 2.971071

Table 6: Rank obtained by Borda Count Voting System, and

identiﬁed Clusters.

Rank Models Cluster

1 KNN 1

2 EIRWM 2

3 EAVR 2

4 EMED 2

5 DT 3

6 MLP 3

8 SVR 4

solely of the SVR technique. Notably, the clusters

identiﬁed by the SK test correspond closely with the

rankings obtained through the Borda count method.

This conﬁrms that the KNN technique remains sta-

tistically the most superior, while the three proposed

ensemble methods consistently outperform the other

individual techniques.

5.4 Features Importance

An important aspect of our investigation was assess-

ing feature importance in explaining the target vari-

able, Effort Test. We employed the ExtraTreesClas-

siﬁer, which uses multiple decision trees to evalu-

ate and rank the signiﬁcance of features within the

dataset.

Table 2 shows the importance scores for each fea-

ture used in our predictive models. The results con-

ﬁrm that all features contribute to the target variable,

aligning with our manual feature selection process

on the original ISBSG dataset. Notably, the ISBSG

dataset contains over 100 features, suggesting that

incorporating additional relevant features could en-

hance the predictive models’ accuracy.

It is important to note that there is currently no

literature speciﬁcally addressing which software fea-

tures are most effective for predicting software testing

activities. Therefore, a more comprehensive analysis

is required to identify the most impactful features for

this purpose.

6 CONCLUSIONS AND FURTHER

WORK

This empirical study explored the effectiveness of ML

techniques in estimating the effort required for soft-

ware testing activities within the SDLC. Four ML

techniques and three heterogeneous ensembles were

examined, with hyperparameters optimized using grid

search. The evaluation employed the Leave-One-Out

Cross-Validation (LOOCV) technique and eight unbi-

ased performance metrics. The key ﬁndings related to

each research question are summarized below:

• (RQ1). The KNN technique consistently outper-

formed the other three ML techniques across all

eight performance metrics.

• (RQ2). Results indicated that the ensemble meth-

ods did surpass the accuracy of the individual

techniques (SVR, DT, and MLP) and show less

performance than KNN. This conclusion was sup-

ported by the SK test.

• (RQ3). All features used in training the ML

techniques were identiﬁed as important; however,

integrating additional features could further en-

hance the models’ predictive capabilities.

Ongoing research is focused on exploring alter-

native ensemble methods, particularly homogeneous

ensembles, which were not covered in this study. Ef-

forts are also underway to improve the selection of

ensemble components. Additionally, acquiring more

relevant datasets for STE is a key priority, as this will

contribute to the development of more robust and ac-

curate STE models.

Software Testing Effort Estimation Based on Machine Learning Techniques: Single and Ensemble Methods

523

REFERENCES

Ajorloo, S., Jamarani, A., Kashﬁ, M., Kashani, M. H., and

Najaﬁzadeh, A. (2024). A systematic review of ma-

chine learning methods in software testing. Applied

Soft Computing, page 111805.

Ali, A. and Gravino, C. (2019). A systematic literature

review of software effort prediction using machine

learning methods. J. Softw. Evol. Process, 31(10):1–

25.

Altman, N. S. (1992). An introduction to kernel and

nearest-neighbor nonparametric regression. Am. Stat.,

46(3):175–185.

Azzeh, M. and Nassif, A. B. (2013). Fuzzy model tree for

early effort estimation. In 2013 12th International

Conference on Machine Learning and Applications,

pages 117–121.

Azzeh, M., Nassif, A. B., and Minku, L. L. (2015). An

empirical evaluation of ensemble adjustment methods

for analogy-based effort estimation. J. Syst. Softw.,

103:36–52.

Charette, R. N. (2005). Why software fails? IEEE Spectr.,

42(9):42–49.

d. A. Cabral, J. T. H., Oliveira, A. L. I., and da Silva, F. Q. B.

(2023). Ensemble effort estimation: An updated and

extended systematic literature review. J. Syst. Softw.,

195:111542.

Elish, M. O., Helmy, T., and Hussain, M. I. (2013). Em-

pirical study of homogeneous and heterogeneous en-

semble models for software development effort esti-

mation. Math. Probl. Eng., 2013.

Foss, T., Stensrud, E., Kitchenham, B., and Myrtveit, I.

(2003). A simulation study of the model evaluation

criterion mmre. IEEE Trans. Softw. Eng., 29(11):985–

995.

Hosni, M. (2023). Encoding techniques for handling cat-

egorical data in machine learning-based software de-

velopment effort estimation. In KDIR, pages 460–467.

Hosni, M. and Idri, A. (2018). Software development effort

estimation using feature selection techniques. In Fron-

tiers in Artiﬁcial Intelligence and Applications, pages

439–452.

Hosni, M., Idri, A., and Abran, A. (2019a). Evaluating ﬁl-

ter fuzzy analogy homogenous ensembles for software

development effort estimation. J. Softw. Evol. Process,

31(2).

Hosni, M., Idri, A., and Abran, A. (2019b). Improved ef-

fort estimation of heterogeneous ensembles using ﬁl-

ter feature selection. In ICSOFT 2018 - Proceedings of

the 13th International Conference on Software Tech-

nologies, pages 405–412. SciTePress.

Hosni, M., Idri, A., Abran, A., and Nassif, A. B.

(2018). On the value of parameter tuning in hetero-

geneous ensembles effort estimation. Soft Comput.,

22(18):5977–6010.

Idri, A., Hosni, M., and Abran, A. (2016). Systematic map-

ping study of ensemble effort estimation. In Proceed-

ings of the 11th International Conference on Evalua-

tion of Novel Software Approaches to Software Engi-

neering, pages 132–139.

Jeffery, R., Ruhe, M., and Wieczorek, I. (2001). Using pub-

lic domain metrics to estimate software development

effort. In Seventh International Software Metrics Sym-

posium. METRICS 2001, pages 16–27.

Labidi, T. and Sakhrawi, Z. (2023). On the value of parame-

ter tuning in stacking ensemble model for software re-

gression test effort estimation. J. Supercomput., page

0123456789.

opez-Mart

ın, C. (2022). Machine learning techniques for

software testing effort prediction. Softw. Qual. J.,

30(1):65–100.

Minku, L. L. and Yao, X. (2013). An analysis of multi-

objective evolutionary algorithms for training ensem-

ble models based on different performance measures

in software effort estimation. In Proceedings of the

9th International Conference on Predictive Models in

Software Engineering - PROMISE ’13, pages 1–10.

Mittas, N. and Angelis, L. (2013). Ranking and cluster-

ing software cost estimation models through a multi-

ple comparisons algorithm. IEEE Trans. Softw. Eng.,

39(4):537–551.

Miyazaki, Y. (1991). Method to estimate parameter values

in software prediction models. Inf. Softw. Technol.,

33(3):239–243.

Myrtveit, I., Stensrud, E., and Shepperd, M. (2005). Re-

liability and validity in comparative studies of soft-

ware prediction models. IEEE Trans. Softw. Eng.,

31(5):380–391.

Radli

nski, Ł. (2023). The impact of data quality on software

testing effort prediction. Electron., 12(7).

Shepperd, M. and MacDonell, S. (2012). Evaluating predic-

tion systems in software project estimation. Inf. Softw.

Technol., 54(8):820–827.

Simon, H. (1999). Neural networks: a comprehensive foun-

dation. MacMillan Publishing Company, 2nd edition.

Song, L., Minku, L. L., and Yao, X. (2013). The impact of

parameter tuning on software effort estimation using

learning machines. In Proceedings of the 9th Interna-

tional Conference on Predictive Models in Software

Engineering.

Wen, J., Li, S., Lin, Z., Hu, Y., and Huang, C. (2012). Sys-

tematic literature review of machine learning based

software development effort estimation models. Inf.

Softw. Technol., 54(1):41–59.

KDIR 2024 - 16th International Conference on Knowledge Discovery and Information Retrieval

524