MEDIATE: Mutually Endorsed Distributed Incentive

Acknowledgment Token Exchange

Philipp Altmann

, Katharina Winter

, Michael K

olle

, Maximilian Zorn

and Claudia Linnhoff-Popien

LMU Munich, Germany

Munich University of Applied Sciences, Munich, Germany

Keywords:

Multi-Agent Systems, Reinforcement Learning, Peer Incentivization, Consensus, Emergent Cooperation.

Abstract:

Recent advances in multi-agent systems (MAS) have shown that incorporating peer incentivization (PI) mecha-

nisms vastly improves cooperation. Especially in social dilemmas, communication between the agents helps to

overcome sub-optimal Nash equilibria. However, incentivization tokens need to be carefully selected. Further-

more, real-world applications might yield increased privacy requirements and limited exchange. Therefore,

we extend the PI protocol for mutual acknowledgment token exchange (MATE) and provide additional analysis

on the impact of the chosen tokens. Building upon those insights, we propose mutually endorsed distributed

incentive acknowledgment token exchange (MEDIATE), an extended PI architecture employing automatic to-

ken derivation via decentralized consensus. Empirical results show the stable agreement on appropriate tokens

yielding superior performance compared to static tokens and state-of-the-art approaches in different social

dilemma environments with various reward distributions.

1 INTRODUCTION

Recent advances in using reinforcement learning (RL)

in multi-agent systems (MAS) demonstrated their

feasibility for real-world multi-agent reinforcement

learning (MARL) applications. Those applications

range from smart grids (Omitaomu and Niu, 2021)

and factories (Kim et al., 2020) to intelligent trans-

portation systems (Qureshi and Abdullah, 2013). To

assess the agents’ cooperation capabilities, social

dilemmas producing tensions between the individual

and collective reward maximization (social welfare)

are often used (Dawes, 1980). Yet, the availability of

communication and exchange is vital to fostering co-

operation between self-interested individuals. How-

ever, besides the autonomous interaction within an

environment, increased privacy requirements might

require instances to conceal information regarding

their current state (Tawalbeh et al., 2020). Peer in-

centivization (PI) is a recent branch of research of-

fering a distinct solution for emergent cooperation

between agents. At its core, PI enables agents to

shape each other’s behavior by exchanging reward to-

kens in addition to the environmental reward (Phan

et al., 2022; Lupu and Precup, 2020). However, for

proper integration and effective incentivization, those

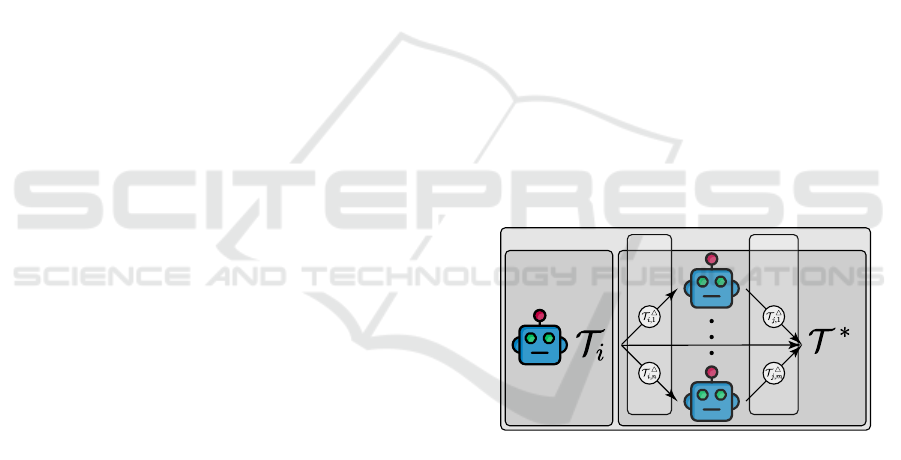
MEDIATE

Token Derivation

Consensus

Request

Response

Figure 1: MEDIATE Architecture deriving a consensual PI

token T

∗

through reciprocal decentralized communication.

exchanged tokens need to be carefully considered, re-

gardless of whether their value is set dynamic or as

a hyperparameter. For the robust and scalable appli-

cability of PI mechanisms in decentralized learning

scenarios, adaptive incentivization tokens and mech-

anisms to agree upon common token values are re-

quired. Yet, current approaches are missing said co-

ordinated adaptability. To overcome these shortcom-

ings, we provide the following contributions:

• We evaluate the effect of different centralized

(common) and decentralized (varying) values for

the incentivization token.

• We propose mutually endorsed distributed incen-

tive acknowledgment token exchange (MEDIATE,

Altmann, P., Winter, K., Kölle, M., Zorn, M. and Linnhoff-Popien, C.

MEDIATE: Mutually Endorsed Distributed Incentive Acknowledgment Token Exchange.

DOI: 10.5220/0013091900003890

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 17th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2025) - Volume 1, pages 33-44

ISBN: 978-989-758-737-5; ISSN: 2184-433X

cf. Fig. 1), an automatic token derivation mecha-

nism based on the agents’ value estimate, and a

consensus mechanism to mediate a global token

maintaining local privacy.

• We provide ablation studies of the introduced to-

ken derivation and the consensus mechanism over

a static token. Benchmark comparisons to state-

of-the-art PI approaches show that MEDIATE can

negotiate appropriate tokens that yield improved

cooperation and social welfare in various social

dilemmas with different reward landscapes.

2 PRELIMINARIES

Social Dilemmas. Game Theory analyzes behavior

among rational agents in cooperative and competi-

tive situations (Russell, 2010; Littman, 2001). So-

cial dilemmas are Markov games that inhibit a spe-

ciﬁc reward structure, which creates tension between

individual and collective reward maximization. Se-

quential social dilemmas (SSD) are temporally ex-

tended social dilemmas, in which the game repeats

over several time steps (Leibo et al., 2017). The

Nash equilibrium is a situation where no agent can

increase its individual reward by changing its strat-

egy if all other agents maintain their current strategy

(Littman, 2001; Sandholm and Crites, 1996). MARL

utilizes SSDs to analyze and experiment with the so-

cial behavior of different learning strategies (Leibo

et al., 2017). To assess the emergence of cooperation,

we employ the Iterated Prisoner’s Dilemma (IPD),

where mutual defection constitutes a Nash equilib-

rium (Axelrod, 1980; Sandholm and Crites, 1996).

To evaluate the scalability of our approach, we use

the Coin Game with two, four, and six agents (Lerer

and Peysakhovich, 2017). Additionally, we use the

Rescaled Coin Game with two agents to assess the ro-

bustness w.r.t. varying reward landscapes. The rate of

own coins versus total coins collected reﬂects over-

all cooperation. For insights on long-term coopera-

tion, we use Harvest, posing a risk of the tragedy of

the commons to self-interested agents (Perolat et al.,

2017; Phan et al., 2022). For further details about the

environments used, please refer to the Appendix.

Peer Incentivization. In MAS, cooperation con-

notes the joining of individual problem-solving strate-

gies of autonomous agents into a combined strategy

(Crainic and Toulouse, 2007). The emergent coop-

eration of learning agents necessitates coordination

(No

e, 2006), which poses a vital challenge to current

communication protocols in decentralized MARL

scenarios (Jaques et al., 2019; K

olle et al., 2023; Alt-

mann et al., 2024b). PI is a recent branch of research,

focussing on agents learning to actively shape the be-

havior of others by sending rewards or penalties (Phan

et al., 2022; Yang et al., 2020). These peer rewards

are processed like environment rewards, enabling the

emergence of cooperation. However, new dynamics

arise through the increased inter-dependency, which

comes with new challenges. Carefully designing this

reward mechanism is essential to achieving a good

outcome (Lupu and Precup, 2020).

Consensus in Multi-Agent Systems. Distributed

systems use consensus algorithms to deduct a global

average of local information (Schenato and Gamba,

2007). For MAS, consensus describes the con-

vergence of agents on a mutual value via commu-

nication (Li and Tan, 2019). A consensus algo-

rithm speciﬁes the execution steps to reach consen-

sus (Han et al., 2013). Bee swarms, bird ﬂocks, and

other group-coordinated species show natural behav-

ior (Amirkhani and Barshooi, 2022) that inspires fur-

ther underlying concepts like leadership, voting, or

decision-making (Conradt and Roper, 2005). Two

main application areas for consensus algorithms are

sensor networks (Yu et al., 2009) and blockchain tech-

nology (Monrat et al., 2019), which has played an in-

tegral role in cryptocurrencies and provides promising

solutions for IoT applications. Consensus in sensor

networks mainly deals with the fusion of distributed

data, especially for time-critical data (Schenato and

Gamba, 2007) and uncertainty in large-scale net-

works (Olfati-Saber and Shamma, 2005). Research

in cryptocurrency and IoT focuses on synchronization

(Cao et al., 2019), agreement (Salimitari and Chatter-

jee, 2018), and veriﬁcation of actions (Lashkari and

Musilek, 2021) between entities in distributed sys-

tems. The number of sophisticated consensus algo-

rithms is growing through the rising importance of de-

centralized coordination mechanisms (Lashkari and

Musilek, 2021) in an increasingly digitally connected

world. Our approach utilizes the cryptographic tech-

nique of additive secret sharing, solving the average

consensus problem for privacy-critical tasks (Li et al.,

2019). MARL research on consensus algorithms has

been increasing recently, intending to reach an opti-

mal joint policy in a decentralized system that is ro-

bust to unreliable agents or adversarial attacks (Figura

et al., 2021). To our knowledge, no research exists

concerning consensus algorithms, PI and RL.

Problem Formulation. We formulate our prob-

lem of a MAS as a stochastic game M =

⟨D, S, Z, A, P, R⟩, with the set of all agents D =

ICAART 2025 - 17th International Conference on Agents and Artiﬁcial Intelligence

{1, . . . , N }, a set S of states s

at time step t, a set

A = ⟨A

, . . . , A

⟩ of joint actions a

= ⟨a

t,i

⟩

i∈D

the transition probability P(s

t+1

| s

, a

), and the

joint reward R(s

, a

) = ⟨r

t,i

⟩

i∈D

∈ R. Further-

more, we assume each agent i to have a neighbor-

hood N

t,i

⊆ D \ {i}, bounding its set of local ob-

servations z

t+1

= ⟨z

t+1,i

⟩

i∈D

∈ Z

, and the agents’

experience tuple ⟨τ

t,i

, a

t,i

, r

t,i

, z

t+1,i

⟩, where τ

t,i

∈

(Z × A

)

is the agent’s history. Agent i selects the

next action based on a stochastic policy π

t,i

|τ

t,i

Simultaneously learning agents cause non-stationary,

i.e., varying transition probabilities over time. The

goal of each self-interested agent i is to ﬁnd a best

response π

∗

that maximizes the expected individual

discounted return:

t,i

∞

k=0

i,t+k

, (1)

with a discount factor γ ∈ [0, 1). From the perspec-

tive of an agent, other agents are part of its environ-

ment, and policy updates by other agents affect the

performance of an agent’s own policy (Laurent et al.,

2011). The performance of π

is evaluated using a

value function V

) = E

t,i

] for all s

∈ S,

with the joint policy π = ⟨π

⟩

j∈D

(Bus¸oniu et al.,

2010). Both the policies π and the value functions

V are approximated by independent neural networks

parameterized by θ and ω, respectively. For sim-

plicity, we omit those for the following and use the

abbreviated forms V

= V

(τ

t,i

) ≈ V

) and

= π

respectively. To measure efﬁciency U of the

whole MAS, we furthermore consider the social wel-

fare (Sandholm and Crites, 1996), measured by the

sum of undiscounted returns over all agents within an

episode until time step T :

U =

i∈D

T −1

t=0

t,i

(2)

Furthermore, we use the fraction of own coins to mea-

sure cooperation based on the coins collected by each

agent:

own coins =

# own coins collected

# total coins collected

(3)

Mutual Acknowledgment Token Exchange

(MATE). MATE is a reciprocal approach to PI

based on a two-phase communication protocol,

as shown in Fig. 2, to exchange acknowledgment

tokens T ≥ 0 for individual reward shaping of r

t,i

depending on a monotonic improvement measure

. MI

t,i

) is deﬁned by the temporal difference

Agent 1

Agent 2

Agent 3

(a) Request phase

Agent 1

Agent 2

Agent 3

(b) Response phase

Figure 2: MATE protocol example. (a) If agent 1 estimates

a monotonic improvement MI

t,1

) ≥ 0 of its situation, it

“thanks” its neighbor agents 2 and 3 by sending an acknowl-

edgment request T as reward. (b) Agent 2 and 3 check if

the request T monotonically improves their own situation

along with their own respective reward. If so, a positive re-

ward T is sent back as a response. If not, a negative reward

−T is sent back.

residual of

w.r.t. some arbitrary reward r

t,i

proposed in (Phan et al., 2022, 2024):

t,i

) = r

t,i

+ γ

(τ

t+1,i

) −

(τ

t,i

) (4)

In the request phase (Fig. 2a), each agent i checks its

current situation via MI

. If MI

t,i

) ≥ 0, the agent

sends a token x

= T as an acknowledgment request

to all other agents j ∈ N

t,i

as a reward. In the re-

sponse phase (Fig. 2b), all request-receiving agents

j ∈ N

t,i

check if the request token x

would improve

their situation along with their own respective reward

t,j

. If MI

t,j

+ x

) ≥ 0, then agent j accepts the

request with a positive response token y

= T . How-

ever if MI

t,j

+ x

) < 0, then agent j rejects the

request with a negative response token y

= −T . Af-

ter the request and response phase, the shaped MATE

reward is computed for each agent i as follows:

ˆr

t,i

= r

t,i

+ max{⟨x

⟩

j∈N

t,i

} + min{⟨y

⟩

j∈N

t,i

}

(5)

In the following, we will use the MATE protocol (Fig.

2) and reward (Eq. 5) without any change and explain

our contributions on top of it.

MEDIATE: Mutually Endorsed Distributed Incentive Acknowledgment Token Exchange

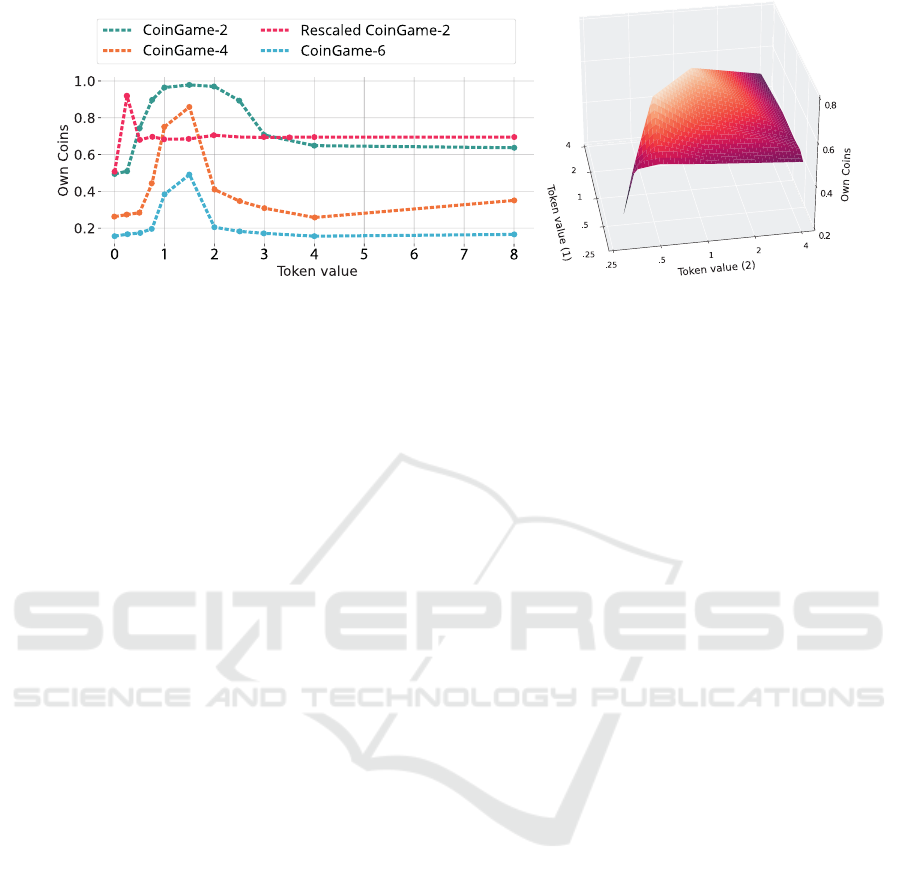
(a) Central token values for CoinGame-2, -4, and -6 (b) Decentralized Token Values for CG-2

Figure 3: Rate of own coins for different tokens when determined centralized (3a) and decentralized (3b).

3 IMPACT OF

INCENTIVIZATION TOKENS

As MATE was previously only evaluated with token

values of 1, we ﬁrst aim to provide additional insights

into the impact of the incentivization token, supply-

ing an extensive hyperparameter analysis, both per-

agent (decentralized, i.e., x

and y

may differ) and

globally (centralized, i.e., x

= y

= T ). Fig. 3a

displays the level of cooperation measured by the

rate of own coins collected for different token val-

ues T ∈ [0, 0.25, 0.5, 0.75, 1, 1.5, 2, 2.5, 3, 4, 8] in

the Coin Game with two, four, and six agents, as

well as the two-agent Coin Game with scaled re-

wards. We averaged all results over ﬁve random

seeds. The graphs display high average levels of co-

operation for value 1 in all settings, except for the

down-scaled Coin Game, where token 1 fails. This in-

dicates that the token value is highly dependent on the

reward landscape. Insufﬁcient (inferior) token values

fail to achieve the collective objective, causing self-

interested behavior. Conversely, over-exploitative (in-

temperate) token values likewise fail to yield cooper-

ative behavior. As the number of agents increases,

a value of 1.5 appears optimal within the presented

range, but the required precision for successful coop-

eration varies. Also, the range of token values that

yield high cooperation narrows, retaining its relative

position but exhibiting an increased sensitivity to the

boundaries of that range. The discrepancy between

the optimal token value of 1.5 and the value of 1 in-

creases in the six-agent Coin Game.

The analysis implies that factors like the domain,

the reward landscape, and the number of agents inﬂu-

ence incentive rewards. The range of tokens with dis-

tinctively high cooperation is solely a function of the

environment rewards but depends on the speciﬁc dy-

namics of the game, making it challenging to predict.

A ﬁxed token value lacks the adaptability required for

diverse settings, making a priori prediction based on

parameter settings a complex task. It becomes evident

that reward structures are not the sole determinants for

selecting appropriate token weights and may not even

be reliably indicative across all scenarios.

To provide further insights into the dynamics in-

troduced by the choice of incentivization token value,

we modiﬁed the protocol to allow the agents to ex-

change disparate tokens. We refer to this mode as de-

centralized. Note that using automated token deriva-

tion in a decentralized setting without a mechanism

for coordination or consensus might result in such

varying token values. Fig. 3b maps the interpolated

cooperation levels in the two-agent Coin Game with

the tokens T ∈ [0.25, 0.5, 1, 2, 4], as values between

1 and 2 have previously shown to be sufﬁcient cen-

tral tokens, employed by both agents, measured by

the rate of own coins. The results reveal that the to-

ken combinations (1, 1) and (2, 2) yield the highest

cooperation rates. Both token values are positioned

in the appropriate token range in the centralized com-

parison (cf. Fig. 3a), and the combinations contain

equal values, which appears to be a signiﬁcant crite-

rion in this context. Although the combination (1, 2)

includes two appropriate values, the cooperation is

decreased compared to the equal-valued exchange.

With increasing discrepancy between the token val-

ues, cooperation further decreases, suggesting a cor-

relation between the degree of value equality and co-

operation. Agents with over-exploitative token values

can greatly impact other agents, especially those with

limited social inﬂuence due to smaller tokens, leading

to a manipulative form of cooperation. Equal but in-

appropriate token values exhibit low performance and

cooperation, which minimizes for (0.25,0.25).

ICAART 2025 - 17th International Conference on Agents and Artiﬁcial Intelligence

Overall, this evaluation suggests that the exchange

of decentralized token values must be appropriate and

equal to provide fairness and induce equal coopera-

tion. Nevertheless, the rate of own coins collected

for all tested tokens excels the performance of na

ıve

learning, reﬂected by token value 0. Conceptually,

these prospects of MATE arise from enabling agents

to share their success, provided the beneﬁts are mu-

tual. As shown before, however, exchanging tokens of

value T = 1 might not always be a sufﬁcient choice

for any given environment.

4 MEDIATE

To elevate PI token values from static hyperparame-

ters to dynamically adaptable domain-speciﬁc quanti-

ties, we propose mutually endorsed distributed incen-

tive acknowledgment token exchange (MEDIATE),

combining two progressions (cf. Fig. 1): First, we

provide an automated mechanism to derive dynamic

agent-based incentivization tokens T

. To ensure

global convergence of said tokens, we secondly pro-

vide a consensus mechanism that ensures the privacy

of the agents’ local information.

Generally, we intend to improve cooperation by

introducing reciprocal participation (via a positive re-

ward or incentive) if agents experience monotonic im-

provement, i.e., their experienced situation is better

than approximated by their local value estimate, caus-

ing a positive temporal difference. By requiring mu-

tual acknowledgment of this improvement, conver-

gence towards a strategy maximizing efﬁciency or so-

cial welfare is attained. Thus, mutual PI acts similarly

to a global value function regularizing policy updates.

To further support this effect, we retrieve the dynamic

token values based on the agents’ local value V

. This

allows us to provide a lightweight extension, not rely-

ing on additional models to be learned (in contrast to

previous automatic incentivization approaches). ME-

DIATE operates decentralized, individually calculat-

ing a token value for each agent based on their re-

spective value functions. As these token values are

directly used to shape the agents’ reward (c.f. Eq. 5),

incentivization is relative to the agents’ value, push-

ing their strategies towards global cooperation (sim-

ilar to the monotonic improvement) while maintain-

ing value privacy (i.e., an agent does not know the

value function of other agents). This assumption en-

sures both independence and decentralization by en-

abling an agent to operate solely based on its domain-

speciﬁc metrics and variables. Alg. 1 depicts the pro-

posed mechanism for deriving and updating individ-

ual tokens.

Algorithm 1: Agent-wise Token Derivation with MEDI-

ATE.

Setup for Agent i ∈ D: T

← 0.1; r

min

← ∞;

← 0

for Epoch ϵ in Epochs; Agent i ∈ D do

← {} ▷ Initialize mean values for epoch

for Rollout ⟨τ

0,i

, a

0,i

, r

0,i

, . . . , τ

T,i

, a

T,i

, r

T,i

⟩ in ϵ

min

← min(r

min

, ⟨r

0...T,i

⟩)

← V

∪

(τ ) ▷ Calculate mean value (6)

end for

← max(T

(∗)

(i)

+ ∇

, 0) ▷ Update local token

(7)

← median(V

)

end for

All agents initially set their token to a small but

non-zero value of 0.1 to differentiate it from a zero-

valued token that would equate to na

ıve learning.

This initialization allows for the immediate incorpo-

ration of the PI mechanism. To ensure an appropriate

acceptance-rejection-ratio and thus an appropriate im-

pact on the behavior of other agents, the token value

must be proportional to the value function. Thus, we

suggest incrementing tokens by the relative difference

between the mean state value estimates across consec-

utive epochs. By doing so, MEDIATE tailors tokens

to the unique dynamics of each domain, thereby fos-

tering equal cooperation across diverse settings. As

a measure of the proﬁt, we derive the mean accumu-

lated value

V of an episode τ of length T similar to

the undiscounted return (cf. Eq. (1)):

(τ) =

t=0

(τ

t,i

)

(6)

refers to the current value approximation of agent

i. Furthermore, we use the median of the mean val-

ues

V over an epoch of episodes to improve stability.

The local tokens T

are adjusted every epoch based on

the difference (∆) between the current median of the

mean values (median(V

)) and the previous median

of the mean value

∇

= α ·

∆(

, median(V

))

· |r

min

|, (7)

with α = 0.1 as a constant comparable to a learning

rate and the absolute value of the lowest encountered

environmental reward r

min

(cf. Alg. 1) as a scaling

factor. Furthermore, we use the previous median of

the mean value

for normalization. Consequently,

sufﬁciently large negative state value estimates can

cause positive tokens, which rise when the value fur-

ther decreases. For negative values, the token thus re-

mains proportionate to the absolute magnitude of the

MEDIATE: Mutually Endorsed Distributed Incentive Acknowledgment Token Exchange

value function. Furthermore, the resulting token value

is clamped to positive values using the max operation

(cf. Alg. 1), sending a zero token otherwise. Resem-

bling the use of a ReLU activation function (Agarap,

2018), this forces the agent to send no incentive when

unable to send a positive. By this, agents adhere to

the principle of Niceness, which is a core principle for

the reciprocal strategy of MATE, implying no intent

of defection in the request (Phan et al., 2022).

However, besides using appropriate tokens, ﬁnd-

ings from the analysis of decentralized tokens also

demonstrated the need for equal token values in the

mutual exchange. Therefore, we extend MEDIATE

with a consensus mechanism to reach an agreement

on a mutual token, increasing equality and reducing

the impact of outliers while preserving the privacy of

the agents’ conﬁdential information using additive se-

cret sharing. All agents set up the consensus exchange

by dividing their token values into shares for all

agents in their neighborhood N , reserving one share

for privacy reasons. The token is only reconstructable

when accounting for all shares, which provides secu-

rity against privacy defectors. In the request phase, all

agents i send the corresponding shares [T

△

i,1

, . . . , T

△

i,n

]

to all n neighbors. Each receiving agent j accumu-

lates its received shares [T

△

j,1

, . . . , T

△

j,m+1

] from its m

neighbors, including its reserved share. In the re-

sponse phase, each agent j sends the accumulated

shares to all its neighbors. Each receiving agent i

obtains the accumulated shares from all neighbors,

which it averages over the number of shares, i.e., the

number of agents N , to obtain the reconstructed con-

sensus token T

∗

i∈N

j∈N

△

i,j

(8)

In domains like Harvest, with only partially con-

nected agents and changing topologies, the consen-

sus protocol includes a multi-iteration response phase.

Each summed share is tagged with an ID, sent to all

neighbors, and forwarded over multiple time steps

to ensure network-wide information dissemination.

To integrate the reconstructed token into the token

derivation mechanism, we propose two different up-

date mechanisms: Isolated updates the local token T

based on the previous local token, which is shared in-

dependently via the consensus protocol: max(T

∇

, 0). In contrast, synchronized replaces the local

token with the reconstructed token T

∗

after the con-

sensus phase: max(T

∗

+∇

, 0). Consequently, only

the token update (cf. Alg. 1) is affected, either syn-

chronized with the consensus token T

∗

or drifting in-

dependently. We will refer to the resulting variants as

MEDIATE-I and MEDIATE-S.

5 RELATED WORK

Various concepts help achieve emergent cooperation

in MAS. Learning with opponent-learning awareness

(LOLA) (Foerster et al., 2018) and stable opponent

shaping (SOS) (Letcher et al., 2019) consider the

learning process of other agents and shape the pol-

icy updates of opponents. Nature and human social

behavior also inspired many concepts. Wang et al.

(2019) developed an evolutionary approach to cre-

ate agents with social behavior by natural selection.

Other work focuses on prosocial agents and intrin-

sic motivation thriving for the manifestation of social

norms (Jaques et al., 2019). Eccles et al. (2019) di-

vided agents into innovators, learning a policy, and

imitators, which reciprocate innovators. Baumann

et al. (2020) insert an external planning agent into the

environment, which can observe all agents and dis-

tribute rewards. Overall, we divide approaches fos-

tering emergent cooperation into constructed artiﬁcial

social assemblies, added intrinsic motivation, and ex-

ternal optimization techniques. Our approach com-

bines those concepts, using socially inspired mutual

acknowledgment to shape the environmental rewards.

A large corpus in PI research focuses on similar

approaches to learning incentives integrated into the

model. Gifting integrates the reward-gifting capabil-

ity into agents’ policies as an additional action. Dif-

ferent reward mechanisms can build upon this con-

cept. In zero-sum gifting, agents receive a penalty

for each sent reward to balance the total sum of re-

wards. Gifting can also be only allowed up to a

ﬁxed budget per episode as an alternative to penal-

ization. With a replenishable budget, the reception of

environment rewards can recharge this budget (Lupu

and Precup, 2020). Learning to incentivize other

learning agents (LIO) is another approach that uses

an incentive function to learn appropriate peer re-

wards. Selecting a reward is not part of the action

space but is learned separately by a second model

(Yang et al., 2020). Like LIO, MEDIATE derives

incentives from the agents’ expected environmental

return. However, in contrast to MEDIATE, LIO re-

quires an additional model to be learned to predict

this value, which causes additional overhead. Learn-

ing to share (LToS) also implements two policies,

one for local objectives set by a high-level policy

(Yi et al., 2021). Peer-evaluation-based dual-DQN

(PED-DQN) lets agents evaluate their received peer

signals w.r.t. their environment rewards with an addi-

tional DQN network (Hostallero et al., 2020). Learn-

ing to inﬂuence through evaluative feedback (LIEF)

learns to reconstruct the reward function of peers via

feedback. The authors call for an investigation be-

ICAART 2025 - 17th International Conference on Agents and Artiﬁcial Intelligence

tween a manual, systematic, and learned construction

of rewards (Merhej and Chetouani, 2021). Fayad and

Ibrahim (2021) use counterfactual simulations to de-

rive inﬂuential actions. The above concepts modify

the agent models or the action space to derive the in-

trinsic rewards. Rather than altering the agents them-

selves, we utilize an additional protocol layer, which

serves as a tool for agents and yields increased ﬂexi-

bility.

Building upon mutual acknowledgment token ex-

change (MATE) (Phan et al., 2022, 2024), we control

the exchange of incentives via a two-phase commu-

nication protocol (c.f. Fig. 2). In the request phase

of each time step, all agents evaluate their mono-

tonic improvement (MI), c.f. Eq. (4), and potentially

send acknowledgment tokens to all neighbors. In the

response phase, agents evaluate their MI w.r.t. the

sum of environment rewards and the received token,

and respond with a positive or negative token. This

two-way handshake allows agents to give feedback

to other agents when incentives are received, which

fosters cooperation and has been shown to outper-

form na

ıve learning and other PI approaches, like LIO

and Gifting, in various benchmarks regarding efﬁ-

ciency and equality metrics (Phan et al., 2022, 2024).

MATE uses a communication layer and thus provides

a lightweight solution with minimal interference with

the agent model. Due to this ﬂexible and privacy-

conserving design, we evaluate our approach as an ex-

tension of MATE. However, note that other protocol

PI solutions can also utilize MEDIATE.

Overall, we aim to eliminate the need to set the ex-

change token beforehand, which is a central limitation

of MATE. Given their direct combination with the ex-

ternal reward, we argue that incentivization tokens

are sensitive parameters to be carefully considered.

Kuhnle et al. (2023) analyze the Harsanyi-Shapley

value to determine the weight of a side payment based

on the strategic strength of a player in two-player

scenarios. Value decomposition networks (Sunehag

et al., 2018), VAST (Phan et al., 2021), and QMIX

(Rashid et al., 2020) decompose the joint action-value

function into agent-based value functions to achieve

cooperation and maximize social welfare. These ap-

proaches are based on a centralized value function,

whereas our work focuses on independent learners in

a fully decentralized setting. MEDIATE also uses the

value function to automatically derive token values

to be mixed with the environmental reward, posing

a lightweight and efﬁcient solution.

6 EXPERIMENTAL RESULTS

To assess the effect of the introduced token deriva-

tion mechanism and the proposed consensus architec-

ture, we ran evaluations comparing isolated and syn-

chronized MEDIATE in the IPD, CoinGame-2, and

CoinGame-4. As an additional ablation, we use a re-

duced version with only the automated decentralized

token derivation (cf. Alg. 1) without any consensus

mechanism, which we refer to as AutoMATE. Addi-

tionally, we compare the above to na

ıve learning and

MATE with a ﬁxed token of 1. We measure coop-

eration in all Coin Game environments by the ratio

between own coins collected (occ) and total coins

collected (tcc): own coins =

|occ|

|tcc|

. We compare

the performance in the IPD and Harvest by the ap-

proaches’ efﬁciency (cf. Eq. (2)) as a metric for social

welfare. Additionally, we compare all MEDIATE ab-

lations w.r.t. the convergence of their token value. To

test the scalability of MEDIATE and its robustness to

varying reward distributions, we provide further eval-

uations in the Rescaled Coin Game-2, CoinGame-

6, and Harvest, including benchmark comparisons to

zero-sum- and budget-gifting and LIO.

Training is conducted for 5000 epochs, compris-

ing ten episodes each. We averaged all of the fol-

lowing results over eight random seeds. If not stated

otherwise, all implementations use their default hy-

perparameters from the corresponding source. Please

refer to the appendix for further environment- and im-

plementation details

6.1 Evaluation of MEDIATE

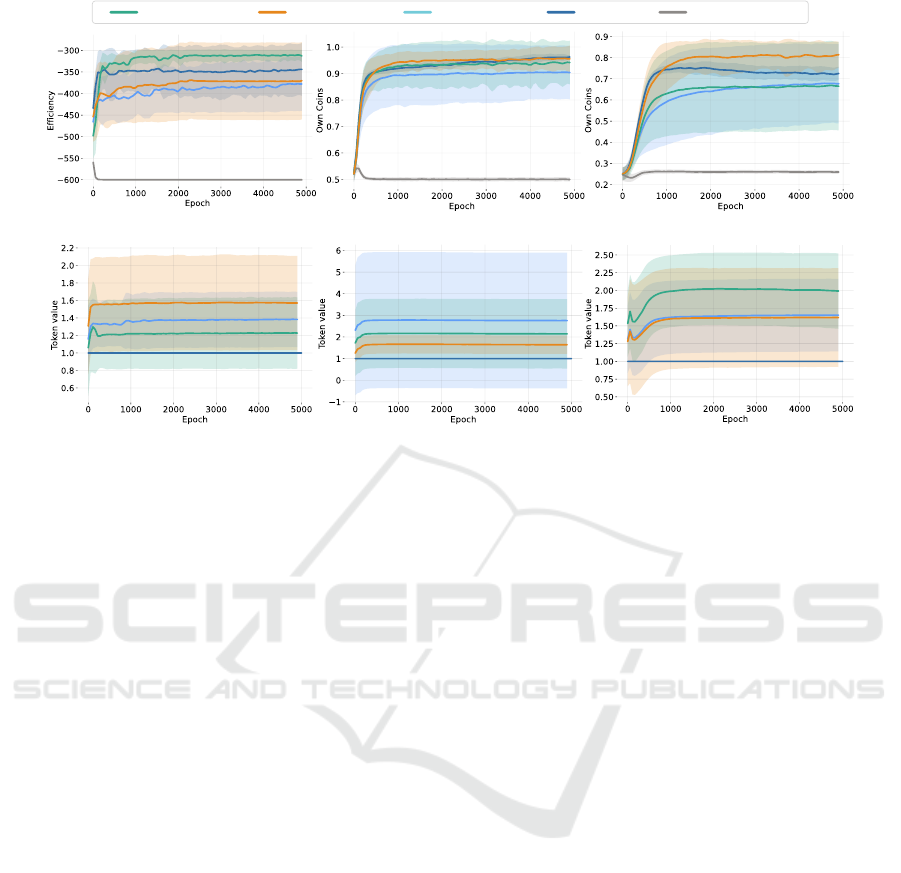
Fig. 4 shows the evaluation results. The graphs indi-

cate that either synchronized or isolated MEDIATE

updates consistently achieve efﬁciency and cooper-

ation levels comparable or superior to MATE in all

experimental settings, which legitimates their further

investigation. As expected, na

ıve learning fails to

reach emergent cooperation, again showcasing the

compared environments’ intricacy.

In general, MEDIATE enhances the performance

of AutoMATE across all settings, except for the two-

agent Coin Game scenario, where isolated updates

neither improve nor deteriorate cooperation. The re-

sults imply that the combined automatic and decen-

tralized mechanism - introduced by MEDIATE - pro-

vides sufﬁcient tokens to replace the original MATE

token value of 1. Furthermore, Figs. 4d-4f show that

all automatically derived tokens converge within the

initial 1000 epochs, indicating the purposeful nature

All required implementations are available at https://

github.com/philippaltmann/MEDIATE.

MEDIATE: Mutually Endorsed Distributed Incentive Acknowledgment Token Exchange

Naive Learning

MATEAutoMATE

MEDIATE-IMEDIATE-S

(a) IPD | Efﬁciency (b) CoinGame-2 | Own Coins (c) CoinGame-4 | Own Coins

(d) IPD | Token Values (e) CoinGame-2 | Token Values (f) CoinGame-4 | Token Values

Figure 4: MEDIATE Evaluation: Comparing the mean Efﬁciency (Fig. 4a) and rate of Own Coins (Fig. 4b, 4c) of Na

ıve

Learning (grey), MATE (blue), AutoMATE (light blue), MEDIATE-I (orange), and MEDIATE-S (green), and the Mean

Token Value (Fig. 4d, 4e, 4f) in the IPD (Fig. 4a, 4d), 2-agent CoinGame (Fig. 4b, 4e), and 4-agent CoinGame (Fig. 4c, 4f).

The shaded areas mark the 95% conﬁdence intervals. Overall, MEDIATE outperforms the compared approaches. Isolated

consensus shows improved adaptability to increasing numbers of agents, while Synchronized consensus shows improved

robustness in the negative-valued IPD.

of the proposed architecture. In comparison, the cor-

responding tokens of AutoMATE and MEDIATE all

converge to higher token values than MATE, which,

according to our preliminary studies, are more op-

timal tokens. Wider conﬁdence intervals in token

convergence are generally associated with reduced

efﬁciency and cooperation, but in the CoinGame-4,

AutoMATE tokens converge to equivalent values as

those with isolated updates. However, although its

conﬁdence interval is narrower, AutoMATE’s perfor-

mance is inferior due to the missing token coordina-

tion between the agents. Comparing the two MEDI-

ATE variants, isolated updates perform better in both

CoinGame settings.

In the negative-valued IPD domain, synchronized

updates show advantages. Overall, in combination

with the token plots, the results show that the update

variant converging to a smaller value, i.e., the respec-

tively less optimistic variant, provides superior tokens

and thus yields improved efﬁciency and cooperation.

Given the absence of a deﬁnitive superior option be-

tween the two MEDIATE variants, we include both in

the benchmark comparisons.

6.2 Benchmark Comparisons

Fig. 5 shows the benchmark results. Table 1 summa-

rizes the ﬁnal performance metrics. The two-agent

Coin Game features down-scaled rewards (RCG-2),

requiring agents to learn cooperation under minimal

positive and negative environment rewards. In con-

trast to the compared approaches, both MEDIATE

variants achieve signiﬁcantly higher rewards and mas-

ter the task. Yet, isolated updates exhibit a slight

performance advantage over synchronized updates.

MATE demonstrates moderate cooperation, slightly

improving upon LIO. In contrast, the gifting methods

and na

ıve learning only show marginal cooperation,

although Gifting-Budget performs comparably better.

These results again highlight the superior adaptability

of MEDIATE to unconventional, potentially challeng-

ing reward scenarios that yield improved applicability

to varying tasks.

In the six-agent Coin Game (CG-6), na

ıve learn-

ing performs worst alongside Gifting-Zerosum and

Gifting-Budget. While LIO shows a marginal

improvement, it still lacks signiﬁcantly behind

MATE and MEDIATE regarding strategic cooper-

ation. MEDIATE-I performs similarly to MATE,

which potentially can be attributed to the limited ca-

pability of isolated updates to manage negative re-

turns. MATE initially demonstrates an optimal learn-

ICAART 2025 - 17th International Conference on Agents and Artiﬁcial Intelligence

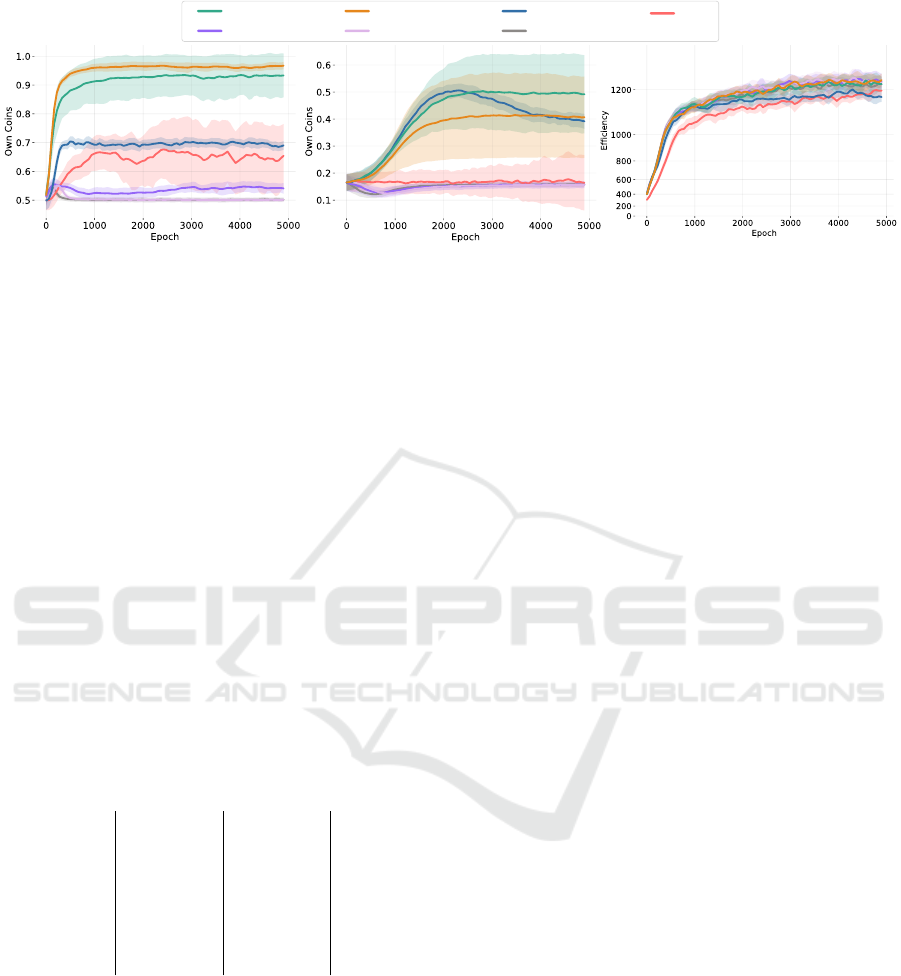
Naive Learning

MATE

MEDIATE-IMEDIATE-S

Gifting-Budget

LIO

Gifting-Zerosum

(a) RCG-2 — Own Coins (b) CG-6 — Own Coins (c) Harvest (6 Agents) — Efﬁciency

Figure 5: Benchmark Comparison: Mean rate of Own Coins (Fig. 5a, 5b) and Efﬁciency (Fig. 5c) of MEDIATE-S (green),

MEDIATE-I (orange), MATE (blue), LIO (red), Budget-Gifting (purple), Zerosum-Gifting (pink) and Na

ıve Learning (grey)

in the Rescaled CoinGame-2 (RCG-2) (Fig. 5a), CoinGame-6 (CG-6) (Fig. 5b), and Harvest (Fig. 5c). The shaded areas

mark the 95% conﬁdence intervals. Across all scenarios, MEDIATE shows superior performance. Generally, using Isolated

consensus shows increased adaptability to the intricate reward landscapes speciﬁcally considered here.

ing curve but deteriorates in performance afterward.

In terms of cooperation, MEDIATE with synchro-

nized updates emerges as performing best.

Harvest demonstrates the ability of MEDIATE to

beneﬁt in partially connected topologies. Here, ME-

DIATE ranks among the top-performing approaches

and enhances the performance of MATE by providing

an appropriate incentivization token. It thus demon-

strates its efﬁcacy in functioning even within unreli-

able environments while preserving privacy over the

agents’ local value information.

Table 1: Final average of the rate of Own Coins in the

Rescaled CoinGame-2 (RCG-2) and CoinGame-6 (CG-6),

and the Efﬁciency in Harvest for synchronized and iso-

lated MEDIATE (MEDIATE-S, MEDIATE-I), AutoMATE,

MATE, LIO, Budget- and Zerosum Gifting (Budget-G,

Zerosum-G), and Na

ıve Learning.

RCG-2 CG-6 Harvest

MEDIATE-S 0.93 ± 0.08 0.50 ± 0.16 1212 ± 20

MEDIATE-I 0.97 ± 0.02 0.41 ± 0.16 1232 ± 17

AutoMATE 0.86 ± 0.08 0.18 ± 0.09 1204 ± 35

MATE 0.69 ± 0.01 0.39 ± 0.03 1177 ± 20

LIO 0.69 ± 0.10 0.17 ± 0.11 1192 ± 20

Budget-G 0.54 ± 0.03 0.16 ± 0.02 1232 ± 23

Zerosum-G 0.50 ± 0.01 0.16 ± 0.01 1230 ± 20

ıve L. 0.50 ± 0.01 0.16 ± 0.01 1220 ± 25

Overall, the evaluations demonstrated that emer-

gent cooperation between agents fosters optimal so-

cial welfare. Appropriate reward weights can boost

equal cooperation in social dilemmas, but such

weights’ appropriateness depends on the domain, the

number of agents, the reward structure, or other fac-

tors. Involving a higher number of agents within a

domain increases the required precision. Our exper-

iments show that a token value of 1 - as proposed

for MATE - is not universally appropriate in all do-

mains or settings. In the down-scaled two-agent Coin

Game, token value 1 is inappropriate, and in the six-

agent Coin Game, it does not achieve optimal coop-

eration. Yet across all domains, MEDIATE exhibits

strong adaptability while consistently delivering su-

perior performance, even in challenging cooperative

tasks such as the six-agent Coin Game, scenarios with

complex reward landscapes, or unreliable environ-

ments with partially connected neighborhoods, like

Harvest.

7 CONCLUSION

In this work, we proposed mutually endorsed dis-

tributed incentive acknowledgment token exchange

(MEDIATE). MEDIATE introduces automated PI to-

kens in decentralized MAS with a consensus architec-

ture and two agent-individual update mechanisms.

Token decentralization allows agents to use dif-

ferent tokens in the exchange. Experiments on the

impact of different tokens in social dilemmas sug-

gest that equal and appropriate token values foster

improved social welfare. MEDIATE integrates the

gradient of the agents’ local value function approxi-

mation to derive appropriate tokens matching the ex-

ternal rewards. To achieve consensus on equal to-

kens, we propose extending the MATE protocol based

on additive secret sharing, enabling the identiﬁca-

tion of the token average through the token exchange

while adhering to privacy requirements. The consen-

sus protocol is independent of the underlying algo-

rithm for token derivation. We furthermore evaluate

two token-update variations: A synchronized mecha-

nism based on the reconstructed global token and an

isolated mechanism using the previous local token.

Benchmark evaluations showed that MEDIATE

MEDIATE: Mutually Endorsed Distributed Incentive Acknowledgment Token Exchange

achieves high social welfare in all tested domains. In

all evaluated settings, MEDIATE improves the per-

formance of MATE and even outperforms or matches

the best-performing baselines. It represents a robust

and adaptive solution capable of ﬁnding appropriate

tokens. Computationally, MEDIATE is comparable

to MATE while overcoming its central limitation of

static token values. The only addition of deriving con-

sented tokens at each update is a sum of constant val-

ues with linear complexity. Furthermore, the token

extends on the value approximation. Thus, compared

to LIO, no additional model needs to be learned.

Yet, even though not apparent in the evaluated

social dilemma environments, this dependence on a

robust value estimate also depicts a central limita-

tion of MEDIATE. Therefore, integrating surrogate

reward metrics like (Altmann et al., 2024a) might im-

prove the overall robustness. Furthermore, the evalu-

ated update mechanisms showed potentially unstable

and prone to outliers. Thus, future work should fo-

cus on producing more accurate tokens, especially for

an increased number of agents, making the overall al-

gorithm more reliable in precision-requiring domains

like the Rescaled CoinGame. Also, while MEDIATE

has been shown to be robust to scaled reward land-

scapes, increasing numbers of agents, and long-term

cooperation scenarios like Harvest, it should be tested

for unreliable connections or defective scenarios.

Overall, MEDIATE provides a lightweight and ro-

bust framework to assess communication consensus

mechanisms with automated peer incentives for emer-

gent cooperation in various scenarios of social dilem-

mas.

ACKNOWLEDGEMENTS

This work is part of the Munich Quantum Valley,

which is supported by the Bavarian state government

with funds from the Hightech Agenda Bayern Plus.

REFERENCES

Agarap, A. F. (2018). Deep learning using rectiﬁed linear

units (relu). arXiv preprint arXiv:1803.08375.

Altmann, P., Ritz, F., Zorn, M., K

olle, M., Phan, T., Gabor,

T., and Linnhoff-Popien, C. (2024a). Discriminative

reward co-training. Neural Computing and Applica-

tions, pages 1–17.

Altmann, P., Sch

onberger, J., Illium, S., Zorn, M., Ritz, F.,

Haider, T., Burton, S., and Gabor, T. (2024b). Emer-

gence in multi-agent systems: A safety perspective.

In Leveraging Applications of Formal Methods, Veri-

ﬁcation and Validation. Rigorous Engineering of Col-

lective Adaptive Systems, ISoLA ’24, pages 104–120.

Springer Nature.

Amirkhani, A. and Barshooi, A. H. (2022). Consensus in

multi-agent systems: a review. Artiﬁcial Intelligence

Review, 55(5):3897–3935.

Axelrod, R. (1980). Effective choice in the prisoner’s

dilemma. Journal of conﬂict resolution, 24(1):3–25.

Baumann, T., Graepel, T., and Shawe-Taylor, J. (2020).

Adaptive mechanism design: Learning to promote co-

operation. In 2020 International Joint Conference on

Neural Networks (IJCNN), pages 1–7. IEEE.

Bus¸oniu, L., Babu

ska, R., and De Schutter, B. (2010).

Multi-agent reinforcement learning: An overview. In-

novations in multi-agent systems and applications-1,

pages 183–221.

Cao, B., Li, Y., Zhang, L., Zhang, L., Mumtaz, S., Zhou,

Z., and Peng, M. (2019). When internet of things

meets blockchain: Challenges in distributed consen-

sus. IEEE Network, 33(6):133–139.

Conradt, L. and Roper, T. J. (2005). Consensus decision

making in animals. Trends in ecology & evolution,

20(8):449–456.

Crainic, T. G. and Toulouse, M. (2007). Explicit and emer-

gent cooperation schemes for search algorithms. In

International Conference on Learning and Intelligent

Optimization, pages 95–109. Springer.

Dawes, R. M. (1980). Social dilemmas. Annual review of

psychology, 31(1):169–193.

Eccles, T., Hughes, E., Kram

ar, J., Wheelwright, S., and

Leibo, J. Z. (2019). Learning reciprocity in com-

plex sequential social dilemmas. arXiv preprint

arXiv:1903.08082.

Fayad, A. and Ibrahim, M. (2021). Inﬂuence-based rein-

forcement learning for intrinsically-motivated agents.

arXiv preprint arXiv:2108.12581.

Figura, M., Kosaraju, K. C., and Gupta, V. (2021). Ad-

versarial attacks in consensus-based multi-agent rein-

forcement learning. In 2021 American Control Con-

ference (ACC), pages 3050–3055. IEEE.

Foerster, J., Chen, R. Y., Al-Shedivat, M., Whiteson, S.,

Abbeel, P., and Mordatch, I. (2018). Learning with

opponent-learning awareness. In Proceedings of the

17th International Conference on Autonomous Agents

and MultiAgent Systems, page 122–130.

Han, Y., Lu, W., and Chen, T. (2013). Cluster consensus

in discrete-time networks of multiagents with inter-

cluster nonidentical inputs. IEEE Transactions on

Neural Networks and Learning Systems, 24(4):566–

578.

Hostallero, D. E., Kim, D., Moon, S., Son, K., Kang, W. J.,

and Yi, Y. (2020). Inducing cooperation through re-

ward reshaping based on peer evaluations in deep

multi-agent reinforcement learning. In Proceedings

of the 19th International Conference on Autonomous

Agents and MultiAgent Systems, pages 520–528.

Jaques, N., Lazaridou, A., Hughes, E., Gulcehre, C., Or-

tega, P., Strouse, D., Leibo, J. Z., and De Freitas, N.

(2019). Social inﬂuence as intrinsic motivation for

multi-agent deep reinforcement learning. In Interna-

ICAART 2025 - 17th International Conference on Agents and Artiﬁcial Intelligence

tional conference on machine learning, pages 3040–

3049. PMLR.

Kim, Y. G., Lee, S., Son, J., Bae, H., and Do Chung, B.

(2020). Multi-agent system and reinforcement learn-

ing approach for distributed intelligence in a ﬂexible

smart manufacturing system. Journal of Manufactur-

ing Systems, 57:440–450.

olle, M., Matheis, T., Altmann, P., and Schmid, K. (2023).

Learning to participate through trading of reward

shares. In Proceedings of the 15th International Con-

ference on Agents and Artiﬁcial Intelligence, ICAART

’23, pages 355–362. SciTePress.

Kuhnle, A., Richley, J., and Perez-Lavin, D. (2023).

Learning strategic value and cooperation in multi-

player stochastic games through side payments. arXiv

preprint arXiv:2303.05307.

Lashkari, B. and Musilek, P. (2021). A comprehensive re-

view of blockchain consensus mechanisms. IEEE Ac-

cess, 9:43620–43652.

Laurent, G. J., Matignon, L., Fort-Piat, L., et al. (2011). The

world of independent learners is not markovian. Inter-

national Journal of Knowledge-based and Intelligent

Engineering Systems, 15(1):55–64.

Leibo, J. Z., Zambaldi, V., Lanctot, M., Marecki, J., and

Graepel, T. (2017). Multi-agent reinforcement learn-

ing in sequential social dilemmas. In Proceedings of

the 16th Conference on Autonomous Agents and Mul-

tiAgent Systems, pages 464–473.

Lerer, A. and Peysakhovich, A. (2017). Maintaining coop-

eration in complex social dilemmas using deep rein-

forcement learning. arXiv preprint arXiv:1707.01068.

Letcher, A., Foerster, J., Balduzzi, D., Rockt

aschel, T., and

Whiteson, S. (2019). Stable opponent shaping in dif-

ferentiable games. In International Conference on

Learning Representations.

Li, Q., Cascudo, I., and Christensen, M. G. (2019). Privacy-

preserving distributed average consensus based on ad-

ditive secret sharing. In 2019 27th European Signal

Processing Conference (EUSIPCO), pages 1–5. IEEE.

Li, Y. and Tan, C. (2019). A survey of the consensus for

multi-agent systems. Systems Science & Control En-

gineering, 7:468 – 482.

Littman, M. L. (2001). Value-function reinforcement learn-

ing in markov games. Cognitive systems research,

2(1):55–66.

Lupu, A. and Precup, D. (2020). Gifting in multi-agent

reinforcement learning. In Proceedings of the 19th

International Conference on autonomous agents and

multiagent systems, pages 789–797.

Merhej, R. and Chetouani, M. (2021). Lief: Learning to in-

ﬂuence through evaluative feedback. In Adaptive and

Learning Agents Workshop (AAMAS 2021).

Monrat, A. A., Schel

en, O., and Andersson, K. (2019). A

survey of blockchain from the perspectives of appli-

cations, challenges, and opportunities. IEEE Access,

7:117134–117151.

e, R. (2006). Cooperation experiments: coordination

through communication versus acting apart together.

Animal behaviour, 71(1):1–18.

Olfati-Saber, R. and Shamma, J. S. (2005). Consensus ﬁl-

ters for sensor networks and distributed sensor fusion.

In Proceedings of the 44th IEEE Conference on Deci-

sion and Control, pages 6698–6703. IEEE.

Omitaomu, O. A. and Niu, H. (2021). Artiﬁcial intelligence

techniques in smart grid: A survey. Smart Cities,

4(2):548–568.

Perolat, J., Leibo, J. Z., Zambaldi, V., Beattie, C., Tuyls, K.,

and Graepel, T. (2017). A multi-agent reinforcement

learning model of common-pool resource appropria-

tion.

Phan, T., Ritz, F., Belzner, L., Altmann, P., Gabor, T., and

Linnhoff-Popien, C. (2021). Vast: Value function fac-

torization with variable agent sub-teams. In Advances

in Neural Information Processing Systems, NeurIPS

’21, pages 24018–24032. Curran Associates, Inc.

Phan, T., Sommer, F., Altmann, P., Ritz, F., Belzner, L.,

and Linnhoff-Popien, C. (2022). Emergent coop-

eration from mutual acknowledgment exchange. In

Proceedings of the 21st International Conference on

Autonomous Agents and Multiagent Systems, pages

1047–1055.

Phan, T., Sommer, F., Ritz, F., Altmann, P., N

ußlein,

J., K

olle, M., Belzner, L., and Linnhoff-Popien, C.

(2024). Emergent cooperation from mutual acknowl-

edgment exchange in multi-agent reinforcement learn-

ing. Autonomous Agents and Multi-Agent Systems,

38(34).

Qureshi, K. N. and Abdullah, A. H. (2013). A survey on in-

telligent transportation systems. Middle-East Journal

of Scientiﬁc Research, 15(5):629–642.

Rashid, T., Samvelyan, M., De Witt, C. S., Farquhar, G., Fo-

erster, J., and Whiteson, S. (2020). Monotonic value

function factorisation for deep multi-agent reinforce-

ment learning. The Journal of Machine Learning Re-

search, 21(1):7234–7284.

Russell, S. J. (2010). Artiﬁcial intelligence a modern ap-

proach. Pearson Education, Inc.

Salimitari, M. and Chatterjee, M. (2018). A survey on con-

sensus protocols in blockchain for iot networks. arXiv

preprint arXiv:1809.05613.

Sandholm, T. W. and Crites, R. H. (1996). Multiagent rein-

forcement learning in the iterated prisoner’s dilemma.

Biosystems, 37(1-2):147–166.

Schenato, L. and Gamba, G. (2007). A distributed consen-

sus protocol for clock synchronization in wireless sen-

sor network. In 2007 46th ieee conference on decision

and control, pages 2289–2294. IEEE.

Sunehag, P., Lever, G., Gruslys, A., Czarnecki, W. M.,

Zambaldi, V., Jaderberg, M., Lanctot, M., Sonnerat,

N., Leibo, J. Z., Tuyls, K., and Graepel, T. (2018).

Value-decomposition networks for cooperative multi-

agent learning based on team reward. In Proceedings

of the 17th International Conference on Autonomous

Agents and MultiAgent Systems, page 2085–2087.

Tawalbeh, L., Muheidat, F., Tawalbeh, M., and Quwaider,

M. (2020). Iot privacy and security: Challenges and

solutions. Applied Sciences, 10(12):4102.

Wang, J. X., Hughes, E., Fernando, C., Czarnecki, W. M.,

nez Guzm

an, E. A., and Leibo, J. Z. (2019).

MEDIATE: Mutually Endorsed Distributed Incentive Acknowledgment Token Exchange

Evolving intrinsic motivations for altruistic behavior.

In Proceedings of the 18th International Conference

on Autonomous Agents and MultiAgent Systems, page

683–692.

Yang, J., Li, A., Farajtabar, M., Sunehag, P., Hughes, E.,

and Zha, H. (2020). Learning to incentivize other

learning agents. Advances in Neural Information Pro-

cessing Systems, 33:15208–15219.

Yi, Y., Li, G., Wang, Y., and Lu, Z. (2021). Learning to

share in multi-agent reinforcement learning. arXiv

preprint arXiv:2112.08702.

Yu, W., Chen, G., Wang, Z., and Yang, W. (2009). Dis-

tributed consensus ﬁltering in sensor networks. IEEE

Transactions on Systems, Man, and Cybernetics, Part

B (Cybernetics), 39(6):1568–1577.

APPENDIX

Iterated Prisoner’s Dilemma. The Iterated Pris-

oner’s Dilemma (IPD) is the repeated game of the Pris-

oner’s Dilemma, depicted in Table 2. At each time step, the

two players must choose between cooperation and defection

to maximize their payoff (Axelrod, 1980; Hostallero et al.,

2020). Mutual defection constitutes a Nash equilibrium. If

both agents defect, no agent is incentivized to change its

strategy to cooperation in the next step if the other agent re-

mains a defector. If both agents switched their strategy to

cooperate, both would receive a lower penalty.

Table 2: Prisoner’s Dilemma reward allocation. Each cell

contains the respective payoffs for each of the two players

based on their choice of cooperation or defection.

Cooperate Defect

Cooperate (-1,-1) (-3,0)

Defect (0,-3) (-2,-2)

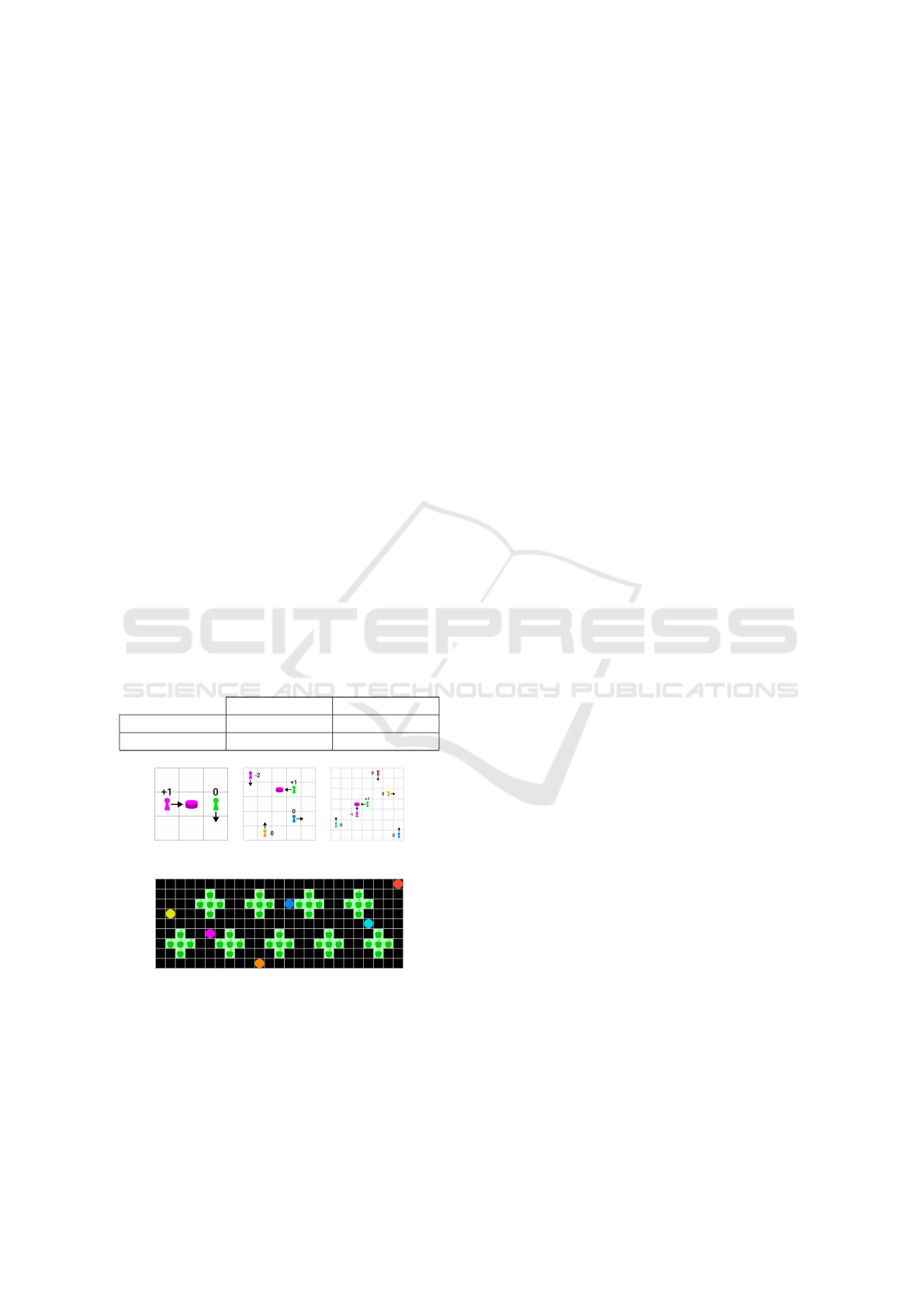
(a) CG-2 (b) CG-4 (c) CG-6

(d) Harvest (6 agents)

Figure 6: Evaluation Environments

Coin Game. Coins or Coin Game is an SSD conceptual-

ized by Lerer and Peysakhovich (2017). The CoinGame-N

comprises N ∈ {2, 4, 6} agents on a 3x3, 5x5, and 7x7

grid respectively (cf. Figs. 6a-6b). A distinct color iden-

tiﬁes each agent. Initially, all N agents and one random-

colored coin spawn at random positions. The color of the

coin matches one of the agents. An agent can distinguish

whether the coin matches its own color or not. The action

space of each agent comprises four directions of movement

A ∈ {left, right, up, down}. A coin is collected when

an agent moves to its position. The environment discards

actions violating its bounds. If an agent collects any coin,

it receives a reward of +1. If the color matches a different

agent, that agent is penalized with −2. If multiple agents

collect a coin simultaneously, the matching agent receives a

penalty of −1. Once a coin is collected, a new coin spawns.

To evaluate varying reward scales, we added the Rescaled

Coin Game-2 variation with downsized rewards (i.e., scaled

by 0.1), such that the positive reward becomes +0.1 and

the penalty weighs −0.2. The ratio between reward and

penalty remains unchanged. Self-interested agents will col-

lect all coins regardless of color since this strategy imposes

only positive rewards on themselves. The Nash equilibrium

is reached if all agents follow this strategy since refraining

from collecting other agents’ coins only reduces an agent’s

own rewards without mitigating the penalties incurred from

the actions of other agents. However, if all agents collect

their own coins, each agent proﬁts from the reduced penal-

ties, and social welfare can be maximized. To measure the

level of strategic cooperation in this domain, we evaluate

the rate of own coins w.r.t. to the total of collected coins.

Harvest. The Commons game is conceptualized by Per-

olat et al. (2017) and adapted by Phan et al. (2022), where

it is named Harvest. In Harvest, agents move on a 25x9-

sized grid to collect apples. The Harvest grid, including the

ﬁxed positioning of the apples, is displayed in Fig. 6d. Ap-

ples have a regrowth rate, which depends on the number of

existing apples in the local area. More apples in the area

cause a higher regrowth rate of collected apples. If no ap-

ples remain in the area, no apples regrow. Self-interested

agents maximize their own apple harvest, but in a MAS,

agents have to refrain from simultaneous apple collection

to avoid the ultimate depletion of resources (the tragedy of

the commons). This requirement is the Nash equilibrium

of Harvest, as a single agent can not improve its rewards

by refraining from apple collection when other agents will

continue to diminish the resources. Only if all agents co-

operate they can maximize their long-term rewards. Agents

can tag other agents to remove them from the game for 25

time steps. (Perolat et al., 2017). In addition to a positive

reward of +1 for an apple harvest, each time step poses a

time penalty of −0.1. Furthermore, agents only have access

to a partial observation surrounding their position. Agents

can only communicate with agents in their neighborhood

in an area of 7x7 tiles. In addition to moving in four di-

rections (as for the coin game), the action space comprises

four actions to tag all neighbor agents in the four directions.

Moving toward a boundary results in no movement. Only

one agent can harvest an apple or tag another agent at a time.

The order of actions at each time step is random.

ICAART 2025 - 17th International Conference on Agents and Artiﬁcial Intelligence