Tutrace: Editable Animated Vector Shape from Video

ıc Vital

Technicolor Group, France

Keywords:

Video, Vectorization, Rotoscopy, Animation, Vector Graphics.

Abstract:

We present a new video vectorization technique for converting a sequence of binary images into an animated

vector shape. Our approach offers the beneﬁt of producing an output that can be directly used in a compositing

software to apply manual edits and corrections, which is often a mandatory constraint for rotoscoping artists

in the VFX industry. Our process initially builds a frame-by-frame vectorization of the input, ﬁnds correspon-

dences between vertices at different frames, and extracts an animated vector shape from the induced graph

structure. Although the presented method is completely automatic, the general approach is ﬂexible and offers

several controls to adjust the ﬁdelity vs. simplicity trade-off in the generated output.

1 INTRODUCTION

In the visual effects (VFX) industry, rotoscoping

artists work primarily with animated shapes (closed

or open 2D curves) as these vector graphics primitives

provide ﬁne control over the ﬁnal result and allow re-

editing in case of feedback from clients, supervisors

or downstream departments. However, using these

animated shapes comes at a cost, as they require sev-

eral hours of careful manual work from trained artists

to be initially created.

On the other hand, image segmentation methods

have matured in the recent years, and it is now pos-

sible to automatically extract a desired object from a

video with great precision in a number of scenarios.

However the lack of control and ability to edit the re-

sults is currently making it difﬁcult for VFX studios

to integrate these methods in their standard workﬂow.

In this work, we propose a method to bridge this

gap, i.e. turn a segmented video (made out of binary

images) into an animated vector shape, which can be

imported in a compositing DCC

such as Nuke or Sil-

houette for re-editing. We call this method Tutrace.

This name originated as a blend between the initial

inspiration for the algorithm, Potrace, and the topol-

ogy of the output, which resembles a tube or tunnel.

The fact that we are targeting DCC-compatible

animated vector shapes imposes some speciﬁc con-

https://orcid.org/0009-0002-7972-9242

Digital Content Creator, i.e. software dedicated to cre-

ating and editing digital content such as 2D/3D geometry,

images, etc.

straints on the structure of the output. More precisely,

this means we must produce closed curves whose ge-

ometry is speciﬁed by a set of keyframes, i.e. frame

values along the timeline where the positions of all

control points are prescribed. Using this representa-

tion, the curve geometry in-between two keyframes is

determined by interpolating the control points posi-

tions.

The main challenge imposed by this structure is

that the number of vertices is ﬁxed for the entire frame

range. By contrast, applying a single-image vector-

ization algorithm to each frame independently would

create vector shapes with a varying number of ver-

tices, adapted to the input geometry. This is particu-

larly visible in areas where details appear or disappear

over the animation: a ﬂat area needs only two vertices

to be represented, but if this area breaks into several

parts then more vertices are needed.

Our algorithm works by ﬁrst vectorizing each

video frame independently, then ﬁnding correspon-

dences between these initial static vector shapes to

extract an animated vector shape, and ﬁnally simpli-

fying it. Our main contribution lies in the central part

of this algorithm, which is the process of going from

a sequence of static vector shapes to an animated vec-

tor shape, thus solving the problem stated above using

an ad-hoc method. The simpliﬁcations performed af-

terwards on the animated shape aim at reducing its

complexity, i.e. the number of animated vertices and

keyframes, thus making the output better suited for

manual editing.

Vital, L.

Tutrace: Editable Animated Vector Shape from Video.

DOI: 10.5220/0013097900003912

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 20th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2025) - Volume 1: GRAPP, HUCAPP

and IVAPP, pages 19-28

ISBN: 978-989-758-728-3; ISSN: 2184-4321

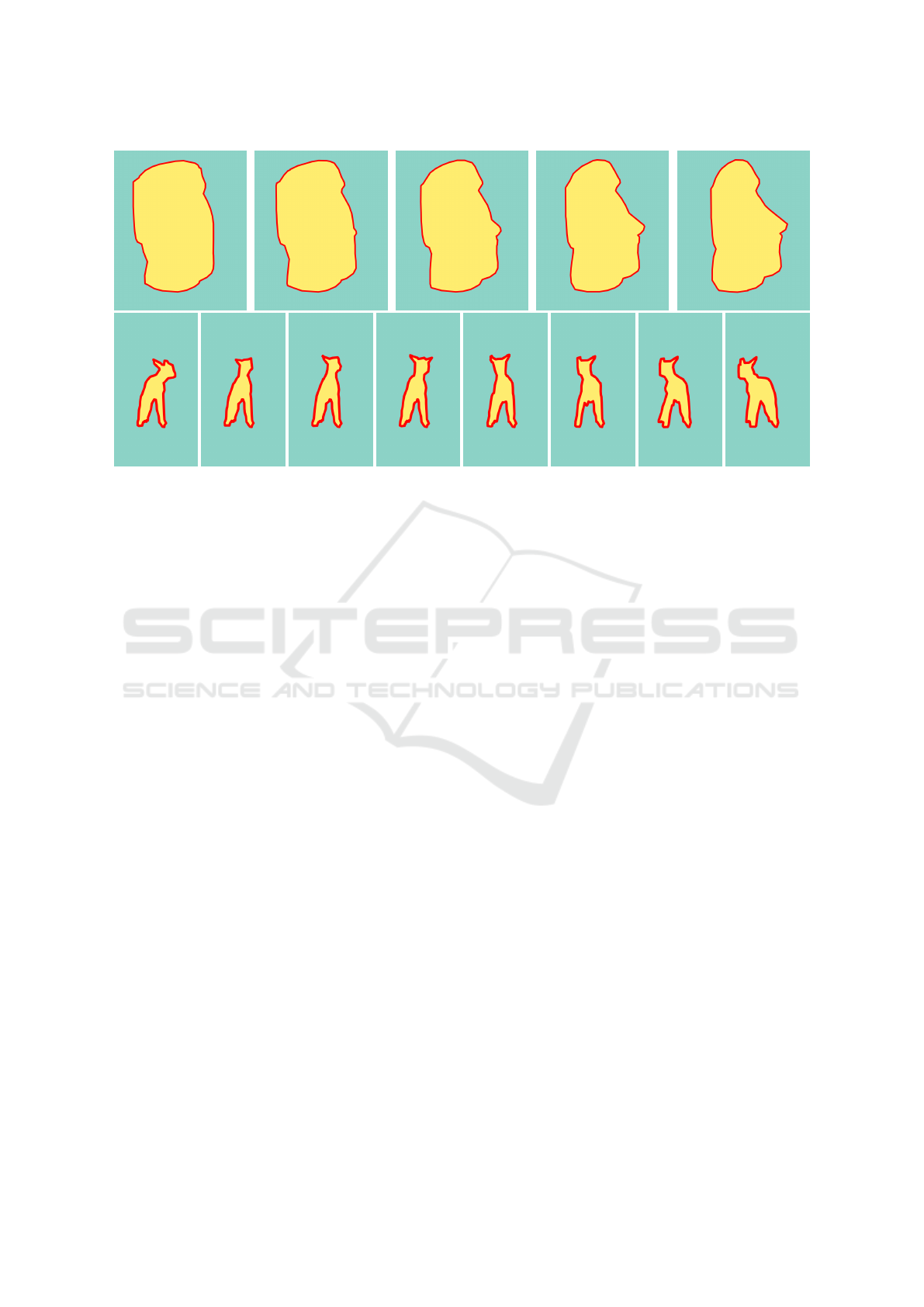
Figure 1: Animated vector shapes generated by Tutrace on the “statue” (ﬁrst row) and “sheep” (second row) sequences, shown

in red and overlaid on the images.

2 RELATED WORK

2.1 Video Object Segmentation

Image segmentation and object segmentation in video

are fundamental problems in computer vision, and

there is now extensive literature on that topic (Yu

et al., 2023) (Yao et al., 2020). Going from object

segmentation in a single image to a sequence of im-

ages is not a trivial task, as temporal coherence has to

be taken into account, and many artifacts can arise.

In this article, we do not present any new seg-

mentation method: this work is complementary to

segmentation, as it takes a binary image sequence as

input and produces an animated vector shape. The

motivation behind this is to provide users with direct

control over the results of an automatic segmentation

process, rather than relying on implicit controls.

2.2 Image Vectorization

There has been much work on single-image vectoriza-

tion, with various algorithms and representations pro-

posed to cover a wide range of inputs: natural images,

cartoon, manga, line drawings (Favreau et al., 2016),

and even pixel art (Kopf and Lischinski, 2011).

These methods can be classiﬁed into two main

categories depending on the representation they work

with, namely meshes or curves. Mesh-based meth-

ods span a wide range of primitives, including Fergu-

son patches (Sun et al., 2007) and triangular B

ezier

patches (Xia et al., 2009). The curve-based methods

also include various primitives, for instance closed

polygons and B

ezier curves (Selinger, 2003) as well

as diffusion curves (Orzan et al., 2008).

In this work, we focus particularly on the context

of rotoscopy, thus adding the constraint that we must

be able to import and edit the vectorization result in a

compositing DCC. Therefore the set of possible prim-

itives we can use is reduced to closed curves, thus

making Potrace (Selinger, 2003) an adequate choice

to base our work on.

2.3 Video Vectorization

Several methods have already been proposed for

video vectorization, however they do not focus on the

same objectives as we do.

(Zhang et al., 2009) proposes a method speciﬁ-

cally tailored for cartoon animation, and focuses on

decomposing the input images into spatially and tem-

porally coherent regions. However the ﬁnal output

it generates is a frame-by-frame vectorization, not an

animated shape.

(Wang et al., 2017) takes a quite different ap-

proach: it considers the input video as a volume with

color information, and the vectorization as a tetrahe-

dral meshing problem. This approach greatly simpli-

ﬁes the spatial-temporal duality and offers a link be-

tween vectorization and the wide literature on mesh

processing, however the output it generates is a tetra-

hedral mesh, which is not usable in any composit-

ing DCC and not easily convertible into an animated

shape.

GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications

(Li et al., 2021) proposes a method based on dif-

fusion curves, producing results of great visual qual-

ity, using a combination of optical ﬂow and shape

matching techniques for temporal coherence. How-

ever once again the output is not an animated shape,

but a frame-by-frame vectorization. In addition, the

output is made out of diffusion curves, which do not

have any topology constraint, and therefore generally

do not form a closed curve, therefore making the out-

put of this algorithm unﬁt to be used in ours.

(Zhang et al., 2023) focuses on motion graphics

video, i.e. animated graphic designs. They address

the problem of motion tracking and layered decompo-

sition, which is of critical importance whenever multi-

ple objects are in the scene. The output they produce,

however, is not a vector shape: each tracked object

is associated with an image inferred from the video

input, called its canonical image, a sequence of per-

frame afﬁne transforms and a sequence of per-frame

z-index depth. In particular, this representation im-

plies that their approach does not handle change in

the objects themselves, such as details appearing and

disappearing throughout the animation, which occurs

quite frequently in the context of rotoscopy and must

not be put aside.

3 MOTIVATION AND OVERVIEW

3.1 Problem Statement

The input data we consider in this work is a ﬁnite se-

quence of images (I

)

0≤ f <F

where F is the number

of frames. All these images share the same dimen-

sions (w, h). In this article we do not take color into

account, we only treat binary images, i.e. images with

pixel values in the set {0, 1}.

We also make another strong assumption on these

images: we assume that in each image, the pixels with

value 1 form a connected component without hole.

We call this component the content of the image. This

assumption greatly simpliﬁes the topology of the ani-

mated content.

The output we want to produce is an animated

shape, i.e. a closed curve deﬁned by a sequence of N

vertices animated over K keyframes. Each keyframe

deﬁnes a ﬁxed 2D position for the vertices, and for

a given frame in-between two keyframes the vertices

positions are linearly interpolated to determine the

shape geometry on that frame. Note that such an an-

imated shape is not necessarily a polygon: the ver-

tices could also be interpreted as control points for a

smooth curve. However, in the work that follows, we

will focus on generating an animated polygon.

3.2 Algorithm Breakdown

The overall workﬂow of the algorithm is quite intu-

itive: we start by vectorizing each image indepen-

dently, then we match the vertices between consec-

utive frames to create animated vertices, thus forming

an animated shape.

However most single-image vectorization algo-

rithms will try to simplify the shape geometry by

removing vertices in “ﬂat” areas, which is problem-

atic for the matching phase. Indeed, if a portion of

the shape is ﬂat at a given frame but “breaks into

two parts” at the following frame, hence creating a

new vertex at the breaking point, we won’t be able

to match this new vertex against the shape at the ﬁrst

frame (see Figure 3a). To overcome this issue, we

make sure that the ﬁrst vectorization step produces a

sequence of densely sampled shapes (see Figure 3b)

and we delay the simpliﬁcation step until the end of

the algorithm, when we have a fully animated shape.

We refer to this ﬁnal simpliﬁcation step as pruning.

In addition, it is quite likely that the matching

phase does not produce 1-to-1 vertex matches be-

tween consecutive frames, which makes the process

of creating animated vertices and joining them into

an animated shape more complex than simply chain-

ing the matches. We call this process untangling.

In summary, our algorithm follows these four

steps, depicted in Figure 2: extract a dense contour

from each image, match the vertices of these contours

between consecutive frames, untangle these matches

to produce an animated shape, and prune the animated

vertices and keyframes on this animated shape.

3.3 Data Structure

The data structure we use in our method is a simpli-

ﬁed version of the work presented in (Dalstein et al.,

2015), which we will call a Tutrace complex.

At the most abstract level, a Tutrace complex is

just a directed graph. A node in this graph is called

a key vertex, and it encodes both a 2D position and a

frame number. As for the edges in this graph, they are

split into two categories: the key edges and the tempo-

ral edges. A key edge always links two key vertices

which have the same frame number, whereas a tempo-

ral edge always links two key vertices with different

frame numbers, and is directed from lower to higher

frame number.

This graph structure is enriched with additional

entities which provide higher-level structures and se-

mantic for working with a Tutrace complex. A key

cycle is a looping path of key edges, and can be seen

as a static vector shape (made out of a single closed

Tutrace: Editable Animated Vector Shape from Video

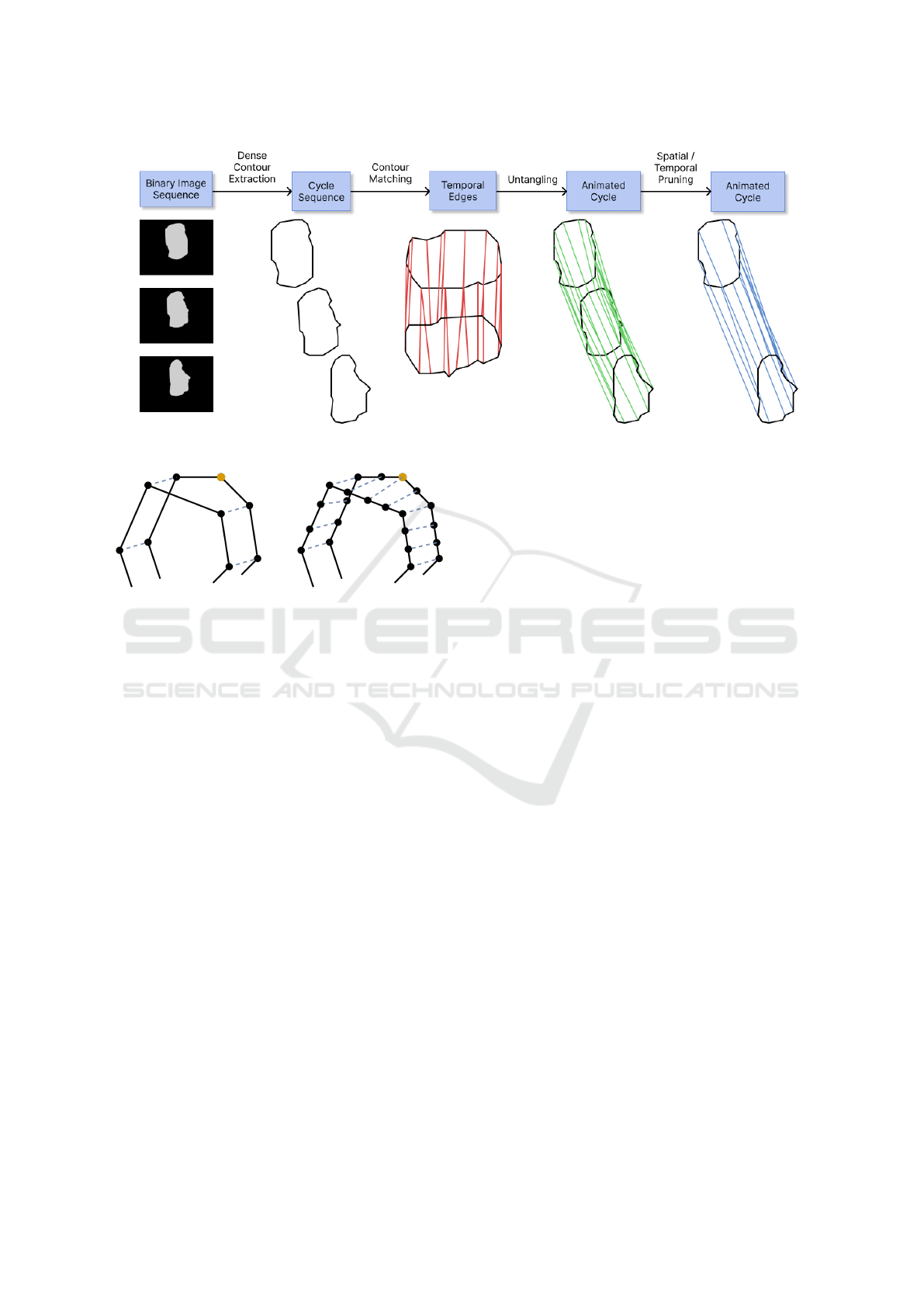
Figure 2: Overview of the Tutrace algorithm.

(a) (b)

Figure 3: Contour matching. Solid lines represent contours

and dashed lines represent matches. (a) Sparse contour. In

this case, there is no good candidate vertex to match the

highlighted vertex. (b) Dense contour. Here, ﬁnding a good

match for the each vertex becomes possible.

curve). A key cycle naturally inherits the frame num-

ber of its key edges. A sequence of key cycles with

increasing frame numbers is called a cycle sequence.

An animated vertex is a path of temporal edges. A

circular sequence of animated vertices is called an an-

imated cycle, and can be seen as an animated vector

shape.

4 DENSE CONTOUR

The ﬁrst step of our algorithm is the extraction of

dense contours. This routine will run on each image

separately, and is very similar to a single-image vec-

torization algorithm, the main difference being that

we wish to keep a dense and regular sampling of

points along the resulting shape.

4.1 Contour Extraction

For a given image, this phase begins by tracing the im-

age’s content, i.e. it generates a closed polygon curve

that follows the boundary of the content’s pixels (see

Figure 4a).

This polygon is the most densely sampled shape

we can get, however since it follows the exact bor-

der of the pixels it also contains some high-frequency

details that we would like to get rid of (staircase ef-

fect) as they do not play a part in the actual shape we

perceive.

4.2 Contour Simpliﬁcation

We add to this ﬁrst tracing step a constrained simpli-

ﬁcation step, i.e. a simpliﬁcation step that obeys the

following constraints: for any two consecutive points

p, q on the output polygon, ||p − q||

< d

max

, with

max

a parameter of the algorithm (see Figure 4b).

To perform this constrained simpliﬁcation we de-

cided to use an iterative algorithm that progressively

decimates edges on the polygon while always respect-

ing the constraint. The decimation is done by us-

ing a 2D adaptation of the edge-contraction technique

based on quadric error metric, introduced in (Garland

and Heckbert, 1997). However, we add an eligibil-

ity condition on edges: we only consider an edge for

contraction if, once contracted, it would not create a

new edge longer than d

max

This algorithm has one main weakness: it may re-

move meaningful details if they are smaller than d

max

To solve this issue, we use the geometrical interpre-

tation of the quadric error metric: it measures the

distance to the lines formed by neighboring edges.

Therefore, in order to keep small details, we add a

second constraint to mark an edge e as eligible: we

ask for its contraction error to be under a given thresh-

old err

max

GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications

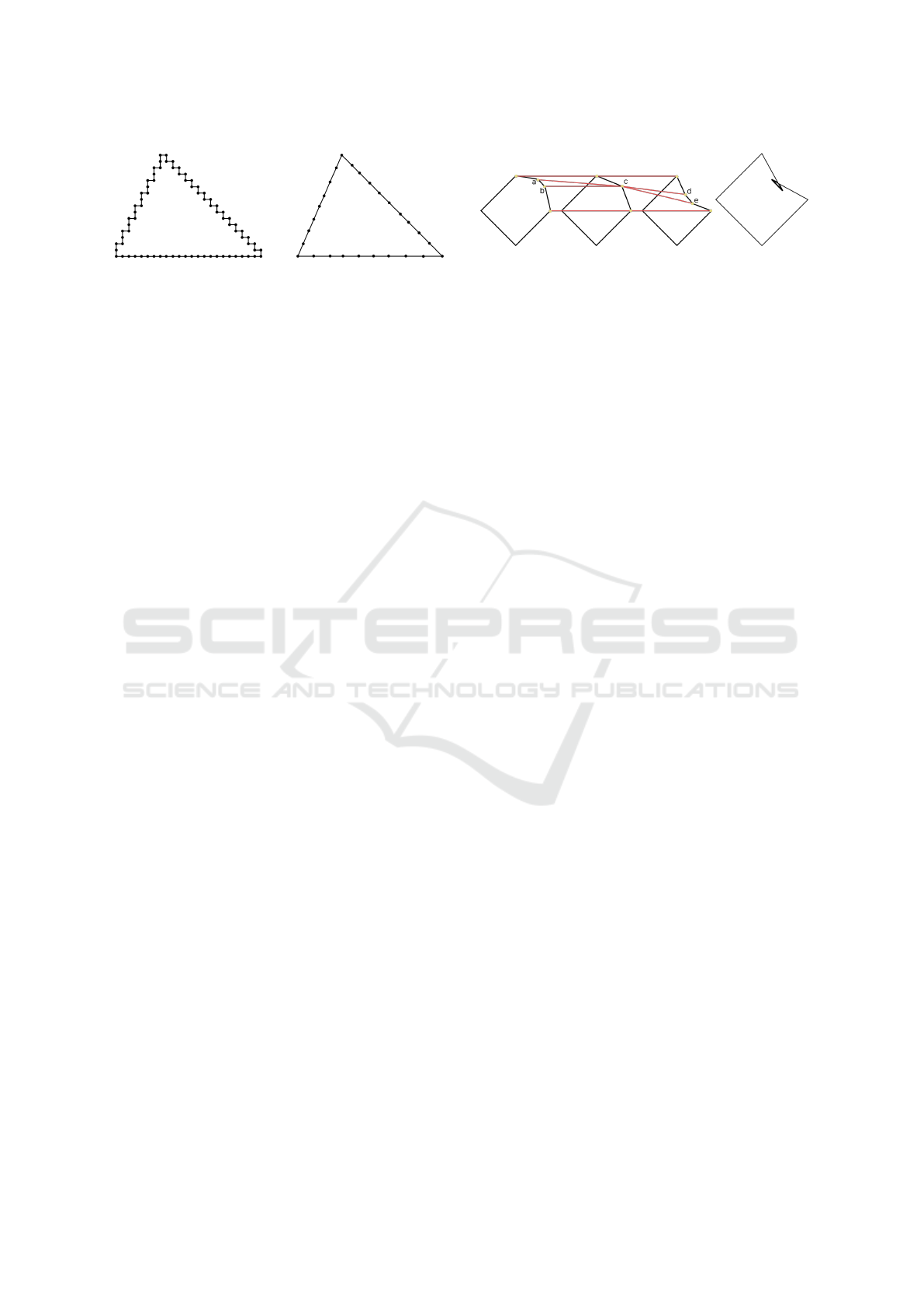
(a) (b)

Figure 4: The two substeps of the dense contour extraction

phase. (a) The border of the image content is extracted, pro-

ducing a perfectly accurate shape. (b) This shape is simpli-

ﬁed to smooth out staircase artifacts. The density constraint

imposes that all edges are smaller than d

max

5 CONTOUR MATCHING

The second step of our algorithm is the matching

of vertices between consecutive frames. Consider a

frame 0 ≤ f < F, we denote the dense contour ex-

tracted from I

as C

= {v

f ,0

, ..., v

f ,n

−1

} where each

f ,i

is a vertex of the dense contour polygon, inter-

preted as a 2D point. For 0 ≤ f < F − 1, the prob-

lem of matching C

with C

f +1

can be seen as ﬁnding

for each v

f ,i

a corresponding vertex v

f +1, j

. Note that

this matching is asymmetric, however this can be cor-

rected by also matching C

f +1

with C

: this will en-

sure that reading the sequence forward or backward

will lead to the same result.

An intuitive way to match v

f ,i

would be to ﬁnd

its nearest neighbor in C

f +1

. However this approach

lacks robustness and leads to unwanted results in

many simple cases. Since we are trying to vectorize a

coherent object moving across a sequence of images,

we can assume that its displacement from one frame

to the next one is “small”. We approximate this small

displacement by a rigid transform on the dense con-

tours. Therefore we can apply a rigid point-set regis-

tration technique to ﬁnd a rigid transform T : R

→ R

that best ﬁts C

onto C

f +1

. Once we have T , we can

match v

f ,i

with C

f +1

by ﬁnding its nearest neighbor

in T

−1

f +1

To perform the rigid point-set registration we use

the ICP algorithm (Besl and McKay, 1992), and we

denote by n

iter

the number of ICP iterations. This

method has the advantage of being fast and simple to

implement. In the case where the displacements be-

tween consecutive contours cannot be approximated

by rigid transforms, we can replace the ICP with more

generic point-set registration methods, such as Coher-

ent Point Drift (Myronenko and Song, 2010).

(a) (b)

Figure 5: In a situation like the one depicted in (a), the

untangling algorithm should favor selecting the animated

vertices a → c → d and b → c → e over a → c → e and

b → c → d. Indeed, in the second scenario the animated

vertices are crossing each other, resulting in a twist artifact

as depicted in (b).

6 UNTANGLING

The third step of our algorithm consists in untangling

the matches, i.e. extracting an animated cycle from

the Tutrace complex we have built so far.

Since the objective of this step is to only change

how the data is structured, we wish to minimize its

impact on the ﬁnal geometry, i.e. keep as many an-

imated vertices as possible, well spread over the en-

tire shape. However we cannot simply keep all the

animated vertices as some of them can “cross” each

other, as shown in Figure 5. In this section we present

an ad-hoc method for extracting animated vertices

which ensures that there will be no such artifact in

the animated cycle.

6.1 Generating Animated Vertices

One way to build animated vertices from the input

data is to compute paths of key vertices connected

with temporal edges. Each path should start at the

ﬁrst frame and end at the last frame. The correspond-

ing animated vertices thus have one key vertex per

frame.

Generating these animated vertices simply

amounts to computing all the paths linking a key

vertex at the ﬁrst frame to a key vertex at the last

frame, which can be achieved with a graph traversal

algorithm. Note that two animated vertices can

potentially share one or more key vertices.

6.2 Circular Ordering and Intervals

Having generated this set of animated vertices, the

core problem of untangling is to select a subset and

structure it in a circular sequence.

For a given frame f let’s denote by kc

the in-

put key cycle at f and (kv

f ,i

)

0≤i<N

its key vertices

indexed in circular order. In addition, for a given ani-

mated vertex av, let’s denote by av( f ) the key vertex

Tutrace: Editable Animated Vector Shape from Video

lying on av at frame f .

Now imagine we select some animated vertices

(av

)

0≤ j<N

, thus forming an animated cycle ac,

which can also be seen as a directed graph with an-

imated vertices as nodes and edges inherited from the

circular ordering. At frame f , we want the induced

subset of key vertices (av

( f ))

0≤ j<N

to respect the

circular ordering of kc

Because of the cyclic nature of the problem, we

cannot say that a key vertex is before or after another

one. However we can say that a key vertex is between

two others if it lies on the path of key edges that con-

nects them. We call key vertex interval between two

key vertices kv and kv

′

(denoted [kv, kv

′

]) the ordered

sequence of key vertices which lie between kv and kv

′

Similarly, we call animated vertex interval between

two animated vertices av and av

′

(denoted [av, av

′

])

the ordered sequence of animated vertices which lie

on the path from av to av

′

in ac. Equipped with these

new notions, we can now say that ac respects the cir-

cular ordering of kc

if (and only if) for each ani-

mated vertex interval [av, av

′

] the induced key vertex

sequence at frame f is a sub-sequence of key vertex

interval [av( f ), av

′

( f )].

6.3 Divide-and-Conquer Approach

Let’s consider a key vertex interval [a, b] and a key

vertex c ∈ [a, b]. We can measure its distance to the

interval bounds by taking the maximum between the

length of the key edge path a → ... → c and the key

edge path c → ... → b. Going further, we can deﬁne an

interval mid-point as a key vertex minimizing the dis-

tance to the bounds. This mid-point deﬁnition can be

extended to animated vertex intervals by taking an an-

imated vertex that minimizes the maximum distance

to the bounds over all frames.

Being able to extract a mid-point from an ani-

mated vertex interval allows us to split it into two

smaller “balanced” parts, and thus provides a way

to construct an animated cycle using a divide-and-

conquer approach (see Algorithm 1 for pseudo-code).

For the initialization, we select an arbitrary animated

vertex av

re f

, add it to the animated cycle ac, and we

exceptionally consider that the interval [av

re f

, av

re f

]

contains all the generated animated vertices. Then,

for each considered interval, we select a mid-point,

add it to ac in-between the interval bounds - thus nat-

urally creating the circular order of ac and respecting

the circular order of the key cycles - and recursively

continue on the two sub-intervals created. The ter-

mination condition for the recursion is met when the

interval is only constituted of its own bounds.

Data: AV : set of animated vertices

Result: ac: animated cycle

= empty circular list;

= empty FIFO structure;

re f

= arbitrary element of AV ;

insert av

re f

in ac;

append (av

re f

, av

re f

, AV ) to Q;

while Q is not empty do

start

= animated vertex;

end

= animated vertex;

= animated vertex interval;

pop 1

element of Q into

(av

start

, av

end

, I);

if I contains only av

start

and av

end

then

continue to the next iteration;

end

ﬁnd mid-point av

mid

∈ I that minimizes

the maximum distance to av

start

and

end

;

insert av

mid

in ac between av

start

and

end

;

append (av

start

, av

mid

, [av

start

, av

mid

]) to

append (av

mid

, av

end

, [av

mid

, av

end

]) to Q;

end

Algorithm 1: Pseudo-code for animated cycle extraction

from the generated animated vertices during untangling.

7 PRUNING

The fourth step of the algorithm is the simpliﬁcation

of the animated cycle generated during the untangling

step. We can perform two kinds of operations to sim-

plify an animated shape: either remove an animated

vertex or remove a keyframe (i.e. all the key vertices

at a given frame). We divide this step into two distinct

pass: a spatial pass that removes animated vertices,

and a temporal pass that removes keyframes.

7.1 Spatial Pruning

In the spatial pruning pass, we interpret the animated

cycle as a directed circular graph where the nodes are

the animated vertices. We then apply an algorithm

similar to what is done in Potrace (Selinger, 2003):

1. we assign to each edge a weight w

base

2. for each path u → ... → v in the original graph of

length at most l

max

we create a new directed edge

u → v and assign it a weight equal to w

base

plus the

maximum geometric error made by short-cutting

the path u → ... → v with the path u → v over all

frames

GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications

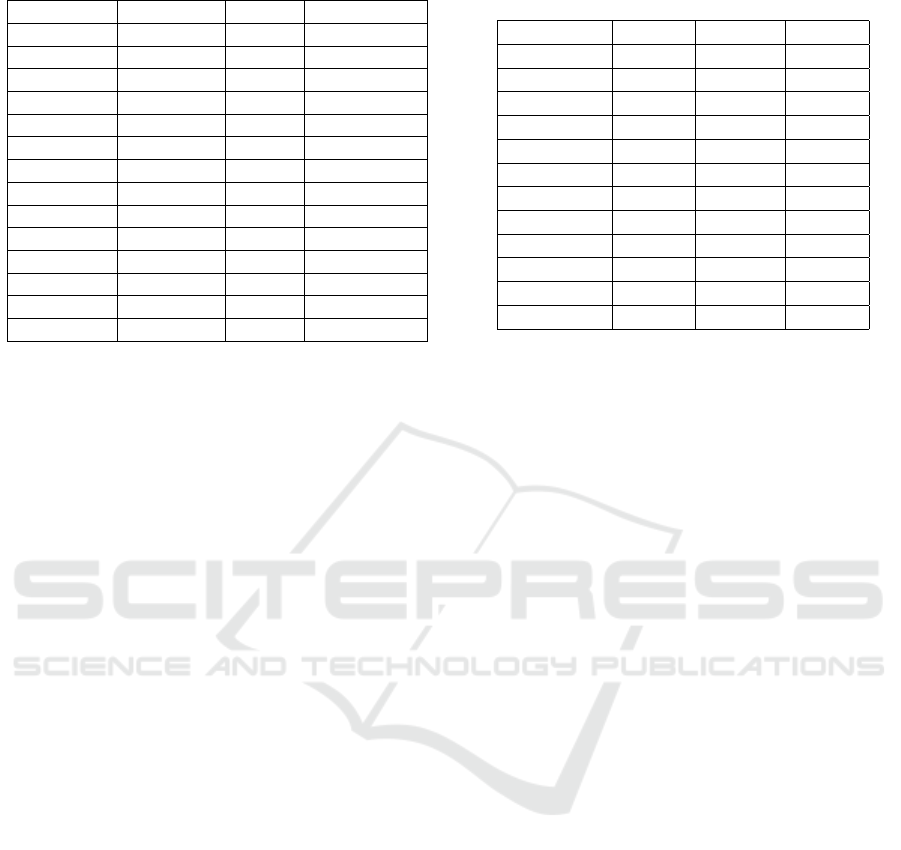
Table 1: Description of evaluation dataset.

Name Dim Frames Source

airplane 1920x1080 50 Synthetic

birdfall 259x327 30 SegTrack V2

blackswan 1920x1080 50 DAVIS 2017

cactus 720x1080 30 Synthetic

car-shadow 1920x1080 40 DAVIS 2017

house 640x480 20 Synthetic

parachute 414x352 51 SegTrack V2

paragliding 1920x1080 70 DAVIS 2017

penguin 384x212 42 SegTrack V2

rallye 1920x1080 50 DAVIS 2017

shark 1080x720 30 Synthetic

sheep 1920x1080 68 DAVIS 2017

statue 640x480 20 Synthetic

worm 480x264 244 SegTrack V2

3. we compute a circuit in this graph that minimizes

the sum of weights, which becomes the new ani-

mated shape.

The main idea behind this algorithm is that we will

shortcut the redundant vertices in areas that remain

ﬂat over the entire animation because the error will be

low.

7.2 Temporal Pruning

In the temporal pruning pass, we view the animated

cycle as a sequence of F key cycles, and we interpret

each key cycle as a vector in R

(with n the number

of animated vertices) by stacking the position of the

animated vertices at a given frame. Using this rep-

resentation we can apply a generalized version for

arbitrary dimension of the Ramer-Douglas-Peucker

line simpliﬁcation algorithm introduced in (Douglas

and Peucker, 1973). We will denote by θ

k f

the er-

ror threshold parameter in the RDP algorithm. This

technique will produce a set of keyframes to keep in

our animated shape, and we can then remove the dis-

carded ones.

The intuition here is that we will remove

keyframes in frame ranges where they can be well ap-

proximated by linear interpolation.

8 EXPERIMENTAL RESULTS

We evaluated our method on a variety of binary image

sequences. Our dataset (Vital, 2024) contains videos

coming from 3 different sources, as it allows us to

cover a wide range of input properties (see Table 1):

synthetic sequences made by rendering only the matte

layer of 3D objects, sequences coming from the Seg-

Track V2 dataset (Li et al., 2013) and sequences com-

Table 2: Rasterization error comparison. Rasterization er-

rors have been mutliplied by 10

for readability.

Name Potrace VTracer Tutrace

airplane 96 4 5

birdfall 37 4 13

blackswan 275 7 11

car-shadow 96 3 13

house 35 16 25

parachute 67 6 10

paragliding 38 0 2

penguin 81 13 22

rallye 35 1 11

shark 239 11 21

sheep 133 2 4

statue 188 9 16

ing from the DAVIS 2017 dataset (Pont-Tuset et al.,

2017).

8.1 Comparison with Frame-by-Frame

Vectorization

We compare our results to what would be obtained

by vectorizing each frame independently. The output

of such a process is not an animated vector shape but

a sequence of static vector shapes, however we can

still compare the rasterization error, i.e. the per-pixel

difference between the input images and the images

obtained by rasterizing the vector shapes.

For the comparison, we use two different vector-

ization algorithms: Potrace (Selinger, 2003) which

has been in use for years in software such as Inkscape,

and VTracer (Pun and Tsang, 2020) which is a more

recent alternative to Potrace. For Potrace, we set the

max

parameter to 0 to generate only polygonal out-

puts, and we disable the curve optimization. Simi-

larly for VTracer we set the output mode to “poly-

gon”. For Tutrace, we use the following parameters:

max

= 20, err

max

= 2, n

iter

= 20, l

max

= 5, w

base

= .5,

and θ

k f

= 3.

It is important to note that even though these tests

provide a good basis for comparison, comparing two

different structures has some limitations: for instance,

we cannot use the number of keyframes in the ani-

mated vector shape as a metric, even though it is an

important factor in the ﬁnal quality.

The evaluation results are displayed in Table 2,

which shows that our method performs quite well

in terms of rasterization error: the results are not as

good as VTracer, but this was expected since frame-

by-frame vectorization has no temporal constraint to

satisfy, however we still out-perform Potrace on every

sequence.

The number of animated vertices generated by

Tutrace: Editable Animated Vector Shape from Video

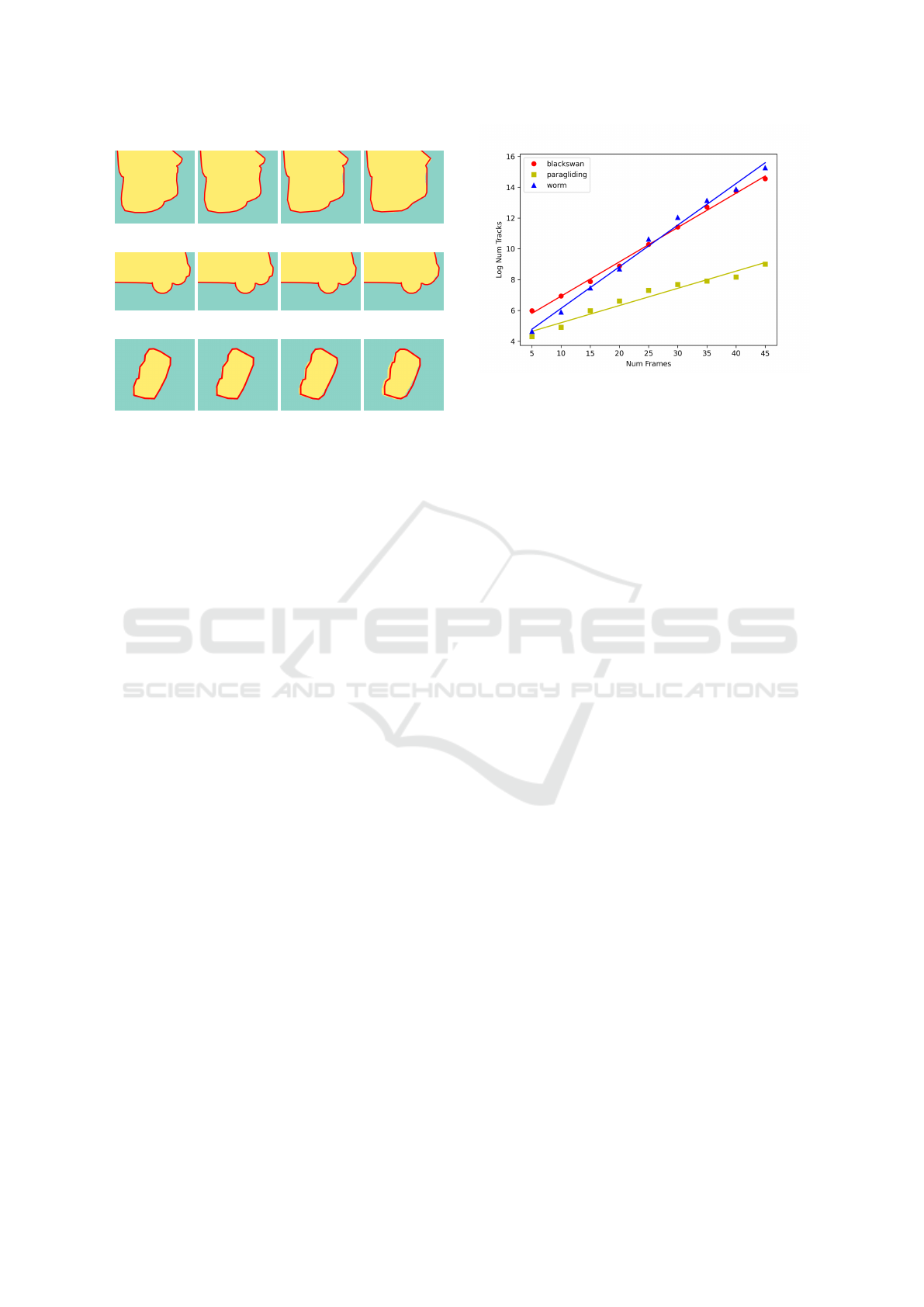
(a) 73 / 10 (b) 73 / 6 (c) 44 / 5 (d) 28 / 4

(e) 161 / 19 (f) 161 / 11 (g) 73 / 13 (h) 73 / 9

(i) 35 / 23 (j) 20 / 12 (k) 20 / 9 (l) 20 / 4

Figure 6: Varying pruning parameters on the “statue”, “car-

shadow” and “parachute” sequences to generate simpler

outputs. Figures are annotated like so: number of animated

vertices / number of keyframes.

our method is comparable to the average number of

vertices generated by Potrace but generally higher

than VTracer. Once again this was expected since

our method has to account for changing geometry

throughout the animation. However if we consider

the output complexity, i.e. the total number of control

points used to deﬁne the shapes, we remark that Tu-

trace is more compact than Potrace on all sequences,

and more compact than VTracer on all sequences ex-

cept 3, namely “blackswan”, “paragliding” and “ral-

lye”.

This experimental comparison shows that, in addi-

tion to generating a very speciﬁc and constraining ge-

ometric structure, Tutrace offers a good compromise

between output quality and complexity.

8.2 Fidelity vs. Simplicity Trade off

The ﬁnal pruning step of our method offers the pos-

sibility to control the complexity of the generated an-

imated shape. The less complex an animated shape

is, the larger the rasterization error. However in some

applications it can be beneﬁcial to be able to gener-

ate coarser shapes, as they are easier to work with.

As shown in Figure 6, by manipulating the pruning

parameters one can obtain various levels of simpliﬁ-

cation and thus easily generate a shape with the ap-

propriate complexity.

8.3 Limitations and Failure Cases

As can be seen in Table 2, two sequences from the

dataset were not present in the comparison: cactus

Figure 7: For the “blackswan”, “paragliding” and “worm”

sequences, we restricted the sequence to a given number of

frames and computed the number of animated vertices to

generate during the untangling step. We display the loga-

rithm of that number, along with a linear approximation to

highlight its exponential growth.

and worm. As explained in more details below, these

sequences reached the limits of what can currently be

achieved with Tutrace.

When working on the worm sequence (which is

particularly long), we have found that the impact of

the number of frames is critical for the performance

of the algorithm. Indeed, since the matching step does

not always produce 1-1 correspondences between key

vertices in adjacent frames, some animated vertices

generated at the beginning of the untangling step will

“split” at each new frame, leading to a combinato-

rial explosion. We measured the number of animated

vertices generated until a given frame for several se-

quences in our dataset. The results are shown in Fig-

ure 7. As we can see, the growth can be well approx-

imated by an exponential growth, with a coefﬁcient

that varies from one sequence to another.

As for the cactus sequence, it is part of the syn-

thetic sequences made speciﬁcally for these experi-

ments: it consists of a static 3D cactus model around

which the camera is turning. As can be seen in Fig-

ure 8, the particular shape of the cactus will generate

many occlusions, with branches appearing, disappear-

ing and reappearing. Even though the Tutrace algo-

rithm was designed to handle occlusions - such as the

nose on the statue sequence shown in Figure 1 - this

particular case is too complex to untangle for our sys-

tem: when a side branch merges into the central trunk,

the empty region between that branch and the trunk

shrinks and disappears quickly, however the particu-

lar elongated shape of that region makes it difﬁcult for

vertices to get matched properly as they will end up

matching against the outer side of the branch instead,

thus creating erroneous animated vertices. Note that

in practice, rotoscoping artists would not work on the

GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications

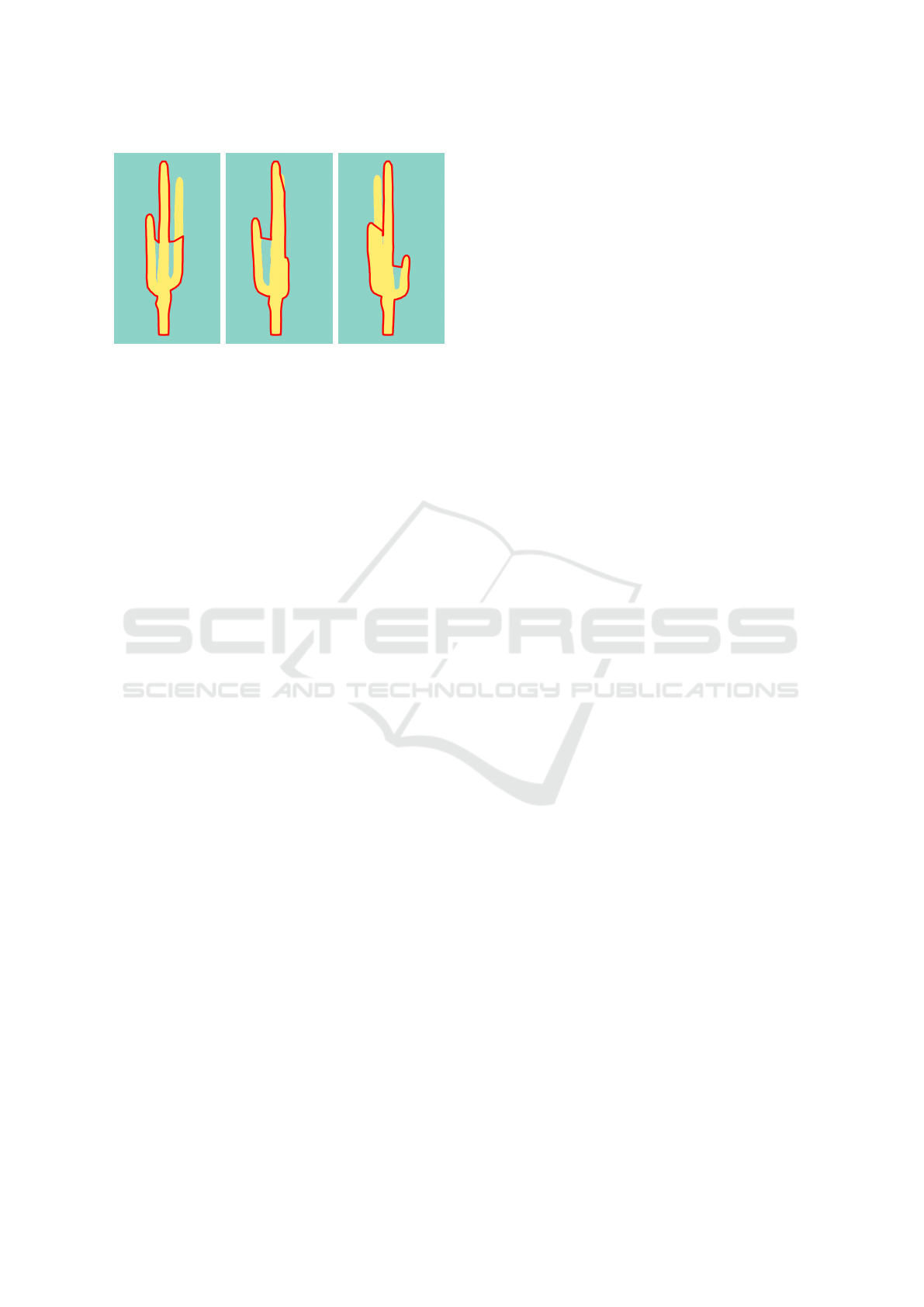
Figure 8: A failure case with the “cactus” sequence.

whole cactus shape at once: they would work on each

branch separately to tackle this occlusion problem.

9 FUTURE WORK

As mentioned previously, an important limitation of

our method is performance, mostly due to the num-

ber of animated vertices that we generate during the

untangling step which can increase quickly with the

number of frames. We see two main ways to over-

come this issue in the future: modify the untangling

algorithm to generate only the necessary animated

vertices and/or cut down the input video into smaller

chunks which will be processed independently and

then merged.

We could also try to reinterpret the untangling

problem as a multi-graph matching task, where the

graphs to match would simply be the key cycles. In-

deed, many advancements have been made in recent

years on this topic (Yan et al., 2016), which would al-

low us to solve the untangling step much faster and

without requiring an ad-hoc method. However such

algorithms are designed to extract collections of cor-

responding nodes in the input graphs, which can be

interpreted in our setting as animated vertices, but not

the structure relating these collections to each other,

i.e. the circular structure of an animated cycle in our

case. Further work would therefore be required to see

if we could extend a multi-graph matching method to

ﬁt our purposes.

Another important topic to investigate is smooth-

ing. Indeed, the shape we currently generate only

contains straight line segments, whereas most image

vectorization methods produce smooth shapes, using

for instance B

ezier segments. Smoothing an animated

vector shape is not a trivial problem, however it would

also have another positive side effect: fewer vertices

would be required to accurately vectorize curved ar-

eas in the input images. (Shao and Zhou, 1996) pro-

poses a curve ﬁtting algorithm that could potentially

ﬁt our purposes, if we could properly adapt the iden-

tiﬁcation of critical points to animated vertices.

It can also be noted that in our pipeline the images

are only fed into the ﬁrst step, and never used again.

Re-using the input images later in the process could

allow us to improve the quality of the animated shape

by ﬁtting its geometry to the input data. Some meth-

ods for optimizing the rasterization error of a vector

shape have been proposed, such as (Li et al., 2020),

which could be extended to include the temporal di-

mension of video vectorization.

Handling multiple objects and occlusions could

also have a major impact, as these types of situations

arise frequently in rotoscopy, for instance when sev-

eral characters interact in the scene. Building on the

work of (Zhang et al., 2023) could be an interesting

starting point as they provide a framework for solving

both object tracking and layer decomposition.

10 CONCLUSION

We have presented a video vectorization algorithm

that works on a binarized input and generates an an-

imated vector shape. The core of our method lies in

the untangling step, which extracts animated vertices

from static shapes and correspondences between their

vertices. We showed that the output quality is com-

parable to frame-by-frame vectorization, with the ad-

vantage of being directly ready to import and edit in

a DCC. Additionally, the user can control the com-

plexity of the animated shape, thus allowing to create

simpler shapes. We hope that this method, with the

ﬂexible multi-step approach it uses, will serve as a

basis for further development in this area, mostly tar-

geting use cases in rotoscopy for VFX.

ACKNOWLEDGEMENTS

Many thanks to Vincent Demoulin for his useful com-

ments and feedback on both Tutrace and this article.

We also thank the anonymous reviewers for helping

us improve this paper. This work was partially sup-

ported by Technicolor Group.

REFERENCES

Besl, P. J. and McKay, N. D. (1992). Method for regis-

tration of 3-d shapes. In Sensor fusion IV: control

paradigms and data structures, volume 1611, pages

586–606. Spie.

Tutrace: Editable Animated Vector Shape from Video

Dalstein, B., Ronfard, R., and Van De Panne, M. (2015).

Vector graphics animation with time-varying topol-

ogy. ACM Transactions on Graphics (TOG), 34(4):1–

12.

Douglas, D. H. and Peucker, T. K. (1973). Algorithms for

the reduction of the number of points required to rep-

resent a digitized line or its caricature. Cartographica:

the international journal for geographic information

and geovisualization, 10(2):112–122.

Favreau, J.-D., Lafarge, F., and Bousseau, A. (2016). Fi-

delity vs. simplicity: a global approach to line drawing

vectorization. ACM Transactions on Graphics (TOG),

35(4):1–10.

Garland, M. and Heckbert, P. S. (1997). Surface simpli-

ﬁcation using quadric error metrics. In Proceedings

of the 24th annual conference on Computer graphics

and interactive techniques, pages 209–216.

Kopf, J. and Lischinski, D. (2011). Depixelizing pixel art.

In ACM SIGGRAPH 2011 papers, pages 1–8.

Li, F., Kim, T., Humayun, A., Tsai, D., and Rehg, J. M.

(2013). Video segmentation by tracking many ﬁgure-

ground segments. In Proceedings of the IEEE Interna-

tional Conference on Computer Vision, pages 2192–

2199.

Li, T.-M., Luk

c, M., Gharbi, M., and Ragan-Kelley, J.

(2020). Differentiable vector graphics rasterization for

editing and learning. ACM Transactions on Graphics

(TOG), 39(6):1–15.

Li, Y., Wang, C., Hong, J., Zhu, J., Guo, J., Wang, J., Guo,

Y., and Wang, W. (2021). Video vectorization via

bipartite diffusion curves propagation and optimiza-

tion. IEEE Transactions on Visualization and Com-

puter Graphics, 28(9):3265–3276.

Myronenko, A. and Song, X. (2010). Point set registra-

tion: Coherent point drift. IEEE Transactions on Pat-

tern Analysis and Machine Intelligence, 32(12):2262–

2275.

Orzan, A., Bousseau, A., Winnem

oller, H., Barla, P., Thol-

lot, J., and Salesin, D. (2008). Diffusion curves: a vec-

tor representation for smooth-shaded images. ACM

Transactions on Graphics (TOG), 27(3):1–8.

Pont-Tuset, J., Perazzi, F., Caelles, S., Arbel

aez, P.,

Sorkine-Hornung, A., and Van Gool, L. (2017). The

2017 davis challenge on video object segmentation.

arXiv preprint arXiv:1704.00675.

Pun, S. and Tsang, C. (2020). Vtracer. https://www.

visioncortex.org/vtracer-docs.

Selinger, P. (2003). Potrace: a polygon-based tracing algo-

rithm.

Shao, L. and Zhou, H. (1996). Curve ﬁtting with bezier

cubics. Graphical models and image processing,

58(3):223–232.

Sun, J., Liang, L., Wen, F., and Shum, H.-Y. (2007). Image

vectorization using optimized gradient meshes. ACM

Transactions on Graphics (TOG), 26(3):11–es.

Vital, L. (2024). Tutrace evaluation videos. {https://doi.org/

10.5281/zenodo.14510189}.

Wang, C., Zhu, J., Guo, Y., and Wang, W. (2017). Video

vectorization via tetrahedral remeshing. IEEE Trans-

actions on Image Processing, 26(4):1833–1844.

Xia, T., Liao, B., and Yu, Y. (2009). Patch-based im-

age vectorization with automatic curvilinear feature

alignment. ACM Transactions on Graphics (TOG),

28(5):1–10.

Yan, J., Yin, X.-C., Lin, W., Deng, C., Zha, H., and Yang,

X. (2016). A short survey of recent advances in graph

matching. In Proceedings of the 2016 ACM on Inter-

national Conference on Multimedia Retrieval, pages

167–174.

Yao, R., Lin, G., Xia, S., Zhao, J., and Zhou, Y. (2020).

Video object segmentation and tracking: A survey.

ACM Transactions on Intelligent Systems and Tech-

nology (TIST), 11(4):1–47.

Yu, Y., Wang, C., Fu, Q., Kou, R., Huang, F., Yang, B.,

Yang, T., and Gao, M. (2023). Techniques and chal-

lenges of image segmentation: A review. Electronics,

12(5):1199.

Zhang, S., Ma, J., Wu, J., Ritchie, D., and Agrawala, M.

(2023). Editing motion graphics video via motion vec-

torization and transformation. ACM Transactions on

Graphics (TOG), 42(6):1–13.

Zhang, S.-H., Chen, T., Zhang, Y.-F., Hu, S.-M., and Mar-

tin, R. R. (2009). Vectorizing cartoon animations.

IEEE Transactions on Visualization and Computer

Graphics, 15(4):618–629.

GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications