Ground Awareness in Deep Learning for Large Outdoor Point Cloud

Segmentation

Kevin Qiu

1 a

, Dimitri Bulatov

1 b

and Dorota Iwaszczuk

2 c

Fraunhofer IOSB Ettlingen, Gutleuthausstrasse 1, 76275 Ettlingen, Germany

Technical University of Darmstadt, Civil and Environmental Engineering Sciences, Darmstadt, Germany

Keywords:

Remote Sensing, RandLA-Net, DTM.

Abstract:

This paper presents an analysis of utilizing elevation data to aid outdoor point cloud semantic segmentation

through existing machine-learning networks in remote sensing, speciﬁcally in urban, built-up areas. In dense

outdoor point clouds, the receptive ﬁeld of a machine learning model may be too small to accurately determine

the surroundings and context of a point. By computing Digital Terrain Models (DTMs) from the point clouds,

we extract the relative elevation feature, which is the vertical distance from the terrain to a point. RandLA-Net

is employed for efﬁcient semantic segmentation of large-scale point clouds. We assess its performance across

three diverse outdoor datasets captured with varying sensor technologies and sensor locations. Integration of

relative elevation data leads to consistent performance improvements across all three datasets, most notably in

the Hessigheim dataset, with an increase of 3.7 percentage points in average F1 score from 72.35% to 76.01%,

by establishing long-range dependencies between ground and objects. We also explore additional local fea-

tures such as planarity, normal vectors, and 2D features, but their efﬁcacy varied based on the characteristics

of the point cloud. Ultimately, this study underscores the important role of the non-local relative elevation

feature for semantic segmentation of point clouds in remote sensing applications.

1 INTRODUCTION

Semantic segmentation of outdoor point clouds, cap-

tured by airborne or terrestrial sensor platforms, is

an important task with use cases in urban planning,

mapping, digital twin creation, and vegetation analy-

sis. They also have applications in vehicle navigation,

infrastructure management and augmented or virtual

reality, where a precise semantic representation of

the real environment is required. Point clouds, as

opposed to 2D orthophotos or 2.5D representations,

enhance spatial understanding and allow delineation

of vertical structures. Outdoor point clouds usu-

ally cover large areas with a considerable number of

points from either LiDAR (Light Detection and Rang-

ing) sensors or computed through photogrammetry.

Therefore, segmentation methods need to be fast and

efﬁcient. Semantic segmentation models based on

deep learning (DL) became widely used with the ad-

vancement of computer processing power and sophis-

https://orcid.org/0000-0003-1512-4260

https://orcid.org/0000-0002-0560-2591

https://orcid.org/0000-0002-5969-8533

ticated architectures, such as PointNet++ (Qi et al.,

2017b), KPConv (Thomas et al., 2019), or RandLA-

Net (Hu et al., 2020). However, these methods may

struggle when applied to very large and dense point

clouds. For example, differentiating a large horizon-

tal (concrete) roof from an asphalt road may require

a large receptive ﬁeld and thus an exaggerated depth

and memory footprint of the neural network, result-

ing in a high computational cost. In point cloud deep

learning, the receptive ﬁeld is characterized by the

number of points rather than metric distances. For

a point cloud with very high point density, this means

that the receptive ﬁeld may only encompass points

within a relatively small spatial area.

One solution could lie in the integration of addi-

tional features into DL pipelines as surrogates for re-

liably large receptive ﬁelds. Fortunately, remote sens-

ing offers a few tools providing long-range context

about the vertical dimension of the environment. In

particular, elevation over ground is the difference be-

tween the vertical distance of a point with its clos-

est terrain point and is considered one of the most

crucial features for class differentiation. Since this

closest terrain point can still be arbitrarily far away

Qiu, K., Bulatov, D. and Iwaszczuk, D.

Ground Awareness in Deep Learning for Large Outdoor Point Cloud Segmentation.

DOI: 10.5220/0013101200003912

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 20th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2025) - Volume 1: GRAPP, HUCAPP

and IVAPP, pages 29-38

ISBN: 978-989-758-728-3; ISSN: 2184-4321

for large off-terrain objects, a so-called Digital Ter-

rain Model (DTM) is required, which involves eval-

uating points over large areas, leading to larger re-

ceptive ﬁelds. There are good conventional methods

for the computation of DTM, without the need for

any labeled points (Bulatov et al., 2014; Piltz et al.,

2016) while our segmantic segmentation workﬂow is,

of course, agnostic to the method of DTM derivation.

Further local features popular in point cloud analy-

sis, like planarity or point densities and distributions

along the z-axis, can also be derived. In DL-based im-

age processing, it has been shown that adding sensi-

ble hand-crafted features improves the overall perfor-

mance (Audebert et al., 2018). One goal of the article

is to ﬁnd out which features are useful in the context

of point cloud segmentation.

We argue that RandLA-Net is an efﬁcient network

with practical relevance in remote sensing, which can

also be easily extended with (hand-crafted) point fea-

tures. Our contributions are as follows: 1) We ex-

tend this network with the relative elevation h

of a

point as well as other point-based 2D and 3D local

features, whereby to calculate h

for airborne point

clouds, we rely on a state-of-the-art point ﬁltering

method (Bulatov et al., 2014). 2) We demonstrate, on

three diverse datasets differing in sensor location, sen-

sor type, landscape type, etc., a consistent improve-

ment of semantic segmentation performance with the

addition of h

; in contrast, the additional value of the

local features varies depending on the dataset.

2 RELATED WORKS

2.1 Point Cloud Semantic Segmentation

Using DL

Convolutional neural networks were extremely suc-

cessful for the segmentation of 2D images, the reason

why some of the ﬁrst approaches for 3D data seman-

tic segmentation were projection-based, like Snap-

Net (Boulch et al., 2018). Also inspired by 2D neu-

ral networks, 3D convolutions discretize the point

cloud into voxels and apply 3D kernels for convolu-

tion (Tchapmi et al., 2017).

The ﬁrst network to directly operate on the points

was the pioneering framework called PointNet (Qi

et al., 2017a), using only shared Multi-Layer Percep-

trons (MLPs) to process the point features. Its succes-

sor, PointNet++ (Qi et al., 2017b), learns hierarchi-

cal local features through multiple layers and down-

sampling using Farthest Point Sampling (FPS). Point-

NeXt (Qian et al., 2022) then improves upon Point-

Net++ with a better training strategy. Other meth-

ods like KPConv (Thomas et al., 2019) use sophis-

ticated learnable kernel-point convolutions. A down-

side of all above-mentioned methods is the large pro-

cessing cost. These networks can either only handle

a small number of points at once due to high mem-

ory use or are computationally expensive, for exam-

ple due to their choice of point sampling method. The

fastest sampling method is random sampling, which

RandLA-Net (Hu et al., 2020) employs. With less

than a tenth of the parameters as KPConv, for exam-

ple, it is optimized for high point throughput and is

therefore well suited for remote sensing applications.

Even though RandLA-Net was published in 2019, no

network surpasses it in both speed and performance

on the S3DIS 6-fold segmentation task as of the re-

cent publication of PointNeXt, as shown in Table 1

in (Qian et al., 2022).

Most recently, transformer-based networks like

PCT (Guo et al., 2021) have become popular in the

research community. The basic transformer archi-

tecture calculates global attention between all input

tokens, which is immensely computationally expen-

sive. Networks like Point Transformer (Zhao et al.,

2021) improve on this by only calculating attention

between neighboring tokens, similar to SWIN Trans-

former (Liu et al., 2021) in the image domain. The

self-attention mechanisms of transformers open the

way to self-supervised methods, where the model

learns inherent features through pretext tasks from

the training data without labels. For example, Point-

MAE (Pang et al., 2022) and Point-M2AE (Zhang

et al., 2022) use point cloud reconstruction as the pre-

text task. Unfortunately, all transformer methods have

a high computational demand and do not yet have a

practical relevance in large outdoor point cloud pro-

cessing.

2.2 Elevation Data and Local Features

in Semantic Segmentation

Digital Elevation Models (DEMs) have long been

used in object detection. In the age of DL in the

2D image domain, the effect of different fusion tech-

niques of RGB and NDSM (Normalized Digital Sur-

face Model, essentially h

in 2D) in the semantic

segmentation of orthophotos was explored in (Qiu

et al., 2022), where the addition of NDSM and IR

information improved the performance of the U-Net

and DeepLabV3+ model; (Audebert et al., 2018)

come to a similar conclusion. In the 3D domain,

many experiments with hand-crafted feature sets have

been performed. Examples are covariance-based fea-

tures (Maas and Vosselman, 1999), fast point feature

GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications

histograms (Rusu et al., 2009), or signatures of a his-

togram of orientations (Tombari et al., 2010). These

features can be subject to a conventional classiﬁer,

such as Random Forest (Breiman, 2001), whereby

e.g., (Mongus et al., 2013) have not even learned

any thresholds, but have used 3D morphological pro-

ﬁles for detecting buildings in LiDAR point clouds.

With DL-based approaches, hand-crafted features re-

lying on local neighborhoods have been superﬂuous,

and therefore features exploiting non-local interac-

tions between points gained popularity. For exam-

ple, (Niemeyer et al., 2014) test different features, and

they ﬁnd that the height above ground is the most

important feature in a Random Forest-based work-

ﬂow, where the neighborhood features of a point

were also considered. However, the receptive ﬁeld

in a Random Forest approach is typically smaller

than in DL, where network depth signiﬁcantly in-

creases the receptive ﬁeld. Furthermore, (Wu et al.,

2019) employ a multi-section plane ﬁtting approach

to roughly extract ground points to assist segmenta-

tion of objects on the ground, whereby ground ﬁl-

tering has been accomplished implicitly in a weakly-

supervised way, such that ground-aware features were

utilized with a suitable attention module. The au-

thors of (Yousefhussien et al., 2018) developed a

network based on PointNet that consumes terrain-

normalized points along with spectral information.

In (Jiang et al., 2022), the ground is detected using a

point-based FCN, and a ground aware attention mod-

ule was added to the segmentation model. In (Liu

et al., 2023), RandLA-Net is trained with additional

remote sensing features. On a LiDAR dataset col-

ored with RGB information, the addition of a sur-

face normal feature brings a slight improvement in

overall mIoU (mean Intersection over Union). The

authors of (Mitschke et al., 2022) use RandLA-Net

in a hyperspectral urban dataset, where the spectral

bands are reduced to an input dimension of 64 us-

ing PCA. Due to its efﬁcient handling of large point

clouds, RandLA-Net is popular in remote sensing

(Chen et al., 2022; Grilli et al., 2023; Mei et al.,

2024).

3 METHODOLOGY

3.1 Preliminaries: RandLA-Net

According to (Qian et al., 2022), RandLA-Net

outperforms competing procedures, such as KP-

Conv (Thomas et al., 2019), PointNet++ (Qi et al.,

2017b), PointNeXt (Qian et al., 2022), its successor,

and Point Transformer (Guo et al., 2021) regarding

the trade-off between accuracy, efﬁciency, and mem-

ory requirements. Even the most recently published

PTv3 (Wu et al., 2024) has over 46M parameters, re-

quiring high-end GPUs while RandLA-Net with its

1.3M parameters is able to run on a single Nvidia

V100 GPU with only 16 GB of memory, which is our

setup. Since our point clouds are large and processing

needs to be fast and efﬁcient, RandLA-Net is a sensi-

ble choice as the network for this paper with practical

relevance.

While we refer to (Hu et al., 2020) for an in-depth

understanding of the network architecture, we provide

here the most necessary details. RandLA-Net uses a

U-Net like structure consisting of an encoder and de-

coder, four layers each, with skip connections. In the

encoder, the number of points is sampled down and

the feature dimension of each point is increased to 512

at the ﬁnal encoder layer. In the decoder, the num-

ber of points is increased back to the original point

cloud while the feature dimension is reduced to the

original eight, but with much higher semantic infor-

mation. Three fully connected layers, a dropout layer

and a softmax follow, resulting in class probabilities

for each point. The name RandLA-Net originates

from the use of Random sampling as the downsam-

pling method to discard 75% of the points after each

layer, reducing the input point size by a factor of 256

at the end of the encoder. Besides, in each encoder

layer, a so-called Local feature Aggregation module

encodes the relative positions and features of neigh-

boring points of each point using only computation-

ally efﬁcient MLPs.

This network is able to process point features ad-

ditional to the x, y and z coordinates, like RGB values,

or those particular features described in the next sec-

tion. The features are ﬁrst scaled to a dimension size

of eight using a fully connected layer and then passed

to the encoder, so the additional features barely affect

the computational complexity of the network. The

training procedure follows the original implementa-

tion with ﬁve layers, an input size of 40,000 points, a

learning rate of 1e-3 and data augmentation. We use a

PyTorch implementation by Idisia Robotics

, whereas

the original authors use TensorFlow.

3.2 Relative Elevation and Local

Features

In this section, we describe the additional point fea-

tures that are added to RandLA-Net to aid the seman-

tic segmentation task. We compute the relative ele-

vation h

and other local features that are popular in

https://github.com/idsia-robotics/

RandLA-Net-pytorch

Ground Awareness in Deep Learning for Large Outdoor Point Cloud Segmentation

traditional point cloud processing and remote sensing

methods.

For h

, we ﬁrst need to derive the Digital Sur-

face Model (DSM) and DTM. The DSM is calculated

by sampling the 3D points into a rectangular, equal-

spaced 2D grid of a suitable resolution. Each grid cell,

or pixel p, therefore deﬁnes a neighborhood U (p) of

3D points. The height value for the DSM of each pixel

is determined as the mean z-value of the at most n = 4

highest points within U. This is to avoid random se-

lection of height values at vertical surfaces, like walls,

and to reduce noise. Because U (p) may be empty, in-

painting is done using the heat equation.

The derivation of DTMs is challenging for noisy

point clouds with different types of objects. There are

nowadays efﬁcient DL-based approaches allowing to

deal with difﬁcult terrains (Gevaert et al., 2018), how-

ever, they usually need some reference data, which

was not available in our case. Thus, we apply a two-

step procedure of (Bulatov et al., 2014) to the DSM,

which we brieﬂy describe in what follows. First,

we identify ground points by considering the circular

neighborhood and applying a minimum ﬁlter. The ﬁl-

ter size should have an order of magnitude that corre-

sponds to the size of the largest off-terrain region, for

example, the largest building, to ensure that at least

one ground point is within the ﬁlter. If it is too small,

points of a building can be spuriously included into

the list of ground points, and if it is too large, smaller

hills and other elevated regions of the DTM may get

lost. Here, some too-large buildings may be interac-

tively masked out. In spite of this, this approach may

have problems in densely built-up regions and also

when there is a high percentage of outliers in the ele-

vation map. As a consequence, the functional that ap-

proximates the ground points should be robust against

outliers in the data. We chose the 2.5D cubic spline

surface computed by minimization of a functional as

in (Bulatov and Lavery, 2010) in the L

-norm:

L(z) = (1 − λ)

∑

m=1

z(x

, y

) − z

+λ

x,y

(

+ 2

)dxdy+

∑

nodes

(

(1)

where {(x

, y

, z

)}

m=1

are the coordinates of the

ground points, z = z(x, y) is the function value of the

point (x, y) for a Sibson-element of a cubic spline,

λ ≈ 0.7 is a data ﬁdelity parameter, and ε is a small

positive scalar, supposed to guarantee numerical sta-

bility. The DTM value for each pixel p is given by the

spline parameters. The difference between the z coor-

dinate of a point and the DTM of the corresponding

pixel yields its relative elevation h

Table 1: Description of the point-wise input features for

RandLA-Net that are utilized in this paper. Abbreviations:

NNs = Nearest neighbors, NV = Normal Vector, Feat. =

Feature, ?D = Dimensionality.

Feat. Description ?D

color RGB information 3D

Rel. height above the terrain 3D

Planarity calculated using cova-

riance matrix of 10 NNs

Absolute value of NV

computed over 100 NNs

σ(z) Variance of the points in U 2D

ν Number of points in U 2D

Using the same neighborhood U, the number of

points per pixel ν and the variance of their elevations

σ(z) are determined. These local features are calcu-

lated in the 2D plane and assigned to every point in

Planarity η and normals n

are derived directly

from the point cloud. From K nearest neighbors of ev-

ery point, we compute the structure tensor. Its eigen-

values λ

, λ

, sorted in descending order, and the

corresponding eigenvectors v

, v

are used to cal-

culate

η =

− λ

, n

= (v

)

, (2)

as well as a few other measures (omnivariance, linear-

ity, etc.) mentioned in the implementation of (Wein-

mann et al., 2015). We chose η and n

in (2) because

planarity turned out to be the most distinctive mea-

sure in many publications (Weinmann et al., 2017),

among others, while the normal vector direction is

not directly coupled to the eigenvalues. Note that

we decided to make this feature invariant with re-

spect to rotations around the xy-plane and modulo

π around z-axis. All 3D features are calculated on

the full point clouds without any downsampling such

as grid sampling. Due to the extreme irregularity of

the point cloud in the terrestrial Toronto3D dataset

(see next section), especially in regions further away

from the sensor path, we decided not to use our two-

step method for DTM computation. Instead, a sim-

ple RANSAC algorithm was used to ﬁnd the ground

plane of each of the four tiles. The resulting elevation

data is not as accurate as in the other datasets, since

the ground is not perfectly ﬂat.

Figure 1 shows the 2D features ν and σ(z) as well

as the steps needed to calculate the relative elevation

information on a tile of the Swiss3DCities dataset.

The number-of-points feature in Fig. 1b, for example,

has high values at building walls and tall vegetation,

where many points are stacked in the z-direction. Ta-

ble 1 shows all features that are used in this paper to

aid semantic segmentation.

GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications

(a) Orthoprojection (b) ν (c) σ(z)

(d) DSM (e) DTM (f) Normalized DSM

Figure 1: View of the orthoprojection, DSM, DTM, NDSM, and 2D features (number of points ν and variance of the points

σ(z) in a “pixel” of an 2D grid) of the ﬁfth Davos tile of the Swiss2DCities dataset. The Normalized DSM, or NDSM, is

two-dimensional and calculated by subtracting the DTM from the DSM.

4 DATASETS

A diverse selection of datasets, listed in Table 2,

were chosen for comprehensive analysis. Different

capturing techniques, e.g. LiDAR vs. Photogramme-

try, and sensor location, e.g. aerial or terrestrial, yield

very different point conﬁgurations.

Swiss3DCities (Can et al., 2021) is an UAV-based

dataset, covering a total area of 2.7 km

from three

different Swiss cities with a ground sampling dis-

tance (GSD) of 1.28 cm. The high-resolution point

clouds were derived photogrammetrically and labeled

into ﬁve classes. The authors emphasize uniform den-

sity and completeness, including on vertical surfaces,

through oblique captures. We use the “medium” den-

sity point clouds and only the ﬁve tiles from the city of

Davos to speed up the training time. For validation,

we use the ﬁfth Davos tile, which consists of about

12.5M points.

The Hessigheim dataset (K

olle et al., 2021) is an

airborne RGB LiDAR dataset of the city Hessigheim

in Germany, with a GSD of 2 cm to 3 cm. The point

density is about 800 points per square meter, but is

quite heterogeneous along the vertical dimension. We

chose the most popular March 2018 capture and cal-

culated the local features using the same parameters

as in Swiss3DCities. The dataset consists of a train,

validation, and test set, but the labels for the latter are

not publicly available, requiring submission for eval-

uation of the approximately 52M points.

The Toronto3D dataset (Tan et al., 2020) is also

captured using LiDAR. However, the sensor was

mounted on a driving vehicle, resulting in large den-

sity variations due to vastly different distances from

the car to the scene. The LiDAR and RGB camera

scans along a 1 km stretch of road are merged, re-

sulting in even more density variation due to varying

speed of the vehicle. The authors deliberately kept all

points of the entire approximately 100 m scan radius

to mimic real life point clouds. The dataset is divided

into four tiles, with the second tile used as validation,

as was instructed by (Tan et al., 2020).

Ground Awareness in Deep Learning for Large Outdoor Point Cloud Segmentation

Table 2: Comparison of the three outdoor point cloud datasets used in this paper.

Dataset Platform Sensor #Points Classes Year

Swiss3DCities Air- Photogram-

67.7M 5 2020

Davos borne metric

Hessigheim Air- Riegl VUX-1LR

125.7M 11 2021

March 2018 borne LiDAR

Toronto3D Vehicle Teledyne Optech

78.3M 8 2020

March 2018 MMLS Maverick LiDAR

5 RESULTS

In the Davos subset of the Swiss3DCities dataset, as

shown in Table 3, the addition of the relative informa-

tion h

feature signiﬁcantly improves the mIoU from

66.70% with just color features to 69.81%. This jump

is larger than after the addition of color features to

the conﬁguration containing point coordinates only.

Adding elevation and all local features improves the

results even more, to an mIoU of 71.20%. The largest

jump in IoU score can be seen in the small urban as-

set class, with the terrain class not far behind. Fig-

ure 2 shows the qualitative results along with the RGB

point cloud and ground truth. The “all” conﬁgura-

tion, using all features listed in Tab 1, in Fig. 2d

shows fewer artifacts, mostly of the urban asset class

(red), than the “color” conﬁguration in Fig. 2c, mak-

ing most other classes like building (blue) and vegeta-

tion (green) more accurate. It should be noted that the

ground truth data provided may not be entirely accu-

rate or comprehensive, partially due to inherent ambi-

guities. For instance, certain objects such as hedges,

man-made structures like walls or entrances to under-

ground parking facilities have been mislabeled as ter-

rain. These areas are however predicted as either ur-

ban asset or building, like in the bottom right corner

of the Figures.

As shown in Table 4, three variations on the Hes-

sigheim dataset were submitted and evaluated. First,

to establish the baseline, a model with just color was

trained, reaching an average F1 score of 72.35%.

Adding relative elevation, the average F1 score im-

proves substantially by almost 4 pp. to 76.01%.

The largest improvements with relative elevation are

the shrub, gravel, and vertical surface class. All of

these classes beneﬁt from the elevation information,

shrubs for example can be better distinguished from

the ground and tree. Most other classes improve as

well. It should be noted that the improvement of large

classes, like of buildings, trees, and the ground, in the

Hessigheim dataset as well as in the Swiss3DCities

dataset, will be less pronounced. This is because the

improvements mainly affect the challenging ambigu-

ous points, which represent a small fraction in large

classes and thus have limited inﬂuence on the overall

score. Adding both elevation and local features, how-

ever, degrades the performance of the network, but

it is still better in terms of mF1 than the color only

conﬁguration. This is attributed to the fact that the

point density, especially on vertical surfaces, is very

heterogeneous in the Hessigheim dataset due to more

down facing LiDAR scan sweeps, whereas the pho-

togrammetric Swiss3DCities dataset has a quite ho-

mogeneous point cloud. This makes features like ν or

σ(z) inconsistent. Furthermore, hand-crafted features

require setting parameters like the number of neigh-

bors, for which sensible choices may differ between

datasets.

Figure 3 shows the qualitative results of the base-

line “color” and “color+h

” conﬁguration, along with

the RGB input point cloud. Since this is the test set, a

ground truth cannot be shown. The detection of roofs

(red) with relative elevation in Figure 3c is slightly

improved, showing less confusion with the urban fur-

niture class (purple). Facades (orange) are also less

confused with the vertical surface class (yellow). The

uneven point density is apparent in the ﬁgures, where

individual LiDAR sweeps can be seen on the verti-

cal surfaces as well as occluded areas like underneath

protruding roofs.

On the last dataset, Toronto3D, relative elevation

brings a small improvement, as seen in Table 5, where

the mIoU jumps over 0.5 pp. to 72.10%. The small

improvement could be explained by the relative ele-

vation not being fully accurate due to the RANSAC

approximation. The addition of local features, how-

ever, severely degrades the performance, making it

worse than the color conﬁguration. One reasonable

explanation is that the features are calculated on the

full point cloud, where the point density varies wildly,

while for RandLA-Net the points and features are ﬁrst

grid sampled (grid size 6 cm, just like the original au-

thors of RandLA-Net did). The downsampling also

increases the receptive ﬁeld in terms of metric dis-

tance, since the point density is drastically reduced,

making h

less impactful. No downsampling was ap-

GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications

Table 3: Performance of RandLA-Net with different feature conﬁgurations on the Davos subset validation tile of the

Swiss3DCities dataset. The ﬁrst conﬁguration only uses the xyz point coordinates.

Features

Mean

IoU

terrain

IoU

constr.

IoU

urban a.

IoU

veget.

IoU

vehicle

- 91.77 66.23 86.54 81.55 17.24 92.43 53.51

color 91.31 66.70 84.76 82.17 16.49 92.17 57.91

color+h

93.08 69.81 87.95 83.17 25.30 94.13 58.50

all 93.31 71.20 88.06 85.19 32.30 93.40 57.15

(a) RGB (b) Ground truth

Figure 2: The results on the ﬁfth Davos validation tile of the Swiss3DCities dataset, with predictions of two conﬁgurations

and corresponding ground truth. Some errors in Fig. 2c that are not present in Fig. 2d are circled in black.

Table 4: Performance of RandLA-Net with different input features on the Hessigheim March 2018 test set.

Feat. OA mF1

F1 L.

Veg.

F1 I.

Surf.

Car

F1 U.

Furn.

Roof

Fac.

Shr.

Tree

Grav.

F1 V.

Surf.

Chi.

color 86.00 72.35 91.53 86.88 61.78 50.64 94.72 79.07 56.75 96.45 30.06 69.30 88.68

color+h

87.67 76.01 92.40 87.52 55.61 49.63 96.52 79.09 64.84 96.76 45.86 78.47 89.42

all 85.24 74.62 90.17 84.11 60.56 49.74 94.63 79.57 63.93 95.70 40.67 72.34 89.42

Table 5: Performance of RandLA-Net on the Toronto 3D L002 validation tile.

Feat. OA

Mean

IoU

uncl.

IoU

road

IoU

r. ma.

IoU

natu.

IoU

build.

IoU

ut. l.

IoU

pole

IoU

car

IoU

fence

color 92.80 71.52 41.47 92.30 56.23 91.95 88.67 83.88 78.37 87.97 22.84

color+h

93.43 72.10 44.52 93.35 62.32 92.67 89.81 84.84 73.73 86.10 21.60

all 90.26 61.66 19.58 90.11 17.78 89.25 81.17 81.01 69.44 84.79 21.78

plied to the other datasets for training or evaluation.

Another reason is that the strong density variation and

occlusion effects make less useful features, especially

the 2D features like ν or σ(z). Density variations are

Ground Awareness in Deep Learning for Large Outdoor Point Cloud Segmentation

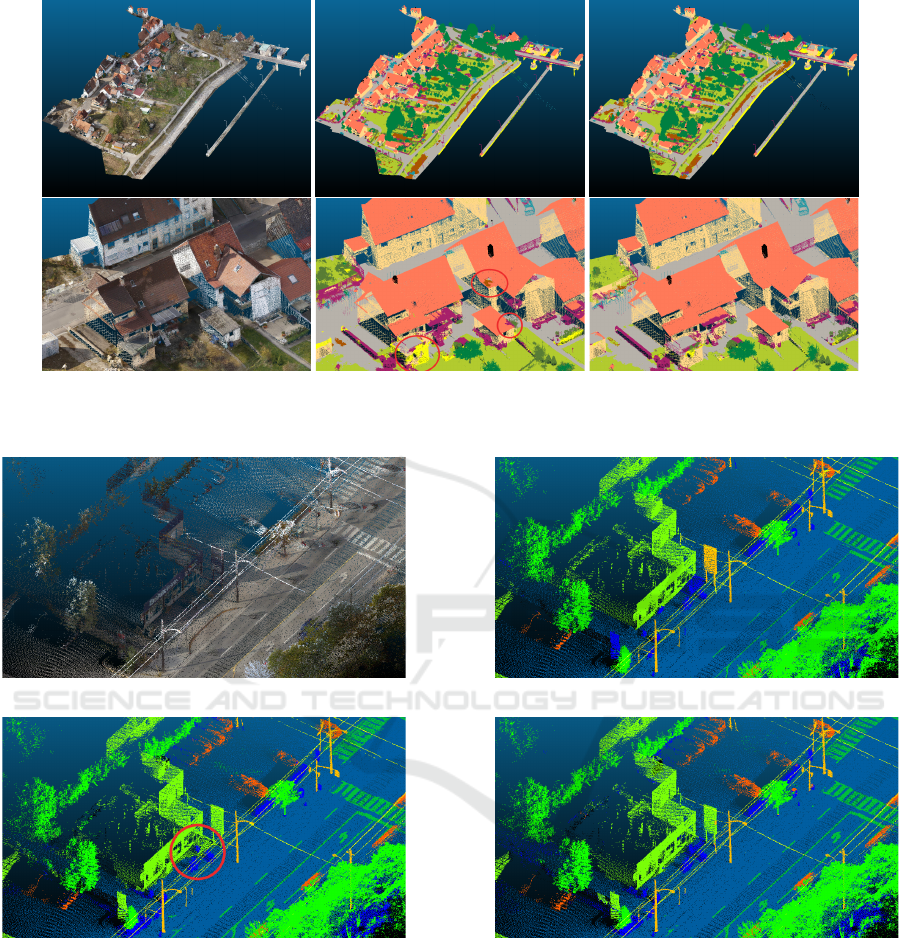
(a) RGB (b) Pred. “color” (c) Pred. “color+h

”

Figure 3: The test set of the Hessigheim March 2018 capture and predictions with different conﬁgurations in its entirety, and

a zoomed in area. Errors in Fig. 3b are circled in red. Ground truth is not publicly available.

(a) RGB (b) Ground truth

”

Figure 4: A zoomed in area of the Toronto3D L002 validation tile with the predictions of two conﬁgurations and ground truth.

The tile has been downsampled using grid sampling. An error in Fig. 4c is circled in red.

also caused by the distance from the vehicle and ve-

hicle speed, both of which are not correlated to useful

information for semantic segmentation. Note that the

results of Toronto3D on vanilla RandLA-Net do not

reach the mIoU of the original authors. This may be

due to weaker hardware or a different implementation

of RandLA-Net. The RGB point cloud, ground truth

and qualitative results are shown in Fig. 4. Small im-

provements can be seen in the delineation of road and

ground. The point density is, of course, highest along

the road, where the vehicle was driven.

6 CONCLUSION AND OUTLOOK

With 3D outdoor point clouds, it is relatively straight-

forward to compute a Digital Terrain Model, or DTM,

using well established methods. Then, the relative el-

GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications

evation of individual points of the point cloud with re-

spect to the ground surface can be determined. A con-

sistent and large improvement in semantic segmen-

tation accuracy of aerial point clouds is achieved by

integrating this relative elevation information into an

existing deep learning network, such as RandLA-Net,

without needing to modify its architecture. This ap-

proach renders the source or method of DTM deriva-

tion irrelevant. It could utilize traditional numerical

methods, DL techniques, or even DTMs from pub-

licly available government data sources. The addi-

tion of the relative elevation feature ensures ground

awareness through a long-range dependency between

ground and object points, especially in cases where

the receptive ﬁeld does not capture the terrain. In

the Hessigheim dataset, the addition of the eleva-

tion information increases the mF1 from 72.35% to

76.01%, and in the Swiss3DCities dataset the mIoU

from 66.70% to 69.81%. Other local features are

less reliably beneﬁcial. Using these local features can

even degrade network performance in more datasets

with more inhomogeneous point distributions, like in

both LiDAR datasets of Hessigheim and Toronto3D.

There are two main reasons for this, which contrast

the relative elevation: 1) The local features depend on

the structure of the point cloud 2) they are quite local-

ized and easily captured by the receptive ﬁeld of the

network.

It is therefore advisable to incorporate relative el-

evation information into classiﬁcation and segmenta-

tion tasks in large outdoor point clouds, which are

typical for remote sensing, whenever feasible. This

recommendation holds not only for 2D scenarios, as

demonstrated in (Qiu et al., 2022) and (Audebert

et al., 2018), but also for 3D point cloud segmentation

tasks using modern deep learning networks, as evi-

denced by the ﬁndings presented in this paper, even

though the input point cloud already implicitly con-

tains the information necessary to derive the DTM.

The effect of relative elevation could be even more

apparent in datasets with larger or taller buildings and

higher resolution.

The prevailing direction in Computer Vision in-

volves shifting towards methods that require fewer

or even no annotated labels at all, as the process of

labeling is often prohibitively expensive. In future

work, we therefore may integrate elevation features

into other point cloud segmentation models and even

explore their effect on self-supervision tasks and in

transformer models.

REFERENCES

Audebert, N., Le Saux, B., and Lef

evre, S. (2018). Beyond

rgb: Very high resolution urban remote sensing with

multimodal deep networks. ISPRS Journal of Pho-

togrammetry and Remote Sensing, 140:20–32.

Boulch, A., Guerry, J., Le Saux, B., and Audebert, N.

(2018). SnapNet: 3D point cloud semantic labeling

with 2D deep segmentation networks. Computers &

Graphics, 71:189–198.

Breiman, L. (2001). Random forests. Machine learning,

45:5–32.

Bulatov, D., H

aufel, G., Meidow, J., Pohl, M., Solbrig, P.,

and Wernerus, P. (2014). Context-based automatic

reconstruction and texturing of 3D urban terrain for

quick-response tasks. ISPRS J. of Photogrammetry

and Remote Sensing, 93:157–170.

Bulatov, D. and Lavery, J. E. (2010). Reconstruction

and texturing of 3D urban terrain from uncalibrated

monocular images using L

splines. Photogrammet-

ric Engineering and Remote Sensing, 76(4):439–449.

Can, G., Mantegazza, D., Abbate, G., Chappuis, S.,

and Giusti, A. (2021). Semantic segmentation on

Swiss3DCities: A benchmark study on aerial pho-

togrammetric 3D pointcloud dataset. Pattern Recog-

nition Letters, 150:108–114.

Chen, J., Zhao, Y., Meng, C., and Liu, Y. (2022). Multi-

feature aggregation for semantic segmentation of an

urban scene point cloud. Remote Sensing, 14(20).

Gevaert, C., Persello, C., Nex, F., and Vosselman, G.

(2018). A deep learning approach to DTM extraction

from imagery using rule-based training labels. ISPRS

J. of Photogrammetry and Remote Sensing, 142:106–

123.

Grilli, E., Daniele, A., Bassier, M., Remondino, F., and

Seraﬁni, L. (2023). Knowledge enhanced neural net-

works for point cloud semantic segmentation. Remote

Sensing, 15(10).

Guo, M.-H., Cai, J.-X., Liu, Z.-N., Mu, T.-J., Martin, R. R.,

and Hu, S.-M. (2021). Pct: Point cloud transformer.

Computational Visual Media, 7:187–199.

Hu, Q., Yang, B., Xie, L., Rosa, S., Guo, Y., Wang, Z.,

Trigoni, N., and Markham, A. (2020). Randla-net:

Efﬁcient semantic segmentation of large-scale point

clouds. In Proceedings of the IEEE/CVF Conference

on Computer Vision and Pattern Recognition, pages

11108–11117.

Jiang, T., Wang, Y., Liu, S., Cong, Y., Dai, L., and Sun,

J. (2022). Local and global structure for urban als

point cloud semantic segmentation with ground-aware

attention. IEEE Transactions on Geoscience and Re-

mote Sensing, 60:1–15.

olle, M., Laupheimer, D., Schmohl, S., Haala, N., Rot-

tensteiner, F., Wegner, J. D., and Ledoux, H. (2021).

The Hessigheim 3D (H3D) benchmark on semantic

segmentation of high-resolution 3D point clouds and

textured meshes from UAV LiDAR and Multi-View-

Stereo. ISPRS Open Journal of Photogrammetry and

Remote Sensing, 1:1–11.

Liu, C., Zhang, Q., Shirowzhan, S., Bai, T., Sheng, Z.,

Wu, Y., Kuang, J., and Ge, L. (2023). The inﬂu-

ence of changing features on the accuracy of deep

Ground Awareness in Deep Learning for Large Outdoor Point Cloud Segmentation

learning-based large-scale outdoor lidar semantic seg-

mentation. In IEEE International Geoscience and

Remote Sensing Symposium (IGARSS), pages 4443–

4446. IEEE.

Liu, Z., Lin, Y., Cao, Y., Hu, H., Wei, Y., Zhang, Z., Lin,

S., and Guo, B. (2021). Swin transformer: Hierarchi-

cal vision transformer using shifted windows. In Pro-

ceedings of the IEEE/CVF International Conference

on Computer Vision, pages 10012–10022.

Maas, H.-G. and Vosselman, G. (1999). Two algorithms for

extracting building models from raw laser altimetry

data. ISPRS Journal of Photogrammetry and Remote

Sensing, 54(2-3):153–163.

Mei, Q., Qiu, K., Bulatov, D., and Iwaszczuk, D. (2024).

Improving deep learning based point cloud classiﬁ-

cation using Markov Random Fields with Quadratic

Pseudo-Boolean Optimization. ISPRS Annals of Pho-

togrammetry, Remote Sensing & Spatial Information

Sciences, 229-236.

Mitschke, I., Wiemann, T., Igelbrink, F., and Hertzberg, J.

(2022). Hyperspectral 3D point cloud segmentation

using RandLA-Net. In Proc. International Conference

on Intelligent Autonomous Systems (IAS-17). Interna-

tional Conference on Intelligent Autonomous Systems.

IAS.

Mongus, D., Luka

c, N., Obrul, D., and

Zalik, B. (2013).

Detection of planar points for building extraction from

LiDAR data based on differential morphological and

attribute proﬁles. ISPRS Annals of the Photogramme-

try, Remote Sensing and Spatial Information Sciences,

2:21–26.

Niemeyer, J., Rottensteiner, F., and Soergel, U. (2014).

Contextual classiﬁcation of lidar data and building ob-

ject detection in urban areas. ISPRS Journal of Pho-

togrammetry and Remote Sensing, 87:152–165.

Pang, Y., Wang, W., Tay, F. E., Liu, W., Tian, Y., and

Yuan, L. (2022). Masked autoencoders for point cloud

self-supervised learning. In Proceedings of the Euro-

pean Conference on Computer Vision, pages 604–621.

Springer.

Piltz, B., Bayer, S., and Poznanska, A.-M. (2016). Vol-

ume based DTM generation from very high resolution

photogrammetric DSMs. The International Archives

of the Photogrammetry, Remote Sensing and Spatial

Information Sciences, 41:83–90.

Qi, C. R., Su, H., Mo, K., and Guibas, L. J. (2017a). Point-

net: Deep learning on point sets for 3d classiﬁcation

and segmentation. In Proceedings of the IEEE Con-

ference on Computer Vision and Pattern Recognition,

pages 652–660.

Qi, C. R., Yi, L., Su, H., and Guibas, L. J. (2017b). Point-

net++: Deep hierarchical feature learning on point sets

in a metric space. Advances in neural information pro-

cessing systems, 30.

Qian, G., Li, Y., Peng, H., Mai, J., Hammoud, H., Elho-

seiny, M., and Ghanem, B. (2022). Pointnext: Revis-

iting pointnet++ with improved training and scaling

strategies. Advances in Neural Information Process-

ing Systems, 35:23192–23204.

Qiu, K., Budde, L. E., Bulatov, D., and Iwaszczuk, D.

(2022). Exploring fusion techniques in U-Net and

DeepLab V3 architectures for multi-modal land cover

classiﬁcation. In Earth Resources and Environmen-

tal Remote Sensing/GIS Applications XIII (SPIE), vol-

ume 12268, pages 190–200. SPIE.

Rusu, R. B., Blodow, N., and Beetz, M. (2009). Fast point

feature histograms (FPFH) for 3D registration. In

IEEE International Conference on Robotics and Au-

tomation, pages 3212–3217. IEEE.

Tan, W., Qin, N., Ma, L., Li, Y., Du, J., Cai, G., Yang,

K., and Li, J. (2020). Toronto-3D: A large-scale mo-

bile LiDAR dataset for semantic segmentation of ur-

ban roadways. In Proceedings of the IEEE/CVF Con-

ference on Computer Vision and Pattern Recognition

Workshops, pages 202–203.

Tchapmi, L., Choy, C., Armeni, I., Gwak, J., and Savarese,

S. (2017). Segcloud: Semantic segmentation of 3d

point clouds. In International Conference on 3D Vi-

sion (3DV), pages 537–547. IEEE.

Thomas, H., Qi, C. R., Deschaud, J.-E., Marcotegui, B.,

Goulette, F., and Guibas, L. J. (2019). Kpconv: Flex-

ible and deformable convolution for point clouds. In

Proceedings of the IEEE/CVF International Confer-

ence on Computer Vision, pages 6411–6420.

Tombari, F., Salti, S., and Di Stefano, L. (2010). Unique

signatures of histograms for local surface description.

In European Conference on Computer Vision, pages

356–369. Springer.

Weinmann, M., Jutzi, B., Hinz, S., and Mallet, C. (2015).

Semantic point cloud interpretation based on optimal

neighborhoods, relevant features and efﬁcient classi-

ﬁers. ISPRS Journal of Photogrammetry and Remote

Sensing, 105:286–304.

Weinmann, M., Jutzi, B., and Mallet, C. (2017). Geomet-

ric features and their relevance for 3D point cloud

classiﬁcation. ISPRS Annals of the Photogramme-

try, Remote Sensing and Spatial Information Sciences,

4:157–164.

Wu, J., Jiao, J., Yang, Q., Zha, Z.-J., and Chen, X. (2019).

Ground-aware point cloud semantic segmentation for

autonomous driving. In Proceedings of the 27th ACM

International Conference on Multimedia, pages 971–

979.

Wu, X., Jiang, L., Wang, P.-S., Liu, Z., Liu, X., Qiao, Y.,

Ouyang, W., He, T., and Zhao, H. (2024). Point trans-

former v3: Simpler faster stronger. In Proceedings

of the IEEE/CVF Conference on Computer Vision and

Pattern Recognition, pages 4840–4851.

Yousefhussien, M., Kelbe, D. J., Ientilucci, E. J., and Sal-

vaggio, C. (2018). A multi-scale fully convolutional

network for semantic labeling of 3D point clouds. IS-

PRS Journal of Photogrammetry and Remote Sensing,

143:191–204. ISPRS Journal of Photogrammetry and

Remote Sensing Theme Issue “Point Cloud Process-

ing”.

Zhang, R., Guo, Z., Gao, P., Fang, R., Zhao, B., Wang, D.,

Qiao, Y., and Li, H. (2022). Point-m2ae: multi-scale

masked autoencoders for hierarchical point cloud pre-

training. Advances in Neural Information Processing

Systems, 35:27061–27074.

Zhao, H., Jiang, L., Jia, J., Torr, P. H., and Koltun, V. (2021).

Point transformer. In Proceedings of the IEEE/CVF

International Conference on Computer Vision, pages

16259–16268.

GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications