Ray-LUT: A Lookup-Based Method for Camera Lens Simulation in
Real-Time Using Ray Tracing
Jan Honsbrok
a
, Sina Mostafawy, Jens Herder
b
and Alina Huldtgren
c
Faculty of Media, Hochschule D
¨
usseldorf, M
¨
unsterstraße 156, 40476 D
¨
usseldorf, Germany
Keywords:
Ray Tracing, Camera, Lens Effects, Optical Simulation, Real-Time, Caching, GPU.
Abstract:
Lens systems have a major influence on the image due to effects such as depth of field or optical aberrations.
The only method to simulate these effects precisely is to trace rays through an actual lens system. This provides
accurate results, but only with high computational effort. To speed up the ray tracing through the lens system,
various acceleration methods have been developed, requiring considerable precomputations. We present a new
method based on the Realistic Camera by Kolb et. al.. Instead of tracing each ray through the lens system, the
rays are precomputed once and stored in a lookup table. In contrast to other methods, our method is simple,
and does not require substantial preprocessing upfront. We can simulate complex effects such as chromatic
aberrations accurately in real-time, regardless the number of lens surfaces in the system. Our method achieves
the same performance as state-of-the-art methods like Polynomial Optics, while maintaining the same number
of samples per pixel.
1 INTRODUCTION
Lens systems cause a variety of effects that lead to
visible changes in the image. Photorealistic ray trac-
ing should therefore not only focus on the light inter-
actions that occur within the scene, as the simulation
of these effects is essential for achieving a photoreal-
istic result. Many lens effects can only be achieved
using ray tracing.
In the movie industry lens effects are simulated in
offline renderings to create a realistic image. Since
lens effects influence the image composition, it is not
possible to judge an image without lens effects. To
not disrupt the creative work of an animator, the im-
pact of a change in the scene has to be visible immedi-
ately. A real-time preview of lens effects is therefore
essential. Figure 1 shows the impact of missing lens
effects in the animation preview.
The Realistic Camera (Kolb et al., 1995) is capa-
ble of simulating these effects accurately, but it is not
suitable for real-time, due to the high computational
costs of ray tracing through the lens system. Meth-
ods exists to reduce the cost of ray tracing, with Poly-
nomial Optics (Hullin et al., 2012) being the most
a
https://orcid.org/0009-0007-3601-1798
b
https://orcid.org/0000-0002-1833-424X
c
https://orcid.org/0000-0002-0542-8626
no depth of field
(a)
with depth of field
without distortionwithout distortion
(b)
with distortionwith distortion
Figure 1: The missing preview of lens effects leads to a
completely different impression of the scene. (a) Depth of
field conveys the depth and proportions of the scene and
directs the viewer’s attention to the chess pieces in front. (b)
Distortion strongly influences horizontal and vertical lines
in the image. Lens: (Angenieux, 1955) Scene: (Sayed et al.,
2023).
promising of these methods. Instead of tracing rays
through the lens system, the way of a ray through the
system is described with a polynomial. Polynomial
Optics can achieve high simulation accuracy while
maintaining real-time capability. Fitting the polyno-
mial requires a substantial amount of computation up-
front, making it impossible to load an arbitrary lens
system interactively at runtime.
A simple method to avoid repetitive and expensive
computations is caching. For the simulation of a lens
system, caching can reduce the costly ray tracing to a
Honsbrok, J., Mostafawy, S., Herder, J. and Huldtgren, A.
Ray-LUT: A Lookup-Based Method for Camera Lens Simulation in Real-Time Using Ray Tracing.
DOI: 10.5220/0013105900003912
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 20th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2025) - Volume 1: GRAPP, HUCAPP
and IVAPP, pages 177-184
ISBN: 978-989-758-728-3; ISSN: 2184-4321
Proceedings Copyright © 2025 by SCITEPRESS – Science and Technology Publications, Lda.
177

simple lookup in memory. In contrast to Polynomial
Optics, the preprocessing time to compute the cache is
only a few milliseconds and can be neglected. An in-
teractive calculation is also possible by progressively
computing the cached samples.
The drawbacks of caching are always the calcu-
lation and memory consumptions of the cache. If the
cached results have to be recalculated for each lookup,
no performance gain can be achieved. High memory
consumptions can make the use of a cache inappro-
priate or even impossible. The recalculation of the
cache is not an issue for the simulation of lens sys-
tems, because only a few cases require a recalculation
in real-time. In case of caching the rays of a lens sys-
tem, the memory requirement depends on the resolu-
tion, the number of samples per pixel and number of
stored wavelengths. Since the resolution and number
of samples per pixel are typically low in real-time sce-
narios, the memory requirement appears justifiable in
view of the performance advantages. Axis symmetry
is applied to reduce the memory usage further.
We contribute a physically accurate method to
simulate lens systems in real-time using ray tracing.
Instead of tracing rays through the lens system for ev-
ery frame, we compute the rays once and store them
into a lookup table. Our method is based on the Real-
istic Camera, allowing us to simulate complex optical
effects accurately. In contrast to other methods, our
method does not require considerable preprocessing.
2 PREVIOUS WORK
(Kolb et al., 1995) introduced the Realistic Camera, a
camera model utilizing sequential ray tracing to accu-
rately simulate lens systems, resulting in images with
complex optical effects. To reduce the number of vi-
gnetted rays, a global exit pupil is precalculated and
explicitly sampled. (Steinert et al., 2011) extended
the Realistic Camera with many photographic effects
and improved the sampling of the exit pupil. Instead
of a global exit pupil, the exit pupil is calculated per
pixel, reducing the number of vignetted rays signifi-
cantly. (Pharr et al., 2016) reduced the computational
effort to calculate per-pixel exit pupils by utilizing ro-
tational symmetry.
For real-time applications many different options
were explored, being either too slow for real-time or
lacking accuracy. (Nießner et al., 2012) used ray trac-
ing on the GPU to simulate human perception through
glasses. To ensure real-time performance only one
sample per pixel is calculated per frame and the re-
sults are accumulated over several frames. Instead of
ray tracing they propose the use of a blur, which is
faster but less accurate. (Joo et al., 2016) optimized
the intersection with aspheric lenses, but could still
not achieve real-time performance using ray tracing.
For real-time applications they demonstrate how to
derive a realistic bokeh texture, which can be used
with a defocus blur. (Lee et al., 2010) demonstrate
that depth peeling can reduce the computational cost
of ray tracing. This approach is less accurate, because
occluded parts of the scene can be missed. (Sauer
et al., 2022) and (Stein et al., 2021) demonstrate how
to use filters for the simulation of progressive additive
lenses. Since the refractive power of these lenses de-
pends on the position on the lens, ray tracing is used
to generate blur or distortion maps. The actual ren-
dering process is conducted using rasterization.
As (Kolb et al., 1995) showed, ray tracing is the
most accurate way to simulate complex lens effects.
The computational cost of ray tracing is high due to
the calculation of intersections and refractions. Var-
ious methods have been investigated to reduce the
computational cost of ray tracing. (Hullin et al., 2011)
reduced the number of traced rays for lens flare sim-
ulation by tracing a grid of rays through the lens sys-
tem and interpolating the results. (Lee and Eisemann,
2013) further developed the method by (Hullin et al.,
2011) and replaced the ray tracing with a 2x2 trans-
formation matrix. This method is fast but lacks non-
linear effects. (Hullin et al., 2012) used polynomi-
als instead of matrices, allowing for non-linear ef-
fects. (Hanika and Dachsbacher, 2014) showed how
the accuracy of the polynomial can be improved by
fitting it using a set of ray traced ground-truth sam-
ples. (Schrade et al., 2016) employed high degree
polynomials to improve the accuracy for wide angle
lenses. They applied orthogonal matching pursuit ad-
ditionally to reduce the number of terms in the poly-
nomial, improving the performance. Applying or-
thogonal matching pursuit can result in nearly expo-
nential time (Zheng and Zheng, 2017a). (Zheng and
Zheng, 2017a) proposed an adaptive approach to re-
duce the number of coefficients, which terminates in
polynomial runtime. Even though (Zheng and Zheng,
2017a) reduced the time to fit the polynomial dras-
tically, they showed it can still take multiple hours.
Loading an arbitrary lens system interactively at run-
time is therefore not possible. Once the polynomial
is fitted Polynomial Optics achieves real-time perfor-
mance.
Recent work also has shown that neural net-
works can be used for lens simulation, the NeuroLens
(Zheng and Zheng, 2017b). While being more accu-
rate than polynomial-based methods, the render times
for complex lenses can be more than twice as high
compared to the polynomial approach. It is therefore
GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications
178

Figure 2: Our method is capable of rendering complex optical aberrations in real-time. This figure shows the aberrations of
three different lenses (Ogawa, 1996; Thorlabs, Inc., 2023; Schade, 1950) in the OpenChessSet scene (Sayed et al., 2023). All
images are rendered using our method in real-time with 30 fps at a resolution of 1600x900 pixels on a NVIDIA GeForce RTX
4070 Ti. (a) is rendered using spectral sampling, (b) and (c) are not and therefore achieve higher sample rates.
questionable if this approach is suitable for real-time
applications; the authors do not provide any informa-
tion on this.
Polynomial Optics is capable of simulating a lens
system physically accurately in real-time, but loading
an arbitrary lens system at runtime is not possible in-
teractively. Many approaches have employed prepro-
cessing to reduce the computational effort at runtime
(Joo et al., 2016; Sauer et al., 2022; Stein et al., 2021;
Hullin et al., 2012; Hanika and Dachsbacher, 2014;
Schrade et al., 2016; Zheng and Zheng, 2017a; Zheng
and Zheng, 2017b), but no one has utilized caching
and reused the rays once they were generated.
3 Ray-LUT
3.1 System Overview
Our method uses a lookup table, avoiding the com-
putational costs of ray tracing and replacing it by a
simple memory lookup, giving us high performance
advantages.
The lookup table is calculated upfront using the
Realistic Camera. To allow for a free moving camera,
the rays are generated at the origin and transformed
to the camera position at render time. Some changes
to the lens system require a calculation in real-time.
Because the Realistic Camera is not suitable for real-
time, the lookup table cannot be recomputed in real-
time. Instead, we perform a progressive recalculation
over multiple frames.
3.2 Ray Generation
We rely on the Realistic Camera implementation by
(Pharr et al., 2016) to generate camera rays. To sim-
ulate the path of a ray through the lens system, the
Realistic Camera uses sequential ray tracing. Each
ray is intersected with each lens surface and refracted
according to Snell’s Law. If the ray hits the lens hous-
ing, it is vignetted. To account for vignetting and the
correct radiance, the Realistic Camera also returns a
weight for each ray. As the implementation by (Pharr
et al., 2016) did not provide support for chromatic
aberrations, we added support for this effect.
Chromatic aberrations are caused by different re-
fraction indices for different wavelengths. Each
wavelength is refracted slightly differently, forming
multiple images on the sensor. To determine the in-
dex of refraction for a given wavelength, we evaluate
the Sellmeier Equation (von Sellmeier, 1871) on each
lens surface, using measured data from manufactur-
ers of optical glasses like Schott (Schott AG, 2023)
or Ohara (Ohara Corporation, 2023). So far, we only
sample wavelengths for R, G and B, but our method
could be extended to arbitrary wavelengths.
Cylindrical surfaces where added to support
anamorphic systems. No aspheric or free-form sur-
faces were implemented so far.
3.3 Recalculation of the Ray-LUT
The rays stored in the lookup table must be calculated
before they can be used. The cache is populated up-
front once. The cached rays depend on various pa-
rameters. If a single parameter changes, all rays have
Ray-LUT: A Lookup-Based Method for Camera Lens Simulation in Real-Time Using Ray Tracing
179

d = 47cmd = 47cm
3spp3spp
d = 57cmd = 57cm
3spp3spp
d = 47cmd = 47cm
chrom. abb., 1sppchrom. abb., 1spp
d = 57cmd = 57cm
chrom. abb., 1sppchrom. abb., 1spp
Figure 3: Image quality of our method during a change
of the focus distance d, with and without chromatic aberra-
tions, using the Canon Zoom (34 surfaces) (Ogawa, 1996).
Since the Ray-LUT is recalculated during the change, the
number of samples per pixel is lower, resulting in a loss of
image quality. The impression of the scene still remains.
to be recalculated. Depending on which parameter
changes there are different requirements for the speed
of the calculation. In most cases, a calculation with
interactive frame rates is sufficient. Changing the de-
scription of the lens system, the aperture, the sensor
size, the resolution or the number of samples per pixel
is typically done during scene setup. In these cases,
a calculation with interactive frame rates is sufficient,
because none of these parameters changes over time.
Changing the camera position, the focus distance or
the zoom of the lens system needs to be possible in
real-time, since these parameters are usually part of
animations. To change the camera position in real-
time, the rays can be generated at the origin and are
transformed to the actual camera position. Changes
of the focus distance and the zoom in real-time can
be handled by performing a progressive calculation
over multiple frames. Only a few samples per pixel
are calculated per frame, ensuring real-time perfor-
mance, but resulting in a temporary loss of quality.
We argue that this is not an issue, since focus or zoom
changes do not happen very often and the loss of qual-
ity is acceptable in a variety of applications. Figure 3
shows an example of the image quality during a focus
change. There is a loss of quality, but the impression
of the scene remains, being suitable for a real-time
preview of animations.
3.4 Storing the Rays
The rays are stored into a flat, contiguous buffer. Sam-
ples of an individual pixel are stored next to each
other. For every ray position, direction and weight are
saved, adding up to a memory consumption of seven
floats per ray. If chromatic aberrations are enabled,
more than one wavelength sample is stored. In our
case, we store three spectral samples.
To reduce the memory consumption, symmetries
can be exploited. Because anamorphic lens systems
are not rotational symmetric, only axis symmetry can
be used. Axis symmetry allows us to only store one
image quadrant, reducing the memory consumption
to one quarter. So far, no interpolation between the
samples has been investigated, but this could be part
of future work.
The memory consumption is calculated based on
the resolution, the number of samples per pixel and
the number of stored wavelength samples. Table 1
shows the memory consumption of different configu-
rations. For real-time scenarios smaller resolutions
and lower sample counts are common. For exam-
ple, the viewport of a digital content creation app
is usually around 1600x900 pixels on a screen with
2560x1440 pixels, since other elements must fit on the
screen. A NVIDIA GeForce RTX 4070Ti can roughly
compute 25 samples per pixel in real-time, using a
pinhole camera. A resolution of 1600x900 pixels and
25 samples per pixels lead to a memory consumption
of 0.94 GB without and 2.82 GB with chromatic aber-
rations. Considering the huge performance benefits,
this seems appropriate.
Table 1: Memory consumption Ray-LUT in gigabytes for
different resolutions and samples per pixel (spp), with and
without chromatic aberrations (CA).
spp Full HD Full HD (CA) 4K 4K (CA)
4 0.05 0.16 0.22 0.65
8 0.11 0.32 0.43 1.3
16 0.22 0.65 0.87 2.6
32 0.43 1.3 1.73 5.19
64 0.87 2.6 3.46 10.38
256 3.46 10.38 13.84 41.53
1024 13.84 41.53 55.37 166.11
4096 55.37 166.11 221.48 664.45
3.5 Implementation Details
We implemented our method using the NVIDIA Op-
tiX Framework (Parker et al., 2010). OptiX was cho-
sen because it is widely used and it was the framework
we had the most experience with. Our results should
apply to every other ray tracing framework. We used
GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications
180

the OptiX Sample application from (Wald and Parker,
2019). This sample application allows the loading of
a scene, the rendering of this scene using ray tracing
and uses a denoiser. The code for primary ray gener-
ation was adjusted to allow switching between differ-
ent camera models. This includes the pinhole camera,
the thin lens model, the Realistic Camera, Polynomial
Optics and our method.
The use of a lookup table gives us a huge perfor-
mance advantage in terms of lens simulation. Achiev-
ing a noise-free result in real-time is not possible, as
real-time constraints prevent rendering enough sam-
ples. For this reason, we combine real-time ray trac-
ing with the NVIDIA OptiX Denoiser to achieve a ray
traced image without noise in real-time.
4 RESULTS
We evaluated our method in terms of performance and
compared our method to the thin lens model, the Re-
alistic Camera and Polynomial Optics. All methods
were implemented on the GPU using NVIDIA OptiX.
For the Realistic Camera, the implementation de-
scribed in 3.2 was used without caching. For Polyno-
mial Optics, we used the method by (Schrade et al.,
2016) because there was a reference implementation
available in their supplementary material. For the
polynomial, we used a degree of 8 and a maximum
number of coefficients of 15. This seemed to be a
good tradeoff between performance and accuracy.
We used the OpenChessSet scene (Sayed et al.,
2023) as a test scene. The scene contains 1,430,950
triangles and 13 textures with a resolution of
2048x2048 pixels. The scene is illuminated by a sin-
gle area light, only lambertian shading is applied to
the surfaces. We also evaluated the different methods
in other scenes, which showed similar results. There-
fore, only the results of the OpenChessSet scene are
presented.
All tests were performed on a test system with
an AMD Ryzen 9 5950X processor with 16 cores,
128 GB of RAM and an NVIDIA GeForce RTX
4070Ti with 12 GB VRAM. Windows 10 was used
as the operating system. All tests were performed at
a resolution of 1600x900 pixels, which is roughly the
size of a viewport in a digital content creation app on
a screen with 2560x1440 pixels.
4.1 Performance
We used a fixed set of lenses to evaluate the perfor-
mance of our method. The lenses were selected by
the count of surfaces in the system, since this aspect
Table 2: Lenses used for performance evaluation.
Lens Surfaces
Biconvex Lens (Thorlabs, Inc., 2023) 3
Angenieux (Angenieux, 1955) 15
Canon (Ogawa, 1996) 34
Panavision (Neil, 2006) 57
is very interesting for performance. Table 2 shows
an overview of the selected lenses. All methods were
tested with each of the lens systems listed above, with
the exception of the Panavision lens for Polynomial
Optics, as no corresponding polynomials could be
generated.
The render time of the individual method was
measured at 25 samples per pixel, with and without
chromatic aberrations. This number of samples was
selected, because it is the maximum number of sam-
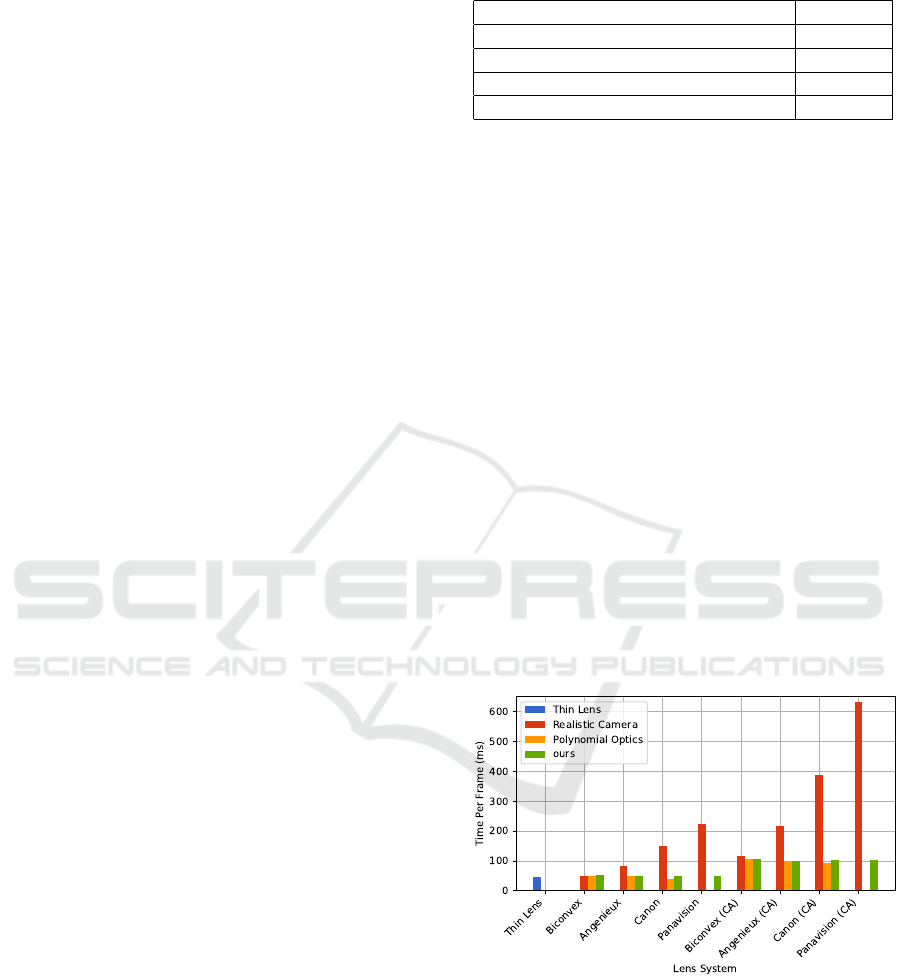
ples the thin lens can still display in real-time. Figure
4 shows the render time the various methods could
achieve.
For the Realistic Camera, the render time grows
linearly with the number of lenses in the system.
The simplest lens is already slower than the thin lens
model. With chromatic aberrations the render time
grows up to 633 ms. Polynomial Optics achieves an
almost constant performance. The performance of our
method is comparable to the thin lens model, regard-
less the number of lenses in the system. With chro-
matic aberrations, the performance is way better than
the Realistic Camera and comparable to Polynomial
Optics.
Figure 4: Render time in ms for different methods and
lenses using 25 samples per pixel, with and without chro-
matic aberrations (CA).
4.2 Achieved Effects
With the Realistic Camera as the foundation of our
method, we can accurately simulate a variety of ef-
fects. Figure 2 shows examples for chromatic aberra-
tions, distortion, spherical aberrations, vignetting and
Ray-LUT: A Lookup-Based Method for Camera Lens Simulation in Real-Time Using Ray Tracing
181

Figure 5: Biconvex Lens, 3 surfaces (Thorlabs, Inc., 2023),
with chromatic aberrations, 6 samples per pixel, 30 fps
(1600x900 pixels). Since the Biconvex Lens is not cor-
rected for chromatic aberrations, they are clearly visible.
curvature of field. Figure 5 shows a perspective of the
OpenChessSet scene using the Biconvex Lens (Thor-
labs, Inc., 2023). We can see the high-quality depth
of field. As the Biconvex Lens is not corrected for
chromatic aberrations, they are clearly visible in the
image.
4.3 Image Quality During Recalculation
Figure 6: F LIP error of our method during progressive re-
calculation compared to cache hit, with and without chro-
matic aberrations (CA). Lower is better.
To recalculate the cache in real-time, we perform a
progressive recalculation with only a few samples per
pixel, resulting in a loss of image quality. To measure
the loss, we rendered two images for each lens using
our method, one with the sample count for progres-
sive recalculation and another one with the full sam-
ple count available on cache hit. We compared those
images to a reference image generated using the Re-
alistic Camera with 4000 samples per pixel and com-
puted the error using F LIP (Andersson et al., 2020).
We chose F LIP because it is a perceptual metric, mod-
eling the perceived difference between two images
when alternating between them. Figure 6 shows the
F LIP error for the various lenses.
Because the rays are generated using the Realistic
Camera, the complexity rises linearly with the num-
ber of lens surfaces. Therefore, lens systems with
more surfaces achieve a smaller number of samples
per pixel during progressive recalculation, resulting
in a larger error. Our method can deliver the same
amount of samples per pixel regardless the complex-
ity of the lens, accordingly, the error in case of a cache
hit is almost constant across all lenses. For lenses with
only a few surfaces, the same number of samples per
pixel can be achieved during recalculation as during
cache hit. With chromatic aberrations, the computa-
tional effort increases, which reduces the number of
samples per pixel during recalculation and increases
the error.
5 DISCUSSION
Like Polynomial Optics, our method can achieve high
performance advantages over the Realistic Camera.
The performance is comparable to Polynomial Optics
and is independent from the number of surfaces in the
lens system.
These performance advantages come at the cost of
high storage requirements, as all rays must be stored
in memory. Axis symmetry is used to reduce to the
memory consumption. In real-time scenarios, a small
number of samples per pixel and a lower resolution is
common, resulting in a memory consumption of mul-
tiple gigabytes. In view of the high performance ad-
vantage the memory requirement appears justifiable.
Like other methods, our method requires prepro-
cessing, which in our case is to compute the cache.
Compared to Polynomial Optics, this is considerably
fast. Even for a lens system with 57 surfaces, we
can compute the cache with 25 samples per pixel in
28 ms. In contrast, Polynomial Optics needs mul-
tiple hours to fit the polynomial (Zheng and Zheng,
2017b). While the polynomial could be fitted upfront,
this is not suitable for use cases in which the lens sys-
tem is not known in advance, for example because
the lens system is still in development and is con-
stantly changing. With our method, it is possible to
get a real-time visualization of any lens system with-
out long preprocessing.
To evaluate the polynomial efficiently at runtime,
Polynomial Optics outputs the fitted polynomial as
c99-Code and compiles it to machine code. Com-
GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications
182

pared to the evaluation of a list of coefficients, perfor-
mance advantages of 20x can be achieved. (Hanika
and Dachsbacher, 2014) To load and simulate an ar-
bitrary lens system at runtime, some kind of compiler
is required, making the setup more complex. In con-
trast, our method just needs some memory.
When changing the focus or zoom of a lens sys-
tem, the Ray-LUT must be recalculated in real-time,
leading to a temporary loss in quality. Our method
is therefore only suitable for applications that can ac-
cept this temporary loss in quality, for example the
real-time preview of animations. The Ray-LUT is not
suitable for use cases in which the final image is gen-
erated in real-time, such as in a virtual studio.
In ophthalmology rendering methods are used to
to plan corrective lenses and evaluate different sur-
gical techniques. With our method, different op-
tions could be visualized in real-time. Our method
promises great potential in this area, but possible ap-
plications have not yet been investigated further.
Given that our method can achieve great perfor-
mance improvements in real-time, it seems natural
that the speed of offline renderings could also be im-
proved. We implemented our method in an offline
ray tracer and evaluated the performance with various
lenses and scenes of different complexity. If the pro-
portion of lens simulation in the overall render time is
high, for example with highly complex lens systems
and simple scenes, the render time can be drastically
reduced. We could observe performance improve-
ments up to 80%. Because resolution and samples
per pixel counts are usually high in offline renderings,
this comes with a huge memory consumption that can
add up easily to several hundreds of gigabytes (see
Table 1). Without a further reduction of the memory
consumption, using our method for offline renderings
is not practical.
6 CONCLUSION AND FUTURE
WORK
We presented a physically accurate method to simu-
late lens systems in real-time using ray tracing. We
showed that the rays of a camera lens are suitable
for caching and that recalculating the cache is not
a problem. Our method was evaluated in multiple
test scenes with lens systems of different complexity,
showing a similar performance as Polynomial Optics.
Lens systems of arbitrary complexity can be simu-
lated in real-time. In contrast to other methods, our
preprocessing step is fast and can be computed inter-
activly.
Our method was developed for the real-time pre-
view of animations in the film industry. There is also
great potential for use in ophthalmology, where ren-
dering methods are used to plan corrective lenses and
evaluate different surgical techniques. Our method
could visualize the possible options accurately in real-
time.
So far, axis symmetry has been employed to re-
duce the storage requirements of the Ray-LUT. For
spherical lenses, rotational symmetricy could reduce
the memory usage further. The rays could be calcu-
lated along an axis of the film and transformed during
rendering according to the the pixel position during
rendering. The memory requirement of a single ray
could be reduced by two floats, by storing one com-
ponent of the position and direction implicitly. In or-
der to make the Ray-LUT independent of the rendered
resolution, the rays could be calculated for just a few
points on the sensor and interpolation could be carried
out in between between these points. This could save
additional memory and computing effort.
If the memory requirement can be significantly
reduced, a precalculation of the Ray-LUT is possi-
ble. Instead of recalculating the Ray-LUT cumula-
tively in real-time when refocusing, rays for several
focus distances could be precalculated and loaded ac-
cordingly when refocusing. In order to only store a
small number of focus distances, an interpolation of
different distances could take place. Until now, such a
procedure was inconceivable due to the high memory
requirements for the various configurations. If nec-
essary, such configurations could be generated in an
offline preprocess and stored on disk.
So far, only spherical and cylindrical lens surfaces
were implemented and evaluated. It would be inter-
esting to extend our method to aspherical or free-form
surfaces. Because prime lenses are common in the
movie industry, we restricted our implementation to
these lens types. It would be interesting to extend our
method to zoom lenses. As zooms are often part of
animations, the recalculation of the cache must hap-
pen in real-time. This could be solved by a progres-
sive recalculation like for changing focus distances.
Spectral renderers take a variety of wavelengths
into account and not just three specific ones, as in
our implementation. Our method allows to store an
arbitrary number of wavelengths; however, this has
not been investigated yet. There are no restrictions
in how the wavelength spectrum is sampled, allowing
to sample green wavelengths more densely to account
for human vision.
Ray-LUT: A Lookup-Based Method for Camera Lens Simulation in Real-Time Using Ray Tracing
183

REFERENCES
Andersson, P., Nilsson, J., Akenine-M
¨
oller, T., Oskarsson,
M., Astr
¨
om, K., and Fairchild, M. D. (2020). Flip:
A difference evaluator for alternating images. Proc.
ACM Comput. Graph. Interact. Tech., 3(2).
Angenieux, P. (1955). Large aperture six component optical
objective. US Patent 2,701,982.
Hanika, J. and Dachsbacher, C. (2014). Efficient monte
carlo rendering with realistic lenses. Computer
Graphics Forum, 33(2):323–332.
Hullin, M., Eisemann, E., Seidel, H.-P., and Lee, S.
(2011). Physically-based real-time lens flare render-
ing. In ACM SIGGRAPH 2011 Papers, SIGGRAPH
’11, New York, NY, USA. Association for Computing
Machinery.
Hullin, M. B., Hanika, J., and Heidrich, W. (2012). Poly-
nomial optics: A construction kit for efficient ray-
tracing of lens systems. Computer Graphics Forum,
31(4):1375–1383.
Joo, H., Kwon, S., Lee, S., Eisemann, E., and Lee, S.
(2016). Efficient ray tracing through aspheric lenses
and imperfect bokeh synthesis. Computer Graphics
Forum, 35(4):99–105.
Kolb, C., Mitchell, D., and Hanrahan, P. (1995). A real-
istic camera model for computer graphics. In Pro-
ceedings of the 22nd Annual Conference on Computer
Graphics and Interactive Techniques, SIGGRAPH
’95, pages 317–324, New York, NY, USA. Associa-
tion for Computing Machinery.
Lee, S. and Eisemann, E. (2013). Practical real-time lens-
flare rendering. In Proceedings of the Eurograph-
ics Symposium on Rendering, EGSR ’13, pages 1–6,
Goslar, DEU. Eurographics Association.
Lee, S., Eisemann, E., and Seidel, H.-P. (2010). Real-
time lens blur effects and focus control. ACM Trans.
Graph., 29(4).
Neil, I. A. (2006). Anamorphic imaging system. US Patent
2006/0050403 A1.
Nießner, M., Sturm, R., and Greiner, G. (2012). Real-
time simulation and visualization of human vision
through eyeglasses on the gpu. In Proceedings of the
11th ACM SIGGRAPH International Conference on
Virtual-Reality Continuum and Its Applications in In-
dustry, VRCAI ’12, pages 195–202, New York, NY,
USA. Association for Computing Machinery.
Ogawa, H. (1996). Zoom lens. US Patent 5,537,259.
Ohara Corporation (2023). Catalog data. https://www.
oharacorp.com/catalog.html.
Parker, S. G., Bigler, J., Dietrich, A., Friedrich, H., Hobe-
rock, J., Luebke, D., McAllister, D., McGuire, M.,
Morley, K., Robison, A., and Stich, M. (2010). Op-
tix: A general purpose ray tracing engine. ACM Trans.
Graph., 29(4).
Pharr, M., Jakob, W., and Humphreys, G. (2016). Phys-
ically Based Rendering: From Theory to Implemen-
tation. Morgan Kaufmann Publishers Inc, San Fran-
cisco, CA, USA, 3rd edition.
Sauer, Y., Wahl, S., and Habtegiorgis, S. W. (2022). Real-
time blur simulation of varifocal spectacle lenses in
virtual reality. In SIGGRAPH Asia 2022 Technical
Communications, SA ’22, New York, NY, USA. As-
sociation for Computing Machinery.
Sayed, M., Sayed, M., Rydalch, C., Elendt, M., Stone, J.,
and Delgado, P. (2023). The open chess set. This work
is licensed under the Creative Commons Attribution
4.0 International License. To view a copy of this li-
cense, visit https://creativecommons.org/licenses/by/
4.0/.
Schade, W. (1950). Petzval-type photographic objective.
US Patent 2500046A.
Schott AG (2023). Optisches Glas: Datenbl
¨
atter.
https://www.schott.com/de-de/products/
optical-glass-p1000267/downloads.
Schrade, E., Hanika, J., and Dachsbacher, C. (2016). Sparse
high-degree polynomials for wide-angle lenses. Com-
puter Graphics Forum, 35(4):89–97.
Stein, N., Rifai, K., Wahl, S., and Lappe, M. (2021). Sim-
ulating lens distortion in virtual reality. In Proceed-
ings of the 13th International Conference on Disabil-
ity, Virtual Reality & Associated Technologies.
Steinert, B., Dammertz, H., Hanika, J., and Lensch, H.
P. A. (2011). General spectral camera lens simulation.
Computer Graphics Forum, 30(6):1643–1654.
Thorlabs, Inc. (2023). N-bk7 bi-convex lenses, un-
coated. https://www.thorlabs.com/newgrouppage9.
cfm?objectgroup id=4847.
von Sellmeier, W. (1871). Zur Erkl
¨
arung der abnormen Far-
benfolge im Spectrum einiger Substanzen. Annalen
der Physik, 219(6):272–282.
Wald, I. and Parker, S. G. (2019). Rtx accelerated ray trac-
ing with optix. In ACM SIGGRAPH 2019 Courses,
SIGGRAPH ’19, New York, NY, USA. Association
for Computing Machinery.
Zheng, Q. and Zheng, C. (2017a). Adaptive sparse polyno-
mial regression for camera lens simulation. The Visual
Computer, 33(6):715–724.
Zheng, Q. and Zheng, C. (2017b). Neurolens: Data-driven
camera lens simulation using neural networks. Com-
puter Graphics Forum, 36(8):390–401.
GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications
184