
Indoor Navigation: Navmesh Applied to Indoor Graph Creation
Maxime Callico
1, 2
, Rodolphe Giroudeau
1
, Benoît Darties
1
and Jean Carrière
2
1
LIRMM, Montpellier, France
2
Woosmap, Montpellier, France
Keywords:
Navmesh, Graph, Shortest Path, Polygon, Convex, Concave, Indoor, Navigation.
Abstract:
This paper explores the adaptation of the Navmesh algorithm, widely used in video games for pathfinding,
to real-world indoor navigation. By applying polygon decomposition techniques, we generate routing graphs
for complex indoor environments. Our results demonstrate that the algorithm is particularly efficient with
orthogonal polygons, commonly found in real-life buildings, due to their structured geometry. We compare
the performance across various polygon types and discuss optimization strategies for path naturalness and
computational efficiency. This work opens pathways for practical applications in indoor navigation.
1 INTRODUCTION
Indoor navigation has become increasingly significant
as spaces like shopping malls, airports, and museums
grow more complex alongside societal advancements
(Diakité and Zlatanova, 2018). Companies currently
provide map services through terminals to help users
locate destinations, but the next step involves real-
time positioning and navigation within these environ-
ments.
This research focuses on generating graphs for in-
door route searches. Presently, maps are manually an-
notated with location data (e.g., train stations, stores),
and vertices are placed at fixed intervals, leading to
dense graphs. Automating this process with polygon
division algorithms could reduce workloads while of-
fering tailored routing solutions based on different ob-
jective functions.
The main goal is to develop an optimal strategy
for creating indoor navigation graphs using Open-
StreetMap (OSM) data. This study adapts the
Mesh Navigation (Navmesh) algorithm proposed by
(Oliva and Pelechano, 2011), which partitions non-
intersecting polygons into convex subsets. Although
Navmesh is widely used in video games (Snook,
2000), this project applies it to indoor navigation.
Unlike road maps, where vertices naturally rep-
resent intersections and edges correspond to roads,
indoor spaces present challenges. Placing vertices
at regular intervals produces overly dense graphs,
while positioning them at entrances/exits fails for
non-convex rooms. A single vertex per room simpli-
fies the graph but yields unrealistic routes. Navmesh,
however, efficiently partitions complex spaces into
routing graphs for realistic navigation, a technique
adapted here.
The algorithm presented in (Oliva and Pelechano,
2011) has limitations: it omits the processing order
for concave angles and assumes minimizing polygons
as its goal without clear justification. This work ex-
plores multiple objective functions to assess the best
approach.
The project begins with implementing the algo-
rithm and conducting tests to evaluate its parameters,
identify limitations, and optimize performance.
The remainder of this paper is organized as fol-
lows: Section 2 reviews related work, Section 3 de-
tails the Navmesh algorithm, Section 4 compares it to
other methods, Section 5 presents results, and Section
6 offers concluding remarks.
2 RELATED WORK
While a significant amount of literature focuses on the
modelization of indoor navigation graphs (Park et al.,
2020)(Zhou et al., 2022)(Noureddine et al., 2020),
fewer works address their automatic generation. The
emphasis often lies on describing models rather than
automating their creation. This gap highlights the
need for more research into methods for automatic
graph generation.
The division of polygons into convex components
is not a new concept. It has been applied to nav-
Callico, M., Giroudeau, R., Darties, B. and Carrière, J.
Indoor Navigation: Navmesh Applied to Indoor Graph Creation.
DOI: 10.5220/0013109800003893
In Proceedings of the 14th International Conference on Operations Research and Enterprise Systems (ICORES 2025), pages 221-228
ISBN: 978-989-758-732-0; ISSN: 2184-4372
Copyright © 2025 by Paper published under CC license (CC BY-NC-ND 4.0)
221

igation since the 1980s in robotics under the term
meadow mapping, introduced by Ronald C. Arkin
(Arkin, 1986). Theoretically, Lingas et al. (1982)
showed that dividing a polygon without holes can
be solved in O(n
4
) time, where n is the polygon’s
number of sides. Numerous other algorithms for
polygon decomposition have been formalized (Her-
tel and Mehlhorn, 2006) (Keil, 2000) (O’Rourke and
Supowit, 1983).
Since the early 2000s, the term Navmesh, of-
ten attributed to Golodetz (Snook, 2000), has gained
prominence, particularly as a pathfinding tool in video
games. Navmesh divides the walkable plane into con-
vex polygons to form a simple graph, producing natu-
ral paths. Extensive research exists on Navmesh gen-
eration for multi-story terrains, dynamic 3D environ-
ments (O’Rourke and Supowit, 1983) (Berseth et al.,
2015), real-time applications (Hale et al., 2021) and
pathfinding (Brewer, 2019). However, applying such
complex algorithms to 2D floor plans—simpler than
video game environments—would be inefficient for
this work.
While methods for manually creating efficient
routing graphs exist (Yuan and Schneider, 2010)
(Jensen et al., 2009), this study seeks an auto-
mated, straightforward approach. The algorithm from
(Oliva and Pelechano, 2011), which offers polyno-
mial complexity, has been chosen. Although generat-
ing Navmesh is NP-hard when minimizing polygons
(Keil, 2000), the resulting solution, while not optimal,
will be shown to be sufficient for our needs.
3 NAVMESH
In this section, the algorithm presented in (Oliva and
Pelechano, 2011) is described, followed by an exam-
ple that illustrates the creation of the graph through
polygon division.
3.1 Description of the Algorithm
Let A = (a
0
,a
1
,...,a
n−1
) be the considered polygon.
Let B = (b
0
,b
1
,..., b
m−1
) be the set of non-convex
vertices of the polygon.
Definition 1 (Trigonometric and Anti-Trigonometric
Direction). A set of points in R
2
is in the trigonomet-
ric (resp. anti-trigonometric) direction if the points
are in an anti-clockwise (resp. clockwise) manner.
Definition 2 (Reflex Angles). Let α be an angle. α is
a reflex angle if α > π.
The goal of the algorithm is to divide the polygon
into a partition of convex polygons. The first stage
α
β
Figure 1: Examples of angles. α is a reflex angle (
3π
2
> π)
but β is not (
π
2
).
involves identifying the reflex angles within the poly-
gon. To achieve this, we iterate over the vertices in
the anti-trigonometric direction. For each vertex a
i
,
we consider the triangle formed by a
i−1
, a
i
, and a
i+1
.
If the triangle lies in the external polygon (resp. in-
ternal polygon) and is in the anti-trigonometric (resp.
trigonometric) direction, then vertex a
i
has a reflex
angle.
To detect these angles, we use the signed area
of a triangle, calculated with the shoelace formula
(Braden, 1986). The signed area determines whether
the triangle is oriented in the anti-trigonometric di-
rection (strictly negative), the trigonometric direction
(strictly positive), or if the points are collinear (equal
to 0). Using this formula, we identify all reflex angles
in the polygon.
Once the concave vertices are identified, the algo-
rithm generates a set of portals. These portals divide
the vertex into two interior angles that are no longer
reflex. We first describe the portal creation process
and then analyze the impact of the order in which con-
cave vertices are processed.
Definition 3 (Concave Vertex). A concave vertex is a
vertex of the original polygon in which interior angle
is a reflex angle. It is also called a notch.
An example of a concave vertex is presented in
Figure 1. α, which is a reflex angle, would be a con-
cave vertex if it was an internal angle inside a poly-
gon.
Let b
i
be in B. In this part, we will suppose all
indices are written modulo n −1. First of all, we have
to find the interest area of b
i
.
Definition 4 (Interest Area). The interest area of a
vertex b
i
is the interior polygon formed by the exten-
sion of its two adjacent sides, e
i−1,i
and e
i,i+1
.
An example of interest area can be found in Figure
2. In that interest area, any straight line coming from
the vertex b
i
will divide the reflex angle into two non-
reflex angles. The object chosen by the algorithm,
i.e. the object closest to the concave vertex inside
of the interest area, will be connected to b
i
, correcting
his reflex angle.
Depending on the closest object, there are three
possible cases:
ICORES 2025 - 14th International Conference on Operations Research and Enterprise Systems
222
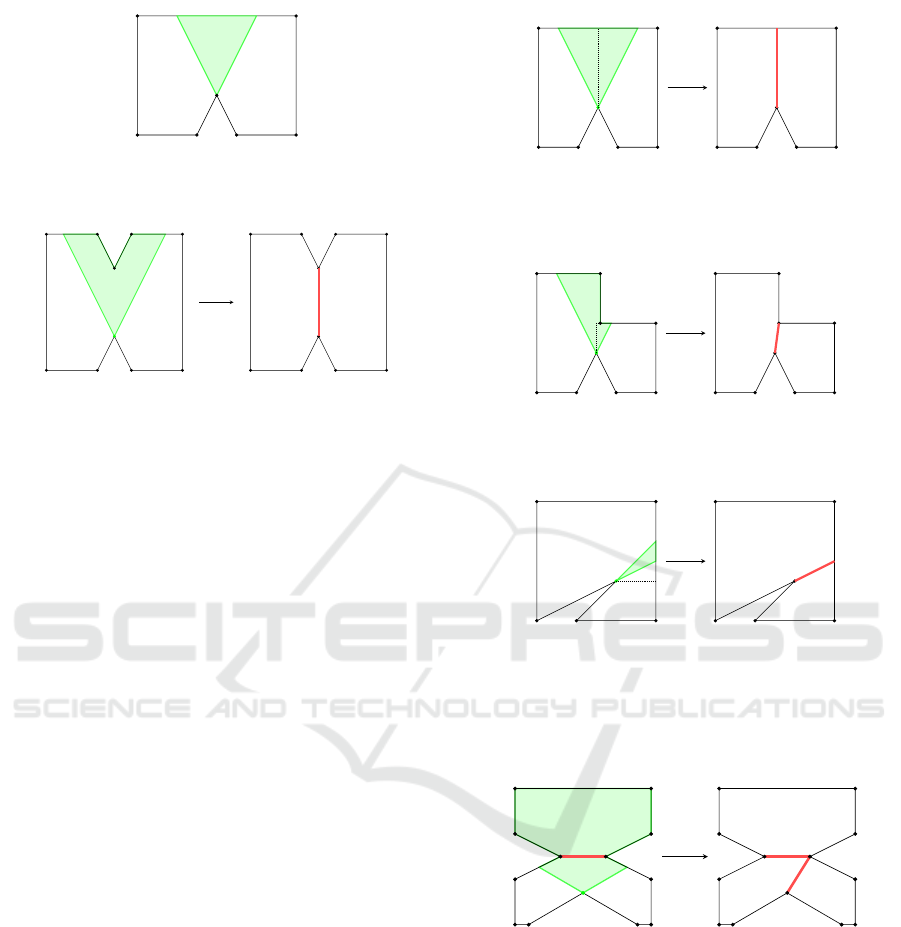
e
i−1,i
e
i−1,i
v
i
θ
v
i−1
v
i+1
I
i
Figure 2: Interest area example. The interest area I
i
, colored
in green, is the interest area of v
i
.
e
i−1,i
e
i−1,i
e
j−1, j
e
j, j+1
b
i
v
i−1
v
i+1
v
j
I
i
Figure 3: Portal from a vertex to another vertex. The closest
element to b
i
in the interest area I
i
is v
j
. On the right, the
resulting portal connecting the two, in red.
• if the closest object is another vertex c
j
, the por-
tal is simply a line between these two vertices. An
example of these kind of portals is found in 3.
• If the closest object is a side of the polygon e
j
,
there are five candidates for the portal. The clos-
est choice is its projection, but it is not necessarily
in the interest area. We can also consider the two
vertices incident to e
j
or the two intersections of
the interest area with e
j
. Figure 4 shows all possi-
ble cases of this step.
• Lastly, if the object is another portal P
j
, we con-
nect the vertex to the closest extremity of P
j
. If
none of these extremities are in the interest area,
we connect it to both of the extremities of the por-
tal. Two examples are shown in 5.
We now know what to do with each concave ver-
tex of the polygon. The question becomes: In which
order are we going to consider the vertices?There are
multiple possible orders:
• Random Order: the random order is the first
possibility. We think adding a random dimension
could allow to better the performances instead of
blindly following the same order for each poly-
gon.
• Trigonometric Order: it would be interesting to
compare the performances to a default order like
this one.
• Biggest (or Smallest) Angle First: dividing the
biggest angles first could give us bigger polygons
from which to create the graph, but smallest inter-
est areas gives us less choice, accelerating perfor-
mance at the cost of some other characteristics.
e
i−1,i
e
i,i+1
e
j
b
i
v
i−1
v
i+1
I
i
(a) Portal from a vertex to a side of the polygon. On the
left, the considered polygon, with b
i
the current vertex and
I
i
the interest area. The projection of e
j
is the closest object
in the area, so the portal on the right connects the two.
e
i−1,i
e
i,i+1
e
j
b
i
I
i
(b) Portal from a vertex to a side of the polygon. The pro-
jection is not in the interest area; the closest object to b
i
is
the extremity of e
j
, so on the right the two objects are con-
nected.
e
i−1,i
e
i,i+1
e
j
I
i
b
i
(c) Portal from a vertex to a side of the polygon. The pro-
jection is not in the interest area; the closet object in the
interest area is the intersection between the extension of
e
i−1,1
. On the right, the two objects connected.
Figure 4: Portals from a vertex to a side of the polygon.
e
i−1,i
e
i,i+1
b
i
p
j
I
i
Figure 5: Portal from a vertex to another portal. On the
left, we see the portal p
j
is the closest object to b
i
inside its
interest area; both extremities are at the same distance, so
we can chose one at random and connect it to b
i
, which is
done on the right.
3.2 Description of the Graph
From the division of the polygon in its different con-
vex parts, we can create the graph by adding a node
for every portal and creating a visibility graph.
Definition 5 (Visibility Graph in a Polygon). Let P be
a polygon. Let V be a set of nodes inside of the poly-
gon. We create E = {(i ∈ V, j ∈ V ),P covers (i, j)}.
Indoor Navigation: Navmesh Applied to Indoor Graph Creation
223

The visibility graph for the nodes V in P is G = (V,E).
The visibility graph contains an edge between ev-
ery two vertices that can see each other; in other
words, it contains an edge between every two vertices
whose edge would be contained inside the polygon.
For our graph, we also add the condition that a
portal acts as an edge of the polygon, i.e. an edge
of the graph would not cross the portals. The next
section contains examples of graph creation.
4 COMPARISON
In this section, we compare the Navmesh method to
other commonly used approaches for indoor graph
generation. Navmesh, while originally developed for
video game pathfinding, has demonstrated significant
potential for real-world applications, such as indoor
navigation in complex environments. However, sev-
eral alternative methods exist, each with their own ad-
vantages and drawbacks.
4.1 Equidistant Nodes
An alternative approach for graph creation involves
covering the polygon with evenly spaced nodes and
connecting adjacent nodes with arcs. As shown in
Figure 6, the graph produced by Navmesh is notably
less dense in comparison. While the equidistant nodes
method is not inherently flawed, it results in overly
dense graphs, which significantly increase the com-
putational cost of finding the shortest path.
4.2 Delaunay Triangulation
Another way of creating the graph is using Delaunay
triangulation (Delaunay, 1934). If we triangulate the
polygon in that way, we can obtain different portals,
and we can create the graph using the same method
used for Navmesh.
Figure 7 shows us a comparison between these
two methods. Density is no longer a problem, but
one of our main goals is the "naturalness of the path",
i.e., that the path chosen in the graph should be as
close as possible to what a human would do. We
see in the Delaunay triangulation graph, the paths we
could find would have a number of π/2 turns, but the
graph generated by Navmesh would, intuitively, find
more natural paths.
(a) Graph created by Navmesh.
(b) Graph created using equidistant nodes.
Figure 6: Comparison between Navmesh and the equidis-
tant nodes method.
5 PRACTICAL RESULTS
5.1 Theoretical Results
This section presents the obtained results. The algo-
rithm has been applied to a set of three different types
of polygons, each varying in size:
• Normal polygons - the algorithm was applied to
randomly generated normal polygons to establish
a performance baseline.
• Orthogonal polygons - these polygons are com-
posed exclusively of 90-degree or 270-degree an-
gles. Intuitively, orthogonal polygons are unions
of rectangular shapes.
• Isothetic polygons - isothetic polygons are con-
structed using two distinct families of lines, where
each family passes through a different common
point, forming a skewed grid.
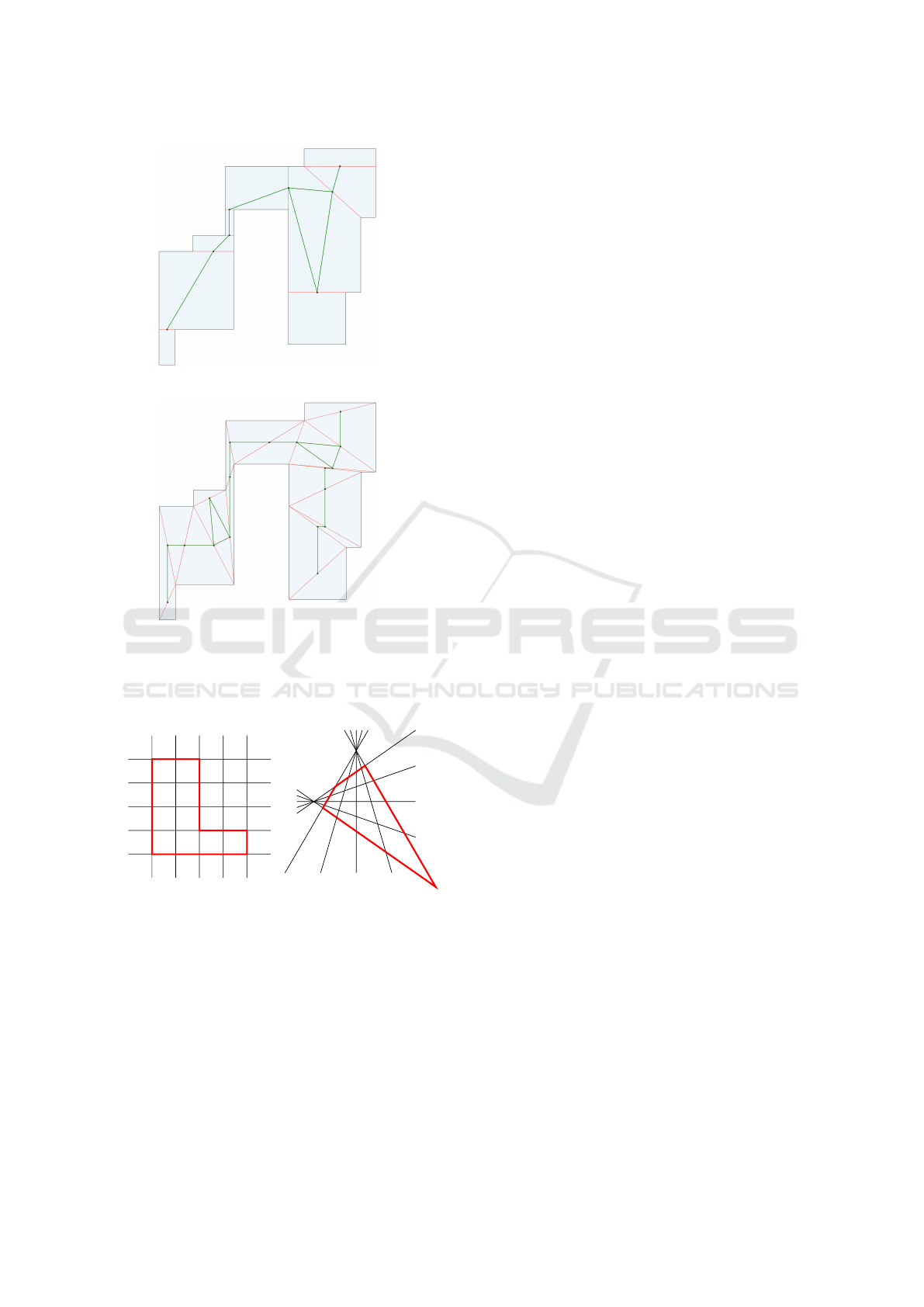
Figure 8 represents an example of both an orthog-
onal polygon and an isothetic polygon.
ICORES 2025 - 14th International Conference on Operations Research and Enterprise Systems
224
(a) Graph created by Navmesh.
(b) Graph created using Delaunay triangula-
tion.
Figure 7: Comparison between Navmesh and the Delaunay
triangulation method.
(a) (b)
Figure 8: On a, an orthogonal polygon, created from a
quadrilateral grid. On (b, an isothetic polygon, formed from
the grid created by two different families of lines passing
through the same common point.
5.1.1 Polygon Generation
To create the test sets, a random number of polygons
was generated using two different polygon genera-
tion methods. For the normal polygons, no restric-
tions were imposed, except for the exclusion of self-
intersecting polygons. The used method allows for
the generation of any polygon, including those with
holes. The technique employed, known as Inward
Denting, is derived from the article "Approaches for
Generating 2D Shapes." (Hada, 2014).
Normal Polygons. The first step in generating nor-
mal random polygons involves selecting n random
points, where n represents the number of vertices in
the final polygon. The randomness of the polygon
arises from these points, as the algorithm itself is de-
terministic and will produce the same polygon when
given the same set of points.
Initially, the convex hull of the set of points must
be determined. Several convex hull algorithms can
be employed for this task, such as the Gift Wrapping
algorithm (Jarvis march) (Jarvis, 1973), or Chan’s al-
gorithm (Chan, 1996). However, this article will not
focus on this aspect.
The subsequent step, which is repeated until no
points remain outside the polygon, involves adding
the node that modifies the perimeter the least. For
each arc of the polygon, the distance to each point is
computed, and the point that contributes the smallest
increase to the perimeter is added, while ensuring the
polygon remains non-intersecting.
Orthogonal and Isothetic Polygons. For orthogo-
nal polygons, we use the cut and expand method pro-
posed in (Tomás and Bajuelos, 2004). The genera-
tion of orthogonal polygons begins with a 2 × 2 grid,
where the grid is considered as a 2 × 2 square. From
this starting point, the grid is expanded, and random
sections are removed to generate an orthogonal poly-
gon. The algorithm is divided into two distinct steps:
the expand step selects a row and column of the grid
for expansion, while the cut step selects one of the
newly created areas to be removed.
When we generate orthogonal polygons on a grid
like in our method, we simply create a grid which can
be transformed into a matrix of size n × n with ones
where the polygon has a square and zeroes where it
does not. For isothetic polygons, we can then generate
the isothetic grid and use that matrix as a template for
that grid.
5.1.2 Results
Tests were executed on a server with 8GB of RAM
and an Intel(R) Xeon(R) with 2.50GHz. The algo-
rithm has been coded in Python; the importance of the
results lies mostly on the comparison between perfor-
mances, more so than on the performance itself.
To begin with, tests on three different types of
polygons, described above with different sizes, rang-
Indoor Navigation: Navmesh Applied to Indoor Graph Creation
225

ing from 20 to 500 nodes per polygon, with 20 poly-
gons generated for each size, are executed. The means
are represented in the graph.
The results in Figure 9 show the performance of
the Navmesh algorithm across normal, orthogonal,
and isothetic polygons of varying sizes. Orthogonal
polygons consistently demonstrate the fastest com-
putation times, even as size increases. This is due
to their simple geometry, which minimizes the need
for complex subdivisions and enables efficient space
partitioning. Since orthogonal polygons often repre-
sent real-world structures like grid-based buildings,
these results highlight the practical applicability of
Navmesh in such environments. Additionally, the
tight error bars indicate consistent performance across
trials, confirming the robustness of the algorithm for
this polygon type.
In contrast, normal and isothetic polygons exhibit
significantly longer computation times as size grows.
Normal polygons, with their irregular shapes, re-
quire more subdivisions to ensure convexity, increas-
ing processing time. Isothetic polygons, despite be-
ing theoretically regular, often introduce small, com-
plex geometries as they scale, contributing to sub-
stantial variability. This variability is evident in their
wider error bars, suggesting less predictable perfor-
mance. These findings emphasize the computational
challenges of irregular geometries and the importance
of selecting appropriate polygon types for efficient
Navmesh execution in real-world applications.
The next tests, shown in Figure 10 are about the
order of the nodes. The original article does not talk
about the order: we take the interest areas of the
notches and we find for each notch its closest element,
but we don’t know in which order the notes are con-
sidered. For this test, we compute how many portals
were added when considering the same polygon using
different orders. We have considered five different or-
ders:
• Normal Order: Notches are processed in a
clockwise order around the polygon.
• Random: Notches are processed in a randomly
determined order.
• Biggest or Smallest Angles First: Notches are
ordered by their internal angle size, with the
largest (or smallest) angles being processed first.
The results show that normal and random pro-
cessing orders perform similarly, with no significant
difference in the number of portals added. How-
ever, starting with the smallest angles increases portal
count, especially for larger polygons, as small inter-
nal angles create complex subdivisions early. In con-
trast, prioritizing larger angles simplifies the problem
earlier, reducing subdivisions. Regardless of order,
portal count grows linearly with polygon size.
For random polygons, the results highlight
promising real-world applications. Orthogonal poly-
gons, common in real buildings, compute signifi-
cantly faster. Additionally, processing the largest an-
gles first reduces portal count and graph density, im-
proving shortest-path search efficiency. These find-
ings are encouraging for practical use cases.
5.2 Real Use Cases
As part of the investigation, a program was developed
to apply the algorithm to real-world cases. By using
a GeoJSON file representing a real building as input,
the program executes the algorithm on the building
and generates a graph, which is then provided to the
user.
Definition 6 (GeoJSON File). A GeoJSON file is a
digital document containing geographical informa-
tion in the form of polygons, lines, or points. The data
is represented in terms of latitude and longitude.
The graphs generated for real-world scenarios are
both natural and accurately reflect the underlying en-
vironment. Figure 11 illustrates an example of a real-
world case processed by the program. The portals
generated are not excessive, and the resulting path
appears natural and intuitive. This outcome demon-
strates the effectiveness of the algorithm in produc-
ing paths that closely mirror real-world navigation
patterns, avoiding the creation of overly complex or
unnatural routes while ensuring computational effi-
ciency.
6 CONCLUSION
This paper shows that the Navmesh concept, widely
used in video games, can be adapted to real-world en-
vironments. The proposed algorithm balances com-
putational complexity and practical use, even with the
NP-hard challenge of polygon division. While not al-
ways optimal, the results prove effective for real-life
cases, especially with simpler structures.
Tests reveal the algorithm performs best on or-
thogonal polygons, typical of real-world buildings,
thanks to their regularity, which simplifies the search
space and reduces execution time. Irregular polygons,
on the other hand, increase complexity as their size
grows. Still, the algorithm remains scalable and effi-
cient, even for larger inputs.
Node processing tests showed that prioritizing the
largest angles reduces portal count, with all orders
ICORES 2025 - 14th International Conference on Operations Research and Enterprise Systems
226

Figure 9: Time spent executing the Navmesh algorithm across different polygon types and sizes. The error bars represent the
95% confidence interval for the results. Isothetic polygons exhibit significantly greater variability while orthogonal polygons
maintain consistently lower and more stable computation times, with barely visible confidence intervals.
Figure 10: Number of portals added per node order considered. The confidence intervals for the biggest angles first strategy
are shown: 95% of the values obtained in our simulations fall within 15% of the value represented on the plot. There are two
middle bars, representing the normal and random values, which have very similar values.
Figure 11: Application of the algorithm to a real use case. In red, the portals created by the algorithm, and in green the
generated graph. In blue, a found shortest path crossing the station.
Indoor Navigation: Navmesh Applied to Indoor Graph Creation
227

maintaining linear growth. Future work will focus on
improving path “naturalness” and optimizing for real-
ism over speed to ensure intuitive navigation solutions
across various polygon types.
Future research will focus on applying this
method to real-world scenarios and further investigat-
ing the “naturalness” of paths. Since the number of
portals directly impacts the graph, future work could
aim to optimize for path realism over speed, ensuring
intuitive and context-appropriate navigation solutions
across various polygon types.
REFERENCES
Berseth, G., Kapadia, M., and Faloutsos, P. (2015). Ac-
clmesh: Curvature-based navigation mesh generation.
In Proceedings of the 8th ACM SIGGRAPH Confer-
ence on Motion in Games, page 97–102.
Braden, B. (1986). The surveyor’s area formula. The Col-
lege Mathematics Journal, 17(4):326–337.
Brewer, D. (2019). Tactical pathfinding on a navmesh.
Game AI Pro, 360:25–32.
Chan, T. M. (1996). Optimal output-sensitive convex hull
algorithms in two and three dimensions. Discrete &
Computational Geometry, 16(4).
Delaunay, B. (1934). Sur la sphère vide. Bulletin de
l’Academie des Sciences de l’URSS. Classe des sci-
ences mathematiques et na, 1934(6):793–800.
Diakité, A. A. and Zlatanova, S. (2018). Spatial subdivi-
sion of complex indoor environments for 3d indoor
navigation. International Journal of Geographical In-
formation Science, 32(2):213–235.
Hada, P. S. (2014). Approaches for generating 2d shapes.
UNLV Theses, Dissertations, Professional Papers,
and Capstones.
Hale, D. H., Youngblood, G. M., and Dixit, P. (2021).
Automatically-generated convex region decomposi-
tion for real-time spatial agent navigation in virtual
worlds. In Proceedings of the AAAI Conference on Ar-
tificial Intelligence and Interactive Digital Entertain-
ment, pages 173–178.
Hertel, S. and Mehlhorn, K. (2006). Fast triangulation of
simple polygons. In Lecture Notes in Computer Sci-
ence, pages 207–218.
Jarvis, R. (1973). On the identification of the convex hull
of a finite set of points in the plane. Information Pro-
cessing Letters, 2(1).
Jensen, C. S., Lu, H., and Yang, B. (2009). Graph model
based indoor tracking. In Proceedings - IEEE In-
ternational Conference on Mobile Data Management,
pages 122–131.
Keil, J. M. (2000). Polygon decomposition. Handbook of
computational geometry, 2:491–518.
Noureddine, H., Ray, C., and Claramunt, C. (2020). Seman-
tic trajectory modelling in indoor and outdoor spaces.
In 2020 21st IEEE International Conference on Mo-
bile Data Management (MDM), pages 131–136.
Oliva, R. and Pelechano, N. (2011). Automatic generation
of suboptimal navmeshes. In MIG’11: Proceedings of
the 4th International Conference on Motion in Games,
pages 328–339.
O’Rourke, J. and Supowit, K. (1983). Some np-hard poly-
gon decomposition problems. IEEE transactions on
information theory, 29:181–190.
Park, J., Goldberg, D. W., and Hammond, T. (2020). A com-
parison of network model creation algorithms based
on the quality of wayfinding results. Transactions in
GIS, 24(3):602–622.
Snook, G. (2000). Simplified 3d movement and pathfind-
ing using navigation meshes. In Game Programming
Gems, pages 288–304. Charles River Media.
Tomás, A. P. and Bajuelos, A. L. (2004). Generating ran-
dom orthogonal polygons. In Current Topics in Artifi-
cial Intelligence, pages 364–373, Berlin, Heidelberg.
Yuan, W. and Schneider, M. (2010). inav: An indoor
navigation model supporting length-dependent opti-
mal routing. In Lecture Notes in Geoinformation and
Cartography, pages 299–313.
Zhou, Z., Weibel, R., Richter, K.-F., and Huang, H. (2022).
Hivg: A hierarchical indoor visibility-based graph for
navigation guidance in multi-storey buildings. Com-
puters, Environment and Urban Systems, 93:101751.
ICORES 2025 - 14th International Conference on Operations Research and Enterprise Systems
228
