Evaluating Transformers Learning by Representing Self-Attention

Weights as a Graph

Rebecca Leygonie

, Sylvain Lobry

and Laurent Wendling

Laboratory LIPADE, Universit

e Paris Cit

e, 45 rue des Saints-P

eres, Paris, 75006, France

Keywords:

Explainability, Graph Visualization, Self-Attention, Health Data.

Abstract:

Transformers architectures have established themselves as the state of the art for sequential data processing,

with applications ranging from machine translation to the processing of Electronic Health Records (EHR).

These complex data present a particular challenge in terms of explainability, which is a crucial aspect for their

adoption in the healthcare ﬁeld, subject to strict ethical and legal requirements. To address this challenge, we

propose an approach to represent learning through graphs by exposing the self-attention links between tokens.

We introduce a metric to assess the relevance of the connections learned by the model, in comparison with

medical expertise. We apply our approach to the Behrt model, designed to predict future hospital visits based

on sequences of previous visits, trained on data from the French National Health Data System. Our exper-

iments show that our method facilitates understanding of model learning, and enables a better appreciation

of the inﬂuence of diagnoses on each other, as well as of the biases present in the data, than global model

evaluation measures.

1 INTRODUCTION

Since their introduction (Vaswani et al., 2017), Trans-

formers architectures (Lin et al., 2022) have been

recognized as the state of the art for processing se-

quential data (Wen et al., 2023), primarily due to

their self-attention mechanism. This mechanism ef-

fectively captures the relationships between different

elements (tokens) of a sequence while minimizing the

vanishing gradient problem (Bengio et al., 1994) of-

ten encountered with recurrent architectures. Some of

the best-known models using this technology include

BERT (Bidirectional Encoder Representations from

Transformers) (Devlin et al., 2019), GPT (Generative

Pre-trained Transformer) (Radford et al., 2018), and

T5 (Raffel et al., 2020), which have revolutionized

the ﬁeld of natural language processing.

Initially introduced for machine translation task

(Vaswani et al., 2017), Transformers are now com-

monly used to process all forms of sequential data,

including Electronic Health Records (EHR) (Nerella

et al., 2023). EHR contains a multitude of complex

data. This includes ICD (International Classiﬁcation

https://orcid.org/0009-0007-1279-9832

https://orcid.org/0000-0003-4738-2416

https://orcid.org/0000-0003-1091-5995

of Diseases)

codes for diagnoses and medications, as

well as demographic information and treatment his-

tories, which are recorded at each patient visit. The

complexity of these data stems not only from their

volume and diversity, but also from their structuring

into temporal sequences, which capture cycles of di-

agnosis, treatment and patient follow-up, including

potential re-admissions.

Although the adaptation of natural language pro-

cessing methods for EHR data is very promising, the

lack of explainability raises legal and ethical issues

that constitute a signiﬁcant obstacle on the deploy-

ment of these methods for decision support in the

healthcare ﬁeld (Amann et al., 2020; Shortliffe et al.,

2018). It is currently possible to explain model learn-

ing by visualizing learned self-attention weights, but

this is done on a few examples, often to show what

the model has learned well, without comparison with

a ground truth (Siebra et al., 2024).

To address this problem, we propose an approach

for understanding and validating the learning of a

model based on self-attention mechanisms. This

framework consists in representing, in the form of

graphs, the links between input tokens, weighted by

the self-attention weights learned by the model. Each

The International Classiﬁcation of Diseases is a med-

ical classiﬁcation used worldwide for epidemiological,

health management and clinical purposes.

Leygonie, R., Lobry, S. and Wendling, L.

Evaluating Transformers Learning by Representing Self-Attention Weights as a Graph.

DOI: 10.5220/0013111400003912

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 20th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2025) - Volume 1: GRAPP, HUCAPP

and IVAPP, pages 695-705

ISBN: 978-989-758-728-3; ISSN: 2184-4321

695

Visit 1: O20 (Hemorrhage in early pregnancy)

Visit 2: J45 (Asthma)

Visit 3: O43 (Placenta anomalies)

Visit 4: O80 (Single spontaneous birth)

diagnostic

correlation

Figure 1: Overview of the proposed approach. Given a sequence of diagnostics input into a Transformer model, we extract

the self-attention weights learned by the model between each pair of tokens and represent them as a graph, where each node

is a diagnostic and each directed edge from node A to node B represents the self-attention weight node A gives to node B

during the model’s prediction. We evaluate this graph against a graph representing medical expertise to assess the relevance

of the self-attention weights learned by the model.

link in the graph thus represents the relative impor-

tance of each token in relation to the others, in a pre-

cise data sample. We then evaluate the graph against

a ground truth collected from experts to obtain a rele-

vance score for the self-attention links learned by the

model. Figure 1 illustrates the proposed approach.

To assess our methodology we apply this approach

to a speciﬁc model, Behrt (Li et al., 2020), which has

been trained on data from the French National Health

Data System (SNDS). This model aims at predicting

the next hospital visit of a patient given a sequence of

previous visits. We apply our approach on two differ-

ent use cases, illustrating the versatility and effective-

ness of our method. The results show that our method

can be used to understand and validate model learn-

ing. In addition, the use of graphical representations

helps users to understand more directly the connec-

tions that the model has learned, which is crucial for

increasing the conﬁdence of healthcare professionals

in using the model’s predictions in concrete clinical

situations. In this work, we introduce four contribu-

tions:

• Contribution 1. We propose a method that graph-

ically represents the interactions between tokens

learned by the model.

• Contribution 2. We propose an approach for

modeling medical expertise as a graph.

• Contribution 3. We introduce a new metric to

evaluate the relevance of the connections learned

by the model by comparing them to medical ex-

pertise.

• Contribution 4. We validate our method through

two use cases.

The paper is structured as follows. In Section 2, we

review existing works on adapting Transformers to

electronic health record (EHR) data, as well as the

explainability methods used to validate these models.

Section 3 details our proposed methodology. Experi-

mental protocols are explained in Section 4, while the

results obtained are presented in Section 5 and dis-

cussed in Section 6.

2 RELATED WORK

2.1 Transformers for Health Data

For several years, researchers have propose to exploit

data from the International Classiﬁcation of Diseases

IVAPP 2025 - 16th International Conference on Information Visualization Theory and Applications

696

(ICD), notably for the task of predicting future diag-

noses (Nerella et al., 2023). Behrt (Li et al., 2020),

an adaptation of BERT for EHR data, is pre-trained

using a masked language model before being trained

on sequences of ICD codes and age data to predict

future diagnoses. Hi-BEHRT (Li et al., 2022), an ex-

tension of Behrt, uses a hierarchical structure to pro-

cess long sequences of medical data more efﬁciently.

Furthermore, Med-BERT (Rasmy et al., 2021) mod-

iﬁes the pre-training task to include the prediction

of length of stay and uses a combination of ICD-9

and ICD-10 codes to predict diabetes and heart fail-

ure. ICD-9 and ICD-10 are two different versions

of disease classiﬁcation. Proposed in 1979, ICD-9

comprises 14, 000 codes covering diagnoses and pro-

cedures. The codes are mainly numerical and fairly

general. Adopted in 1990 and implemented in many

countries in the early 2000s, ICD-10 is much more

detailed, with around 70, 000 diagnostic codes. It pro-

vides a much more precise description of diseases and

their symptoms. HiTANet (Hierarchical Time-aware

Attention Network) (Luo et al., 2020) incorporates a

temporal vector to represent the time elapsed between

consecutive visits, combined with the embedding of

the original visit to predict future diagnoses on three

disease-speciﬁc databases. Finally, RAPT (Represen-

tAtion by Pre-training time-aware Transformer) (Ren

et al., 2021) integrates an explicit duration vector with

additional pre-training tasks such as similarity predic-

tion and reasonableness checking to address issues

of insufﬁcient data, incompleteness, and the typical

short sequences of EHR data. RAPT is evaluated

for predicting pregnancy outcomes, risk periods, as

well as diagnoses of diabetes and hypertension dur-

ing pregnancy.

2.2 Validation of Self-Attention Links

Among the studies that use Transformer-type archi-

tectures on electronic health record (EHR) data, those

that evaluate model performance by validating the

self-attention links learned by the model fall into two

groups. The ﬁrst category includes works that assess

the relevance of self-attention weights through a few

selected examples. Among these works, the authors

of LSAN (Ye et al., 2020), using a hierarchical at-

tention module, randomly select samples to analyze

which symptoms receive the most attention during

each visit for risk prediction. Others, such as the au-

thors of Behrt (Li et al., 2020), Med-BERT (Rasmy

et al., 2021) and (Meng et al., 2021), use the bertviz

(Vig, 2019) tool to visualize interactions between di-

agnoses with signiﬁcant self-attention weights. This

tool allows to visualize self-attention links between

pairs of elements in a sentence, by choosing from the

attention heads and layers of the model.

The second category includes work that modi-

ﬁes the representation of input data, making self-

attention weights more interpretable. For example,

(Dong et al., 2021) represent data as graphs linking

domain concepts. This modiﬁcation of the data rep-

resentation improves the explainability of the atten-

tion mechanism, as it relies on the attention weights

assigned to each graph instance and not just on the

direct relationships between inputs and outputs. Sim-

ilarly, (Peng et al., 2021) introduce ontologies as input

data, demonstrating that it is possible to obtain more

interpretable medical codes links.

Theses works aims to interpret and validate model

learning through self-attention, but experiments in the

EHR ﬁeld are often limited to validating performance

through manually evaluated visual examples. In this

work, we propose a method that evaluates the learn-

ing of self-attention links by representing them as a

graph and comparing them to a ground truth also rep-

resented as a graph. To represent self-attention links

as a graph, we ﬁrst extract these weights (Section 3.1)

during inference of a Behrt (Li et al., 2020) model,

by choosing a speciﬁc layer. These weights show the

attention that each token gives to every other token in

the same sequence. In parallel with this collection of

data for all sequences, we identify the most inﬂuen-

tial tokens for prediction, by analyzing their gradient

(Section 3.2). We then use these information to con-

struct a directed graph (Section 3.3). In this graph, the

tokens of importance are the source nodes, and they

are connected to the other tokens to which they are

linked in the sequences. We also add self-attention

links between tokens that are linked to those identi-

ﬁed as important, illustrating the interactions and self-

attention weights between the different tokens playing

a primary or secondary role in the prediction made by

the model. Finally, we evaluate the graph by measur-

ing the weight of directed edges common to those of

a graph representing ground truth (Section 3.4).

3 METHODOLOGY

Figure 2 illustrates the different steps of our method-

ology.

3.1 Creation of the Global Attention

Matrix

Let T = {t

, t

, . . . , t

} be a set (or vocabulary) of V

distinct tokens. We consider a labeled dataset X =

, y

)

i∈J1;NK

consisting of N sequences X

and their

Evaluating Transformers Learning by Representing Self-Attention Weights as a Graph

697

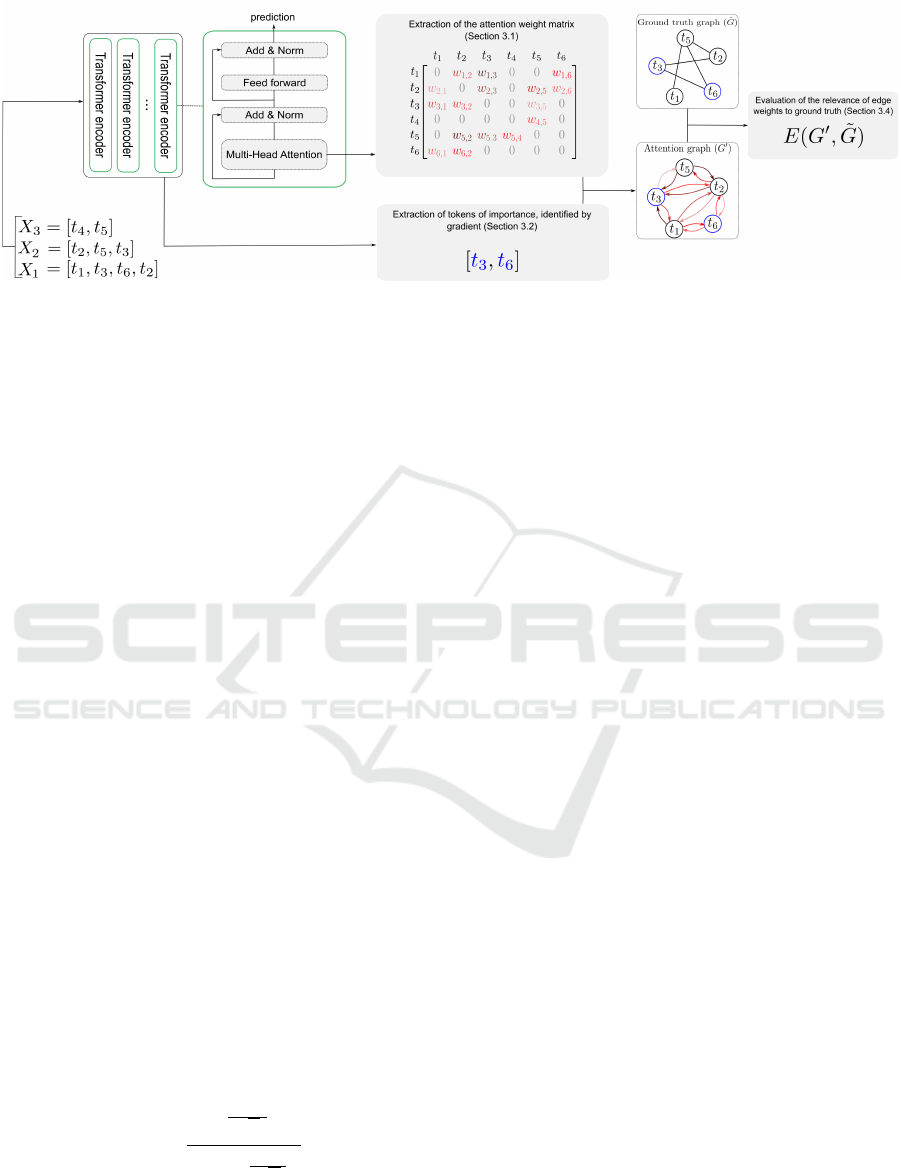
Figure 2: Stages of the proposed methodology: from the sequences given as input to a Transformer, we identify tokens of

importance by gradient analysis. A global attention matrix is constructed in which each token assigns a weight (denoted

w) to all other tokens in a global vocabulary, provided that both tokens coexist in the same sequence. Then, we extract a

self-attention subgraph G

′

by starting with the important tokens (blue nodes) and adding all the tokens (black nodes) to which

they are linked in the global attention matrix. A directed edge linking two nodes in G

′

is weighted by the self-attention weight

that the source node assigns to the target node. We evaluate the relevance of the self-attention weights learned by the model

using the evaluation function E, which compares the attention graph G

′

with the graph representing ground truth, denoted

associated ground truth y

. Speciﬁcally, each X

a sequence of tokens (x

, . . . , x

), where z

∈ N and

∀j ∈ J1, z

K, x

∈ T . We feed each sequence X

into a

Transformer trained to predict ˆy

. If the model’s pre-

diction ˆy

matches the true label y

, we retrieve the at-

tention matrix A

of size z

×z

during the processing

of X

through the model:







1,1

1,2

··· a

1,z

2,1

2,2

··· a

2,z

··· a







(1)

where each element a

m,n

represents the self-attention

that the token x

in the sequence X

gives to the to-

ken x

in the same sequence. Speciﬁcally, in a Trans-

former layer, the self-attention a

m,n

is calculated by

projecting x

into a query vector Q

= W

and x

into a key vector K

, where, W

and W

rep-

resent the learned weight matrices. These query and

key vectors are used to compute a raw self-attention

score via a dot product, which is then divided by the

dimension of the key vectors (the size of the embed-

dings used to represent each token in the key space).

Finally, this normalized score is passed through a soft-

max function that converts it into probabilities, result-

ing in :

m,n



·K

√



∑

l=1



·K

√



(2)

where z

is the total number of tokens in the sequence

. Note that the self-attention a

m,n

in the matrix is

calculated as the mean of the attention that token x

gives to token x

in all the attention heads of the se-

lected layer.

Once we’ve retrieved the self-attention weights

for each peer in each sequence, we aggregate these

weights into a global attention matrix G of size (V ×

V ) where V is the size of the token vocabulary T . Fi-

nally, the matrix G is nothing other than an adjacency

matrix representing the self-attention links between

all tokens. This matrix lists the values of the self-

attention weights of all possible pair links among all

tokens in the global vocabulary. Speciﬁcally, G syn-

thesize the attention that each token t

gives to each

other token t

across all analyzed sequences. For each

pair of tokens (t

, t

), we identify all occurrences of

these tokens in different sequences and accumulate

the corresponding self-attention values for these to-

kens from the A

matrices associated with each se-

quence. We collect these values into a set S

= {a

′

| x

′

= t

, x

′

= t

m, n ∈ {1, . . . , V }, m

′

, n

′

∈ {1. . . , z

}}

(3)

Each element G[m, n] of the matrix is then calcu-

lated by taking the median of these values from the

set S

G[m, n] = Median(S

) (4)

Note that we choose to take the median value to

avoid potential outliers. Finally, G[m, n] captures the

level of attention that each token t

gives to every

other token t

across all sequences, reﬂecting the cen-

tral tendency of the intensity of interaction between

any pair of tokens in the dataset.

IVAPP 2025 - 16th International Conference on Information Visualization Theory and Applications

698

3.2 Identiﬁcation of Important Tokens

For each sequence X

where the model correctly pre-

dicts the label ˆy

, we recover the gradient ∆(x

) of

each token x

in X

by performing a backpropagation

pass. The gradients allow us to measure the inﬂuence

of each token on the prediction. Knowing that the

model makes a good prediction, gradients with higher

values indicate a more signiﬁcant contribution to the

model’s decision (Simonyan et al., 2014). For each

token in the vocabulary T that appears in at least one

correctly predicted sequence, we calculate the median

importance of the gradients associated with that to-

ken.

Finally, we select a predeﬁned number g of

the most important tokens according to these me-

dian gradient measures, thus identifying those tokens

that most consistently and signiﬁcantly inﬂuence the

model’s correct predictions.

3.3 Self-Attention Graph Generation

We aim to construct a self-attention graph G

′

that rep-

resents the interactions between tokens as learned by

the model. In other words, we extract a subgraph from

the global attention matrix by selecting the relation-

ships between a chosen set of tokens (nodes). In this

section, we explain how we select the nodes of the

graph.

To create an interpretable and comparable graph,

we use the g tokens with the most signiﬁcant gradients

as the initial nodes of G

′

. Then, we expand this ini-

tial set by adding any token t

from the global vocab-

ulary T , for which the self-attention G[m, n] is non-

zero, where the token t

or t

belongs to the initial

set of g tokens of importance. Thus, the set of nodes

in G

′

includes the initial g tokens and all the tokens

directly linked to them, with their associated median

self-attention weights. We construct a directed graph

where each pair (t

, t

) among the nodes of G

′

is con-

nected by a directed edge from t

to t

if G[m, n] is

non-zero. The directed edges are weighted by the cor-

responding values of G, which quantify the intensity

of self-attention t

gives to t

3.4 Evaluation of the Self-Attention

Learned by a Model

We want to evaluate in an automated way the qual-

ity of the self-attention connections between tokens

learned by an attention-based model. To do this, we

compare these connections to a reference, represented

by a graph

G. For our experiments we have imple-

mented a protocol for the creation of the reference

graph by medical experts, detailed in Section 4.4.

This ground-truth graph,

G, contains the same nodes

as the graph G

′

because we want to evaluate the inter-

actions (directed edges) and not the tokens (nodes),

which depend essentially on the sequences used. We

wish to evaluate whether the model has learned a good

distribution of self-attention weights compared to es-

tablished expertise. For this, we introduce an eval-

uation method that takes into account the weight of

edges, which is not the case for classical evaluation

measures such as precision or recall. Evaluation is

performed by calculating the difference between the

weighted proportion of G

′

directed edges common to

G and the weighted proportion of G

′

directed edges

not common to

G. The evaluation function, which we

call E, is calculated as follows:

E(G

′

G) = w

−w

out

(5)

where:

• w

∑

(m,n)∈G

′

∩

∑

(m,n)∈G

′

, is the weighted proportion

of directed edges in the graph G

′

that are also

present in the ground truth

G, i.e. the number of

′

directed edges included in

G weighted by their

weight and normalized by the weighted number

of directed edges in G

′

• w

out

∑

(m,n)∈G

′

,(m,n)̸∈

∑

(m,n)∈G

′

, is the weighted propor-

tion of directed edges in G

′

that are not conﬁrmed

The evaluation function E measures the alignment be-

tween the graph G

′

and the ground truth

G. It ranges

from -1 to 1, where a score of 1 is reached when all

directed edges of G

′

are included in

G, and -1 when

no directed edges are included. Scores between 0 and

1 indicate that directed edges included in

G are more

heavily weighted than those not included, reﬂecting

a predominance of matches. Conversely, scores be-

tween -1 and 0 indicate that directed edges not in-

cluded in

G are more heavily weighted, reﬂecting a

predominance of mismatches.

4 EXPERIMENTS

We evaluate our method using an attention-based

model, trained by the Lab Sant

e of the Direction de

la recherche, des

etudes, de l’

evaluation et des statis-

tiques (Drees

). To test the validity of the graphs

generated from self-attention weights and links, we

set up a protocol for creating ground truth graphs in

collaboration with the medical experts in the depart-

ment.

https://drees.solidarites-sante.gouv.fr

Evaluating Transformers Learning by Representing Self-Attention Weights as a Graph

699

4.1 Model

We wish to study the learning of a model based on at-

tention mechanisms, speciﬁcally adapted to the anal-

ysis of medical data. For our experiments, we use the

model Behrt, a variant of BERT, trained on the task

of predicting patient diagnoses during future hospital

visit, based on a historical sequence of visits.

4.1.1 Data

The data on which the model was trained comes

from the MCO (M

edecine, Chirurgie, Obst

etrique) ta-

bles of the PMSI (Programme de M

edicalisation des

Syst

emes d’Information) of the SNDS. Each hospi-

tal visit is characterized by a set of diagnoses, in-

cluding a principal diagnosis and, where applicable,

a related diagnosis, as well as several associated diag-

noses, which enrich the context of the principal diag-

nosis.

4.1.2 Training Task

The model is trained on a multi-class and multi-label

classiﬁcation task. This means that the label to be

predicted can contain several different classes. The

classes are represented by 2053 diagnoses coded ac-

cording to the 10th revision of ICD, which is the list

of codes that classify diseases and medical problems.

The model training process is divided into two dis-

tinct phases to reﬁne the predictive capabilities of the

model, specializing it to meet the speciﬁc require-

ments of the medical ﬁeld:

1. Prediction of masked words, where the model

learns to identify and restore hidden elements in

the training data.

2. Fine-tuning of the pre-trained model to specif-

ically adapt it to the task of predicting diagnoses

for upcoming hospital visits.

The training of the model for masked word predic-

tion was conducted on individuals having more than 2

hospital visits and at least 3 diagnostic codes, drawn

from two samples. A random sample of 4% of the

SNDS data covering the period from 2008 to 2017,

and a sample considering all SNDS data from 2018

to 2021. The dataset for the masked word prediction

contains 14, 59M samples. The training of the model

for predicting diagnoses of the next hospital visit is

carried out on individuals having at least 4 visits in

their medical history, using the same datasets as the

ﬁrst phase. The dataset for the ﬁne-tuning, i.e the pre-

diction of the next hospital visit contains 5, 94M sam-

ples. In both datasets, the minimum numbers of visits

and codes in the sequence are imposed to ensure that

the training sample contains sufﬁciently diverse med-

ical paths and thus avoid overﬁtting.

4.2 Use Cases

We apply our method during the model inference

phase, retrieving the medical histories of individuals

for whom the model has correctly predicted the next

visit, i.e. the diagnosis to be predicted is in the top 2

of predictions. We ensure that the other diagnosis in

the top 2 is contextually related to the predicted diag-

nosis, reinforcing the relevance of our interpretation

of importance gradients. We are working on two dis-

tinct use cases, based on different samples of test data.

These use cases concern the prediction of incident di-

agnoses, meaning that the diagnosis to be predicted

does not appear in the input sequence. This approach

makes it possible to precisely analyze the inﬂuence of

previous diagnoses on predictions.

4.2.1 Use Case of Childbirth

The class childbirth includes the following ICD10

codes: (O80) single spontaneous delivery; (O81) sin-

gle delivery by forceps and suction cup; (O82) single

delivery by caesarean section; (O83) other assisted

single deliveries; and (O84) multiple deliveries. We

select 2000 individuals for whom the visit to be pre-

dicted contains a label of the childbirth class, which

is not in the sequence we give as model input. On the

sample used, the model makes a good prediction for

190 individuals.

4.2.2 Use Case of Hypertensivity

The hypertensivity is deﬁned by the following ICD10

codes: (I10) essential hypertension; (I11) hyperten-

sive heart disease; (I12) hypertensive nephropathy;

(I13) hypertensive cardionephropathy; and(I15) sec-

ondary hypertension. As in the case of childbirth, we

randomly select 2000 individuals for whom the visit

to be predicted contains the diagnosis I10 and none

of the hypertensivity class labels is in the sequence

corresponding to the medical history. On the sample

used, the model makes a good prediction for 514 in-

dividuals.

4.3 Generation of Graph G

′

from Behrt

in Inference

For each use case, the creation of the graph begins by

retrieving the attention matrices for each individual,

taken from the last layer of the Behrt model. Next,

we build a global median attention matrix of dimen-

sions 2053 ×2053, where 2053 represents the number

IVAPP 2025 - 16th International Conference on Information Visualization Theory and Applications

700

of possible diagnoses. We also extract the gradient for

each diagnosis from the sequence representing an in-

dividual’s medical history, which we give as input to

the model. This enables us to identify, for each indi-

vidual, which diagnoses most inﬂuenced the predic-

tion. We then calculate the median of the gradients

per diagnosis.

For both use cases and to preserve conﬁdentiality,

we limit ourselves to the study of diagnoses or pairs of

diagnoses present in at least ﬁve distinct medical path-

ways. This method allows us to maintain anonymity

while preserving analytical relevance. Consequently,

some diagnoses selected from the g diagnoses of im-

portance may not appear in our graph if their connec-

tions with other diagnoses do not appear in the re-

quired minimum of ﬁve distinct medical pathways.

Similarly, a connection between two diagnoses will

not be visible in the graph if the pair of diagnoses does

not appear in at least ﬁve distinct sequences. Thus, for

both use cases, the number of signiﬁcant diagnoses

identiﬁed by the median gradient value is arbitrarily

chosen so that the generated graph contains enough

directed edges.

4.3.1 Use Case of Childbirth

We select the 10 most inﬂuential diagnoses accord-

ing to the median value of their gradient (represented

by blue-bordered nodes in Figure 3a). From these

diagnoses, we extract the self-attention subgraph G

′

that links important nodes to other associated nodes

in the global attention matrix, as well as links be-

tween added nodes (nodes that are not part of the set

of importance diagnoses). Figure 3a illustrates the

overall graph showing the self-attention relationships

between the importance diagnoses, the diagnoses to

which they are connected in the global attention ma-

trix, and the links between these diagnoses. More pre-

cisely, an directed edge from node A to node B in the

same graph is weighted by the median self-attention

that A gives to B. The weight is represented by the

color of the directed edge.

4.3.2 Use Case of Hypertensivity

We identify the 46 most signiﬁcant diagnoses accord-

ing to the value of their gradients. As with the child-

birth use case, these diagnoses are then connected to

the other tokens associated with them in the global at-

tention matrix, and the directed edges of the graph are

weighted according to the self-attention weight. The

graph for this use case is shown in ﬁgure 3b.

https://icd.who.int/browse10/2019/en

4.4 Creation of the Ground Truth

Graph

To interpret the links between diagnoses learned by

the Behrt model through the mechanics of attention,

we want to compare them with a ground truth, which

translates into medical expertise. Self-attention, al-

though signiﬁcant in our model, has no direct and ob-

vious correspondence in the medical context. In order

to validate or invalidate these links, we have designed

a protocol aimed at healthcare professionals, involv-

ing the creation of a graph of relationships between

diagnoses. This graph is designed to be undirected

and unweighted.

The protocol is based on two lists of diagnoses:

the ﬁrst, called ”gradients”, contains the diagnoses

we have identiﬁed as important for prediction. The

second, called ”other”, includes diagnoses that are

related to the ”gradient” diagnoses according to the

global attention matrix. To produce a graph that faith-

fully reﬂects the clinical reality of the two use cases

presented, we called on the expertise of two Drees

medical experts to form clusters. We speciﬁcally

asked them to link each diagnosis from the ”other”

list to one or more diagnoses from the ”gradient” list,

taking into account the existence of a contextual cor-

relation between them. This correlation may concern

elements such as comorbidity, causality, impact on

treatment, clinical implication, or coding frequency.

4.5 Evaluation of G

′

Relative to

We evaluate the self-attention weights of the graph

′

in relation to the ground truth

G by calculating

E(G

′

G). Because G

′

is directed, and

G is not, we

consider the edges of

G to be bidirectional edges. The

aim is to analyze G

′

according to different thresh-

olds that determine which directed edges are taken

into account. More speciﬁcally, we aim to determine

whether there is a threshold where the directed edges

of G

′

in common with

G are correctly identiﬁed by

the model as being signiﬁcant, i.e. the weight of these

directed edges is greater than that of directed edges

not included. For each threshold established, we con-

sider only those directed edges of G

′

whose weight

exceeds that threshold. We then remove the isolated

nodes from G

′

and keep the same nodes in

G. The

results of this evaluation, depending on the thresholds

chosen, are presented in Section 5.

Evaluating Transformers Learning by Representing Self-Attention Weights as a Graph

701

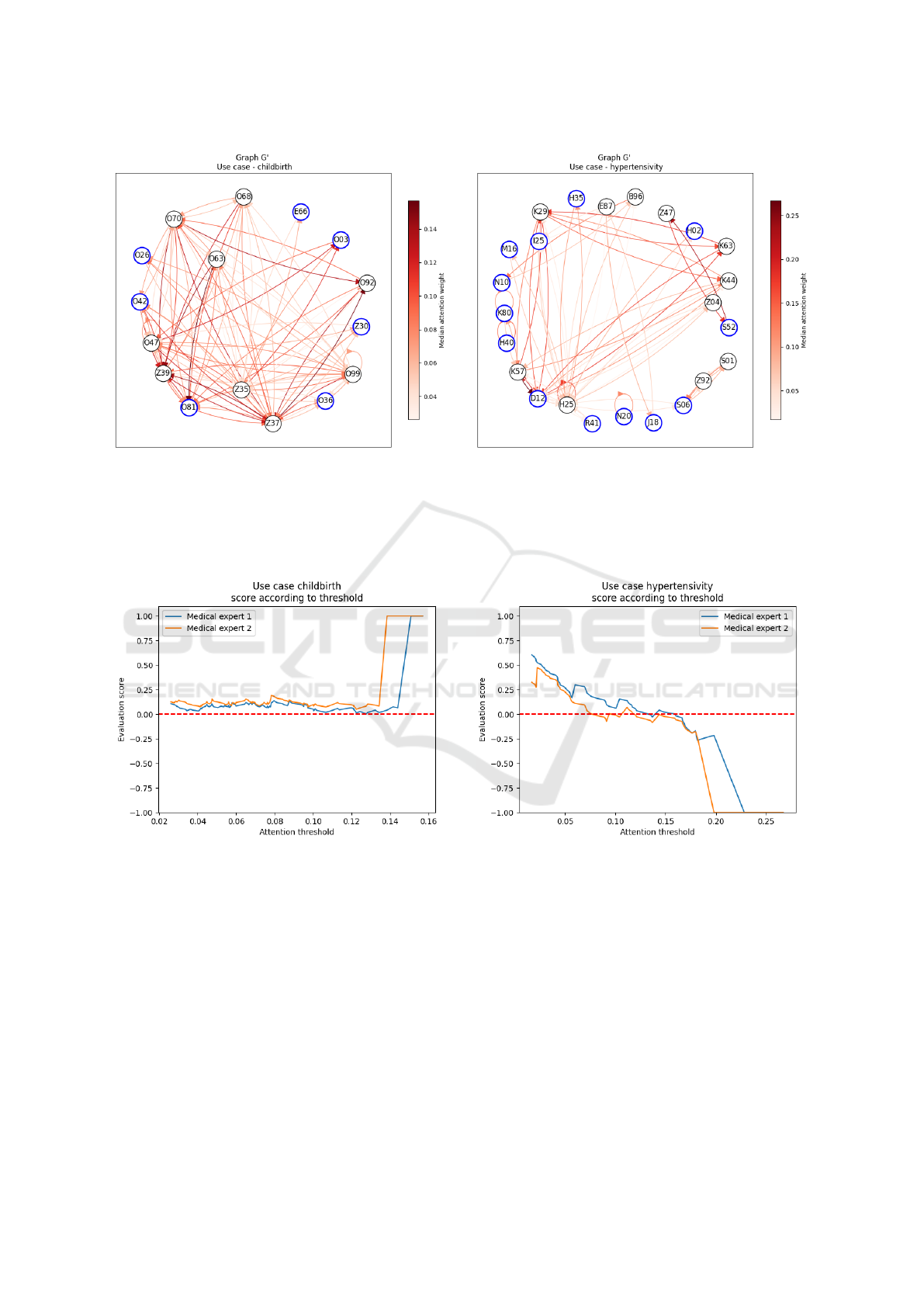
(a) (b)

Figure 3: Graphs obtained from our approach applied to the Behrt model in inference. The visualizations were generated

using the NetworkX python package. (a) use case of childbirth, (b) use case of hypertensivity. Nodes with a blue border

are diagnoses identiﬁed by the gradient as being important for prediction. Nodes with a black border are the diagnoses to

which the importance nodes are linked in the global attention matrix. An directed edge from node A to node B has a color

corresponding to the median weight of self-attention that A gives to B. Descriptions of ICD10-coded diagnoses in the nodes

are referenced online

(a) (b)

Figure 4: Curves illustrating the evolution of the evaluation score as a function of the self-attention threshold used to select

directed edges in the G

′

graph. (a) corresponds to use case of childbirth, and (b) to use case of hypertensivity. In both ﬁgures,

the blue curve represents the evaluation of the graph in relation to the medical expertise of the ﬁrst doctor, while the orange

curve reﬂects the evaluation in relation to the second doctor. A red dotted line located for score=0 is included to facilitate

visualization of evaluation scores that become negative.

5 RESULTS

We are testing our evaluation method on two use

cases: the prediction of a diagnosis signaling child-

birth, and a case revealing a diagnosis of essential hy-

pertension. To do this, we evaluate the graph gen-

erated from the information extracted during infer-

ence phase of the Behrt model, by comparing it with

ground truths obtained via the protocol described in

Section 4.4 and involving two medical experts. This

evaluation consists in computing the difference be-

tween the weighted proportion of directed edges com-

mon to the ground truths and those not included, i.e.

those not validated by the ground truths. We adjust

the threshold above which directed edges are con-

sidered in the graph G

′

to determine whether, above

IVAPP 2025 - 16th International Conference on Information Visualization Theory and Applications

702

a certain threshold, directed edges included in the

ground truths have a more signiﬁcant weight than

those excluded. This allows us to determine whether a

speciﬁc threshold produces a graph that most closely

approximates the ground truth.

The curves evaluating the score of G

′

in relation

to ground truths are shown for each use case in Fig-

ure 4. For the case of childbirth (see Figure 4a), we

observe that above a threshold of 0.13 or 0.15, de-

pending on the ground truth, the score reaches 1. This

indicates that all the directed edges of G

′

are included

G, conﬁrming the existence of a threshold beyond

which the directed edges correspond precisely to the

ground truth and demonstrating that the model cor-

rectly assigns high self-attention weights to the rele-

vant directed edges. Before this threshold, the score

remains positive but does not exceed 0.25, suggesting

that, although some directed edges are not included in

the ground truth, their inﬂuence is relatively minor.

On the other hand, in the case of hypertensivity

(see Figure 4b), the curves show a constant decay,

meaning that the higher the directed edge selection

threshold, the fewer directed edges are in common

with the ground truth, or their weight is less than those

excluded. These results indicate that, in this use case,

the model fails to pay sufﬁcient attention to diagnosis

pairs validated by the expert.

6 DISCUSSION

We develop a method for automatically evaluating the

links between tokens learned by an attention-based

model, using the Behrt architecture, trained by the

Lab Sant

e (Drees) on SNDS data. We analyze the

learning of the model on a task that can be evaluated

by an expert: the prediction of a diagnosis. More

precisely, the model we use is trained to predict the

next hospital visit from a sequence of previous visits,

which does not contain the diagnosis to be predicted,

which we call an incident diagnosis. We graphically

represent the model’s learning by linking diagnoses

identiﬁed as important by their gradient to the diag-

noses to which they are linked via the self-attention

learned by the model. The representation we pro-

pose makes it easier for medical experts to understand

how the Behrt model is learned. It enables the anal-

ysis of self-attention links between tokens, which can

be compared to correlations between diagnoses in the

medical ﬁeld.

Our approach enables a more granular assess-

ment of model learning than would be possible with

global measures such as precision or recall. Indeed,

the framework we propose facilitates visualization

and evaluation of the diagnostic links learned by the

model, and enables learning to be adjusted according

to these observations. Although the model does not

achieve a high recall rate - correctly diagnosing 190

out of 2000 individuals in the case of childbirth and

514 out of 2000 in the case of hypertensivity - our ap-

proach is applied to determine whether these results

are the result of overﬁtting. Analyses reveal that the

model establishes more relevant diagnostic links for

childbirth than for hypertensivity, which is surprising

given the better recall rate observed for hypertensiv-

ity. This anomaly is interpreted as being due to the

complexity of the hypertensivity case, which presents

a wide variety of diagnostic pathways that can lead

to correct predictions. These results demonstrate the

added value of our approach, whose analysis creates

a direct link between the training data used and the

performance obtained, enabling potential adjustment

of the sample used.

In our experiments, we developed a protocol for

creating a ground truth graph, which allows us to eval-

uate the graph of self-attention links learned by the

model. The curves shown in Figure 4 indicate that the

evaluation score of the model graph, relative to the

ground truth graph, follows the same trend, indepen-

dently of the medical expertise being compared. This

ﬁnding suggests that our proposed protocol succeeds

in establishing a ground truth that reﬂects shared med-

ical knowledge, thus reinforcing the validity of the

established ground truth as representative of general

medical expertise. The protocol for establishing the

ground truth does not take into account the weight-

ing of edges, as there is no direct and obvious cor-

respondence with self-attention in the medical con-

text. In the future, we would like to develop a method

to weight the edges established by medical expertise,

in order to more accurately evaluate the self-attention

weighting adopted by the model.

Finally, the proposed method offers an accurate

assessment of model learning based on attention

mechanisms, which is fundamental in the medical

ﬁeld. Indeed, understanding how the model learns is

crucial to being able to use its predictions to make in-

formed decisions.

7 CONCLUSION

Our method aims to validate the learning of models

based on self-attention mechanisms by representing

the learned links as graphs and evaluating their rele-

vance to a graph that represents the ground truth. This

approach enabled us to gain a better understanding of

how a BERT-type model works, speciﬁcally trained to

Evaluating Transformers Learning by Representing Self-Attention Weights as a Graph

703

predict the diagnosis of the next hospital visit based

on a series of previous visits. Our experiments on

two distinct use cases revealed that the case where the

model showed better initial performance established

less relevant diagnostic links than in the case where

the model appeared a priori to perform less, underlin-

ing the importance of a detailed analysis of learned

relationships.

We have also developed a method for creating a

ground truth from a simple-to-implement protocol.

Although we have considered ground truths deﬁned

individually by different medical experts, a future ap-

proach could be to unify these various truths into a

single one. Furthermore, the protocol for establish-

ing the reference graph does not take into account the

weighting of edges, as there is no direct correspon-

dence with self-attention in the medical context. In

the future, we would like to develop a method for

weighting the edges established by medical expertise,

thus enabling a more accurate assessment of the self-

attention distribution assigned by the model.

To extract a subgraph from the global attention

matrix, which we call the self-attention graph, we

start with g tokens considered important for predic-

tion based on their associated gradients. The num-

ber g is chosen to have a graph with enough edges to

evaluate. Subsequently, we would like to extract the

graph using a less arbitrary initialization, for example

by extracting weakly connected components based on

a self-attention threshold in the global attention ma-

trix. This would also allow us to evaluate the different

components derived from the global attention matrix

against those from a richer reference graph.

To generate the graph, we used the self-attention

weights of the last layer of the model. However, we

plan to explore the weights of other layers in the fu-

ture and design a method for integrating the atten-

tion of all layers, in order to better evaluate learning.

Furthermore, the self-attention weight between two

tokens is calculated by averaging the self-attention

weights from all attention heads in the last layer. In

our future work, we plan to analyze each attention

head individually to examine whether the associated

weights may have distinct interpretations in the med-

ical context. Finally, we aggregate the self-attention

weights between two tokens by calculating the me-

dian of these weights in all sequences combined. In

future work, we’d like to study the impact of the

choice of aggregation operation.

Finally, the results obtained showed that our ap-

proach enables a different performance analysis to

that obtained with global evaluation measures. In-

deed, in the two use cases studied, our method re-

vealed biases linked to the training data, which were

not detectable with recall measures, for example. In

this way, our approach facilitates understanding and

conﬁdence in the predictions made by a model, thanks

to an automatic but thorough analysis of its learning.

ACKNOWLEDGEMENTS

We thank Milena Suarez Castillo and Javier Nicolau

for allowing this collaboration, the Lab Sant

e team for

the model developpement and the medical experts Di-

ane Naouri, Albert Vuagnat, and Constance Prieur for

their valuable expertise and the time dedicated to this

work. Their active participation in the validation ex-

ercises greatly contributed to the quality of our study.

REFERENCES

Amann, J. et al. (2020). Explainability for artiﬁcial intel-

ligence in healthcare: a multidisciplinary perspective.

BMC medical informatics and decision making, 20.

Bengio, Y. et al. (1994). Learning long-term dependencies

with gradient descent is difﬁcult. IEEE Transactions

on Neural Networks, 5(2):157–166.

Devlin, J. et al. (2019). BERT: Pre-training of deep bidi-

rectional transformers for language understanding. In

Conference of the North American Chapter of the As-

sociation for Computational Linguistics: Human Lan-

guage Technologies, Volume 1 (Long and Short Pa-

pers), pages 4171–4186. Association for Computa-

tional Linguistics.

Dong, G. et al. (2021). Semi-supervised graph instance

transformer for mental health inference. In 2021 20th

IEEE International Conference on Machine Learning

and Applications, pages 1221–1228.

Li, Y. et al. (2020). BEHRT: transformer for electronic

health records. Scientiﬁc reports, 10(1):7155.

Li, Y. et al. (2022). Hi-BEHRT: hierarchical transformer-

based model for accurate prediction of clinical

events using multimodal longitudinal electronic health

records. IEEE journal of biomedical and health infor-

matics, 27(2):1106–1117.

Lin, T. et al. (2022). A survey of transformers. AI open,

3:111–132.

Luo, J. et al. (2020). HiTANet: Hierarchical time-aware

attention networks for risk prediction on electronic

health records. In 26th ACM SIGKDD International

Conference on Knowledge Discovery & Data Mining,

pages 647–656.

Meng, Y. et al. (2021). Bidirectional representation learning

from transformers using multimodal electronic health

record data to predict depression. IEEE journal of

biomedical and health informatics, 25(8):3121–3129.

Nerella, S. et al. (2023). Transformers in healthcare: A

survey. arXiv preprint arXiv:2307.00067.

IVAPP 2025 - 16th International Conference on Information Visualization Theory and Applications

704

Peng, X. et al. (2021). Sequential diagnosis prediction

with transformer and ontological representation. In

2021 IEEE International Conference on Data Mining,

pages 489–498.

Radford, A. et al. (2018). Improving language understand-

ing by generative pre-training.

Raffel, C. et al. (2020). Exploring the limits of transfer

learning with a uniﬁed text-to-text transformer. Jour-

nal of machine learning research, 21(140):1–67.

Rasmy, L. et al. (2021). Med-BERT: pretrained contextual-

ized embeddings on large-scale structured electronic

health records for disease prediction. NPJ digital

medicine, 4(1):86.

Ren, H. et al. (2021). RAPT: Pre-training of time-aware

transformer for learning robust healthcare representa-

tion. In Proceedings of the 27th International Confer-

ence on Knowledge Discovery & Data Mining, pages

3503–3511.

Shortliffe, E. H. et al. (2018). Clinical decision support in

the era of artiﬁcial intelligence. Jama, 320(21):2199–

2200.

Siebra, C. A. et al. (2024). Transformers in health: a sys-

tematic review on architectures for longitudinal data

analysis. Artiﬁcial Intelligence Review, 57(2):1–39.

Simonyan, K. et al. (2014). Deep inside convolutional net-

works: visualising image classiﬁcation models and

saliency maps. In International Conference on Learn-

ing Representations.

Vaswani, A. et al. (2017). Attention is all you need. Ad-

vances in neural information processing systems, 30.

Vig, J. (2019). A multiscale visualization of attention in

the transformer model. In 57th Annual Meeting of

the Association for Computational Linguistics: Sys-

tem Demonstrations, pages 37–42.

Wen, Q. et al. (2023). Transformers in time series: a survey.

In 32nd International Joint Conference on Artiﬁcial

Intelligence, pages 6778–6786.

Ye, M. et al. (2020). Lsan: Modeling long-term depen-

dencies and short-term correlations with hierarchical

attention for risk prediction. In 29th ACM Interna-

tional Conference on Information & Knowledge Man-

agement, pages 1753–1762.

Evaluating Transformers Learning by Representing Self-Attention Weights as a Graph

705