Approximation of Inertial Measurement Unit Data to Time Series

Kinematic Data Through Correlation Analysis and Machine Learning

William Fr

ohlich

1 a

, Rafael Bittencourt

, Sandro Rigo

2 b

, Rafael Baptista

1 c

and C

esar Marcon

1 d

School of Technology, Pontiﬁcal Catholic University of Rio Grande do Sul (PUCRS), Porto Alegre, Brazil

Universidade do Vale do Rio dos Sinos (UNISINOS), S

ao Leopoldo, Brazil

Keywords:

Gait Analysis, Inertial Measurement Units, Kinematic, Machine Learning, Correlation.

Abstract:

Accurate results are traditionally obtained in gait analysis using gold-standard methods such as motion cap-

ture with kinematic cameras and force platforms in biomechanics labs. However, these techniques are ex-

pensive, time-consuming, and require controlled environments, limiting their accessibility for more clinical

and research applications. This study explores the potential of inertial measurement units as a cost-effective

alternative. We focused on extracting features from Inertial Measurement Unit (IMU) data, such as accelera-

tion and angular velocity, and derived metrics like speed and angular acceleration to approximate the accuracy

of kinematic camera data. Following extensive preprocessing of inertial and kinematic datasets, we applied

analytical methods, including Pearson correlation and cross-correlation, to identify signiﬁcant relationships

between the two data sources. We employed the most strongly correlated features to train Machine Learning

models, Clustering techniques to assess the consistency and reliability of the results, and the Random Forest

algorithm to train and evaluate the models’ capacity for time series prediction. Our ﬁndings suggest that cer-

tain aspects of IMU data strongly correlate with kinematic outcomes. This indicates that IMUs can replicate

results traditionally obtained through more complex and costly methods under speciﬁc conditions.

1 INTRODUCTION

Gait analysis is a critical tool for diagnosing neurode-

generative diseases, optimizing athletic performance,

and understanding the broader implications of gait

on health and lifestyle. Traditionally, motion capture

systems using kinematic cameras and plantar pres-

sure measurements have been the gold standard for

precise gait analysis due to their accuracy and ability

to capture detailed biomechanical data (Zhang et al.,

2017) (Jakob et al., 2021). However, these methods

come with signiﬁcant limitations, such as being ex-

pensive, requiring specialized equipment, and being

performed in controlled laboratory environments, re-

stricting their accessibility in clinical and research set-

tings (Benson et al., 2018).

In response to these challenges, Inertial Measure-

ment Units (IMUs) have emerged as a promising al-

ternative. IMUs are portable, cost-effective, and ver-

satile, allowing for gait analysis outside traditional lab

settings (Akhtaruzzaman et al., 2016) (Kotiadis et al.,

2010). Despite their potential, the data collected by

https://orcid.org/0000-0003-3551-2623

https://orcid.org/0000-0001-8140-5621

https://orcid.org/0000-0003-1937-6393

https://orcid.org/0000-0002-7811-7896

IMUs must be validated against gold-standard meth-

ods like optical motion capture to ensure accuracy and

reliability (Kvist et al., 2024). This validation is es-

sential for IMUs to be considered viable substitutes

or complements of established technologies.

Biomechanics and gait assessments are funda-

mental for identifying locomotor issues, playing a

crucial role in personalized rehabilitation and ath-

letic performance enhancement (Benson et al., 2018)

(Akhtaruzzaman et al., 2016). Wearable devices, es-

pecially IMUs, have gained attention due to their con-

venience and ability to capture gait data in real-world

environments. However, the challenge remains in

ensuring that the data obtained from wearables can

achieve the precision of traditional motion capture

labs (Kvist et al., 2024).

Motion capture systems with high-precision cam-

eras and force platforms provide high accuracy, cap-

turing joint angles, stride length, speed, and muscle

activity. In contrast, wearable sensors lack the ac-

curacy of lab-based methods, but they are versatile

and can record real-time data continuously (Kotiadis

et al., 2010). We compare these approaches, explor-

ing their current applications and identifying the re-

search gaps related to wearable IMU and kinematic

data integration.

Fröhlich, W., Bittencourt, R., Rigo, S., Baptista, R. and Marcon, C.

Approximation of Inertial Measurement Unit Data to Time Series Kinematic Data Through Correlation Analysis and Machine Learning.

DOI: 10.5220/0013115800003911

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 18th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2025) - Volume 2: HEALTHINF, pages 75-86

ISBN: 978-989-758-731-3; ISSN: 2184-4305

One of the leading research challenges is corre-

lating IMU data with kinematic data obtained from

motion capture systems (Silva and Stergiou, 2020).

A strong correlation would validate IMUs as reliable

tools for capturing gait metrics, making them suitable

for broader applications. Artiﬁcial intelligence (AI)

and Machine Learning (ML) are particularly well-

suited for this task, as they can process large datasets,

uncover complex patterns, and model relationships

between inertial and kinematic data (Silva and Ster-

giou, 2020) (Benson et al., 2018).

This study investigates how IMU data, such as ac-

celeration, gyroscope, roll, and yaw, correlate with

camera kinematic data. We applied Pearson correla-

tion and cross-correlation techniques to identify sig-

niﬁcant relationships between the two datasets. Based

on these correlations, we developed Machine Learn-

ing models to predict kinematic parameters using

IMU data. The subsequent validation of these mod-

els and cluster analysis offers valuable insights into

the feasibility of using IMUs as complementary or al-

ternative tools to traditional motion capture.

Using these correlations as a foundation, we de-

veloped ML models, including Random Forest (RF)

and Linear Regression (LR), to predict kinematic pa-

rameters from IMU data. This approach leverages

the capacity of AI and ML to process large datasets

and uncover complex, nonlinear relationships be-

tween wearable sensor data and biomechanical mea-

surements (Silva and Stergiou, 2020) (Benson et al.,

2018). In summary, wearable IMUs offer signiﬁcant

advantages in terms of ﬂexibility and real-world ap-

plicability, but achieving the same level of precision

as traditional motion capture is still a challenge. By

integrating AI-driven models, we provide a step for-

ward in bridging the gap between IMU and kinematic

data.

2 RELATED WORK

Biomechanics and gait assessment are essential tools

for identifying locomotion problems, with signiﬁ-

cant impact across various ﬁelds, including personal-

ized rehabilitation strategies and athletic performance

enhancement (Benson et al., 2018) (Akhtaruzzaman

et al., 2016). Understanding human biomechanics

can improve health outcomes, reﬁne athletic abilities,

and accelerate recovery processes (Silva and Stergiou,

2020). In recent years, wearable devices for gait anal-

ysis have gained popularity due to their portability

and ease of use, allowing gait analysis outside tradi-

tional biomechanics labs (Benson et al., 2018). How-

ever, it is crucial to validate wearable data using gold-

standard methods to ensure accuracy and precision

(Kvist et al., 2024).

Biomechanics laboratories, equipped with high-

speed cameras, force platforms, and electromyo-

graphs, capture detailed movement data during walk-

ing (Akhtaruzzaman et al., 2016). These labs of-

fer precise information on joint angles, stride length,

speed, and muscle activity, making them the gold

standard for gait analysis (Jakob et al., 2021) (Zhang

et al., 2017). On the other hand, wearable sensors pro-

vide a more versatile alternative, although they gener-

ally do not achieve the same level of accuracy and

precision (Akhtaruzzaman et al., 2016). These de-

vices typically consist of inertial sensors placed on

key body areas, recording real-time movement with-

out environmental restrictions (Kotiadis et al., 2010).

Despite the advantages of wearables, a research

gap exists in correlating data from inertial sensors

with data from biomechanics labs that use opti-

cal cameras for motion capture (Zhou et al., 2020)

(Tsakanikas et al., 2023) (Silva and Stergiou, 2020).

Many studies focus on speciﬁc diagnoses, like Parkin-

son’s disease detection, rather than directly compar-

ing the datasets (Borz

ı et al., 2023) (da Rosa Tavares

et al., 2023). Correlation analysis is crucial to assess

how well kinematic data matches inertial data (De-

sai et al., 2024) (He et al., 2024) (Kvist et al., 2024)

(Ripic et al., 2023) (Rousanoglou et al., 2024). Still,

preprocessing steps, such as ﬁltering and data nor-

malization, are needed before analysis. Furthermore,

clustering techniques could enhance data grouping

and identiﬁcation using artiﬁcial intelligence (Caldas

et al., 2020) (Kim et al., 2022) (Nguyen et al., 2019).

This study aims to explore the differences be-

tween motion capture labs and wearable sensors and

to evaluate state-of-the-art applications of both tools

in gait analysis. Speciﬁcally, it seeks to identify re-

search gaps related to correlating kinematic and in-

ertial data, potentially contributing to establishing a

gold-standard approach using inertial data alone.

3 METHODOLOGY

Figure 1 shows the methodology used to evaluate

the similarities and correlations between kinematic

gait data obtained from gold-standard motion cap-

ture systems and inertial data collected from wear-

able sensors. The process begins with data collec-

tion (Subsection 3.1) in a biomechanics laboratory

equipped with high-speed cameras and a wearable

IMU system. After collecting the data, we conducted

experiments to determine the optimal preprocessing

steps, drawing from state-of-the-art approaches, as

HEALTHINF 2025 - 18th International Conference on Health Informatics

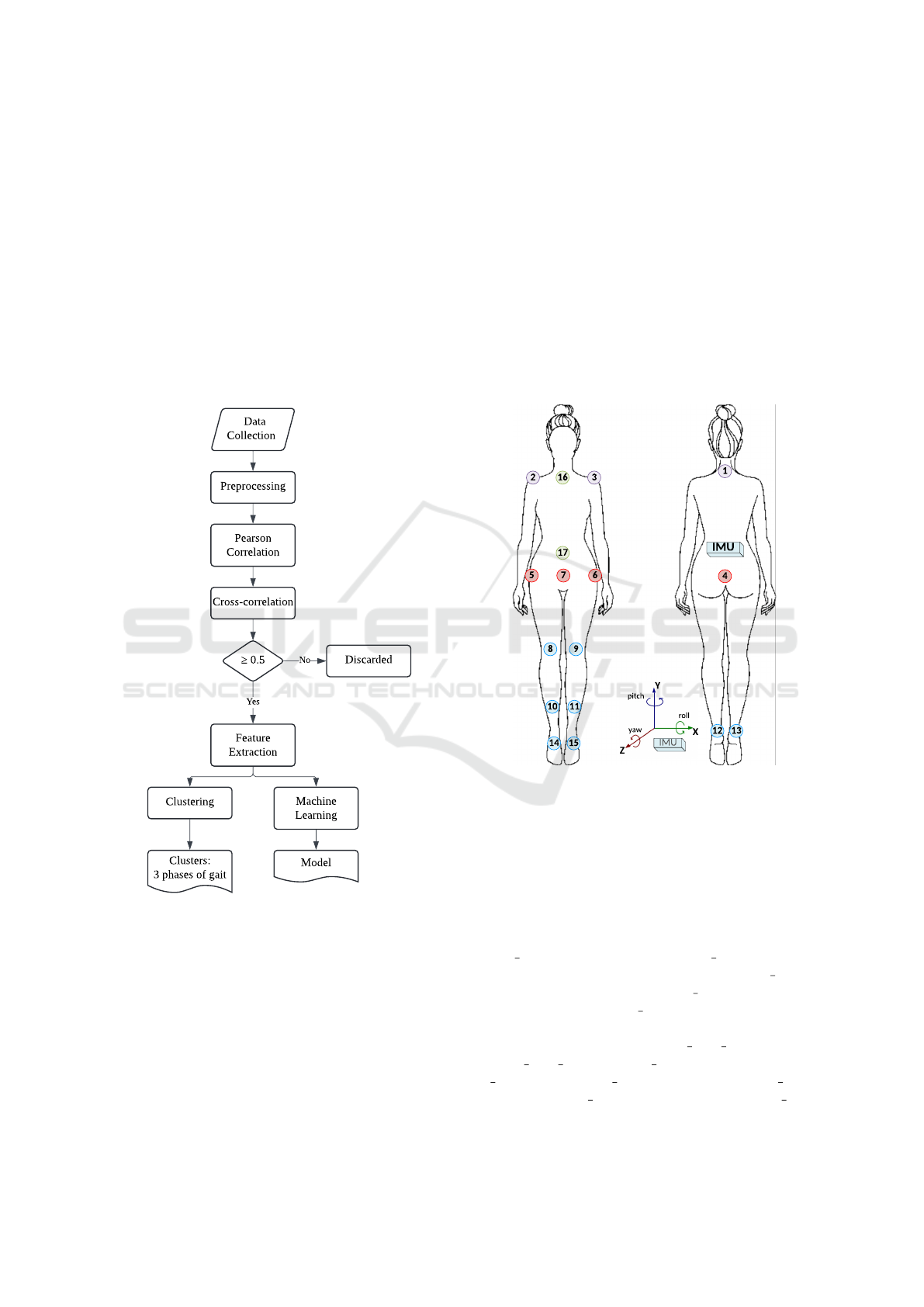
discussed in Subsection 3.2. Next, we applied cor-

relation algorithms to analyze the relationships and

similarities between the kinematic and inertial data

(Subsection 3.3). Based on these correlation results,

we used AI algorithms to perform cluster analysis

(Subsection 3.5), focusing on the three phases of gait:

double stances and single stances with the left and

right feet. Finally, we conducted exploratory Machine

Learning experiments (Subsection 3.6) using RF and

Linear Regression algorithms. These stages formed

the basis for training models to evaluate how well in-

ertial data can capture gait patterns compared to the

gold-standard kinematic data and evaluate the feature

importance in each model of the kinematic points.

Figure 1: Flowchart for evaluating similarities and correla-

tion between kinematic and inertial data.

3.1 Data Collection

The data collection experiments had the ethics com-

mittee’s approval and followed a standardized gait

analysis protocol, where participants walked along a

straight path, stepped over a force platform, and then

returned. The procedure was conducted using the

equipment from the GaitLab biomechanics laboratory

(BTS Bioengineering, 2024b), which includes mo-

tion capture cameras and a force platform. The wear-

able sensor used in the experiments was the GWalk

(BTS Bioengineering, 2024a), a device positioned

on the participants’ lumbar region that collects iner-

tial data from accelerometers and gyroscopes, includ-

ing acceleration (acc) and rotational motion (gyro),

both on three axes, and roll (roll), pitch (pitch), and

yaw (yaw) orientation angles. Figure 2 illustrates the

placement of the wearable IMUs on the participants

during data collection. It also shows the orientation

of the data relative to the X, Y, and Z axes and the

direction of data rotation. The raw data were ex-

tracted from the computers using software to collect

data from the devices.

Figure 2: Placement of kinematic points and wearable

IMUs for the data collection experiments.

The data from the biomechanics laboratory in-

clude many kinematic points, but to make the study

more efﬁcient and focused, we have selected the key

points based on the state of the art (Delval et al.,

2021). We categorized these points into groups, ac-

cording to point in Figure 2: for the Upper Trunk, we

selected the C7 cervical vertebra (c7 - 1), right shoul-

der (r should - 2), and left shoulder (l should - 3); for

the Lower Trunk, we chose the sacrum (sacrum s - 4),

right anterior superior iliac crest (r asis - 5), left ante-

rior superior iliac crest (l asis - 6), and the midpoint

between the iliac crests (MIDASIS - 7). For the legs,

the selected points are the right (r knee 1 - 8) and left

knee (l knee 1 - 9), right (r mall - 10) and left ankle

(l mall - 11), right (r heel - 12), and left heel (l heel

- 13), and right (r met - 14) and left metatarsal (l met

- 15). Two additional valuable points are the average

Approximation of Inertial Measurement Unit Data to Time Series Kinematic Data Through Correlation Analysis and Machine Learning

shoulder position (PO - 16) and the center of mass

(SHO - 17). In the collected kinematic data, as shown

in Figure 2, the X-axis represents lateral movement,

the Y-axis represents upward movement, and the Z-

axis represents forward walking movement. In addi-

tion to the inertial data, force platforms provide mea-

surements for both feet (r f orce and l f orce) along

three axes. The collected dataset

is available for re-

production

3.2 Data Preprocessing

In gait analysis, abrupt changes along the X, Y, and Z

axes, particularly derived from acceleration data, rep-

resent the rate of change of acceleration over time.

This information is vital as it highlights sudden shifts

in the forces acting on the body, which may indicate

speciﬁc gait events or irregularities.

We developed data processing and analysis rou-

tines using Python 3.10, employing libraries such as

NumPy, Pandas, Scipy, and Scikit-Learn. Data pre-

processing is crucial in ensuring the data is clean,

consistent, and ready for advanced analysis. The pre-

processing workﬂow incorporated multiple steps, all

guided by the latest methodologies in gait analysis

and supported by relevant research (Millecamps et al.,

2015), (Burdack et al., 2020), (Parashar et al., 2023).

After loading the data, the ﬁrst step addressed data

issues, often represented as ”Not a Number” (NaN),

which can arise from various reasons. Proper han-

dling of NaNs is crucial, as they can skew results or

degrade model performance if left unaddressed. Ini-

tially, we removed NaNs from the start and end of the

ﬁles, where the absence of data likely corresponded

to periods outside the recorded movement. Next, we

conducted experiments by imputing NaNs with the

mean of surrounding values to ﬁll in the gaps. How-

ever, in cases where data was missing due to speciﬁc

conditions, such as during the swing phase when the

force platforms might not detect force, we replaced

NaNs with zeros, indicating the absence of foot con-

tact with the platform. After experimenting with these

imputation methods, the optimal solution was replac-

ing missing data caused by a technical failure with the

mean of the surrounding data and imputing zeros for

data not captured by the force platforms. This strat-

egy ensured that the data remained as accurate and

unbiased as possible for further analysis.

We applied interpolation techniques to address

gaps further. Linear interpolation, in particular, es-

timated missing values based on neighboring data

points. This approach assumes a smooth transition

www.kaggle.com/datasets/wrfrohlich/artemis-dataset

between known values, making it ideal for time se-

ries data like gait measurements, where maintaining

continuity is crucial for accurate analysis.

Next, we ﬁltered the data to reduce the noise of the

signal. We tested with Butterworth ﬁlters, including

low-pass, band-pass, and high-pass conﬁgurations.

The low-pass Butterworth ﬁlter proved the most ef-

fective, eliminating high-frequency noise while pre-

serving crucial patterns in the sensor data. For both

the GaitLab data sampled at 250 Hz and the GWalk

data sampled at 100 Hz, we applied a 3.0 Hz cutoff

frequency with a 5th-order ﬁlter. This low-pass ﬁl-

ter was particularly advantageous, as it retained the

essential low-frequency components critical for gait

analysis.

Following noise reduction, we normalized the

data, ensuring that all features were on the same scale,

preventing any single feature from dominating the

analysis. We tested standardization, which adjusts

data to have a mean of zero and a standard devia-

tion of one, and Min-Max scaling, which rescales data

to a ﬁxed range. Min-Max scaling yielded better re-

sults, particularly for datasets with features on differ-

ent scales, by preserving the relative importance of

each feature while ensuring uniform analysis.

The ﬁnal preprocessing step was data merging, an

essential task given the equipment’s differing sam-

pling rates, such as 250 Hz for GaitLab and 100 Hz

for GWalk. Temporal alignment of the datasets is nec-

essary to ensure accurate comparison and integration.

This was accomplished by merging the data based on

precise timestamps from each system, allowing for

synchronized analysis of the gait cycles captured by

both kinematic cameras and inertial sensors.

Through these comprehensive preprocessing

steps, we ensured the data was of high quality,

accurately reﬂecting the subjects’ movements, and

ready for the following stages of correlation analysis

and ML model development.

3.3 Data Correlations

The correlation analysis between kinematic, force,

and inertial data is crucial for identifying similarities

and relationships between these datasets. This anal-

ysis is the foundation for validating whether IMUs

can effectively replicate the results traditionally ob-

tained through more complex and expensive meth-

ods. In this study, we employed Pearson correlation

(Section 3.3.1 and cross-correlation (Section 3.3.2

techniques to assess the degree of similarity between

the data from these different sources. Based on the

strongest relationships between IMU and kinematic

points, we will move forward using AI techniques.

HEALTHINF 2025 - 18th International Conference on Health Informatics

3.3.1 Pearson Correlation Analysis

Pearson correlation evaluates the strength and direc-

tion of the linear relationship between two quanti-

tative variables. The Pearson correlation coefﬁcient

ranges from -1 to 1. A value of -1 indicates a per-

fect negative correlation, 0 indicates no correlation,

and 1 indicates a perfect positive correlation. By cal-

culating the Pearson correlation between acceleration

data from inertial sensors and the positional data of

speciﬁc points on the body, we aimed to determine

whether the movements detected by the IMUs are ac-

curately reﬂected in the kinematic displacements ob-

served. This correlation analysis was performed for

each kinematic dataset, focusing on key inertial points

corresponding to relevant body segments.

The kinematic data were systematically grouped

by body parts, such as lower limbs, upper limbs, and

trunk; we conducted correlation analyses to under-

stand how different body regions interacted with the

inertial data. This systematic approach allowed us to

identify which body parts and associated kinematic

data most closely aligned with the inertial measure-

ments and improved the visualization of the matrices.

The Pearson correlation analysis initially under-

stood the linear relationships between the kinematic

and inertial datasets. By computing the Pearson cor-

relation coefﬁcients for each pair of kinematic and in-

ertial data points, we could identify instances where

the inertial data closely matched the kinematic data.

This step is essential in determining whether the

IMUs could capture the same movement patterns as

the more precise kinematic systems.

3.3.2 Cross-Correlation Analysis

Following the Pearson correlation analysis, we

extended our investigation by applying a cross-

correlation technique, which is particularly valuable

for time series data as it measures the similarity be-

tween two signals over different time lags. This

method shifts one signal relative to the other and cal-

culates the correlation at each time shift, identifying

the time lag that produces the highest correlation.

Even though the data were pre-aligned based on

the collection time, cross-correlation provided a more

reﬁned analysis by determining the optimal tempo-

ral alignment between the inertial and kinematic sig-

nals. This precise alignment maximized the accuracy

of the subsequent analyses, ensuring that the inertial

data could be directly compared to the kinematic data

at their most correlated time points.

We performed cross-correlation analyses for each

combination of kinematic and inertial data points,

systematically identifying which kinematic points ex-

hibited the highest correlation with the inertial sen-

sors. We established a threshold of 0.5 for the corre-

lation coefﬁcient, ensuring that only the most relevant

and strongly correlated data points were considered.

However, some kinematic points did not reach this

threshold, indicating a weaker relationship with the

inertial data. To address this, we implemented fea-

ture extraction techniques to enhance the correlation

by deriving additional relevant metrics from the in-

ertial data, thereby ensuring that all kinematic points

had some degree of correspondence with the inertial

measurements.

The combined use of Pearson correlation and

cross-correlation provided an understanding of the

relationships between kinematic and inertial data.

These analyses demonstrated that, under the right

conditions, inertial sensors could replicate kinematic

data with high accuracy.

3.4 Features Extraction

We performed feature extraction from the inertial data

to analyze correlations between inertial and kinematic

data. In gait analysis, feature extraction from iner-

tial data is crucial for establishing meaningful cor-

relations with kinematic data. Inertial data from ac-

celerometers and gyroscopes capture the forces and

rotations acting on the body during movement. How-

ever, to make these data comparable and correlatable

with kinematic data, which describe the actual move-

ment of body segments, it is essential to extract and

transform the raw information into features that re-

ﬂect the dynamic and kinematic aspects of the move-

ment.

These features facilitate the identiﬁcation of

movement patterns, enhancing our understanding of

how forces and rotations inﬂuence body motion.

Some extracted features include velocities (vel) along

the X, Y, and Z axes. Velocity data, calculated by in-

tegrating acceleration data over time in each axis, is

a fundamental feature that describes the translational

movement of body segments. We obtained the angu-

lar acceleration (ang acc gyro) in the X, Y, and Z axes

from the derivative of gyroscope data, which mea-

sures the rotation rate along the respective axes. This

angular acceleration provides insights into how body

parts rotate, which is essential for understanding the

rotational movement of segments, such as the rotation

of the trunk or limbs.

We obtained the magnitude of acceleration

(mag acc) from the square root of the sum of the

squares of the accelerations along each of the three

axes, representing the total intensity of the force act-

ing on the body, yielding the total force associated

Approximation of Inertial Measurement Unit Data to Time Series Kinematic Data Through Correlation Analysis and Machine Learning

with the movement. Similarly, the magnitude of an-

gular velocity (mag gyro) is calculated from the rota-

tions measured by the gyroscopes. The harsh varia-

tion ( jerk) along the X, Y, and Z axes, coming from

the derivative of the acceleration, represents the accel-

eration rate change over time, providing information

about abrupt modiﬁcations in the forces acting on the

body.

Finally, position (pos) along the three axes was

obtained by integrating the velocity data over time.

This enabled us to estimate where the body segments

are located in space, approaching a kinematic mea-

sure derived from velocity. Extracting these features

from inertial data is relevant for identifying similari-

ties between inertial and kinematic data and thus ﬁnd-

ing relationships in the IMU data that correspond to

the behavior of all inertial points.

3.5 Clustering

After the correlation and cross-correlation analysis,

it is crucial to evaluate whether the correlations ob-

served between inertial and kinematic points can be

veriﬁed using AI algorithms for pattern clustering and

point correlation. Clustering after correlation analysis

allows for identifying similar patterns, which is es-

sential for better understanding the biomechanics of

movement and differentiating subgroups of interest.

A new stage of data preparation is required to

perform the clustering process. We based our ap-

proach on the correlation data between inertial and

kinematic points with the highest Pearson and cross-

correlation coefﬁcients for a more accurate clustering

process. We set a minimum correlation threshold of

0.5 between the inertial and kinematic points. Since

the objective of this study is to assess whether kine-

matic data can be inferred from inertial data, the data

were grouped so that for each kinematic point, all in-

ertial data or features extracted from the inertial data

were aggregated. Thus, all inertial data with a correla-

tion greater than 0.5 were grouped for each kinematic

point.

Next, the data needed to be resized for cluster-

ing using the K-Means algorithm. We experimented

with two-dimensionality reduction techniques: Prin-

cipal Component Analysis (PCA) and t-distributed

Stochastic Neighbor Embedding (t-SNE). The choice

of dimensionality reduction method is crucial for fa-

cilitating the visualization and interpretation of the

formed clusters.

The data were transformed into a lower-

dimensional space for each speciﬁed method, PCA

or t-SNE. This step aims to reduce data complexity

and improve clustering efﬁciency. We performed ex-

periments using both methods, but PCA resulted in

more tightly grouped and better-deﬁned clusters. The

number of clusters (n = 3) was selected based on crite-

ria that balance the internal homogeneity of the clus-

ters with the distinction between them. This selection

was guided by the three phases of gait: left leg swing,

stance, and right leg swing.

We evaluated the clusters using the Silhouette

Score, Calinski-Harabasz Score, and Davies-Bouldin

Index metrics that provide a quantitative view of clus-

ter cohesion and separation, essential for validating

the clustering results. After the initial clustering re-

sults, we proceeded to the step where the data were

time-shifted according to the lag that yielded the best

results in the cross-correlation analysis. With these

adjustments, the clusters showed a signiﬁcant im-

provement compared to the data without the time-

shift adjustments related to the lag of the clusters.

3.6 Machine Learning

The next step in evaluating the similarities between

kinematic and inertial data is assessing how well an

ML algorithm can train a model and predict values in

time series. To achieve this, we opted for an RF-based

approach to predict kinematic gait variables, and com-

plementary experiments were performed using Linear

Regression for performance comparison.

The data follows from the conclusions drawn in

the Pearson correlation and cross-correlation analy-

sis stages, selecting values with a correlation modulus

greater than 0.5, whether positive or negative, and us-

ing the time-shift adjustments. Cross-correlation data

is helpful in assessing the temporal delay (lags) be-

tween IMU variables and the body points captured by

the cameras.

The data was organized in a tabular format, where

the input variables (X) are the IMU readings and the

output variable (Y) is the coordinate of a speciﬁc body

point. n inertial data points correspond to one kine-

matic value, as performed in the clustering experi-

ment. The dataset was split into training and test sets,

with 80% for training and 20% for testing.

We ﬁrst implemented the RF algorithm, as state-

of-the-art research indicates it performs well in train-

ing time series data related to gait. It is particularly

effective with correlated and nonlinear variables. As

a complementary evaluation, we implemented LR,

which seeks to establish a linear relationship between

the input, IMU, and output kinematic variables.

To assess the performance of the models, we cal-

culated several metrics that are well-suited for time

series analysis, including Mean Squared Error (MSE),

which represents the average squared error between

HEALTHINF 2025 - 18th International Conference on Health Informatics

the predictions and actual values; R-Squared (R

), in-

dicating the proportion of variance explained by the

model; Mean Absolute Error (MAE), which evalu-

ates the average absolute error between predictions

and actual values; Mean Absolute Percentage Error

(MAPE), representing the average percentage error

between predictions and actual values; and Relative

Absolute Error (RAE), which compares the model’s

total absolute error to that of a simple baseline model.

We conducted an additional evaluation to under-

stand which adjustments might be necessary to dis-

tribute IMU data during training for each kinematic

point. We used the Feature Importance attribute from

the RF model for this. Feature Importance helps iden-

tify the contribution of each feature in the training

process, highlighting those with little relevance or de-

tecting features that may introduce bias, leading to

overﬁtting or poor model performance.

4 RESULTS AND DISCUSSION

This section encompasses three parts: the ﬁrst focuses

on the Pearson Correlation results (Section 4.1), in the

sequence Cross-correlation (Section 4.2) results ob-

tained, and the third Section 3.5 discusses and evalu-

ates the clustering analysis’s outcomes.

4.1 Pearson Correlation Analysis

The Pearson correlation analysis shows a strong

match between the IMU and kinematic data in several

instances, particularly regarding vertical foot move-

ment and lateral trunk motion. This strong correlation

suggests that wearables can accurately capture large

displacements or rotations around speciﬁc axes, align-

ing closely with the patterns observed in the kine-

matic data. In some instances, however, the rota-

tions detected by the IMUs correlate inversely with

the movements seen in the kinematic data, indicat-

ing that the IMUs might be measuring rotations oppo-

site to the linear motion. Nevertheless, more complex

movements, such as accelerations along certain axes

or speciﬁc rotations, show lower correlations, indicat-

ing limitations in the IMU sensors’ ability to capture

small-scale movements or intricate dynamic patterns.

One key ﬁnding is the high correlation between

the Z-axis acceleration (acc z) and the c7

point (lo-

cated at the base of the neck), with a value of 0.6259

that indicates the vertical movement recorded by the

accelerometer is strongly linked to the motion of

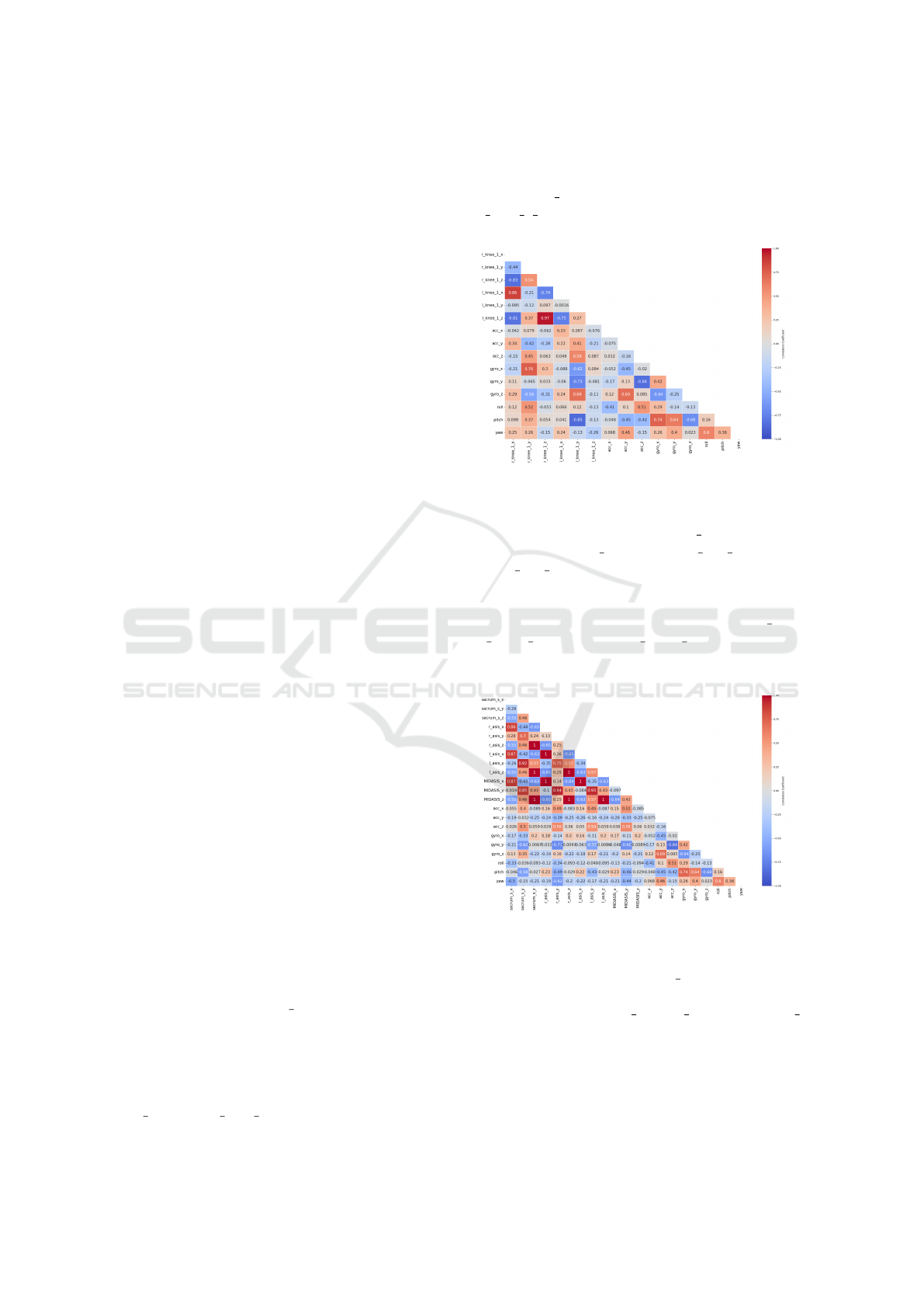
the neck. When analyzing the foot and leg points

(Figure 3), we see a higher correlation between the

gyro x and the r knee 1

point (0.7616), suggesting

that the gyroscope on the X-axis effectively captures

the lateral motion of the right knee. Additionally,

for the gyro z-axis, there is a strong correlation with

l knee 1 y (0.6866), reinforcing the relationship be-

tween Z-axis rotations and knee movement.

Figure 3: Correlation matrix of upper leg data against IMU.

The trunk points of Figure 4 show notable nega-

tive correlations between the gyro y-axis and points

such as MIDASIS y (-0.6773), r asis y (-0.7107),

and l asis y (-0.5705), suggesting the Y-axis rota-

tion could be related to an opposite or compensatory

movement in the pelvis and waist points. Regard-

ing force plates, correlations between gyro x and

r f orce x (-0.5781) and r f orce y (-0.5133) indicate

that the gyroscopes may capture the impact or force

exerted on the right leg during motion.

Figure 4: Correlation matrix of trunk data against IMU.

In terms of velocity and displacement, the linear

velocities along the X-axis (vel x) stand out with ex-

tremely high correlations (close to 1.0) with several

body points, such as c7 z, SHO z, and MIDASIS z,

among others in both the upper and lower body, sug-

gesting coordinated and consistent movement in a

speciﬁc direction during gait.

The most signiﬁcant correlations in the analyzed

groups exceed 0.5, highlighting the IMU’s ability

Approximation of Inertial Measurement Unit Data to Time Series Kinematic Data Through Correlation Analysis and Machine Learning

to capture movements related to kinematic points,

mainly vertical and rotational.

When the correlation threshold is lowered to 0.4,

more moderate correlations emerge, especially in hor-

izontal movements and regions that are harder to mea-

sure precisely, such as lateral movements of the trunk

and head. Despite this, most correlations remain

above this threshold, supporting that IMUs can ex-

tract useful information for analysis similar to kine-

matic data across multiple dimensions.

The fact that most correlations are above 0.5 or

0.4 suggests that the IMU sensors capture movement

accurately compared to kinematic points, particularly

regarding vertical and rotational movements. How-

ever, there are limitations in lateral movements and

speciﬁc acceleration axes, where correlations tend to

be lower.

4.2 Cross-Correlation Analysis

These cross-correlation data highlight the relation-

ships between inertial device variables and kinematic

variables of anatomical reference points. Cross-

correlation measures how two-time series shift rela-

tive to each other, while lag represents the time dif-

ference between the two signals that maximizes this

correlation. This step is essential to align the data and

optimize their correlation.

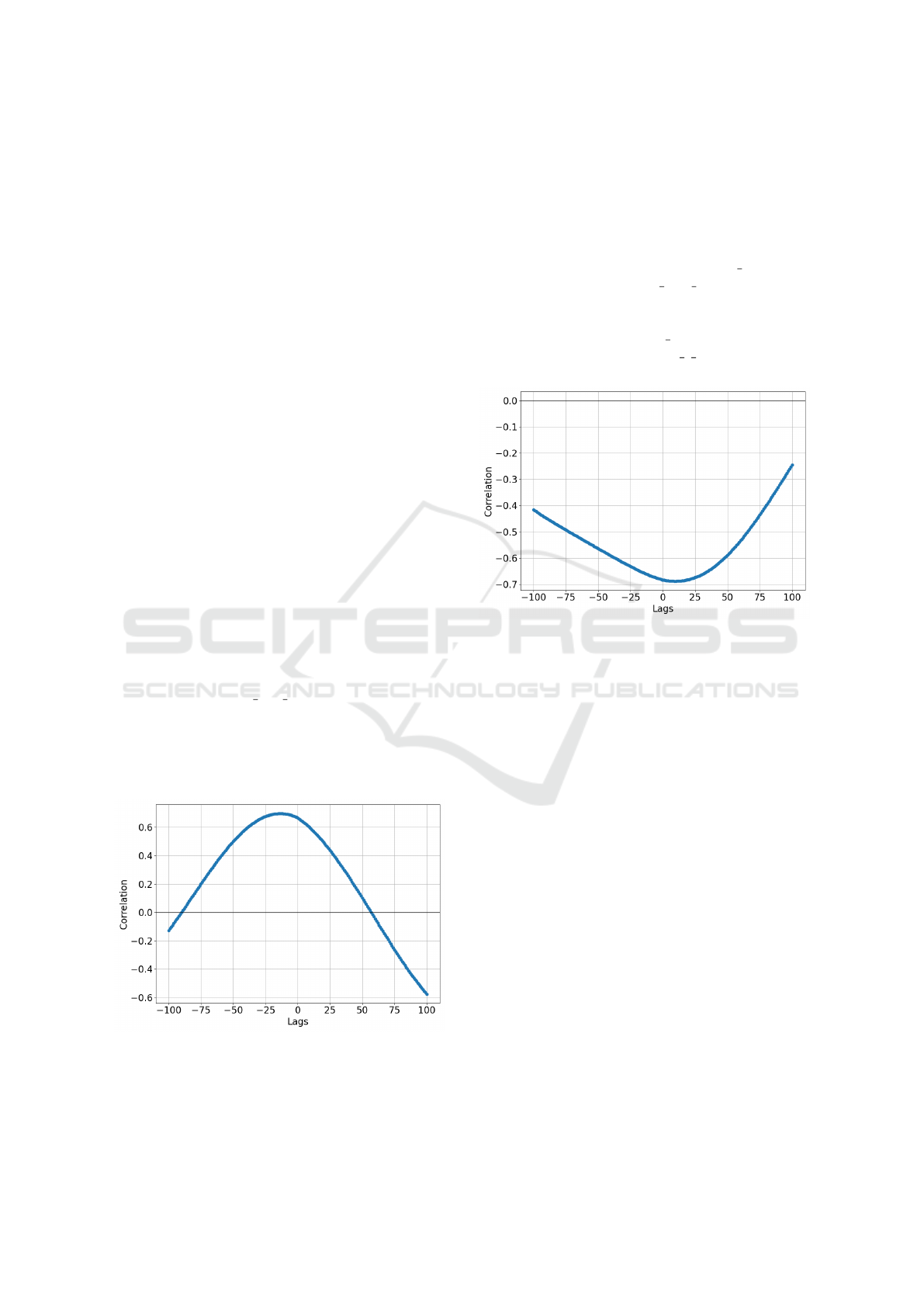
For instance, the X-axis acceleration from the ac-

celerometer is strongly correlated with the vertical

displacement of the r asis y (Figure 5), hip region,

with a lag of 34 samples. Similarly, the Z-axis rota-

tion from the gyroscope is highly correlated with the

Y-axis force of the right leg’s force point, showing a

lag of 72 samples, suggesting a relatively strong syn-

chronization.

Figure 5: Cross-correlation matrix of trunk data against

IMU.

The Z-axis acceleration is closely correlated with

the vertical movement of the C7 point located at the

upper back, indicating synchronized vertical motions

between the trunk and the vertical acceleration mea-

sured by the device. Some variables display signif-

icant negative correlations, which could indicate op-

posing movements or inverse relationships between

the forces/movements captured by the sensors. For

example, the Y-axis accelerometer (acc y) and the

right heel Y-axis position (r heel y) have a correla-

tion of -0.82 (Figure 6), suggesting that as Y-axis ac-

celeration increases, the right heel’s vertical position

decreases. Similarly, the gyro y-axis rotation and the

sacrum Y-axis position (sacrum s y) have a negative

correlation of -0.77.

Figure 6: Cross-correlation matrix of trunk data against

IMU.

The analysis shows strong correlations between

IMU and kinematic data for several variables, with

some correlations being exceptionally high (above

0.8). However, there is a need for temporal align-

ment (lag) to improve the precision of the match be-

tween the two data types. Additionally, it is crucial

to consider that some variables have negative corre-

lations, suggesting a more complex dynamic in the

movement. These ﬁndings indicate that, with adjust-

ments in lag and a deeper analysis of inversely corre-

lated variables, it is possible to achieve effective inte-

gration between IMU and kinematic data to describe

movement accurately.

4.3 Clustering Analysis

Based on the clustering data involving IMU variables

and kinematic points, we analyzed kinematic and in-

ertial data. We grouped the inertial points that exhib-

ited the highest correlation with each kinematic point,

taking into account the most appropriate lag for each

relationship. The metrics used to evaluate the clusters

were the Silhouette Score, Calinski-Harabasz Score,

and Davies-Bouldin Index. When graphically analyz-

ing the clusters, we observe the variables along the

HEALTHINF 2025 - 18th International Conference on Health Informatics

axes as Principal Component 1 and Principal Compo-

nent 2. These represent the two dimensions of the data

transformed through PCA, capturing the most signif-

icant variations. Principal Component 1 accounts for

the direction of maximum variance, while Principal

Component 2 captures the second most signiﬁcant

variance in the data.

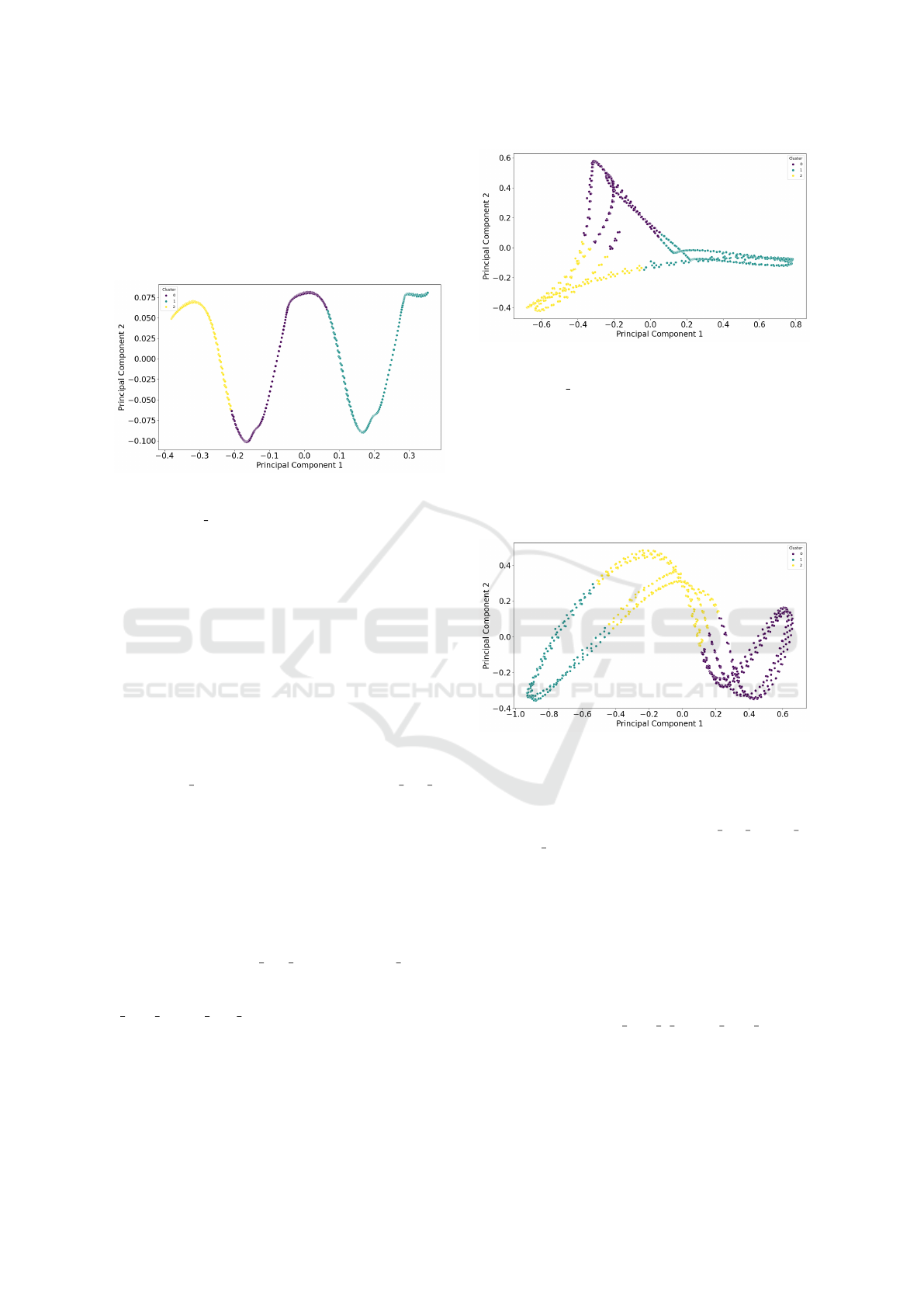
Figure 7: Clustering using K-Means for 3 clusters with PCA

and adjustment of inertial data according to the best lag.

The left ankle l mall point on the Z-axis and inertial data

with the best correlation.

The Silhouette Score (SS), which ranges from -1

to 1, measures how well a data point is associated with

its cluster compared to others. Figure 7 displays that

most variable pairs achieved SS values around 0.5 to

0.65, indicating that the clusters are reasonably well-

formed. Scores above 0.6 are considered good, while

those below 0.4 may suggest an overlap between clus-

ters.

The Calinski-Harabasz metric measures disper-

sion within and between clusters; a higher score in-

dicates better separation between clusters. Figure 8

shows that the variables related to the X-axis of the

left knee (l knee) and the left metatarsal (l met x)

stood out with scores above 5000, indicating excellent

separation between these clusters. Conversely, pairs

like the right metatarsal on the X-axis and sacrum on

the Y-axis displayed lower scores below 1500, sug-

gesting poor separation.

The Davies-Bouldin Index evaluates the similar-

ity rate between clusters. Unlike the other metrics, a

lower value indicates that the clusters are more com-

pact and well-separated. We observed higher indices

for variables such as r asis y and MIDASIS y, sug-

gesting that these clusters may be poorly deﬁned or

exhibit signiﬁcant overlap. In contrast, variables like

l mall z and l heel z showed low values, indicating

that these clusters are compact and distinct.

An analysis of the X and Z axes, such as C7

on the X-axis, the right shoulder on the Z-axis, and

the left mall on the Z-axis, revealed higher Silhou-

ette Scores (> 0.55) and lower Davies-Bouldin In-

Figure 8: Clustering using K-Means for 3 clusters with PCA

and adjustment of inertial data according to the best lag.

The left knee l knee point on the X-axis and inertial data

with the best correlation.

dex values (0.5–0.7) (Figure 9, suggesting that the

clusters associated with these axes are well-deﬁned.

We can conclude that movements or displacements

along these axes are more easily distinguishable by

the clusters, particularly in segments like the knee and

metatarsal.

Figure 9: Clustering using K-Means for 3 clusters with PCA

and adjustment of inertial data according to the best lag.

The center of mass SHO point on the X-axis and inertial

data with the best correlation.

Concerning the Y-axis, such as c7 y, r should y,

MIDASIS y, the Silhouette Scores were relatively low

(around 0.35–0.4), while the Davies-Bouldin Index

values were higher (0.9). These ﬁndings suggest that

the clusters along the Y-axis may not be as well-

deﬁned, possibly due to the complexity of vertical

movement during gait, which tends to be more contin-

uous with fewer abrupt changes. For the Y-axis, con-

ducting additional experiments and seeking comple-

mentary approaches to improve the data quality will

be necessary.

Variables such as l

knee 1 z and l mall z exhib-

ited high Calinski-Harabasz Scores and low Davies-

Bouldin Index values, indicating that the movements

of the knees and ankles, particularly in the sagittal

plane, are well-separated in clusters, reﬂecting the

importance of these joints in propulsion and phase

Approximation of Inertial Measurement Unit Data to Time Series Kinematic Data Through Correlation Analysis and Machine Learning

transitions during gait. Regarding central points like

the sacrum on the Z-axis (sacrum s z) and the mid-

point between the point of the iliac crest on the X-axis

(MIDASIS x), we observed a combination of favor-

able results, with Silhouette Scores above 0.6 and low

Davies-Bouldin Index values, indicating that the clus-

ters for these central body points are well-separated.

The variables l mall z, l knee 1 z, l met x, and

MIDASIS x demonstrated an excellent combination

of clustering metrics, meaning that they are well-

suited to describe different phases of gait or variations

in movement. However, variables associated with the

Y-axis, such as r asis y, r met x, and MIDASIS y, in-

dicate that the clusters are not well-deﬁned, suggest-

ing that the data or movements captured along these

axes do not vary signiﬁcantly between phases or sub-

jects or that substantial overlap exists.

4.4 Machine Learning Analysis

The evaluation metrics reveal that using IMU data,

the Random Forest (RF) model performed robustly

in predicting gait kinematic points. Most kine-

matic points, such as c7 z, r should z, l should z,

sacrum s z, and r mall z, showed low MSE, around

−7

, indicating high accuracy in predictions. When

assessing R

values, we observed results close to 1, as

0.99996 for c7 z, suggesting the model captures al-

most all the variance, providing a good ﬁt for these

parameters. However, some points like l met y (R-

Squared of 0.995) and r met y (R

of 0.997) showed

a lower performance in terms of variance explanation,

suggesting the model may struggle with these speciﬁc

cases. Still, these values remain above 0.99, which

overall represents strong performance.

We observed low MAE values, such as the right

shoulder on the Z-axis (r should z) with 0.00045, in-

dicating that the predictions are very close to the ac-

tual values in measurement units. The MAPE for

most points is extremely low, such as 0.0011% for

c7 z. However, points like MIDASIS y (MAPE of

10%) and r met y (MAPE of 5%) showed higher er-

rors, indicating that the model has more difﬁculty ac-

curately predicting these points, likely due to the in-

creased complexity of the Y-axis data.

The data suggests the model performs consistently

across predictions in the X, Y, and Z directions, with

larger errors occurring along the Y-axis, such as in left

heel (l heel y) and left metatarsal (r met y), which

may be attributed to greater variability in human

movement along this axis, associated with vertical

motion during gait. Comparing the LR results with

those of RF, we observe that RF has superior overall

performance regarding data ﬁt (R-Squared) and pre-

diction accuracy (MSE, MAE, RAE, MAPE), espe-

cially for more complex variables. Linear Regres-

sion performs reasonably but with more signiﬁcant

variation in results and higher errors for many vari-

ables, suggesting it does not capture the non-linearity

present in gait data as effectively.

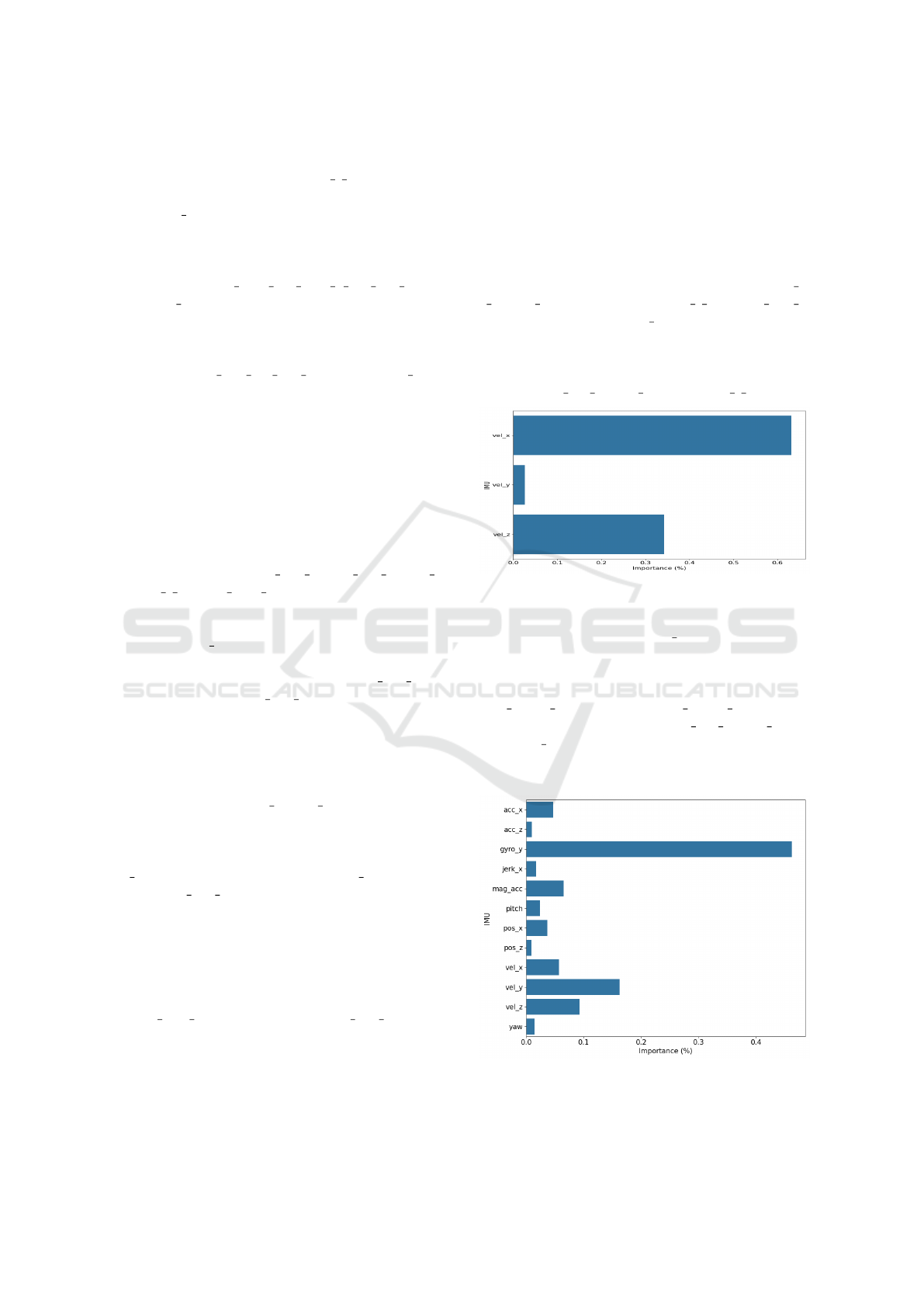
Considering the feature importance in the RF

model, we found that for many points, such as c7 x,

r should x (Figure 10), sacrum s x, and l asis x,

speed along the X-axis (vel x) plays a signiﬁcant role

compared to other variables, with velocity along this

axis being a strong predictor in the model. Veloc-

ity along the Z-axis is also relevant, particularly for

points like c7 x, r should z, and sacrum s z.

Figure 10: Feature importance of IMU data in training the

right shoulder X-axis model.

Speed along the Y-axis (vel y) shows variable im-

portance, often lower than the X and Z axes, indi-

cating that lateral velocity may be less crucial to the

overall gait behavior. Variables related to acceleration

(acc x, acc z) and position (pos x, pos z) show sig-

niﬁcant importance, such as in c7 y, r should y, and

MIDASIS y (Figure 11), suggesting that these vari-

ables may be linked to critical gait events, like direc-

tion changes or acceleration/deceleration.

Figure 11: Feature importance of IMU data in training the

model for the midpoint between the iliac crests on the Y-

axis.

HEALTHINF 2025 - 18th International Conference on Health Informatics

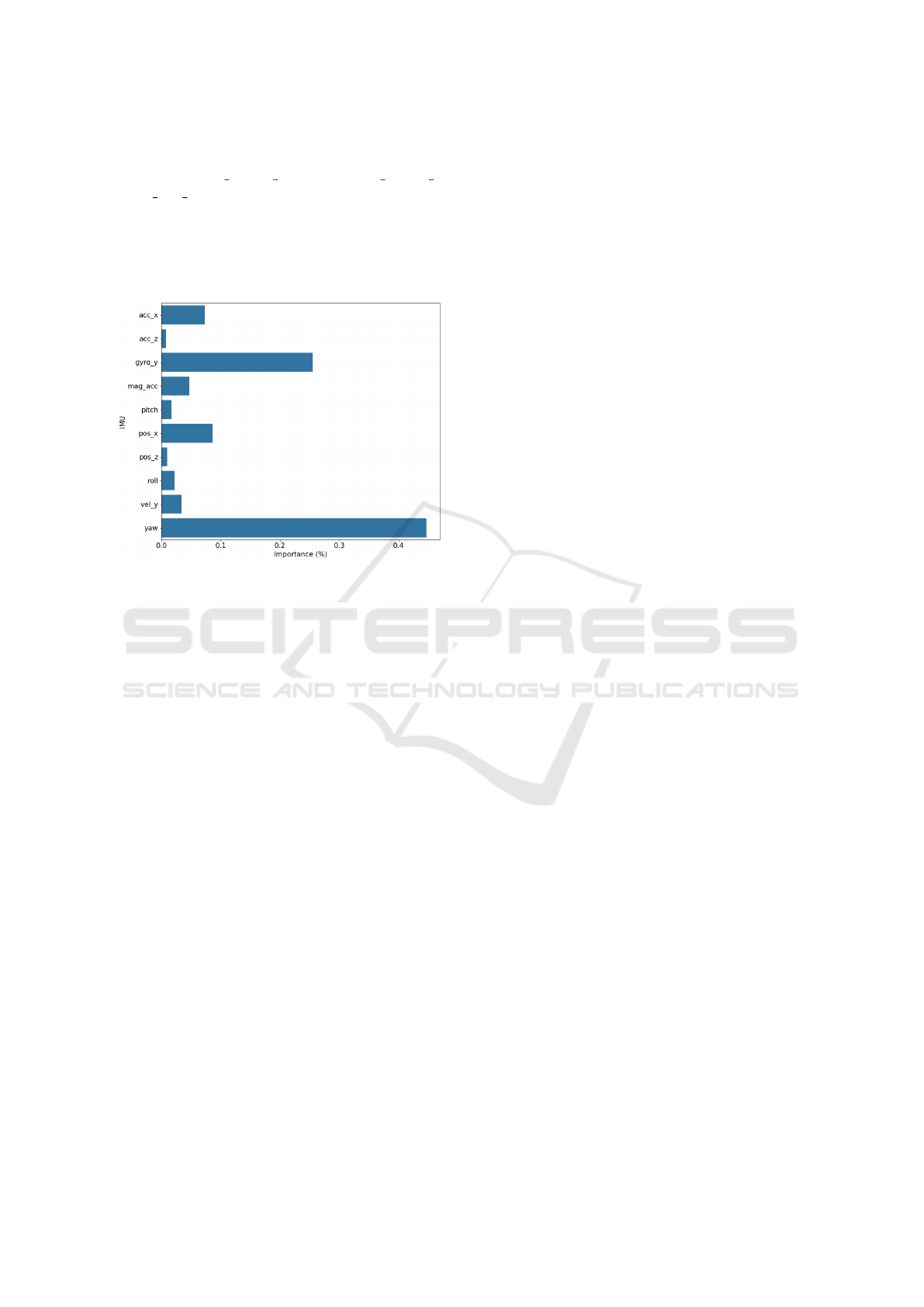
Yaw shows relevant importance for speciﬁc

points, such as r should y (Figure 12), l should x,

and r asis y, indicating that rotational movement

around the vertical axis is signiﬁcant for predicting

kinematic data. Roll and pitch exhibit relatively lower

importance, suggesting that while they inﬂuence gait,

they are less critical in determining the overall move-

ment.

Figure 12: Feature importance of IMU data in training the

model for the right shoulder on the Y-axis.

5 CONCLUSION

This study evaluated the similarity between signals

from biomechanics laboratories, considered the gold

standard in gait analysis, and inertial data from wear-

able devices, which are more accessible and cost-

effective. Achieving the same mathematical results

from different gait analysis instruments would repre-

sent a signiﬁcant breakthrough in the ﬁeld. To assess

the correspondence between the two datasets, some

experiments were conducted, comprising data col-

lection followed by preprocessing and various math-

ematical analyses, including artiﬁcial intelligence

models to predict kinematic points based on sensor

data.

Pearson correlation analysis presented promis-

ing results with good correspondence between IMU

sensor data and kinematic data, particularly in ver-

tical movements and rotations along speciﬁc axes.

Anatomical points, such as the base of the neck (C7)

and the right knee, exhibited strong correlations, sug-

gesting that inertial sensors can reliably capture key

movements. However, accelerations on the y-axis and

lateral motions showed lower correlations, revealing

a limitation of the IMU sensors in detecting small

displacements or intricate movements. Additionally,

some negative correlations suggest that the sensors

may be capturing rotations or movements opposite to

expectations, which could reﬂect natural compensa-

tions in the body during gait–an important factor that

may not necessarily be a ﬂaw but should be consid-

ered.

Cross-correlation analysis emphasized the need

for temporal alignment between inertial and kine-

matic data. The signiﬁcant time lags observed be-

tween some variables indicate delays that should be

corrected to improve the accuracy of the correlations.

Clustering analysis revealed that movements along

the X and Z axes, especially around the knee and an-

kle joints, are well-deﬁned and show clear separation

between clusters. However, clustering movements

along the Y-axis posed challenges, with low scores on

the Silhouette and Davies-Bouldin indices indicating

difﬁculties distinguishing these movements.

Improving the temporal alignment between IMU

and kinematic data is essential. Lateral movements

and speciﬁc accelerations also require more attention,

suggesting the need for new experiments or more sen-

sitive sensors. Despite these challenges, the positive

results indicate that using inertial sensors remains a

promising avenue, particularly for capturing large dis-

placements and rotations, with great potential for in-

tegration into more gait analysis systems.

The RF model performed excellently in predicting

kinematic points based on sensor data, with low error

rates and high R-Squared values for most points. A

few points with higher MAPE and RAE could bene-

ﬁt from further reﬁnement, potentially through model

architecture or input data adjustments. The RF ap-

proach appears effective and well-suited for predict-

ing kinematic gait data.

For future work, it is essential to focus on improv-

ing the data related to the Y-axis and reﬁning the clus-

tering across all anatomical points. Additionally, the

application of Machine Learning algorithms for time

series analysis holds promise, enabling more accurate

predictions and automatic pattern detection in gait. As

these techniques evolve, the accuracy and utility of in-

ertial data will be expected to improve, making wear-

ables increasingly effective tools for gait analysis in

clinical and athletic settings.

REFERENCES

Akhtaruzzaman, M., Shaﬁe, A., and Khan, M. (2016).

Gait analysis: Systems, technologies, and impor-

tance. Journal of Mechanics in Medicine and Biology,

16(07):1630003.

Benson, L., Clermont, C., Bo

snjak, E., and Ferber, R.

(2018). The use of wearable devices for walking and

Approximation of Inertial Measurement Unit Data to Time Series Kinematic Data Through Correlation Analysis and Machine Learning

running gait analysis outside of the lab: A systematic

review. Gait and Posture, 63:124–138.

Borz

ı, L., Sigcha, L., Rodr

ıguez-Mart

ın, D., and Olmo,

G. (2023). Real-time detection of freezing of gait

in parkinson’s disease using multi-head convolutional

neural networks and a single inertial sensor. Artiﬁcial

Intelligence in Medicine, 135:102459.

BTS Bioengineering (2024a). BTS G-WALK - Wire-

less Sensor for Gait Analysis. https://www.

btsbioengineering.com/products/g-walk/. Accessed:

2024-08-31.

BTS Bioengineering (2024b). BTS GAITLAB - 3D Mo-

tion Analysis System. https://www.btsbioengineering.

com/products/bts-gaitlab/. Accessed: 2024-08-31.

Burdack, J., Horst, F., Giesselbach, S., Hassan, I., Daffner,

S., and Sch

ollhorn, W. I. (2020). Systematic compar-

ison of the inﬂuence of different data preprocessing

methods on the performance of gait classiﬁcations us-

ing machine learning. Frontiers in Bioengineering and

Biotechnology, 8.

Caldas, R., Sarai, R., Buarque de Lima Neto, F., and Mark-

ert, B. (2020). Validation of two hybrid approaches for

clustering age-related groups based on gait kinematics

data. Medical Engineering & Physics, 78:90–97.

da Rosa Tavares, J., Ullrich, M., Roth, N., Kluge, F.,

Eskoﬁer, B., Gaßner, H., Klucken, J., Gladow, T.,

Marxreiter, F., da Costa, C., da Rosa Righi, R., and

Vict

oria Barbosa, J. (2023). utug: An unsupervised

timed up and go test for parkinson’s disease. Biomed-

ical Signal Processing and Control, 81:104394.

Delval, A., Betrouni, N., Tard, C., Devos, D., Dujardin,

K., Defebvre, L., Labidi, J., and Moreau, C. (2021).

Do kinematic gait parameters help to discriminate

between fallers and non-fallers with parkinson’s dis-

ease? Clinical Neurophysiology, 132(2):536–541.

Desai, R., Martelli, D., Alomar, J., Agrawal, S., Quinn, L.,

and Bishop, L. (2024). Validity and reliability of in-

ertial measurement units for gait assessment within a

post stroke population. Topics in Stroke Rehabilita-

tion, 31(3):235–243. PMID: 37545107.

He, Y., Chen, Y., Tang, L., Chen, J., Tang, J., Yang, X., Su,

S., Zhao, C., and Xiao, N. (2024). Accuracy valida-

tion of a wearable imu-based gait analysis in healthy

female. BMC Sports Science, Medicine and Rehabili-

tation, 16(1):2.

Jakob, V., K

uderle, A., Kluge, F., Klucken, J., Eskoﬁer,

B., Winkler, J., Winterholler, M., and Gassner, H.

(2021). Validation of a sensor-based gait analysis sys-

tem with a gold-standard motion capture system in pa-

tients with parkinson’s disease. Sensors, 21(22).

Kim, H., Kim, Y.-H., Kim, S.-J., and Choi, M.-T. (2022).

Pathological gait clustering in post-stroke patients us-

ing motion capture data. Gait & Posture, 94:210–216.

Kotiadis, D., Hermens, H., and Veltink, P. (2010). Inertial

gait phase detection for control of a drop foot stimula-

tor: Inertial sensing for gait phase detection. Medical

Engineering and Physics, 32(4):287–297.

Kvist, A., Tinmark, F., Bezuidenhout, L., Reimeringer, M.,

Conradsson, D., and Franz

en, E. (2024). Validation

of algorithms for calculating spatiotemporal gait pa-

rameters during continuous turning using lumbar and

foot mounted inertial measurement units. Journal of

Biomechanics, 162:111907.

Millecamps, A., Lowry, K., Brach, J., Perera, S., Redfern,

M., and Sejdi

c, E. (2015). Understanding the effects

of pre-processing on extracted signal features from

gait accelerometry signals. Computers in Biology and

Medicine, 62:164–174.

Nguyen, A., Roth, N., Ghassemi, N., Hannink, J., Seel, T.,

Klucken, J., Gassner, H., and Eskoﬁer, B. (2019). De-

velopment and clinical validation of inertial sensor-

based gait-clustering methods in parkinson’s dis-

ease. Journal of NeuroEngineering and Rehabilita-

tion, 16(1):77.

Parashar, A., Parashar, A., Ding, W., Shabaz, M., and Rida,

I. (2023). Data preprocessing and feature selection

techniques in gait recognition: A comparative study of

machine learning and deep learning approaches. Pat-

tern Recognition Letters, 172:65–73.

Ripic, Z., Nienhuis, M., Signorile, J., Best, T., Ja-

cobs, K., and Eltoukhy, M. (2023). A comparison

of three-dimensional kinematics between markerless

and marker-based motion capture in overground gait.

Journal of Biomechanics, 159:111793.

Rousanoglou, E., Foskolou, A., Emmanouil, A., and

Boudolos, K. (2024). Inertial sensing of the abdomi-

nal wall kinematics during diaphragmatic breathing in

head standing. Biomechanics, 4(1):63–83.

Silva, L. and Stergiou, N. (2020). Chapter 7 - the basics

of gait analysis. In Stergiou, N., editor, Biomechanics

and Gait Analysis, pages 225–250. Academic Press.

Tsakanikas, V., Ntanis, A., Rigas, G., Androutsos,

C., Boucharas, D., Tachos, N., Skaramagkas, V.,

Chatzaki, C., Kefalopoulou, Z., Tsiknakis, M., and

Fotiadis, D. (2023). Evaluating gait impairment in

parkinson’s disease from instrumented insole and imu

sensor data. Sensors, 23(8).

Zhang, Y., Wang, M., Awrejcewicz, J., Fekete, G., Ren, F.,

and Gu, Y. (2017). Using gold-standard gait analy-

sis methods to assess experience effects on lower-limb

mechanics during moderate high-heeled jogging and

running. Journal of visualized experiments : JoVE,

127:55714.

Zhou, L., Tunca, C., Fischer, E., Brahms, C., Ersoy, C.,

Granacher, U., and Arnrich, B. (2020). Validation of

an imu gait analysis algorithm for gait monitoring in

daily life situations. In Annual International Confer-

ence of the IEEE Engineering in Medicine and Biol-

ogy Society (EMBC), pages 4229–4232.

HEALTHINF 2025 - 18th International Conference on Health Informatics