Double Descent Phenomenon in Liquid Time-Constant Networks,
Quantized Neural Networks and Spiking Neural Networks
Hongqiao Wang and James Pope
a
School of Engineering Mathematics and Technology, University of Bristol, U.K.
Keywords:
Double Descent, LTC, QNN, SNN.
Abstract:
Recent theoretical machine learning research has shown that the traditional U-shaped bias-variance trade-off
hypothesis is not correct for certain deep learning models. Complex models with more parameters will fit
the training data well, often with zero training loss, but generalise poorly, a situation known as overfitting.
However, some deep learning models have shown to generalise even after overfitting, a situation known as
the double descent phenomenon. It is important to understand which deep learning models exhibit this phe-
nomenon for practitioners to design and train these models effectively. It is not known whether more recent
deep learning models exhibit this phenomenon. In this study, we investigate double descent in three recent neu-
ral network architectures: Liquid Time-Constant Networks (LTCs), Quantised Neural Networks (QNNs), and
Spiking Neural Networks (SNNs). We conducted experiments on the MNIST, Fashion MNIST, and CIFAR-
10 datasets by varying the widths of the hidden layers while keeping other factors constant. Our results show
that LTC models exhibit a subtle form of double descent, while QNN models demonstrate a pronounced dou-
ble descent on CIFAR-10. However, the SNN models did not show a clear pattern. Interestingly, we found
the learning rate scheduler, label noise, and training epochs can significantly affect the double descent phe-
nomenon.
1 INTRODUCTION
1.1 Double Descent Overview
In machine learning, the generalisation ability of a
model is an important factor in evaluating model per-
formance. The generalisation ability is determined by
a combination of bias and variance. Bias is defined as
the error between the predicted and true values of a
model. It is a measure of the model’s ability to fit the
training data. Meanwhile, variance is used to describe
the extent to which a model’s predictions vary across
different training data sets. It measures the model’s
sensitivity to the training data. The conventional wis-
dom is that overly simple models have a high bias due
to their inability to learn complex patterns in the data.
As model complexity continues to increase, the bias
of the model decreases and the generalisation abil-
ity improves. However, overly complex models have
high variance due to overfitting caused by a high re-
liance on noise in the training data. In other words, the
generalization ability, represented by test error, forms
a
https://orcid.org/0000-0003-2656-363X
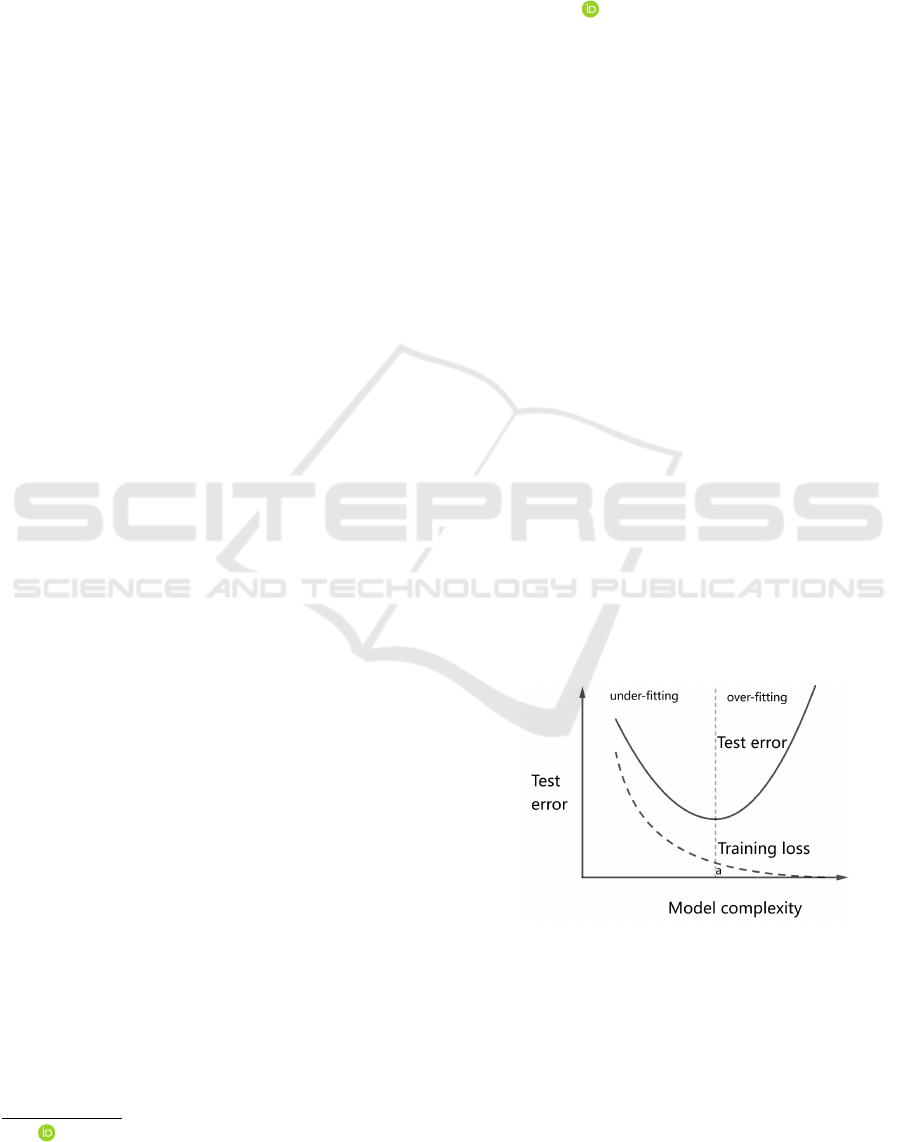
a U-shaped curve with respect to model complexity,
and the key issue is to find the point where variance
and bias can be traded off (Geman et al., 1992) (Hastie
et al., 2001). The U-shaped curve shown in Figure 1.
Figure 1: U-Shaped curve.
However, the traditional biased variance trade-off
seems to be imperfect in some modern deep neural
networks. In 2018, Belkin first proposed the phe-
nomenon of double descent and confirmed its exis-
tence in neural network models (Belkin et al., 2019).
The double descent curve shown in figure 2 refers to
the fact that after the traditional U-shaped curve, the
Wang, H. and Pope, J.
Double Descent Phenomenon in Liquid Time-Constant Networks, Quantized Neural Networks and Spiking Neural Networks.
DOI: 10.5220/0013133900003890
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 17th International Conference on Agents and Artificial Intelligence (ICAART 2025) - Volume 3, pages 351-359
ISBN: 978-989-758-737-5; ISSN: 2184-433X
Proceedings Copyright © 2025 by SCITEPRESS – Science and Technology Publications, Lda.
351

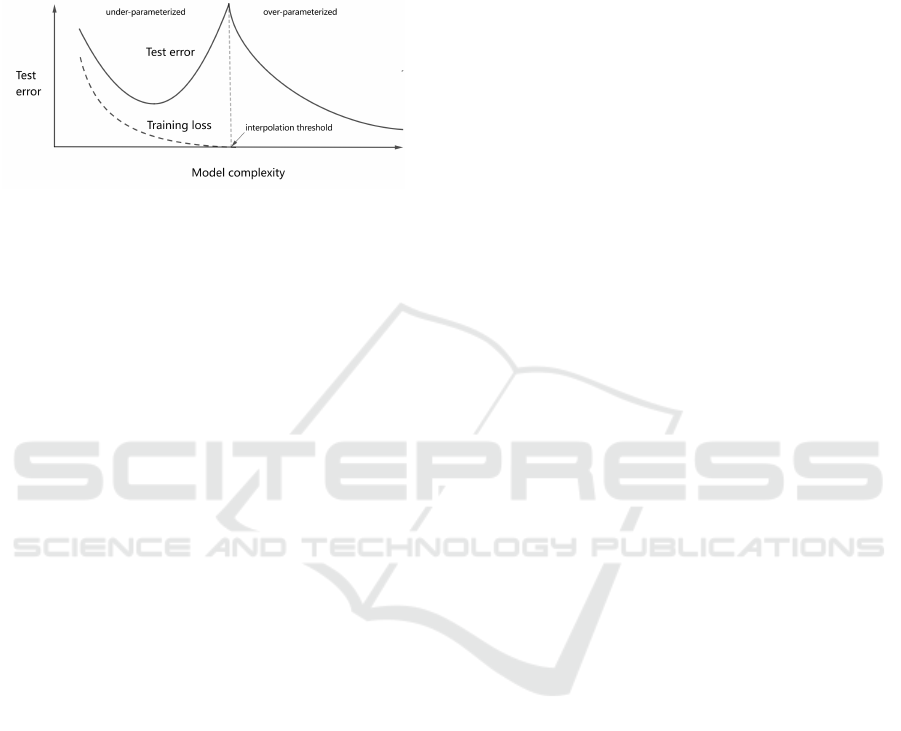
generalisation error on the right side of the interpola-
tion threshold point (Salakhutdinov, 2017) decreases
again due to the increase in model complexity. Specif-
ically, beyond the interpolation threshold, empirical
observations indicate an enhancement in the model’s
generalization performance.
Figure 2: Double Descent Curve.
The causes and characteristics of the double de-
scent curve have been analysed by many researchers,
but the reasons for this phenomenon are not yet fully
understood. Moreover, the presence of the double de-
scent phenomenon remains underexplored in many
types of neural networks, which poses challenges
for researchers in understanding and optimizing these
models.
1.2 Study Aims
Belkin (Belkin et al., 2019) and Lafon (Lafon and
Thomas, 2024) identified the double descent curve
in RFF and ReLU models. This phenomenon has
also been verified in ResNets, CNNs, and Transform-
ers (Nakkiran et al., 2021). Shi (Shi et al., 2024)
further validated double descent in GCNs (Kipf and
Welling, 2017), graph attention networks (Veli
ˇ
ckovi
´
c
et al., 2017), GraphSAGE (Hamilton et al., 2017), and
Chebyshev graph networks (Defferrard et al., 2016).
However, the double descent phenomenon remains
under-explored in many neural network models.
Liquid Time-Constant Networks (LTCs), Quan-
tised Neural Networks (QNNs), and Spiking Neural
Networks (SNNs) represent advancements in neural
network design, each with distinct advantages like
adaptability, reduced computational needs, and bio-
logical plausibility. LTCs regulate first-order dynam-
ical systems for time series forecasting (Hasani et al.,
2021). QNNs reduce computational complexity by
quantising weights and activations into low precision
values while retaining accuracy (Guo, 2018) (Hubara
et al., 2018). SNNs, inspired by biological systems,
process spatiotemporal data efficiently using spike
timing (Tavanaei et al., 2019).
This study aims to explore whether double descent
manifests in these architectures and under what condi-
tions. Factors such as training data size, noise, model
complexity, epochs, optimizer, and learning rate may
influence its occurrence. We designed double descent
experiments with varying hidden layer widths while
keeping other parameters constant to investigate these
effects and improve training practices, especially re-
garding overfitting and model complexity.
1.3 Study Contributions
Our results show that the LTC model observes a slight
double descent on a network depth of 5, but over-
all the test error curve shows a decreasing trend and
eventually stabilises at a low value, demonstrating
good generalizability.
For the QNN model, a significant double descent
phenomenon was observed in both the MNIST and
CIFAR-10 datasets. The results show that increasing
epoch weakens the trend of the second decline. Im-
portantly, we also find that adding data noise aggra-
vates the double descent phenomenon, while adding a
learning rate scheduler eliminates it.
In contrast, the SNN model does not show a dou-
ble descent phenomenon on the MNIST dataset. In-
stead, the test error curve shows a traditional U-
shaped pattern without the learning rate scheduler,
while after adding it, the test error decreases and then
remains low.
In summary, our results show that SNNs do not
exhibit double descent behaviour, whereas LTCs and
QNNs exhibit double descent in specific situations.
Furthermore, the finding that adding a learning rate
scheduler may eliminate the double descent phe-
nomenon is novel. The study of this phenomenon can
provide valuable insights into their performance and
guide the future development of neural network re-
search.
2 BACKGROUND
2.1 Double Descent
The double descent phenomenon, an important re-
cent discovery in deep learning, extends the classical
U-shaped bias-variance trade-off curve. It describes
how test error first decreases, then increases, and fi-
nally decreases again after overfitting as neural net-
work complexity grows. This suggests that increas-
ing model capacity beyond an interpolation threshold
can improve generalization, contrary to the traditional
view that overfitting leads to poor generalization.
Belkin et al. (Belkin et al., 2019) first identified
this secondary drop in test error, proposing that larger
ICAART 2025 - 17th International Conference on Agents and Artificial Intelligence
352

function spaces allow models to discover smoother
interpolation functions, reducing test error. Lafon
and Thomas (Lafon and Thomas, 2024) extended this
analysis, showing how both explicit (e.g., regular-
ization) and implicit biases (from gradient descent)
help select models that generalize well even in over-
parameterized settings.
Nakkiran et al. introduced the concept of Effective
Model Complexity (EMC) to explain how double de-
scent also depends on training epochs, not just model
size (Nakkiran et al., 2021). The EMC expression is
as follows:
EMC
D,ε
(T ) := max
{
n | E
S∼D
n
[Error
S
(T (S))] ≤ ε
}
(1)
Neal et al. (Neal et al., 2018) and Hastie et al.
(Hastie et al., 2022) further analysed bias and variance
behavior in over-parameterized models. The general-
ization error, represented by the formula:
Err( f ) = Bias
2
( f )+ Var( f ) (2)
provides theoretical insight into how bias and vari-
ance change as model complexity increases.
Empirical studies have confirmed double descent
across various models and datasets, including CNNs
(Geiger et al., 2020) and graph neural networks (Shi
et al., 2024). Derezinski et al. (Derezinski et al.,
2020) highlighted the role of implicit regularization,
and Nakkiran and Bansal (Nakkiran et al., 2021)
showed that proper regularization can suppress dou-
ble descent. Pagliardini et al. (Pagliardini et al.,
2018) used decision boundary analysis to explore how
model width affects generalization. Pezeshki et al.
(Pezeshki et al., 2022) reveal that the essence of the
test error’s double descent behavior over training time
lies in the learning dynamics of different features on
varying time scales.
All of the above theoretical explanations share a
common view that classical VC-theory cannot explain
double descent in large over-parameterized networks.
However, Cherkassky and Lee (Cherkassky and Lee,
2024) demonstrate that the phenomenon of double de-
scent can be effectively explained using VC theory by
linking generalization performance to the minimiza-
tion of VC-dimension through Structural Risk Mini-
mization (SRM) and weight norm control.
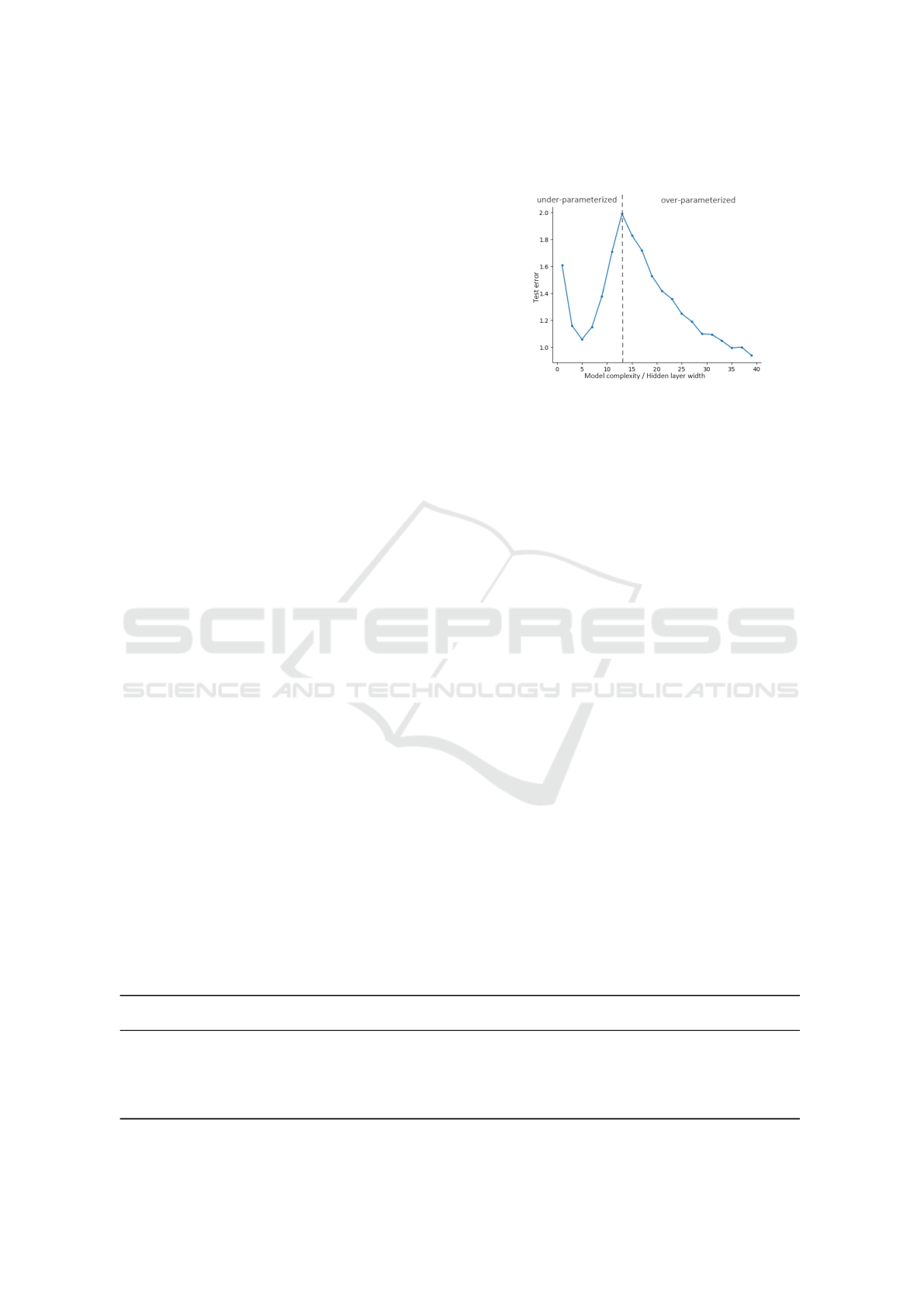
Figure 3: CNN Double Descent Curve.
To validate the existence of double descent, we
replicated Nakkiran et al.’s experiments (Nakkiran
et al., 2021) using a 4-layer CNN on CIFAR-10, in-
creasing layer width. The results, shown in Figure 3,
confirmed the double descent phenomenon. This
model will serve as the basis for our work on quan-
tised networks.
3 METHODOLOGY
3.1 Overview of Double Descent
Experimental
The focus of all experiments was to understand how
the test error curve manifests under different condi-
tions when the model complexity increasing. Model
complexity can be increased by three methods: in-
creasing units in a hidden layer, adding layers, or
combining both. Each experiment with different set-
ting varied the network width and different experi-
ments varied the number of layers to analyse its im-
pact on test error to explore the occurrence of the
double descent phenomenon. Table 1 shows the ap-
proaches taken to increase model complexity and out-
lines the experimental conditions for LTC, QNN, and
SNN models.
Liquid Time-Constant Networks (LTCs). We uti-
lized networks of four different depths, consisting of
Table 1: Experiment Settings for LTC, QNN, and SNN Models.
Model Depths Widths Optimizer Scheduler Epochs Dataset
LTC 1, 3, 5, 10 1–63 (step 2) SGD/Adam with/without 50 Fashion MNIST
QNN 2, 4 1–63 (step 2) SGD/Adam with/without 20, 50, 80 MNIST, CIFAR-10
SNN 2, 4 10–2000 (step 50) SGD with/without 50 MNIST
Double Descent Phenomenon in Liquid Time-Constant Networks, Quantized Neural Networks and Spiking Neural Networks
353

1, 3, 5, and 10 layers. The width of each hidden layer
was varied from 1 to 63, increasing in increments of 2.
After this, we further confirm whether the double de-
scent phenomenon would occur by conducting addi-
tional experiments on a 5-layer LTC network but with
a reduced step size of change in network width from
2 to 1. We built LTC models with multiple LTC lay-
ers followed by a fully connected output layer. Each
LTC layer updates its hidden state using the following
equation:
h
t
= τh
t−1
+ (1 − τ)·ReLU(W
in
· x
t
+W
rec
· h
t−1
+ b)
where h
t
is the hidden state at time t, τ is the time con-
stant, W
in
and W
rec
are input and recurrent weights,
and b is the bias term. ReLU was selected for its sim-
plicity and effectiveness.
Quantized Neural Networks (QNNs). For CIFAR-
10, we varied network complexity by increase param-
eter c from 1 to 63 and used Adam and SGD optimiz-
ers across different training epochs (20, 50, 80), la-
bel noise (0%, 10%, 20%), with and without learning
rate scheduler. For MNIST, we conducted two exper-
iments: one using the same architecture and settings
as CIFAR-10 (10% label noise, 50 training epochs,
without learning rate scheduler), and a second with a
simplified QNN to explore the effect of reduced net-
work complexity. The QNN was based on a 5-layer
CNN, quantised using PyTorch’s Quantisation-Aware
Training (QAT).
Spiking Neural Networks (SNNs). We used models
with two different depths, consisting of 2 and 4 layers.
The width of each hidden layer was varied from 10
to 2000, increasing in increments of 50. Our models
used a two-layer and a four-layer architectures with
fully connected layers followed by Leaky Integrate-
and-Fire (LIF) neurons.
4 RESULTS
The summary of results of all the experiments are
shown in appendix.
4.1 Experiment 1: Liquid
Time-Constant Networks
In our experiments, we assessed the double de-
scent phenomenon and generalization performance
of Liquid Time-Constant (LTC) networks with vary-
ing depths (1, 3, 5, 10 layers) on the Fash-
ion MNIST dataset. The models were trained
for 50 epochs using the SGD optimizer and the
InverseSquareRootScheduler learning rate sched-
uler. Training without the scheduler resulted in
vanishing gradients, which prevented convergence.
All LTC networks demonstrated strong generaliza-
tion, with test error curves decreasing sharply as net-
work width increased and stabilizing at consistently
low values. Notably, the traditional U-shaped bias-
variance curve was absent.
Of particular note is the behavior of the 5-layer
LTC network, where the test error curve exhibited a
subtle indication of double descent within the hidden
layer width range of 1 to 10. The training error curve
for this model can be seen to reach the interpolation
threshold at approximately width 5, which is about
the starting point for the test error to begin its sec-
ond decline. This fact is consistent with the theory
of double descent which is the test error will fall a
second time after the interpolation threshold reached
and further increases the likelihood of a double de-
scent occurring in the 5-layer LTC network. However,
this observation remains inconclusive, as the fluctua-
tions could be attributed to training instability rather
than a definitive double descent behaviour. To investi-
gate further, we conducted an additional experiments
with narrower width increments (increasing the hid-
den layer width by one unit at a time). The results
continued to suggest a potential double descent pat-
tern: the test error initially decreased as the hidden
layer width increased from 1 to 3, slightly increased
at width 4, and then decreased again. However, due to
the short duration of the error increase, it is difficult
to definitively confirm the presence of double descent
in the LTC network.
Despite this ambiguity, our results imply that LTC
networks may indeed be susceptible to double descent
under certain conditions. However, the inherent sim-
plicity of the Fashion MNIST dataset likely resulted
in a rapid decline in training loss. This rapid conver-
gence and the small size of the interpolation thresh-
old may have caused the upward trend in test error
to begin diminishing before it could fully manifest.
Consequently, this could have obscured our ability
to clearly observe the presence of the double descent
phenomenon. Future will be to evaluate double de-
scent using the different layers and datasets.
The ultimate goal of training a network is to min-
imize test error to achieve optimal generalization.
While we cannot definitively claim to have observed
the double descent phenomenon in LTC networks, the
consistent reduction in test error across all network
depths as network width increased, demonstrates that
the networks ultimately achieved robust generaliza-
tion performance, meeting our primary objectives.
In addition to using the SGD optimizer, we ex-
plored the network using the Adam optimizer. Re-
sults shown in Figure 4 (b), revealed gradient vanish-
ICAART 2025 - 17th International Conference on Agents and Artificial Intelligence
354

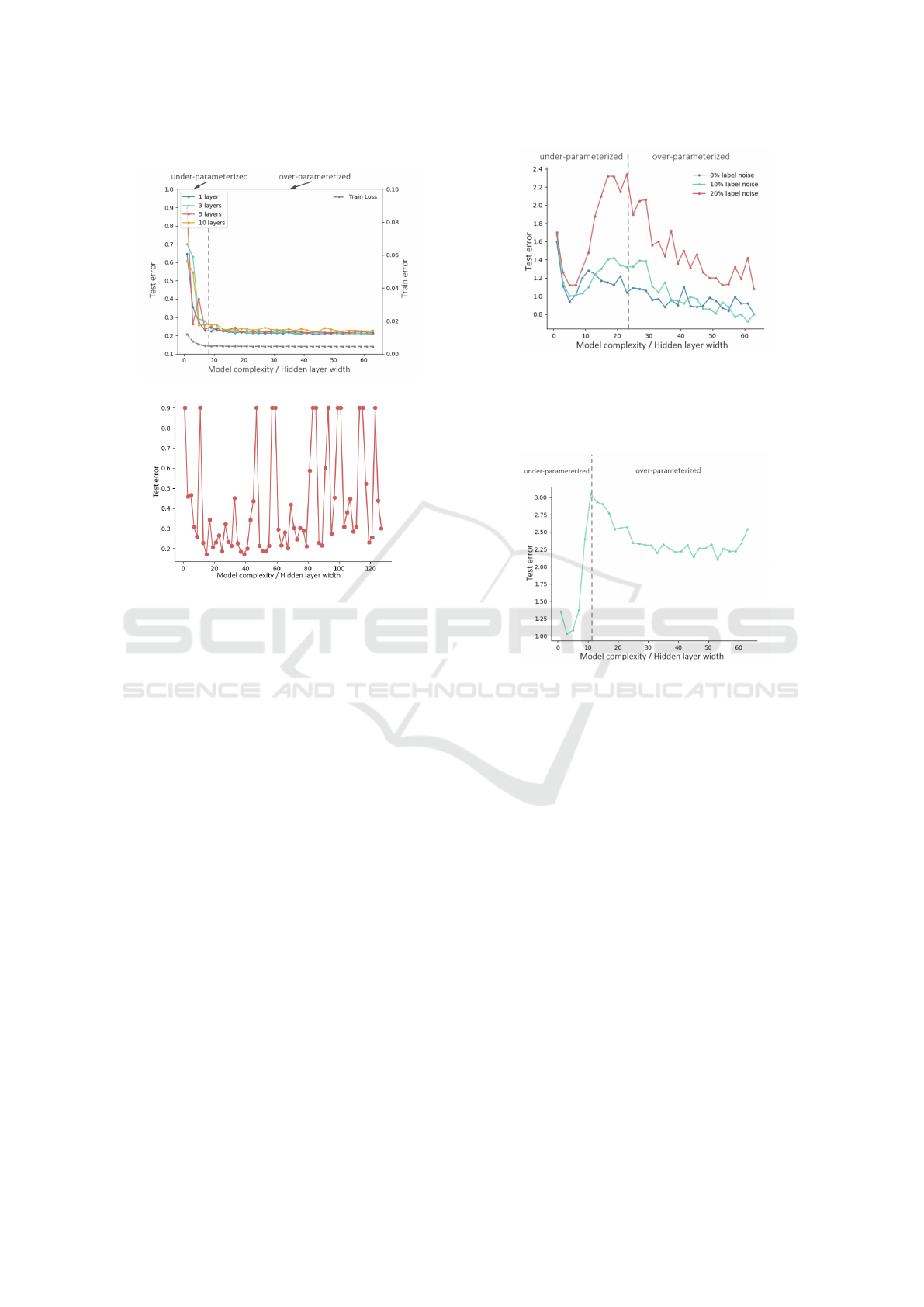
(a)
(b)
Figure 4: (a) Test error curves for 1, 3, 5, and 10-layer
LTC networks on Fashion MNIST using the SGD optimizer.
LTCs did not show clear double descent phenomenon but
generalized well. (b) Test error curves for 5-layer LTC net-
works on Fashion MNIST using the Adam optimizer. LTC
did not show double descent phenomenon and generalized
poorly.
ing and unstable test errors, resulting in inferior gen-
eralization compared to SGD. Based on these find-
ings, we recommend using the SGD optimizer when
training LTC networks on simple datasets like Fash-
ion MNIST. Expanding both network width and depth
can improve generalization without significant risk of
overfitting. Future work will examine double descent
across more diverse datasets and network configura-
tions.
4.2 Experiment 2: Quantised Neural
Networks
In our second set of experiments, we investigated the
behavior of Quantized Neural Networks (QNNs) on
CIFAR-10 to understand how quantization impacts
the double descent phenomenon and generalization.
Initial experiments used the Adam optimizer (learn-
ing rate 0.001, 50 epochs) under varying label noise
levels (0, 0.1, 0.2), as shown in Figure 5. Results
confirmed that quantization does not eliminate dou-
ble descent. Moreover, the data noise did not disrupt
Figure 5: Test error curve for 4-layer QNN models with
label noise (0, 0.1, 0.2) using Adam optimizer, 50 epochs,
without learning rate scheduler on CIFAR-10. QNNs show
significant double descent phenomenon and this trend be-
comes more pronounced with increasing label noise.
Figure 6: Test error curve for 4-layer QNN with 0.1 label
noise using Adam optimizer, 80 epochs, without learning
rate scheduler on CIFAR-10. As the number of training
epochs increases, the double descent trend becomes less no-
ticeable and the generalisation capacity decreases.
the double descent phenomenon, and increasing label
noise exacerbated the double descent phenomenon.
We then extended the training epochs to 80, keep-
ing the learning rate at 0.001 and label noise at 0.1
(Figure 6). This weakened the magnitude of the sec-
ond descent but notably worsened generalization per-
formance, especially at higher model complexities,
suggesting that network models with double descent
phenomena do not always get good generalisation
performance by simply increasing the model com-
plexity and train epoch.
To understand this decline in performance, we
conducted additional experiments where we moni-
tored both training and test errors across all epochs.
The results revealed that, particularly in networks
with large hidden layer widths, test error initially de-
creased but subsequently increased as training con-
tinued. This suggests that prolonged training (i.e.,
excessive training epochs) can diminish the model’s
generalization ability.
Double Descent Phenomenon in Liquid Time-Constant Networks, Quantized Neural Networks and Spiking Neural Networks
355

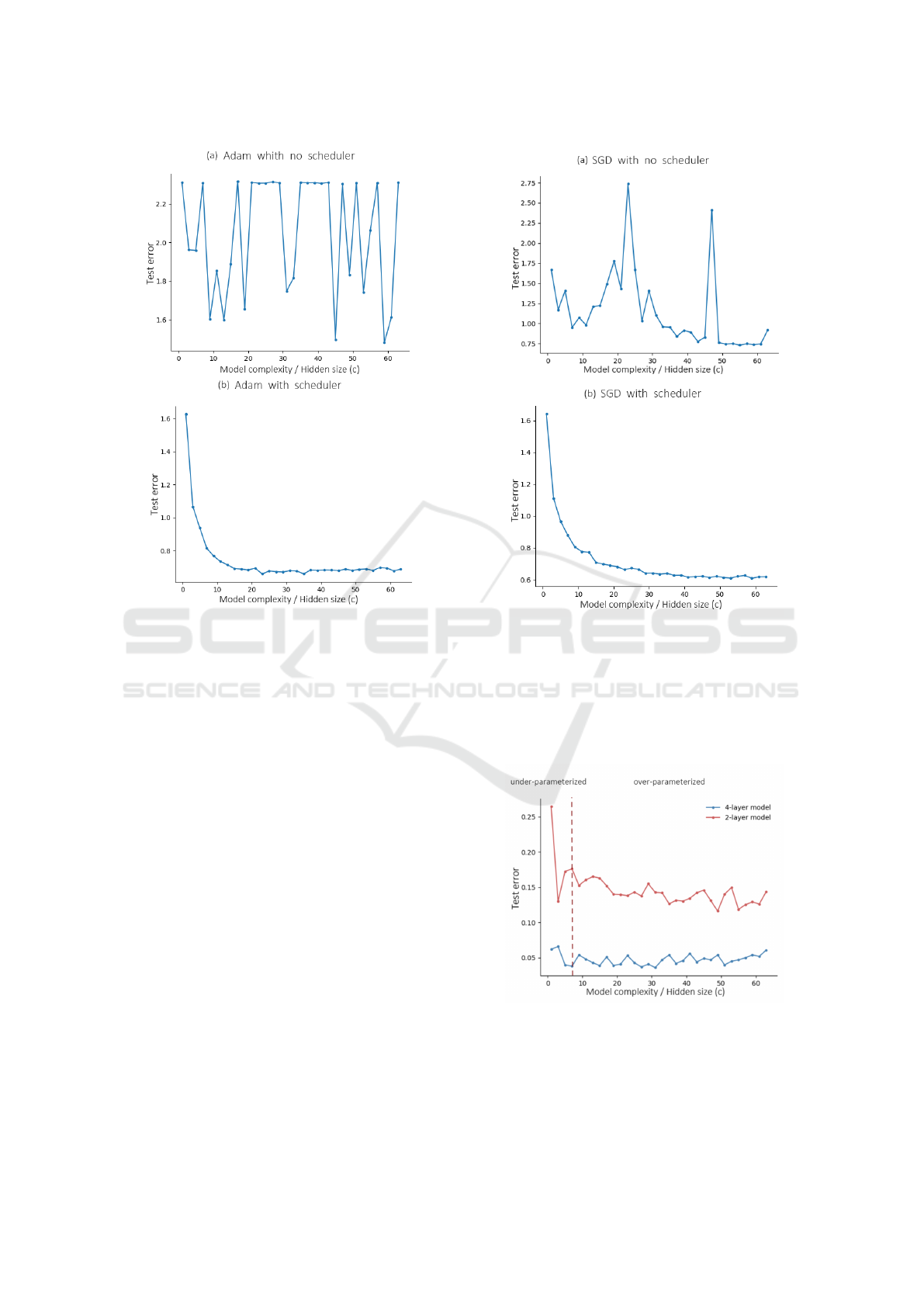
Figure 7: (a) Test error curve for 4-layer QNN with 0.1 la-
bel noise using Adam optimizer with higher learning rate
and 20 epochs, without learning rate scheduler on CIFAR-
10. The test error curve did not show double descent trend
and was highly unstable, indicating weak generalization
ability. (b) Test error curve for 4-layer QNN with 0.1 la-
bel noise using Adam optimizer with higher learning rate
and 20 epochs, with learning rate scheduler on CIFAR-10.
The test error curve did not show double descent trend but
demonstrated strong generalization ability.
To address this, we reduced training epochs to 20
and increased the learning rate to 0.1. However, the
larger learning rate introduced instability due to ex-
ploding gradients, as shown in Figure 7(a). Incorpo-
rating the StepLR scheduler (Figure 7(b)) effectively
eliminated the double descent phenomenon and im-
proved generalization performance.
To explore whether the choice of optimizer af-
fects the double descent phenomenon, we replaced
Adam with SGD under the same conditions. Without
a scheduler, the double descent pattern persisted but
remained unstable (Figure 8(a)). Adding the StepLR
scheduler stabilized the test error curve and improved
generalization (Figure 8(b)). Overall, SGD outper-
formed Adam in generalization performance but did
not entirely eliminate double descent.
In the two experiments conducted on the MNIST
dataset, the results are illustrated in Figure 9. The
blue line represents the performance of the original
Figure 8: (a) Test error curve for 4-layer QNN with 0.1 label
noise using SGD optimizer with higher learning rate and 20
epochs, without learning rate scheduler on CIFAR-10. The
test error curve demonstrated double descent trend but re-
mained unstable. (b) Test error curve for 4-layer QNN with
0.1 label noise using SGD optimizer with higher learning
rate and 20 epochs, with learning rate scheduler on CIFAR-
10. The test error curve did not show double descent trend
but demonstrated strong generalization ability.
Figure 9: Test error curve for 2- and 4-layer QNNs with 0.1
label noise using Adam optimizer, 50 epochs, without learn-
ing rate scheduler on MNIST. The 2-layer model exhibited
the double descent phenomenon, whereas the 4-layer model
did not.
ICAART 2025 - 17th International Conference on Agents and Artificial Intelligence
356

QNN model which does not show the double descent
behaviour, while the red line depicts the results from
the simplified QNN model which show the double
descent behaviour. When comparing the blue line
with the corresponding results in Figure 9, it becomes
evident that when the experimental model and con-
figuration remain unchanged, the use of a simpler
dataset allows the model to learn the underlying pat-
terns more effectively, leading to better generalization
performance. However, although the simplified QNN
model exhibited the double descent phenomenon, as
shown by the red line, the generalization performance
of the model was worse than complex model.
Through these experiments, we have established
several important conclusions and recommendations
for training QNNs:
1. Persistence of Double Descent. quantisation does
not negate the occurrence of the double descent phe-
nomenon. The characteristic double descent behav-
ior observed in the original CNN architecture persists
in the quantised version, confirming that the quan-
tisation process alone does not eliminate this phe-
nomenon.
2. Data Noise. Increased data noise may exacerbate
the double descent phenomenon
3. Mitigating Overfitting. Several techniques,
including reducing the learning rate, introducing a
learning rate scheduler, and limiting the number of
training epochs, effectively mitigate overfitting. In
particular, the learning rate scheduler helps to elim-
inate the double descent phenomenon without affect-
ing the generalisation ability of the model.
4. Model Complexity vs. Generalization. Our ex-
periments indicate that simply increasing model com-
plexity does not guarantee improved generalization.
Even if there is a double descent behaviour, if the
learning rate and training duration are not adjusted
properly, the test error during the second descent may
not drop below the U-curve lowest point or, in some
cases, the traditional U-shaped curve may replace the
double descent curve entirely. In such instances, the
generalization error continues to rise after reaching its
initial minimum, with no subsequent decline.
5. Optimizer and Scheduler The choice of optimizer
and the use of a learning rate scheduler are crucial fac-
tors influencing the behavior of QNNs. In our exper-
iment, SGD is better than Adam Optimizer but both
can lead to unstable training outcomes and a notice-
able decline in generalization performance, particu-
larly under conditions of high learning rates and ex-
tended training durations. However, when combined
with a learning rate scheduler, the model can provide
a more stable and robust generalization performance.
In conclusion, when training QNNs, particularly
on complex datasets like CIFAR-10, we must pay
careful attention to the selection of optimizer, learn-
ing rate, training duration, and the use of learning rate
schedulers. These factors play a crucial role in in-
fluencing the model’s generalization performance and
the occurrence of the double descent phenomenon.
Future research should continue to explore these vari-
ables in order to further optimize the training of more
type of QNNs.
4.3 Experiment 3: Spiking Neural
Networks
In this study, we investigated the double de-
scent phenomenon and generalization performance
of Spiking Neural Networks (SNNs) using two
models with different depths (2 and 4 LIF lay-
ers) on the MNIST dataset. Each model was
tested under two conditions: with and without the
InverseSquareRootScheduler learning rate sched-
uler.
Across all experiments, the double descent phe-
nomenon did not manifest, regardless of network
depth or the use of a scheduler. Without the scheduler,
both networks exhibited traditional U-shaped test er-
ror curves, indicating overfitting as model complex-
ity increased. The simpler 2-layer network consis-
tently achieved lower test errors, suggesting that in the
absence of a learning rate scheduler, increasing the
model’s complexity—whether by expanding the hid-
den layer width or by adding more layers—can lead to
overfitting, thereby compromising the model’s ability
to generalize effectively.
In contrast, introducing the
InverseSquareRootScheduler significantly
improved generalization, with test error curves
initially decreasing and then stabilizing at low levels
as model complexity increased. The 2-layer net-
work continued to outperform the 4-layer network,
highlighting the superior generalization of simpler
models.
These results indicate that SNNs do not exhibit
double descent under the studied conditions, with
overfitting being the primary challenge. The re-
sults also emphasize the crucial role of the learning
rate scheduler in enhancing the generalization perfor-
mance of SNNs. The scheduler effectively mitigated
U-shaped error profiles and improved stability and
generalization, particularly for simpler datasets like
MNIST.
In summary, experiments with SNNs demonstrate
that double descent does not exist. For practitioners
using SNNs, it is recommended to use a learning rate
scheduler to manage overfitting and thoughtfully con-
Double Descent Phenomenon in Liquid Time-Constant Networks, Quantized Neural Networks and Spiking Neural Networks
357

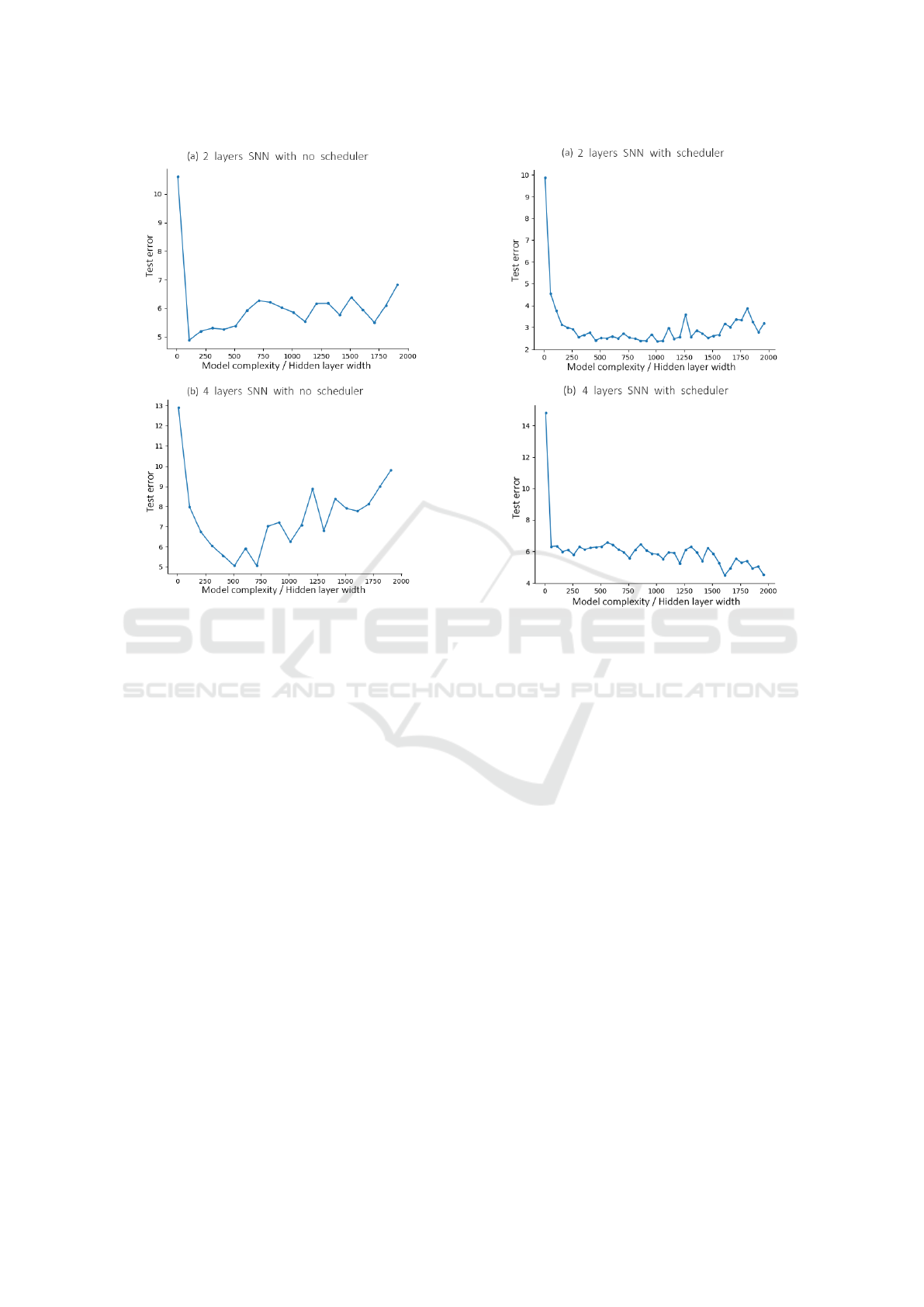
Figure 10: When the scheduler was not used, the test error
exhibited a U-shaped curve. (a) Test error curve for 2-layer
SNN without learning rate scheduler, without label noise,
using SGD optimizer, 50 epochs on MNIST. (b) Test er-
ror curve for 4-layer SNN without learning rate scheduler
on MNIST, without label noise, using SGD optimizer, 50
epochs on MNIST.
sider the trade-offs associated with increasing model
complexity.
5 CONCLUSION
Our study explores the double descent phenomenon
in three recent deep learning models. QNNs exhibited
clear double descent on CIFAR-10, while LTCs only
showed some evidence of it, requiring further valida-
tion. SNNs did not display double descent. We found
that learning rate schedulers, optimizers, and training
epochs significantly influence double descent. Future
work will involve broader experiments with varied pa-
rameters, optimizers, schedulers, and models, includ-
ing FNNs, RNNs, and GANs.
We believe that double descent reflects the behav-
ior of dynamically learning features by the model dur-
ing training, signifying that the model first learns shal-
low features and subsequently captures deeper, more
complex features. Models exhibiting this pattern of-
Figure 11: Although the double descent phenomenon still
did not occur after using the scheduler, the model ultimately
achieved strong generalization ability. (a) Test error curve
for 2-layer SNN with learning rate scheduler, without label
noise, using SGD optimizer, 50 epochs on MNIST. (b) Test
error curve for 4-layer SNN with learning rate scheduler
on MNIST, without label noise, using SGD optimizer, 50
epochs on MNIST.
ten demonstrate strong generalization. However, the
absence of the double descent phenomenon does not
necessarily indicate good or poor generalization per-
formance. For instance, a model may quickly learn
sufficient features, causing the test error curve to de-
cline rapidly and stabilize at a low value without ex-
hibiting a second increase. Conversely, the test error
curve may take on a U-shaped pattern, as observed
in SNN models trained without a learning rate sched-
uler. The reasons behind the lack of double descent
phenomenon in SNNs, however, require further inves-
tigation.
In summary, we believe that double descent is
generally a favorable phenomenon for generaliza-
tion. However, researchers should not explicitly aim
to achieve double descent; instead, they should re-
main focused on the ultimate goal of machine learn-
ing—achieving better generalization. To this end, se-
lecting appropriate hyperparameters and adopting ef-
ficient learning rate schedulers, as demonstrated in
ICAART 2025 - 17th International Conference on Agents and Artificial Intelligence
358

this study, can be effective strategies.
REFERENCES
Belkin, M., Hsu, D., Ma, S., and Mandal, S. (2019). Recon-
ciling modern machine-learning practice and the clas-
sical bias–variance trade-off. Proc. Natl. Acad. Sci.
U.S.A., 116(32):15849–15854.
Cherkassky, V. and Lee, E. H. (2024). To understand dou-
ble descent, we need to understand vc theory. Neural
Networks, 169:242–256.
Defferrard, M., Bresson, X., and Vandergheynst, P. (2016).
Convolutional neural networks on graphs with fast lo-
calized spectral filtering. In Advances in Neural Infor-
mation Processing Systems (NeurIPS), volume 29.
Derezinski, M., Liang, F. T., and Mahoney, M. W.
(2020). Exact expressions for double descent and
implicit regularization via surrogate random design.
In Larochelle, H., Ranzato, M., Hadsell, R., Balcan,
M., and Lin, H., editors, Advances in Neural Infor-
mation Processing Systems, volume 33, pages 5152–
5164. Curran Associates, Inc.
Geiger, M., Jacot, A., Spigler, S., Gabriel, F., Sagun, L.,
d’Ascoli, S., Biroli, G., Hongler, C., and Wyart, M.
(2020). Scaling description of generalization with
number of parameters in deep learning. J. Stat. Mech.
Theory Exp., 2020(2):023401.
Geman, S., Bienenstock, E., and Doursat, R. (1992). Neu-
ral networks and the bias/variance dilemma. Neural
Comput., 4(1):1–58.
Guo, Y. (2018). A survey on methods and theo-
ries of quantized neural networks. arXiv preprint
arXiv:1808.04752.
Hamilton, W., Ying, Z., and Leskovec, J. (2017). Inductive
representation learning on large graphs. In Advances
in Neural Information Processing Systems (NeurIPS),
volume 30.
Hasani, R., Lechner, M., Amini, A., Rus, D., and Grosu, R.
(2021). Liquid time-constant networks. In Proc. AAAI
Conf. Artif. Intell., volume 35, pages 7657–7666.
Hastie, T., Montanari, A., Rosset, S., and Tibshirani, R. J.
(2022). Surprises in high-dimensional ridgeless least
squares interpolation. Ann. Stat., 50(2):949–986.
Hastie, T., Tibshirani, R., and Friedman, J. (2001). The Ele-
ments of Statistical. Learning, Data Mining, Inference
and Prediction, volume 1.
Hubara, I., Courbariaux, M., Soudry, D., El-Yaniv, R., and
Bengio, Y. (2018). Quantized neural networks: Train-
ing neural networks with low precision weights and
activations. J. Mach. Learn. Res., 18(187):1–30.
Kipf, T. N. and Welling, M. (2017). Semi-supervised clas-
sification with graph convolutional networks. In Proc.
Int. Conf. Learn. Represent. (ICLR).
Lafon, M. and Thomas, A. (2024). Understanding the
double descent phenomenon in deep learning. arXiv
preprint arXiv:2403.10459.
Nakkiran, P., Kaplun, G., Bansal, Y., Yang, T., Barak, B.,
and Sutskever, I. (2021). Deep double descent: Where
bigger models and more data hurt. J. Stat. Mech. The-
ory Exp., 2021(12):124003.
Neal, B., Mittal, S., Baratin, A., Tantia, V., Scicluna, M.,
Lacoste-Julien, S., and Mitliagkas, I. (2018). A mod-
ern take on the bias-variance tradeoff in neural net-
works. arXiv preprint arXiv:1810.08591.
Pagliardini, M., Gupta, P., and Jaggi, M. (2018). Un-
supervised learning of sentence embeddings us-
ing compositional n-gram features. arXiv preprint
arXiv:1703.02507.
Pezeshki, M., Mitra, A., Bengio, Y., and Lajoie, G. (2022).
Multi-scale feature learning dynamics: Insights for
double descent. In International Conference on Ma-
chine Learning, pages 17669–17690. PMLR.
Salakhutdinov, R. (2017). Deep learning tu-
torial at the simons institute, berkeley.
Available: https://simons.berkeley.edu/talks/
ruslan-salakhutdinov-01-26-2017-1.
Shi, C., Pan, L., Hu, H., and Dokmani
´
c, I. (2024). Ho-
mophily modulates double descent generalization in
graph convolution networks. Proc. Natl. Acad. Sci.
U.S.A., 121(8):e2309504121.
Tavanaei, A., Ghodrati, M., Kheradpisheh, S. R., Masque-
lier, T., and Maida, A. (2019). Deep learning in spik-
ing neural networks. Neural Netw., 111:47–63.
Veli
ˇ
ckovi
´
c, P., Cucurull, G., Casanova, A., Romero, A., Li
`
o,
P., and Bengio, Y. (2017). Graph attention networks.
arXiv preprint arXiv:1710.10903.
Double Descent Phenomenon in Liquid Time-Constant Networks, Quantized Neural Networks and Spiking Neural Networks
359