A Two-Stage Extended Kalman Filter-Based Approach Against FDI

Cyber-Attack in Intelligent and Connected Vehicles

Bin Sun

1 a

, Shichun Yang

1 b

, Yu Wang

, Jiayi Lu

and Yaoguang Cao

1,2 c

School of Transportation Science and Engineering, Beihang University, Beijing, China

State Key Lab of Intelligent Transportation System, Beihang University, Beijing, China

{sunbin2022, yangshichun, lujiayi, caoyaoguang}@buaa.edu.cn, wangyu 200105@163.com

Keywords:

Cybersecurity, False Data Injection, Two-Stage Extended Kalman Filter, Intelligent and Connected Vehicles.

Abstract:

With the widespread integration of artiﬁcial intelligence and telecommunication technologies in vehicles, the

challenge of cybersecurity in Intelligent and Connected Vehicles (ICVs) has gained signiﬁcant attention. A

typical and high-risk cyber-attack technique involves False Data Injection (FDI) into sensors through the net-

work, resulting in deviations in subsequent planning and control algorithm outcomes. Existing approaches

suffer from limited robustness, being suitable only for simple models or requiring extensive data for the train-

ing model, which limits their practicality. Therefore, this paper proposes a method based on a Two-stage

Extended Kalman Filter (TSEKF), which not only detects cyber-attacks but also restores the vehicle’s true

motion state, thereby enhancing the robustness of vehicle ego state perception. The experimental results

demonstrate that the proposed method exhibits strong performance across various motion scenarios, offering

an effective solution for the safe operation of ICVs.

1 INTRODUCTION

Intelligent and Connected Vehicles (ICVs) are a fu-

ture trend, integrating advanced technologies and im-

proving travel efﬁciency, but also introducing security

risks due to external information exchange. Protect-

ing vehicle sensors from cyber-attacks is essential for

safe operation(Mwanje et al., 2024).Common cyber

attacks include FDI, DRA, and DoS. FDI is the most

typical, injecting false data into vehicle sensors, lead-

ing to inaccurate algorithms and potential safety risks

(Ju et al., 2022). This paper focuses on detecting FDI

attacks.

Cyber-attack detection for ICVs can be classi-

ﬁed into three main categories. The ﬁrst category is

model-based attack detection methods, which design

an observer based on the vehicle’s dynamic model,

assuming that modeling and measurement uncertain-

ties have upper bounds. An attack is detected when

the measurement innovation exceeds a threshold. The

work in (He et al., 2021) focuses on sensor attack de-

tection using a saturation-like observer. The meth-

ods proposed in (Dutta et al., 2018), and (Abdol-

https://orcid.org/0009-0008-4998-0974

https://orcid.org/0000-0003-3426-7988

https://orcid.org/0000-0002-6107-2425

lahi Biron et al., 2016) utilize a sliding mode observer

for attack detection, characterized by a simple design

process and some robustness to modeling uncertain-

ties. However, observer-based methods are primarily

suited for deterministic system models, offering sim-

plicity but limited performance under imperfect com-

munication.The second category involves attack de-

tection based on machine learning techniques. These

methods utilize machine learning to achieve attack

detection. In (Ju et al., 2020), Support Vector Ma-

chines (SVM) is employed to detect speed and posi-

tion sensor attacks during vehicle following. Hsiao-

Chung Lin et al. developed an Atta detection model

using a pre-trained VGG16 deep learning classiﬁer

to learn attack behavior features and classify threats

(Lin et al., 2022). Several scholars (Hossain et al.,

2020), (Lokman et al., 2019), (Han et al., 2018),

(Javed et al., 2021) have used foundational classiﬁers

to detect anomalies in CAN messages, such as De-

cision Trees, Logistic Regression and Support Vec-

tor Classiﬁers. Wei Lo et al. implemented a hybrid

network combining Convolutional Neural Networks

(CNN) and Long Short-Term Memory networks to

automatically extract spatial and temporal features

from vehicular network trafﬁc for attack detection (Lo

et al., 2022). However, machine learning-based de-

tection faces two major challenges: the inability to

Sun, B., Yang, S., Wang, Y., Lu, J. and Cao, Y.

A Two-Stage Extended Kalman Filter-Based Approach Against FDI Cyber-Attack in Intelligent and Connected Vehicles.

DOI: 10.5220/0013137900003941

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 11th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2025), pages 301-308

ISBN: 978-989-758-745-0; ISSN: 2184-495X

301

quantify cyber-attacks and potential signiﬁcant per-

formance degradation in the presence of measurement

noise. Additionally, effective detection and mitigation

of cyber-attacks require substantial amounts of real

data, which involves considerable effort in data col-

lection and labeling. The last category is hybrid meth-

ods that integrate model-based approaches with arti-

ﬁcial intelligence. The literature (Wang et al., 2020)

presents a method that cascades CNN with a χ

de-

tector, where CNN ﬁrst detects and removes anoma-

lous sensor data, followed by the χ

detector to iden-

tify undetected anomalies. Although this approach

shows performance improvements, the detection re-

sults rely heavily on CNN training. Guo et al. de-

signed a machine learning method that combines bat-

tery dynamics and vehicle kinematic models to de-

tect cyber-attacks on electric vehicles in various driv-

ing scenarios (Guo et al., 2021). Linxi Zhang et

al. merge traditional rule-based intrusion detection

techniques with emerging machine learning methods,

striking a balance between detection accuracy and ef-

ﬁciency (Zhang and Ma, 2022). Although each of the

three aforementioned methods has its strengths and

weaknesses in attack detection, they all primarily em-

phasize anomaly detection in the data, neglecting the

estimation of the vehicle’s true state.

The Kalman ﬁlter helps estimate vehicle states in

noisy settings. However, it struggles with inaccurate

models or biased sensor data. The Two-stage Kalman

Filter (TSKF) was initially proposed to addresses ran-

dom biases (Keller and Darouach, 1997). This pa-

per introduces a Two-stage Extended Kalman Filter

(TSEKF) for nonlinear systems to detect and mitigate

cyber-attacks in ICVs. It identiﬁes cyber-attacks and

estimates vehicle states via a dual-stage process. The

performance of the method is validated for different

vehicle motions.

The remainder of the paper is organized as fol-

lows. Section II introduces the vehicle dynamics

modeling. Section III discusses the modeling of

cyber-attacks and the detection methods using the

TSEKF algorithm. Section IV describes the experi-

ment results of the TSEKF in various motion states.

Finally, Section VI summarizes the entire paper.

2 VEHICLE DYNAMICS

In the extened Kalman Filter prediction step, a twin-

track model is utilized to model the lateral and lon-

gitudinal vehicle dynamics, thereby enhancing the

precision of vehicle state estimation (Henning and

Sawodny, 2016). The model consists of a nonlinear

dynamic state equation combined with a linear output

Figure 1: Double-track model of vehicle lateral dynamic

modal.

equation:

˙x = r(x, u), x(0) = x

y = Cx + F

(x) f

. (1)

The state vector of the dynamic equations is:

x = [

x,V

y,V

x,I

y,I

]

, (2)

with longitudinal velocity v

y,V

, lateral velocity v

x,V

yaw rate

, longitudinal acceleration a

x,I

and lateral

acceleration a

y,I

.The subscript for the state variables

indicates the reference coordinate system for mea-

surements: I for the inertial coordinate system, V for

the vehicle coordinate system, and T

for the tire co-

ordinate system. The tire numbering is as follows: 1

for the left front, 2 for the right front, 3 for the left

rear, and 4 for the right rear. The coordinate system is

shown in 1.

The control input vector of the model of the dy-

namic equations is:

u =



δ T

b1,T

b2,T

b3,T

b4,T

d1,T

d2,T

d3,T

d4,T



, (3)

with the front steering angle δ, the barking moment

bi,T

and driving moment T

di,T

of four wheels.

2.1 Non-Linear Tier Model

The torque balance equations for the four wheels are

as follows:

i,T

= −r

(tire)

· F

ix,V

− T

bi,T

+ T

di,T

, (4)

where θ

is the moment of inertia of an individual

tire around its rotational axis, r

(tire)

is the tire radius,

and F

xi,V

is the longitudinal ground force acting on the

tire in the vehicle driving direction.

The tire model used in this study is a simpliﬁed

version of the Magic Formula Tire (MFT) model (Di-

eter et al., 2018), based on the MFT 5.2 model pro-

posed by Pacejka (Pacejka, 2012), and includes a

VEHITS 2025 - 11th International Conference on Vehicle Technology and Intelligent Transport Systems

302

complete set of parameters. The fundamental equa-

tions are as follows:

i,V

= F

i(max)

sin(C arctan(B

∥

))



0 1



∥

i(max)

= DµF

(1 + k

−F

(5)

The parameters B,C, D,k

and k

represent the

initial slope, saturation shape, peak tire force, longitu-

dinal scaling factor, and tire load coefﬁcient, respec-

tively. These parameters describe the characteristic

relationship curve between slip and tire force, but do

not have physical units. The maximum transferable

force F

i(max)

increases with tire load F

, which can be

calculated as in reference (Dieter et al., 2018). How-

ever, as the load continues to increase, the rate of in-

crease of the maximum force gradually decreases, a

relationship determined by the coefﬁcient k

(Best,

2014).

The inputs for the tire model (5) are the longitudi-

nal slip k

and the lateral slip angle α

. For each tire,

these are represented as:





. (6)

The longitudinal slip k

is calculated as:

tire

i,T

− v

xi,T

. (7)

The side slip angle α

is deﬁned by











δ − arctan



y,V

x,V

−s



,i = 1

δ − arctan



y,V

x,V



,i = 2

−arctan



y,V

−l

x,V

−s



,i = 3

−arctan



y,V

−l

x,V



,i = 4

. (8)

As shown in Figure 1, l

and l

represent the dis-

tances from the vehicle’s center of gravity to the front

and rear axles, respectively, s

is half of the vehicle’s

width.

2.2 Vehicle Dynamic Model

The general equation for the horizontal motion of a

vehicle can be expressed as follows:

˙v

x,V

∑

i=1

ix,V

y,V

˙v

y,V

∑

i=1

iy,V

−

x,V

∑

i=1

iz,V

(9)

All kinetic quantities, tire forces, and moments are

illustrated in Figure 1. In equation (9), m represents

the vehicle’s mass, θ

denotes the moment of inertia

of the entire vehicle about the z axis, while F

ix,V

and

iy,V

are the horizontal components of the respective

tire forces in the x or y direction. M

iz,V

represents the

moments generated by these forces around the vehi-

cle’s center of gravity (COG).

It is important to note that the additional trans-

lational acceleration caused by the rotating reference

frame has been accounted for in equation (10), but the

accelerations in inertial coordinates are calculated as:

x,I

∑

i=1

ix,V

y,I

∑

i=1

iy,V

, (10)

The complete model is derived by combining

equations (9) with a nonlinear tire model (5),

f (x,u) =







∑

i=1

ix,V

y,V

∑

i=1

iy,V

−

x,V

∑

i=1

iz,V

∆t



∑

i=1

ix,V

− a

x(∆t),I



∆t



∑

i=1

iy,V

− a

y(∆t),I









. (11)

The parameters used in the vehicle dynamic

model and MFT tire model proposed in this study

are listed in Table 1. These parameters were obtained

from the open database of the simulation software.

3 CYBER-ATTACK MODELING

AND TSEKF-BASED

APPROACH

The nonlinear vehicle dynamics model established

in Chapter 2 can be discretized using the 4th-order

Runge-Kutta method:

= f

k−1

) + w

k−1

= Cx

+ v

, (12)

with the state vector x

∈ R

, control input u

∈ R

and observation vector y

∈ R

. Here, w

∈ R

, w

∼

N (0,Q) and v

∈ R

, v

∼ N (0,R) denote process

and measurement noise, respectively, both of which

are assumed to follow a normal distribution with a

mean of zero. The covariance matrices Q and R rep-

resent the process noise and measurement noise co-

variance, respectively. Sensor noise captures the ran-

dom uncertainty present during the measurement pro-

cess. Process noise reﬂects external inﬂuences, such

A Two-Stage Extended Kalman Filter-Based Approach Against FDI Cyber-Attack in Intelligent and Connected Vehicles

303

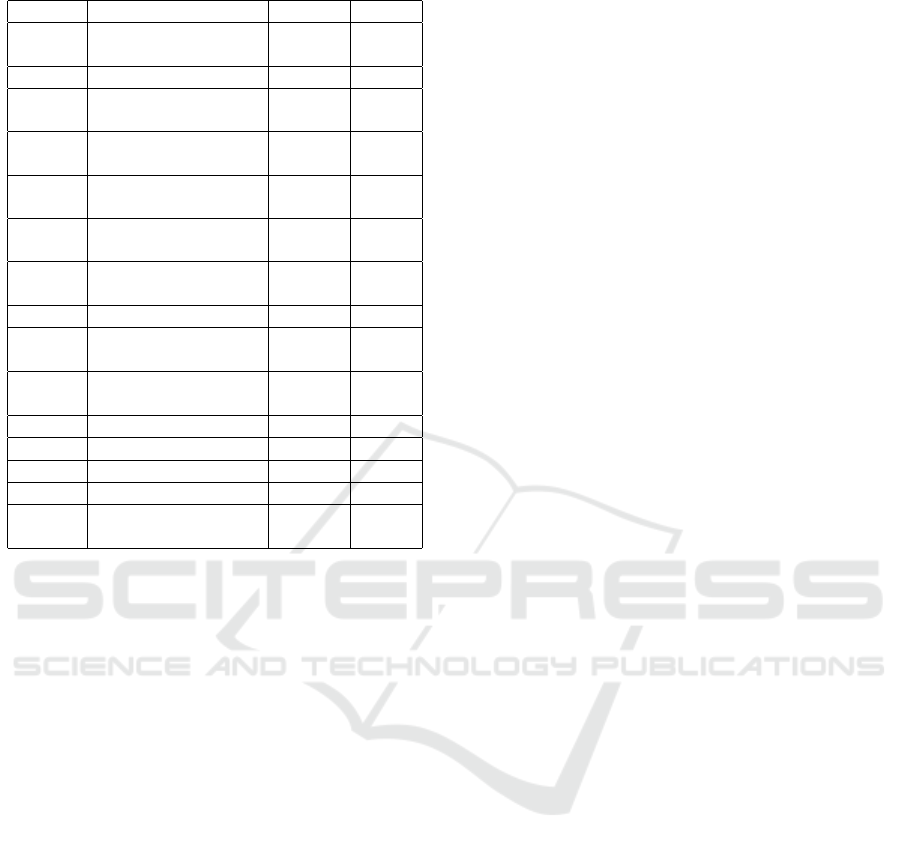
Table 1: Modelling Parameters.

Symbol Description Value Unit

µ Friction coefﬁcient

of road surface

0.8 -

Nominal tire load 5150 N

Longitudinal scaling

factor

1.1743 -

Degenerative tire

load factor

0.1342 -

B Initial slope parame-

ter

10.4962 -

C Shape factor for satu-

ration region

1.5402 -

D Inﬂuences maximum

tire force peak

1.1006 -

m Vehicle mass 2100 kg

Moment of inertia for

Vehicle

2549 kg · m

Moment of inertia for

tires

2.1 kg · m

Distance cog to front 1.27 m

Distance cog to rear 1.37 m

tire

tire radius 0.34 m

Half track-width 0.81 m

g gravitational acceler-

ation constant

9.81 m/s

as wind force and road surface irregularities. Addi-

tionally, internal non-parametric input uncertainties,

such as actuator delays, are neglected; we assume that

the response of actuators, like steering, is rapid. Sim-

ilar uncertainties for other parameters are also disre-

garded.

In equation (13), the state observation matrix C is

chosen as follows:

C =







1 0 0 0 0

0 1 0 0 0

0 0 1 0 0







. (13)

3.1 Cyberthreat Modelling

FDI is one of the most prevalent forms of cyber-

attacks, where attackers, unaware of system param-

eters or previous event data, directly introduce er-

roneous information into the original data. This

manipulation can result in signiﬁcant discrepancies

in speed, acceleration, and other critical parame-

ters, leading downstream decision-making processes

to rely on incorrect motion states for path planning.

Consequently, the safety constraints derived from

these decisions are based on ﬂawed states, rendering

them ineffective and posing substantial safety risks of

ICVs. FDI attack can be modeled as follows (Tan

et al., 2017):



+ v

+ F

+ v

k < τ

k ≥ τ

. (14)

Here, the subscript k indicates the value at a given

discrete time k; b represents the bias/attack vector

added to the measurements; F denotes the observa-

tion matrix of the attack vector, illustrating how b in-

ﬂuences the system’s observations; and τ is the mo-

ment when the attack is activated.

Thus, considering the cyber-attack, the dynamics

described by equation (13) can be updated to

= f

k−1

) + w

k−1

= Cx

+ F · b

+ v

, (15)

with cyber threat b

∈ R

We assume that the cyber-attack is stationary dur-

ing the attack duration and can be modeled as a Gaus-

sian random process

k+1

= b

+ w

f ,k

, (16)

where w

b,k

∈ R

, w

b,k

∼ N (0,Q

) represents the un-

certainty of the attack magnitude.

For cyber-attacks, this paper considers FDI in the

form of erroneous data in longitudinal velocity, lat-

eral velocity, yaw rate, longitudinal acceleration, and

lateral acceleration, speciﬁcally:

b =





. (17)

The output matrix of the attack is related to the state

variables, speciﬁcally as follows:

(x) =







0 0 0

1 0 0

0 1 0

0 0 1







. (18)

The measurement output when b = 0 is:

y = [

x,V

y,V

x(∆t),I

y(∆t),I

]

. (19)

3.2 Two-Stage Extended Kalman Filter

By dividing state estimation and attack estimation

into two stages, the TSEKF effectively reduces

the computational complexity associated with high-

dimensional parameters. The ﬁrst stage focuses on

estimating the true state of the vehicle’s motion, while

the second stage concentrates on estimating the mag-

nitude of the cyber-attack. Consequently, the ﬁrst

stage can be redesigned based on different vehicle

model parameters, and the second stage can be opti-

mized to reduce false positive rates and shorten attack

detection times. These two stages operate relatively

independently, with no mutual interference, making

VEHITS 2025 - 11th International Conference on Vehicle Technology and Intelligent Transport Systems

304

Figure 2: The proposed TSEKF algorithm.

the algorithm particularly well-suited for application

in the ﬁeld of intelligent and connected vehicles.

The overall framework of the algorithm is illus-

trated in Figure 2. In the ﬁrst stage of vehicle motion

state prediction, the inputs u

, the attack prior esti-

mate

k|k−1

, and state transformation Γ

k|k−1

are used

to predict the state. Then, the measurement values y

are utilized to compute the corrected motion state esti-

mate. This corrected state estimate

k+1|k+1

is subse-

quently used in the second stage for detecting cyber-

attacks, yielding a corrected attack estimate

k|k

, that

serves as the prior estimate for the next iteration. The

prediction of cyber-attack detection

k|k−1

leverages

the prior estimate of the attack and determines the

next state transition Γ

k|k−1

The subscript k|k − 1 indicates that at time step k,

measurements up to time step k−1 are used. Utilizing

the nonlinear motion equations (13) and combining

them with the current cyber-attack estimate, the prior

state is predicted for the vehicle’s motion state:

ˆx

k|k−1

= f

( ˆx

k−1|k−1

k−1

k−1|k−1

). (20)

The prior estimate of the cyber-attack is computed

based on the assumed stationary characteristics of the

cyber-attack:

k|k−1

k−1|k−1

. (21)

According to the principles of the Extended

Kalman Filter (EKF), the approximate linearized state

transition Jacobian matrix for the nonlinear system is

obtained through numerical computation using ﬁnite

difference methods:

∂ f

∂x

. (22)

According to equation (23), the self-covariance of

the vehicle motion state estimation error is calculated

as follows:

xx,k+1|k

= A

xx,k|k

+ Q. (23)

The self-covariance of the estimation error for the

cyber-attack, based on equation (22) and the uncer-

tainty of the cyber-attack process, is given by the fol-

lowing result:

bb,k+1|k

= P

f f ,k|k

+ Q

. (24)

The state and attack cross-covariance matrix can

be computed using the state transition matrix and the

static assumption of the cyber-attack, resulting in:

xb,k+1|k

= A

xb,k|k

. (25)

To eliminate the cross-covariance from equation

(26), the state transformation should be processed as

follows:



k|k−1





−Γ

k|k−1

0 I



ˆx

k|k−1





ˆx

k|k−1

− Γ

k|k−1



. (26)

By applying the state transformation, the two

phases of the EKF can be effectively separated. The

new system state

x is a linear combination of the sys-

tem state and the attack state, while the attack estima-

tion state

b =

b remains unchanged. Here, I

and I

are appropriately dimensioned identity matrices. Ac-

cording to reference (May et al., 2023), it can be ex-

pressed in an iterative calculation as a form indepen-

dent of the cross-covariance:

k|k−1

= A

k−1

k−1|k−1

bb,k−1|k−1

−1

bb,k|k−1

. (27)

When the measurement value is y

obtained, the

corrected kinematic state estimate is given by:

˜x

k|k

= ˜x

k|k−1

+ K

˜x,k

− F

y,k

k|k−1

−C

k+1

ˆx

k+1|k

(28)

with Kalman gain for state estimate K

˜x,k

, and calcu-

lated by

˜x,k

= P

˜x,k|k−1

−1

˜x,k

. (29)

Similar to the classic EKF algorithm, in equation

(31), S

˜x,k

represents the covariance of the observation

error

˜x,k

= C

˜x,k|k−1

+ R. (30)

The posterior estimate of the cyber-attack is given

by:

k|k−1

+ K

b,k

− F

y,k

k|k−1

), (31)

with

= y

−C

( ˜x

k|k−1

+ Γ

k|k−1

). (32)

Similarly, the Kalman gain for attack estimate K

b,k

= P

bb,k|k−1

−1

f ,k+1

, (33)

where β

and S

f ,k+1

are calculated as follows:

= F

y,k

k|k−1

(34)

f ,k+1

= β

k+1

f f ,k+1|k

k+1

+ S

x,y,k+1

. (35)

Finally, the error covariance for the next time step

is updated using the following calculation:

˜x ˜x,k|k

= (I − K

˜x ˜x,y,k

˜x ˜x,k|k−1

(36)

bb,k|k

= (I − K

f ,k

bb,k|k−1

. (37)

A Two-Stage Extended Kalman Filter-Based Approach Against FDI Cyber-Attack in Intelligent and Connected Vehicles

305

4 EXPERIMENT RESULTS AND

DISCUSSION

Various driving maneuvers were constructed in the

simulation environment, including linear drive and

circular drive, to simulate vehicle dynamics in single-

directional movement, as well as coupled lateral and

longitudinal movements. Different types of data in-

jection attacks were designed to evaluate the perfor-

mance of the proposed TSEFK algorithm. The covari-

ance of process noise Q, measurement noise R, and

attack noise Q

was conﬁgured as diagonal matrices,

with the value of diagonal elements set as 3 × 10

−4

1 × 10

−5

and 2 × 10

−3

, respectively.

4.1 Linear Drive

Two driving maneuvers, with constant speed and ac-

celeration, were designed to test the algorithm per-

formance under cyber-attacks targeting longitudinal

speed and longitudinal acceleration, respectively.

(a) Cyber-attack Estimate (b) Vehicle State

Figure 3: Linear Drive.

For the constant-speed scenario, the vehicle speed

was set at 50 km/h (≈ 16m/s), , reﬂecting typical ur-

ban trafﬁc. At t = 1s, an FDI attack was initiated on

the longitudinal speed of the vehicle, with the attack

magnitude b

= 4(m/s). Figure (3a) illustrates the al-

gorithm estimation of cyber-attack magnitude. When

the cyber-attack (solid red line) occurs, the proposed

algorithm immediately detects it, with the estimated

attack magnitude on longitudinal speed (solid green

line) converging to the actual attack value within ap-

proximately 1 second. However, it should be noted

that when the cyber-attack is initiated, there is signif-

icant ﬂuctuation in the estimated attack magnitudes

for both longitudinal and lateral acceleration. This is

because acceleration is the derivative of speed; thus,

any substantial deviation in speed measurements may

not only reﬂect direct attacks on speed, but may also

indicate an attack in acceleration. Over time, the esti-

mated values for acceleration converge toward zero.

Figure (3b) presents the actual state, the measured

state (without TSEFK), and the estimated state gen-

erated by the proposed algorithm (with TSEFK). Fol-

lowing a cyber-attack, the measured value displays an

immediate deviation. Although the estimated value

increases slightly, they rapidly reduce and converge

to the actual state within approximately 1 second.

(a) Cyber-attack Estimate (b) Vehicle State

Figure 4: Linear Accelerated Drive.

For the acceleration scenario, the vehicle speed

was also set at 50 km/h (≈ 16m/s), while an FDI

attack was initiated in the longitudinal acceleration,

with the attack magnitude b

= 2(m/s

). The attack

can be detected immediately and its magnitude sta-

bilizes within 1 second. Unlike in Figure (3a), the

estimated attack magnitudes for other variables re-

main close to zero. As explained previously, accelera-

tion is the derivative of other variables and determines

their rate of change. Therefore, when acceleration is

attacked, it exhibits a deviation independently, unaf-

fected by deviations in other variables. In Figure (4b),

the vehicle estimated state return to the actual state af-

ter a slight increase.

4.2 Circular Drive

We used the circular motion to test the algorithm’s

evaluation of the vehicle’s lateral motion state indi-

cators, with the steering angle ﬁxed at 0.1 rad and

the vehicle speed set to the previously mentioned

50km/h. At t = 0.7s, a FDI attack was initiated at the

(a) Cyber-attack Estimate (b) Vehicle State

Figure 5: Circular Drive.

VEHITS 2025 - 11th International Conference on Vehicle Technology and Intelligent Transport Systems

306

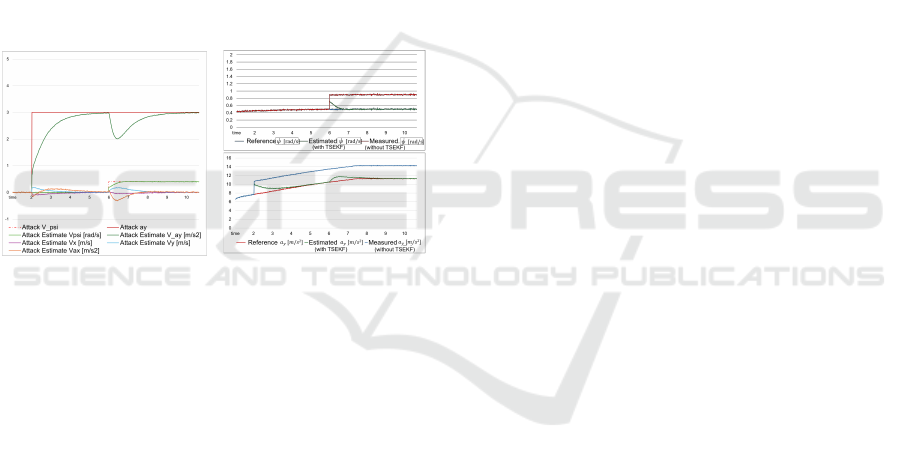
lateral speed. Similarly to the linear constant speed

scenario, Figure (5a) shows that following the attack

(solid red line) at the lateral speed, the corresponding

estimated attack value (solid green line) rises swiftly

and converges to the actual attack magnitude within

approximately 1 second. Similarly, an attack on lat-

eral speed causes ﬂuctuations in the estimated attack

value for acceleration, but these ultimately converge

to zero around 2 seconds. In Figure (5b), the algo-

rithm’s estimated values experience a slight increase

before converging to the actual lateral speed.

To further validate the algorithm’s performance

under combined motion conditions, we introduced an

acceleration scenario to the constant-speed circular

motion. The steering angle was kept constant at 0.1

rad, while the vehicle speed increased uniformly from

50km/h to 70km/h. At t = 2s, an FDI attack with

= 3(m/s) was initiated in the lateral acceleration,

followed by another FDI attack with b

= 0.4(rad/s)

on the yaw rate at t = 6s.

(a) Cyber-attack Estimate (b) Vehicle State

Figure 6: Circular Accelerated Drive.

In Figure(6a), when only a lateral acceleration at-

tack is applied (solid red line), similar to the longitu-

dinal acceleration attack, the attack magnitude is ef-

fectively tracked. This causes only minor ﬂuctuations

in the estimated attack values for other variables. The

actual lateral acceleration of the vehicle, in the ab-

sence of attack, is also accurately estimated. How-

ever, when a cyber-attack is applied to the yaw rate

(dashed red line), it induces a change in the estimated

attack values not only for yaw rate but also for ac-

celeration. This occurs because lateral acceleration

is one of the factors causing yaw rate change; thus,

when the yaw rate deviates due to a cyber-attack, the

algorithm may also infer that lateral acceleration has

been attacked, resulting in a perceived shift. However,

over time, the estimated value for the lateral accelera-

tion attack converges to its actual value. This ﬂuctua-

tion also affects the vehicle state estimation, as shown

in Figure (6b): for the acceleration state estimation,

there is a noticeable deviation from the vehicle’s true

state between 6 and 7 seconds, though this deviation

remains much smaller than that of the direct measure-

ment. For the yaw rate state estimation, after a slight

increase, it swiftly converges to the vehicle’s actual

state.

In summary, the TSEKF algorithm effectively de-

tects cyber-attack magnitudes and estimates vehicle

state within 1–2 seconds under various driving con-

ditions. It performs better in estimating attacks and

states when targeting acceleration, though attacks on

speed-related variables cause some ﬂuctuations in the

acceleration estimates. Despite this, the estimated

values remain signiﬁcantly closer to the true state

compared to direct measurements without TSEKF.

5 CONCLUSION

In this paper, we propose a TSEKF-based cyberse-

curity approach to address FDI attacks in ICVs. By

separating state and attack estimation into two stages,

the method reduces computational complexity while

achieving accurate state estimation and attack detec-

tion across various vehicle states. The experimen-

tal results demonstrate strong stability and robustness

against FDI attacks under different driving conditions.

In the ﬁrst stage, the algorithm accurately estimates

vehicle motion states despite attacks, while in the

second stage it effectively detects and estimates sen-

sor data deviations, providing robust protection. This

research expands the application of Kalman ﬁlters

in ICV security and lays a foundation for advanced

cyber-attack protection mechanisms.

In summary, the proposed method offers a promis-

ing solution to ensure the safety of ICV and counter

cyber threats. Future work could explore the integra-

tion of additional attack patterns and multisensor fu-

sion techniques to enhance protection in complex sce-

narios.

ACKNOWLEDGEMENTS

This work is supported by National Key R&D

Program of China (Grant No.2023YFB3107400),

National Key R&D Program of China (Grant

No.2022YFB2503300) and the National Natural Sci-

ence Foundation of China (No. U22A202101).

REFERENCES

Abdollahi Biron, Z., Dey, S., and Pisu, P. (2016). Sen-

sor fault diagnosis of connected vehicles under im-

perfect communication network. In Dynamic Sys-

A Two-Stage Extended Kalman Filter-Based Approach Against FDI Cyber-Attack in Intelligent and Connected Vehicles

307

tems and Control Conference, volume 50695, page

V001T16A003. American Society of Mechanical En-

gineers.

Best, M. C. (2014). A new empirical ‘exponential’ tyre

model. International Journal of Vehicle Design. Pub-

lisher: Inderscience Publishers Ltd.

Dieter, S., Manfred, H., and Roberto, B. (2018). Vehicle

dynamics: modeling and simulation.

Dutta, R. G., Yu, F., Zhang, T., Hu, Y., and Jin, Y. (2018).

Security for Safety: A Path Toward Building Trusted

Autonomous Vehicles. In 2018 IEEE/ACM Interna-

tional Conference on Computer-Aided Design (IC-

CAD), pages 1–6. ISSN: 1558-2434.

Guo, L., Ye, J., and Yang, B. (2021). Cyberattack Detection

for Electric Vehicles Using Physics-Guided Machine

Learning. IEEE Transactions on Transportation Elec-

triﬁcation, 7(3):2010–2022.

Han, M. L., Kwak, B. I., and Kim, H. K. (2018). Anomaly

intrusion detection method for vehicular networks

based on survival analysis. Vehicular Communica-

tions, 14:52–63.

He, X., Hashemi, E., and Johansson, K. H. (2021). Dis-

tributed control under compromised measurements:

Resilient estimation, attack detection, and vehicle pla-

tooning. Automatica, 134:109953.

Henning, K.-U. and Sawodny, O. (2016). Vehicle dynamics

modelling and validation for online applications and

controller synthesis. Mechatronics, 39:113–126.

Hossain, M. D., Inoue, H., Ochiai, H., Fall, D., and

Kadobayashi, Y. (2020). LSTM-Based Intrusion De-

tection System for In-Vehicle Can Bus Communica-

tions. IEEE access : practical innovations, open solu-

tions, 8:185489–185502.

Javed, A. R., ur Rehman, S., Khan, M. U., Alazab, M.,

and G, T. R. (2021). CANintelliIDS: Detecting In-

Vehicle Intrusion Attacks on a Controller Area Net-

work Using CNN and Attention-Based GRU. IEEE

Transactions on Network Science and Engineering,

8(2):1456–1466.

Ju, Z., Zhang, H., Li, X., Chen, X., Han, J., and Yang, M.

(2022). A Survey on Attack Detection and Resilience

for Connected and Automated Vehicles: From Vehi-

cle Dynamics and Control Perspective. IEEE Trans-

actions on Intelligent Vehicles, 7(4):815–837.

Ju, Z., Zhang, H., and Tan, Y. (2020). Distributed Deception

Attack Detection in Platoon-Based Connected Vehicle

Systems. IEEE Transactions on Vehicular Technol-

ogy, 69(5):4609–4620.

Keller, J.-Y. and Darouach, M. (1997). Optimal two-stage

Kalman ﬁlter in the presence of random bias. Auto-

matica, 33(9):1745–1748. Publisher: Elsevier.

Lin, H.-C., Wang, P., Chao, K.-M., Lin, W.-H., and Chen,

J.-H. (2022). Using Deep Learning Networks to

Identify Cyber Attacks on Intrusion Detection for In-

Vehicle Networks. Electronics, 11(14):2180. Pub-

lisher: Multidisciplinary Digital Publishing Institute.

Lo, W., Alqahtani, H., Thakur, K., Almadhor, A., Chan-

der, S., and Kumar, G. (2022). A hybrid deep learn-

ing based intrusion detection system using spatial-

temporal representation of in-Vehicle network trafﬁc.

Vehicular Communications, 35:100471. Publisher:

Elsevier.

Lokman, S.-F., Othman, A. T., and Abu-Bakar, M.-H.

(2019). Intrusion detection system for automotive

Controller Area Network (CAN) bus system: a review.

EURASIP Journal on Wireless Communications and

Networking, 2019(1):184.

May, M. P., Henning, K.-U., and Sawodny, O. (2023). Ex-

perimental validation of sensor fault estimation for ve-

hicle dynamics with a nonlinear tire model. Control

Engineering Practice, 141:105725.

Mwanje, M. D., Kaiwartya, O., Aljaidi, M., Cao, Y., Ku-

mar, S., Jha, D. N., Naser, A., and Lloret, J. (2024).

Cyber security analysis of connected vehicles. IET

Intelligent Transport Systems.

Pacejka, H. B. (2012). Semi-Empirical Tire Models. Tire

and Vehicle Dynamics, pages 149–209. Publisher: El-

sevier.

Tan, R., Nguyen, H. H., Foo, E. Y. S., Yau, D. K. Y.,

Kalbarczyk, Z., Iyer, R. K., and Gooi, H. B. (2017).

Modeling and Mitigating Impact of False Data Injec-

tion Attacks on Automatic Generation Control. IEEE

Transactions on Information Forensics and Security,

12(7):1609–1624.

Wang, Y., Masoud, N., and Khojandi, A. (2020). Real-time

sensor anomaly detection and recovery in connected

automated vehicle sensors. IEEE transactions on

intelligent transportation systems, 22(3):1411–1421.

Publisher: IEEE.

Zhang, L. and Ma, D. (2022). A Hybrid Approach To-

ward Efﬁcient and Accurate Intrusion Detection for

In-Vehicle Networks. IEEE access : practical inno-

vations, open solutions, 10:10852–10866.

VEHITS 2025 - 11th International Conference on Vehicle Technology and Intelligent Transport Systems

308