A Novel Pairing-Free ECC-Based Ciphertext-Policy Attribute-Based

Proxy Re-Encryption for Secure Cloud Storage

Shivangi Shukla

and Sankita J. Patel

Department of Computer Science and Engineering, Sardar Vallabhbhai National Institute of Technology, Surat,

Gujarat 395007, India

Keywords:

Pairing-Free, Elliptic Curve Cryptography, Access Control, CP-ABPRE, Cloud Storage.

Abstract:

Proxy re-encryption (PRE) is a cryptographic primitive enabling data owner to delegate ciphertext access rights

without leaking underlying plaintext to honest-but-curious cloud servers. The delegation of ciphertext access

rights enhances the efﬁciency of outsourced data on cloud servers. Ciphertext-policy attribute-based proxy re-

encryption (CP-ABPRE) employs PRE in attribute-based encryption to enable ciphertext transformation from

speciﬁed access policy to new access policy without leaking underlying plaintext. However, current state-of-

the-art schemes incorporate expensive bilinear pairing operations to transform ciphertext access policy. The

escalating adoption of cloud computing in real-time applications demands a pairing-free CP-ABPRE mecha-

nism for resource-limited users in the network. The agenda of this paper, for the ﬁrst time, is to design a novel

pairing-free elliptic curve cryptography (ECC) based ciphertext-policy attribute-based proxy re-encryption,

abbreviated as ECC-CP-ABPRE scheme. It incorporates linear secret sharing scheme (LSSS) for the expres-

siveness of access policies. To reduce overall communication and computational overheads, ECC-CP-ABPRE

scheme replaces expensive bilinear pairing operations with scalar multiplication on elliptic curve. The security

analysis illustrates that ECC-CP-ABPRE scheme is secure under collusion attack and ensures data conﬁden-

tiality. Furthermore, the performance evaluation demonstrates that ECC-CP-ABPRE scheme incurs signiﬁcant

reduction in computational and communication overheads than existing CP-ABPRE schemes.

1 INTRODUCTION

In the modern era of Internet, cloud computing has

become mainstream solution for outsourcing data that

can be accessed anytime and anywhere (Wang et al.,

2023). Although cloud computing offers reliable and

cost-effective data storage, users are reluctant to cloud

services as they lose physical control over their out-

sourced data. Furthermore, cloud service providers

are untrusted third parties that can access or disclose

outsourced data to unauthorized organizations for ﬁ-

nancial beneﬁts (Dhakad and Kar, 2022). Thus, data

conﬁdentiality and access control mechanisms are

pivotal security requirements for cloud storage.

CP-ABE associates user’s secret key with at-

tributes, and ciphertext incorporates access policy

deﬁned over attributes of the system. The cipher-

text can be decrypted only if user’s attribute secret

key satisﬁes access policy in the ciphertext (Bethen-

court et al., 2007). However, CP-ABE lacks the

provision of encrypted data sharing in collaborated

https://orcid.org/0000-0001-8945-2721

scenarios. It is not desirable in practical scenarios

that require frequent ciphertext-policy updates. Ad-

ditionally, heavy computational overheads incurred

in decrypting ciphertext and encrypting plaintext un-

der new access policy are inconvenient for resource-

limited data users in the network. Thus, PRE tech-

nique is integrated with CP-ABE, known as CP-

ABPRE, to enable efﬁcient sharing of encrypted data

stored on clouds. (Liang et al., 2009) ﬁrst introduced

CP-ABPRE to enable ciphertext transformation from

speciﬁc access policy to new access policy. Assume

a delegator (i.e. original data user) wants to delegate

access rights of CT

under access policy AP

to dele-

gatee (i.e. shared data user) that satisﬁes access policy

. The original data user generates re-encryption

key for ciphertext transformation of CT

under AP

and transmits it to proxy server. The

semi-trusted proxy server transforms CT

under AP

to CT

under AP

without gaining underlying plain-

text or secret keys of participating data users.

The existing CP-ABPRE schemes are based on

expensive bilinear pairings that impede in escalating

Shukla, S. and Patel, S. J.

A Novel Pairing-Free ECC-Based Ciphertext-Policy Attribute-Based Proxy Re-Encryption for Secure Cloud Storage.

DOI: 10.5220/0013138600003899

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 11th International Conference on Information Systems Security and Privacy (ICISSP 2025) - Volume 1, pages 225-233

ISBN: 978-989-758-735-1; ISSN: 2184-4356

225

adoption of cloud computing in real-time applications

of smart cities incorporating resource-constrained

end-users (Rezaeibagha et al., 2021). This motivates

us to design a lightweight CP-ABPRE scheme that ef-

ﬁciently shares encrypted data on clouds. The salient

contributions are:

•To enhance the efﬁciency of CP-ABPRE schemes,

we propose a novel pairing-free ECC-CP-ABPRE

that eliminates expensive bilinear pairing with scalar

multiplications on elliptic curves.

•Security analysis illustrates that ECC-CP-ABPRE is

resilient against collusion attack, offers speciﬁcity of

re-encryption keys and data conﬁdentiality. Perfor-

mance evaluation illustrate its efﬁciency.

2 RELATED WORK

(Liang et al., 2009) designed CP-ABPRE with access

policy based on AND gates of positive and negative at-

tributes. (Luo et al., 2010) extended it for AND gates

access policy based on negative, multi-value attributes

and wildcards, and (Liang et al., 2015) designed adap-

tively chosen-ciphertext secure CP-ABPRE for arbi-

trary network settings. (Yang et al., 2016) designed

CP-ABPRE that enables user revocation by facilitat-

ing cloud server with re-encryption keys from each

data owner to data user however, it necessitates PRE

for each data access request. (Deng et al., 2020) pro-

posed CP-ABPRE that enables partial decryption of

re-encrypted ciphertext by proxy server to minimize

computational overhead. (Ge et al., 2021) designed

CP-ABPRE to support veriﬁability wherein shared

data user veriﬁes correctness of re-encrypted data and

proxy server proves its fairness if the re-encryption

process is performed honestly. (Zhou et al., 2021) de-

signed CP-ABPRE with accountability to trace mali-

cious users. However, it lacks revocation mechanism

for such malicious data users to prevent any further

unauthorized access. (Chen et al., 2022) proposed

CP-ABPRE for encrypted sharing of medical data

that facilitates user revocation mechanism in health-

care centres. However, existing CP-ABPRE schemes

incorporate complex bilinear pairing to update or

modify access policy of ciphertext. It is inefﬁcient

for cloud-based applications in real-world resource-

constrained environments such as smart homes etc.

Thus, designing of lightweight CP-ABPRE scheme

that supports access rights delegation of ciphertext is

an interesting open problem. In this direction, we

aim to design a lightweight ECC-based CP-ABPRE

scheme while retaining security of the system.

3 PRELIMINARIES

The preliminaries are as follows:

1.Access Structure: Assume P = {P

...,P

} de-

notes set of parties. AS ⊆ 2

is monotone if ∀B,C :

if B ∈ AS and B ⊆ C then C ∈ AS. The access struc-

ture (respectively, monotonic access structure) is a

collection (respectively, monotone collection) AS

of non-empty subsets of P i.e., AS ⊆ 2

0. The sets

in AS are authorized sets, else unauthorized sets.

AS incorporates all authorized set of attributes.

2.LSSS: The secret sharing scheme

∏

based on set of

parties is called as LSSS if: (a) Shares of all partic-

ipating entities form a vector over Z

. (b) There ex-

ists share-generating matrix A of l × n and function

ρ where ρ(i) ∈ P , i ∈ {1,2,...,l}. Assume column

vector ⃗v = (s,v

,...,v

) where v

,...,v

∈ Z

are randomly chosen and s ∈ Z

is secret to be

shared, then A · v denotes vector of l shares of s

related to

∏

, and A

·⃗v belongs to ρ(i). Note that

no such constants exists for any unauthorized at-

tribute set. Linear construction property of LSSS:

Let

∏

be LSSS for AS and S |= (A,ρ) denotes that

S is authorized attribute set hence, it satisﬁes ac-

cess structure AS and assume I = {i : ρ(i) ∈ S} ⊂

{1,2...,l}. Suppose for

∏

, λ

are valid shares

of s then, constants {c

∈ Z

}

i∈I

exists such that

∑

i∈I

· λ

= s. These {c

} can be found in poly-

nomial time with knowledge of A and I (Beimel,

1996). Any unauthorized set with corresponding

matrix includes no target vector (1,0,...,0) in row

span of I. Also, it will incorporate a vector

⃗

d such

that d · (1,0,...,0) = −1 and

⃗

d · A

= 0 for all i ∈ I.

3.ECC: Elliptic curve E

(a,b) is deﬁned on ﬁnite

ﬁeld F

as y

= x

+ ax + b (mod p) and 4a

27b

̸= 0 where p is large prime number and a, b are

elements of F

(Miller, 1985). Given Q = k.G where

G is group generator of order q, it is hard to calcu-

late k in polynomial time. ECDLP is more difﬁcult

to solve than integer factorization hence, requiring

smaller key size than RSA. Alice and Bob performs

following: (a) Key Generation: Alice selects private

key s

∈ Z

and computes public P

= s

.G Bob se-

lects private s

∈ Z

and computes public P

= s

(b) Encryption: Alice maps plaintext m to point

M, selects random integer k ∈ Z

, computes CT

k.G, CT

= M + k.P

and transmits {CT

,CT

} to

Bob. (c) Decryption: Bob utilizes his s

to compute

− s

.CT

= M + k.P

− s

k.G = M. Bob maps

M to obtain m.

4.DDH Assumption: Assume P is cyclic group of

prime order q with G as generator, and b,c are ran-

dom integers in Z

. Given (G,bG,cG,bcG) to A , it

is difﬁcult to distinguish between bcG ∈ P and ran-

ICISSP 2025 - 11th International Conference on Information Systems Security and Privacy

226

dom R ∈ P. The algorithm B’s advantage in solv-

ing DDH assumption is ε if Prob[B (G,bG,cG,Z =

bcG) = 0] − Prob[B(G, bG, cG, Z = R) = 0]| ≥ ε

Deﬁnition 1. The DDH assumption holds if the

advantage of polynomial time algorithm in solving

DDH problem is at most negligible.

4 SYSTEM OVERVIEW

This section elaborates system architecture, threat

model, and formal structure of ECC-CP-ABPRE.

Public

Parameters

Attribute Authority

Secret Key

Proxy Server

Data Owner

Cloud Server

Original Ciphertext

Original Data User

Ciphertext

Re-encrypted

Ciphertext

Re-encyption Key

Re-encrypted Ciphertext

Original Ciphertext

Shared Data Users

Original

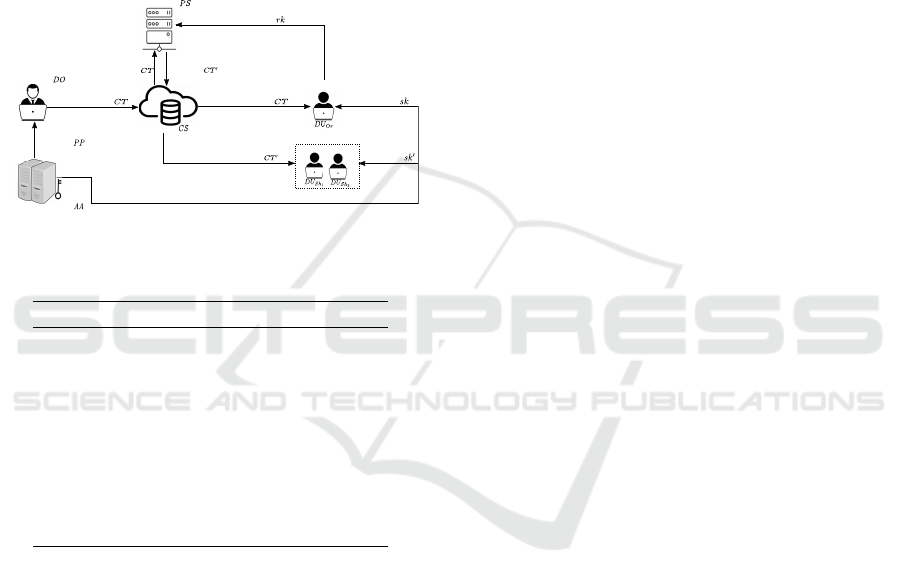
Figure 1: System Architecture of ECC-CP-ABPRE.

Table 1: Notations Summary.

Notation Description

AA, DO Attribute authority, Data owner

CS, PS Cloud server, Proxy server

, DU

Original data user, Shared data user

A, C Adversary, Challenger

A Share-generating matrix

ρ Associate rows of A to attribute

U, S Universal attribute set, DU’s attribute set

Public key of attribute i

msk, PP Master secret key, public parameters

sk, rk Secret key of DU, Re-encryption key

CT , CT

′

Original, Re-encrypted ciphertext

⃗

λ, ⃗w Random vectors

4.1 System Architecture

The entities incorporated are: AA is trusted third

party responsible for system initialization, generates

PP and distributes sk to data users. Fig. 1 and Ta-

ble 1 depict and describe, respectively, entities and

notations of ECC-CP-ABPRE. DO formulates access

policy over system attributes and encrypts ans stores

his data as CT on CS. CS and PS are honest-but-

curious entities that execute all authorized requests

but attempt to retrieve some information from results.

The CS stores ciphertexts generated by participating

entities, and PS generates CT

′

using CT and rk of

DU. DU request access to ciphertext stored on CS

and can successfully decrypt it if corresponding at-

tributes satisfy the underlying access policy. DU are

categorized as delegator i.e. DU

and delegatee i.e.

. DU

that satisﬁes the access policies of CT ,

generates rk to update the ciphertext-policy. CT

′

can

be decrypted by DU

with their sk

′

that satisﬁes the

updated ciphertext-policy.

4.2 Threat Model and Security

Requirements

An unauthorized user without valid secret key is an

adversary A that attempts to gain underlying plain-

text of encrypted data. A attempts following attacks:

ﬁrstly, A colludes with CS and PS to download and

decrypt either CT or CT

′

to gain underlying plaintext.

Secondly, PS leverages rk to update access policy of

unspeciﬁed ciphertext (i.e. rk that does not satisﬁes

ciphertext-policy). Following are security goals:

Data conﬁdentiality: It ensures that the outsourced

encrypted data should be decrypted by authorized en-

tities with valid sk that satisfy ciphertext-policy. Sim-

ilarly, CT

′

should be decrypted by authorized users

that satisfy the updated access policy in CT

′

. Addi-

tionally, the underlying plaintext of both CT and CT

′

should be inaccessible to both CS and PS.

Speciﬁcity of re-encryption keys: The rk issued by

should re-encrypt the speciﬁed ciphertext (i.e.

rk generated for policy update of speciﬁed cipher-

text). This rk should neither re-encrypt unspeciﬁed

ciphertexts nor deduce any other valid re-encryption

keys to re-encrypt other ciphertexts in CS.

4.3 Formal Structure

ECC-CP-ABPRE incorporates following algorithms:

•Setup(λ,U) → (PP,msk): AA inputs U and security

parameter λ to generate msk and PP.

•KeyGenr(S, msk) → sk: AA inputs msk and user’s at-

tribute set S and outputs secret key sk for S.

•Enc(m,(A,ρ)) → CT : DO generates CT by encrypt-

ing m under (A,ρ).

•Dec

(CT, sk) → m/⊥: DU

with sk executes this

algorithm to decrypt CT . If attribute set S |= (A, ρ)

then m is generated as output, otherwise symbol ⊥

that indicates either CT is invalid or S ⊭ (A,ρ).

•ReEncKeyGenr(sk,(A

′

,ρ

′

),CT ) → rk: DU

with

sk of S where S |= (A, ρ), outputs rk. It inputs up-

dated (A

′

,ρ

′

), CT under (A,ρ), sk, and outputs rk.

•ReEncr(CT, rk) → CT

′

: PS inputs CT , rk to generate

′

which is outsourced on CS.

•Dec

(CT

′

,sk

′

) → m/⊥: DU

with sk

′

of S

′

decrypts

′

. It inputs sk

′

, CT

′

under (A

′

,ρ

′

), and outputs m

if S

′

|= (A

′

,ρ

′

), else ⊥ for S

′

⊭ (A

′

,ρ

′

) or invalid CT

′

A Novel Pairing-Free ECC-Based Ciphertext-Policy Attribute-Based Proxy Re-Encryption for Secure Cloud Storage

227

4.4 Security Model

ECC-CP-ABPRE adopts selective model where ad-

versary commits challenge policy before security

game similar to (Waters, 2011; Ge et al., 2021).

Semantic Security: Sem-O and Sem-R security

game illustrates semantic security of original and re-

encrypted ciphertext, respectively.

Game Sem-O: ECC-CP-ABPRE is original cipher-

text semantic secure if A’s advantage is negligible.

Initialization: A selects challenge (A

′′

,ρ

′′

Setup: C outputs {PP,msk} and provides PP to A.

Query Phase 1: A queries: (1) O

(S): A

queries sk with S, C executes KeyGenr(S, msk)

and outputs sk to A. (2) O

(S,(A

′

,ρ

′

),CT ):

A queries rk on (S,(A

′

,ρ

′

)) wherein S ⊭

′

,ρ

′

). C computes sk = KeyGenr(S,msk),

rk = ReEncKeyGenr(sk,(A

′

,ρ

′

),CT ), and sends

rk to A . (3) O

(S,(A

′

,ρ

′

),CT ): A queries

re-encrypted ciphertext on (S,(A

′

,ρ

′

),CT )

where C computes sk = KeyGenr(S, msk),

rk = ReEncKeyGenr(sk,(A

′

,ρ

′

),CT ), CT

′

ReEncr(CT, rk) and transmits CT

′

to A. A

cannot execute: (1)O

(S) if S |= (A

′′

,ρ

′′

)

(2)O

(S,(A

′

,ρ

′

),CT ) if S |= (A

′′

,ρ

′′

) and A

queried O

′

) where S

′

|= (A

′

,ρ

′

)

Challenge: A transmits (m

) of same length to

C . C calculates challenge CT

′′

= Enc(m

,(A

′′

,ρ

′′

))

where β ∈ {0,1} and sends CT

′′

to A.

Query Phase 2: A queries similar to Query

Phase 1 except: (1) O

(S) if S |= (A

′′

,ρ

′′

) (2)

(S,(A

′

,ρ

′

),CT ) and O

′

) if S |= (A

′′

,ρ

′′

) and

′

|= (A

′

,ρ

′

) (3) O

(S,(A

′

,ρ

′

),CT

′′

) and O

′

) if

S |= (A

′′

,ρ

′′

) and S

′

|= (A

′

,ρ

′

)

Guess: A outputs guess bit β

′

. A wins if β

′

β. A’s advantage to win this game is deﬁned as

Adv

Sem−O

(λ) = |Prob[β

′

= β] − 1/2

Game Sem-R: ECC-CP-ABPRE is re-encrypted ci-

phertext semantic secure if the advantage of A is neg-

ligible in the below game.

Initialization: A selects (A

′′

,ρ

′′

Setup: C generates {PP,msk} and provides PP to A.

Query Phase 1: A queries: (1)O

(S): A queries

sk with S, C executes sk = KeyGenr(S,msk) and

transmits sk to A. (2) O

(S,(A

′

,ρ

′

),CT ): A

queries rk on (S,(A

′

,ρ

′

)) wherein S ⊭ (A

′

,ρ

′

C computes sk = KeyGenr(S, msk) and rk =

ReEncKeyGenr(sk,(A

′

,ρ

′

),CT ), and returns rk to A.

A cannot execute O

(S) if S |= (A

′′

,ρ

′′

Challenge: A transmits (m

) of same length to C .

C computes challenge CT

′′′

as CT = Enc(m

,(A,ρ)),

rk = ReEncKeyGenr(S,(A

′′

,ρ

′′

),CT ), CT

′′′

ReEncr(CT, rk) where β ∈ {0, 1} and S |= (A,ρ). C

returns CT

′′′

to A.

Query Phase 2: A queries similar to Query Phase 1

except O

(S) if S |= (A

′′

,ρ

′′

Guess: A outputs guess bit β

′

There is no constraint on re-encryption query i.e. A

generates appropriate rk followed by re-encryption

query hence, omitted in this game. A’s advantage to

win this game is Adv

Sem−R

(λ) = |Prob[β

′

= β] −1/2|

Deﬁnition 2. The ECC-CP-ABPRE is semantic se-

cure if both Sem-O and Sem-R are secure.

5 ECC-CP-ABPRE

CONSTRUCTION

ECC-CP-ABPRE incorporates following algorithms:

(

(λ

λ,

)

): AA generates (p,E

(a,b),G) with se-

curity parameter λ as input. Assume hash function

H : {0,1}

∗

→ Z

∗

for one-way mapping of ID

to el-

ements in Z

∗

. AA inputs U = {A

,...,A

} and

for each A

∈ U, AA selects random a

∈ Z

as secret

key and computes PK

= a

.G as public key for A

AA secretly stores msk = {a

...,a

} and publicize

PP = {U,PK

,PK

,...PK

,G,H} as PP.

(

)

): AA inputs S and msk, and assigns

unique ID

to DU and generates random r

∈ Z

, ∀i ∈

S to compute sk

i,ID

= a

+ H(ID

).r

. Finally, AA

securely transmits sk = {sk

i,ID

,∀i ∈ S} to DU.

(

(A,

,ρ

ρ)

)

))

)

): DO performs following:

1.DO maps m to point M on E

(a,b), selects random

s ∈ Z

to calculate CT

= M + s.G

2.DO selects

⃗

λ = (s, v

,...,v

) ∈ Z

and ⃗w =

(0,ζ

,ζ

,...,ζ

) ∈ Z

. Assume A

denotes x

row

of A where x = [1,l], DO calculates λ

⃗

λ · A

⊺

and w

= ⃗w · A

⊺

where A

⊺

denotes transpose of A

Further, for all x = [1,l], DO computes: CT

1,x

.G + w

.PK

ρ(x)

and CT

2,x

= w

.G DO transmits

CT = ((A, ρ),CT

,{CT

1,x

,CT

2,x

}

x=[1,l]

) to CS.

(

T ,

)

): DU

with S and sk = {sk

x,ID

,∀x ∈

S} decrypts CT as follows:

1.DU

generates X = {x|ρ(x) ∈ S}. If S |= (A,ρ)

then, there exists {c

∈ Z

}

x∈X

such that

∑

(1,0,. .. , 0). DU

computes:

∑

1,x

−

∑

2,x

.sk

ρ(x),ID

∑

.G + w

.PK

ρ(x)

−



∑

.G + w

ρ(x)

H(ID

).G



∑

.G − w

ρ(x)

H(ID

).G (1)

2.DU

utilizes constant set {c

∈ Z

}

x∈X

∑

x∈X

= s and

∑

x∈X

= 0. DU

computes:

∑

.G − c

ρ(x)

H(ID

).G = s.G (2)

3.DU

calculates point M as M = CT

−s.G. Finally,

generates m by mapping point M on E

(a,b).

ICISSP 2025 - 11th International Conference on Information Systems Security and Privacy

228

(

′

,ρ

′

)

T )

)

): DU

with sk of

S considers CT under (A,ρ) and new (A

′

,ρ

′

) as input

and computes rk. DU

can generate rk only if S |=

(A,ρ), else symbol ⊥ is generated. DU

computes:

1.For (A, ρ), DU

generates {c

∈ Z

}

x∈X

such that

∑

x∈X

· A = (1,0, 0, . . . , 0) where X = {x|ρ(x) ∈

S}. DU

computes s.G using (1) and (2), gener-

ates random s

′

∈ Z

and computes rk

= s

′

.G − s.G.

2.Assume A

′

is of size l

′

× n

′

and A

′

denotes y

row of A

′

where y = [1, l

′

]. DU

selects two ran-

dom vector

⃗

′

= (s

′

,...,v

′

) ∈ Z

and ⃗w

′

(0,ζ

′

,ζ

′

,...,ζ

′

) ∈ Z

. DU

calculates λ

′

⃗

′

⊺

and w

′

⃗

′

· A

′

⊺

where A

′

⊺

denotes transpose

of A

′

. Further, for all y = [1, l

′

], DU

computes

1,y

= λ

′

.G + w

′

.PK

ρ(y)

and rk

2,y

= w

′

3.DU

transmits re-encryption key rk =

((A

′

,ρ

′

),rk

,{rk

1,y

,rk

2,y

}

y=[1,l

′

]

(

T ,

)

): PS inputs CT =

((A,ρ),CT

,{CT

1,x

,CT

2,x

}

x=[1,l]

), rk =

((A

′

,ρ

′

),rk

,{rk

1,y

,rk

2,y

}

y=[1,l

′

]

) and computes

transformed ciphertext as CT

′

= CT

+ rk

M + s.G + s

′

.G − s.G = M + s

′

.G. For all y = [1,l

′

PS computes CT

′

1,y

= rk

1,y

, CT

′

2,y

= rk

2,y

and sends

′

= ((A

′

,ρ

′

),CT

′

,{CT

′

1,y

,CT

′

2,y

}

y=[1,l

′

]

) to CS.

(

′

)

): DU

with S

′

and sk

′

{sk

′

y,ID

,∀y ∈ S

′

} decrypts CT

′

as:

1.DU

generates set Y = {y|ρ

′

(y) ∈ S

′

}. If S

′

,ρ

′

) then, there exists {c

′

∈ Z

}

y∈Y

such that

∑

′

= (1, 0, 0, . . . , 0). DU

performs:

′

∑

′

1,y

−

∑

′

2,y

.sk

′

ρ(y),ID

∑

′

.G + w

′

.PK

ρ(y)

−



∑

′

.G + w

′

ρ(y)

H(ID

).G



∑

′

.G − w

′

ρ(y)

H(ID

).G (3)

2.DU

utilizes {c

′

∈ Z

}

y∈Y

∑

y∈Y

′

= s

′

and

∑

y∈Y

′

= 0. Hence, DU

computes:

∑

′

∑

′

.G − c

′

ρ(y)

H(ID

).G = s

′

.G (4)

3.DU

computes M = CT

′

− s

′

G. DU

calculates m

by mapping point M on E

(a,b).

Correctness of Original Ciphertext

M = CT

− c



∑

1,x

−

∑

2,x

.sk

ρ(x),ID



= CT

− c



∑

.G +

∑

.PK

ρ(x)

−

∑

−

∑

ρ(x)

H(ID

).G



= CT

− c



∑

.G +

∑

.G −

∑

−

∑

ρ(x)

H(ID

).G



= CT

− c



∑

.G −

∑

ρ(x)

H(ID

).G



= CT

−



∑

.G −

∑

ρ(x)

H(ID

).G



= CT

− s.G = M + s.G − s.G = M

It should be noted that

∑

= s and

∑

= 0.

Correctness of Re-Encrypted Ciphertext

M = CT

′

− c

′



∑

′

1,y

−

∑

′

2,y

.sk

′

ρ(y),ID



= CT

′

− c

′



∑

′

.G +

∑

′

.PK

ρ(y)

−

∑

′

−

∑

′

ρ(y)

H(ID

).G



= CT

′

− c

′



∑

′

.G +

∑

′

.G −

∑

′

−

∑

′

ρ(y)

H(ID

).G



= CT

′

− c

′



∑

′

.G −

∑

′

ρ(y)

H(ID

).G



= CT

′

−



∑

′

.G −

∑

′

ρ(y)

H(ID

).G



= CT

′

− s

′

.G = M + s

′

.G − s

′

.G = M

It should be noted that

∑

′

= s

′

and

∑

′

= 0.

6 SECURITY PROOF

Semantic security of ECC-CP-ABPRE is as follows:

Theorem 1. The ECC-CP-ABPRE scheme is seman-

tic secure under the DDH assumption.

Proof. As per semantic security in Deﬁnition 2, fol-

lowing two lemma proves Sem-O and Sem-R security.

Lemma 1. ECC-CP-ABPRE is Sem-O secure under

the DDH assumption.

Proof. Assume probability polynomial time (PPT), A

breaks Sem-O security with non-negligible probabil-

ity ε > 0, then there exists PPT algorithm B that dis-

tinguishes between random tuples and DDH with ad-

vantage of ε/2. Challenger C selects random b, c ∈

, β ∈ {0,1} and R ∈ P. Assume G is generator

of group P with order q. Then Z = bcG if β = 0,

else Z = R. C transmits (G, bG, cG, Z) to B. B main-

tains secret and re-encryption keys lists that are empty

initially: (i) Li

: records (S, sk

) tuple. (ii) Li

stores (S, (A

′

,ρ

′

),rk,ind) tuple where ind = 1 indi-

cates valid rk and ind = 0 indicates random rk. B

executes the following:

Initialization: A provides challenge (A

′′

,ρ

′′

) to B .

Setup: B selects random a

∈ Z

and computes PK

b.G as public key for A

where i = [1,n]. B transmits

PP = {PK

,PK

,...,PK

,G,H} to A.

Query Phase 1: In this phase: (1)O

(S): A queries

on S and B conﬁrms whether S ⊭ (A

′′

,ρ

′′

). If un-

satisﬁed, B outputs ⊥ otherwise, B selects r

∈ Z

and computes sk

= a

b + H(ID

).r

where ID

de-

notes identity of A . (2)O

(S,(A

′

,ρ

′

),CT ): B veri-

ﬁes if S |= (A

′′

,ρ

′′

) and there exists (S

′

,sk

′

) in Li

where S

′

|= (A

′

,ρ

′

) then, ⊥ is generated as output.

A Novel Pairing-Free ECC-Based Ciphertext-Policy Attribute-Based Proxy Re-Encryption for Secure Cloud Storage

229

Else if S |= (A

′′

,ρ

′′

) and no entry (S

′

,sk

′

) exists in

where S

′

|= (A

′

,ρ

′

) then, B generates random

rk and (S, (A

′

,ρ

′

),rk,0) is added to Li

. Otherwise,

B queries O

(S) to receive sk

, computes rk using

ReEncKeyGenr and (S,(A

′

,ρ

′

),rk,1) is added to Li

(3)O

(S,(A

′

,ρ

′

),CT ): If S |= (A

′′

,ρ

′′

) and there ex-

ists (S

′

,sk

′

) in Li

wherein S

′

|= (A

′

,ρ

′

) then, ⊥

is generated as output. Else, if (S,(A

′

,ρ

′

),rk,0) or

(S,(A

′

,ρ

′

),rk,1) exists in Li

, B encrypts CT with

rk. Otherwise, B queries O

(S,(A

′

,ρ

′

),CT ) to com-

pute rk followed by re-encryption of CT with rk.

Challenge: A selects and transmits (m

) of same

length to B . B ﬂips a coin β and selects ran-

dom s ∈ Z

⃗

λ = (s,v

,...,v

) ∈ Z

and ⃗w =

(0,ζ

,ζ

,...,ζ

) ∈ Z

. B generates challenge ci-

phertext CT

′′

= M

+ s.G, CT

′′

1,x

= λ

G + a

ρ(x)

and CT

′′

2,x

= w

c.G where x = [1,l

′′

], λ

⃗

λ · A

′′

⊺

= ⃗w · A

′′

⊺

and M

denotes plaintext m

on ellip-

tic curve. B returns this challenge ciphertext CT

′′

{(A

′′

,ρ

′′

),CT

′′

,{CT

′′

1,x

,CT

′′

2,x

}

x∈[1,l

′′

]

} to A .

Query Phase 2: Similar to Query Phase 1 with con-

straints mentioned in Sem-O model.

Guess: A outputs a guess β

′

. If B outputs 0, then Z =

bcG and β

′

= β; else, B returns 1 indicating Z = R.

Analysis: If Z = bcG, then CT

′′

is perfect ciphertext.

Thus, Prob[B (G,bG,cG,Z = bcG) = 0] = 1/2 + ε. If

Z = R then Prob[B(G,bG, cG, Z = R) = 0] = 1/2 .

Hence, the advantage of B in breaking security is:

Adv

Sem−O

(Prob[B(G,bG,cG,Z = bcG) = 0]

+ Prob[B (G, bG, cG, Z = R) = 0]) −

(

+ ε +

) −

Thus, B can solve DDH assumption with ε.

Lemma 2. ECC-CP-ABPRE scheme is Sem-R secure

under the DDH assumption.

Proof. Assume PPT A breaks Sem-O security with

non-negligible probability ε > 0, then there exists

PPT algorithm B that distinguishes between random

tuple and DDH with advantage ε/2.

Initialization, Setup and Query Phase 1 is same as

Lemma 1.

Challenge: A selects (m

) of same size and trans-

mits to B . B selects S where S ⊭ (A

′′

,ρ

′′

) and out-

puts sk

and rk = ReEncKeyGenr(sk

,(A

′′

,ρ

′′

),CT ).

B ﬂips a coin β and selects (A,ρ) where S |= (A,ρ)

and computes CT = Enc(m

,(A,ρ)). B calculates

′′′

= ReEncr(CT, rk) and returns CT

′′′

to A.

Query Phase 2: Similar to Query in Sem-R model.

Guess: A outputs guess β

′

. If B outputs 0, it indicates

Z = bcG & β

′

= β; else, B outputs 1 indicating Z = R.

Analysis: If Z = bcG, then CT

′′′

is perfect ciphertext.

Thus, Prob[B (G,bG,cG,Z = bcG) = 0] = 1/2 + ε. If

Z = R then Prob[B(G,bG, cG, Z = R) = 0] = 1/2 .

Hence, the advantage of B in breaking security is:

Adv

Sem−R

(Prob[B(G,bG,cG,Z = bcG) = 0]

+ Prob[B (G, bG, cG, Z = R) = 0]) −

(

+ ε +

) −

Thus, B can solve DDH assumption with non-

negligible advantage ε.

Hence, Theorem 1 is proved.

7 SECURITY ANALYSIS

The security analysis are as follows:

Data Conﬁdentiality: In ECC-CP-ABPRE, only

valid users with corresponding attributes satisfying

access policy can decrypt ciphertext. The security

is based on ECDLP which ensures inefﬁcacy of in-

valid users to compute master secret key {a

} from

= a

.G in polynomial time. In Enc, assume M

mapped as m.G on elliptic curve where m ∈ Z

and

DO selects random s ∈ Z

thus, CT

= (m + s).G.

Note that CT

denotes a random point on elliptic curve

from A ’s viewpoint hence, leaks no valuable infor-

mation about M. Also, secret s is split by λ

us-

ing LSSS that can be recovered by DU’s attributes

satisfying (A,ρ). Thus, any invalid user with at-

tributes not satisfying (A,ρ), there exits no corre-

sponding rows A

such that

∑

= (1,0,0 ...,0)

where x = [1,l]. Hence, secret s, ﬁrst entry of vector

⃗

λ cannot be computed thereby, ensuring data conﬁ-

dentiality of CT . In ReEncKeyGenr, DU

computes

= (s

′

−s).G which denotes random point on ellip-

tic curve. Thus, PS acquires no valuable information

from rk

due to ECDLP. In ReEncr with (A

′

,ρ

′

), PS

computes CT

′

= (m + s

′

).G where random m,s

′

∈ Z

Similar to CT , ECDLP and LSSS ensures security of

′

. Thus, invalid user with attributes not satisfying

′

,ρ

′

), there exits no corresponding rows A

′

such

that

∑

′

= (1,0,0 . . . , 0) where y = [1,l

′

]. Hence,

secret s

′

, ﬁrst entry of vector

⃗

′

cannot be computed

thereby, ensuring data conﬁdentiality of CT

′

Resistant to Collusion Attack: ECC-CP-ABPRE

should resist collusion attack i.e. if multiple users

collude their secret keys, they should be incapable in

ICISSP 2025 - 11th International Conference on Information Systems Security and Privacy

230

ciphertext decryption unless at-least one user can de-

crypt ciphertext independently. KeyGenr generates sk

that binds unique ID

of DU and random r

with at-

tributes of corresponding user. Hence, sk of differ-

ent DU cannot be combined successfully to decrypt

ciphertext. Assume Alice with attribute A, and Bob

with attributes C and D, collude to gain underlying

plaintext in ciphertext-policy (A ∨ B) ∧C ∧D. Neither

of them can decrypt the ciphertext individually, Alice

computes D

Alice

∑

.G − w

Alice

ρ(x)

H(ID

Alice

)G and

Bob computes D

Bob

∑

.G − w

Bob

ρ(x)

H(ID

Bob

for some x. Note that Alice and Bob have

H(ID

Alice

) ̸= H(ID

Bob

) and r

Alice

ρ(x)

̸= r

Bob

ρ(x)

in their sk.

Hence, they cannot compute constant set {c

∈ Z

such that

∑

= (1,0, 0, . . . , 0) and are unable to

compute sG thus, resistant to collusion attack.

Speciﬁcity of Re-Encryption Key: In ECC-CP-

ABPRE, rk should re-encrypt speciﬁed ciphertext i.e.

rk generated for policy update of speciﬁed ciphertext.

To update (A,ρ) to (A

′

,ρ

′

), DU

in ReEncKeyGenr

generates random s

′

∈ Z

and computes rk

= s

′

G −

sG for original ciphertext CT

= M + sG under (A,ρ).

Thus, any unspeciﬁed ciphertext CT

∗

= M

∗

G un-

der (A

∗

,ρ

∗

) cannot be re-encrypted with rk

as it re-

quires re-encryption key incorporating s

∗

G. Also, it

is difﬁcult to compute other re-encryption keys from

rk = {rk

,{rk

1,y

,rk

2,y

}

y=[1,l

′

]

} due to random s

′

hence, ensuring speciﬁcity of re-encryption keys.

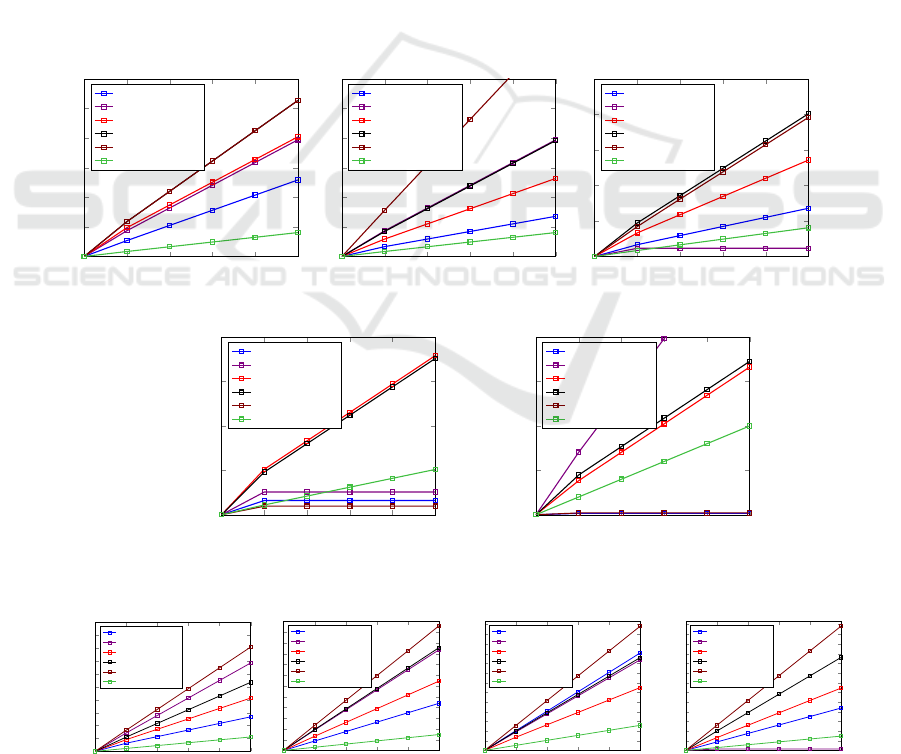
8 PERFORMANCE ANALYSIS

ECC-CP-ABPRE is compared with existing schemes

by incorporating Java pairing-based cryptography

package (De Caro and Iovino, 2011) for pairing op-

erations on Type 1 symmetric pairing G × G → G

with 512-bit supersingular curve of embedding degree

2, size of the elliptic curve is 512 bits, the order of the

elliptic curve group is 160 bits that are implemented

10 20 30 40

0.5

1.5

2.5

·10

Attributes

Communication overhead (in bytes)

(Yang et al., 2016)

(Deng et al., 2020)

(Ge et al., 2021)

(Zhou et al., 2021)

(Chen et al., 2022)

ECC-CP-ABPRE

(a) Re-encryption Key.

10 20 30 40

0.5

1.5

2.5

·10

Attributes

Communication overhead (in bytes)

(Yang et al., 2016)

(Deng et al., 2020)

(Ge et al., 2021)

(Zhou et al., 2021)

(Chen et al., 2022)

ECC-CP-ABPRE

(b) Original Ciphertext.

10 20 30 40

0.5

1.5

2.5

·10

Attributes

Communication overhead (in bytes)

(Yang et al., 2016)

(Deng et al., 2020)

(Ge et al., 2021)

(Zhou et al., 2021)

(Chen et al., 2022)

ECC-CP-ABPRE

10 20 30 40

2,000

4,000

6,000

8,000

Attributes

Communication overhead (in bytes)

(Yang et al., 2016)

(Deng et al., 2020)

(Ge et al., 2021)

(Zhou et al., 2021)

(Chen et al., 2022)

ECC-CP-ABPRE

(d) Public Key.

10 20 30 40

2,000

4,000

6,000

8,000

Attributes

Communication overhead (in bytes)

(Yang et al., 2016)

(Deng et al., 2020)

(Ge et al., 2021)

(Zhou et al., 2021)

(Chen et al., 2022)

ECC-CP-ABPRE

(e) Secret Key.

Figure 2: Comparison of Computational Overhead(in bytes).

10 20 30 40

Attributes

Computational overhead (in sec)

(Yang et al., 2016)

(Deng et al., 2020)

(Ge et al., 2021)

(Zhou et al., 2021)

(Chen et al., 2022)

ECC-CP-ABPRE

(a) Encrypt Plaintext.

10 20 30 40

Attributes

(Yang et al., 2016)

(Deng et al., 2020)

(Ge et al., 2021)

(Zhou et al., 2021)

(Chen et al., 2022)

ECC-CP-ABPRE

(b) Decrypt CT .

10 20 30 40

Attributes

(Yang et al., 2016)

(Deng et al., 2020)

(Ge et al., 2021)

(Zhou et al., 2021)

(Chen et al., 2022)

ECC-CP-ABPRE

10 20 30 40

Attributes

(Yang et al., 2016)

(Deng et al., 2020)

(Ge et al., 2021)

(Zhou et al., 2021)

(Chen et al., 2022)

ECC-CP-ABPRE

(d) Decrypt CT

′

Figure 3: Comparison of Communication Overhead(in sec).

A Novel Pairing-Free ECC-Based Ciphertext-Policy Attribute-Based Proxy Re-Encryption for Secure Cloud Storage

231

using laptop conﬁguration of Intel Core i5-1135G7 @

2.40 GHz, 8 GB RAM. For communication overhead,

|G|, |G

, |P|, and |Z

| denotes size of elements in

G, G

, ECC point and random element in Z

. |G|,

|, |P| and |Z

| are 1024 bits, 2048 bits, 320 bits

and 160 bits, respectively. ECC-CP-ABPRE incurs

less communication overhead to send rk and CT com-

pared with (Yang et al., 2016; Deng et al., 2020; Ge

et al., 2021; Zhou et al., 2021; Chen et al., 2022) as

in Fig. 2(a) and 2(b), respectively. To transmit CT

′

ECC-CP-ABPRE performs better than (Yang et al.,

2016; Ge et al., 2021; Zhou et al., 2021; Chen et al.,

2022) as in Fig. 2(c) however, it is increased com-

pared with (Deng et al., 2020) as latter scheme lever-

ages PS to perform partial decryption of ciphertext in

re-encryption. To transmit public key and secret key

as in Fig. 2(d) and 2(e), ECC-CP-ABPRE increases

by ≈320n bits and ≈160n

′

bits, respectively, com-

pared to (Yang et al., 2016; Chen et al., 2022). This

can be circumvented as AA transmits these keys once

during system initialization and user registration.

For computational overhead comparison, T

EX P

, T

and T

represent as time for expo-

nential operation in G, multiplication operation in G,

bilinear pairing, scalar multiplication, and point addi-

tion in ECC, respectively. T

EX P

, T

and

are 0.0765 sec, 0.0118 sec, 0.1099 sec, 0.0220

sec and 0.0002 sec, respectively. ECC-CP-ABPRE

requires signiﬁcantly less computation overhead than

(Yang et al., 2016; Deng et al., 2020; Ge et al., 2021;

Zhou et al., 2021; Chen et al., 2022) to encrypt plain-

text, decrypt original ciphertext and re-encrypt ci-

phertext as shown in Fig. 3(a), 3(b), and 3(c) re-

spectively. To decrypt CT

′

, ECC-CP-ABPRE out-

performs (Yang et al., 2016; Ge et al., 2021; Zhou

et al., 2021; Chen et al., 2022) as in Fig. 3(d). How-

ever, computational overhead in (Deng et al., 2020) is

less than ECC-CP-ABPRE as it leverages PS to par-

tially decrypt CT in re-encryption phase. Nonethe-

less, computational overhead in re-encryption phase

is signiﬁcantly increased as PS performs both re-

encryption and partial decryption of CT as in Fig.

3(c). Hence, the overall computational overhead of

ECC-CP-ABPRE is less than (Deng et al., 2020).

Thus, the overall efﬁciency of ECC-CP-ABPRE sur-

passes (Yang et al., 2016; Deng et al., 2020; Ge et al.,

2021; Zhou et al., 2021; Chen et al., 2022) in terms of

communication and computational overheads.

9 CONCLUSION

This paper designs a novel pairing-free ECC-based

CP-ABPRE to enable efﬁcient sharing of encrypted

data in clouds. ECC-CP-ABPRE replaces expensive

bilinear pairing operations with scalar multiplications

to update ciphertext-policy. The security analysis il-

lustrates semantic security of both original ciphertext

and re-encrypted ciphertext under DDH assumption.

It ensures data conﬁdentiality and speciﬁcity of re-

encryption keys while resisting collusion attack. The

performance results demonstrate its efﬁciency. In fu-

ture, ECC-CP-ABPRE will be extended to trace and

revoke malicious data users leaking their secret keys

to unauthorized users in the system.

REFERENCES

Beimel, A. (1996). Secure schemes for secret sharing and

key distribution. Technion-Israel Institute of technol-

ogy, Faculty of Computer Science.

Bethencourt, J., Sahai, A., and Waters, B. (2007).

Ciphertext-policy attribute-based encryption. In 2007

IEEE symposium on security and privacy (SP’07),

pages 321–334. IEEE.

Chen, J., Wang, J., Yin, X., and Ning, J. (2022). A ﬁne-

grained medical data sharing scheme with ciphertext

reencryption. Wireless Communications and Mobile

Computing, 2022.

De Caro, A. and Iovino, V. (2011). jpbc: Java pairing based

cryptography. In 2011 IEEE symposium on computers

and communications (ISCC), pages 850–855. IEEE.

Deng, H., Qin, Z., Wu, Q., Guan, Z., and Zhou, Y. (2020).

Flexible attribute-based proxy re-encryption for efﬁ-

cient data sharing. Information Sciences, 511:94–113.

Dhakad, N. and Kar, J. (2022). Eppdp: An efﬁcient privacy-

preserving data possession with provable security in

cloud storage. IEEE Systems Journal.

Ge, C., Susilo, W., Baek, J., Liu, Z., Xia, J., and Fang, L.

(2021). A veriﬁable and fair attribute-based proxy re-

encryption scheme for data sharing in clouds. IEEE

Transactions on Dependable and Secure Computing.

Liang, K., Au, M. H., Liu, J. K., Susilo, W., Wong, D. S.,

Yang, G., Yu, Y., and Yang, A. (2015). A secure

and efﬁcient ciphertext-policy attribute-based proxy

re-encryption for cloud data sharing. Future Gener-

ation Computer Systems, 52:95–108.

Liang, X., Cao, Z., Lin, H., and Shao, J. (2009). Attribute

based proxy re-encryption with delegating capabili-

ties. In Proceedings of the 4th International Sympo-

sium on Information, Computer, and Communications

Security, pages 276–286.

Luo, S., Hu, J., and Chen, Z. (2010). Ciphertext policy

attribute-based proxy re-encryption. In International

Conference on Information and Communications Se-

curity, pages 401–415. Springer.

Miller, V. S. (1985). Use of elliptic curves in cryptogra-

phy. In Conference on the theory and application of

cryptographic techniques, pages 417–426. Springer.

Rezaeibagha, F., Mu, Y., Huang, K., Chen, L., and Zhang,

L. (2021). Toward secure data computation and out-

ICISSP 2025 - 11th International Conference on Information Systems Security and Privacy

232

source for multi-user cloud-based iot. IEEE Transac-

tions on Cloud Computing.

Wang, M., Xu, L., Hao, R., and Yang, M. (2023). Secure

auditing and deduplication with efﬁcient ownership

management for cloud storage. Journal of Systems

Architecture, 142:102953.

Waters, B. (2011). Ciphertext-policy attribute-based en-

cryption: An expressive, efﬁcient, and provably se-

cure realization. In International workshop on public

key cryptography, pages 53–70. Springer.

Yang, Y., Zhu, H., Lu, H., Weng, J., Zhang, Y., and Choo,

K.-K. R. (2016). Cloud based data sharing with ﬁne-

grained proxy re-encryption. Pervasive and Mobile

computing, 28:122–134.

Zhou, X., Xu, K., Wang, N., Jiao, J., Dong, N., Han, M.,

and Xu, H. (2021). A secure and privacy-preserving

machine learning model sharing scheme for edge-

enabled iot. IEEE Access, 9:17256–17265.

A Novel Pairing-Free ECC-Based Ciphertext-Policy Attribute-Based Proxy Re-Encryption for Secure Cloud Storage

233