Who Knows Who: A Context-Based Approach to

Network Generation for Social Simulations

Veronika Kurchyna

∗

, Philipp Fl

ugger, Ye Eun Bae, Jan Ole Berndt and Ingo J. Timm

German Research Center for Artiﬁcial Intelligence (DFKI),

Cognitive Social Simulation, Behringstr. 21, 54296 Trier, Germany

Keywords:

Synthetic Population, Network Generation, Agent-Based Modelling.

Abstract:

Established network models (small-world, preferential attachment, random, etc.) often fail to capture the full

range of characteristics observed in real social networks, potentially limiting the transferability of model re-

sults. To address this limitation, we propose a Contextual Network Model that is superimposed on a synthetic

population. The model takes into account sociodemographic agent-traits and location data, such as workplaces

and frequent leisure activities, to construct a realistic network. To showcase the effect of network topology

on model dynamics, we investigate a Susceptible-Infectious-Removed (SIR) model with information diffu-

sion by comparing our proposed network model with the aforementioned established network models. The

study identiﬁes an earlier, lower peak of infectious agents, along with a greater number of susceptible agents

remaining at the end of the simulation for the proposed network model. Moreover, the study underscores the

measurable impact of network topology on model behaviour, revealing different expansion rates and patterns

in the information diffusion process. Additionally, this work offers instructions for a customisable implemen-

tation of a contextual network model generator for other agent-based models and populations.

1 INTRODUCTION

Recent phenomena, such as pandemics or opinion

dynamics in social media have driven the develop-

ment of numerous simulation models. These mod-

els are aimed at gaining insight into the function-

ing of social mechanisms, such as the dual causal-

ity between individual and collective actions during

an epidemic (Palomo-Briones et al., 2022), assess-

ing interventions like non-pharmaceutical interven-

tions during the COVID-19 pandemic (Kerr et al.,

2021), and optimizing the allocation of scarce re-

sources, such as water distribution (Khorshidi et al.,

2024). Such models differ, among other aspects,

in their complexity regarding agent behaviour and

the socio-spatial networks of interactions and trans-

missions (Lorig et al., 2021). Ideally, social net-

works generated for agent-based social simulations

should mirror their real-world counterparts by ex-

hibiting observable properties and measurable prop-

erties. However, common approaches often disre-

gard contextual information, such as the nature of

the network, the characteristics of nodes, or the dis-

tribution of edges. In reality, social relations are

∗

Corresponding author

shaped by personal attributes, such as age and edu-

cation, along with common activities like workplaces

or frequent leisure activities (McPherson et al., 2001).

We propose a method for generating a context-based

network model, along with a prototype implementa-

tion, designed to compare against classical social net-

work approaches in agent-based models (ABM). This

method focuses on replicating properties that charac-

terise real-world social networks.

2 BACKGROUND AND RELATED

WORK

We introduce the main observable properties of social

networks and classical approaches to network gener-

ation. Additionally, we investigate how comparable

network model approaches are implemented in the

context of agent-based models.

2.1 Characteristics of Social Networks

Social networks can be represented by graphs, where

agents are depicted as nodes and their social relations

as edges (Marin and Wellman, 2011). Arbitrary sets

342

Kurchyna, V., Flügger, P., Bae, Y. E., Berndt, J. O. and Timm, I. J.

Who Knows Who: A Context-Based Approach to Network Generation for Social Simulations.

DOI: 10.5220/0013141900003890

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 17th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2025) - Volume 1, pages 342-350

ISBN: 978-989-758-737-5; ISSN: 2184-433X

of edges (like the Erd

os-R

enyi random network) do

not necessarily form a realistic representation of a so-

cial network. Hamill and Gilbert (2009) aggregated

essential structural properties of social networks as

identiﬁed by various researchers:

• Low Density. Only a fraction of possible connec-

tions exists in social network graphs.

• Limited Personal Network Size. The number of

social contacts is limited, higher numbers increas-

ingly unlikely, eventually approaching zero.

• Variation in Personal Network Size. The size of

personal networks varies, with some individuals

having large networks while others have smaller

networks.

• Fat-Tail Distribution. Extreme values occur

more often compared to a normal distribution.

• Assortativity. High-degree nodes are more likely

to connect with other high-degree nodes, while

low-degree nodes tend to link with other low-

degree nodes. This results in clusters of agents

with similar connectivity levels.

• High Clustering. A node’s connections tend to

be interconnected, reﬂecting the transitivity of so-

cial relations (Bruggeman, 2013). This property

can be quantiﬁed using the average clustering co-

efﬁcient.

• Communities. Communities are characterized by

a high local clustering coefﬁcient, with most con-

nections concentrated within the community and

relatively few edges extending to nodes outside

the community.

• Short Path Lengths. Nodes are reachable over a

small number of edges from any other node in the

network, leading to a small-world effect.

2.2 Properties of Social Relations

In addition to large-scale effects on the entire net-

work, speciﬁc properties of social relations help ex-

plain how those relations between agents are formed.

• Homophily. Individuals seek ties to similar peo-

ple across sociodemographic, behavioural, and in-

trapersonal dimensions. A hierarchical relation-

ship of characteristics has been found - some

traits, such as ethnicity, are stronger associ-

ated with homophilic preference than other at-

tributes (McPherson et al., 2001).

• Reciprocity. Symmetry is favoured over unre-

ciprocated connections in social relations (Hal-

linan, 1978). Asymmetric ties are resolved by

breaking off contact or by transforming into a

mutual relationship (Cook and Emerson, 1987).

As such, friendship is modelled as an undirected

edge (Krackhardt, 2003).

• Transitivity. Individuals tend to be friends with

the friends of their friends, which is a smaller-

scale symptom of the high clustering of networks.

The risk of circularity makes this a non-trivial

issue (Arentze et al., 2012). An iterative ap-

proach is typically used to model transitive rela-

tionships (Arentze et al., 2013).

• Assortativity. People frequently associate with

people of similar connection degrees, meaning

that individuals with large contact networks most

frequently connect to others with similarly large

networks and vice versa for low-connected indi-

viduals (Badham and Stocker, 2010).

2.3 Network Models

Four types of network models are commonly used in

social simulations (Hamill and Gilbert, 2009). These

models only receive basic parameters as input to gen-

erate the edges between nodes. These approaches pro-

vide a valuable benchmark, offering a foundational

framework for novel approaches.

• Regular Lattice. Each node is linked to its

four neighbors in a spatially explicit network.

The result yields a uniform distribution of de-

grees (Hamill and Gilbert, 2009).

• Random Network. Nodes can connect to any

other node. While the degree is not limited, ob-

servations show that most nodes are likely to have

a similar degree. Nodes with signiﬁcantly fewer

or more edges are rare (Barab

asi and Bonabeau,

2003).

• Small-World. By rewiring a few edges in a regu-

lar lattice model, short path lengths and high clus-

tering are achieved (Watts and Strogatz, 1998).

Regarding the characteristics of social networks,

this approach improves upon the previous two

networks in terms of social network characteris-

tics (Dorogovtsev and Mendes, 2003).

• Preferential Attachment. The scale-free model

is characterized by new nodes connecting to ex-

isting nodes with a greater number of links at a

higher probability. The result features highly con-

nected hubs and nodes with signiﬁcantly different

numbers of edges (Barab

asi and Albert, 1999).

Who Knows Who: A Context-Based Approach to Network Generation for Social Simulations

343

2.4 Related Work: Approaches to Social

Network Generation

Other approaches leverage domain-speciﬁc knowl-

edge from social sciences and social network analysis

to better represent real-life structures.

Local interactions occurring during agents’ move-

ment in space offer a method for modelling contacts

between agents as they move and cross paths (Caux

et al., 2014). While networks grow organically in this

manner, this approach violates the assortativity cri-

terion typical of social networks. Alternatively, fol-

lowing the proposed ego-network approach of Conti

et al. (2011), networks are initialised based on dif-

ferent types of relationships, resulting in a hierarchi-

cal structure of social groups. This approach demon-

strates the way relationships can be classiﬁed, poten-

tially independent of the way these contacts were cho-

sen.

As an in-between approach, social circles map

agents and relationships onto a continuous space,

where proximity indicates closer relationships. The

social reach (radius of social circle) limits the size

of the personal network of an agent. A small social

reach may characterize the network of a family or

close friends, while a large social reach may repre-

sent acquaintances, such as work colleagues (Hamill

and Gilbert, 2009). Moreover, Kapeller et al. (2019)

investigated the impacts of homophilic attribute dis-

tributions on a basic diffusion model by separating

the processes of network generation (structural prox-

imity) and attribute distribution (attribute proximity).

They found that homophilic distribution is essential

for a more accurate analysis of collective behaviour

Talaga and Nowak (2019) and also examined the ex-

tent of homophily necessary to accurately represent

typical social networks by combining it with a ran-

dom edge rewiring. They concluded that homophily

plays a crucial role in generating social networks and

is versatile to be applied across various social struc-

tures.

3 DESCRIPTION OF

CONTEXTUAL NETWORK

MODELS IN THE STUDY

Based on the characteristics of social networks and

related works, we provide a guideline for generating a

context-based network by leveraging individual-level

attributes from a synthetic population.

3.1 Determining Homophilic

Preferences

The model applies the concept of homophily

where similarity positions individuals closer to each

other (Hamill and Gilbert, 2009). Social distance

is explicitly incorporated by computing pairwise dis-

tances between agents. People in proximity are pre-

ferred over remote agents during the initial network

generation process to ensure homophilic preferences

for social relations. Depending on the type of at-

tribute (categorical or metric), appropriate similarity

measures like the Euclidean distance or the Jaccard

index are applied.

Although geographic location may be considered

as the most fundamental form of homophily (McPher-

son et al., 2001), the introduction of new means of

digital communication may have dampened this ef-

fect (Kaufer and Carley, 1984). To incorporate the

increasing relevance of digital interaction patterns,

we exclude location-dependent attributes for one part

(∼10%) of the overall edges in the network.

The average personal network sizes range from

69 to 109 individuals, with large conﬁdence intervals

making it challenging to determine the exact size of

a network (Lindenfors et al., 2021). This information

can be used to parameterize a fat-tailed distribution,

enabling the sampling of personal network sizes for

each agent. By incorporating personal network size

as an individual-level attribute during the similarity

computation, an assortative bias can be integrated into

the network.

3.2 Incorporating Transitivity

To capture the transitive tendency of social relations,

the process begins by adding a subset of edges to the

ﬁnal graph, referred as the inner circle, which repre-

sents the closest contacts for each agents. This sub-

set can then be used to enhance the similarity for any

node x that is connected to node z through a path with

length = 2 without repeated edges. In other words,

the likelihood of nodes x and z forming a relation in

the following step is increased if they share a common

node y in their neighborhood.

This is done to avoid what Arentze et al. call

“a problem of endogeneity”. Incorporating transitiv-

ity into the network generation process requires in-

formation on mutual connections or common friends.

However, identifying these connections is only possi-

ble after the network has been created (Arentze et al.,

2012, 2013), as they depend on the existing relation-

ships between nodes. A multi-step procedure thus al-

lows the identiﬁcation of transitivity-enhancing con-

ICAART 2025 - 17th International Conference on Agents and Artiﬁcial Intelligence

344

nections by identifying common connections of two

agents. The remaining contacts, referred to as the

outer circle, are then added based on the updated sim-

ilarities, with edges iteratively added between agents

exhibiting the highest similarity.

3.3 Social Network Constraints

To construct a realistic network, the approach pre-

sented so far has to adhere to the constraints listed

in section 2 (Hamill and Gilbert, 2009). Many of

these constraints can be directly addressed by choos-

ing an appropriate edge distribution (or personal net-

work size distribution). We chose a gamma distribu-

tion, which requires shifting and scaling to align with

typical network sizes (Lindenfors et al., 2021). This

way a low network density can be achieved, though

the exact magnitude of network density is directly in-

ﬂuenced by the examined population size, as the sam-

pled network sizes represent absolute rather than rel-

ative values. However, this effect can be neglected

when working with sufﬁciently large populations.

The applied parameterized gamma distribution ex-

hibits a fat-tail, while simultaneously limiting the

probability of extraordinary high values. Sampling

from this distribution yields personal networks that

vary in size, exhibit a fat-tail distribution, show a low

density for typical population sizes, and have a practi-

cal size limit due to increasingly unlikely probabilities

for higher values.

Assortativity represents one of the main properties

that differentiates established network models, such

as Preferential Attachment, from models focused on

the representation of social relations. At its core, as-

sortativity describes a homophilic preference of nodes

to connect to other nodes with a similar degree. This

allows us to incorporate the node degree into the sim-

ilarity computation as described in section 3.1. By

adjusting the weight of this attribute when calculating

similarities, the ﬁnal network can be made more or

less assortative.

As clustering and transitivity represent two

closely related topics in graph theory (Schank and

Wagner, 2005), our iterative implementation of the

inner and outer circle results in an improved global

clustering coefﬁcient compared to approaches with-

out transitivity during the network generation process.

Communities are characterized by a high local

clustering coefﬁcient, while being only loosely con-

nected to the networks remaining nodes. This loose

connection to other nodes primarily depends on the

distribution of the agents attributes. By employing

similarity measures such as the Jaccard index, these

loose connections can be emphasized, in contrast to

the more uniform connections expected by the Eu-

clidean distance. This works because we apply the

Jaccard index as a binary similarity coefﬁcient that

produces polarized similarity values ∈ {0, 1}. Ulti-

mately, the resulting community structure of the ﬁ-

nal network, heavily depends on whether such struc-

tures exist in the provided attribute distribution of the

agents.

Short path lengths are realized by including digi-

tal relations in the similarity computation. These re-

lations, which form independently of location, tend

to connect distant clusters of agents, as they are not

constrained by spatial proximity.

Reciprocity can be simply implemented by adding

the inverse edge for each contact, ensuring that the

relationships are always mutual.

4 USE CASE: INFORMATION

DIFFUSION

To illustrate the impact of network structure on model

behaviour, transmission processes such as informa-

tion diffusion or disease spreads are well suited. We

demonstrate the effects of this network generation ap-

proach with a synthetic population simulating infor-

mation diffusion using a SIR model.

4.1 Synthetic Population Generation

Synthetic populations, simulated to mimic real popu-

lations, are pivotal in research, especially microsimu-

lation, providing substitutes for real data due to cost

and privacy issues. They facilitate detailed individual-

level modeling and analysis when direct data access is

limited or too expensive to obtain (Barthelemy and

Toint, 2013). Commonly generated using Iterative

Proportional Fitting (IPF), synthetic populations align

aggregated data with speciﬁc sociodemographic at-

tributes (Frick, 2004) such as age, gender and house-

hold location (Cajka et al., 2010). These attributes

ensure accurate representation but may be limited by

available data.

We use a synthetic population to generate a re-

alistic social network, requiring detailed information

about individuals. Our example population is based

on Kaiserslautern, Germany, with about 100,000 peo-

ple, based on 2011 census data and household grids.

We apply to assign workplaces, schools, and kinder-

gartens to each person. Using synthetic populations

enhances credibility compared to randomly generated

ones and alleviates privacy concerns, as no personal

data is involved. An exemplary excerpt with three

households is shown in Table 1.

Who Knows Who: A Context-Based Approach to Network Generation for Social Simulations

345

4.2 Simulating Information Diffusion

Using Epidemic Models

Information Diffusion (ID) is the ﬂow of informa-

tion between entities in a network (Li et al., 2017),

similarly to disease contagion that involves suscepti-

ble nodes and active spreaders. Infection dynamics

are characterised by state transitions between differ-

ent groups. The most typical model of contagion is

the Susceptible-Infectious-Removed Model (SIR)(Li

et al., 2017), which will be used in this example.

This model class proves to be quite versatile, be-

cause the slight modiﬁcations to the groups and tran-

sition processes between them are allowing to adapt

the model to various scenarios. Some models within

this class incorporate additional agent groups, such

as an exposed (E) group (e.g. the SEIR model), pro-

viding a more precise representation of speciﬁc pro-

cesses.

4.3 Agent-Based Model for Evaluation

Epidemic models like the SIR model, are easy to ap-

ply to information diffusion use cases (Li et al., 2017).

An initial set of infectious agents start the process by

infecting (informing) each of their immediate neigh-

bors in the network. Each susceptible (uninformed)

neighbor then adopts the information with a global

probability P

, or rejects it. If the information is

adopted, the agent becomes infectious (informed) and

spreads the information to all immediate neighbors in

the following simulation step (t +1). Such agents can

switch groups once more by being removed. In this

state, the agent is neither spreading the information

nor is susceptible to it.

We focus on the examination of differences in

model behaviour based on the underlying graph struc-

ture. The main independent variable is the type of

network: the proposed context network, as well as

three classical network models: Erd

os-R

enyi (ran-

dom) (Newman et al., 2002), Barab

asi–Albert (Pref-

erential Attachment) (Barab

asi and Bonabeau, 2003)

and Watts–Strogatz (Small World) (Watts and Stro-

gatz, 1998). Besides that, the inﬂuence of the SIR

model parameters will be observed. To avoid parame-

ter conﬁgurations obscuring differences between the

network models, each of the SIR parameters is in-

Table 1: Excerpt of synthetic population for Kaiserslautern.

household person

id size location type id age gender workplace

1400 3 7.76 49.46 Couple with child(ren) 2578 33 Female

2579 37 Male 2071

2580 7 Male

3900 1 7.77 49.44 Single Person Household 7224 52 Female 1851

6900 2 7.75 49.43 Couple, no children 12675 43 Female 1808

12676 50 Male 669

Table 2: Levels of independent variables.

Variable Level 1 Level 2 Level 3 Level 4

Network Model Context Random Pref. Attach. Small-World

Initially Infected 0.01% 0.1% 1%

Infection Probability 0.0001 0.001, 0.01

Recovery Probability 0.001 0.01 0.1

cluded as independent variables in the experiment de-

sign: the infection probability, P

∈ [0, 1] , recovery

probability P

∈ [0, 1], and the amount of initially in-

fected nodes i ∈ [0, 1] at t = 0. The dependent vari-

ables include the temporal evolution of SIR states,

providing insights into the pattern of the infection

spread on different network graphs. The simulation

experiment uses a factorial design documented in Ta-

ble 2, for a total of 324 combinations. Each parameter

conﬁguration was simulated for 10 iterations to mini-

mize the effect of random ﬂuctuations.

5 SIMULATION RESULTS AND

EVALUATION

The ﬁrst evaluation metric is ensuring the correct

properties of the proposed network model, especially

in comparison to alternative approaches. The results

of the experimental comparison are summarised in

Table 3. The context network model achieves most

of the observed real-world characteristics.

Table 3: Summary of characteristics of examined network

models based on (Hamill and Gilbert, 2009).

Context Random Pref. Attach. Small-World

Low density ! ! ! !

Ego network size limited ! ! # !

Variation in ego network size ! Limited ! Limited

Fat-tail ! # ! #

Assortative ! # # #

High clustering ! # # !

Small-world effect ! ! ! !

The distribution of edges varies drastically be-

tween the different network models. Table 4 refer-

ences the measured properties of node degrees. The

context network model (CNM), in contrast to other

models, can reach a minimum of 4 edges for an agent.

Agents with such a low degree can lead to infections

(information spreading) not reaching all parts of the

graph, thus leading to a higher number of agents re-

maining susceptible (uninformed) at the end of the

simulation.

Figure 1 showcases how the network model im-

pacts diffusion dynamics, in particular regarding the

timing and magnitude of the peak of infections. In

particular, the CNM reaches a lower peak than the

other models, and a slower decline of infections (in-

formation spreading). This ﬁgure shows the results

for an infection probability (deﬁned as θ) of 0.001,

ICAART 2025 - 17th International Conference on Agents and Artiﬁcial Intelligence

346

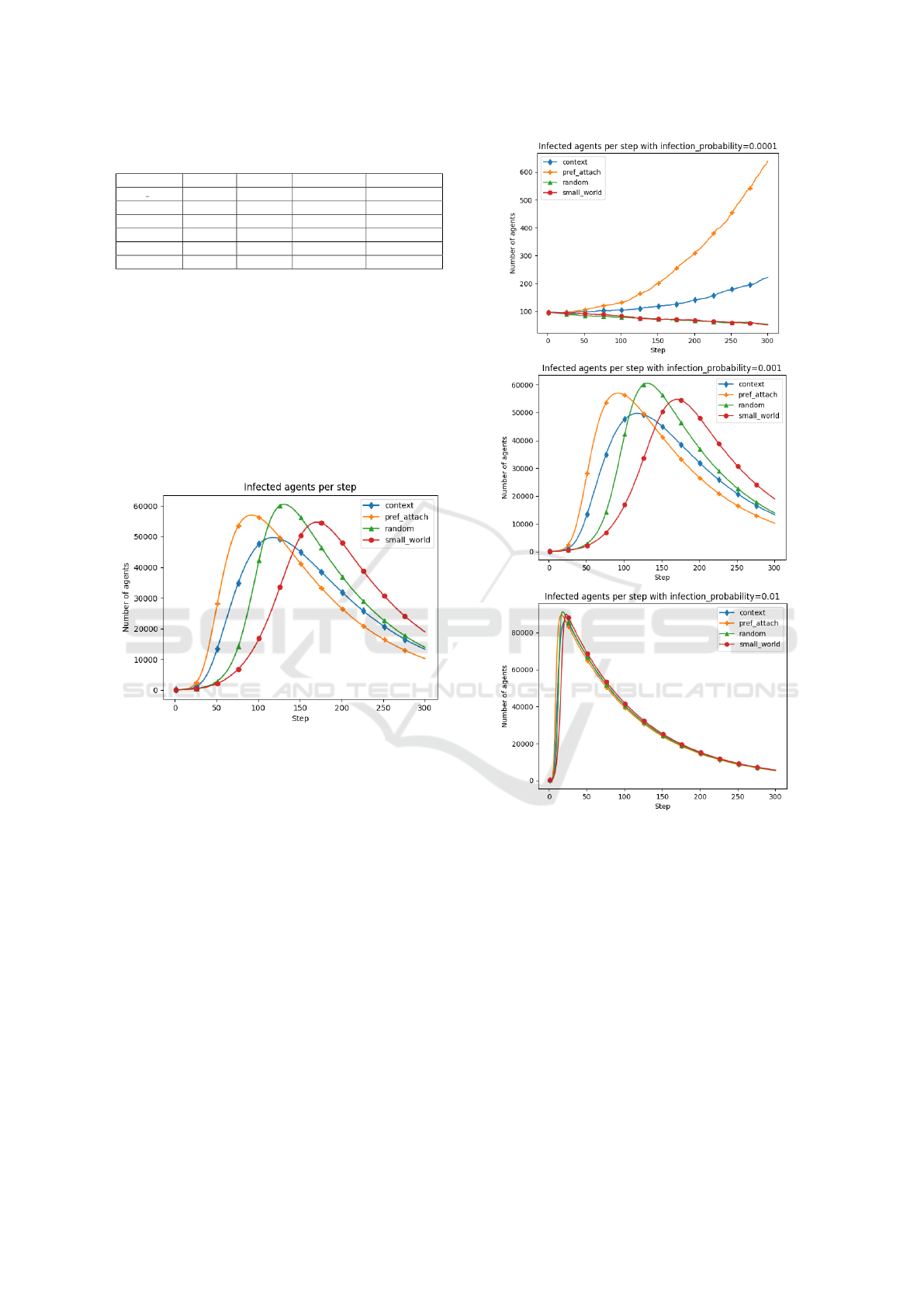
Table 4: Properties of edge distribution.

Context Random Pref. Attach Small-World

num edges 4516587 4516016 4498708 4500824

mean 92 92 92 92

std 41 10 111 2

min 4 55 46 82

max 313 137 3454 102

median 87 92 65 92

and those for other θ values of 0.0001 and 0.01. The

results are summarised in Figure 2. For a low θ, the

major ﬁnding is the existence of a critical threshold

min

required for the maintenance of infection dy-

namics. For a high infection probability θ, the dif-

ferences between the networks are visually indistin-

guishable, with a positively right-skewed distribution

mainly determined by the recovery rate. When sim-

ulating with parameter conﬁgurations close to those

thresholds, the network structure can signiﬁcantly in-

ﬂuence the course of the model.

Figure 1: Infected per step for infection probability 0.001.

Further, Figure 3 displays another important prop-

erty of the different network models: altered state

transitions in the SIR model. The context model

retains some agents in the susceptible (uninformed)

state at the end of the simulation - this suggests that

there are clusters of agents that were not reached by

the infections (information), likely due to the exis-

tence of agents with few edges as shown in Table 4.

This is an important observation for different use

cases in which the rate of spread and the connectiv-

ity of all nodes are critical factors. As a particu-

lar example, crisis communications and other time-

sensitive application areas are relevant: on a realis-

tic network model, information cannot spread sufﬁ-

ciently fast across the entire network and peer-to-peer

communication may not be suited to reach all agents

in the network. The initial structure of such a network

could greatly impact the results of emerging com-

munication topologies (Banerjee et al., 2020). Sim-

ilarly, in contexts where interventions on an existing

Figure 2: Side-by-Side comparison of infectious agents for

infection probabilities 0.0001 , 0.001 and 0.01.

network intend to either accelerate or slow down the

spread of a transmission, the network topology im-

pacts the effect of the analysed measures.

6 CONCLUSION AND OUTLOOK

The generation of realistic synthetic populations for

social simulations is a recurrent topic, often inves-

tigated in regards to the properties of resulting net-

works, rather than the impact of different topolo-

gies on model behaviour. This work proposes the

context-based network model, integrating concepts

derived from social sciences. Unlike traditional ap-

Who Knows Who: A Context-Based Approach to Network Generation for Social Simulations

347

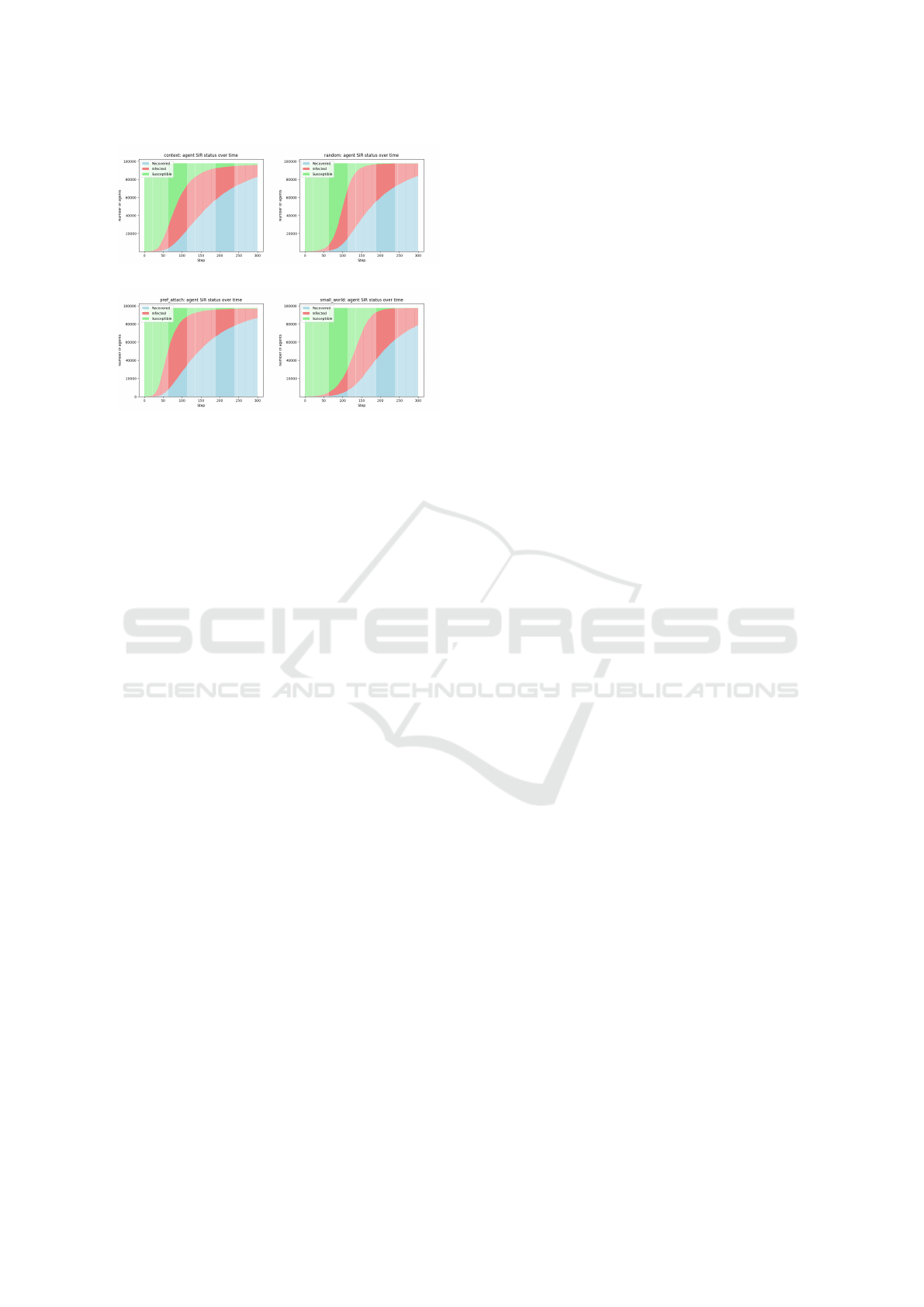
(a) (b)

Figure 3: Comparison of state transitions in each step for

(a) Context model, (b) Random network, (c) Preferential

Attachment and (d) Small-World.

proaches relying on random or probabilistic deci-

sions, the CNM plausibilizes network generation by

combining applicable concepts, like homophily or

transitivity, with sociodemographic information ob-

tained from a synthetic population. The incorporation

of a CNM, can improve the validity and transferabil-

ity of results generated by simulation studies.

6.1 Summary of Network Generation

To implement a generation procedure which imposes

a realistic network on a given synthetic population,

two major methods were used: based on empirical re-

search, such as Dunbar’s number (Lindenfors et al.,

2021), a shifted and scaled gamma distribution was

found for which sampling the number of edges per

node exhibits a fat right tail, representing individu-

als with very large ego-networks, while the x-axis

of the distribution is limited to positive integer val-

ues. When applying this distribution on a reason-

ably large node population, a network with a low den-

sity is achieved. As the sampled number of edges

falls within the above described range, the number

of nodes directly impacts the resulting density of the

network. For larger networks, the effect is negligible;

however, when sampling for a relatively small node

population, the absolute number of edges can result

in a network with a higher density.

Assortativity, high clustering and the small-

worldness were implemented using a similarity-based

approach. Social relations exhibit homophilic prefer-

ences, which can be applied to different traits, such

as age, sex and the number of social contacts. By

calculating a weighted similarity matrix, agents with

the highest similarity are connected to each other in

a two-phase process: ﬁrst, a highly clustered, assor-

tative network was formed based on similarity scor-

ing with applicable demographic attributes. Second,

virtual relations were included by removing locations

from the similarity computation to create location-

independent relations taking place in digital spaces.

This two-phase process establishes a small-world ef-

fect in the network.

When dealing with homogeneous anonymous

nodes lacking differentiating factors, applying an ap-

propriate edge distribution can achieve half of the de-

sired social network characteristics. Applying reshuf-

ﬂing algorithms, such as the assortativity tuning al-

gorithm by Xulvi-Brunet and Sokolov (2004), further

reﬁnes the network to mirror real-world social net-

work properties. This enables the development of a

more efﬁcient and versatile model, suitable for diverse

social network modeling requirements, without ne-

cessitating in-depth domain-speciﬁc knowledge about

social relations.

6.2 Summary of Statistical Properties

While the examination of networks is not entirely

novel, as already explored e.g. by Badham and

Stocker (2010), the comparison of a realistic net-

work against established classics presents a further

contribution towards understanding the impact of net-

work topology on social dynamics in artiﬁcial soci-

eties. The evaluation of the CNM was thus compared

against three classic network models: Erd

os-R

enyi,

Barab

asi–Albert and Watts–Strogatz (random, pref-

erential attachment, small-world, respectively). The

models were compared in the context of an epidemic

spread simulation, using the SIR model to observe the

impact of the network on diffusion dynamics.

The structural comparison between the graphs in-

dicated varying standard deviations regarding edge

distributions, with the CNM ranking in between the

more tightly clustered models (random and small-

world) and the more spread out preferential attach-

ment model. These factors entailed observable dif-

ferences in the simulation results. The higher stan-

dard deviation and assortativity of the CNM led to

an early peak infection (spread) rate with more sus-

ceptible agents at the end of the simulation. The

earlier peaks can be attributed to the higher degree

of some nodes compared to the random and small-

world models, while the remaining susceptible (unin-

formed) agents are due to weakly connected nodes,

with a degree signiﬁcantly lower than the mean.

When analyzing variations of selected simulation

parameters (speciﬁc scenarios for infection, recovery

probability, etc.), the degree distribution proved to

ICAART 2025 - 17th International Conference on Agents and Artiﬁcial Intelligence

348

be more impactful. Due to the higher connectivity

of some nodes, the infection rate of the CNM and

preferential attachment model increases under spe-

ciﬁc scenarios (e.g. low infection probability). In

contrast, the infection (information spread) fades out

relatively quickly for the random and small-world

models. These threshold values, drastically impact

the course of the infection and should thus be consid-

ered when developing a simulation model. Other sce-

narios (e.g. high infection probability) minimize the

observable differences between the models, but keep

their ordinal structure regarding the statistical mea-

sures (mean, standard deviation, etc.) intact.

6.3 Challenges and Further Work

The presented CNM, assumes homophily as the dom-

inant force affecting the structure of social relations.

In reality, many more concepts inﬂuence relation for-

mation, some of which were considered and inte-

grated during this work (e.g. reciprocity, transitivity),

while others like communities remain unattended.

Identifying and integrating each relevant factor, with-

out them interfering, remains a challenging task. Each

additional concept increases the technical and compu-

tational complexity, and should thus only be included,

if it is inherently relevant for the research task and

does not interfere with already incorporated concepts.

Depending on the size of the network to compute, a

revised similarity calculation approach (less compar-

isons, GPU Cluster, parallelization, etc.) might be

needed to reduce computation time and space con-

straints.

Reciprocity was assumed for this network, yet un-

reciprocated relations can be needed for some use

cases. The proposed CNM can be easily adapted to

support such relations by utilizing a directed graph.

Due to the symmetry of the applied distance mea-

sures, most relations that form within the network are

reciprocated, as both agents initiate an edge connec-

tion. However, some relations form unilateral, as one

of the connected agents is not included in the most

similar agent list of the other. In a directed graph,

this would result in an unreciprocated relation with

a directed edge. The social circles model provides

an example of unreciprocated relations with differ-

ent social reaches among agents(Hamill and Gilbert,

2009). The impact of such unreciprocated relations

offers grounds for further examination.

Finally, the experiment results imply the existence

of isolated nodes in the CNM (see Figure 3. For fur-

ther understanding of these network structures, an in-

depth examination is required to identify if remaining

susceptible agents are evenly spread throughout the

network, or if they are clustered together in commu-

nities. Given the emphasis on the importance of such

isolated graph components for practical use case ap-

plications, it is crucial to not only look at aggregate-

level results, but also at the agent-level dynamics dur-

ing individual simulation runs. This is particularly

important when evaluating the realism of a simula-

tion – while most models can yield a realistic top-level

behaviour after calibration to replicate real world ob-

servations, the underlying causes generating these ef-

fects are not studied closer when validating via pa-

rameter ﬁtting. Assuming that most reasonable mod-

els can be calibrated to produce realistic output, the

aggregated observations alone are not sufﬁcient to

analyse the structural differences and emergent ef-

fects leading to these results.

Instead of comparing different networks based on

their ability to replicate real data, analysis should

rather focus on the process and characteristics of the

approach, such as network resilience in case of node

failures, the impact of particular network generation

steps or the impact of evolving social networks over

the course of the simulation.

Overall, the CNM is an approach using little ac-

tual domain knowledge and expert input, which cre-

ates a social network for a given synthetic population

that mirrors real-life characteristics while maintaining

relevant traits such as shared activities and locations.

The inclusion of further traits for similarity compu-

tation and adjustment of parameters for the distribu-

tion of edges among nodes allows for a high degree

of customization ﬁt for different use cases, types of

networks and available agent data.

ACKNOWLEDGEMENTS

This work is part of the results of GreenTwin Project,

funded by the Federal Ministry for the Environment,

Nature Conservation, Nuclear Safety and Consumer

Protection (BMUV) (Grant No. 67KI31073C)

REFERENCES

Arentze, T., Berg, P., and Timmermans, H. (2012). Mod-

eling social networks in geographic space: Approach

and empirical application. Environment and Planning

A, 44.

Arentze, T., Kowald, M., and Axhausen, K. W. (2013).

An agent-based random-utility-maximization model

to generate social networks with transitivity in geo-

graphic space. Social Networks, 35(3):451–459.

Badham, J. and Stocker, R. (2010). The impact of network

Who Knows Who: A Context-Based Approach to Network Generation for Social Simulations

349

clustering and assortativity on epidemic behaviour.

Theoretical Population Biology, 77(1):71–75.

Banerjee, I., Warnier, M., and Brazier, F. M. T. (2020).

Self-organizing topology for energy-efﬁcient ad-hoc

communication networks of mobile devices. Complex

Adaptive Systems Modeling, 8(1):7.

Barab

asi, A.-L. and Bonabeau, E. (2003). Scale-free net-

works. Scientiﬁc american, 288(5):60–69.

Barab

asi, A.-L. and Albert, R. (1999). Emergence of scal-

ing in random networks. Science, 286(5439):509–

512.

Barthelemy, J. and Toint, P. L. (2013). Synthetic population

generation without a sample. Transportation Science,

47(2):266–279.

Bruggeman, J. (2013). Social Networks: An Introduction.

Routledge.

Cajka, J. C., Cooley, P. C., and Wheaton, W. D. (2010).

Attribute assignment to a synthetic population in sup-

port of agent-based disease modeling. Methods Rep

RTI Press, 19(1009):1–14.

Caux, R. D., Smith, C., Kniveton, D., Black, R., and Philip-

pides, A. O. (2014). Dynamic, small-world social

network generation through local agent interactions.

Complex., 19:44–53.

Conti, M., Passarella, A., and Pezzoni, F. (2011). A model

for the generation of social network graphs.

Cook, K. S. and Emerson, R. M. (1987). Social exchange

theory.

Dorogovtsev, S. and Mendes, J. (2003). Evolution of

Networks: From Biological Nets to the Internet and

WWW. Oxford University Press.

Frick, M. (2004). Generating synthetic populations using

ipf and monte carlo techniques: Some new results. Ar-

beitsberichte Verkehrs-und Raumplanung, 225.

Hallinan, M. T. (1978). The process of friendship forma-

tion. Social Networks, 1(2):193–210.

Hamill, L. and Gilbert, N. (2009). Social circles: A sim-

ple structure for agent-based social network models.

Journal of Artiﬁcial Societies and Social Simulation,

12(2):3.

Kapeller, M. L., J

ager, G., and F

ullsack, M. (2019). Ho-

mophily in networked agent-based models: a method

to generate homophilic attribute distributions to im-

prove upon random distribution approaches. Compu-

tational Social Networks, 6:1–18.

Kaufer, D. S. and Carley, K. M. (1984). Communication at

A Distance: The Inﬂuence of Print on Sociocultural

Organization and Change. Routledge, New York, 1st

edition. Subjects: Education, Humanities.

Kerr, C. C., Stuart, R. M., Mistry, D., Abeysuriya, R. G.,

Rosenfeld, K., Hart, G. R., N

nez, R. C., Cohen,

J. A., Selvaraj, P., Hagedorn, B., et al. (2021). Co-

vasim: an agent-based model of covid-19 dynam-

ics and interventions. PLOS Computational Biology,

17(7):e1009149.

Khorshidi, M. S., Nikoo, M. R., Al-Rawas, G., Bahrami,

N., Al-Wardy, M., Talebbeydokhti, N., and Gan-

domi, A. H. (2024). Integrating agent-based model-

ing and game theory for optimal water resource allo-

cation within complex hierarchical systems. Journal

of Cleaner Production, 482:144164.

Krackhardt, D. (2003). The Strength of Strong Ties: The

Importance of Philos in Organizations. In Networks

in the Knowledge Economy. Oxford University Press.

Li, M., Wang, X., Gao, K., and Zhang, S. (2017). A survey

on information diffusion in online social networks:

Models and methods. Information, 8(4):118.

Lindenfors, P., Wartel, A., and Lind, J. (2021). Dun-

bar’s number deconstructed. Biology Letters,

17(5):20210158. Epub 2021 May 5.

Lorig, F., Johansson, E., and Davidsson, P. (2021). Agent-

based social simulation of the covid-19 pandemic: A

systematic review. Journal of Artiﬁcial Societies and

Social Simulation, 24(3):5.

Marin, A. and Wellman, B. (2011). Social network analy-

sis: An introduction. The SAGE handbook of social

network analysis, pages 11–25.

McPherson, M., Smith-Lovin, L., and Cook, J. M. (2001).

Birds of a feather: Homophily in social networks. An-

nual review of sociology, 27(1):415–444.

Newman, M. E. J., Watts, D. J., and Strogatz, S. H.

(2002). Random graph models of social networks.

Proceedings of the National Academy of Sciences,

99(suppl 1):2566–2572.

Palomo-Briones, G. A., Siller, M., and Grignard, A. (2022).

An agent-based model of the dual causality between

individual and collective behaviors in an epidemic.

Computers in biology and medicine, 141:104995.

Schank, T. and Wagner, D. (2005). Approximating clus-

tering coefﬁcient and transitivity. Journal of Graph

Algorithms and Applications, 9(2):265–275.

Talaga, S. and Nowak, A. (2019). Homophily as a

process generating social networks: insights from

social distance attachment model. arXiv preprint

arXiv:1907.07055.

Watts, D. J. and Strogatz, S. H. (1998). Collective dynamics

of ‘small-world’ networks. Nature, 393(6684):440–

442.

Xulvi-Brunet, R. and Sokolov, I. M. (2004). Reshuf-

ﬂing scale-free networks: From random to assortative.

Phys. Rev. E, 70:066102.

ICAART 2025 - 17th International Conference on Agents and Artiﬁcial Intelligence

350