Slice Reconciliation in Continuous-Variable Quantum Key Distribution

Using Discrete Modulation

Margarida Almeida

1,2 a

, Armando N. Pinto

1,2 b

and Nuno A. Silva

1 c

Instituto de Telecomunicac¸

oes, University of Aveiro, Campus Universit

ario de Santiago, 3810-193 Aveiro, Portugal

Department of Electronics, Telecommunications and Informatics, University of Aveiro, Campus Universit

ario de Santiago,

3810-193 Aveiro, Portugal

{mralmeida, anp, nasilva}@ua.pt

Keywords:

Quantum Key Distribution, Continuous-Variable, Discrete Modulation, Higher-Order Constellations,

Information Reconciliation, Slice Reconciliation, Multidimensional Reconciliation.

Abstract:

Information reconciliation is a critical component of Continuous-Variable Quantum Key Distribution (CV-

QKD) systems. This particular step of the CV-QKD system signiﬁcantly affects the extraction key rate. Pre-

vious studies that incorporate higher-order discrete modulation (DM) while accounting for the information

reconciliation step in the computation of the extraction key rate of CV-QKD systems have focused on multidi-

mensional reconciliation. However, higher-order DM formats, such as 64-Quadrature Amplitude Modulation

(QAM), enable higher signal-to-noise ratios (SNRs) where slice reconciliation is known to outperform mul-

tidimensional reconciliation. In this work, we compare the performance of multidimensional reconciliation

and slice reconciliation in DM-CV-QKD systems. Our ﬁndings demonstrate that slice reconciliation delivers

superior performance at metropolitan distances. At 20 km, using slice reconciliation with 3 slices of code

rates 0, 0.01, and 0.6 increases the key rate by more than 400 times when compared to multidimensional

reconciliation with a code rate of 0.05. This signiﬁcant performance boost more than compensates for the

higher computational time associated with slice reconciliation. With the proper optimization of the number of

slices, and of the code rate per slice, slice reconciliation is a valid option for real-world implementations of

DM-CV-QKD systems using higher-order constellations.

1 INTRODUCTION

Quantum Key Distribution (QKD) is a revolution-

ary technique to ensure the secure communication

between two distant parties without relying on any

computational assumption (Pirandola et al., 2020).

In that sense, QKD guarantees unconditional secu-

rity by exploiting the inherent properties of quantum

states (Pirandola et al., 2020). In the ﬁeld of quan-

tum cryptography, Continuous-Variable (CV) QKD

has gained signiﬁcant attention due to its compati-

bility with existing telecommunication infrastructure

and its potential for high key rates over metropolitan

distances (Zhang et al., 2019).

In CV-QKD, information is typically encoded in

the quadratures of coherent states using Gaussian

Modulation (GM) (Laudenbach et al., 2018). While

GM has been theoretically proven to be optimal in

https://orcid.org/0000-0003-1812-5971

https://orcid.org/0000-0003-2101-5896

https://orcid.org/0000-0002-6309-6818

terms of key rates, its practical implementation poses

several challenges. This is due to the need for op-

toelectronic modulators with inﬁnite extinction ra-

tios (Liu et al., 2021; Denys et al., 2021) and the com-

plexity of generating truly Gaussian-distributed ran-

dom variables (Liu et al., 2021).

Discrete Modulation (DM) has been proposed as

a practical alternative to GM for real-world imple-

mentations (Leverrier and Grangier, 2011). In DM,

information is encoded using speciﬁc constellations,

such as M-symbol Phase Shift Keying (M-PSK),

which offer experimental simplicity (Ghorai et al.,

2019; Kleis et al., 2017; Lin and L

utkenhaus, 2020).

Notably, higher-order constellations, especially M-

symbol Quadrature Amplitude Modulation (M-

QAM), can approach the performance of GM (Denys

et al., 2021). Experimental demonstrations of

64-, 256-, and 1024-QAM for CV-QKD have been re-

ported in (Roumestan et al., 2021a; Roumestan et al.,

2021b). However, like most CV-QKD implementa-

tions, these experiments omitted the critical step of in-

Almeida, M., Pinto, A. N. and Silva, N. A.

Slice Reconciliation in Continuous-Variable Quantum Key Distribution Using Discrete Modulation.

DOI: 10.5220/0013142200003902

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 13th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2025), pages 79-86

ISBN: 978-989-758-736-8; ISSN: 2184-4364

formation reconciliation. As a result, the reported key

rates do not accurately reﬂect the actual performance

of the system in a real-world scenario (Almeida et al.,

2023a; Almeida et al., 2023b).

In the information reconciliation step, Alice and

Bob correct discrepancies between their respective

measurement outcomes due to noise and other im-

perfections in the quantum channel. The efﬁciency

of this process directly impacts the overall perfor-

mance of the QKD system. Information reconcilia-

tion was proposed for small-order DM-CV-QKD sys-

tems (Leverrier et al., 2008) considering sign rec-

onciliation, originally applied to GM-CV-QKD sys-

tems (Li et al., 2019). In GM-CV-QKD, reconcilia-

tion methods such as multidimensional reconciliation

and slice reconciliation are commonly employed (Li

et al., 2019; Wang et al., 2022; Leverrier et al., 2008;

Wen et al., 2021). Multidimensional reconciliation

relies on a transformation step, being particularly ef-

fective for low signal-to-noise ratios (SNRs) due to

its lossless rotation (Wang et al., 2022). On the other

hand, slice reconciliation operates through a quanti-

zation step (Feng et al., 2021), enabling the distilla-

tion of more than one bit per symbol per measured

quadrature, and showing higher efﬁciency at higher

SNRs (Wang et al., 2022; Van Assche et al., 2004).

In (Almeida et al., 2023a; Almeida et al., 2023b),

the impact of the reconciliation efﬁciency and of the

frame error rate (FER) of the information reconcilia-

tion step on the extraction key rate was studied. These

works showed the importance of accounting for the

information reconciliation step when optimizing the

parameters of the system. Notwithstanding, only mul-

tidimensional reconciliation was considered. Since

the use of higher-order DM formats allow for higher

SNRs, it is of the most importance to study the impact

of slice reconciliation on the extraction key rate of

DM-CV-QKD systems. Remark that in (Yang et al.,

2023) a comparison between multidimensional recon-

ciliation and slice reconciliation is provided consid-

ering only Gaussian modulation, and not DM. This

through the comparison of state-of-the-art works us-

ing only one of the reconciliation methods in differ-

ent conditions. Moreover, (Yang et al., 2023) com-

pares both reconciliation methods regarding only the

information reconciliation step, and not the extraction

key rate. Here we compare how the performance of

multidimensional and slice reconciliation affect the

extraction key rate of DM-CV-QKD systems, under-

standing which method is the most beneﬁcial for DM-

CV-QKD systems in each SNR scenario. With this

study we intend to bridge the gap between theoretical

performance and real-world applicability, paving the

way for more robust and efﬁcient quantum communi-

cation systems. From the results, slice reconciliation

is a valid candidate for the reconciliation of keys in

CV-QKD systems using higher-order DM, allowing

for higher extraction rates than multidimensional rec-

onciliation at metropolitan distances.

In the following sections, we provide a detailed

theoretical background on DM-CV-QKD and infor-

mation reconciliation, describing the computation of

the extraction key rate for CV-QKD using higher-

order DM in Section 2. In Section 3 we brieﬂy explain

multidimensional reconciliation and slice reconcilia-

tion. Section 4 is focused on the results of the study

and their discussion. Finally, Section 5 presents the

ﬁnal conclusions.

2 KEY RATE FOR CV-QKD

USING HIGHER-ORDER

CONSTELLATIONS

A CV-QKD system can be divided into two pri-

mary components: the physical layer and the post-

processing layer. The physical layer is responsible

for the exchange of quantum states over the quantum

channel between the two parties, typically referred to

as Alice (the sender) and Bob (the receiver). Here, the

quantum channel is considered to be optical ﬁber. The

post-processing layer encompasses the critical steps

of parameter estimation, information reconciliation,

and privacy ampliﬁcation. This layer ensures that the

keys generated are identical, secure, and free from

eavesdropping.

In DM-CV-QKD, the quantum coherent states are

given by speciﬁc points in a constellation diagram.

The constellation points are geometric and proba-

bilistic shaped to optimize the performance of the

system. In this work, we use 64-QAM following

the Boltzmann-Maxwell distribution for probabilistic

shaping to approximate the optimum performance of

GM (Denys et al., 2021; Roumestan et al., 2021b;

Almeida et al., 2023a). The in-phase and quadrature

points of the 64-QAM constellation are deﬁned by

|α

k,l

| = (k + il)

)/(2

∑

k,l

√

+ l

) with k, l

equidistant values between -1 and 1, V

the modula-

tion variance, and P

k,l

= exp



−ν(k

+ l

)



∑

k,l

the probability of the states under the Boltzmann-

Maxwell distribution. The parameter ν is optimized

to maximize the secret key rate.

The secret key rate, K, of a DM-CV-QKD system

is given by:

K =

[βI

−χ

−∆(n)], (1)

where I

is the mutual information between Bob and

PHOTOPTICS 2025 - 13th International Conference on Photonics, Optics and Laser Technology

Alice computed considering DM (Essiambre et al.,

2010), χ

is the Holevo bound between Bob and Eve

considering heterodyne detection, reverse reconcilia-

tion and collective Gaussian attacks, computed fol-

lowing (Becir et al., 2012), β is the reconciliation ef-

ﬁciency, and ∆(n), computed from (Leverrier et al.,

2010), accounts for the ﬁnite-size effects, consider-

ing the close approximation between 64-QAM and

GM (Roumestan et al., 2021a). The ratio

accounts

for the fact that N −n states are reserved for parame-

ter estimation. The computation of χ

involves the

Z parameter, which is deﬁned as (Denys et al., 2021)

Z = 2



1/2

ˆaτ

1/2

ˆa

†



−

ξW. (2)

Here T

is the channel’s transmission, ξ

is the excess noise, Tr (·) is the trace of ·,

τ =

∑

k,l

|α

k,l

⟩⟨α

k,l

| is the density matrix

describing the average state sent by Alice,

W =

∑

k,l



⟨α

k,l

|ˆa

†

ˆa

|α

k,l

⟩−|⟨α

k,l

|ˆa

|α

k,l

⟩|



ˆa

= τ

1/2

ˆaτ

−1/2

, and ˆa and ˆa

†

are the annihilation

and creation operators on Alice’s system, respec-

tively. Due to the ﬁnite-size effects, the values of

and ξ are adjusted to their respective lower and

upper bounds with a probability of at least 1 −ε

respectively (Leverrier et al., 2010).

The reconciliation efﬁciency β ensures that only

the correct amount of information is extracted, pre-

venting potential security breaches. The FER is

another critical metric, indicating the proportion of

frames that remain uncorrected after the reconcilia-

tion step. The FER parameter is used to compute the

ﬁnal extraction key rate of the system, given by

extraction

(1 −FER)[βI

−χ

−∆(n)]. (3)

3 RECONCILIATION OF

SYMMETRIC KEYS FOR

CV-QKD SYSTEMS

In the post-processing layer, the information recon-

ciliation step ensures that the discrepancies between

Alice’s and Bob’s raw data, X and Y , due to the

noise in the quantum channel are mitigated, leading

to identical keys at Alice’s and Bob’s side. Two of the

most prominent reconciliation methods in CV-QKD

are multidimensional reconciliation and slice recon-

ciliation, each with distinct advantages depending on

the system’s conditions.

Multidimensional reconciliation is particularly ef-

fective in the low SNR environment, by leverag-

ing a lossless rotation of the data points in higher-

dimensional spaces to align Alice’s and Bob’s raw

data. The dimension d of multidimensional recon-

ciliation can take the value of 1, 2, 4 and 8 (Lever-

rier et al., 2008). Due to its improved performance,

here we consider d equal to 8 (Leverrier et al., 2008;

Feng et al., 2021). Multidimensional reconciliation

starts by organizing Alice’s and Bob’s raw data, X and

Y , into 8-dimensional vectors x = (x

,...,x

) and

y = (y

,...,y

), respectively. Bob then generates

a binary random sequence, m, using a true random

number generator and the respective 8-dimensional

sequences u =

√

[(−1)

,(−1)

,...,(−1)

]. To

proceed, Bob computes the rotation matrix M(y,u) =

∑

i=1

(y,u)Q

which maps y into u through

M(y,u)y = u. Here α

(y,u) are the coordinates of

u on the orthogonal basis [Q

y,Q

y,...,Q

y], ob-

tained by doing α

(y,u) =



−1



, with T and Q

de-

tailed in (Leverrier et al., 2008). The rotation matrix

M(y,u) is sent to Alice as side information. By know-

ing M(y,u), Alice can compute the noisy version of u,

v = M(y,u)x. Using the sum-product algorithm, Al-

ice can obtain the best estimate of the binary random

sequence m, thus obtaining the raw binary key. For

such, the log-likelihood ratio for the priori message

probabilities, r

, is given by (Feng et al., 2021)

= −

log



8 + (v

−1)

8 + (v

+ 1)



. (4)

For multidimensional reconciliation, and considering

heterodyne detection, the reconciliation efﬁciency is

given by

, (5)

where R is the code rate of the low-density parity

check (LDPC) matrix used.

On the other hand, slice reconciliation is partic-

ular efﬁcient for higher SNR environments by quan-

tizing the key data into slices. Moreover, it allows

the extraction of more than one bit per symbol per

quadrature, which increases efﬁciency when the chan-

nel conditions are favorable (Wang et al., 2022). Slice

reconciliation starts by quantifying Y into m sets of bi-

nary data, (Y

,··· ,Y

), using a quantization func-

tion Q(y) : R → {0,1}

, as provided in (Wen et al.,

2021). The quantization function is obtained by divid-

ing the set of real numbers into 2

intervals T (Y ), de-

ﬁned by 2

−1 variables τ

,τ

,··· ,τ

−1

. The inter-

val a with 1 ≤a ≤ 2

is deﬁned by the set {x : τ

a−1

≤

x ≤ τ

} where τ

= −∞ and τ

= +∞ (Van Assche

et al., 2004). The 2

intervals, i.e. τ

,τ

,··· ,τ

−1

are equidistant (Wen et al., 2021) and deﬁned by max-

imizing the mutual information between X and T (Y )

(Wang et al., 2022). The best bit assignment method

assigns the least signiﬁcant bit to the ﬁrst slice Q

(y).

Then, each bit is subsequently assigned up to the

Slice Reconciliation in Continuous-Variable Quantum Key Distribution Using Discrete Modulation

most signiﬁcant bit, which is assigned to the last slice

(x) (Van Assche et al., 2004). This ensures that the

ﬁrst slice contains only noisy values that helps Bob

narrow down his guess as quickly as possible. This

ensures that the slices can be corrected with as lit-

tle leaked information as possible. The sum-product

algorithm is applied to each slice at a time. The log-

likelihood ratio for the priori message probabilities,

, is given by (Guo et al., 2020):

= log





∑

a:y

erf



−x

√

2σ



−erf



a−1

−x

√

2σ



∑

′

erf



′

−x

√

2σ



−erf



′

−1

−x

√

2σ







(6)

where x ∈ X are the points of Alice’s discrete con-

stellation, erf(·) is the error function, and σ

T η

ξ+

1 + ξ

thermal

. For slice reconciliation, and considering

heterodyne detection, the reconciliation efﬁciency is

given by (Wang et al., 2022)

2(H(T (Y )) −

∑

i=1

(1 −R

))

, (7)

where R

is the code rate of the LDPC matrix used for

slice i, and (Wang et al., 2022)

H(T (Y )) = −

∑

log

, (8)

where P

a−1

√

2πV

exp



−



, and V

T η

2⟨n⟩ +

T η

ξ + 1 + ξ

thermal

is the variance of Bob’s

states.

4 RESULTS AND DISCUSSION

Through a simulation of a CV-QKD system using 64-

QAM, with multidimensional and slice reconciliation

for the information reconciliation step, we obtained

the FER associated to each reconciliation method for

different SNR values of the CV-QKD system (Fig. 1).

Since differences were found in the relationship be-

tween the FER and the SNR depending on the trans-

mission distance, the simulations were conducted for

discrete transmission distances between 0 and 80 km,

in intervals of 10 km. This differences are due to the

impact of the transmission distance on the noise of the

system and on the optimization of the slice intervals

for slice reconciliation. Due to the high computation

time of the information reconciliation step, only 10

states were considered for the simulation. In Fig. 1,

we present the FER results of the simulations as a

function of the SNR for the different transmission dis-

tances, alongside the respective ﬁt curves. Despite the

simulations being conducted for various possibilities

of code rates for multidimensional reconciliation and

for various combinations of code rates for slice rec-

onciliation, in Fig. 1 we only present results consid-

ering multidimensional reconciliation with code rate

R = 0.05 (Fig. 1a)), slice reconciliation with 2 slices

of code rates R

= 0.05 and R

= 0.4 (Fig. 1b)), and

slice reconciliation with 3 slices of code rates R

= 0,

= 0.01 and R

= 0.6 (Fig. 1c)).

In line with state-of-the-art, multidimensional rec-

onciliation is well ﬁt for smaller SNRs, while slice

reconciliation allows the reconciliation for higher

SNRs (Fig. 1). Remark that slice reconciliation has

associated heights, since each code rate (with a dif-

ferent LDPC matrix) is applied to each slice. From

a practical perspective, it is important to analyze the

role of the reconciliation efﬁciency and of the FER

on the computation of the extraction key rate. This

0 0.1 0.2 0.3 0.4 0.5

Signal-to-Noise Ratio

a) Multidimensional reconciliation (R = 0.05)

100

Frame Error Rate

0 km

10 km

20 km

30 km

40 km

50 km

60 km

70 km

80 km

0 2 4 6 8 10

Signal-to-Noise Ratio

b) Slice reconciliation (2 slices: R

= 0.05, R

= 0.4)

100

Frame Error Rate

0 km

10 km

20 km

30 km

40 km

50 km

60 km

70 km

80 km

0 1 2 3 4 5

Signal-to-Noise Ratio

c) Slice reconciliation (3 slices: R

= 0, R

= 0.01, R

= 0.6)

100

Frame Error Rate

0 km

10 km

20 km

30 km

40 km

50 km

60 km

70 km

80 km

Figure 1: FER as a function of the SNR for different trans-

mission distances, considering (a) multidimensional recon-

ciliation with code rate 0.05, (b) slice reconciliation with 2

slices of code rates 0.05 and 0.4, and (c) slice reconciliation

with 3 slices of code rates 0, 0.01 and 0.6.

PHOTOPTICS 2025 - 13th International Conference on Photonics, Optics and Laser Technology

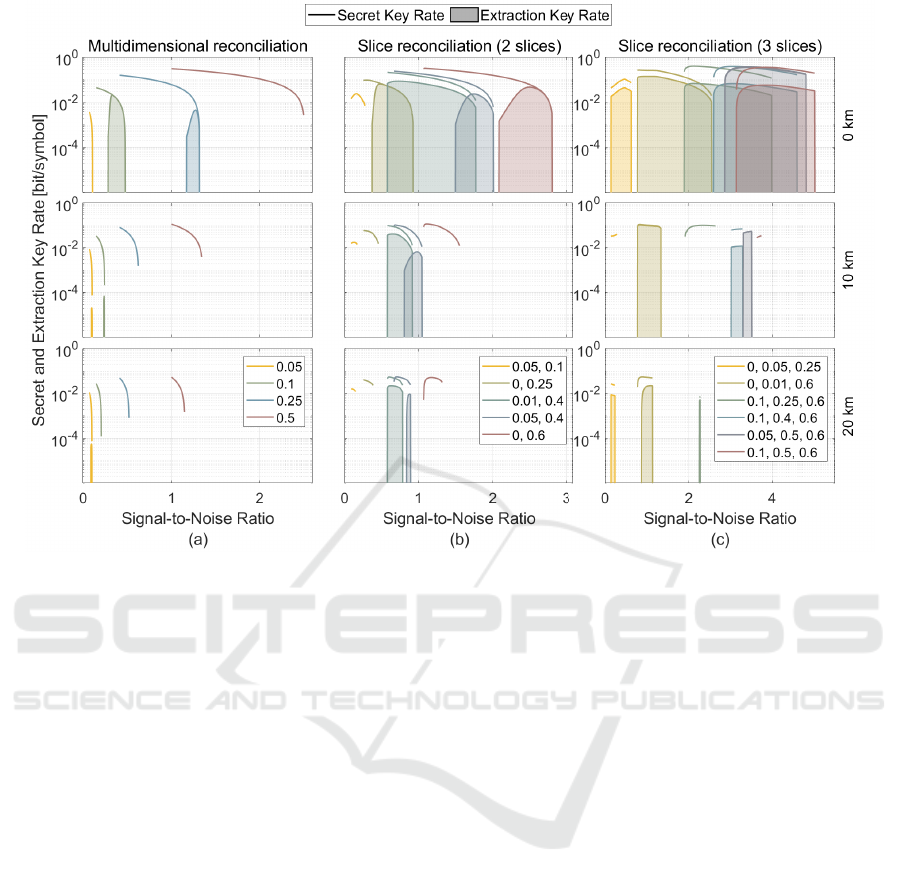
Figure 2: Secret key rate, given by Eq. 1, and extraction key rate, given by Eq. 3, as a function of the SNR for 0, 10 and 20

km, considering (a) multidimensional reconciliation for different code rates, (b) slice reconciliation with 2 slices for different

code rate combinations, and (c) slice reconciliation with 3 slices for different code rate combinations. This considering 10

states exchanged between Alice and Bob for parameter estimation and key extraction, 64-QAM, a transmission coefﬁcient of

0.2 dB/km, a detection efﬁciency η of 0.76, an excess noise ξ of 0.046 SNU, and a thermal noise ξ

thermal

of 0.35 SNU.

for both multidimensional and slice reconciliation. In

that sense, we compare the use of slice reconcilia-

tion with the use of multidimensional reconciliation,

to better understand if the higher correction capabil-

ities of slice reconciliation in the high SNR regime

can be beneﬁcial for the key extraction in CV-QKD

systems using higher-order DM which usually allows

for higher SNR than the low cardinality constellations

initially considered in the literature.

In Fig. 2 we present the secret key rate, given by

Eq. 1, and the extraction key rate, given by Eq. 3, as

a function of the SNR for 0, 10 and 20 km, consider-

ing multidimensional reconciliation for different code

rates (Fig. 2a)), and slice reconciliation with 2 and 3

slices for different code rate combinations (Fig. 2b)

and Fig. 2c)). The extraction key rate was computed

by estimating the FER depending on the SNR using

the ﬁt curves to the results of the simulations of the

CV-QKD system (Fig. 1).

For multidimensional reconciliation, higher code

rates of the LDPC code result in higher secret key

rates, given by Eq. 1, at higher SNRs, due to

the higher reconciliation efﬁciency, computed using

Eq. 5. Notwithstanding, using a LDPC with code

rate 0.5 (the highest code rate considered) does not

allow for any key extraction even in a back-to-back

conﬁguration (Fig. 2a)). This is due to the impact of

the FER on the extraction key rate, given by Eq. 3,

which, for code rate 0.5 is unitary for SNRs below

than 2.5. Decreasing the code rate of the LDPC ma-

trix to a code rate of 0.25 allows key extraction in a

back-to-back conﬁguration, but at smaller rates than

using a LDPC with code rate 0.1. At 0 km, the code

rate 0.1 allows the extraction of 0.02 bit/symbol at an

SNR of 0.33, while the code rate 0.25 can only ex-

tract 0.005 bit/symbol at an SNR of 1.27 (Fig. 2a)).

For higher transmission distances, smaller code rates

of 0.05 and 0.1 must be considered, with the LDPC

matrix of code rate 0.05 allowing key extraction at a

rate of 5.6 ×10

−5

bit/symbol at 20 km for an SNR of

0.09.

Generally, the use of slice reconciliation using 2

slices also allows for higher secret key rates, given

by Eq. 1, at higher SNRs by increasing the sum of

the code rates of the LDPC codes considered for each

slice (Fig. 2b)). The same conclusion cannot be drawn

for slice reconciliation using 3 slices in what concerns

to the secret key rate, with code rate combinations of

0.1, 0.25, 0.6 and 0.1, 0.4, 0.6 achieving higher secret

key rates than code rate combinations of 0.1, 0.5, 0.6

Slice Reconciliation in Continuous-Variable Quantum Key Distribution Using Discrete Modulation

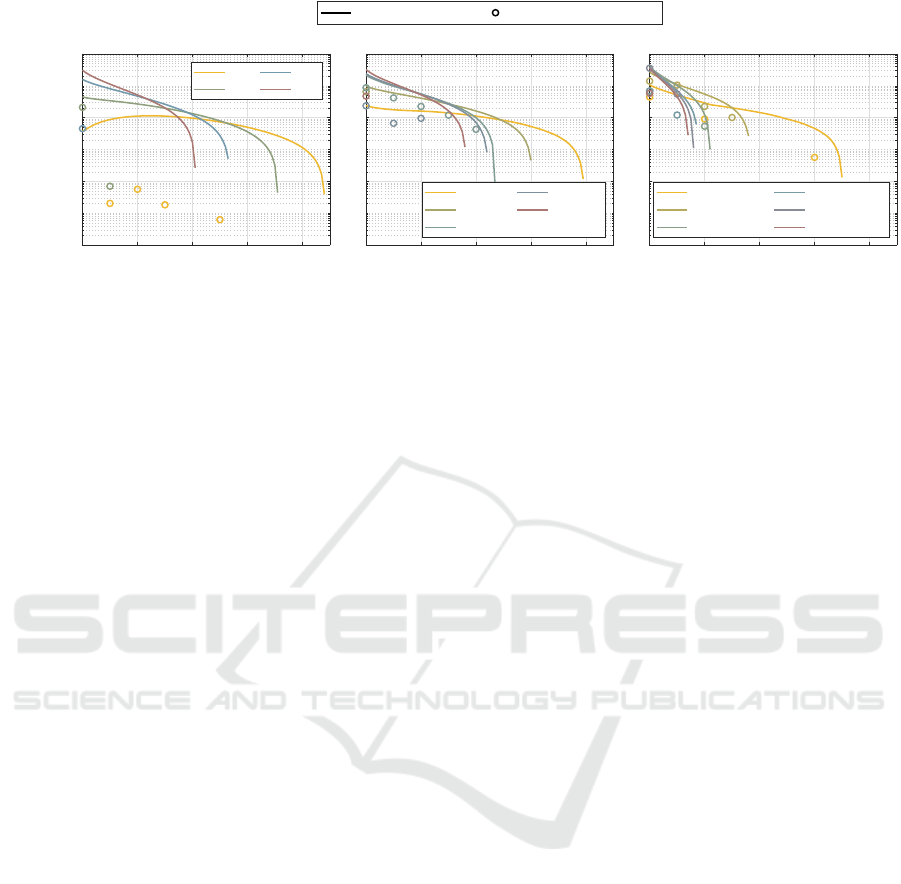
0 20 40 60 80

Transmission Distance [km]

(a)

-6

-4

-2

Secret and Extraction

Key Rate [bit/symbol]

Multidimensional reconciliation

0.05

0.1

0.25

0.5

0 20 40 60 80

Transmission Distance [km]

(b)

-6

-4

-2

Slice reconciliation (2 slices)

0.05, 0.1

0, 0.25

0.01, 0.4

0.05, 0.4

0, 0.6

0 20 40 60 80

Transmission Distance [km]

(c)

-6

-4

-2

Slice reconciliation (3 slices)

0, 0.05, 0.25

0, 0.01, 0.6

0.1, 0.25, 0.6

0.1, 0.4, 0.6

0.05, 0.5, 0.6

0.1, 0.5, 0.6

Secret Key Rate Extraction Key Rate

Figure 3: Secret key rate, given by Eq. 1, and extraction key rate, given by Eq. 3, as a function of the transmission distance

with the SNR optimized, considering (a) multidimensional reconciliation for different code rates, (b) slice reconciliation with

2 slices for different code rate combinations, and (c) slice reconciliation with 3 slices for different code rate combinations.

This considering 10

states exchanged between Alice and Bob for parameter estimation and key extraction, 64-QAM, a

transmission coefﬁcient of 0.2 dB/km, a detection efﬁciency η of 0.76, an excess noise ξ of 0.046 SNU, and a thermal noise

thermal

of 0.35 SNU.

(Fig. 2c)).

The impact of the FER of the information rec-

onciliation step is not as critical for slice reconcilia-

tion as it is for multidimensional reconciliation. In

a back-to-back situation, slice reconciliation with 3

slices of code rates 0.05, 0.5, and 0.6 can extract

0.358 bit/symbol, while slice reconciliation with 2

slice of code rates 0.01 and 0.4 can only extract 0.087

bit/symbol. This corresponds to 17.9 and 4.35 times

more than multidimensional reconciliation with code

rate 0.1. At 10 km and 20 km the key rate ex-

tracted when using slice reconciliation with 3 slices

of code rates 0, 0.01, and 0.6 is 150 times and 402

times greater than using multidimensional reconcilia-

tion with code rate 0.1 and 0.05, respectively (Fig. 2)).

Remark however that, with higher transmission dis-

tances, the range of the SNRs for which key extraction

is possible decreases. This turns the practical imple-

mentation of the CV-QKD system more difﬁcult by

requiring a precise setting of the modulation variance

in the system to ensure the proper SNR depending on

the remaining practical conditions of the system.

In Fig. 3, the secret key rate is presented as a func-

tion of the transmission distances considering mul-

tidimensional reconciliation for different code rates

(Fig. 3a)), and slice reconciliation with 2 and 3 slices

for different code rate combinations (Fig. 3b) and

Fig. 3c)). The secret key rate was maximized con-

sidering an optimization of the SNR. Remark that

smaller code rates for multidimensional reconcilia-

tion, and smaller sums of code rates for the code rate

combinations for slice reconciliation tend to allow a

positive secret key rate for higher transmission dis-

tances (Fig. 3). In this regard, multidimensional rec-

onciliation maximizes the transmission distance for

which the secret key rate is positive, being followed

by slice reconciliation with two slices.

When accounting for the FER in the computation

of the extraction key rate, given by Eq. 3, the use of

slice reconciliation increases the extraction key rate

by several orders of magnitude, for metropolitan dis-

tances up to 60 km. Notwithstanding, one must prop-

erly choose the code rates to use in slice reconcilia-

tion, not only to ensure the maximization of the ex-

traction key rate, but also key extraction, since not all

code rate combinations may allow for key extraction.

Moreover, despite the use of 3 slices generally yield-

ing greater performance in terms of extraction key

rate than the use of 2 slices, one must also consider-

ing the computation time associated to the additional

number of slices because a reduced performance in

terms of extraction key rate may be compensated by

the reduced computation time.

5 CONCLUSION

The impact of the reconciliation efﬁciency and of the

FER of the information reconciliation step must be

accounted on the computation of the extraction key

rate of CV-QKD systems. By comparing the perfor-

mance of multidimensional reconciliation and slice

reconciliation in terms of the extraction key rate in

DM-CV-QKD systems, we show that slice reconcilia-

tion allows for better performances than multidimen-

sional reconciliation for transmission distances up to

60 km. At 0 km and 10 km, slice reconciliation with

3 slices can extract 17.9 and 150 times more bits

PHOTOPTICS 2025 - 13th International Conference on Photonics, Optics and Laser Technology

per symbol than multidimensional reconciliation with

code rate 0.1. This using the code rate combinations

of 0.05, 0.5 and 0.6 at 0 km and 0, 0.01, and 0.6 at

10 km, for slice reconciliation. At 20 km the key rate

extracted when using slice reconciliation with 3 slices

of code rates 0, 0.01, and 0.6 increases to 402 times

the extraction rate when using multidimensional rec-

onciliation with code rate 0.05. Such increase in per-

formance largely compensates the higher computa-

tion time associated to slice reconciliation. Remark

that the information reconciliation step must be opti-

mized to maximize the extraction key rate in DM-CV-

QKD systems. This accounting both for the method

(multidimensional or slice reconciliation), but also for

the code rates used and for the number of slices con-

sidered, in the case of slice reconciliation.

In this study only a reduced number of options

were considered for the code rate combinations for

slice reconciliation with 2 and 3 slices. This mainly

due to high computation time, which results in limited

statistic in the analysis of the FER depending on the

SNR and on the transmission distance. An improved

study should consider the implementation of the in-

formation reconciliation step in the graphics process-

ing unit (GPU) or in a ﬁeld programmable gate array

(FPGA) for increased processing speed. Currently,

the information reconciliation step is implemented in

the central processing unit (CPU), resulting in long

processing times, decreasing the number of the sim-

ulations conducted. With a faster implementation of

the information reconciliation step, the detailed study

of the FER as a function of the SNR should consider

at least 10

states per simulation of the CV-QKD

system for a better statistical analysis, and greater

LDPC matrices, for increased performance. Doing

so, would improve the estimation of the FER consid-

ered for the computation of the extraction key rate,

improving the conclusions on which information rec-

onciliation method is the best ﬁt for a particular CV-

QKD system, depending on the system’s conditions.

Moreover, it would allow the proper assessment of the

critical points or thresholds for the SNR that deter-

mine when the of multidimensional or slice reconcil-

iation is more advantageous. This is especially im-

portant when choosing the code rates that maximize

the key extraction rate of the system. Furthermore,

an improved analysis should considered all possibili-

ties of code rate combinations for slice reconciliation,

and should study the application of slice reconcilia-

tion with more than 3 slices to better understand if the

increase of the number of slices is always beneﬁcial,

or if it exists an optimum number of slices.

ACKNOWLEDGMENTS

This work was supported in part by Fundac¸

ao para

a Ci

encia e a Tecnologia (FCT) through national

funds, by the European Regional Development Fund

(FEDER), through the Competitiveness and Inter-

nationalization Operational Programme (COMPETE

2020) of the Portugal 2020 framework, under the

PhD Grant UI/BD/153377/2022, and co-funded by

the European Defence Industrial Development Pro-

gramme (EDIDP) under the project DISCRETION

(S12.858093), and by the European Union’s Hori-

zon Europe research and innovation programme un-

der the project ”Quantum Security Networks Partner-

ship” (QSNP, grant agreement No 101114043).

REFERENCES

Almeida, M., Pereira, D., Fac

ao, M., Pinto, A. N., and

Silva, N. A. (2023a). Reconciliation Efﬁciency Impact

on Discrete Modulated CV-QKD Systems Key Rates.

Journal of Lightwave Technology, 41(19):6134–6141.

Almeida, M., Pinto, A. N., and Silva, N. A. (2023b).

Modulation variance optimization in discrete modu-

lated CV-QKD systems | SPIE Sensors + Imaging.

In EMERGING IMAGING AND SENSING TECH-

NOLOGIES FOR SECURITY AND DEFENCE, Ams-

terdam, Netherlands. SPIE.

Becir, A., El-Orany, F. A. A., and Wahiddin, M. R. B.

(2012). Continuous-variable quantum key distri-

bution protocols with eight-state discrete modula-

tion. International Journal of Quantum Information,

10(01):1250004.

Denys, A., Brown, P., and Leverrier, A. (2021). Explicit

asymptotic secret key rate of continuous-variable

quantum key distribution with an arbitrary modula-

tion. Quantum, 5:540.

Essiambre, R.-J., Kramer, G., Winzer, P. J., Foschini, G. J.,

and Goebel, B. (2010). Capacity limits of optical

ﬁber networks. Journal of Lightwave Technology,

28(4):662–701.

Feng, Y., Wang, Y.-J., Qiu, R., Zhang, K., Ge, H.,

Shan, Z., and Jiang, X.-Q. (2021). Virtual channel

of multidimensional reconciliation in a continuous-

variable quantum key distribution. Physical Review

A, 103(3):032603.

Ghorai, S., Grangier, P., Diamanti, E., and Leverrier, A.

(2019). Asymptotic Security of Continuous-Variable

Quantum Key Distribution with a Discrete Modula-

tion. Physical Review X, 9(2):021059.

Guo, D., He, C., Guo, T., Xue, Z., Feng, Q., and Mu, J.

(2020). Comprehensive high-speed reconciliation for

continuous-variable quantum key distribution. Quan-

tum Information Processing, 19(9):320.

Kleis, S., Rueckmann, M., and Schaeffer, C. G. (2017).

Continuous variable quantum key distribution with a

Slice Reconciliation in Continuous-Variable Quantum Key Distribution Using Discrete Modulation

real local oscillator using simultaneous pilot signals.

Optics Letters, 42(8):1588.

Laudenbach, F., Pacher, C., Fung, C.-H. F., Poppe, A.,

Peev, M., Schrenk, B., Hentschel, M., Walther, P., and

ubel, H. (2018). Continuous-Variable Quantum Key

Distribution with Gaussian Modulation-The Theory of

Practical Implementations. Advanced Quantum Tech-

nologies, 1(1):1800011.

Leverrier, A., All

eaume, R., Boutros, J., Z

emor, G., and

Grangier, P. (2008). Multidimensional reconciliation

for a continuous-variable quantum key distribution.

Physical Review A, 77(4):042325.

Leverrier, A. and Grangier, P. (2011). Continuous-

variable quantum key distribution protocols with

a non-Gaussian modulation. Physical Review A,

83(4):042312.

Leverrier, A., Grosshans, F., and Grangier, P. (2010). Finite-

size analysis of a continuous-variable quantum key

distribution. Physical Review A, 81(6):062343.

Li, Q., Wen, X., Mao, H., and Wen, X. (2019). An im-

proved multidimensional reconciliation algorithm for

continuous-variable quantum key distribution. Quan-

tum Information Processing, 18(1):25.

Lin, J. and L

utkenhaus, N. (2020). Trusted detector

noise analysis for discrete modulation schemes of

continuous-variable quantum key distribution. Physi-

cal Review Applied, 14(6):064030.

Liu, W.-B., Li, C.-L., Xie, Y.-M., Weng, C.-X., Gu, J., Cao,

X.-Y., Lu, Y.-S., Li, B.-H., Yin, H.-L., and Chen, Z.-B.

(2021). Homodyne Detection Quadrature Phase Shift

Keying Continuous-Variable Quantum Key Distribu-

tion with High Excess Noise Tolerance. PRX Quan-

tum, 2(4):040334.

Pirandola, S., Andersen, U. L., Banchi, L., Berta, M.,

Bunandar, D., Colbeck, R., Englund, D., Gehring, T.,

Lupo, C., Ottaviani, C., Pereira, J. L., Razavi, M.,

Shamsul Shaari, J., Tomamichel, M., Usenko, V. C.,

Vallone, G., Villoresi, P., and Wallden, P. (2020). Ad-

vances in quantum cryptography. Advances in Optics

and Photonics, 12(4):1012.

Roumestan, F., Ghazisaeidi, A., Renaudier, J., Brindel, P.,

Diamanti, E., and Grangier, P. (2021a). Demonstra-

tion of probabilistic constellation shaping for contin-

uous variable quantum key distribution. In Optical

Fiber Communication Conference (OFC) 2021, page

F4E.1, Washington, DC. Optica Publishing Group.

Roumestan, F., Ghazisaeidi, A., Renaudier, J., Vidarte,

L. T., Diamanti, E., and Grangier, P. (2021b). High-

rate continuous variable quantum key distribution

based on probabilistically shaped 64 and 256-QAM.

In 2021 European Conference on Optical Communi-

cation (ECOC), pages 1–4, Bordeaux, France. IEEE.

Van Assche, G., Cardinal, J., and Cerf, N. (2004). Reconcil-

iation of a Quantum-Distributed Gaussian Key. IEEE

Transactions on Information Theory, 50(2):394–400.

Wang, X., Wang, H., Zhou, C., Chen, Z., Yu, S., and Guo,

H. (2022). Continuous-variable quantum key distribu-

tion with low-complexity information reconciliation.

Optics Express, 30(17):30455.

Wen, X., Li, Q., Mao, H., Wen, X., and Chen, N.

(2021). An Improved Slice Reconciliation Protocol

for Continuous-Variable Quantum Key Distribution.

Entropy, 23(10):1317.

Yang, S., Yan, Z., Yang, H., Lu, Q., Lu, Z., Cheng, L., Miao,

X., and Li, Y. (2023). Information reconciliation of

continuous-variables quantum key distribution: Prin-

ciples, implementations and applications. EPJ Quan-

tum Technology, 10(1):40.

Zhang, Y., Li, Z., Chen, Z., Weedbrook, C., Zhao, Y.,

Wang, X., Huang, Y., Xu, C., Zhang, X., Wang, Z., Li,

M., Zhang, X., Zheng, Z., Chu, B., Gao, X., Meng,

N., Cai, W., Wang, Z., Wang, G., Yu, S., and Guo,

H. (2019). Continuous-variable QKD over 50 km

commercial ﬁber. Quantum Science and Technology,

4(3):035006.

PHOTOPTICS 2025 - 13th International Conference on Photonics, Optics and Laser Technology