Galerkin Enhanced Graph-Based FEM for Interactive Fracture and

Sculpting Applications

Avirup Mandal

1,∗ a

, Parag Chaudhuri

2 b

and Subhasis Chaudhuri

3 c

Department of Computer Science and Engineering, Indian Institute of Technology Palakkad, Kanjikode, India

Department of Computer Science and Engineering, Indian Institute of Technology Bombay, Mumbai, India

Department of Electrical Engineering, Indian Institute of Technology Bombay, Mumbai, India

Keywords:

Interactive Fracture, Graph-Based FEM, Galerkin Multigrid, Sculpting.

Abstract:

Physically-based fracture and cutting simulations are rarely incorporated in interactive graphics systems be-

cause the required computation stiﬂes the speed of interaction. We enhance a physically based method for

object deformation and fracture by using multigrid approximations to expedite the full dynamics solve of the

system. Our method combines a Galerkin multigrid approach with the graph-based Finite Element Method so

that remeshing-free fracture and cutting simulation can be done by solving the system dynamics on a hierarchy

of coarse to ﬁne meshes while accumulating residual error that is fully resolved only at the coarsest level. We

demonstrate the effectiveness of our algorithm by using it to develop an interactive virtual sculpting framework

that enables users to shape object meshes in a physically consistent manner. We compare our method with

other state-of-the-art virtual 3D object editing solutions to show that our method can provide better physically

consistent solutions at interactive speeds.

1 INTRODUCTION

Fracture simulation is crucial in various graph-

ics applications for immersive virtual content cre-

ation. Applications such as video games, mixed re-

ality experiences, and surgical simulators require vi-

sually appealing fracture simulations and instanta-

neous interaction feedback. To achieve high frame

rates with physical plausibility, stable large-time-

step simulations for fracture simulations, the Fi-

nite Element Method (FEM) (O’Brien and Hodgins,

1999) (Pfaff et al., 2014) (Chitalu et al., 2020),

Boundary Element Method (BEM) (Hahn and Woj-

tan, 2015) (Hahn and Wojtan, 2016). Material Point

Method (MPM) (Wolper et al., 2019) (Wolper et al.,

2020) are widely used. These methods utilize an

implicit time integration scheme; however, they are

computationally expensive, and the computational

cost increases with the number of cracks in the object

https://orcid.org/0000-0002-2322-4440

https://orcid.org/0000-0002-1706-5703

https://orcid.org/0000-0002-1680-0016

∗

Some part of this work was done when Avirup Man-

dal was a PhD student at the Department of Electrical Engi-

neering, Indian Institute of Technology Bombay

mesh. As a result, these methods are often restricted

to low-resolution objects for real-time simulations.

To address these issues, researchers have been ex-

ploring alternative approaches to fracture simulation

that offer real-time interaction feedback while main-

taining visual ﬁdelity. A recent approach, graph-

based FEM (Mandal et al., 2023), predicts the evo-

lution of cracks in a remeshing-free manner and runs

independently of the number of cracks. Thus, graph-

based FEM is faster and more stable than the existing

fracture simulation algorithms. However, this method

alone is not sufﬁcient for interactive fracture simula-

tions at high frame rates on high-resolution meshes.

We present an interactive fracture and cutting

simulation framework based on graph-based FEM,

accelerated using a Galerkin multigrid method.

Even though the Galerkin multigrid method for de-

formable object simulation exists in literature (Xian

et al., 2019), combining a multigrid method with a

remeshing-free fracture simulation is neither obvious

nor trivial.

1.1 Contribution

Our contribution lies in being the ﬁrst to develop a

physically based fracture and cutting algorithm that

Mandal, A., Chaudhuri, P. and Chaudhuri, S.

Galerkin Enhanced Graph-Based FEM for Interactive Fracture and Sculpting Applications.

DOI: 10.5220/0013142800003912

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 20th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2025) - Volume 1: GRAPP, HUCAPP

and IVAPP, pages 65-76

ISBN: 978-989-758-728-3; ISSN: 2184-4321

can run at interactive rates. To that end, we com-

bine the Galerkin multigrid method (Xian et al., 2019)

with a graph-based Finite Element Method (Mandal

et al., 2023). In our algorithm, we interleave the so-

lution of system dynamics on a hierarchy of coarse

to ﬁne meshes with remeshing-free fracture simula-

tion on the ﬁne mesh. This allows us to resolve the

fracture or cut accurately while it amortizes the cost

of solving the full system dynamics via repeated ap-

proximate solutions at multiple mesh levels. The ac-

cumulated residual error is ﬁnally fully resolved on

the coarsest level mesh.

We present multiple examples of fracture using

our Galerkin-enhanced graph-based FEM. We study

and characterize the tradeoff between speed and phys-

ical accuracy when using our method in comparison

to other solutions representing state-of-the-art. We

develop an interactive cutting and sculpting applica-

tion based on our method and show various sculpt-

ing examples of the same. A user study is pre-

sented to validate the physical plausibility, ease of

use, and responsiveness of the developed application

and method.

The rest of the paper is organized as follows. We

start with a discussion of the related state of the art

in Section 2. Section 3 brieﬂy explains graph-based

FEM and the Galerkin multigrid method. This is fol-

lowed by fracture and sculpting simulation results for

various materials in Section 4. Section 5 contains de-

tails about the user experiments. Finally, in Section 6,

we conclude our paper by presenting a few potential

future directions of our work.

2 RELATED WORK

We begin with an overview of deformable solids, fol-

lowed by a review of fast deformation simulation al-

gorithms and methods for mesh-based and meshless

fracture simulation.

The Finite Element Method (FEM) is widely

used for deformation modeling. A co-rotational

model with Cauchy linear strain was proposed by

uller and Gross, 2004). Other researchers, such

as (Bargteil et al., 2007), (Irving et al., 2004), and

(Stomakhin et al., 2012), looked into large plastic

ﬂow. (Smith et al., 2018) studied extreme ﬂesh de-

formation using Neo-Hookean elasticity and later ex-

tended their work to more isotropic models. (Xu

et al., 2015) proposed a novel algorithm for arbitrary

elastic energy design, and (Kim et al., 2019) devel-

oped an inversion-free anisotropic elastic density.

Position-Based Dynamics (PBD) and shape

matching (Chentanez et al., 2016) are fast simulation

methods that can be used in real-time applications.

PBD is extended to work with large meshes (M

uller,

2008), fast ﬂuids (Macklin and M

uller, 2013), and

the uniﬁed NVIDIA Flex framework. Following simi-

lar ideas of PBD, Projective Dynamics (PD) (Bouaziz

et al., 2014) method is proposed for fast real-time so-

lutions, which is later extended and generalized with

ADMM (Overby et al., 2017). However, the perfor-

mance of Projective Dynamics is dependent on the

pre-factorization of a direct solver, which can pose

challenge due to the high memory requirements for

extremely high-resolution meshes. In addition, the

convergence of position-based dynamics is not sufﬁ-

cient for simulating stiff objects with high resolutions.

To overcome these, (Xian et al., 2019) proposed

a Galerkin multigrid method for efﬁcient memory us-

age in fast deformable object simulation, which we

merge with graph-based FEM to simulate fracture and

cutting interactively.

Fracture simulation algorithm in computer graph-

ics began with Terzopoulos and Fleischer (Terzopou-

los and Fleischer, 1988), with early algorithms using

mass-spring dynamics (Hirota et al., 2000). FEM-

based brittle fracture technique was introduced by

(O’Brien and Hodgins, 1999) and later extended to

ductile fracture (O’Brien et al., 2002). Remeshing

issues during fracture led to solutions such as local

mesh reﬁnement (Wicke et al., 2010) and gradient

ﬂow (Chen et al., 2014). (Molino et al., 2004) in-

troduced the Virtual Node Algorithm (VNA) to avoid

remeshing. Using XFEM (Koschier et al., 2017),

VNA was improved by appropriate mass conservation

after fracture.

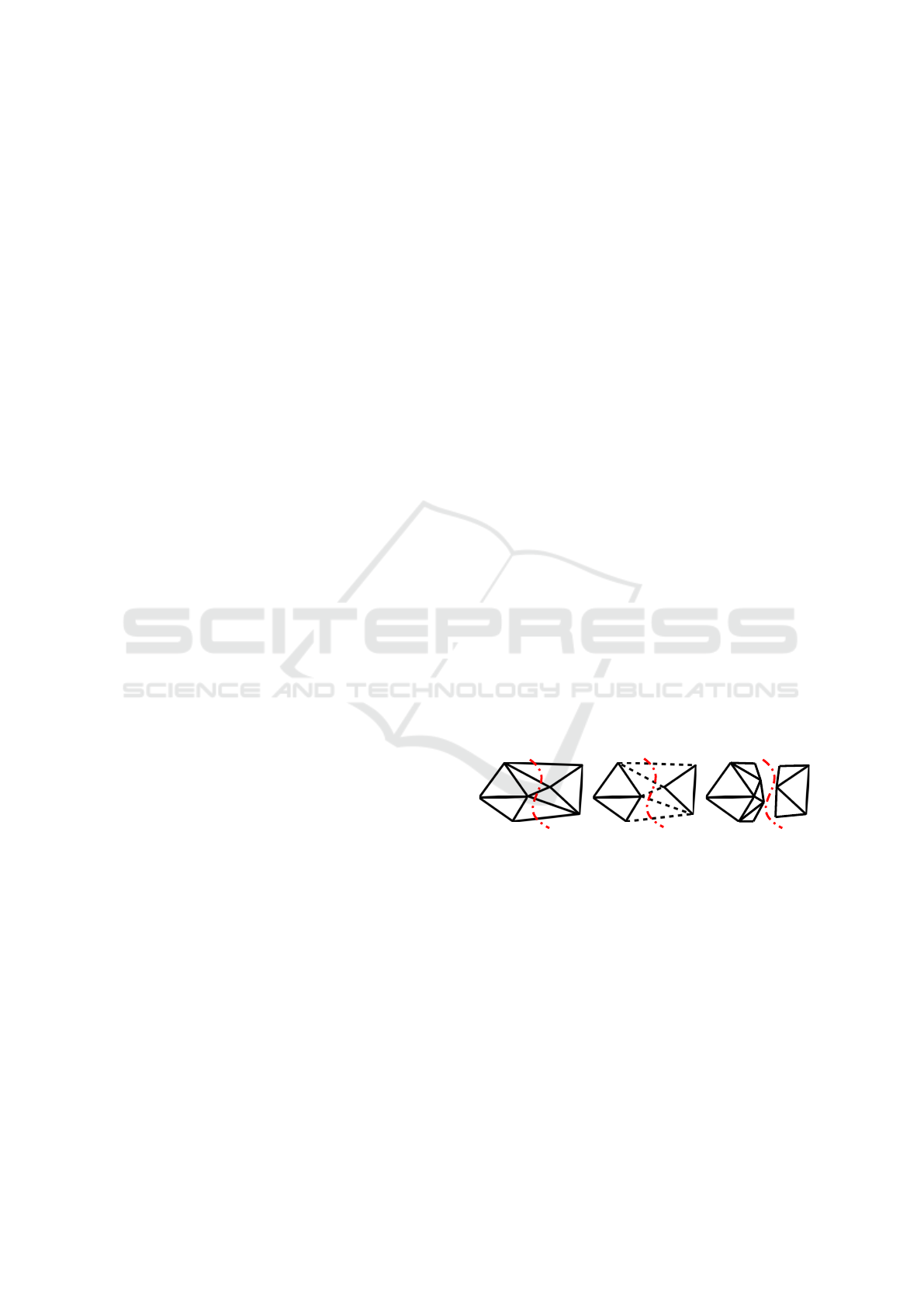
(a) (b)

(c)

Fracture line

Figure 1: (a) Original mesh with a fracture, (b) Computa-

tional mesh (M

), with damaged edges (dotted lines), on

which system dynamics get evaluated, (c) Mesh for visu-

alization (M

) is split and the fracture surface is recon-

structed.

Boundary Element Methods (BEM) for fracture

simulation was introduced by (James and Pai, 1999)

for brittle materials. This work was later extended

by (Hahn and Wojtan, 2015) for faster simulation.

Grid-free Material Point Method (MPM) (Stomakhin

et al., 2013) for ductile fracture simulation is pro-

posed in (Wolper et al., 2019) (Wolper et al., 2020),

which is later extended by (Fan et al., 2022) to simu-

late brittle fractures.

Graph-based FEM (Gra-FEA), developed

GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications

by (Khodabakhshi et al., 2016), simulates brittle

fracture and scales well for high-resolution meshes

without remeshing. This has been extended to

3D dynamic simulations for both brittle and ductile

fractures (Mandal et al., 2023) (Mandal et al., 2022b),

but simulating deformable bodies at an interactive

rate remained challenging.

3 GALERKIN ENHANCED

GRAPH-BASED FEM

We brieﬂy explain graph-based FEM for fracture

simulation ﬁrst and then present the details of the

Galerkin multigrid-based enhancement.

3.1 Graph-Based FEM

Graph-based FEM (Mandal et al., 2023) is a fast,

remeshing-free method to simulate the fracture of

both ductile and brittle materials. Given a computa-

tional volumetric mesh, M

, made of tetrahedral ele-

ments, M

induces a graph where vertices and edges

of the mesh become the nodes and edges of the graph.

The stress of a tetrahedral element, ∆

, of the mesh

is then projected along the direction of edges of the

graph formed by the edges of the tetrahedra.

= σ

cos

+ σ

cos

+ σ

cos

+ σ

cosφ

+ σ

cosφ

+ σ

cosφ

(1)

where σ

represents the normal stress along the edge

formed by nodes m and n and σ

i j

, ∀i, j ∈ {x,y,z} are

Cartesian components of Piola Kirchhoff stress. Sim-

ilarly φ

, ∀k ∈ {x,y,z} is the angle of the edge with k

axis. The edge is marked as damaged if σ

exceeds a

threshold. A damaged edge is never repaired in subse-

quent simulation steps. Next, the hyper-elastic strain

energy of the element, Ψ

, is recalculated to include

the effect of the damaged edge as

f rac

= ζ (Ψ

) (2)

where ζ denotes the update function based on the

damaged edge. This newly reformulated strain en-

ergy adds more freedom to the vertices of the broken

edge for movement. Thus, if all the edges connecting

a vertex get labeled as damaged, it can move indepen-

dently and M

never needs to be remeshed. Subse-

quently the internal elastic force, f

int

∂Ψ

f rac

∂u

and

tangent stiffness matrix, k

∂f

int

∂u

are also updated

using the new strain energy; u

being the node dis-

placement vector of the ﬁnite element. Additionally,

using a kernel of support R

, the diffusion of cracks

inside M

can be controlled. A larger R

value pro-

duces more diffused cracks and vice versa.

A visualization surface mesh, M

, is maintained

in addition to M

and is the same as the outer surface

of volumetric mesh initially. M

needs to be split, and

the fracture surfaces must be reconstructed to render

the fracture. Remeshing M

does not affect the M

shown in Figure 1. The complete ﬂow of the fracture

process is summarized in Algorithm 1. Please refer

(Mandal et al., 2023) for further details about graph-

based FEM.

Algorithm 1: Fracture Simulation using Graph-based FEM.

1: for Each element in M

2: Calculate stress along the edges σ

i j

3: if σ

i j

> σ

thres

then

4: Label the edge in as fractured in M

5: Update strain energy density Ψ

6: Update internal force f

int

7: Update stiffness matrix k

8: Remesh the M

for visualization

9: end if

10: end for

3.2 Galerkin Enhanced Graph-Based

FEM

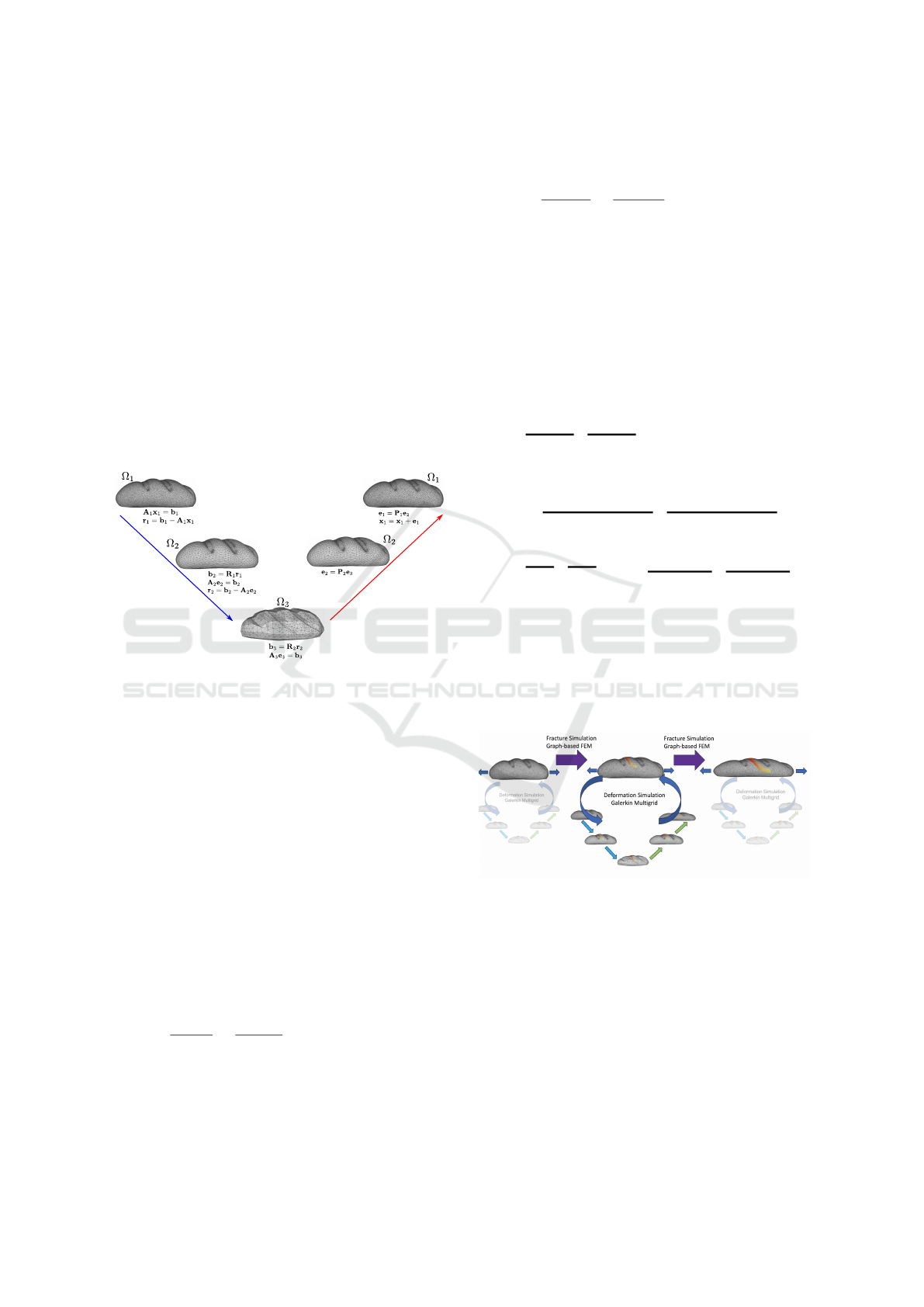
A Galerkin multigrid method can be conceived as an

iterative method of solving a set of linear systems of

an object mesh by passing it down to increasingly

coarser resolution meshes at multiple levels (Xian

et al., 2019). As shown in Figure 2, the set of lin-

ear systems is deﬁned from ﬁner to coarser resolution

meshes.

For deformation object simulation using FEM, the

discretized linear system equation for the implicit

backward Euler method is written as (Sin et al., 2013)



M + ∆t



| {z }

∆v = ∆t



ext

− f

int

− ∆tKv



| {z }

(3)

where M,K,f

int

& f

ext

denote system mass matrix,

tangent stiffness matrix, internal and external vectors

respectively. v

& ∆v denote current velocity incre-

mental velocity at time t. These parameters are con-

structed using element-level parameters.

M =

∑

e∈n

tet

, K =

∑

e∈n

tet

int

∑

e∈n

tet

int

, f

ext

∑

e∈n

tet

ext

(4)

Galerkin Enhanced Graph-Based FEM for Interactive Fracture and Sculpting Applications

where n

tet

is number of tetrahedra in the object mesh.

Initially, the linear system at the ﬁnest level

of the Galerkin multigrid method, A

= b

(see

Equation 3) is solved using Gauss-Seidel or Jacobi

solver. However, they are stopped much earlier be-

fore convergence is reached. An early stop of these

iterative methods produces a smooth error. The

smooth/residual error is deﬁned as

= b

− A

(5)

Even though the solver is stopped early, the high-

frequency error at each level gets removed quickly,

leaving only low-frequency error in the system. The

low-frequency error is then passed to the next level

containing a coarser resolution mesh. The error then

becomes a high-frequency error at that lower level.

At each timestep, we run an iteration of graph-based

Restriction

Interpolation

Figure 2: Galerkin multigrid deformation simulation:

The system equation is solved in multiple levels using ﬁner

to coarser meshes. At each level, the solver is terminated

much earlier before convergence, and the residual error is

passed to the next level.

FEM to compute the fracture only at the ﬁnest level

of the object mesh. This is depicted in Figure 3. To

do this, we calculate normal stress along the edges of

the ﬁnest-level mesh using Equation 1. The edge is

considered damaged if the stress value along an edge

exceeds a critical threshold and subsequently uses the

reformulated internal hyper-elastic strain energy den-

sity as given in Equation 2. The graph-based FEM

requires no volume remeshing after fracture i.e., the

initial tetrahedral mesh remains the same throughout

the simulation. However, updated strain energy im-

plies an update of internal force and tangent stiffness

matrix, as explained below. The internal force vector

takes the following form.

int

∗

∂Ψ

f rac

∂u

∂ζ(Ψ

)

∂u

= ζ

′

(Ψ

)Ψ

′

= ζ

′

(6)

where f

′

denotes the derivative of function f . In the

last equality, ζ

′

(Ψ

) is written as ζ

′

for the sake of

brevity. Similarly, the tangent stiffness matrix can be

expressed as

∗

∂

f rac

∂u

∂(ζ

′

)

∂u

= ζ

′′

′

+ ζ

′

′′

(7)

where f

int

∗

and k

∗

are the updated internal force vector

and tangent stiffness matrix for tetrahedral ﬁnite ele-

ment. The exact values of ζ

′

and Ψ

′

can be obtained

following the algorithms presented in (Mandal et al.,

2023). Finally, using Equation 6, 7 and 4, we can

rewrite the ﬁnest level system Equation 3 for Galerkin

enhanced graph-based FEM as follows.

M + ∆t

∑

e∈n

tet

∗

| {z }

∆v

= ∆t

ext

−

∑

e∈n

tet

int

∗

− ∆t

∑

e∈n

tet

∗

| {z }

=⇒



M + ∆t

∗



{z }

∆v = ∆t



ext

− f

int

∗

− ∆tK

∗



| {z }

(8)

Notice that the fracture simulation cycle is not re-

peated on the coarser level meshes as depicted in Fig-

ure 3. However, the various effects of fracture, such

as extra degrees of freedom to the mesh vertices due

to fracture, are propagated to these levels using in-

terpolation matrices. When Equation 8 is solved us-

Figure 3: Galerkin multigrid-based deformation simulation

is combined with graph-based FEM for fracture simulation.

ing some popular solver like Gauss-Seidel or Jacobi

solver, it produces a smooth residual error. The resid-

ual at the ﬁnest level is expressed in Equation 5. It is

propagated to the next level using restriction matrix,

= R

(9)

In more general form, at the coarser level, l + 1, the

residual from level l (similar to Equation 5), is re-

stricted using the restriction matrix, R

l+1

= R

(10)

GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications

The error update to the vertices of the level l + 1

is computed, again using a few iterations of a popular

solver.

l+1

= b

l+1

(11)

where similar to Equation 8, A

l+1

and b

l+1

are the

system matrix and column vector of level l + 1 re-

spectively. Subsequently, the residual for level l + 1

is computed as

l+1

= b

l+1

− A

l+1

(12)

After the solver solves the system dynamics at the

coarsest level, the error values at each level are inter-

polated back to the ﬁner level using prolongation or

interpolation matrix P

= P

l+1

(13)

At the ﬁnest level, the next position is updated using

= x

+ e

Since the solver at each level can be stopped early,

and only errors of lower frequency get propagated to

coarser levels, it is not necessary to re-discretize the

system matrix using the Finite Element Method on the

coarser mesh in the Galerkin multigrid method, un-

like pure geometry-based multigrid methods. More-

over, as the whole system is solved in multiple lev-

els, each running just a few iteration loops of some

conventional solver, the entire system runs at an in-

teractive frame rate. Graph-based FEM adds negligi-

ble computational complexity per se while simulating

fracture inside an object mesh. Thus, Galerkin multi-

grid enhanced graph-based FEM is capable of render-

ing fracture in a real-time, interactive manner.

The parameters from the ﬁner to the coarser level

or vice-versa are passed using symmetric restriction

and interpolation matrices at each level l, R

and P

l+1

= R

(14)

Also, R

= P

. The matrices A

denote linear systems

matrices at l

level. The number of levels depends on

the initial system size and the speciﬁc demand of the

application.

The whole process is summarized in Algorithm 2.

If we consider cutting instead of fracture, everything

remains the same except that the user initiates the

crack lines instead of the stress threshold.

A multi-level hierarchy is built by uniformly sam-

pling vertices at various resolutions. Then, the R

and P

Galerkin projection matrices are set up using

skinning-space coordinates with piece-wise constant

interpolation weights.

3.3 Galerkin Grid Hierarchy and

Projection Matrices

Given an object mesh consisting of n vertices, the

coarser level mesh grids are constructed using the fur-

Algorithm 2: Galerkin enhanced Graph-based FEM.

Set up d-level grid hierarchy, Ω

,.. .Ω

2: Construct the projection matrices U

,.. .U

Compute and store the multi-level system matri-

ces A

,.. .A

4: Compute and store the multi-level external force

vectors b

,.. .b

for Each element in object mesh do

6: Calculate mesh fracture using Algorithm 1

end for

8: for Each level l do

Update collision and fracture constraints (e.g.

internal force) to A

with Equation 14

10: Solve the system equation, A

= b

using a

conventional solver (e.g. GS, CG, PCG)

Compute residual, r

with Equation 12

12: Pass it down to the next level, l + 1, with

Equation 10

end for

14: Interpolate the solution back to the ﬁnest level

with Equation 13

thest point sampling method (Brandt et al., 2018),

which is a special case of the k-means++ algo-

rithm (Arthur and Vassilvitskii, 2007). As depicted

in Figure 4, let us denote the set of all the vertices,

, of the full resolution mesh by Ω

. The vertex set,

Ω

, of the immediate next level coarser mesh contains

number of vertices and is a subset of Ω

Ω

⊆ Ω

, k

≤ k

(15)

The set Ω

is ﬁrst initialized with a random vertex

in Ω

. Using Dijkstra’s algorithm, we compute the

geodesic distances to Ω

of all other vertices. Finally,

the most distant vertex in Ω

\Ω

is picked and added

to the set Ω

. The geodesic distances to the new Ω

are updated in the next iteration. This process is re-

peated until the size of Ω

becomes k

. In the same

way, even lower-resolution grids, Ω

, Ω

, ... Ω

are constructed, if required. However, please note that

the meshes at the coarser levels are not explicitly con-

structed. Instead, interpolation and restriction matri-

ces are used to project the parameters of nodes from

a ﬁner mesh to the nodes of a coarser mesh and vice

versa. The full process is explained in the next sec-

tion.

Downsample Downsample

Figure 4: Galerkin grid hierarchy construction. Ω

contains

the vertices on the l

level grid and Ω

l+1

⊆ Ω

Each node in a mesh at any level is assumed to

Galerkin Enhanced Graph-Based FEM for Interactive Fracture and Sculpting Applications

possess twelve degrees of freedom. The interpolation

between different levels is constructed using Linear

Blending Skinning (LBS).

∑

i j

(16)

where y

∈ R

3×1

is position of i

vertex, T

∈ R

3×4

the afﬁne transformation matrix of the j

control han-

dle, Y

∈ R

4×1

is the homogeneous coordinate of the

rest-pose position of vertex i, and ω

i j

is the weight of

handle j to vertex i. Rewriting and rearranging Equa-

tion 16 over all vertices gives the following relation.

Y = Uq (17)

where Y =



,.. .y

n−1



is the position of all ver-

tices at the ﬁnest level;

q = [vec(T

),vec(T

),.. .vec(T

n−1

)] ∈ R

12k×1

de-

notes all the skinning space degrees of freedom; and

U ∈ R

3n×12k

is the linear transformation matrix be-

tween q and Y. Each block of U can be written down

explicitly as U

i j

= ω

i j

⊗ I

∈ R

3×12

where ⊗I

a Kronecker product with a 3×3 identity matrix. Fol-

lowing the same argument, the interpolation between

multiple coarser levels can be calculated below.

= U

l+1

(18)

Finally, the interpolation matrix P for different levels

are deﬁned as P

= U

. To maintain the symmetry of

the system matrix while using the Galerkin multigrid

projection method, the restriction matrix is set to R

The weight parameters ω

i j

are piecewise constant

weights i.e, ω ∈ {0,1}. These weights introduce more

high-frequency errors in the system. However, as

discussed earlier, the high-frequency errors produced

due to these non-smooth weights get suppressed in

the coarser levels. Further details about the Galerkin

multigrid method for deformation simulation can be

found in (Xian et al., 2019).

4 RESULTS

This section presents multiple simulation examples of

interactive cutting and fracture using our method. We

also compare our method to the existing state-of-the-

art FEM methods developed to simulate deformation

and fracture.

All the experiments presented here are carried out

with an Intel i7-9750H octa-core processor, 16GB

DDR4 RAM, and a single Nvidia RTX 2060 GPU

with 6 GB of graphics memory. All the simulation

examples are parallelized using CUDA. In all our sim-

ulations, the blue nodes on the mesh denote ﬁxed

points.

Figure 5: Our Galerkin enhanced graph-based FEM fracture

and cutting simulation algorithm drives an interactive vir-

tual sculpting framework. Here, we show a model sculpted

using our framework.

Parameters and frame per second (fps) values for

each simulation result are presented in Table 1.

Table 1: Parameters for simulation experiments.

Simulation #Tet Grid Setup fps

Armadillo (Fig. 7) 160k 50/1000/all 34.9

Human body (Fig. 6) 40k 50/all 127.2

Sphere (Fig. 14) 34.9k 50/all 118.7

Steak (Fig. 8) 186.1k 50/1000/all 24.7

Charpy test (Fig. 12) 28k 50/all 152.5

4.1 Galerkin Grid Setup

Before presenting the results, we quickly explain the

grid structure of the Galerkin method. All the results

are accompanied by a grid setup depicted as

level

/level

n−1

/.. ./level

/level

/all. It denotes the

number of vertices at each level of the Galerkin grid

mesh, and ‘all’ denotes the vertices of the ﬁnest level

input mesh.

We perform a study of the grid structure on vari-

ous parameters as follows. We notice that increasing

the number of levels contributes little to the speed-up

or accuracy of the simulation. We use volume gain

to characterize accuracy in these results. In multigrid

Galerkin, the solver at each level is terminated after

a few ﬁxed user-deﬁned number of steps, even before

the convergence is attained. However, if the number

of these steps is increased, the error gets reduced at

the expense of simulation time. For example, we sim-

ulated a sphere hanging under gravity (see Figure 14)

with a 50/all grid setup. At the ﬁnest level, we use a

Gauss-Seidel/Jacobi solver with three cycles, and at

the coarser level, a Conjugate Gradient (CG) solver

with 20 cycles or a direct solver. The simulation runs

at 118.7 frames/sec with a volume error 19%. How-

ever, if the cycles of PCG and CG are increased to

30 and 200, respectively, the simulation runs at 23.8

frames/sec with a volume error of 11%.

GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications

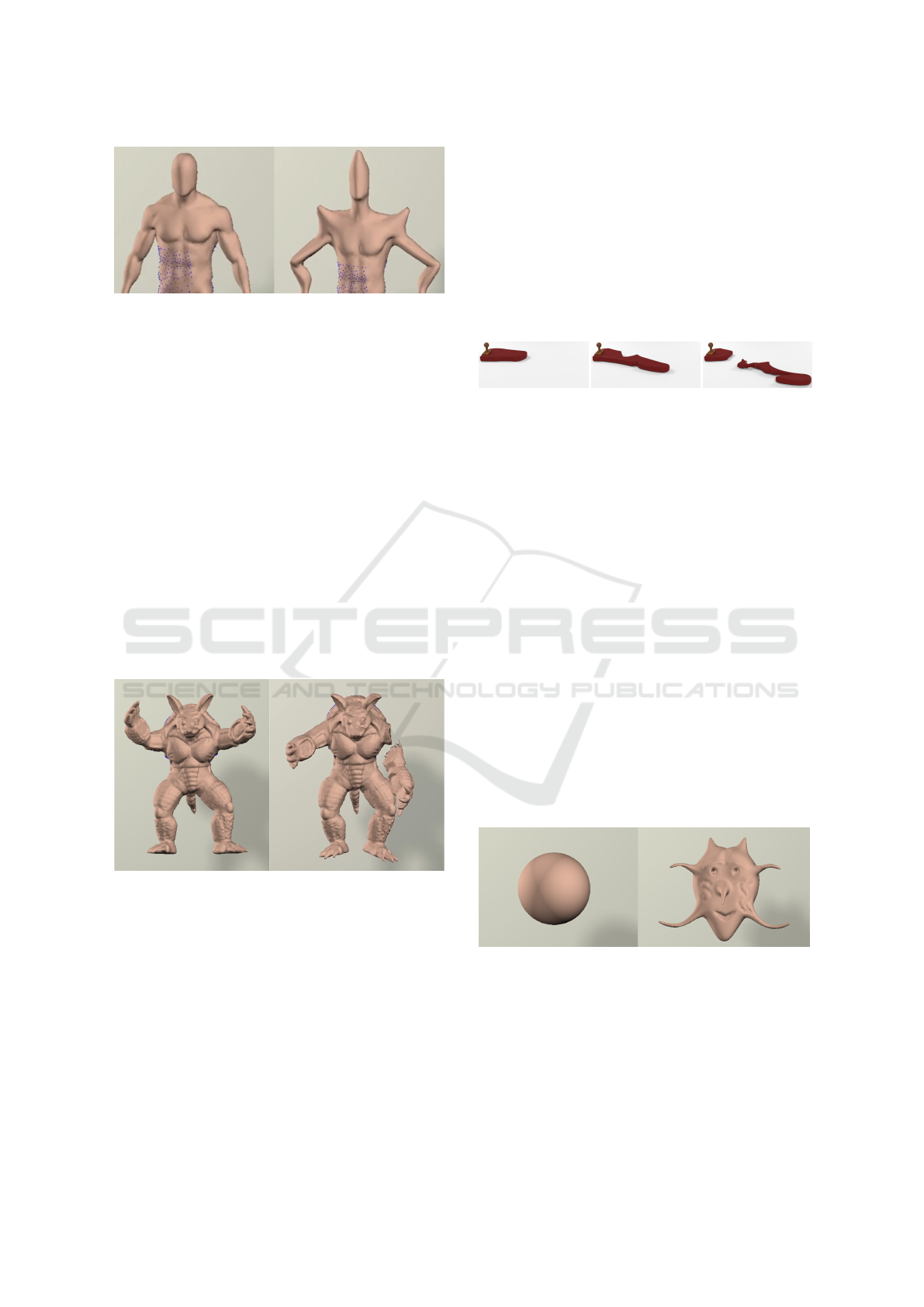
Figure 6: Illustration of the original (left) and deformed hu-

man body model for Galerkin multigrid method (right).

4.2 Deformation and Cutting

Deformation on a human body mesh using Galerkin-

enhanced graph-based FEM is shown in Figure 6. The

human body mesh comprises 40k tetrahedra, and the

simulation runs at 127.2 frames/sec, with a grid set up

of 50/all.

Is-XFEM (Mandal et al., 2022a) also uses multi-

resolution meshes to achieve interactive deformation

and cutting. We compare our method to the im-

plementation of Is-XFEM presented by Mandal et

al. (Mandal et al., 2022a). For the sake of fair com-

parison, unlike the original implementation, the Is-

XFEM method is run on a single thread without hap-

tic feedback. The Is-XFEM simulation runs at 4.1

frames/sec when no cut is present and 3.5 frames/sec

when one cut is introduced. The frame rate keeps on

decreasing as the number of cuts increases.

Figure 7: Illustration of an original (left) and fractured

(right) armadillo mesh.

In Figure 7, we render the fracture of an armadillo

mesh using Galerkin multigrid method augmented

with graph-based FEM. In the ﬁgure, the left arm of

the armadillo is detached from its body when pulled

by the user. The armadillo model consists of 160k

tetrahedra and runs at 34.9 frames/sec with a grid

setup of 50/1000/all. This same cutting simulation of

the armadillo mesh requires 1.4 sec/frame if Is-XFEM

is used. Therefore Galerkin multigrid with graph-

based FEM is around ×25 faster than Is-XFEM.

4.3 Fracture Simulation

In Figure 8, we simulate the fracture of a steak

clamped at one end and pulled at the other. The steak

mesh consists of 186.1k tetrahedra. Galerkin multi-

grid method combined with graph-based FEM ren-

ders the simulation at 24.7 frames/sec with a grid set

up of 50/1000/all. The simulation stays physically

plausible and runs at an interactive rate even for such

a high-resolution mesh.

Figure 8: A piece of steak consisting of 186.1k tetrahedra is

torn apart from pulling at one end. This is simulated using

Galerkin-enhanced graph-based FEM. Galerkin-enhanced

graph-based FEM runs at 24.7 frames/sec.

4.4 Interactive Fracture and Cutting

Simulation

We use Galerkin multigrid to accelerate the deforma-

tion simulation while using graph-based FEM to re-

solve the fracture on the ﬁnest level of the mesh. This

allows us to simulate fracture and cutting at interac-

tive rates.

We develop a virtual sculpting application using

our method. Figure 5 shows a screenshot of our ap-

plication. The application provides a user with vari-

ous tools for mesh manipulation and simple naviga-

tional components to orient those. These sculpting

tools include knives, deformation brushes, and an-

choring tools. We used our application to create vari-

ous sculpting examples and conducted a user study to

gauge its efﬁcacy. We present these results in the next

section.

Figure 9: Original (left) and sculpted (right) Sphere model

using Galerkin multigrid framework.

Our interactive virtual sculpting application can

handle multiple sculpting operations performed on an

object mesh in real-time. At the end of the sculpting

operations, the volumetric tetrahedral and visualiza-

tion triangular mesh are affected. Users can save, ex-

port, or import any of these sculpted meshes, whether

tetrahedral or triangular, for using them in the same

Galerkin Enhanced Graph-Based FEM for Interactive Fracture and Sculpting Applications

or other applications. Moreover, after sculpting, our

method always generates a water-tight visualization

mesh convenient for further use in different applica-

tions.

In Figure 9, an amateur volunteer sculpted a scary

mask starting from a simple sphere model using our

application. In Figure 5, another user sculpted a

model starting from a simple sphere mesh.

4.5 Comparison Study

Figure 10 compares the sculpting generated using two

distinct methods. On the left side of the ﬁgure, we ob-

serve the deformed shapes of different limbs of a hu-

man body, obtained through a solely geometry-driven

technique such as Blender’s grab brush (Blender

Foundation, 2023). On the right side, we present sim-

ilar results with the physics-based sculpting approach,

developed using our Galerkin-enhanced graph-based

FEM.

The illustration distinctly highlights the merits of

our physics-based sculpting method for improving

volume preservation, even without any explicit input

regarding the surface structure of the object mesh.

Better volume preservation results in sculpted shapes

that are faithful to their original forms. In contrast,

traditional geometry-based tools tend to collapse the

volume and generate unrealistic structures.

Figure 10: The left column shows the deformation re-

sults of a human body using a geometry-driven technique

Blender’s grab brush. The right column illustrates the same

deformations using our physics-based Galerkin-enhanced

graph-based FEM. Notice that our physically-based sculpt-

ing framework improves local volume preservation.

Kelvinlets, as introduced in (De Goes and James,

2017), are fundamental solutions of linear elasticity

for singular loads. They enable the real-time render-

ing of physically accurate mesh deformations. How-

ever, the deformation generated by Kelvinlets moves

as if it is embedded in an inﬁnite elastic continuum.

Consequently, these embedded deformations some-

times produce unintended and undesirable non-local

interactions. For example, in Figure 11 (left), ob-

serve the deformation of the left leg of a human body

mesh. It is rendered by applying a Kelvinlet kernel

as depicted in the inset. As can be seen, there are

unrealistic nonlocal deformations induced in the left

hand of the body (red circled), despite being geodesi-

cally far away from the deformed leg. In contrast, our

Galerkin-enhanced graph-based FEM does not suffer

from this limitation and is capable of rendering local

deformation accurately as illustrated on the right side

of Figure 11.

Figure 11: Left leg of human body mesh is deformed by

applying a Kelvinlet kernel as depicted in the inset (left).

However, it produces undesirable and non-local deforma-

tion to the geodesically distant components of the body (red

circled). In contrast, our Galerkin-enhanced graph-based

FEM can render local deformation accurately.

4.6 Validation Results

A Charpy Impact test is a standard experiment per-

formed in an undergraduate strength of materials lab-

oratory. We simulate the Charpy Impact test using our

method and with regular graph-based FEM. In the ex-

periment, a notched steel specimen is held on the two

ends, and a swinging pendulum hits it in the middle,

as depicted in the top row of Figure 12. After the col-

lision, the specimen gets split into two disjoint pieces.

The same test is performed using normal graph-based

Figure 12: Charpy Impact Test: The top row shows the

simulation with Galerkin-enhanced graph-based FEM and

the bottom row with normal graph-based FEM. The left-

most image in each row shows the conﬁguration of the

Charpy test. When hit by a swinging pendulum (shown with

the moving square block), the notched specimen gets split

into two pieces.

FEM as depicted in the bottom row of Figure 12. As

evident from the images graph-based FEM has better

GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications

at preserving ﬁner details and rendering correct de-

formation. The notched bar consists of 28k tetrahe-

dra. While Galerkin multigrid method runs at 152.5

frames/sec with a grid set up of 50/all, regular graph-

based FEM runs at around 4.7 frames/sec. In Fig-

ure 13, we plot the load-crack mouth opening dis-

placement (CMOD) curve obtained from our simu-

lated Charpy impact test experiment. The solid blue

line with a shaded envelope is the experimental load-

CMOD curve from real physical experiments and the

dotted magenta line represents the same curve derived

from the XFEM simulation, as reported by (Areias

and Belytschko, 2005). The dashed red line and

green dashed-dotted line denote the plot for our sim-

ulation set-up using Galerkin-enhanced graph-based

FEM and normal graph-based FEM respectively. The

ﬁgure shows that our experimental results closely fol-

low the real-world laboratory experiment results.

Figure 13: The plot compares the load-crack mouth open-

ing displacement (CMOD) curve of the simulated Charpy

impact test with ground truth curves from actual laboratory

experiments.

5 DISCUSSION AND USER

EXPERIMENT

Even though our method runs much faster than the

existing state-of-the-art deformation simulation tech-

niques, the gain in speed comes at the cost of some

accuracy. We compare the accuracy of the Galerkin-

enhanced graph-based FEM with standard FEM with

different constitutive models in terms of volume gain

(of an incompressible material) as shown in Table 2.

We use a high Poisson ratio (≈ 0.48) for our ex-

periment. In Figure 14, we simulate a sphere that

hangs under gravity and is hinged at the top. This

hanging sphere is simulated with different algorithms

using various hyper-elastic strain energies as ex-

plained in Table 2. As evident from the table, com-

pared to our method, only Co-rotational FEM (Irv-

ing et al., 2004) performs poorly in terms of vol-

ume preservation. However, more recent constitutive

models used in FEM deformation simulation like In-

vertible Principal-Stretch Material design (Xu et al.,

2015) (Sin et al., 2013), stable Neo-Hookean (Smith

et al., 2018) introduce less error than our method.

Thus if volume gain is used as a metric for accu-

Figure 14: A sphere mesh is ﬁxed at the top and hangs under

gravity.

racy for deformation simulation, then we see that our

method clearly trades some accuracy to gain speed

of computation. This is a result of the multi-scale

approximate solve of the system dynamics in the

Galerkin multigrid method.

Table 2: Volume gain in different existing consecutive mod-

els using various hyper-elastic strain energies.

Method Vol. Gain

Co-rot. FEM (Irving et al., 2004) 85%

Inv. N-Hkn (Sin et al., 2013) 3.2%

Inv. StVK (Sin et al., 2013) 10.7%

Stb. N-Hkn (Smith et al., 2018) 4.3%

Our Method (Xian et al., 2019) 19%

5.1 User Study

We conducted a user study to evaluate our interac-

tive application for all the virtual sculpting operations

available in it. The data collection methodology was

suitably evaluated and approved by an ethics commit-

tee of Indian Institute of Technology Bombay, India

and all participants’ data was suitably anonymized.

Figure 15: Making a dent on a real clay ball (left) and a

virtually simulated ball (right).

We recruited ten participants (aged between 25 to

35 years) to take part in our experiments. None of the

participants reported any ailment. All the participants

have normal or corrected-to-normal vision and during

the experiment, they use their dominant hand.

First, we give a brief demo of our virtual sculpt-

ing framework to the participants. At the start of the

experiment, the participants are asked to mould a ball

Galerkin Enhanced Graph-Based FEM for Interactive Fracture and Sculpting Applications

of clay with a stick and knife to get acquainted with

real-world sculpting. The user then puts his/her elbow

on the handle of the chair and holds the mouse to in-

teract with the virtual environment. Figure 15 depicts

the deformation of a real clay sphere and compares

it with a similar deformation, simulated on a virtual

sphere using our framework. Similar results are de-

picted in Figure 16.

Figure 16: Shapes made by participants using a real clay

ball (left) and a virtually simulated ball (right).

During the study, we asked all the participants

to use the deformation and cutting tools on a sphere

mesh. Moreover, the participants are also asked to de-

form and cut the same sphere mesh using Blender. In

order to ensure a fair comparison, we prohibited the

participants from utilizing any other tools available in

Blender, with the exception of the elastic deform and

cutting knife functionalities. To eliminate any bias in-

duced by the order of use of the two systems, half of

the participants are exposed to Blender ﬁrst and then

our framework, while for the other half, the sequence

is reversed. After ﬁnishing the experiments, the par-

ticipants are asked to rate both of the frameworks on

a scale of 1 (very poor) to 10 (very good) in terms of

the following three parameters.

• Physical realism: How closely does the interac-

tion with the virtual material in our sculpting ap-

plication match the interaction with real clay?

• Ease of use: How easy and intuitive is it to use the

sculpting tools to manipulate the virtual material

or object in our sculpting application?

• Responsiveness: While interacting with the ob-

ject during the sculpting, is there any lag between

the interaction being done and the visual update?

The t-test (Rice, 2006) is a commonly used tool

to analyze whether the differences between groups of

data are statistically signiﬁcant. In our experiment,

we ﬁrst ascertain if the user opinions differed signif-

icantly between the two groups, (a) those who used

Blender ﬁrst and (b) those who used our framework

ﬁrst. The null hypothesis in this t-test the user rating

patterns indicate that there is a signiﬁcant difference

between the sculpting experience in Blender and our

framework, for each of the measured parameters. If

the p-value is below a certain threshold (0.05 is a uni-

versally accepted criterion), the null hypothesis is re-

jected. The p-value for each parameter is reported in

Table 3. In all cases, the p-value is below 0.05, which

implies that both strategies are equally effective.

Table 3: P-value for the t-test.

Parameter p-value

Physical realism 0.0071

Ease of use 0.0383

Responsiveness 0.0001

The mean, median, and standard deviation of the

ratings of the user feedback are listed in Table 4. As

evident from the Table, the users rate their experience

using our application for virtual sculpting very favor-

ably. Moreover, the low value of standard deviation

denotes a lower disagreement of opinion among users.

Blender is a professional-grade tool with years of de-

velopment experience, and our application’s ratings

match it closely for the virtual sculpting task. We be-

lieve that our framework preserves physical plausibil-

ity and has the potential to deliver satisfactory results

for various kinds of shape modeling and design tasks.

Our method is also valuable for computing physically

plausible haptic feedback in gaming.

Table 4: Mean, median, and standard deviation of user feed-

back from the study.

Method Parameter Mean Median Std

Ours Physical realism 8.45 8.75 0.43

Ease of use 8.85 9.00 0.61

Responsiveness 9.35 9.00 0.58

Blender Physical realism 9.25 9.00 0.26

Ease of use 9.75 10.0 0.26

Responsiveness 9.90 10.0 0.22

6 LIMITATIONS AND FUTURE

WORK

Our work introduces a Galerkin-enhanced graph-

based FEM algorithm for interactive, real-time frac-

ture and cutting simulation. Our method can ren-

der fractures for extremely high-resolution meshes at

an interactive rate without any computational over-

head, regardless of the number of cracks introduced

within the object mesh. Using this algorithm, we

develop an interactive virtual sculpting framework

and present various dynamic simulation scenarios to

demonstrate its effectiveness and usability. We com-

pare our method with existing techniques and real-

world experiments to evaluate its performance. Our

method holds promise for various applications, in-

cluding 3D virtual surgery, asset creation, and more.

Our method enables the interactive simulation of

GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications

fractures in high-resolution meshes; however, it has

certain limitations in its current form. To achieve real-

time performance, we prioritize computational efﬁ-

ciency over accuracy in volume preservation. As a

result, the algorithm faces challenges in generating

and maintaining intricate crack patterns. A promising

future research direction is enhancing volume preser-

vation accuracy while maintaining real-time perfor-

mance. Implementing volume correction techniques

at each Galerkin grid level could be a potential ap-

proach to address this limitation.

REFERENCES

Areias, P. M. A. and Belytschko, T. (2005). Analysis

of three-dimensional crack initiation and propagation

using the extended ﬁnite element method. Interna-

tional Journal for Numerical Methods in Engineering,

63(5):760–788.

Arthur, D. and Vassilvitskii, S. (2007). K-means++: The

advantages of careful seeding. In Proceedings of the

Eighteenth Annual ACM-SIAM Symposium on Dis-

crete Algorithms, SODA ’07, page 1027–1035, USA.

Society for Industrial and Applied Mathematics.

Bargteil, A. W., Wojtan, C., Hodgins, J. K., and Turk, G.

(2007). A ﬁnite element method for animating large

viscoplastic ﬂow. ACM Trans. Graph., 26(3):16–es.

Blender Foundation (2023). Blender 3.6.4 lts. https://www.

blender.org/ Last accessed on 2-10-2023.

Bouaziz, S., Martin, S., Liu, T., Kavan, L., and Pauly, M.

(2014). Projective dynamics: Fusing constraint pro-

jections for fast simulation. ACM Transactions on

Graphics, 33(4).

Brandt, C., Eisemann, E., and Hildebrandt, K. (2018).

Hyper-reduced projective dynamics. ACM Transac-

tions on Graphics, 37(4).

Chen, Z., Yao, M., Feng, R., and Wang, H. (2014). Physics-

inspired adaptive fracture reﬁnement. ACM Trans.

Graph., 33(4).

Chentanez, N., M

uller, M., and Macklin, M. (2016). Real-

time simulation of large elasto-plastic deformation

with shape matching. In Proceedings of the ACM SIG-

GRAPH/Eurographics Symposium on Computer Ani-

mation, SCA ’16, page 159–167, Goslar, DEU. Euro-

graphics Association.

Chitalu, F. M., Miao, Q., Subr, K., and Komura, T. (2020).

Displacement-correlated xfem for simulating brittle

fracture. Computer Graphics Forum, 39(2):569–583.

De Goes, F. and James, D. L. (2017). Regularized kelvin-

lets: Sculpting brushes based on fundamental solu-

tions of elasticity. ACM Trans. Graph., 36(4).

Fan, L., Chitalu, F. M., and Komura, T. (2022). Simulat-

ing brittle fracture with material points. ACM Trans.

Graph., 41(5).

Hahn, D. and Wojtan, C. (2015). High-resolution brittle

fracture simulation with boundary elements. ACM

Trans. Graph., 34(4).

Hahn, D. and Wojtan, C. (2016). Fast approximations for

boundary element based brittle fracture simulation.

ACM Trans. Graph., 35(4).

Hirota, K., Tanoue, Y., and Kaneko, T. (2000). Simulation

of three-dimensional cracks. The Visual Computer,

16:371 – 378.

Irving, G., Teran, J., and Fedkiw, R. (2004). Invert-

ible ﬁnite elements for robust simulation of large de-

formation. In Proceedings of the 2004 ACM SIG-

GRAPH/Eurographics Symposium on Computer An-

imation, SCA ’04, pages 131–140, Goslar Germany,

Germany. Eurographics Association.

James, D. L. and Pai, D. K. (1999). Artdefo: Accurate

real time deformable objects. In Proceedings of the

26th Annual Conference on Computer Graphics and

Interactive Techniques, SIGGRAPH ’99, page 65–72,

USA. ACM Press/Addison-Wesley Publishing Co.

Khodabakhshi, P., Reddy, J. N., and Srinivasa, A. (2016).

Grafea: a graph-based ﬁnite element approach for

the study of damage and fracture in brittle materials.

Meccanica, 51:3129 – 3147.

Kim, T., De Goes, F., and Iben, H. (2019). Anisotropic elas-

ticity for inversion-safety and element rehabilitation.

ACM Trans. Graph., 38(4).

Koschier, D., Bender, J., and Thuerey, N. (2017). Robust

extended ﬁnite elements for complex cutting of de-

formables. ACM Trans. Graph., 36(4).

Macklin, M. and M

uller, M. (2013). Position based ﬂuids.

ACM Transactions on Graphics, 32(4).

Mandal, A., Chaudhuri, P., and Chaudhuri, S. (2022a).

Interactive physics-based virtual sculpting with hap-

tic feedback. Proceedings of the ACM on Computer

Graphics and Interactive Techniques, 5(1).

Mandal, A., Chaudhuri, P., and Chaudhuri, S. (2022b).

Simulating fracture in anisotropic materials contain-

ing impurities. MIG ’22, New York, NY, USA. Asso-

ciation for Computing Machinery.

Mandal, A., Chaudhuri, P., and Chaudhuri, S. (2023).

Remeshing-free graph-based ﬁnite element method

for fracture simulation. Computer Graphics Forum,

42(1):117–134.

Molino, N., Bao, Z., and Fedkiw, R. (2004). A virtual node

algorithm for changing mesh topology during simula-

tion. In ACM SIGGRAPH 2004 Papers, SIGGRAPH

’04, page 385–392, New York, NY, USA. Association

for Computing Machinery.

uller, M. (2008). Hierarchical position based dynamics.

In Workshop on Virtual Reality Interactions and Phys-

ical Simulations.

uller, M. and Gross, M. (2004). Interactive virtual ma-

terials. In Proceedings of Graphics Interface 2004,

GI ’04, page 239–246, Waterloo, CAN. Canadian

Human-Computer Communications Society.

O’Brien, J. F., Bargteil, A. W., and Hodgins, J. K. (2002).

Graphical modeling and animation of ductile fracture.

ACM Trans. Graph., 21(3):291–294.

O’Brien, J. F. and Hodgins, J. K. (1999). Graphical model-

ing and animation of brittle fracture. In Proceedings

of the 26th Annual Conference on Computer Graph-

ics and Interactive Techniques, SIGGRAPH ’99, page

Galerkin Enhanced Graph-Based FEM for Interactive Fracture and Sculpting Applications

137–146, USA. ACM Press/Addison-Wesley Publish-

ing Co.

Overby, M., Brown, G. E., Li, J., and Narain, R. (2017).

Admm ⊇ projective dynamics: Fast simulation of hy-

perelastic models with dynamic constraints. IEEE

Transactions on Visualization and Computer Graph-

ics, 23(10):2222–2234.

Pfaff, T., Narain, R., de Joya, J. M., and O’Brien, J. F.

(2014). Adaptive tearing and cracking of thin sheets.

ACM Trans. Graph., 33(4).

Rice, J. A. (2006). Mathematical Statistics and Data Anal-

ysis. Belmont, CA: Duxbury Press., third edition.

Sin, F. S., Schroeder, D., and Barbi

c, J. (2013). Vega: Non-

linear fem deformable object simulator. Computer

Graphics Forum, 32(1):36–48.

Smith, B., Goes, F. D., and Kim, T. (2018). Stable neo-

hookean ﬂesh simulation. ACM Trans. Graph., 37(2).

Stomakhin, A., Howes, R., Schroeder, C., and Teran, J. M.

(2012). Energetically consistent invertible elasticity.

In Proceedings of the 11th ACM SIGGRAPH / Eu-

rographics Conference on Computer Animation, EU-

ROSCA’12, pages 25–32, Aire-la-Ville, Switzerland,

Switzerland. Eurographics Association.

Stomakhin, A., Schroeder, C., Chai, L., Teran, J., and Selle,

A. (2013). A material point method for snow simula-

tion. ACM Trans. Graph., 32(4).

Terzopoulos, D. and Fleischer, K. (1988). Modeling inelas-

tic deformation: Viscolelasticity, plasticity, fracture.

SIGGRAPH Comput. Graph., 22(4):269–278.

Wicke, M., Ritchie, D., Klingner, B. M., Burke, S.,

Shewchuk, J. R., and O’Brien, J. F. (2010). Dy-

namic local remeshing for elastoplastic simulation.

In ACM SIGGRAPH 2010 Papers, SIGGRAPH ’10,

New York, NY, USA. Association for Computing Ma-

chinery.

Wolper, J., Chen, Y., Li, M., Fang, Y., Qu, Z., Lu, J., Cheng,

M., and Jiang, C. (2020). Anisompm: Animating

anisotropic damage mechanics. ACM Trans. Graph.,

39(4).

Wolper, J., Fang, Y., Li, M., Lu, J., Gao, M., and Jiang, C.

(2019). Cd-mpm: Continuum damage material point

methods for dynamic fracture animation. ACM Trans.

Graph., 38(4).

Xian, Z., Tong, X., and Liu, T. (2019). A scalable

galerkin multigrid method for real-time simulation of

deformable objects. ACM Transactions on Graphics,

38(6).

Xu, H., Sin, F., Zhu, Y., and Barbi

c, J. (2015). Nonlinear

material design using principal stretches. ACM Trans-

actions on Graphics, 34(4).

GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications