
Fast Detection of Jitter Artifacts in Human Motion Capture Models
Mateusz Pawłowicz
a
, Witold Alda
b
and Krzysztof Boryczko
c
AGH University of Krakow, Cracow, Poland
{mpawlowicz, alda, boryczko}@agh.edu.pl
Keywords:
Character Animation, Motion Capture, Jitter, Animation Datasets, BVH.
Abstract:
Motion capture is the standard when it comes to acquiring detailed motion data for animations. The method is
used for high-quality productions in many industries, such as filmmaking and game development. The quality
of the outcome and the time needed to achieve it are incomparable with the keyframe-based manual method.
However, the motion capture data sometimes gets corrupted, which results in animation artifacts that make it
unrealistic and unpleasant to watch. An example of such an artifact is a jitter, which can be defined as the rapid
and chaotic movement of a joint. In this work, we focus on detecting the jitter in animation sequences created
using motion capture systems. To achieve that, here is proposed a multilevel analysis framework that consists
of two metrics: Movement Dynamics Clutter (MDC) and Movement Dynamics Clutter Spectrum Strength
(MDCSS). The former measures the dynamics of a joint, while the latter metric allows the classification of a
sequence of frames as a jitter. The framework was evaluated on popular datasets to analyze the properties of
the metrics. The results of our experiments revealed that two of the popular animation datasets, LAFAN1 and
Human3.6M, contain instances of jitter, which was not known before inspection with our method.
1 INTRODUCTION
Motion capture (MoCap) is currently the most potent
method for realistic human animations in movies and
video games. It has many advantages compared to tra-
ditional frame-by-frame creation and procedural an-
imation formulas. With motion capture techniques,
animators can quickly obtain even very complex and
unique motion, thus drastically reducing overall costs
and production time. Motion capture also has its
drawbacks and disadvantages. It requires expensive
and complex equipment, including cameras, sensors,
and sophisticated software. Moreover, to get the most
out of this technology, it is also required to cooperate
with professionally trained motion capture actors.
The method itself brings about several technical
issues that may limit its effectiveness. The first well-
known problem is the need for proper calibration of
the whole system, including the configuration of cam-
eras and sensors and the correct illumination of the
screen. The second common issue, especially with
marker-based solutions, is the occlusion of the sen-
sors and/or too fast movement of the sensor, which
may cause ”losing” it by the software. The actor also
a
https://orcid.org/0009-0008-2109-505X
b
https://orcid.org/0000-0002-6769-0152
c
https://orcid.org/0000-0002-3392-3739
has physical limitations, but we omit them here.
Instead, we notice that the recorded motion cap-
ture animation is often noisy and contains spikes, jit-
ter, gaps, and other errors and artifacts. Such data
must be cleaned up in a post-processing procedure
for smooth and realistic movement. Many tools can
help clean up, with popular ones such as Blender,
Maya, and MotionBuilder among them. There are
also several denoising algorithms, starting from rel-
atively simple ones and ending with sophisticated
machine learning-based approaches (Holden, 2018).
Still, the processing of raw data is long and often
painstaking. Even though we are aware of using post-
processing algorithms, we can easily find final anima-
tions stored in databases that have errors and produce
unnatural motion. Checking the quality of recorded
animation simply by carefully observing the motion
is a natural process that takes much time.
This paper aims to address this problem by finding
measures that can help us detect jitter in animation
sequences through automatic analysis of the dataset
itself. Our contributions are as follows:
• We propose two metrics: Movement Dynam-
ics Clutter (MDC) metric to detect dynamic and
irregular movement of a joint and DFT-based
Movement Dynamics Clutter Spectrum Strength
(MDCSS) metric for detecting jitter in these
Pawłowicz, M., Alda, W. and Boryczko, K.
Fast Detection of Jitter Artifacts in Human Motion Capture Models.
DOI: 10.5220/0013144400003912
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 20th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2025) - Volume 1: GRAPP, HUCAPP
and IVAPP, pages 77-88
ISBN: 978-989-758-728-3; ISSN: 2184-4321
Proceedings Copyright © 2025 by SCITEPRESS – Science and Technology Publications, Lda.
77

movements;
• We suggest an analysis method that allows the in-
spection of joint movement dynamics in anima-
tion datasets at various levels: dataset level, se-
quence level, and frame level;
• We evaluate our analysis method to verify
its properties and compare popular animation
datasets concerning jitter presence;
• Using our proposed metrics, we also detect in-
stances of jitter in two widely-used animation
datasets: LAFAN1 (Harvey et al., 2020) and Hu-
man3.6M (Ionescu et al., 2014).
2 RELATED WORK
2.1 Errors and Animation Data
Clean-up
The technical aspect of MoCap technology is not cru-
cial for our paper. We assume that we get the data
”as is” and do not make improvements in the data ac-
quisition process. However, we have to make even a
general analysis of the used technology, as it has an
important impact on types of errors and artifacts in
the animation sequences.
We may distinguish two main approaches to
gathering motion data: marker-based and marker-
less. Optical-based motion capture (OMC) (Callejas-
Cuervo et al., 2023) is the most popular and reli-
able method in the first group. Currently, it has out-
performed others, such as inertial or magnetic mark-
ers. It uses either passive, reflective markers or active
LED markers. Despite their advantages, optical mark-
ers have certain flaws, such as occlusion when mark-
ers hide from the camera or fast marker movements,
which cause gaps and noisy animation. The occa-
sional change of marker position (e.g., when slipped
or detached) adds extra distortion. It is also well
known that the optical markers system is excellent in
the coarse movement of the entire body. At the same
time, it loses control of tiny details (such as fingers)
and gestures, which often move unnaturally. A com-
prehensive overview of the detection and classifica-
tion of errors in optical MoCap systems can be found
in (Skurowski and Pawlyta, 2022).
In the second group, the markerless approach, we
have depth-sensing cameras that can capture motion
without physical markers, thus being convenient and
comfortable for the actors. However, this method
needs a clean-up process to improve the quality of
motion. It can be based on smoothing and denois-
ing algorithms, beneficial for cheap home motion cap-
ture systems with, say, a single RGBD camera (Hoxey
and Stephenson, 2018), where smoothing is achieved
in two steps: by getting rid of positions that differ
by more than 5 percent from the average and sub-
sequently using the Kalman filter. Similar solutions
based on moving average, B-spline smoothing, and
Kalman filter are presented in (Ardestani and Yan,
2022).
2.2 Animation Dataset Analysis
Animation of data collected by motion capture sys-
tems has a spatiotemporal nature. This data consists
of poses that sample continuous movement performed
by an actor at different frames (timesteps). Frames
can be described in various file formats, one of which
is the BVH format (Meredith and Maddock, 2001).
It represents a hierarchy of joints, as well as anima-
tion details, such as framerate (FPS) and number of
frames. Then it follows with the global position of
a skeleton root and local rotations of all the joints in
each frame. This format is one of the most popular, as
it has public specifications and describes well human
movements.
Such animation created from motion capture data
has many applications in the modern world. It appears
in movies, computer games (Geng and Yu, 2003) and
in the entertainment industry (Bregler, 2007). Less
recognizable applications are analyses for automatic
recognition and classification of the type of human
movement (Kadu and Kuo, 2014; Ijjina and Mohan,
2014; Patrona et al., 2018). This technology is also
used in industry (Menolotto et al., 2020), where it is
most often a component of real-time systems. Re-
gardless of the application, the quality of the final ef-
fect largely depends on the quality of the data that
constitute information about the movement sequence.
Hence, a preliminary analysis is often carried out to
detect potential errors and imperfections.
Even with the best motion capture data, some
post-processing is usually being done. The role of
data denoising is of increasing importance because
the quality of animation is something that the human
eye can verify instantly. It is always a non-trivial task;
however, currently, the process itself becomes more
and more automatic. There are several elaborate algo-
rithms. In (Liu et al., 2014) the authors present a so-
phisticated, hence classical approximation algorithm.
Holden in (Holden, 2018) uses an innovative method
based on neural networks to map the positions and ro-
tations of an animated skeleton based on the raw posi-
tions of markers captured by a motion capture system.
Some well-known utility programs that pro-
cess animation data include Matlab MoCap Tool-
GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications
78

box (Burger and Toiviainen, 2013) and RMo-
Cap (Hachaj and Ogiela, 2020). The first is a set of
Matlab functions for visualization and statistical anal-
ysis (e.g., calculation of mean, standard deviation) of
various metrics in motion capture data (e.g., velocity,
acceleration). The toolbox is still being maintained
and developed. It also allows us to perform Princi-
pal Component Analysis (PCA) on the animation se-
quence to derive complexity-related movement fea-
tures. The second solution uses the R programming
language package with a similar purpose, i.e., to vi-
sualize, analyze, and perform statistical processing. It
allows motion correction to reduce foot skating and
motion averaging to remove random errors, provided
that a motion has been recorded multiple times. The
solution also includes utility for conversions between
hierarchical and direct kinematic models.
Other work focused on comparing data from mo-
tion capture for particular purposes. Four metrics
were proposed to distinguish the motion of the hand
of a subject who suffered cerebral palsy from the reg-
ular movement of the hand (Montes et al., 2014).
Those metrics are logarithmic dimensionless jerk,
mean arrest period ratio, peaks metric, and spectral
arc length, among which the latter achieved the best
results. Another piece of research compared various
motion capture systems by collecting treadmill walk-
ing animations (Manns et al., 2016). The authors per-
formed the analysis using PCA and calculated Shan-
non entropy to compare four different systems: three
marker-based and one markerless. This analysis was
correlated with the fact that the markerless solution
gives a lower quality of captured animation than other
solutions.
Recently, a new framework for analysis of lo-
comotive datasets has been proposed that could be
used, e.g., for the motion matching approach (Abiche-
quer Sangalli et al., 2022). It focuses on the cover-
age of linear and angular speeds of animated charac-
ters, frame usage frequency, planned locomotion path,
used and unused animations, transition cost, and num-
ber. The solution also incorporates visualization of
linear and angular speed coverage across the anima-
tion dataset. It allows for identifying types of transi-
tions in motion matching that may be difficult to per-
form due to the lack of animation sequences with cor-
responding speeds.
2.3 Anomaly Detection in Time Series
Jitter detection in animation can also be viewed as
an anomaly detection problem applied to time se-
ries. Among the commonly used methods for this
purpose are PCA, Savitzky-Golay, and Kalman filters
and recurrent neural networks, such as those based on
LSTM and GRU layers. As qualitative artifact de-
tection in animation is a rarely addressed topic, we
would like to briefly present approaches used in mul-
tivariate time series anomaly detection problems re-
lated to other fields. Many learning-based approaches
suffer from inaccuracies at an early stage due to ini-
tialization time. An outlier-resistant sampling can be
used in conjunction with domain-specific clustering
algorithms to mitigate such an issue in online ser-
vices systems (Ma et al., 2021). Recent literature also
uses a weighted hybrid algorithm that combines mul-
tiple methods (e.g., moving median, Kalman filter,
Savitzky-Golay filter) for anomaly detection in long-
term cloud resource usage planning (Nawrocki and
Sus, 2022). Moreover, deep ensemble models were
successfully applied in intrusion monitoring applica-
tions and fraud detection (Iqbal et al., 2024).
3 DATASET ANALYSIS METHOD
3.1 Definition of Movement Dynamics
Clutter (MDC) Metric
Animation sequences based on data collected by mo-
tion capture systems allow modeling movement in
great detail. However, this data can also contain some
artifacts that impact the realism of the actions cap-
tured by the actor. An example of such errors is jit-
ter, which can be described as a rapid and chaotic
movement of a joint. The magnitude of the noise in-
troduced by this phenomenon can vary from barely
noticeable to very disruptive. As a result, on many
occasions, rotations of joints change rapidly, and the
skeleton’s bones twist unnaturally. Although there are
some automatic ways to mitigate this problem (e.g.,
applying Savitzky-Golay smoothing), it is often the
case that animators need to perform a manual review
or statistical analysis to take care of the issue.
To address this inconvenience, we decided to de-
sign a metric that can be used to detect jitter and com-
pare animation sequences and datasets in terms of the
presence of jitter. In order to achieve that, this metric
also needs to consider various technical aspects re-
lated to this data. The spatiotemporal data is multi-
dimensional, which makes it hard to analyze quickly
without any aggregation. The structure of a skeleton
can also be different between datasets, which trans-
lates to different numbers of joints and their hier-
archy. Two animation sequences from two datasets
could vary in terms of recording framerate. Finally,
the scale of the skeleton can differ between datasets,
as most animation formats define poses using simply
Fast Detection of Jitter Artifacts in Human Motion Capture Models
79

Figure 1: A visualization of MDC metric calculation
method. Positions of joint j in the 3 consecutive frames
are indicated as p
j,t
, p
j,t+1
and p
j,t+2
. These positions are
used to derive velocities v
j,t
and v
j,t+1
to calculate length
of dv
j,t:t+1
and angle α
j,t
, which are core components of
the suggested metric.
abstract floats. All these problems must be considered
when designing a metric that allows us to compare
any two animation sequences.
Therefore, we suggest a Movement Dynamics
Clutter (MDC) metric that considers all the mentioned
technical aspects. The definition of calculation for a
single joint can be seen in Equation 1. We identified
that the core nature of the jitter is chaotic changes in
both the velocity of a joint (v
j,t
, v
j,t+1
) and the angle
of these velocities (α
j,t
) between consecutive frames t
and t +1 (illustrated in Figure 1). The angle is defined
in radians and squared to smooth the metric in case of
minor changes and amplify significant changes. This
information can be derived from most animation for-
mats, as all that is needed are the global positions of
all the joints. We also normalize the metric by mul-
tiplying by FPS (F) and dividing by the sum of the
lengths of all the bones of the skeleton (S). These two
operations allow us to standardize the calculated val-
ues concerning the time and space dimensions of the
datasets. Normalization of space dimensions could
also be achieved by calculating the height of the skele-
ton instead of the sum of the bone lengths. However,
this proved to be cumbersome without manual work,
as the rest of the poses of skeletons in MoCap datasets
are not always T-poses or A-poses, making it hard to
calculate the distance from feet to head.
MDC
j,t
=
F
S
α
2
j,t
||dv
j,t:t+1
|| (1)
The metric can also be generalized for the calcula-
tion at the frame level by simply aggregating the val-
ues from all joints using the maximum (Equation 2);
as for a frame, the crucial information is whether there
is jitter in any of the joints. Although this loses some
detail, it allows for easy, high-dimensional data anal-
ysis. Moreover, the metric can also be averaged over
consecutive frames W (a window) to further aggregate
the MDC metric (Equation 3) and, e.g., apply it to the
whole dataset.
MDC
t
= max
j∈J
MDC
j,t
(2)
MDC
W
=
1
|W |
|W |
∑
t=1
MDC
t
(3)
3.2 Movement Dynamics Clutter
Spectrum Strength (MDCSS)
Metric
While the proposed MDC metric can detect chaotic
movement successfully, it does not distinguish it from
a single rapid joint movement. An example of such a
rapid movement might be a dynamic stomp when a
character’s foot bounces off the floor. As we sam-
ple continuous movement, the change in the velocity
vectors between consecutive frames could be angled
to almost 180
◦
. According to Equation 1, this results
in a very high metric value for the joint and, conse-
quently, for the entire frame. Our analysis indicated
this problematic scenario when comparing the regular
animation sequence from the LAFAN1 dataset with
the jittery sequence from Contemporary Dance (Aris-
tidou et al., 2017). The dynamic stomp of the charac-
ter in the first sequence achieves an indistinguishable
value of the MDC metric from the jitter that occurs on
the left hand of the second animated character, which
is demonstrated in Figure 2. The highlighted window
refers to these examples, and as can be seen, the MDC
metric has an even higher value for stomp than for jit-
ter.
To address this shortcoming, we decided to treat
our metric as a signal and look for periodicity in it.
We achieve this by calculating the discrete Fourier
transform (DFT) using the FFT algorithm on a sliding
time window W , which consists of multiple consecu-
tive frames. For most of our experiments, we used a
window that reflected a third of a second, as it gives
a satisfying sample size for all the common FPS con-
figurations in motion capture animation sequences.
The actual values of DFT represent the energy dis-
tribution between frequencies, so this mechanism is
expected to differentiate the problematic cases. In
regular movement, we do not expect a peak of en-
ergy on any particular frequency, as our MDC metric
usually has low values. On the other hand, when jit-
ter occurs, we could expect that some frequencies will
dominate in terms of energy value, since jitter causes
regular spikes in the MDC metric.
Therefore, as our second metric for jitter analysis,
we use a maximum of real DFT components, omitting
the base frequency component (since it is just a sum
of the values of the signal samples). We call that met-
ric Movement Dynamics Clutter Spectrum Strength
(MDCSS). Assuming that the sequence of values of
GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications
80
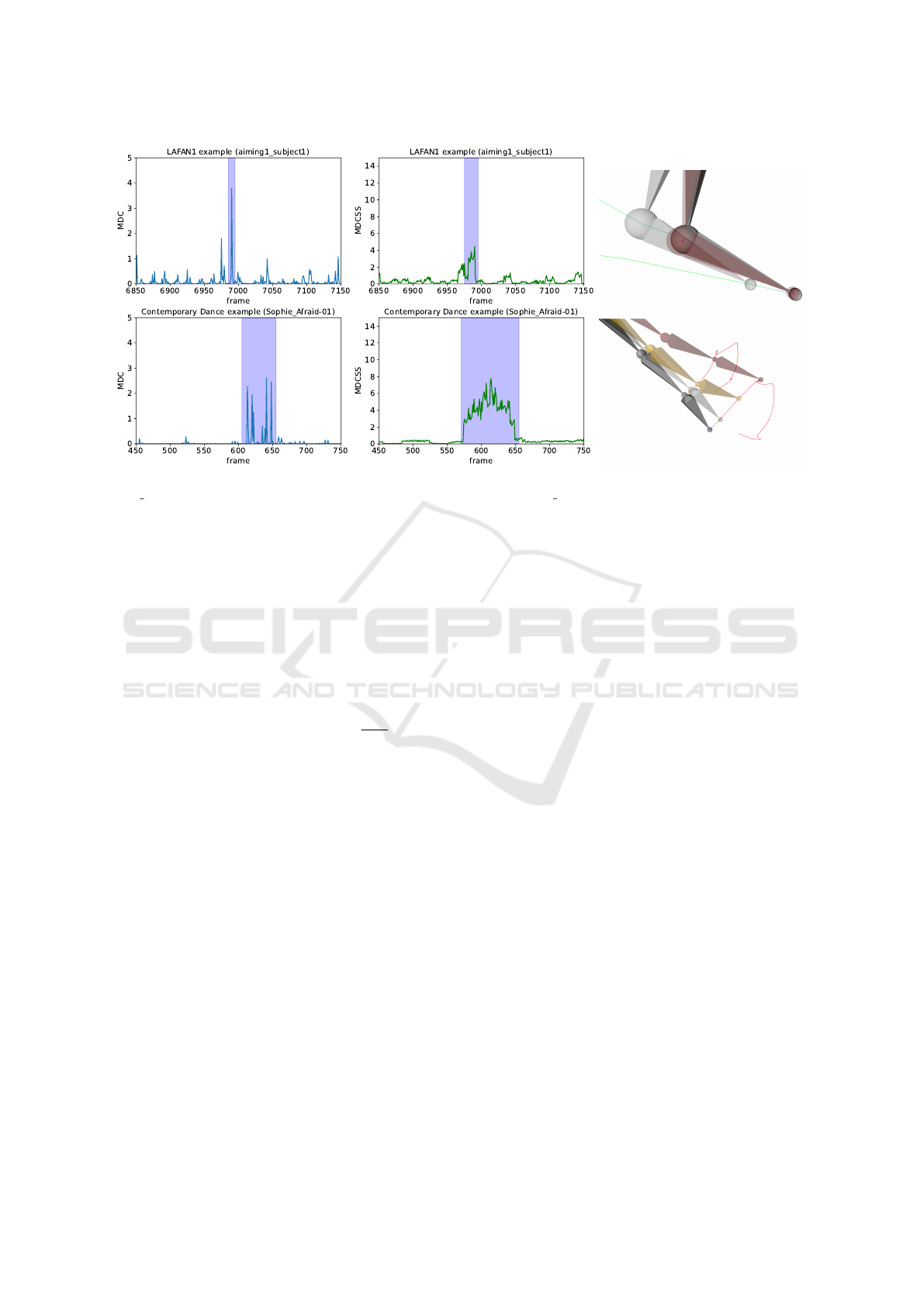
Figure 2: Comparison of MDC (blue) and MDCSS (green) metrics on dynamic stomp in LAFAN1 example (aim-
ing1 subject1) and short jitter at the left hand in Contemporary Dance (Sophie Afraid-01). The animation of these examples
is visualized on the right using joint colors. The gray frames are preceding the event, while the colored frames are related to
the event. For LAFAN1 (30 FPS), visualization has a step of 1 frame. For Contemporary Dance, the preceding frames are 12
frames apart, while the event frames are two frames apart. The trajectories of the joints are also visualized using color lines
(green - preceding trajectory, red - following trajectory), with points indicating joint locations in subsequent frames.
our MDC metric in window W could be defined as
MDC
W
(according to Equation 4), MDCSS metric can
be expressed as in Equation 5.
MDC
W
= {MDC
t
}
t=0,1,...,|W |−1
(4)
MDCSS
W
=
|W |−1
max
k=1
(
Re
|W |−1
∑
t=0
MDC
t
e
−i2πkt
|W |
!)
(5)
With the MDCSS metric defined in this manner,
we empirically assigned metric thresholds so that the
characteristics of the movement in the window could
be categorized. A window with value FM
W
< 8
can be considered a window with regular movement,
without any significant jitter artifacts or extraordinary
dynamics. Beyond that value, we observed some in-
stances of the artifact and many rapid movements per-
formed by the character. A window with FM
W
∈
[8, 20] is at the warning level. Such a fragment of an
animation is likely to contain some dynamic move or,
on some occasions, could contain some less chaotic
instances of jitter. It is advised to inspect such parts
of an animation sequence. Lastly, any window with
FM
W
> 20 should be treated as one with erroneous
data with jitter. This threshold was determined by in-
specting the most dynamic joint moves in the tested
datasets, which were not jitter.
3.3 Dataset Analysis Methodology
By using both metrics in conjunction, we can ana-
lyze animation data at various levels of detail: dataset
level, animation sequence level, and frame level. As
the metrics are based solely on the global positions of
joints, they can be applied to most formats of anima-
tion data.
At the dataset level, the MDC and MDCSS met-
rics can be averaged with respect to the total number
of frames. This statistic can be used to quantify the
jitter and unpredictability of the dataset. Properly cal-
culated values can then be used to compare different
datasets, independently of the joint hierarchy, fram-
erate, or scale used for the skeleton representing the
animated character.
The metrics can also be used at the dataset level,
i.e., by averaging each animation sequence. This
method allows pinpointing the sequence that is an
outlier when it comes to quality. Such problematic
animation could be, e.g., re-recorded while avoiding
the issue that caused the jitter or fixed in the post-
processing stage. Moreover, this approach can be
used to compare jitter in animation sequences from
different datasets using a single number.
In some cases, excluding entire animation se-
quences would result in having a small dataset. Here,
frame-level analysis of the MDCSS metric of anima-
tion sequences can be used. The metric calculated
Fast Detection of Jitter Artifacts in Human Motion Capture Models
81

on a sliding window makes distinguishing parts with
jitter from those without it possible. The jittery parts
(error level) could then be filtered out from the dataset
instead of removing the whole sequence, if such a
solution fits the purpose of use. On the other hand,
the parts at a warning level with dynamic movement
should be inspected, provided that they are detected
in an unexpected fragment of animation (e.g., a non-
dynamic one). This warning may indicate a slightly
noticeable jitter there. Furthermore, frame-level anal-
ysis can also be used to compare two animation se-
quences from two different datasets in greater detail
than using a single number (as in Figure 2).
Finally, the MDC metric allows us to perform the
jitter inspection at the joint level in a single frame. If a
given window has a high value of the MDCSS metric,
we can inspect the MDC metric values in that window
and find the frames with values that are outliers. In
these frames, we can inspect the distribution of MDC
values across the skeleton’s joints. It allows for the se-
lection of the subset of joints that cause a high metric
value and are likely to be jittery. This level of analysis
helps when analyzing warning levels of the MDCSS
metric. It also allowed us to detect the subsampling
problem in the case of a stomp in one of the anima-
tion sequences in the LAFAN1 dataset (Figure 2).
4 EXPERIMENTS AND
DISCUSSION
4.1 Popular Evaluated Datasets
For the evaluation of the suggested metrics, we de-
cided to use several popular datasets. Their quantita-
tive details are presented in Table 1.
The LAFAN1 (Harvey et al., 2020) consists of
animation sequences captured by five actors in a
production-grade motion capture studio in collabora-
tion with Ubisoft. The subjects perform various ac-
tions, such as moving and aiming weapons, walk-
ing, running, fighting, or navigating obstacles. The
authors have published the dataset in the BVH file
format. It has been used in various research publi-
cations, most commonly to test the performance of
neural networks used for motion in-betweening (Qin
et al., 2022; Ren et al., 2023; Oreshkin et al., 2024).
Human3.6M (Ionescu et al., 2014) is a dataset
dedicated to the estimation of human poses, but it also
contains animation data captured from motion capture
to match these poses. The shared animation part of
the dataset was captured at 50 FPS by seven actors
performing different actions (e.g., walking, phoning,
eating). The data is available as CDF (Common Data
Format) files in various parameterization formats. We
exported the animation in BVH format based on pose
data with angles and subsampled it to 25 FPS, as this
setup was also used to benchmark results for machine
learning models in research (Harvey et al., 2020).
Two more datasets were collected by Bandai
Namco Research (Kobayashi et al., 2023) that con-
tain short animation sequences performed in vari-
ous styles. The first dataset consists of 17 activities
(e.g., fighting, dancing, waving hands) recorded in 15
styles. The other has 10 action types (mostly loco-
motion and hand actions) performed in 7 styles but in
much larger quantities. Both datasets were published
in the BVH animation format.
Contemporary Dance (Aristidou et al., 2017) is
another dataset that contains dances performed by
nine actors in various moods (e.g., bored, afraid, an-
gry, or relaxed). The dataset is also a part of a much
larger AMASS dataset (Mahmood et al., 2019). It was
shared in various formats (BVH, FBX, C3D) to in-
crease accessibility, but the BVH file format contains
some very noticeable instances of jitter. We used this
animation format, as the animation quality is much
worse compared to other datasets.
4.2 Experiments Setup
All the metric evaluation experiments were performed
on a machine with AMD Ryzen 9 5950X, 64 GB
DDR4 RAM, and RTX 3080 TI. Due to large vol-
umes of data, we calculated metrics using PyTorch
with GPU acceleration. We used Python 3.10.14 for
experiments, along with PyTorch 2.4.0 and NumPy
1.26.4. We derived the positions of joints based on the
BVH format of animation using forward kinematics.
All animation and motion path visualizations were
created using Blender 4.2.2. We used a time window
of
1
3
s when calculating the MCDSS metric in the ex-
periments and the same thresholds as defined in Sec-
tion 3.2.
4.3 Comparison of Popular Datasets
We benchmark our metrics by evaluating them on all
the datasets mentioned in Section 4.1. We perform
dataset-level analysis to calculate the average metrics
values for these datasets and count the number of er-
rors and warnings detected. We also count the number
of error and warning windows as a chain of consecu-
tive frames classified similarly. These windows could
be used to count the number of instances of jitter or
dynamic movement.
The experiment outcome was collected in Table 2
and Table 3. As expected, Contemporary Dance has
GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications
82
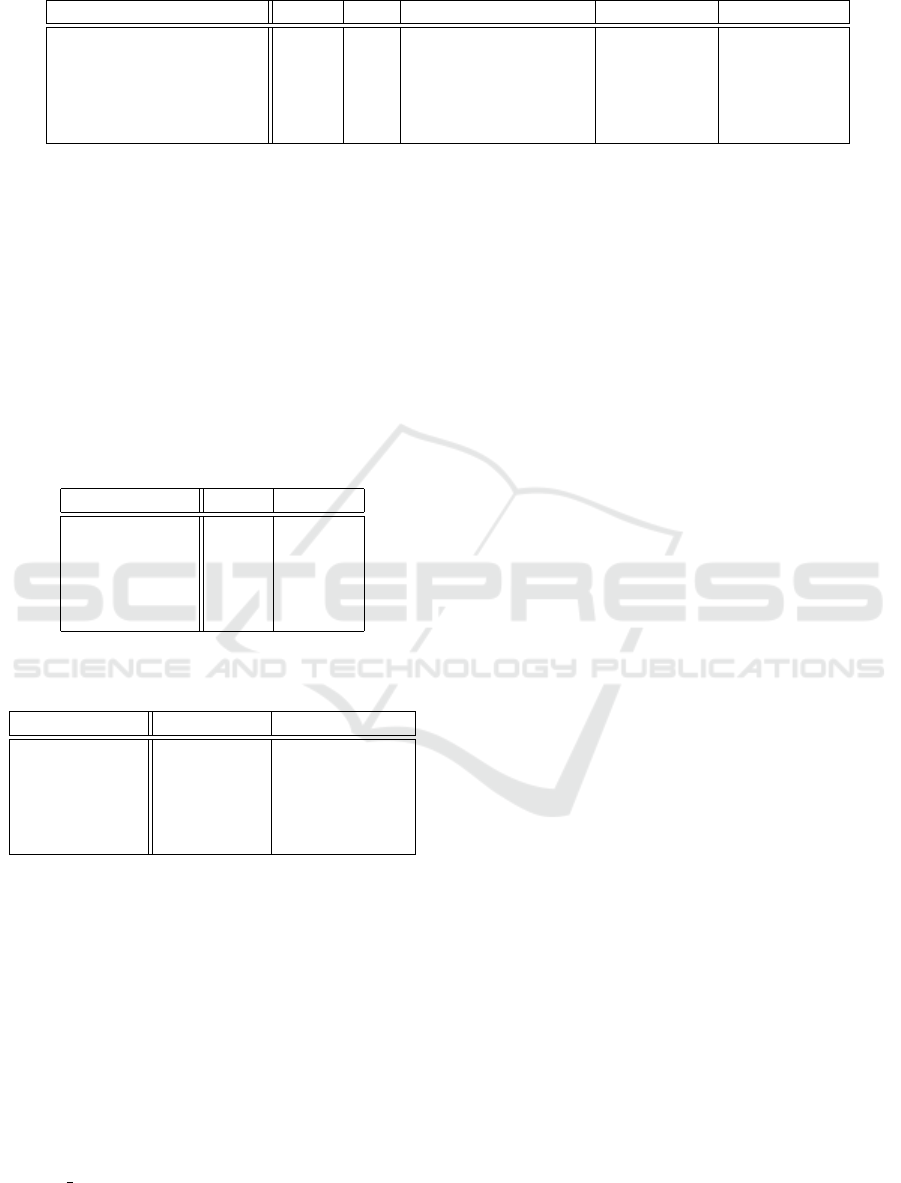
Table 1: Comparison of datasets’ properties used for the experiments.
Dataset Joints FPS Animation sequences Total frames Total time [s]
LAFAN1 22 30 77 496,672 16,556
Human3.6M 25 25 210 263,743 10,550
Bandai Namco Dataset 1 22 30 175 36,665 1,222
Bandai Namco Dataset 2 22 30 2,902 384,931 12,831
Contemporary Dance 31 120 133 989,150 8,242
the highest metrics scores due to multiple jitter in-
stances. The average value of the MDCSS metric
strongly deviates from the other datasets and suggests
that every frame in that dataset is at a warning level.
The large numbers of error and warning frames and
windows further signify it. Bandai Namco Dataset 2
achieves the best results, as most animations there do
not contain much character movement and are not as
dynamic as some sequences in other datasets. Both
Bandai Namco datasets do not contain errors accord-
ing to our MDCSS metric.
Table 2: Average metrics values per frame for tested
datasets.
Dataset MDC MDCSS
Contemporary 0.408 8.109
LAFAN1 0.113 0.462
Bandai 1 0.106 0.431
Bandai 2 0.084 0.409
Human3.6M 0.099 0.396
Table 3: Number of error and warning frames (f) and win-
dows (w) in the compared datasets.
Dataset Errors (f/w) Warnings (f/w)
Contemporary 85372/7543 77892/17563
LAFAN1 16/6 206/140
Bandai 1 0/0 45/43
Bandai 2 0/0 469/458
Human3.6M 21/17 355/205
All the datasets, except for Contemporary Dance,
achieve relatively similar average values for our met-
rics. However, in both LAFAN1 and Human3.6M,
our metrics detected errors. We conducted further in-
vestigation using frame-level analysis and found that
both datasets contain short instances of jitter on these
error windows. Human3.6M contains very short er-
rors in many animation sequences (e.g., in the se-
quence ”Sitting Down” performed by subject 5) and
looks like short occlusions. Artifacts are most com-
monly found in the hands. In the case of LAFAN1,
all the errors are present in a single animation se-
quence, ”Obstacles 5,” performed by subject 3 (ob-
stalces5
subject3). The sequence contains dynamic
maneuvers, such as running, jumping, and tripping
over. In some instances, it looks like the motion cap-
ture system mismatched the position of all the joints,
resulting in a visible discontinuity and jumps in the
motion path of the character. On other occasions, it
again looks like the reason is occlusion. Two warn-
ings are also detected in this sequence: a barely no-
ticeable short foot jitter and a dynamic landing from
a jump.
We decided to manually remove the instances of
jitter at error levels from the LAFAN1 example by
applying interpolation between keyframes to compare
the metrics’ values with and without artifacts in the
animation. While the manual adjustment of the posi-
tions of character joints seemed to give a more real-
istic result, we would like to disclose that we are not
professional animators, and the actual realism of the
fixed animation could be further improved. The main
objective of the adjustment was to remove the jitter
from the sequence, which was achieved. The output
of the frame-level analysis of this animation clip is
presented in Figure 3. We can see that the application
of changes causes our MDCSS metric to return to the
normal range of values. This reinforces the usabil-
ity of our framework in detecting instances of jitter in
animation sequences.
4.4 Detecting Artificial Jitter in
LAFAN1 Dataset
To evaluate our MDCSS metric comparatively, we de-
cided to benchmark it on the detection of artificial
jitter added to a subset of the LAFAN1 dataset. We
are unaware of any other research that focused on de-
tecting this type of artifact, so we chose to compare
against some commonly used methods for anomaly
detection in multidimensional time series. We se-
lected the PCA and Savitzky-Golay filter to serve as a
baseline for comparison.
The methods were benchmarked on animation se-
quences performed by subject 3, as real jitter is also
present. Artificial jitter was added to all the ani-
mation sequences except the one that contains ac-
tual instances of the artifact. This was achieved by
corrupting every 10-second window of the animation
with a 0.25-1s jittery fragment applied to a single
skeleton joint. The displacement of the joint loca-
Fast Detection of Jitter Artifacts in Human Motion Capture Models
83
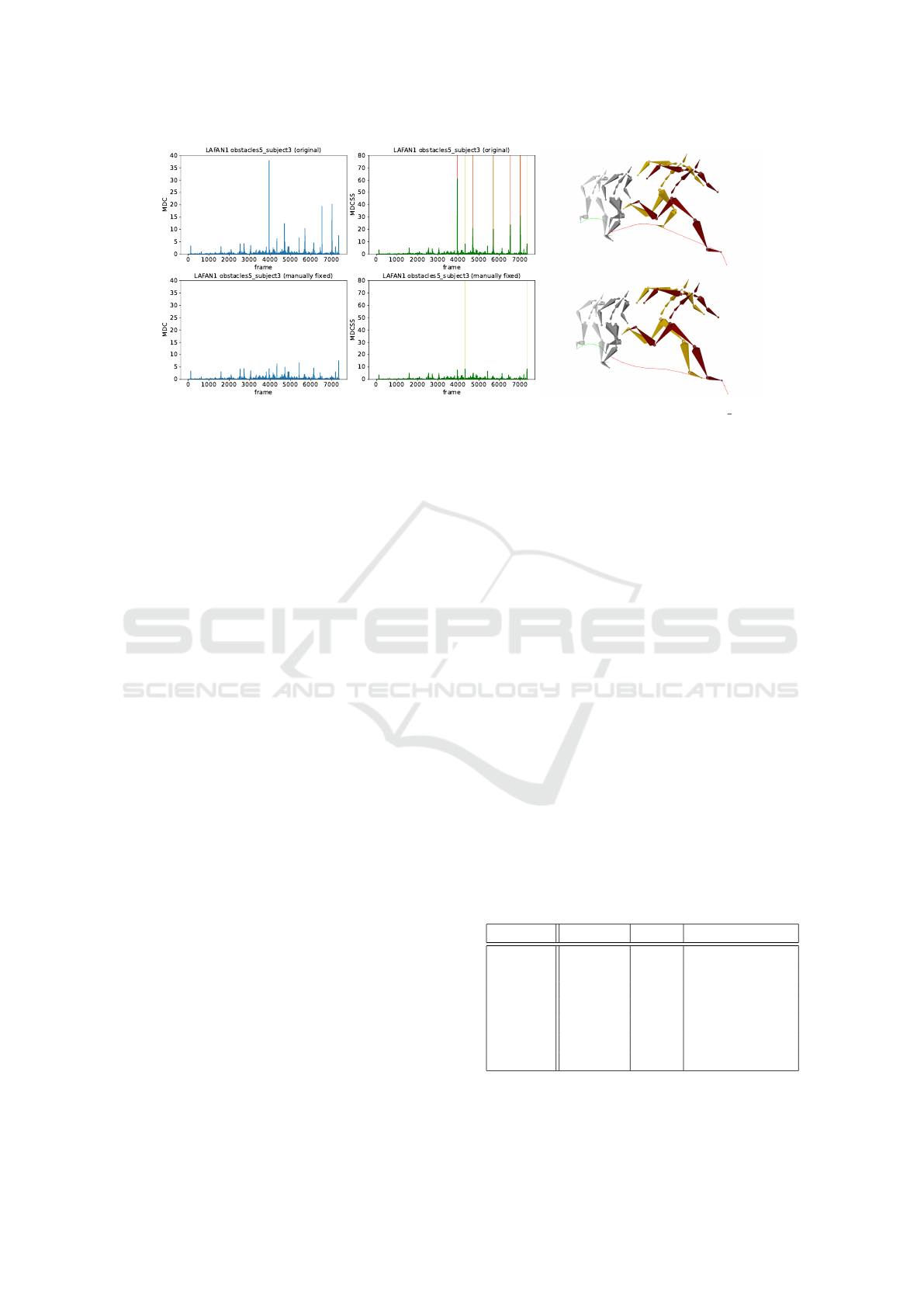
Figure 3: Comparison of metrics before and after manually attempting to fix animation sequence obstacles5 subject3 from
LAFAN1 dataset. The yellow and red zones on the plots correspond to warning and error event intervals. The visualization
on the right shows a jitter instance around frame 4700. Yellow and red frames are one frame apart. In the original sequence,
the left leg of the character is unnaturally twisted in the yellow frame and makes a sudden correction in the red frame. The
fixed version does not have this artifact. Some preceding frames with jitter have been omitted to improve visibility in the top
example.
tion is added to all its coordinates according to the
normal distribution N (0, σ). We parameterized σ us-
ing skeleton length and tested the following values of
σ: 0.02S, 0.0175S, 0.015S, 0.0125S, 0.01S, 0.0075S
and 0.005S. This methodology contains a simplifica-
tion, as displacement of the joint location does not
preserve its length. The sequence with real jitter was
not altered in any way to benchmark the methods in a
real-life scenario.
The detection was carried out on 10-frame clips.
A jittery window was classified as detected if a 10-
frame clip intersects it, and the method labeled it as
anomalous. A normal clip was defined as one that
does not intersect any jitter window.
Our MDCSS metric has a naturally defined error
level, so we used that to classify anomalous clips.
We decided on 22 principal components while per-
forming PCA and using the quadratic reconstruction
error as the detection metric. Dimensionality reduc-
tion is performed on the joint acceleration vectors in
each frame (reduction of 660-dimensional data), and
we extract the maximum reconstruction error over all
joints and clip frames. This offers an opportunity
to pinpoint the joint that caused the jitter, similar to
what our MDC metric allows. The clip is classified
as anomalous when the reconstruction error exceeds
1.5 times the maximum seen in the training dataset.
We used the rest of the LAFAN1 dataset as training
data to fit the PCA model to regular data. Finally,
the Savitzky-Golay filter was configured to analyze
10 frames and smooth using second-degree polyno-
mials. We use the same jitter detection method as for
PCA, setting the error threshold to 5.5. All acceler-
ation vectors were normalized by skeleton scale and
framerate, similarly to Equation 1.
The results of the experiment are averaged over
10 repetitions. All the methods managed to detect
the real jitter instances with the described configura-
tions. We present a comparison of the F1 score from
the experiment in Table 4, as well as the recall and
precision in Table 5. Our metric remains quite com-
parable in terms of the F1 score and even outperforms
other methods on most values of σ, although only
slightly. Further inspection reveals that precision is
the strong side of our MDCSS metric while remaining
only slightly behind when it comes to recall. In terms
of recall, the Savitzky-Golay filter is the best for most
noise levels. We also performed frame-level analysis
to visualize the behavior of MDCSS metric on a sin-
gle example from that dataset. Figure 4 presents the
sample animation sequence for σ = 0.0125S, which
shows that spikes in our metric align with artificial
jitter windows.
Table 4: F1 score of compared methods on LAFAN1 dataset
for different values of σ in N (0, σ). Best results are high-
lighted in bold.
σ MDCSS PCA Savitzky-Golay
0.02S 0.832 0.778 0.778
0.0175S 0.852 0.824 0.823
0.015S 0.857 0.870 0.868
0.0125S 0.823 0.883 0.884
0.01S 0.683 0.723 0.714
0.0075S 0.332 0.200 0.189
0.005S 0.012 0.000 0.001
GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications
84
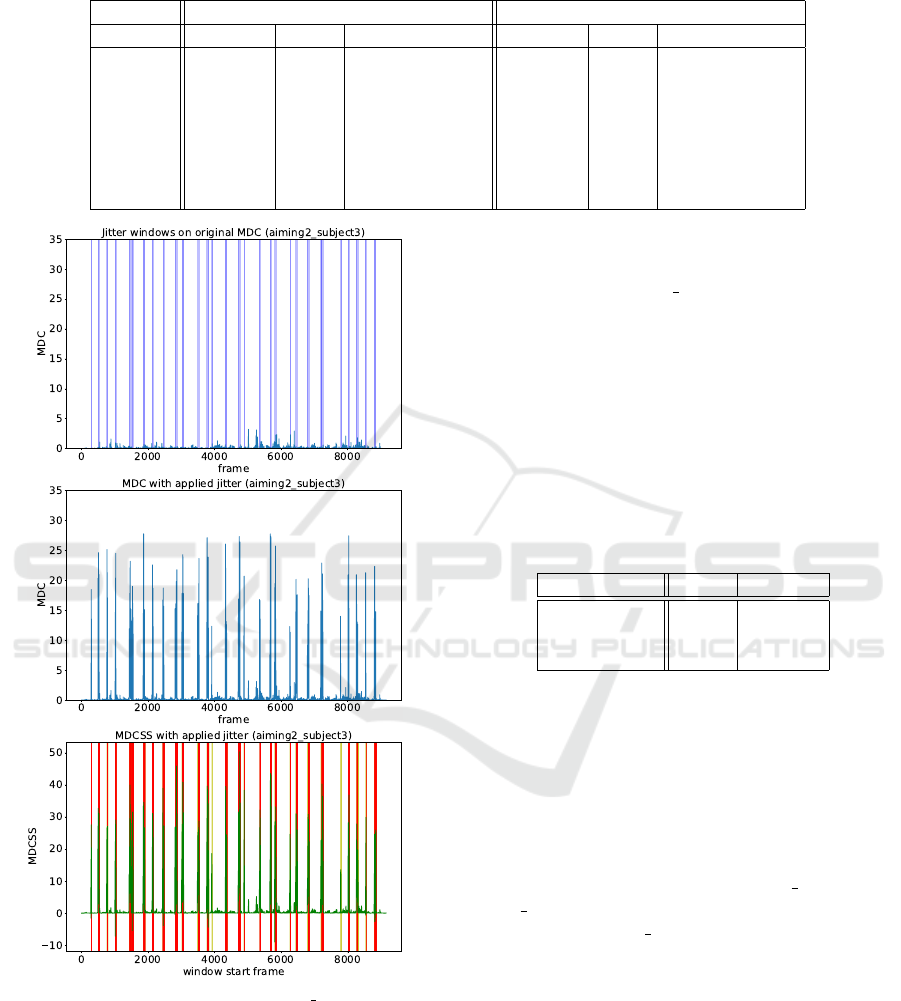
Table 5: Precision and recall of compared methods on LAFAN1 dataset for different values of σ in N (0, σ). Best results are
highlighted in bold.
Recall Precision
σ MDCSS PCA Savitzky-Golay MDCSS PCA Savitzky-Golay
0.02S 0.955 0.996 0.997 0.737 0.639 0.637
0.0175S 0.927 0.990 0.991 0.789 0.705 0.704
0.015S 0.869 0.973 0.970 0.846 0.787 0.786
0.0125S 0.757 0.884 0.884 0.904 0.882 0.884
0.01S 0.536 0.586 0.574 0.942 0.945 0.950
0.0075S 0.200 0.112 0.105 0.978 0.974 0.969
0.005S 0.006 0.000 0.0004 0.900 0.000 0.100
Figure 4: Metrics values for the aiming2 subject3 exam-
ple from LAFAN1 dataset. Highlighted windows in the top
chart indicates where artificial jitter was added according to
N (0, 0.0125S) distribution.
4.5 Scale Invariance
We also decided to verify the invariance of the skele-
ton scale of the proposed metrics. To verify this prop-
erty, we conducted frame-level and dataset-level anal-
yses on the Contemporary Dance dataset. For the
frame-level analysis, we used an example animation
sequence called ”Sophie Afraid-01”. We artificially
scaled the size of the skeleton as well as the root posi-
tion from source BVH files using scales x0.1 and x2.
Figure 5 presents the results of the frame-level
analysis in the example for all test scales. The met-
ric plots are indistinguishable, having the same values
and warning and error windows. The dataset-level
analysis presented in Table 6 further confirms this.
For all given scales, the value of our metrics is the
same when calculated across the whole dataset.
Table 6: Average metrics values per frame on the Contem-
porary Dance dataset for different skeleton scales.
Scale MDC MDCSS
x1 (baseline) 0.408 8.109
x0.1 0.408 8.109
x2 0.408 8.109
4.6 Analysis of Different MDCSS Time
Window Lengths
To further analyze the properties of our MDCSS
metric, we decided to compare how it changes
for different lengths of time windows used. We
achieved that by conducting frame-level analysis for
two examples from LAFAN1 - aiming1 subject1 and
fight1 subject2 - and one example from Contempo-
rary Dance - Sophie Afraid-01. The first example
from LAFAN1 represents regular, non-dynamic an-
imation, while the other example from that dataset
contains plenty of dynamic punches, kicks, and jump-
kicks. On the other hand, the example from Contem-
porary Dance is filled with jittery fragments of anima-
tion and is used to refer to jitter detection properties.
We analyze the following time windows: 0.1s, 0.2s,
0.25s, 0.33s, 0.5s, 0.67s, and 1s. Since we operate on
frames, we round down the number of frames in the
case of FPS indivisibility.
The MDCSS metric values for these examples
Fast Detection of Jitter Artifacts in Human Motion Capture Models
85
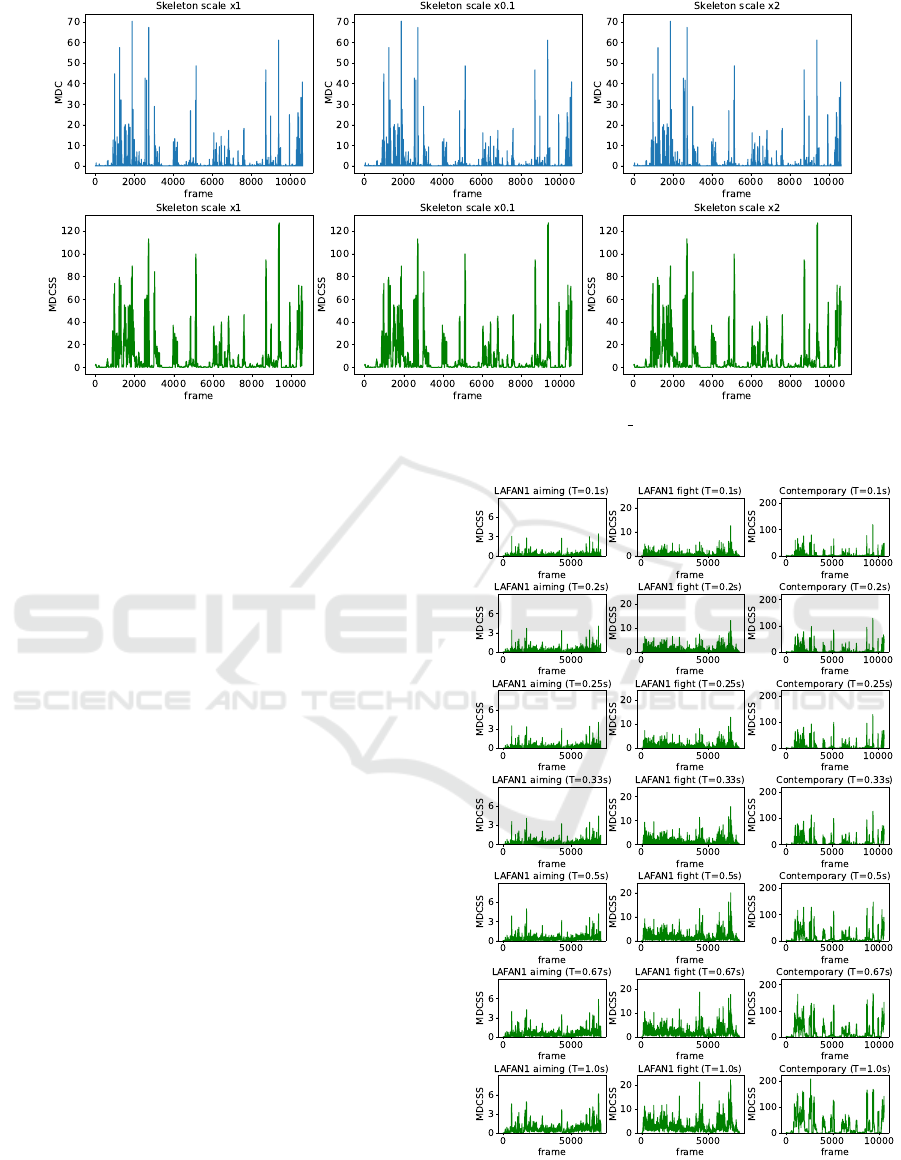
Figure 5: Comparison of metrics for Contemporary Dance example (sequence Sophie Afraid-01) for different scales of the
skeleton.
are plotted in Figure 6. Our analysis suggests that
increasing the time window also magnifies the val-
ues of the metric. The values that are magnified the
most are the ones that correspond to jittery or dy-
namic fragments. This observation makes sense be-
cause a longer time window contains more samples,
and therefore, more energy to be distributed. In the
case of a jitter, more energy might accumulate under
the same frequency, magnifying the value of the MD-
CSS metric.
4.7 Limitations
Our current definition of the animation analysis
method has some limitations. The most important
limitation of our metrics is that a jitter that does not
change the core trajectory of the joint will probably
not be detected. Although this limits the detection ca-
pabilities of our metrics, it also reduces the visibility
of such a jitter.
Our metric also achieves the best values if all char-
acter’s joints start moving in the same direction. An
example of a scenario is a character in a T-pose with
the root joint moving in a straight line. Some ani-
mation formats also allow for the rotation of a bone
around its vertical axis. Such a scenario would also
not be detected by our metrics, as it operates solely
on the positions of joints, not the rotation of bones.
While these shortcomings of our metrics are concern-
ing, they are unlikely to occur in most motion capture
animation sequences.
Figure 6: Comparison of MDCSS values calculated on 3
chosen animation sequences. Each sequence is represented
as a column and each row represents a different length of
time window.
GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications
86

5 DISCUSSION
As the results of the method comparison suggest, our
framework proves to be quite comparable with base-
lines while requiring no fitting to the dataset, in con-
trast to PCA. Moreover, the PCA method requires a
constant number of input variables, which makes it
unfit for working on multiple skeletons with various
hierarchies. The MDCSS metric also proved its use-
fulness in real cases, as we managed to detect undis-
covered jitter in the LAFAN1 dataset. This dataset
is widely used in research to evaluate neural models.
The found jitter instances are located in the training
part of the dataset and negatively influence the train-
ing process of such models, thus affecting the output
result used in the evaluation. We think that our frame-
work could be used to perform preprocessing checks
on motion capture datasets and filter out in such appli-
cations. The proposed metrics consider problematic
technical aspects, which should make such integra-
tion relatively easy.
6 FUTURE WORK
In our subsequent work, we would like to address
some of the limitations of our work, especially the
problem of detecting jitter that does not change the
joint trajectory. We identified that this scenario is
problematic for our analysis framework. Address-
ing this issue could greatly increase the number of
detected jitter instances. One possible solution is to
monitor the rotations of the bones instead of the po-
sitions of the joints. While this approach is likely to
address this problem, it would restrict applications of
our framework, as such data is not always available
for animation sequences. Instead, we would like to
try to solve this problem by inspecting the characteris-
tics of the trajectory. We also aim to experiment with
automatic correction using smoothing algorithms and
neural models in sequences classified as errors by our
metrics.
In addition, we plan to evaluate the proposed
metrics against the performance of neural models to
find a correlation between the value of the metric
and the performance of state-of-the-art neural models.
This work will focus mainly on the warning level of
our MDCSS metric, as we hypothesize that such se-
quences contain more irregular joint movements and
could be harder to predict by neural networks. This
could potentially help us to understand the shortcom-
ings and problematic animation sequences of current
research related to machine learning applications in
frame generation.
7 CONCLUSIONS
In this work, we proposed a novel framework for jit-
ter detection in animation datasets that consists of two
metrics: MDC and MDCSS. The framework can op-
erate at multiple levels of detail and allows datasets to
be compared with different skeleton scales, numbers
of joints, and FPS. We also evaluated this framework
on several popular datasets to prove its usefulness.
Our experiments found that two of the popular ani-
mation datasets, LAFAN1 and Human3.6M, contain
instances of jitter, which was not known before. This
further emphasizes the need for jitter detection frame-
works in professional motion capture environments,
such as the one proposed in this work. The compar-
ison with commonly used anomaly detection meth-
ods also proved that our framework is well-suited for
this task requiring no adjustments or fitting to anima-
tion data. We hope that our metrics can contribute
in the future to cleaning motion capture datasets used
for machine learning purposes, as well as improving
the overall quality of animation by detecting jittery
sequences early in motion capture recordings.
ACKNOWLEDGEMENTS
The research presented in this article was partially
supported by the funds of the Polish Ministry of Sci-
ence and Higher Education, assigned to the AGH Uni-
versity of Krakow (Faculty of Computer Science).
REFERENCES
Abichequer Sangalli, V., Hoyet, L., Christie, M., and Pettr
´
e,
J. (2022). A new framework for the evaluation of
locomotive motion datasets through motion match-
ing techniques. In Proceedings of the 15th ACM
SIGGRAPH Conference on Motion, Interaction and
Games, MIG ’22, New York, NY, USA. Association
for Computing Machinery.
Ardestani, M. M. and Yan, H. (2022). Noise reduction
in human motion-captured signals for computer an-
imation based on b-spline filtering. Sensors (Basel,
Switzerland), 22(12).
Aristidou, A., Zeng, Q., Stavrakis, E., Yin, K., Cohen-Or,
D., Chrysanthou, Y., and Chen, B. (2017). Emotion
control of unstructured dance movements. In Proceed-
ings of the ACM SIGGRAPH / Eurographics Sympo-
sium on Computer Animation, SCA ’17, New York,
NY, USA. Association for Computing Machinery.
Bregler, C. (2007). Motion capture technology for enter-
tainment [in the spotlight]. IEEE Signal Processing
Magazine, 24(6):160–158.
Fast Detection of Jitter Artifacts in Human Motion Capture Models
87

Burger, B. and Toiviainen, P. (2013). MoCap Toolbox – A
Matlab toolbox for computational analysis of move-
ment data. In Bresin, R., editor, Proceedings of the
10th Sound and Music Computing Conference, pages
172–178, Stockholm, Sweden. KTH Royal Institute of
Technology.
Callejas-Cuervo, M., Espitia-Mora, L. A., and V
´
elez-
Guerrero, M. A. (2023). Review of optical and inertial
technologies for lower body motion capture. Journal
of Hunan University Natural Sciences, 50(6).
Geng, W. and Yu, G. (2003). Reuse of motion capture data
in animation: A review. In International Conference
on Computational Science and Its Applications, pages
620–629. Springer.
Hachaj, T. and Ogiela, M. (2020). Rmocap: an r language
package for processing and kinematic analyzing mo-
tion capture data. Multimedia Systems, 26.
Harvey, F. G., Yurick, M., Nowrouzezahrai, D., and Pal, C.
(2020). Robust motion in-betweening. ACM Trans.
Graph., 39(4).
Holden, D. (2018). Robust solving of optical motion cap-
ture data by denoising. ACM Transactions on Graph-
ics (TOG), 37(7):1–12.
Hoxey, T. and Stephenson, I. (2018). Smoothing noisy
skeleton data in real time. In EG 2018 - Posters. The
Eurographics Association.
Ijjina, E. P. and Mohan, C. K. (2014). Human action recog-
nition based on mocap information using convolution
neural networks. In 2014 13th International Confer-
ence on Machine Learning and Applications, pages
159–164.
Ionescu, C., Papava, D., Olaru, V., and Sminchisescu, C.
(2014). Human3.6m: Large scale datasets and pre-
dictive methods for 3d human sensing in natural envi-
ronments. IEEE Transactions on Pattern Analysis and
Machine Intelligence, 36(7):1325–1339.
Iqbal, A., Amin, R., Alsubaei, F. S., and Alzahrani, A.
(2024). Anomaly detection in multivariate time se-
ries data using deep ensemble models. PLOS ONE,
19(6):1–25.
Kadu, H. and Kuo, C.-C. J. (2014). Automatic human mo-
cap data classification. IEEE Transactions on Multi-
media, 16(8):2191–2202.
Kobayashi, M., Liao, C.-C., Inoue, K., Yojima, S., and
Takahashi, M. (2023). Motion capture dataset for
practical use of ai-based motion editing and styliza-
tion.
Liu, X., Ming Cheung, Y., Peng, S.-J., Cui, Z., Zhong,
B., and Du, J.-X. (2014). Automatic motion capture
data denoising via filtered subspace clustering and low
rank matrix approximation. Signal Process., 105:350–
362.
Ma, M., Zhang, S., Chen, J., Xu, J., Li, H., Lin, Y., Nie,
X., Zhou, B., Wang, Y., and Pei, D. (2021). Jump-
Starting multivariate time series anomaly detection for
online service systems. In 2021 USENIX Annual Tech-
nical Conference (USENIX ATC 21), pages 413–426.
USENIX Association.
Mahmood, N., Ghorbani, N., Troje, N. F., Pons-Moll, G.,
and Black, M. J. (2019). AMASS: Archive of motion
capture as surface shapes. In International Conference
on Computer Vision, pages 5442–5451.
Manns, M., Otto, M., and Mauer, M. (2016). Measuring
motion capture data quality for data driven human mo-
tion synthesis. Procedia CIRP, 41:945–950. Research
and Innovation in Manufacturing: Key Enabling Tech-
nologies for the Factories of the Future - Proceedings
of the 48th CIRP Conference on Manufacturing Sys-
tems.
Menolotto, M., Komaris, D.-S., Tedesco, S., O’Flynn, B.,
and Walsh, M. (2020). Motion capture technology in
industrial applications: A systematic review. Sensors,
20(19):5687.
Meredith, M. and Maddock, S. C. (2001). Motion capture
file formats explained. Department of Computer Sci-
ence, University of Sheffield.
Montes, V. R., Quijano, Y., Chong Quero, J. E., Ayala,
D. V., and P
´
erez Moreno, J. C. (2014). Comparison
of 4 different smoothness metrics for the quantitative
assessment of movement’s quality in the upper limb
of subjects with cerebral palsy. In 2014 Pan American
Health Care Exchanges (PAHCE), pages 1–6.
Nawrocki, P. and Sus, W. (2022). Anomaly detection in the
context of long-term cloud resource usage planning.
Knowl. Inf. Syst., 64(10):2689–2711.
Oreshkin, B. N., Valkanas, A., Harvey, F. G., M
´
enard, L.-
S., Bocquelet, F., and Coates, M. J. (2024). Mo-
tion in-betweening via deep δ-interpolator. IEEE
Transactions on Visualization and Computer Graph-
ics, 30(8):5693–5704.
Patrona, F., Chatzitofis, A., Zarpalas, D., and Daras, P.
(2018). Motion analysis: Action detection, recogni-
tion and evaluation based on motion capture data. Pat-
tern Recognition, 76:612–622.
Qin, J., Zheng, Y., and Zhou, K. (2022). Motion in-
betweening via two-stage transformers. ACM Trans.
Graph., 41(6).
Ren, T., Yu, J., Guo, S., Ma, Y., Ouyang, Y., Zeng, Z.,
Zhang, Y., and Qin, Y. (2023). Diverse motion in-
betweening from sparse keyframes with dual posture
stitching. IEEE Transactions on Visualization & Com-
puter Graphics, (01):1–12.
Skurowski, P. and Pawlyta, M. (2022). Detection and classi-
fication of artifact distortions in optical motion capture
sequences. Sensors, 22(11).
GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications
88
