Iterative Environment Design for Deep Reinforcement Learning Based
on Goal-Oriented Specification
Simon Schwan
a
and Sabine Glesner
b
Software and Embedded Systems Engineering, Technische Universit
¨
at Berlin, Straße des 17. Juni 135, Berlin, Germany
Keywords:
Reinforcement Learning, Requirements Specification, Iterative Development, Goals, Environment Design.
Abstract:
Deep reinforcement learning solves complex control problems but is often challenging to apply in practice for
non-experts. Goal-oriented specification allows to define abstract goals in a tree and thereby, aims at lowering
the entry barriers to RL. However, finding an effective specification and translating it to an RL environment
is still difficult. We address this challenge with our idea of iterative environment design and automate the
construction of environments from goal trees. We validate our method based on four established case studies
and our results show that learning goals by iteratively refining specifications is feasible. In this way, we
counteract the common trial-and-error practice in the development to accelerate the use of RL in real-world
applications.
1 INTRODUCTION
Reinforcement Learning (RL) has emerged as a
promising solution for complex control problems
such as collision avoidance (Everett et al., 2021) in
autonomous driving. RL agents learn through interac-
tions with their environment, being rewarded for de-
sirable behavior. The initial step in the development
of RL solutions involves defining an environment in
form of a Markov decision process (MDP). Despite
the potential of RL, the definition of the environment
requires significant experience and expertise and of-
ten involves trial-and-error. This results in very high
entry barriers for developers that are experts in their
application domain, but not RL. Thereby, these barri-
ers limit the application of RL in practice drastically.
Goal-oriented specification (Schwan et al., 2023)
enables to specify goals in a tree structure, which al-
lows to abstract from technical details of RL. How-
ever, at this point, goal-oriented specification is miss-
ing definitions of how to automatically construct en-
vironments from goal tree specifications. These def-
initions are needed to make the approach applicable
by enabling the training of RL agents from goal trees.
Moreover, it is challenging to develop effective spec-
ifications on the first try because of many interdepen-
dent design choices. These choices come not only
a
https://orcid.org/0009-0002-4085-1777
b
https://orcid.org/0009-0003-6946-3257
from defining the environment, but also from training
agents on the environment.
With this work, we close the gap and address
the challenge of constructing environments from goal
trees to enable iterative goal-oriented design. Our
key idea is to design RL environments in iterations of
three phases: specifying goals, training agents, evalu-
ating the results for future improvements. To achieve
this, our two main contributions are as follows:
1. We introduce a method for automatically con-
structing environments from goal trees. Thereby,
we enable the training of RL agents from these
specifications.
2. We instantiate our method with definitions for a
specific set of goal tree components. By care-
fully choosing these definitions, we ensure that
goal tree refinements lead to an increase of the re-
warding feedback to the agent and create the op-
portunity for iterative improvements.
Together, manually refining specifications and au-
tomatically constructing environments from them, en-
ables domain experts to train agents while focusing
on the goals rather than the technical details. At the
same time, we reduce time-consuming tasks of con-
structing the environment manually in each iteration.
This makes iterative environment design from goal-
oriented specifications practical, and we evaluate our
method through four case studies from the Farama
Gymnasium (Farama Foundation, 2024). First, we
240
Schwan, S. and Glesner, S.
Iterative Environment Design for Deep Reinforcement Learning Based on Goal-Oriented Specification.
DOI: 10.5220/0013148500003890
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 17th International Conference on Agents and Artificial Intelligence (ICAART 2025) - Volume 2, pages 240-251
ISBN: 978-989-758-737-5; ISSN: 2184-433X
Proceedings Copyright © 2025 by SCITEPRESS – Science and Technology Publications, Lda.

infer goals from the original environments to enable
goal-oriented specification. Second, we define mul-
tiple goal trees for each case study. Third, we train
agents for each automatically constructed environ-
ment and analyze the results.
1
The paper is structured as follows. We relate
our work to existing research (Section 2). Then, we
describe preliminaries (3) such as MDPs and goal-
oriented specification. Subsequently, we introduce
our running example (4) and define our automated
construction of environments from goal trees (5). We
evaluate our method (6) and conclude (7).
2 RELATED WORK
With the increasing use of artificial intelligence (AI)
systems, Requirements Engineering for AI (RE4AI)
(Ahmad et al., 2023) becomes relevant. The survey
identifies the Unified Modeling Language (UML) and
goal-oriented requirements engineering (GORE) to be
the prevalent modeling languages in RE4AI. Rein-
forcement learning is a methodology that addresses
problems within the context of a specific theoretical
framework: the Markov decision process. Our spec-
ification method enables requirements engineering
that is inspired by GORE (Van Lamsweerde, 2001)
but tailored to the specific framework of RL. A sur-
vey of Human-in-the-loop (HITL) RL (Retzlaff et al.,
2024) examines existing research. It identifies the
HITL paradigm to be of utmost importance and pro-
poses that humans, i.e. developers, domain experts
and users, interact with the RL system in four sequen-
tial phases: agent development, agent learning, agent
evaluation, agent deployment. In alignment with the
theoretical findings of the survey, we introduce our it-
erative design approach according to the initial three
phases. However, we do not consider the agent de-
ployment.
We base our specification language on goals,
which are used in several other RL methods (Schaul
et al., 2015; Andrychowicz et al., 2017; Florensa
et al., 2018; Jurgenson et al., 2020; Chane-Sane et al.,
2021; Okudo and Yamada, 2021; Ding et al., 2023;
Okudo and Yamada, 2023). These methods focus
on improving the training efficiency and we identify
three major directions: (1) using goals to shape and
make the reward dense (Okudo and Yamada, 2021,
2023; Ding et al., 2023); (2) the division of a ma-
jor goal into subgoals (Jurgenson et al., 2020; Chane-
Sane et al., 2021) such as following intermediate way-
points on a trajectory; (3) learning goals simultane-
1
Code and results are available at https://doi.org/10.
6084/m9.figshare.26408821.v1
ously (Schaul et al., 2015; Andrychowicz et al., 2017;
Florensa et al., 2018) to improve generalizability. In
contrast, our approach uses goals to specify require-
ments and enable iterative environment design instead
of focusing on training efficiency.
Furthermore, the idea of goal-oriented specifica-
tion is to integrate existing RL techniques into the
specification and training procedure. In this con-
text, we review existing goal-based methods. Of-
ten, goal-based methods can be automatically applied
(Andrychowicz et al., 2017; Florensa et al., 2018;
Chane-Sane et al., 2021; Jurgenson et al., 2020) to
train RL agents. Hindsight experience replay (HER)
(Andrychowicz et al., 2017) enables to learn many
goals from the same episode by relabeling the target
goals of the terminal state. Thus, HER improves gen-
eralizability by learning from unsuccessful episodes.
While we find HER promising to be integrated into
our training, other approaches (Florensa et al., 2018;
Jurgenson et al., 2020; Chane-Sane et al., 2021) need
to have specifically tailored RL algorithms. These
methods stand in contrast to our approach that en-
ables learning from standard, model-free RL algo-
rithms. Subgoal-based reward shaping (Okudo and
Yamada, 2021, 2023) relies on the manual specifica-
tion of ordered subgoals to guide the agent. We may
be able to integrate it into goal-oriented specification
by developing a corresponding goal-tree operator.
Finally, there are other specification languages for
RL that are related to our work. While (Hahn et al.,
2019) specifies RL objectives in an ω-regular lan-
guage, most languages (Li et al., 2017; Jothimurugan
et al., 2019, 2021; Cai et al., 2021; Hammond et al.,
2021) are based on linear temporal logic, which al-
lows them to specify temporal properties. These lan-
guages enable the design of reward with theoretical
guarantees such as providing policy invariance. How-
ever, these theoretical considerations do not guarantee
that deep RL algorithms converge because of statis-
tical optimization. In contrast, our method integrates
training into the iterative environment design to coun-
teract unpredictable side effects.
3 PRELIMINARIES
This section first provides preliminaries for reinforce-
ment learning, followed by goal-oriented specifica-
tion.
Reinforcement Learning. A reinforcement learn-
ing problem is formally modeled as a Markov deci-
sion process (MDP) (Sutton and Barto, 2018) by a
tuple (S,A,P,R) with S being the space of all states
Iterative Environment Design for Deep Reinforcement Learning Based on Goal-Oriented Specification
241

satisfying the Markov property, A being the space of
all actions, P(s,a, s
′
) = Pr[s
t+1
= s
′
|s
t
= s,a
t
= a] be-
ing the transition probability and R : S × A × S → R
being the immediate reward. The RL agent inter-
acts with the MDP and collects samples in form of
episodes τ = (s
1
,a
1
,r
1
,s
t+1
,...,s
T −1
,a
T −1
,r
T −1
,s
T
)
with states s
i
∈ S, actions a
i
∈ A, rewards r
i
=
R(s
i
,a
i
,s
i+1
) and the terminal state s
T
at time T .
The objective of RL algorithms is to find a policy
π : S → A, also named agent, that maximizes the ex-
pected cumulative and discounted reward, i.e. re-
turn R(τ) =
∑
T
i=0
γ
i
r
i
, with discount factor γ ∈ [0,1].
Depending on the parameters, R(s
t
,a
t
,s
t+1
) denotes
the reward and R(τ) the return. A popular RL algo-
rithm is Proximal Policy Optimization (PPO) (Schul-
man et al., 2017), a policy gradient method that up-
dates in small steps by a clipped surrogate objective.
PPO can optimize for discrete and continuous actions.
There are several methods to specify reward.
Sparse reward, i.e. rewarding only on success, has
the advantage of defining a single and clear objective.
However, the agent may not be able to experience this
sparse reward because it does not reach the associated
success states. In this case, it is possible to shape the
reward to a dense function or to sparsely reward in in-
termediate states. If the reward R consists of multiple
components R
i
as in multi-objective RL, a common
choice is to scalarize using the weighted linear sum
of the components. This enables the use of single-
objective RL algorithms (Roijers et al., 2013).
Throughout the paper, we assume state spaces S to
be feature spaces S : S
A
× S
B
× S
C
× ... consisting of a
set of features F = {A, B,C,...} where a state s ∈ S is
a tuple s = (s
A
,s
B
,s
C
,...).
Goal-Oriented Specification. Goal-oriented spec-
ification (Schwan et al., 2023) introduces the speci-
fication of goals for RL agents in a hierarchical tree
structure. The approach formalizes the separation of
Markov decision processes into immutable aspects,
i.e. the initial environment, and the engineered as-
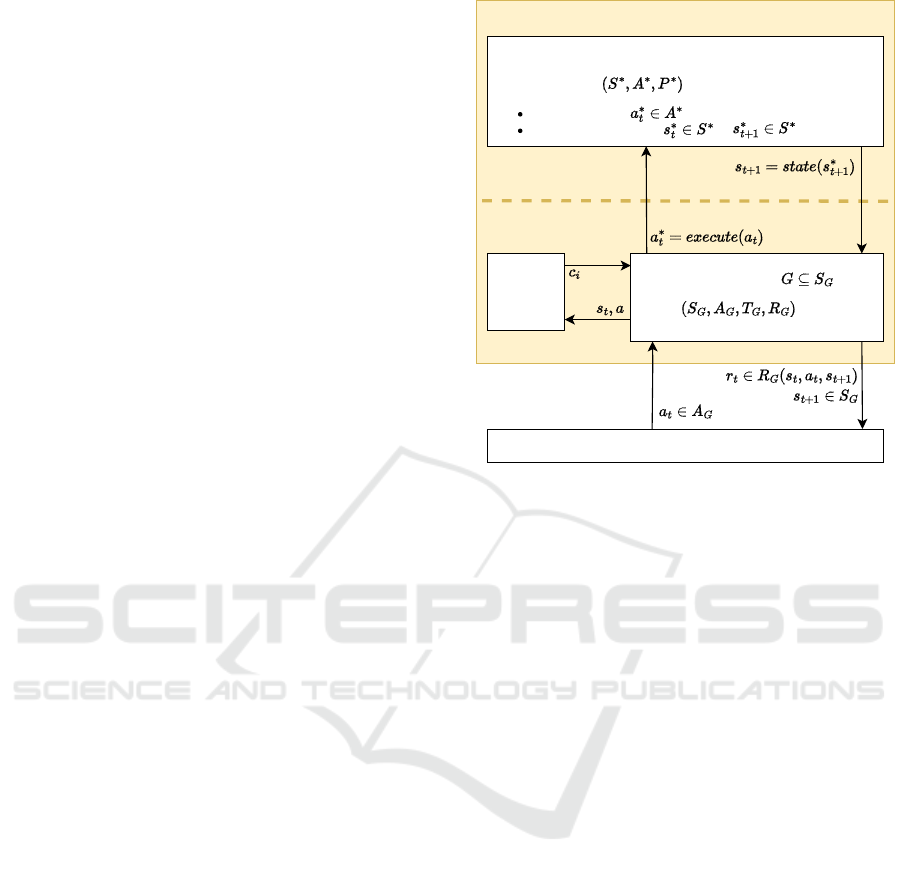
pects, i.e. requirements as depicted in Figure 1. The
initial environment is a three tuple (S
∗
,A
∗
,P
∗
) with
S
∗
being the initial state space (e.g. available sen-
sors), A
∗
being the initial action space (e.g. actua-
tors) and P
∗
being the initial transition probabilities
(e.g. physics of the world or a simulation). These
aspects are immutable and cannot be modified dur-
ing specification. Requirements are the counterpart
to the initial environment. They include aspects of
MDPs that can be designed or manipulated by the
engineer to solve a problem with RL. Formally, re-
quirements are a tuple (S
G
,A
G
,T
G
,R
G
) that belong to
a goal space G ⊆ S
G
. The state space S
G
contains
Environment (MDP)
Initial Environment
Executes action
Transitions from state to
Requirementsof Goal
Agent
engineered
aspects
fixed
aspects
Constraint
Automaton
counter
Figure 1: Composed environment (Markov decision pro-
cess) from the initial environment and requirements.
feature-engineered states. The action space is defined
by A
G
, which contains possibly abstracted actions that
may differ from the initial environment. The termina-
tion space T
G
: S
G
× A
G
contains state-action pairs for
which episodes in the MDP terminate. This allows to
constrain undesired transitions in P
∗
for state-actions
(s,a) ∈ T
G
. The reward R
G
: S×A×S is a single scalar
reward function that implicitly inherits the objective
associated with the goal G.
Figure 1 shows how the initial environment and
requirements are combined to construct an environ-
ment in form of an MDP. To do so, it is necessary to
specify a mapping between the requirements and the
initial environment based on two functions. The first
function state : S
∗
→ S
G
enables the conversion of the
initial state space S
∗
to the feature-engineered state
space of the requirements S
G
. The agent chooses its
next action a
t
∈ A
G
based on the converted states. It
is necessary to execute this action in the initial envi-
ronment, which the definition of execute : A
G
→ A
∗
enables. Then, the environment proceeds to its next
state.
Furthermore, goal-oriented specification (Schwan
et al., 2023) introduces the ability to specify goals in
a tree. The idea is to construct a requirements tuple
from a goal-tree specification, but exact definitions
are not presented in the original work. Each node in
the tree contains its own goal space and requirements.
The construction of these requirements is defined by
the following tree components: leaf nodes, operators,
annotations. Leaf nodes are the atomic units for goals
ICAART 2025 - 17th International Conference on Agents and Artificial Intelligence
242

X
-1
1
Y
0
Figure 2: Pendulum environment.
in the tree and include an associated goal space G.
Goals can be hierarchically structured by a generic
operator (S
G
,A
G
,T
G
,R
G
) =
J
N
i
(S
i
,A
i
,T
i
,R
i
) that al-
lows to refine the parent goal G into N subgoal nodes.
In addition, nodes can be annotated with distance an-
notations that guide the agent to the goal space as well
as safety constraints. Safety constraints are specified
by their constraint state-action space C : S × A and
the number of allowed constraint violations δ
C
∈ N
where cnt
C
: S × A → {0,1} counts a constraint viola-
tion (s,a) ∈ C with 1.
4 RUNNING EXAMPLE
We illustrate our work using the Pendulum case study
from Farama Gymnasium (Farama Foundation, 2024)
that is shown in Figure 2. The objective of the case
study is learning to stabilize a circular pendulum in
an upright position. The state space S
∗
⊆ R
3
contains
three features, i.e. the X and Y position and the angu-
lar velocity α
V
. Actions a ∈ R define the torque that
is applied to the pendulum.
The objective of the pendulum is implicitly de-
fined by the given reward function. However, to use
goal-oriented specification, we need explicit goals as
sections of the state space. Through empirical mea-
surements on trained agents based on the original re-
ward, we examine the terminal states of the episodes.
Based on the results, we define the goal space such
that a successfully trained agent consistently reaches
the goal at the end of an episode. For the Pendulum
case study, we define the goal G
Pend
with constants
c
i
as standing upright at (s
X
,s
Y
) = (1,0) with a tol-
erance of 15 degrees (c
X
= sin(15) ≈ 0.966, c
Y
=
sin(15) ≈ 0.259) with low angular velocity below the
threshold c
α
V
= 0.25:
G
Pend
= {(s
X
,s
Y
,s
α
V
)|s
X
≥ c
X
,|s
Y
| ≤ c
Y
,
|s
α
V
| ≤ c
α
V
}
(1)
In the following, we simplify the notation of goal
spaces by using {s
X
≥ c
X
,|s
Y
| ≤ c
Y
,|s
α
V
| ≤ c
α
V
}
analogously.
5 AUTOMATED CONSTRUCTION
OF ENVIRONMENTS FROM
GOAL TREE SPECIFICATIONS
In this section, we present our two main contributions
to evolve goal-oriented specification (Schwan et al.,
2023) and make iterative design of RL agents from
goal trees practical. First, we introduce our goal tree
processing algorithm that automatically constructs a
single, composite requirements tuple at the root. Our
algorithm is generic with respect to leaf nodes, op-
erators and annotations from the goal tree. Thereby,
it allows the development of future components inte-
grating further RL methods. Second, we introduce a
specific set of definitions for leaf nodes, operators and
annotations that instantiate the generic parts of our al-
gorithm. These definitions allow the construction of
environments from which RL agents can be directly
trained and evaluated. We leverage the fact that goal-
oriented specification allows specifying the same goal
in a variety of goal trees. According to our definitions,
node refinements increase the rewarding feedback to
the agent. Therefore, each refined goal tree specifi-
cation leads to the construction of a unique environ-
ment variant. Together, our algorithm and definitions
allow us to automatically construct unique environ-
ments that can be used to train RL agents and analyze
their behavior. Finally, this enables iterative environ-
ment design from goal-oriented specification.
Next, we introduce our algorithm followed by the
definitions that instantiate the generic construction.
For clarity, we use the terminology of specifying for
manually engineered aspects of the goal tree specifi-
cation and constructing for our automated construc-
tion of requirements.
We implement a depth-first traversal to recursively
construct the composite requirements as shown in Al-
gorithm 1. The algorithm process node(node,S,A)
receives a node as input for which we construct the
output requirements (S
G
,A
G
,T
G
,R
G
) and the goal
space G. Additionally, it receives a state space
S and an action space A as input. We create
a single requirements tuple for a specification by
starting the process at the root node of the tree
process node(root,S
root
,A
root
). Here, S
root
and A
root
are the direct result from the specified state(...) and
execute(...) functions as presented in Section 3. Our
algorithm processes a node in three sequential steps
as follows.
First, we construct a requirements tuple for the
node under construction. Nodes may be either a leaf
or an operator node. Leaf nodes have a specified goal
space G = goal(node), from which we construct the
requirements tuple according to our definitions below.
Iterative Environment Design for Deep Reinforcement Learning Based on Goal-Oriented Specification
243

Data: node, S, A
Result: G, (S
G
,A
G
,T
G
,R
G
)
/* Step 1: Process leaf or operator */
if node is leaf then
G = goal(node)
(S
G
,A
G
,T
G
,R
G
) = lea f (S,A,G)
else
r =
/
0
for c ∈ children(node) do
(S
i
,A
i
,T
i
,R
i
),G
i
= process node(c, S, A)
r ← r ∪ {(S
i
,A
i
,T
i
,R
i
)}
end
G, (S
G
,A
G
,T
G
,R
G
) =
J
N
i
(S
i
,A
i
,T
i
,R
i
), G
i
end
/* Step 2: Process node annotations */
for a ∈ annotations(node) do
(S
G
,A
G
,T
G
,R
G
) ← build(a, (S
G
,A
G
,T
G
,R
G
))
end
/* Step 3: Process root specifics */
if node is root then
insert G into T
G
for all actions
end
return G, (S
G
,A
G
,T
G
,R
G
)
Algorithm 1: Our algorithm process node(node,S,A) im-
plements a recursive depth-first traversal of a goal tree spec-
ification to construct composite requirements.
Operator nodes have children, and we recursively
construct their requirements (S
i
,A
i
,T
i
,R
i
) depth-first
by calling process node(c,S, A). Subsequently, we
combine these requirements using the generic opera-
tor
J
. This generic approach enables us to extend our
specification language in the future. However, we in-
troduce the specific definitions of our
V
-operator be-
low. Second, we adapt the requirements according
to the annotations of the node. We sequentially pro-
cess these annotations by updating the requirements
(←) according to our definitions as introduced below.
Third, we end the training of episodes if the agent en-
ters the root goal space. We do so by inserting the goal
space G into the termination space T
G
at the root.
Following, we introduce definitions for each goal
tree component: leaf nodes,
V
-operator, distance and
constraint annotations. We use these definitions to
automatically construct the requirements tuple at the
root according to Algorithm 1. The result is a unique
environment for each goal tree specifying identical
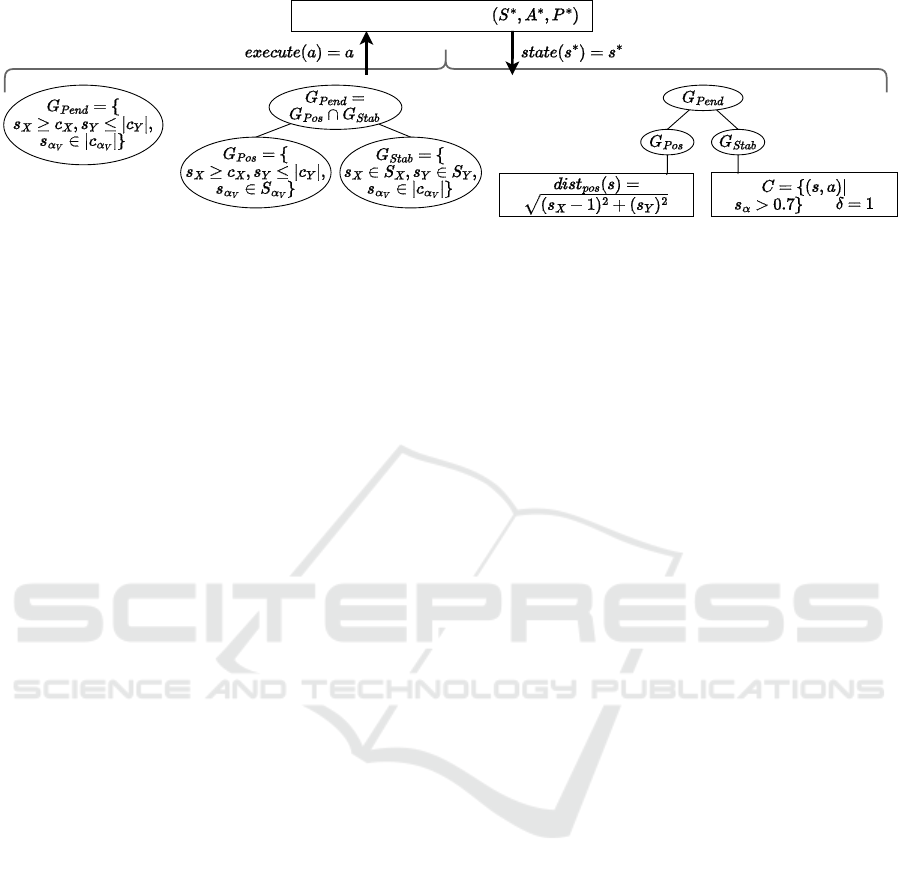
goals. We illustrate all definitions by applying them
to our running example from Section 4 using the three
goal tree specifications as shown in Figure 3.
Leaf Nodes. Leaf nodes are the atomic units of
goals in goal-oriented specification. Each leaf node
contains a specified goal space G ⊆ S
G
, which is the
section of the state space that the agent aims to reach.
We construct the requirements (S
G
,A
G
,T
G
,R
G
) for a
leaf by calling lea f (S,A,G) as shown in Algorithm 1.
The observation and action space need to conform
with the other components of the tree. For leaf nodes,
we externally define these by the structure of the tree:
S
G
= S ∧ A
G
= A
S and A are given as input into the lea f function.
The reward of a leaf node needs to give feedback
to the agent when it reaches the goal space. At the
same time, it is possible to specify goal trees that com-
pose multiple leaf goals. We define the reward R
G
as
follows:
R
G
(s
t
,a
t
,s
t+1
) =





1 s
t
̸∈ G, s
t+1
∈ G
−1 s
t
∈ G
,
s
t+1
̸∈ G
0 else
The positive reward for entering the goal space S
t+1
∈
G may be sufficient if the leaf is the only goal in the
tree. However, goal-oriented specification enables the
composition of leaf nodes through operators, and it
may be possible that an agent again exits the goal
space. For this reason, we neutralize the positive re-
ward with a negative reward of the same magnitude to
prevent the recurrent collection of positive rewards.
The termination space T
G
defines state-action pairs
at which episodes are terminated. For the same rea-
son of composing leaf nodes, we do not terminate
episodes when reaching the goal of a leaf node. In-
stead, we initialize the termination space of a leaf
node as the empty space:
T
G
=
/
0
Still, we terminate episodes when the agent enters the
composite goal at the root as shown in step three of
Algorithm 1.
The simplest goal tree for our running example
is to specify a leaf node with the goal space G
Pend
from Eq. 1 at the root (Figure 3.a). This specification
results in a reward function with a sparse positive
reward when the agent successfully reaches the
goal and episodes terminate. Nevertheless, this
specification may prove challenging during training.
Depending on the size and the dynamics of the
environment as well as the exploration strategy,
the agent may not be able to reach goal states and
experience reward.
V
-operator Node. The
V
-operator enables the
specification of simultaneous subgoals. For this rea-
son, our definitions follow the semantics of intersect-
ing subgoal spaces G =
T
N
i
G
i
. We instantiate the
generic operator
J
from Algorithm 1 by defining
(S
G
,A
G
,T
G
,R
G
) =
V
N
i
(S
i
,A
i
,T
i
,R
i
). Our definitions
ICAART 2025 - 17th International Conference on Agents and Artificial Intelligence
244

with
a) b) c)
Pendulum Initial Environment
Figure 3: Three goal tree specifications (a-c) for the same goal G
Pend
with increasing specification details (left to right)
combined with the Pendulum initial environment.
enable the construction of the composite requirements
tuple of the parent goal as follows.
To enable the composition of child nodes, we de-
fine state and action spaces of the parent and its chil-
dren to be identical:
∀i.S
G
= S
i
∧ A
G
= A
i
Moreover, this definition allows the intersection of the
goal spaces to construct the parent goal space accord-
ing to our semantics. The reward of our
V
-operator
node should compose reaching the goals of its chil-
dren. Our recursive algorithm constructs the require-
ments tuple of the child nodes first. These require-
ments include reward components R
i
for each child
node. We use these components and define the parent
reward R
G
to be the cumulated weighted sum:
R
G
(s
t
,a
t
,s
t+1
) =
N
∑
i
ω
i
R
i
(s
t
,a
t
,s
t+1
)
By default, we weight the reward components equally
with ω
i
= 1/N. However, this definition introduces
the challenge of weighting, which is a non-trivial and
often time-consuming manual task in reward design.
Nevertheless, it defines a reward shape that increases
the feedback to the agent by rewarding the success
of reaching intermediate subgoals. For this reason,
our
V
-operator allows for refinement of a goal and
enables the construction of unique requirements while
preserving the goal space at the root. We define the
termination space of the parent to terminate episodes
whenever a child indicates termination:
T
G
=
N
[
i
T
G
i
For example, the
V
-operator enables us
to refine the root goal G
Pend
of Figure 3.a
into two child goals for reaching the position
G
Pos
= {s
X
≥ c
X
,|s
Y
| ≤ c
Y
,s
α
V
∈ α
V
} and stabilizing
the pendulum G
Stab
= {s
X
∈ X,s
Y
∈ Y,|s
α
V
| ≤ c
α
V
}
as shown in Figure 3.b. While the goal space at the
root remains the same G
Pend
= G
Pos
∩ G
Stab
, the use
of the
V
-operator leads to a weighted sparse reward
shape with R
Pend
= ω
Pend,0
R
Pos
+ ω
Pend,1
R
Stab
. We
omit the reward parameters R(s
t
,a
t
,s
t+1
) for illustra-
tion. In contrast to the constructed requirements from
Figure 3.a, not only the overall goal of the root is
rewarded but also intermediate steps when reaching
a child goal space. Thus, the
V
-operator increases
the feedback to the agent, and we can construct a
unique environment variant from the goal tree.
Annotations. Tree nodes can be annotated in goal-
oriented specification. Thereby it is possible to con-
strain undesirable behavior or increase feedback to
the agent by guiding it towards the desired goal.
Each annotation modifies the requirements tuple of its
node, which we denote by the left arrow (←) in step
2 of Algorithm 1. For each additional reward compo-
nent, we specify a weight for balancing.
In goal-oriented specification, safety constraints
are specified by their constraint action-state space
C : S × A, along with the number of permitted vio-
lations δ ∈ N. However, differing state transitions for
identical states violate the Markov property. This may
be the case for terminating episodes or penalizing
the agent when the violation boundary δ is reached.
To preserve the Markov property for constraint viola-
tions, we make the violation counter transparent to the
agent. To achieve this, we construct an extended state
space S
G
← S
G
× N by adding a violation counter s
C
with:
s
C
= δ −
T
∑
t
cnt
C
(s
t
,a
t
)
The construction entails updating the state and termi-
nation spaces for other tree components with the ex-
tended state space to comply with our definitions. For
instance, the state spaces are identical for parent and
Iterative Environment Design for Deep Reinforcement Learning Based on Goal-Oriented Specification
245

child nodes according to definitions of the
V
-operator.
For this reason, we need to update the state and ter-
mination spaces of adjacent tree components when
adding the constraint violation counter. Furthermore,
we integrate the additional state feature into a con-
straint automaton as shown in Figure 1 that counts
constraint violations. If an episode contains λ con-
straint violations, we end it. We do so by modifying
the termination space to include states with a violation
counter of s
C
= 0:
T
G
← T
G
∪ {(s,a)|s
C
= 0}
Finally, we add a penalty to the original reward as
follows:
R
Pen
(s
t
,a
t
,s
t+1
) =
(
−1 (s
t
,a
t
) ∈ C
0 else
Distance annotations of goal-oriented specifica-
tion enable to guide the agent towards the goal. The
allow a dense reward shaping by specifying a Eu-
clidean distance function dist : S
G
→ R with
dist(s) =
q
(s − g)
2
for a goal state g ∈ G. From this, we construct a
potential-based reward shape (Ng et al., 1999):
R
Dist
(s
t
,a
t
,s
t+1
) = dist(s
t
) − dist(s
t+1
)
Finally, we add the dense reward component R
Dist
to
the existing reward of the requirements.
Figure 3.c illustrates a third tree specification in
which the refined subgoals G
Pos
and G
Stab
are an-
notated. The sparse reward of G
Pos
is shaped by a
dense reward constructed from the specified distance
dist
Pos
(s) =
p
(s
X
− 1)
2
+ (s
Y
− 0)
2
to the top center
position. To restrict exploration of the state space
with high angular velocities of s
α
≥ 0.7, we annotate
the stabilization node by specifying the safety con-
straint C with δ = 1. Note: we introduce the con-
straint C for illustration purpose only and we do not
use it in our experiments.
From the annotated specification in Figure 3.c, we
construct a structured reward function at our root re-
quirements with weighted components as follows:
R
Pend
=ω
Pend,0
(
position goal
z }| {
ω
Pos,0
R
Pos
+ ω
Pos,1
R
Dist
)
+ω
Pend,1
(ω
Stab,0
R
α
+ ω
Stab,1
R
Pen
| {z }
stabilization goal
)
Each reward component strictly belongs to one of
the nodes with goal spaces G
Pos
and G
Stab
. The
weights ω
Pend,i
allow to balance between the position
and stabilization goals whereas the weights ω
Pos,i
and ω
Stab,i
balance the proportions of the inner
reward. Again, we construct requirements for a
goal tree specification with the same goal space
at the root. However, our definitions enable us to
construct a unique and trainable environment variant.
At this point, we have evolved goal-oriented spec-
ification by enabling the automated construction of
environments from goal trees. Furthermore, we con-
struct unique requirements that increase the feedback
to the agent for each goal tree refinement. In the fol-
lowing section, we use our automated construction to
train RL agents on a series of specifications in four
case studies and evaluate the results.
6 EXPERIMENTS & DISCUSSION
With experiments on four existing case studies from
Farama Gymnasium (Farama Foundation, 2024), we
examine two key questions for iterative environment
design: (1) Can we specify goal trees from which
agents are trained to achieve the specified goals? (2)
How can the refinement of tree specifications be used
in the iterative design of RL environments? To answer
these questions, we first present our experimental de-
sign and setup in Section 6.1 and discuss the results
subsequently in Section 6.2.
6.1 Experiment Design and Setup
We evaluate our specification language on four case
studies from Farama Gymnasium (Farama Founda-
tion, 2024), encompassing control problems with dis-
crete and continuous action spaces: Acrobot, Pendu-
lum, MountainCarContinuous, LunarLander. Origi-
nally, each case study represents a trainable RL envi-
ronment, which we call baseline. Each baseline in-
cludes a reward that implicitly defines the objective.
For each case study, we follow our key idea of de-
signing RL environments in iterations of specifying
goals, training agents and evaluating the results.
Initially, we focus on training the baseline and
identify goals in the state space that are necessary to
use goal-oriented specification. For this purpose, we
use Proximal Policy Optimization (PPO) (Schulman
et al., 2017) because of to its versatility in handling
both discrete and continuous action spaces along with
the minimal tuning effort required. We manually tune
hyperparameters for PPO to ensure that the agents can
solve the tasks. For fairness, we use these baseline-
tuned parameters for all experiments of the case study
and reduce bias from hyperparameter tuning. Finally,
ICAART 2025 - 17th International Conference on Agents and Artificial Intelligence
246

Table 1: Complete list of experiment configurations for our case studies.
Acrobot-v1 Pendulum-v1 MountainCar
Continuous-v0
LunarLander-v2
State Space S
Cos,θ
1
× S
Sin,θ
1
× S
Cos,θ
2
× S
Sin,θ
2
× S
α
Vel
,θ
1
× S
α
Vel
,θ
2
× S
Height
b
S
X
× S
Y
× S
α
S
X
× S
Vel
S
X
× S
Y
× S
X,Vel
× S
Y,Vel
×S
α
× S
α,Vel
× S
Leg
1
× S
Leg
2
Goals
a
G
Height
:
1.0 ≤ s
Height
≤ 3.0
G
Position
:
0.966 ≤ s
X
≤ 1.0
−0.259 ≤ s
Y
≤ 0.259
G
Stabilization
:
− 0.25 ≤ s
α
≤ 0.25
G
Position
:
0.45 ≤ s
X
≤ 1.0
G
Velocity
:
−0.03 ≤ s
Vel
≤ 0.07
G
Position
:
− 0.2 ≤ s
X
≤ 0.2
− 0.05 ≤ s
Y
≤ 0.05
G
Velocity
:
− 0.1 ≤ s
X,Vel
≤ 0.1
− 0.1 ≤ s
Y,Vel
≤ 0.1
G
Stabilization
:
0.1 ≤ s
α
≤ 0.1
− 0.1 ≤ s
α,Vel
≤ 0.1
G
LegsGrounded
:
s
Leg
1
= 1, s
Leg
2
= 1
Distance
Annotations
dist
Height
(s) =
q
(s
Height
− 1.5)
2
dist
Position
(s) =
p
(s
X
− 1)
2
dist
Velocity
(s) =
p
(s
X
− 0.07)
2
dist
Position
(s) =
q
s
2
X
+ s
2
Y
dist
Velocity
(s) =
q
s
2
X,Vel
+ s
2
Y,Vel
dist
Stabilization
(s) =
p
s
2
α
Constraints - - - δ
Crash
= 1
C
Crash
= {(s, a)|
(s
X
≤ −0.2∨s
X
≤ 0.2)∧S
y
≤ 0.2}
PPO
Hyper-
parameters
c
- - (use_sde=True) batch_size=32, n_steps=1024,
n_epochs=4, gae_lambda=0.98,
gamma=0.999, , ent_coef=0.01
d
a
We only state the relevant features for each goal. There are no further restrictions on other state space features.
b
We expand the state space by S
Height
with height = −cos(θ
1
) − cos(θ
2
+ θ1) through our state(...) function to enable the
specification of a height goal.
c
If not stated differently, we use the default PPO parameters from Stable Baselines (DLR-RM, 2024b). Most importantly,
these are: gamma=0.99, learning_rate=0.0003, batch_size=64, n_steps=2024, n_epochs=10, gae_lambda=0.95,
ent_coef=0.0, use_sde=False
d
We use optimized hyperparameters from RLZoo (DLR-RM, 2024a), a training framework with published hyperparameters
we extract goal states as described for our running ex-
ample in Section 4. Table 1 lists the goals and hyper-
parameters for reproducibility.
Based on the identified goals, we define up to three
goal tree specifications for each case study. With each
iteration, we increase the specification details refining
the previous tree similar to Figure 3. Our first spec-
ification consists of a single root leaf node, which
includes the goal space that is the intersection of all
identified goals. Second, we refine this root node by
the
V
-operator into subgoal nodes. Finally, we cre-
ate a third specification by annotating the leaf nodes
with distance metrics as given in Table 1. For the
Acrobot case study, we have identified only one goal
and, therefore, we do not include an
V
-operator re-
fined specification. Additionally, for the LunarLander
case study, we impose a safety constraint (see Table 1)
representing the crash penalty from the baseline envi-
ronment.
From each specification, we automatically con-
struct an environment variant. We proceed to train
agents for each variant and measure their performance
by inspecting the individual success rate for each
goal. We do so by defining success based on a goal
space G, counting how often the agent reaches the
goal at the terminal state s
T,i
over N episodes:
success
G
(π) =
1
N
N
∑
τ
i
∼π
(
1 ,s
T,i
∈ G
0 else
Finally, we manually tune the weights of the re-
ward components of those case studies, in which the
agents converge to a local maximum and are therefore
unable to learn all goals.
Iterative Environment Design for Deep Reinforcement Learning Based on Goal-Oriented Specification
247

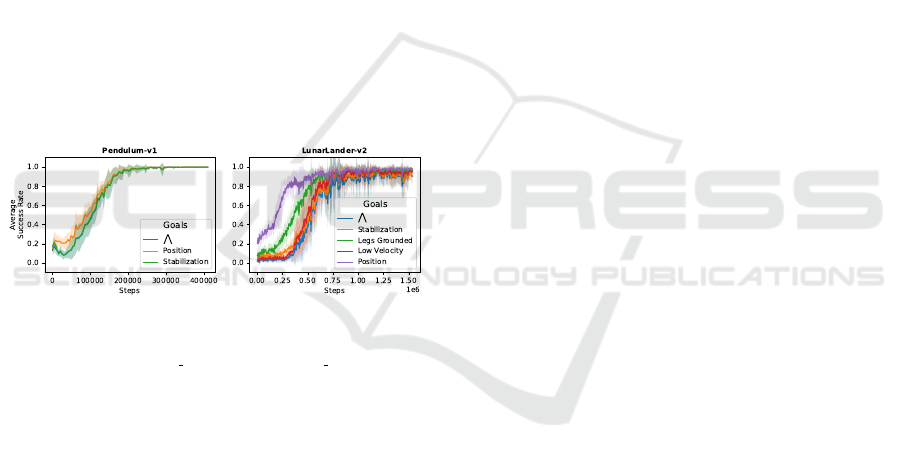
Figure 4: Our results show the success rate of the individual goals with one row per case study. Each column encompasses a
single specification scenario with increasing specification details from left to right.
For reproducibility, we adhere to the following
setup. Each result is averaged over 10 independent
runs with random initialization. We train our agents
with PPO from Stable Baselines (DLR-RM, 2024b)
with tuned hyperparameters Table 1. We normalize
the reward function weights for each environment as
follows: for each of the N reward components of a
node, the weight is
1
N
; the hard safety constraint from
the LunarLander results in a penalty of −1; each dis-
tance reward shape is divided by a specified maxi-
mum distance d to the goal.
6.2 Discussion of Results
The results of our experiments across the four case
studies are depicted in Figure 4. Each row corre-
sponds to one case study, while each column repre-
sents one of the four experimental scenarios: base-
line, single goal,
V
-operator refined goal, with dis-
tance. The graphs illustrate the success metric for
each goal listed in Table 1, providing comparability
across the scenarios, even though the baseline and
single goal scenario do not encompass these goals
directly. The following paragraphs present and dis-
cuss the results for each case study individually and
we conclude with a summary of our findings.
Acrobot. We identify a single goal to reach a spe-
cific height For the Acrobot environment. Thus, we
do not apply the
V
-operator. The baseline scenario
shows convergence, achieving the height goal consis-
tently over all runs. The single goal scenario reaches
about 60 % success rate at the end of training with
high variance. This high variance is caused because
ICAART 2025 - 17th International Conference on Agents and Artificial Intelligence
248

in only 6 out of 10 training runs, the agents can reach
the goal. The agents do not receive any reward in the
remaining four runs due to the sparsity of the reward.
Therefore, the agents cannot converge to a solution.
Incorporating the distance annotation in the last sce-
nario resolves this exploration issue effectively, and
we achieve similar performance to the baseline.
Pendulum. In the baseline of the Pendulum envi-
ronment, the goals are learned consistently. The sin-
gle goal scenario achieves success in 8 out of 10
runs. The
V
-operator refined scenario presents a
more intricate result, in which the refined sparse re-
ward facilitates reliable learning of the stabilization
goal but reaching the target position is more difficult
to achieve. Here, half of the 10 agents converge to
a local optimum where they stabilize the pendulum
without achieving the position goal. The position dis-
tance annotation alleviates this problem by provid-
ing an additional dense reward. However, only by
manually weighting the position and stabilization re-
wards, we can resolve the conflict between the goals.
With this, we achieve more precise convergence to the
goals compared to the baseline as shown in Figure 5.
Figure 5: Results with manual weights for the Pendu-
lum (ω
position
= 0.8, ω
stabilization
= 0.2) and LunarLander
(ω
stabilization
= 50, ω
legs grounded
= 20, ω
low velocity
= 100,
ω
position
= 200) case studies.
MountainCarContinuous. Originally, the Moun-
tainCarContinuous case study is built to introduce an
exploration challenge. This challenge is evident in
the results of the baseline scenario, where the goal is
achieved in only 4 out of 10 runs. We observe similar
difficulties across all three of our specification scenar-
ios. In our
V
-operator refined with distance scenario,
we achieve the goal in 6 out of 10 runs. Improving
the exploration and specific tuning of PPO can resolve
the exploration challenge for the baseline (Kapoutsis
et al., 2023). We strongly believe that our method
yields comparable results with similar tuning efforts,
although this remains to be tested. Nevertheless, we
observe that learning performance improves based on
our refinements with increasing specification detail.
Furthermore, during the design of the case study,
we have experienced the performance degradation for
a different goal tree specification. Specifically, an-
notating the position goal node with the x distance
to the goal states introduces unexpected complexity
into the problem. Here, the trained agents consis-
tently learned to stand still at the bottom of the moun-
tain, while avoiding the negative reward required to
attempt climbing the mountain at high velocity.
LunarLander. The LunarLander case study in-
volves the learning of four goals. The baseline
scenario reaches approximately 80 % success in
achieving the overall
V
-operator goal. While the
sparse reward proves insufficient in the single goal
scenario, the
V
-operator refined scenario enhances
this sparsity by rewarding each goal individually.
Despite this, achieving all goals simultaneously
remains challenging. Our distance annotations
scenario mitigates this issue for the stabilization
goal. Nonetheless, in most runs, the agents converge
to a local optimum, stabilizing without reaching
the landing position. Manual weighting corrects
this imbalance by prioritizing the position goal as
depicted in Figure 5 and we achieve more precise
convergence compared to the baseline.
To conclude our evaluation, we identify known
limitations of our method. Subsequently, we summa-
rize our results with respect to the two key questions
introduced at the beginning of this section.
Our method entails two limitations. First, spec-
ifying complex goals in the state space requires a
state structure for which it is possible and sufficient to
handcraft these goals. While this is theoretically pos-
sible, in practice it hinders the use of our method in
high-dimensional state spaces such as learning from
raw pixels. Second, we have experienced that specific
refinements of goals can lead to undesired and unex-
pected behavior of the trained agents as described in
the results of the MountainCarContinuous case study.
However, this does not contradict our approach of it-
erative environment design but rather emphasizes the
need for iterations. Nevertheless, it is important to
recognize the possibility of degrading results after a
refinement.
Finally, we examine the results regarding our two
key questions. First, we have shown the ability to
specify and learn goal tree specifications sufficiently
for all four case studies. Our results show that we
can consistently learn the goals in three out of four
cases with manually defined weights. For the re-
maining MountainCarContinuous case study, we have
achieved similar results compared to the baseline and
we have learned to reach the goals in 6 out of 10 runs.
Second, the ability to specify goal trees and automat-
ically construct environments, enables iterations by
Iterative Environment Design for Deep Reinforcement Learning Based on Goal-Oriented Specification
249

evaluating a specification from trained agents. Our
findings indicate that single goals with sparse re-
wards, often, do not provide enough feedback for
effective learning. However, the results of our
V
-
operator consistently improve by providing a refined
reward for the goal. Additionally, the
V
-operator en-
ables to balance possibly conflicting goals by weight-
ing the inner reward components while the distance
annotations help to guide the agent towards other-
wise challenging goals. In contrast, we would like
to point out that goal tree refinements do not always
yield improvements in learning the goals. Therefore,
iterations can also include reverting or adapting prior
changes to the specification. Nevertheless, our results
show that we can iteratively improve on learning the
specified goals. In the following section, we conclude
and present future work.
7 CONCLUSION
In this work, we have introduced iterative environ-
ment design for reinforcement learning based on goal-
oriented specification (Schwan et al., 2023). We
evolve goal-oriented specification and make it practi-
cal with two contributions. First, we introduce our au-
tomated method to construct RL environments from
goal tree specifications. Thereby, we enable the train-
ing of agents from these specifications to evaluate
their behavior for future improvements. Second, we
enable iterative goal tree refinements by introducing
definitions for leaf nodes, the
V
-operator and annota-
tions. To evaluate our method, we have trained agents
in four case studies with up to three specification sce-
narios each. With manually tuned weights of the re-
ward components, we achieve goal success rates sim-
ilar to the baselines but with higher precision. Finally,
our results show that goal tree refinements can be used
to iteratively improve the learning of specified goals.
Through iterative environment design, we oppose the
common trial-and-error practice to facilitate the ap-
plication of reinforcement learning.
In future work, we plan on automating the man-
ual weighting of reward components from our
V
-
operator to further reduce time-consuming manual
tasks. Moreover, we aim at enhancing our specifica-
tion method to be practical for high-dimensional state
spaces. Finally, introducing new operators can enable
specifying and learning temporal abstractions. With
this, we follow our idea to overcome the common
trial-and-error practice and facilitate the development
of RL solution for domain experts.
ACKNOWLEDGEMENTS
This work has been partially funded by the Fed-
eral Ministry of Education and Research as part of
the Software Campus project ZoLA - Ziel-orientiertes
Lernen von Agenten (funding code 01IS23068).
REFERENCES
Ahmad, K., Abdelrazek, M., Arora, C., Bano, M., and
Grundy, J. (2023). Requirements engineering for
artificial intelligence systems: A systematic map-
ping study. Information and Software Technology,
158:107176.
Andrychowicz, M., Wolski, F., Ray, A., Schneider, J., Fong,
R., Welinder, P., McGrew, B., Tobin, J., Abbeel, P.,
and Zaremba, W. (2017). Hindsight experience re-
play. In Advances in Neural Information Processing
Systems, pages 5048–5058.
Cai, M., Xiao, S., Li, B., Li, Z., and Kan, Z. (2021). Re-
inforcement Learning Based Temporal Logic Control
with Maximum Probabilistic Satisfaction. In 2021
IEEE International Conference on Robotics and Au-
tomation (ICRA), pages 806–812.
Chane-Sane, E., Schmid, C., and Laptev, I. (2021). Goal-
Conditioned Reinforcement Learning with Imagined
Subgoals. In Proceedings of the 38th International
Conference on Machine Learning, volume 139, pages
1430–1440.
Ding, H., Tang, Y., Wu, Q., Wang, B., Chen, C.,
and Wang, Z. (2023). Magnetic Field-Based Re-
ward Shaping for Goal-Conditioned Reinforcement
Learning. IEEE/CAA Journal of Automatica Sinica,
10(12):2233–2247.
DLR-RM (2024a). RL Baselines3 Zoo: A Train-
ing Framework for Stable Baselines3 Reinforce-
ment Learning Agents. https://github.com/DLR-RM/
rl-baselines3-zoo. [Last accessed on July 17th, 2024].
DLR-RM (2024b). Stable-Baselines3. https://github.com/
DLR-RM/stable-baselines3. [Last accessed on July
17th, 2024].
Everett, M., Chen, Y. F., and How, J. P. (2021). Colli-
sion avoidance in pedestrian-rich environments with
deep reinforcement learning. IEEE Access, 9:10357–
10377.
Farama Foundation (2024). Gymnasium: An API standard
for reinforcement learning with a diverse collection of
reference environments. https://gymnasium.farama.
org/. [Last accessed on July 12th, 2024].
Florensa, C., Held, D., Geng, X., and Abbeel, P. (2018).
Automatic goal generation for reinforcement learning
agents. In International conference on machine learn-
ing, pages 1515–1528.
Hahn, E. M., Perez, M., Schewe, S., Somenzi, F., Trivedi,
A., and Wojtczak, D. (2019). Omega-Regular Objec-
tives in Model-Free Reinforcement Learning. In Tools
and Algorithms for the Construction and Analysis of
Systems, pages 395–412.
ICAART 2025 - 17th International Conference on Agents and Artificial Intelligence
250

Hammond, L., Abate, A., Gutierrez, J., and Wooldridge,
M. (2021). Multi-Agent Reinforcement Learning with
Temporal Logic Specifications. In AAMAS ’21: 20th
International Conference on Autonomous Agents and
Multiagent Systems, pages 583–592. ACM. arXiv:.
Jothimurugan, K., Alur, R., and Bastani, O. (2019). A
composable specification language for reinforcement
learning tasks. Advances in Neural Information Pro-
cessing Systems, 32.
Jothimurugan, K., Bansal, S., Bastani, O., and Alur, R.
(2021). Compositional reinforcement learning from
logical specifications. Advances in Neural Informa-
tion Processing Systems, 34:10026–10039.
Jurgenson, T., Avner, O., Groshev, E., and Tamar, A. (2020).
Sub-Goal Trees a Framework for Goal-Based Rein-
forcement Learning. In Proceedings of the 37th In-
ternational Conference on Machine Learning, volume
119 of Proceedings of Machine Learning Research,
pages 5020–5030.
Kapoutsis, A. C., Koutras, D. I., Korkas, C. D., and
Kosmatopoulos, E. B. (2023). ACRE: Actor-Critic
with Reward-Preserving Exploration. Neural Comput.
Appl., 35(30):22563–22576.
Li, X., Vasile, C. I., and Belta, C. (2017). Reinforcement
learning with temporal logic rewards. IEEE Interna-
tional Conference on Intelligent Robots and Systems,
pages 3834–3839.
Ng, A. Y., Harada, D., and Russell, S. (1999). Policy invari-
ance under reward transformations : Theory and ap-
plication to reward shaping. 16th International Con-
ference on Machine Learning, 3:278–287.
Okudo, T. and Yamada, S. (2021). Subgoal-Based Re-
ward Shaping to Improve Efficiency in Reinforcement
Learning. IEEE Access, 9:97557–97568.
Okudo, T. and Yamada, S. (2023). Learning Potential
in Subgoal-Based Reward Shaping. IEEE Access,
11:17116–17137.
Retzlaff, C. O., Das, S., Wayllace, C., Mousavi, P., Afshari,
M., Yang, T., Saranti, A., Angerschmid, A., Taylor,
M. E., and Holzinger, A. (2024). Human-in-the-Loop
Reinforcement Learning: A Survey and Position on
Requirements, Challenges, and Opportunities. J. Artif.
Intell. Res., 79:359–415.
Roijers, D. M., Vamplew, P., Whiteson, S., and Dazeley,
R. (2013). A survey of multi-objective sequential
decision-making. Journal of Artificial Intelligence Re-
search, 48:67–113.
Schaul, T., Horgan, D., Gregor, K., and Silver, D. (2015).
Universal value function approximators. In 32nd In-
ternational Conference on Machine Learning.
Schulman, J., Wolski, F., Dhariwal, P., Radford, A., and
Klimov, O. (2017). Proximal Policy Optimization Al-
gorithms. CoRR.
Schwan, S., Kl
¨
os, V., and Glesner, S. (2023). A Goal-
Oriented Specification Language for Reinforcement
Learning. In International Conference on Modeling
Decisions for Artificial Intelligence, pages 169–180.
Springer.
Sutton, R. S. and Barto, A. G. (2018). Reinforcement learn-
ing: An introduction. MIT press.
Van Lamsweerde, A. (2001). Goal-oriented requirements
engineering: A guided tour. Proceedings of the IEEE
International Conference on Requirements Engineer-
ing, pages 249–261.
Iterative Environment Design for Deep Reinforcement Learning Based on Goal-Oriented Specification
251