A Whole New World: Can Virtual Reality Help to Understand
Non-Euclidean Geometries?
Ma
´
e Mavromatis
1 a
, Ronan Gaugne
2 b
, R
´
emi Coulon
3 c
and Val
´
erie Gouranton
1 d
1
Universit
´
e Rennes, INSA Rennes, Inria, CNRS, IRISA, France
2
Universit
´
e Rennes, Inria, CNRS, IRISA, France
3
Universit
´
e de Bourgogne, CNRS, IMB, France
Keywords:
Virtual Reality, Education, Simulation, Non-Euclidean Geometry, User Study.
Abstract:
With the democratisation of digital technologies, new pedagogical approaches are emerging that leverage
these innovative media to enhance student engagement and promote different ways of learning. This article
compares three learning modalities—slides, screen, and VR—in terms of knowledge acquired, time spent,
and usability. The slides modality involves an illustrated slide presentation, the screen modality uses an on-
screen simulation with navigation, and the VR modality shows the same simulation in virtual reality with a
Head-Mounted Display (HMD). In this study, we investigated the impact of these modalities on students’
understanding of the essential properties of the unintuitive non-Euclidean geometries S
3
and H
3
. All three
modalities helped participants improve their answers to the mathematics questionnaire, though further research
is needed to fully exploit the unique benefits of virtual reality.
1 INTRODUCTION
Virtual reality (VR) is advancing rapidly, with signifi-
cant progress in fields like medicine, entertainment,
and education. As VR becomes more accessible,
many studies focus on its potential to enhance student
learning (Mikropoulos and Natsis, 2011). New educa-
tional opportunities are emerging, widely recognized
as beneficial. The use of VR in education is expected
to grow, particularly in mathematics, where it im-
proves motivation and performance (Lai and Cheong,
2022). VR immerses students in a virtual world,
enhancing their mathematical reasoning and spatial
skills (Kaufmann and Schmalstieg, 2003).
A key advantage of VR is its ability to represent
3D objects in a 3D environment, aiding 3D thinking
and mental transformation, which 2D technologies
cannot provide (Hedburg and Alexander, 1994). This
is especially useful in geometry, particularly non-
Euclidean geometries, which are counter-intuitive and
difficult to understand due to their conflict with clas-
sical geometry. Several studies have explored inno-
a
https://orcid.org/0000-0001-9089-7859
b
https://orcid.org/0000-0002-4762-4342
c
https://orcid.org/0000-0003-0233-5974
d
https://orcid.org/0000-0002-9351-2747
vative ways to teach these geometries (Sukestiyarno
et al., 2023).
However, few studies examine VR’s role in teach-
ing non-Euclidean geometries. This work aims to
assess the impact of VR on learning non-Euclidean
geometries, comparing it to screen simulations and
traditional slide-based explanations, to determine if
immersion helps students understand these abstract
spaces.
In a user study, we created three learning environ-
ments for non-Euclidean geometries, tested with par-
ticipants from diverse backgrounds. The key math-
ematical properties of each geometry, requiring var-
ious skills, are presented in section 3. Understand-
ing of the geometries was assessed before and after
the experiment to measure the effectiveness of these
environments and compare them. The experiment in
section 5 shows participants improved their answers
to the mathematics questionnaire, with no statistically
significant difference between the three modalities.
Mavromatis, M., Gaugne, R., Coulon, R. and Gouranton, V.
A Whole New World: Can Virtual Reality Help to Understand Non-Euclidean Geometries?.
DOI: 10.5220/0013150900003912
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 20th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2025) - Volume 1: GRAPP, HUCAPP
and IVAPP, pages 231-238
ISBN: 978-989-758-728-3; ISSN: 2184-4321
Proceedings Copyright © 2025 by SCITEPRESS – Science and Technology Publications, Lda.
231

2 RELATED WORKS
2.1 VR in Mathematics Education
Virtual reality has made significant progress in edu-
cation, with current research focusing on its use to
teach real-world phenomena and provide immersive
learning experiences for students (Lai and Cheong,
2022). Studies suggest that students are interested in
using virtual reality as part of their courses (Baxter
and Hainey, 2019).
Using virtual reality as a teaching aid in math-
ematical geometry is an innovative approach. Im-
mersive technologies like VR offer many advantages
(Cevikbas et al., 2023), such as increasing motiva-
tion, providing a different learning experience, and
enhancing effectiveness (Osypova et al., 2021). Vir-
tual reality can help students grasp complex concepts
and reduce misunderstandings (Mikropoulos and Nat-
sis, 2011). However, some studies show mixed re-
sults. For example, a study on virtual reality for mul-
tivariable calculus found that students sometimes per-
formed worse on certain questions after using the VR
application, though results varied. Measuring these
effects is challenging, as comparing VR environments
with traditional classrooms is difficult (Kang et al.,
2020).
Virtual reality learning aids have key benefits,
such as boosting motivation, visualizing abstract con-
cepts, and stimulating interest in new knowledge
(Wang et al., 2018). VR also allows students to play
virtual characters, manipulate geometries, and learn
geometry concepts (Guerrero Idrovo et al., 2016).
One of the key advantages of VR over other tech-
nologies is its ability to represent three-dimensional
(3D) objects in a 3D world, which is particularly use-
ful in geometry.
2.2 VR Geometry Teaching Platforms
Virtual reality mathematical geometry teaching plat-
forms such as ClassVR, VRMath and GeoGebra are
available on the market today. The ClassVR plat-
form provides an operating record system that al-
lows teachers to understand how students learn us-
ing the platform. The VRMath platform provides vir-
tual geometric mathematical objects, such as cylin-
ders, cones and trigonometric cones. GeoGebra is a
three-dimensional drawing platform that provides a
learning space in which students can add points and
lines in virtual space to create a 3D virtual object.
Research continues to use virtual reality to develop
immersive learning systems for geometric mathemat-
ics (Su et al., 2022). Recently, the MathworldVR vir-
tual reality (WebVR) application has been proposed
for teaching higher mathematics concepts that require
spatial abilities. It allows, for example, the manipula-
tion of input variables of parametric functions, which
reduces the time needed by students to understand the
underlying principles of a given mathematical theory
(Takac, 2020).
2.3 Non-Eucliean Geometry Education
Over the past few decades, there has been increas-
ing recognition that mathematics is considered a dif-
ficult subject, requiring changes in teaching meth-
ods and tools to boost students’ interest and partici-
pation (Gambini and L
´
en
´
art, 2021). Non-Euclidean
geometry, in particular, is abstract and challenging
to learn. Multiple studies have used different ap-
proaches to support students in their learning process.
For example, one study assessed the impact of an
ethnomathematics approach on students’ spatial abil-
ities for Euclid’s, Lobachevsky’s, and Riemann’s ge-
ometries, finding a positive influence on spatial skills
(Sukestiyarno et al., 2023). Another explored teach-
ing non-Euclidean concepts using astronomical im-
ages, where students learned to calculate distances
and areas on the Moon’s surface, aiding their under-
standing of geodesics and spherical triangles (Caerols
et al., 2021). An experiment compared Euclidean
and non-Euclidean geometries to help students’ un-
derstand geometric properties and challenge their per-
ceptions of mathematics (Gambini, 2021). Other re-
search has focused on integrating non-Euclidean ge-
ometry into high school curricula to broaden perspec-
tives and clarify concepts like undefined terms in Eu-
clidean geometry (Buda, 2017).
The use of technology has created new dynam-
ics in teaching geometry, enhancing students’ under-
standing. For instance, a study involving technology
in teaching hyperbolic geometry through Poincar
´
e’s
Disk found it increased student engagement and
helped them understand key concepts of this geom-
etry (Kotarinou and Stathopoulou, 2017).
2.4 Deriving the Approach
The value of virtual reality in education is being
increasingly studied, yet its potential use in non-
Euclidean geometry remains unexplored. This area
of mathematics is complex and unintuitive, and could
benefit from new methods of visualization and un-
derstanding. In this study, we focused on designing
the pedagogical content of the different experimental
conditions and examining the user experience (cyber-
sickness, acceptability, usability, and behavior).
GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications
232

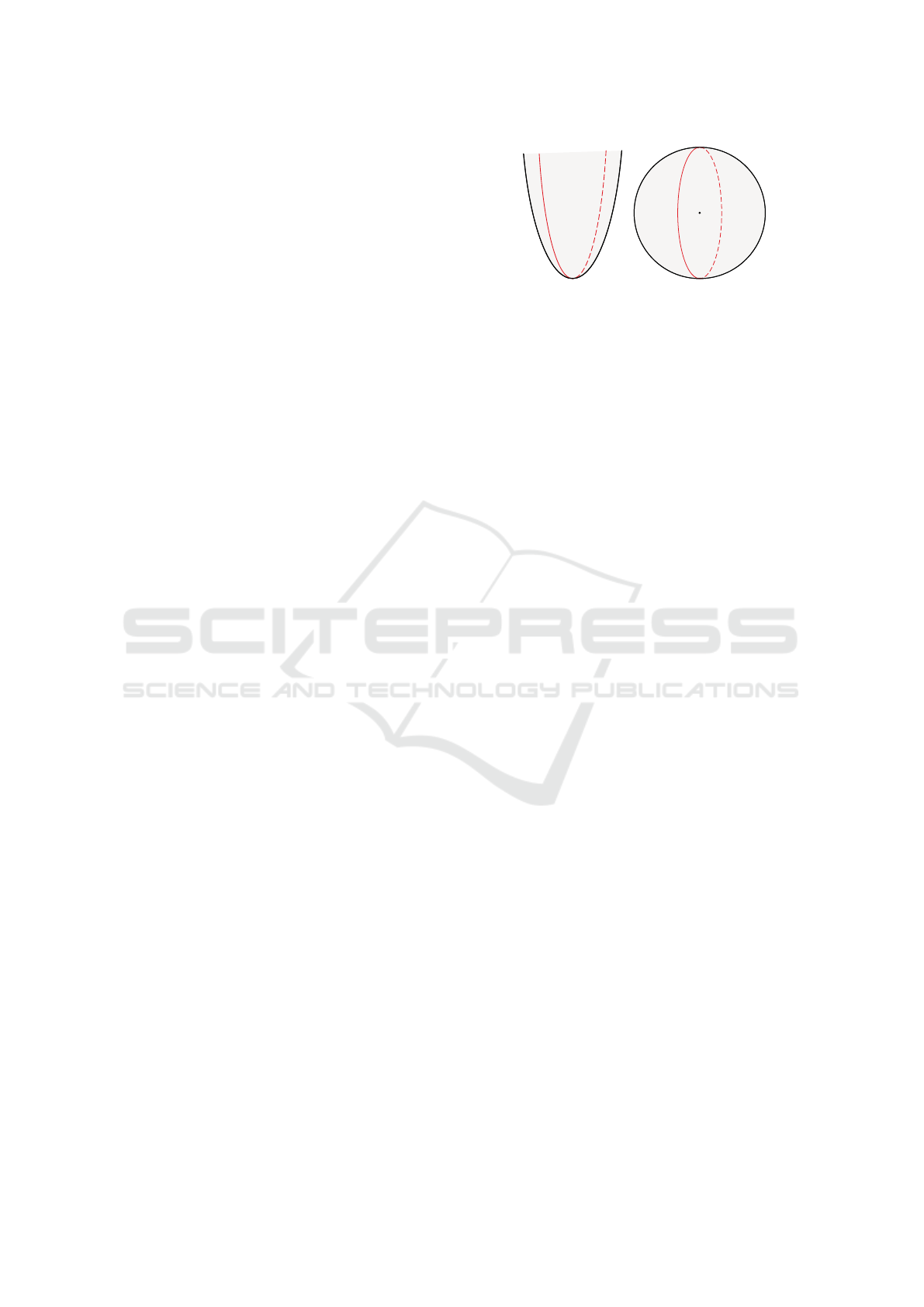
3 UNDERLYING
MATHEMATICAL CONCEPTS
Euclidean geometry is well-known, but alternative 2D
geometries, such as the sphere and hyperboloid (see
Fig. 1), also exist. In three dimensions, Thurston’s
geometrization theorem (Thurston, 1986), proven by
Perelman (Eres et al., 2010), classifies all possible ge-
ometries into eight distinct models. These include the
familiar 3D Euclidean space, along with seven non-
Euclidean geometries, such as spherical geometry S
3
and hyperbolic geometry H
3
. The sphere S
2
and hy-
perboloid H
2
are used throughout the article to illus-
trate their specificities.
3.1 S
3
and H
3
S
3
(resp. H
3
) is the 3D analogue of the 2D sphere
(resp. hyperbolic plane) in R
3
. We model S
3
as the
unit sphere in R
4
and H
3
as the Minkowski hyper-
boloid. The distance between two points P
1
and P
2
is the length of the shortest curve joining them. Both
S
3
and H
3
are homogeneous and isotropic (all points,
resp. directions, are equivalent).
3.2 Mathematical Notions and Related
Properties
Geodesics: A geodesic (see Fig. 1) in a space S is
a curve in S that locally minimises the distance trav-
elled. It is the analogue of a straight line in a plane.
Holonomy: The holonomy of a connection mea-
sures how parallel transport along closed loops alters
the geometric information. This change results from
the connection’s curvature. For example, Fig. 2 shows
the orientation changes of an observer traveling along
the sides of a triangle on a 2D sphere.
Conjugate Points: Conjugate points indicate when
geodesics fail to minimise length globally. For exam-
ple, on a sphere, geodesics passing through the North
Pole can be extended to the South Pole, meaning seg-
ments containing both poles do not minimise length.
Any pair of antipodal points on the 2D sphere are con-
jugate points.
Objects Visible in Front of and Behind: The
geodesics of the sphere are great circles centered at
the sphere’s center (see Fig. 1). As a result, an object
in front of an observer on S
3
is also visible behind,
as a light ray can travel along the geodesic passing
c
Figure 1: Left, an hyperboloid in 2D. Right, a sphere in 2D.
The analogues to H
3
and S
3
in 2D. In red, a geodesic.
through the object in both directions and return to the
observer.
Distance Between Objects: The shape of
geodesics varies across geometries, and even
within a single geometry, affecting how distances
are perceived. In particular, size is not always an
indicator of distance (see Fig. 3).
Right Angled Regular Polygons: Due to space
curvature, the properties of polygons vary across ge-
ometries. For example, the triangle obtained by cut-
ting a sphere in eight similar pieces is a right angled
equilateral triangle (see Fig. 2), while in Euclidean
geometry, the sum of a triangle’s angles is always
180°. In H
3
, one can construct any n-gone with n ≥ 5
as a right angled regular polygon.
4 METHOD
This work aims to design and evaluate a VR-based
learning environment for non-Euclidean geometries.
This section covers the simulation method, the design
focusing on key properties of the geometries, and the
evaluation approach.
4.1 Simulating Non-Euclidean Spaces
Common rendering software does not support non-
Euclidean geometries, as light rays follow straight
lines in traditional engines. Based on the method in
(Coulon et al., 2022), we implemented a raymarching
renderer that traces rays along the geodesics of the
geometry. Other renderers for Thurston geometries
include (Weeks, ; Berger, 2015; Kopczy
´
nski et al.,
2017; Velho et al., 2020). Illumination is computed
using Phong’s model.
4.2 Learning Environment Design
During the experiment’s design, we aimed to iden-
tify key properties of the chosen geometries, focusing
A Whole New World: Can Virtual Reality Help to Understand Non-Euclidean Geometries?
233

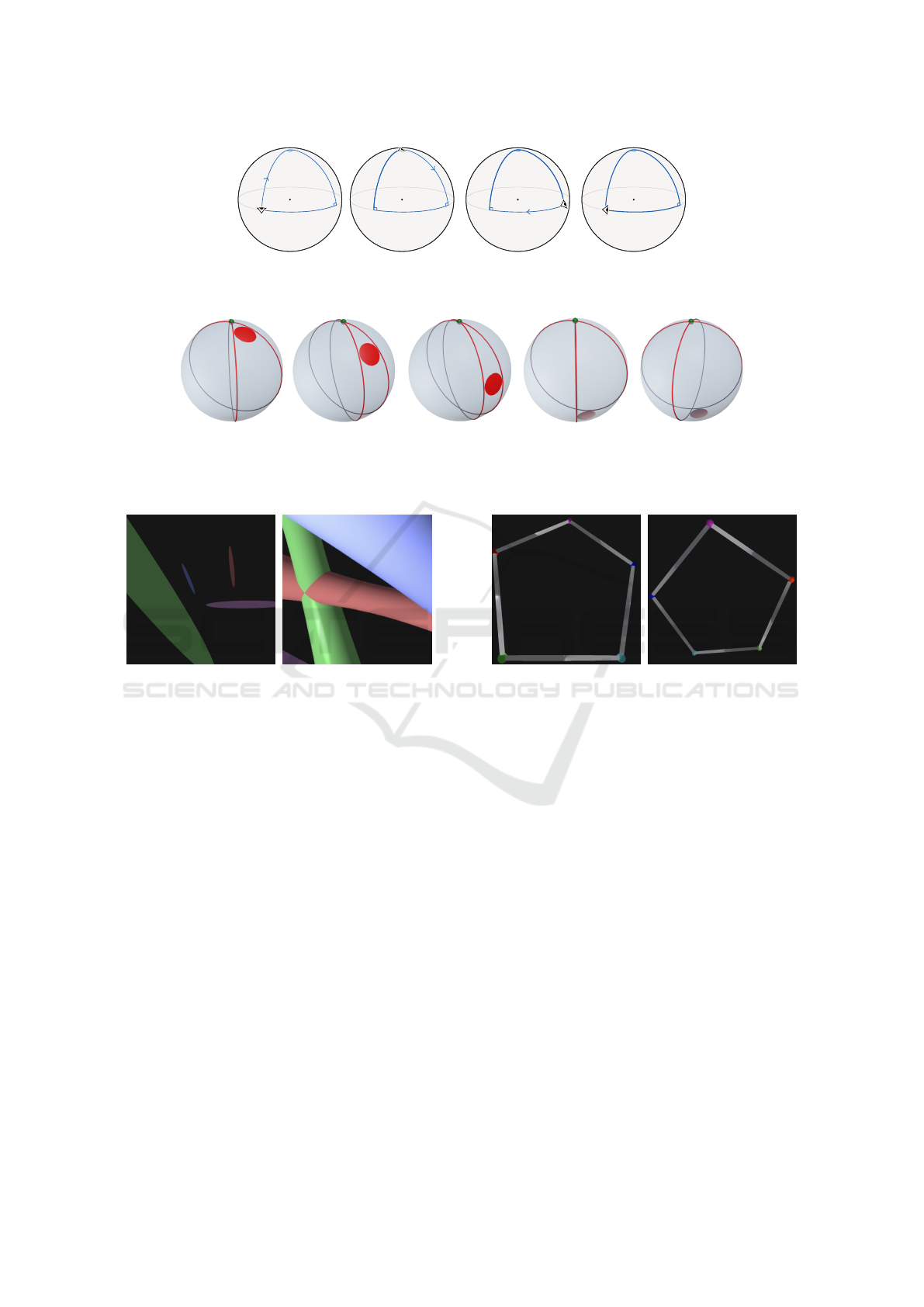
c
c
c
c
Figure 2: Illustration of the principle of holonomy on a 2-dimensional sphere. The observer moves along a right angles
triangle without ever turning. Their orientation changes as they move along the triangle. When they have completed a full
turn of the triangle, they have completed a quarter turn in terms of orientation.
Figure 3: This series of figures illustrates the proportion of an observer’s field of view occupied by an object as a function
of its distance from the observer. The object here is the red disc, while the observer is the green dot. The two red geodesics
tangent to the disc form an angle corresponding to the size of the disc as perceived by the observer. This angle decreases and
then increases as the disc moves from the observer’s position to the antipodal position.
Figure 4: Screenshot of the virtual environment featuring
four infinite cylinders placed around geodesics in H
3
(left)
and S
3
(right).
on both simple properties like distance and geodesics,
and more complex ones like holonomy. We also con-
sidered the logical order for presenting these prop-
erties, as some concepts build on others. Presenting
them randomly would have been irrelevant. This sec-
tion presents these properties in order and explains
how they were introduced to the participants.
Geodesics: The aim was to enable participants to
identify the shape of geodesics in S
3
and H
3
. The vir-
tual environment included four infinite cylinders po-
sitioned around four geodesics (see Figure 4).
Objects Visible in Front of and Behind: This
property only concerned S
3
. The aim was for partici-
pants to see that objects visible in front of them were
also visible behind them. The virtual environment in-
cluded a finite cylinder and a sphere.
Distance: The aim was for participants to under-
stand that distance estimation differs between geome-
Figure 5: Screenshots of the right angled pentagon in H
3
from two different points of view.
tries. To illustrate this, spheres in the virtual environ-
ment were coloured based on their distance from the
user: light for close spheres and dark for distant ones.
The environment consisted of two spheres and finite
cylinders regularly positioned in space.
Conjugate Points: This property applied only to
S
3
and aimed to help participants understand conju-
gate points. The virtual environment featured a finite
cylinder and a sphere, both color-coded by distance
from the user. In the VR and screen conditions, partic-
ipants were asked to identify the position where they
would feel enclosed by one of the objects.
Right Angled Regular Polygons: The goal was to
demonstrate that polygonal properties vary across ge-
ometries. Participants were shown regular polygons
with right angles: an equilateral triangle with right an-
gles in S
3
(see Figure 2) and a regular pentagon with
right angles in H
3
(see Figure 5). We explained on
the UIs and slides that polygons with more than five
sides can be constructed as right-angled regular poly-
GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications
234

Figure 6: The user is immersed in a tiled hyperbolic space
made up of sphere complements. This tiling reveals pillars
that highlight the rotations in the environment caused by
holonomy.
gons in H
3
. In the VR and screen conditions, partic-
ipants moved around to observe the angles, while in
the slides condition, they viewed a drawing.
Holonomy: The aim was to help participants under-
stand the effect of holonomy for a geometry dweller.
The virtual environment featured a tiled space where
“pillars” appeared (see Figure 6). In the VR condi-
tion, participants made squares with their head and
observed the environment. In the screen condition,
they used the keyboard to move the camera and ob-
serve the environment. In the slides condition, a series
of drawings illustrated how the observer’s orientation
changed as they walked along the right-angled poly-
gon from the previous slide (see Figure 2).
5 EXPERIMENT
The aim of this experiment was to explore the impact
of three technologies (VR, screen, slides) on under-
standing non-Euclidean geometries. In the VR and
screen conditions, participants navigated a virtual en-
vironment and focused on one property of the geom-
etry per scene. In the slides condition, participants
worked through one slide per property. They were
free to spend as much time as needed on each prop-
erty, exploring the environment in the VR and screen
conditions, and reading the slides in the slides condi-
tion. Participants were divided into two groups: ex-
perts (mathematics students at the Master’s or PhD
level) and novices (students in preparatory classes or
computer scientists).
5.1 Participants and Apparatus
19 experts participants took part in the experiment (5
females, 12 males, 1 other, 1 preferred not to answer),
aged 19 to 28 (X = 22, SD = 2.5) and 21 novices par-
ticipants took part in the experiment (3 females, 16
males, 2 other), aged 19 to 60 (X = 26, SD = 8.8).
Figure 7: From left to right: Slides, Screen, and VR setups.
All participants were students recruited on our cam-
pus or computer scientists from the lab. They did
not receive any financial compensation. All had nor-
mal or corrected vision. Participants were divided
into three groups for the three conditions (see Fig-
ure 7), with the groups balanced according to their
registration order. Those in the VR condition were
immersed in the virtual environment using an Oculus
HMD and associated controllers. The VR experiment
was conducted using a desktop computer ensuring a
minimum of 80 fps under all conditions, developed
using Unity 2023.2 The experiment was approved by
the local ethics committee (COERLE 2024-37).
5.2 Experimental Protocol and Design
After signing the consent form, participants com-
pleted a demographic questionnaire and were briefed
on the experiment’s purpose. They were given a
document explaining the mathematical concepts they
would encounter; the expert version was technical,
while the novice version was more general. Partici-
pants then took a math questionnaire to assess their
baseline understanding of the first geometry. De-
pending on their assigned condition, participants were
equipped with the appropriate setup: VR equipment
for the vr condition, or a screen, mouse, and keyboard
for the screen or slides conditions. The experiment
consisted of two blocks, each corresponding to one
geometry (S
3
or H
3
). Each block had scenes address-
ing different properties (6 scenes for S
3
, 4 for H
3
).
Participants in the VR or screen conditions filled out
a sickness questionnaire after each scene (i.e. each
property). After completing the first block, partici-
pants re-took the math questionnaire for the first ge-
ometry and then completed it for the second geome-
try. The same procedure was followed for the second
block, with the sickness questionnaire completed af-
ter each property. After finishing the second block,
participants filled out the math questionnaire for the
second geometry and completed an acceptance ques-
tionnaire.
The order of geometries was counterbalanced.
Participants in the VR or screen conditions spent
around 20 minutes per block, while the slides con-
dition took approximately 45 minutes in total.
A Whole New World: Can Virtual Reality Help to Understand Non-Euclidean Geometries?
235

Figure 8: Drawings presented to participants when answer-
ing the maths questionnaire about H
3
.
Figure 9: Drawings presented to participants when answer-
ing the maths questionnaire about S
3
.
5.3 Experimental Data
Subjective Measures. For the VR and screen con-
ditions, we used the VRSQ questionnaire (Kim et al.,
2018) to assess the participants’ VR sickness level.
After the experiment, participants in all three con-
ditions completed a subset of the UTAUT2 question-
naire with 7-point Likert scale answers (Venkatesh
et al., 2012) to assess acceptance. We excluded
the UTAUT2 sections “social influence”, “habit” and
“price value”, as they were irrelevant to our study.
Objective Measures. We measured the time spent
on each scene or slide based on the condition, as well
as the displacement in the virtual environment for par-
ticipants in the VR and screen conditions.
Before and after each block, participants com-
pleted a custom math questionnaire, created in col-
laboration with a mathematician. The questionnaire
included six questions, one for each property, where
participants chose a single answer. An option “the
experiment does not allow me to answer” was always
available. Below are the detailed questions and possi-
ble answers, excluding the neutral option:
• The geodesics of this geometry have a shape like:
For this question, participants had to pick one of
the drawings of Figure 8 when answering about
H
3
, and of Figure 9 when answering about S
3
.
• In this geometry, an object is generally visible: in
a single location / it depends on the objects and
their geometric characteristics / in two places, in
front and behind you / in three places, forming
a triangle around you / in five places, forming a
pentagon around you.
• In this geometry, how can you estimate the dis-
tance from an object to you? by relying on its size
when its distance from you varies. / item it is not
possible to estimate it. / depending on its position
relative to other objects in the environment.
1
2
3
4
5
6
7
condition
effort
intention
motivation
performance
section
score
modalite
vr
screen
slides
Figure 10: Box plot of UTAUT2 section results by section
and modality.
• In this geometry, there are: no pair of special posi-
tions. / one pair of special positions. / all diamet-
rically opposed position pairs play a special role.
/ a variable finite number of special position pairs.
/ a pair of positions visible in no direction.
• In this geometry, the regular polygons with right
angles are: the triangle. / the square. / the pen-
tagon. / polygons with more than five vertices. /
there are no regular right-angled polygons.
• In this geometry, we can observe holonomy. What
does this effect correspond to? a luminous halo
around the objects. / a reflection of the environ-
ment. / a rotation of the environment. / distortion
of distant objects.
5.4 Hypotheses and Results
Building on our literature review and the experimental
protocol, we formulated the following hypotheses:
[H1] Globally, the VR modality will enable better
progress on the mathematics questionnaire.
[H2] Participants will prefer the vr condition, as im-
mersion in the virtual environment is more enjoyable
than studying slides. The use of a headset enhances
this sense of immersion compared to the on-screen
version. This preference will be reflected in the hedo-
nic motivation scores of the UTAUT questionnaire.
Data were analysed using non parametric statistics
due to the limited number of participants.
Subjective Measures. The VRSQ questionnaire
showed similar results across conditions and geome-
tries. A Wilcoxon test revealed no statistically sig-
nificant differences. The ratings (0-100) were low
(screen X = 4.2, SD = 5.7; vr X = 9.6, SD = 9.2),
indicating that cybersickness was not an issue.
GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications
236

−6
−3
0
3
6
Screen Slides VR
modality
score
Timing
before
after
Figure 11: Box plot of mean scores in the math question-
naire before and after the experiment for each modality.
The subset of the UTAUT2 questionnaire gave sim-
ilar results among conditions (vr X = 4.8, SD = 0.9;
screen X = 5.4, SD = 0.8; slides X = 5.0, SD = 1.0).
We found no statistically significant difference while
running a Kruskal-Wallis test (see Figure 10, χ
2
=
2.1, df = 2, p = 0.3). We can still observe that moti-
vation seems higher for the vr and screen conditions
than for the slides condition (see Figure 10).
Objective Measures. To analyse the mathematics
questionnaire, we assigned a score to each answer
as follows: a correct answer is worth +1, a wrong
answer is worth −1, and a neutral answer (“the ex-
periment does not allow me to answer”) is worth
0. The total score ranged from −6 to +6. Paired
Wilcoxon tests revealed that each modality showed
significantly better scores after the experiment than
before (p < 0.01, see Figure 11).
To explore this further, we computed the mean
score change before and after the experiment for each
condition. For all participants, the slides condition
increased the average score by 2.1 points, the screen
condition, by 3 points, and the VR condition, by 3.3
points. We then computed this change separately for
experts and novices. Experts showed slightly more
progress, with their scores increasing by 2.4 points
in the slides condition, 3 points in the screen condi-
tion, and 3.6 points in the VR condition, compared to
novices, who saw increases of 1.9 points in the slides
condition, 3 points in the screen condition, and 2.9
points in the vr condition. However a Kruskal-Wallis
test did not reveal a statistically significant difference
(p = 0.4) between the modalities.
The amount of time spent and the amount of dis-
placement achieved in each scene (i.e. for each prop-
erty) were analyzed using a logistic regression to de-
termine whether they impacted the mathematics ques-
tionnaire scores. However, this analysis did not result
in a model that could establish a correlation between
time/displacement and score. This inability to con-
struct such a model occurred because a large propor-
tion of both correct and incorrect responses fell within
the same time or displacement intervals, making it
difficult to create a reliable model.
5.5 Discussion
The results show that all modalities led to progress,
but the difference between the VR modality and the
others was not statistically significant. Thus, we can-
not confirm or reject our hypothesis [H1].
Similarly, no significant difference was found in
responses to the “hedonic motivation” section of the
UTAUT questionnaire, although responses for VR and
screen were higher and more clustered. Therefore,
hypothesis [H2] cannot be confirmed or rejected.
To maximize comparability between the three
modalities, we simplified the VR and screen exper-
iments. We avoided complex interactions, which
would have reduced comparability. However, this
simplification likely missed unique features of each
modality: physical interaction in VR, precise key-
board/mouse control on screen, and the limited inter-
activity of slides. One hypothesis for the small differ-
ences between modalities is this oversimplification.
Finally, based on math questionnaire scores and
informal feedback, we found that the experiment re-
quired a higher level of mathematics than expected.
The introductory document, meant to explain the vo-
cabulary, used advanced formalism and concepts that
prevented some participants from developing the ex-
pected skills.
6 CONCLUSION AND FUTURE
WORKS
In this experiment we explored the differences be-
tween the three conditions vr, screen and slides for
learning the properties of the non-Euclidean geome-
tries S
3
and H
3
. We have implemented a simulation
of these geometries that allows them to be visualised
and immersed inside both in virtual reality and on
screen. We have also built a scenario that allows the
key properties of these geometries to be tackled in a
short space of time.
The results obtained encourage us to continue this
work, in particular by reducing the presence of math-
ematical formalism, increasing the user’s ability to in-
teract with the system, and reinforcing the pedagogi-
cal approach. It is interesting to gain a better under-
standing of what virtual reality can and cannot do for
A Whole New World: Can Virtual Reality Help to Understand Non-Euclidean Geometries?
237

mathematics education, particularly in areas as com-
plex as non-Euclidean geometries. Virtual reality is a
powerful tool that could enable any scientist in train-
ing to become more proficient at modelling and ge-
ometrising problems.
ACKNOWLEDGEMENTS
This work was supported in part by grants from
CNRS 80 Prime ThurstonVR, DemoES AIR ANR-
21-DMES-0001, Equipex+ Continuum ANR-21-
ESRE-0030
REFERENCES
Baxter, G. and Hainey, T. (2019). Student perceptions of
virtual reality use in higher education. Journal of Ap-
plied Research in Higher Education, 12.
Berger, P. (2015). Espaces Imaginaires. http://
espaces-imaginaires.fr.
Buda, J. K. (2017). Integrating non-euclidean geometry into
high school.
Caerols, H., Carrasco, R., and Asenjo, F. (2021). Using
smartphone photographs of the moon to acquaint stu-
dents with non-euclidean geometry. American Journal
of Physics, 89.
Cevikbas, M., Bulut, N., and Kaiser, G. (2023). Exploring
the benefits and drawbacks of ar and vr technologies
for learners of mathematics: Recent developments.
Systems, 11.
Coulon, R., Matsumoto, E., Segerman, H., and Trettel, S.
(2022). Ray-marching thurston geometries. Experi-
mental Mathematics, 31.
Eres, L., Besson, G., Boileau, M., Maillot, S., and Porti, J.
(2010). Geometrisation of 3-manifolds. 13.
Gambini, A. (2021). Five years of comparison between eu-
clidian plane geometry and spherical geometry in pri-
mary schools: An experimental study. European Jour-
nal of Science and Mathematics Education, 9.
Gambini, A. and L
´
en
´
art, I. (2021). Basic geometric con-
cepts in the thinking of in-service and pre-service
mathematics teachers. Education Sciences, 11(7).
Guerrero Idrovo, G., Ayala, A., Mateu, J., Casades, L., and
Alaman, X. (2016). Integrating virtual worlds with
tangible user interfaces for teaching mathematics: A
pilot study. Sensors, 16.
Hedburg, J. and Alexander, S. (1994). Virtual reality in ed-
ucation: Defining researchable issues. Educational
Media International, 31.
Kang, K., Kushnarev, S., Pin, W., Ortiz, O., and Shihang, J.
(2020). Impact of virtual reality on the visualization
of partial derivatives in a multivariable calculus class.
IEEE Access, PP.
Kaufmann, H. and Schmalstieg, D. (2003). Schmalstieg, d.:
Mathematics and geometry education with collabora-
tive augmented reality. computers & graphics 27(3),
339-345. Computers & Graphics, 27.
Kim, H. K., Park, J., Choi, Y., and Choe, M. (2018). Virtual
reality sickness questionnaire (vrsq): Motion sickness
measurement index in a virtual reality environment.
Applied Ergonomics, 69.
Kopczy
´
nski, E., Celi
´
nska, D., and
ˇ
Ctrn
´
act, M. (2017). Hy-
perRogue: Playing with hyperbolic geometry. In Pro-
ceedings of Bridges 2017: Mathematics, Art, Music,
Architecture, Education, Culture, Phoenix, Arizona.
Tessellations Publishing.
Kotarinou, P. and Stathopoulou, C. (2017). ICT and Lim-
inal Performative Space for Hyperbolic Geometry’s
Teaching.
Lai, J. W. and Cheong, K. H. (2022). Adoption of virtual
and augmented reality for mathematics education: A
scoping review. IEEE Access, 10.
Mikropoulos, T. and Natsis, A. (2011). Educational vir-
tual environments: A ten-year review of empirical re-
search (1999–2009). Computers & Education, 56.
Osypova, N., Kokhanovska, O., Yuzbasheva, G., and
Kravtsov, H. (2021). Implementation of Immersive
Technologies in Professional Training of Teachers,
pages 68–90.
Su, Y.-S., Cheng, H.-W., and Lai, C.-F. (2022). Study of
virtual reality immersive technology enhanced math-
ematics geometry learning. Frontiers in Psychology,
13.
Sukestiyarno, Y. L., Nugroho, K. U. Z., Sugiman, S.,
and Waluya, B. (2023). Learning trajectory of non-
euclidean geometry through ethnomathematics learn-
ing approaches to improve spatial ability. Eurasia
Journal of Mathematics, Science and Technology Ed-
ucation.
Takac, M. (2020). Application of web-based immersive vir-
tual reality in mathematics education. In 2020 21th In-
ternational Carpathian Control Conference (ICCC).
Thurston, W. P. (1986). Hyperbolic structures on 3-
manifolds, i: Deformation of acylindrical manifolds.
Annals of Mathematics, 124.
Velho, L., da Silva, V., and Novello, T. (2020). Immersive
visualization of the classical non-euclidean spaces us-
ing real-time ray tracing in VR. In Proceedings of
Graphics Interface 2020, GI 2020, pages 423–430.
Venkatesh, V., Thong, J., and Xu, X. (2012). Consumer
acceptance and use of information technology: Ex-
tending the unified theory of acceptance and use of
technology. MIS Quarterly, 36:157–178.
Wang, S.-T., Liu, L.-M., and Wang, S.-M. (2018). The de-
sign and evaluate of virtual reality immersive learning
- the case of serious game “calcium looping for carbon
capture”. In 2018 International Conference on System
Science and Engineering (ICSSE).
Weeks, J. Curved Spaces. a flight simulator for mul-
ticonnected universes, available from http://www.
geometrygames.org/CurvedSpaces/.
GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications
238