Uniting Mcdonald’s Beta and Liouville Distributions to Empower

Anomaly Detection

Oussama Sghaier

, Manar Amayri

and Nizar Bouguila

Concordia Institute for Information Systems Engineering (CIISE), Concordia University,

1455 Blvd. De Maisonneuve Ouest, Montreal, H3G 1T7, QC, Canada

sghaieroussama63@gmail.com, {manar.amayri, nizar.bouguila}@concordia.ca

Keywords:

Mcdonald’s Beta-Liouville, Normality Scores, Support Vector Machine, Anomaly Detection.

Abstract:

In this paper, we examine the McDonald’s Beta-Liouville distribution, a new distribution that combines the

key features of the Liouville and McDonald’s Beta distributions, in order to address the issue of anomaly iden-

tiﬁcation in proportional data. Its primary advantages over the standard distributions for proportional data,

including the Dirichlet and Beta-Liouville, are its ﬂexibility and capacity for explanation when working with

this type of data, thanks to its variety of presented parameters. We provide two discriminative methods: a fea-

ture mapping approach to improve Support Vector Machine (SVM) and normality scores based on choosing a

speciﬁc distribution to approximate the softmax output vector of a deep classiﬁer. We illustrate the advantages

of the proposed methods with several tests on image and non-image data sets. The ﬁndings show that the

suggested anomaly detectors, which are based on the McDonald’s Beta-Liouville distribution, perform better

than baseline methods and classical distributions.

1 INTRODUCTION

The identiﬁcation of uncommon occurrences that de-

viate from typical behavior, or anomaly detection

(Chandola et al., 2009; Fan et al., 2011), has expe-

rienced continuous innovation to increase accuracy

and efﬁcacy. It is now a popular topic in many ap-

plications and is very important in many domains, in-

cluding computer vision, medical, network security,

and animal behavior (Topham et al., 2022; Epaillard

and Bouguila, 2019). This task remains difﬁcult since

anomalies have few occurrences, making it difﬁcult to

obtain aberrant samples. Robust techniques are des-

perately needed to model anomalies. Within the ﬁeld

of anomaly detection, where one looks for abnormal

patterns in the data, discriminative methods are com-

monly used to distinguish between normal and abnor-

mal data points. Support vector machines (SVMs)

and the isolation forest (IF) (Liu et al., 2008) are some

of the techniques that have been found to be useful

in this area, despite their challenges. However, it is

important to note that such approaches may be sensi-

tive towards certain settings called hyperparameters,

or they might fail on some data types altogether. Re-

https://orcid.org/0009-0002-0077-5300

https://orcid.org/0000-0002-5610-8833

https://orcid.org/0000-0001-7224-7940

searchers have investigated several strategies to ad-

dress these issues. Some have looked at distribution-

based approaches to gain a deeper understanding of

the data structure (Scholkopf and Smola, 2002), while

others have created algorithms that, without relying

largely on hyperparameters, offer a score to each data

point reﬂecting its degree of normality (Golan and El-

Yaniv, 2018).

This work aims to demonstrate how discrimina-

tive techniques (SVM with feature mapping and Nor-

mality Scores) can be used to get excellent results

in anomaly detection tasks. Our objective with the

normality score technique is to develop a novel sys-

tem that, in the testing phase, assigns a normal-

ity score to each sample after it has been trained

using a transformed set of normal samples during

the training phase. Lastly, the reason for choosing

SVM speciﬁcally among traditional discriminative al-

gorithms is that they have become a common learning

tool that yields benchmark results due to their compu-

tational efﬁcacy, especially in high-dimensional fea-

ture spaces. The challenge encountered in develop-

ing the two approaches lies in effectively modeling

proportional data, which imposes the constraints of

non-negativity and unit sum. Traditionally, data mod-

eling has relied heavily on the Gaussian distribution,

but its rigidity proves inadequate for handling propor-

Sghaier, O., Amayri, M. and Bouguila, N.

Uniting Mcdonald’s Beta and Liouville Distributions to Empower Anomaly Detection.

DOI: 10.5220/0013164100003929

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 27th International Conference on Enterprise Information Systems (ICEIS 2025) - Volume 1, pages 181-190

ISBN: 978-989-758-749-8; ISSN: 2184-4992

181

tional data. Recognizing this limitation, researchers

have turned to the Dirichlet family of distributions as

a more ﬂexible and precise alternative (Golan and El-

Yaniv, 2018; Sghaier et al., 2023; Bouguila and Ziou,

2006; Seﬁdpour and Bouguila, 2012; Bouguila and

Ziou, 2005c; Bouguila and Ziou, 2005b; Bouguila

and Ziou, 2005a; Amirkhani et al., 2021). This shift

underscores a departure from the constraints inherent

in the Gaussian distribution, offering a more adapt-

able framework for accurately representing propor-

tional data. Studies by authors in (Golan and El-

Yaniv, 2018) and (Sghaier et al., 2023) have explored

the use of Dirichlet and Multivariate Beta distribu-

tions, respectively, to approximate output vectors of

deep classiﬁers. Furthermore, Dirichlet and its gen-

eralized counterpart have found application in mod-

eling feature mapping functions within SVM (Rah-

man and Bouguila, 2021). In real applications, how-

ever, the Dirichlet distribution is less dependable due

to the considerable interdependencies among the ran-

dom variables (Wong, 1998; Fan et al., 2017; Epail-

lard and Bouguila, 2016). Furthermore, multinomial

cells and relative placements between categories are

not taken into consideration by the Dirichlet distribu-

tion (Oboh and Bouguila, 2017; Zamzami et al., 2020;

Nguyen et al., 2019). Moreover, inadequate parame-

terization limits the amount of variation and covari-

ance that may be captured in a set of data.

To tackle these challenges, Beta-Liouville from

Liouville family was proposed in (Bouguila, 2012a;

Bouguila, 2012b; Fan and Bouguila, 2013). It has

two additional parameters compared to Dirichlet. In

this context, and utilizing McDonald’s Beta to model

data on the support [0,1] (Forouzanfar et al., 2023b;

Forouzanfar et al., 2023a; Forouzanfar et al., 2023c),

we choose to extend the Beta-Liouville distribution in

our work and create the McDonald’s Beta-Liouville

distribution. McDonald’s Beta-Liouville has three

extra parameters compared to Dirichlet (Fan and

Bouguila, 2012) which gives the data modeling ad-

ditional degrees of freedom. Additionally, the extra

shape factors can alter the tail weights, simultane-

ously modify the kurtosis and skewness, and raise the

distribution’s entropy.

The following succinctly describes the primary

contributions of this work: 1) Based on McDonald’s

Beta and Liouville distributions, we suggest a novel

distribution appropriate for proportional data; 2) We

introduce a deep anomaly detector for images and

non-images, predicated on a broad assumption for

the softmax predictions vector. We present McDon-

ald’s Beta-Liouville distribution for estimating the

classiﬁer’s output vector; 3) We utilize McDonald’s

Beta-Liouville distribution to construct a novel fea-

ture mapping function in SVM.

The rest of this article is organized as follows:

We discuss related work to anomaly detection in sec-

tion 2. In section 3, we propose a new distribution

based on McDonald’s Beta and Liouville distribu-

tions. Section 4 contains a detailed description of

the normality scores-based transformation architec-

ture. We present our McDonald’s Beta-Liouville fea-

ture mapping function of SVM in section 5. Section 6

is devoted to the experimental results when we eval-

uate the effectiveness of our approaches and compare

them to several baseline methods. In section 7, we

conclude our work.

2 RELATED WORK

In prior studies, researchers have explored diverse ap-

proaches for anomaly detection, with a particular fo-

cus on normality scores and SVM feature mapping.

For instance, in (Golan and El-Yaniv, 2018; Sghaier

et al., 2023), an innovative architecture was proposed

involving geometric transformations applied to im-

age data, followed by classiﬁcation using a Dirich-

let (Golan and El-Yaniv, 2018) (or Multivariate Beta

in (Sghaier et al., 2023)) distribution-based normal-

ity scores function during testing. Regarding trans-

formations, we can refer to (Qiu et al., 2021), where

the authors described Neural Transformation Learn-

ing for Anomaly Detection (NeuTraL AD), an end-to-

end process for anomaly detection employing learn-

able transformations. The two parts of the NeuTraL

AD are an encoder and a ﬁxed set of learnable trans-

formations. They are both simultaneously trained on

a contrastive loss that is deterministic (DCL). Addi-

tionally, the work in (Zhang et al., 2020) introduced

a semi-supervised method utilizing GANs and frame

prediction to generate normality scores during testing.

Talking about SVM, it has emerged as a

formidable tool in anomaly detection, as highlighted

in (Hosseinzadeh et al., 2021), where various machine

learning techniques were integrated with SVM clas-

siﬁers for abnormality identiﬁcation. Deep learning

techniques were also coupled with SVM, as exempli-

ﬁed in (Erfani et al., 2016), which employed DBN

for feature extraction followed by one-class SVM

training. Notably, feature mapping functions have

been pivotal in enhancing SVM performance, espe-

cially in handling proportional data. The work pro-

posed by (Nedaie and Najaﬁ, 2018) introduced a fea-

ture mapping function based on the Dirichlet distribu-

tion, which demonstrated effectiveness across various

tasks involving proportional data. Building upon this,

(Rahman and Bouguila, 2021) sought to leverage the

ICEIS 2025 - 27th International Conference on Enterprise Information Systems

182

explanatory capabilities of generalized Dirichlet and

Beta-Liouville distributions to develop a more ﬂex-

ible feature mapping function for modeling propor-

tional data. These previous endeavors provide valu-

able insights and pave the way for further exploration

in the realms of normality scores and SVM feature

mapping for anomaly detection.

3 MCDONALD’S

BETA-LIOUVILLE

DISTRIBUTION

A K-dimensional vector X follows a Liouville distri-

bution with parameters (α

, ··· , α

) and density gen-

erator g(.) if its pdf (probability density function) is

deﬁned by (Fang, 2018; Hu et al., 2019):

p(X|α

, ··· , α

) = g(u)

∏

i=1

−1

Γ(α

)

(1)

where u =

∑

i=1

< 1, and 0 < X

< 1, i = 1, · · · , K.

One common choice of the generator function is:

g(u) =

Γ(

∑

i=1

)

∑

i=1

−1

f (u) (2)

where f (.) is the pdf of the variable u, as a result, we

can obtain a new expression of the pdf of Liouville

distribution:

p(X) =

Γ(

∑

i=1

)

∑

i=1

−1

f (u)

∏

i=1

−1

Γ(α

)

(3)

The Beta distribution, with its two shape parameters

allowing it to approximate any arbitrary distribution,

is a convenient option for u (Bouguila and Elguebaly,

2012). Nevertheless, in this particular context, an ex-

tended version of the Beta distribution, known as Mc-

Donald’s Beta (Manoj et al., 2013), includes three

shape parameters instead of the usual version’s two.

It can therefore ﬁt data more ﬂexibly. McDonald’s

Beta has the ability to accurately reﬂect skewness and

kurtosis in data due to its extra feature, which is very

useful when modeling real-world data (Forouzanfar

et al., 2023b). Furthermore, the third extra shape pa-

rameter adjusts tail weights and raises the entropy of

the generated distribution. For modeling the random

variable u in our study, we select the McDonald’s Beta

distribution, whose pdf is provided by (Manoj et al.,

2013):

f (u|α, β, λ) =

λu

αλ−1

(1 − u

)

β−1

B(α, β)

(4)

with:

B(a, b) =

Γ(a)Γ(b)

Γ(a + b)

(5)

represents the Beta function and Γ(.) denotes the

Gamma function, u is a scalar where 0 ≤ u ≤ 1,

and α, β, λ > 0 We obtain the expression of the pdf

for our proposed distribution for work, which is the

McDonald’s Beta-Liouville distribution, by using the

McDonald’s Beta as the density function for u in

Eq(2), and injecting Eq(4) in Eq(3) by considering

u =

∑

k=1

. The full expression is given as follows:

p(X|α

, ··· , α

, α, β, λ) =

Γ(

∑

k=1

)Γ(α + β)

Γ(α)Γ(β)

∑

k=1

(

αλ−

∑

k=1

)





1 −

∑

k=1





β−1

∏

k=1

−1

Γ(α

)

(6)

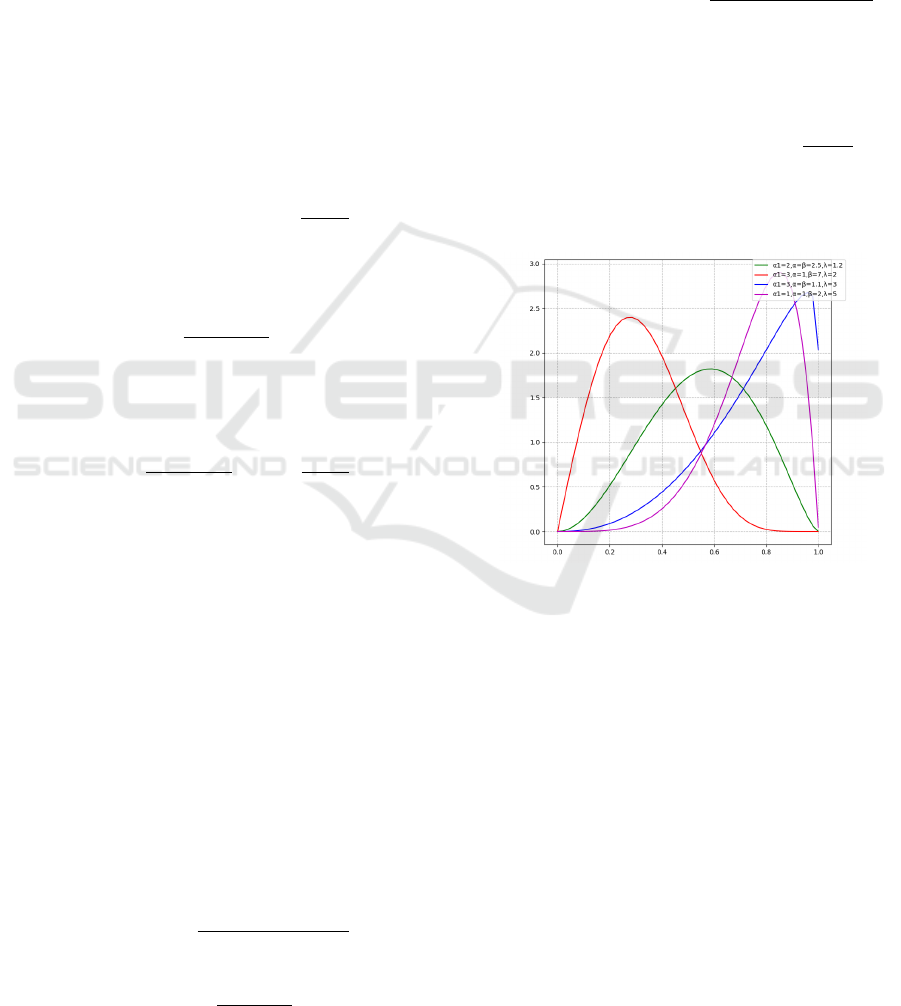
Figure(1) displays some examples of McDonald’s

Beta-Liouville distribution for different parameters.

Figure 1: McDonald’s Beta-Liouville Distribution.

4 MCDONALD’S

BETA-LIOUVILLE

NORMALITY SCORES

4.1 General Framework of the

Proposed Architecture

In this work, we highlight the application of a nor-

mality score in anomaly detection. The core notion of

this concept is as follows: Take into consideration X

as the totality of data samples, each labeled as ”Nor-

mal” or ”Anomaly”. A classiﬁer named C(x) is to be

developed, and its objective is to take a sample x, re-

turn 1 if x is in the set of normal samples termed X,

and 0, otherwise. We must ﬁrst construct a scoring

Uniting Mcdonald’s Beta and Liouville Distributions to Empower Anomaly Detection

183

function called n

(x) and compare its value to a preset

threshold known as λ in order to accomplish that. We

can conclude whether or not our sample is an abnor-

mality based on this comparison.

(x) =

(

1 n

(x) ≥ λ

0 n

(x) < λ.

As determining an appropriate threshold value λ is

not the main challenge in this work, we will ignore

the limited binary decision problem and focus only

on the proper generation of the score function. We

need appropriate measures in order to evaluate the

score function for that. In our work, we determine

the trade-off of the normality score function by set-

ting the Area Under the Receiver Operating Charac-

teristic as our metric. The process starts by apply-

ing a collection of geometric adjustments in the form

of ∆ =

{

, T

, . . . T

}

to the input image data. We

can illustrate the efﬁcacy of this kind of transforma-

tion by showing that it can retain the spatial details of

the normal sample, as the geometric structure of the

original image and its transformed counterpart will

be almost the same (Golan and El-Yaniv, 2018). We

build numerous neural networks based on dense lay-

ers followed by an auto-encoder for non-image data.

The usefulness of neural network-based dense layers,

which retain the structure of the vector data even af-

ter undergoing linear transformations, can be used to

support the choice to deploy them. The purpose of

the auto-encoder is to enhance feature extraction. The

output of this phase is the transformed data:

≜



(x), j) : x ∈ X, T

∈ ∆



where j is the index of transformation, T

is the cor-

responding transformation, x is the given sample and

X is the set of normal samples. In this case, a new

label is assigned to each transformed sample which is

the index of transformation. Then, we fed the trans-

formed data to a deep classiﬁer. In our study, we set

the Wide Residual Networks (WRN) (Zagoruyko and

Komodakis, 2016) as our classiﬁer.

In the second stage of our proposed architecture,

we focus on building our normality scores for ev-

ery sample x ∈ X from the softmax prediction vec-

tor y(T

(x)) produced by the classiﬁer for T

(x) (the

sample x being transformed by the i

transformation).

The normality scores function is the sum of the log-

likelihoods of the distributions of {y(T

(x))}

i=1,···,K

where K is the total number of transformations.

(x) =

K−1

∑

i=0

log p(y(T

(x))|T

) (7)

We decide to use McDonald’s Beta-Liouville distribu-

tion to approximate y(T

(x)). When data points range

from 0 to 1, it makes sense. In addition, its covari-

ance structure is stronger than that of traditional dis-

tributions like the Dirichlet. The McDonald’s Beta-

Liouville log-likelihood function is convex because it

belongs to the exponential family, making it simple to

identify the maximum. In order to estimate the dis-

tribution parameters, we create maximum likelihood

estimators using the modiﬁed normal data.

4.2 Mcdonald’s Beta-Liouville

Normality Scores Expression

In this section, we approximate y(T

(x)) with Mc-

Donald’s Beta-Liouville distribution: y(T

(x)) ∼

McDonald

′

sBL(θ

) with θ

= (α

, ··· , α

, ··· , a

, b

, ··· , b

, p

, ··· , p

). Injecting the

expression of McDonald’s BL pdf in Eq(6) into the

normality scores expression in Eq(7), we obtain the

following expression of n

(x):

(x) =

K−1

∑

i=0

log

Γ(

K−1

∑

k=0

)

K−1

∑

i=0

logΓ(

)

−

K−1

∑

i=0

log(Γ(

)) −

K−1

∑

i=0

log



Γ(

)



K−1

∑

i=0

log(

)

K−1

∑

i=0

−

K−1

∑

k=0

log

K−1

∑

k=0

[y(T

(x))]

K−1

∑

i=0

(

− 1)log





1 −

K−1

∑

k=0

[y(T

(x))]





K−1

∑

i=0

K−1

∑

k=0

(

− 1)log([y(T

(x))]

)

−

K−1

∑

i=0

K−1

∑

k=0

log(Γ(

)) (8)

the estimators of α

, α

, β

, and λ

are denoted by the

following expressions:

, and

. The expres-

sion of n

(x) can be made simpler by removing all the

terms that are independent of the sample values. This

leaves us with:

(x) =

K−1

∑

i=0

−

K−1

∑

k=0

log

K−1

∑

k=0

[y(T

(x))]

K−1

∑

i=0

(

− 1)log





1 −

K−1

∑

k=0

[y(T

(x))]





K−1

∑

i=0

K−1

∑

k=0

(

− 1)log([y(T

(x))]

)−

K−1

∑

i=0

K−1

∑

k=0

log(Γ(

))

(9)

ICEIS 2025 - 27th International Conference on Enterprise Information Systems

184

Using the Fixed Point Iteration, the expressions of the

estimated parameters are the following at iteration t:

= Ψ

−1

K−1

∑

j=0

,t−1

N−1

∑

j=0

log(c

)

−

N−1

∑

j=0

log

K−1

∑

m=0

, k = 0···K − 1 (10)

i,t

= Ψ

−1



i,t−1



i,t−1

N−1

∑

j=0

log

K−1

∑

k=0

(11)

i,t

= Ψ

−1



i,t−1



N−1

∑

j=0

log





1 −

K−1

∑

k=0

i,t−1





(12)

(13)

where:

Q =

N−1

∑

j=0

(

i,t−1

− 1)

log



∑

K−1

k=0



∑

K−1

k=0



i,t−1

1 −



∑

K−1

k=0



i,t−1

−

N−1

∑

j=0

i,t−1

log

K−1

∑

k=0

(14)

with C = (c

)

j=1···N,k=1···K

is the matrix where the

raw equals to y(T

)), x

is the sample j in the

normal samples set X.

5 MCDONALD’S

BETA-LIOUVILLE FEATURE

MAPPING IN SVM

5.1 Support Vector Machines Classiﬁer

SVM is a well-known and often used supervised

learning solution. Empirically, across numerous stud-

ies and applications, it has proven to have signiﬁcant

generalization capabilities. SVMs are effective in de-

termining the optimal decision boundaries that max-

imize the margin between many classes in a dataset

(Cortes and Vapnik, 1995). The SVM optimization

problem’s primal representation is provided by:

min

w,b,ε

∥

∑

(15)

subject to

(i)

φ(X

) + b) > 1 − ε

, i = 1··· , N (16)

> 0, i = 1··· , N (17)

where N is the number of samples, X

is the normal-

ized version of the i

sample in the data set, and y

the corresponding label.

In SVM, the regularization strength is controlled by

the hyperparameter C. It lessens the overﬁtting of the

model by applying a penalty to the misclassiﬁed data

points. It balances the trade-off between obtaining

a broader margin (lower complexity) and minimiz-

ing the classiﬁcation error (higher complexity). The

feature mapping function from the input space χ to

the feature space H is denoted by φ(X

) in (16). If

no additional features are added or taken out of the

data, it is equal to the input data. Instead of being

< φ(X

), φ(X

) > in this instance, the kernel K - the in-

ner product between data points - becomes < X

, X

The slack variable ε

is provided to solve the prob-

lem of non-lineary separated data, and

∑

repre-

sents the upper bound of the generalization error. The

dual problem can be solved computationally for huge

datasets. When the constraints are loosened via La-

grange multipliers, the dual solution becomes,

max

∑

−

∑

(i)

( j)

< φ(X

), φ(X

) >

(18)

subject to

0 < γ

< C,

∑

(i)

= 0, i = 1··· , N (19)

In this case, the decision function of SVM becomes:

f (X) =

∑

(i)

< φ(X

), φ(X) > (20)

5.2 Mcdonald’s Beta-Liouville SVM

Feature Mapping Function

This section focuses on selecting the feature mapping

function to solve the dual and primal problems, as

stated in (15) and (18), respectively. The selection

of φ(X ) for improved modeling is contingent upon

the data’s structure. Using the beneﬁts of the Mc-

Donald’s Beta-Liouville distribution to model propor-

Uniting Mcdonald’s Beta and Liouville Distributions to Empower Anomaly Detection

185

tional data, the following can be used to create a po-

tential feature mapping function:

) =











i j

, j = 1, ··· , K

Γ(

∑

k=1

)Γ(α+β)

Γ(α)Γ(β)

1 −



∑

k=1



β−1



∑

k=1



(

αλ−

∑

k=1

)

∏

k=1

−1

Γ(α

)

, j = K + 1

(21)

As can be seen from (21)’s suggested feature map-

ping function, the input dimension has risen by 1. Di-

versity is introduced into the data set by the new fea-

ture. Furthermore, it offers more information about

how the original characteristics were distributed over-

all. Sorting aberrant samples can be made easier with

this additional representation information. Newton

Raphson’s approach can be used to estimate the pa-

rameters using the initial input data set in a manner

similar to that described in (Nedaie and Najaﬁ, 2018).

After obtaining the training parameters, we were able

to formulate McDonald’s Beta-Liouville SVM (Mc-

Donald’s BL SVM) in a novel way as follows:

min

w,b,ε

K+1

∑

(22)

subject to

(i)

φ(X

) + b) > 1 − ε

, i = 1··· , N (23)

> 0, i = 1··· , N (24)

A new expression of McDonald’s BL SVM can be

formulated as follows:

min

w,b,ε

K+1

∑

(25)

subject to

(i)

(

∑

+ w

K+1

Γ(

∑

k=1

)Γ(α +β)

Γ(α)Γ(β)

λ×

∑

k=1

(

αλ−

∑

k=1

)





1 −

∑

k=1





β−1

∏

k=1

−1

Γ(α

)

> 1 − ε

, i = 1··· , N (26)

> 0, i = 1··· , N (27)

6 EXPERIMENTAL RESULTS

6.1 Feature Mapping SVM Results

Three subsets of Fashion MNIST (Xiao et al., 2017)

data and three more from MNIST (Baldominos et al.,

2019) data served as the foundation for our analysis

in this section. We take 2000 samples from each of

the following classes: 1, 2, and 3 to serve as anomaly

classes for the three subsets, respectively (class 1 is

the anomaly class of the ﬁrst subset, class 2 is the

anomaly class of the second subset, and class 3 is

the anomaly class of the third subset). We consider

the class 0 to be the normal class (10000 samples).

We thus set the anomalous rate to 16%. Using var-

ious SVM kernels, including Linear, RBF (Radial

Basis Function), and Polynomial kernels, we com-

pare the performance of our proposed method, Mc-

Donald’s Beta Liouville for feature mapping in SVM

(McDonald’s BL SVM), against baseline SVM and

two state-of-the-art benchmarking methods: Dirich-

let SVM (Dir SVM) and Beta-Liouville SVM (BL

SVM).

Our experiments on the Fashion MNIST dataset

revealed consistent improvements in classiﬁcation

performance achieved by McDonald’s BL SVM

across different SVM kernels. Notably, when em-

ploying the Linear kernel, McDonald’s BL SVM out-

performed baseline SVM, Dir SVM, and BL SVM

across all classes, with F1 scores of 90.86% (Class

1), 89.7% (Class 2), and 73.41% (Class 3) com-

pared to 87.64%, 88.88%, 87.77%, and 84.03%,

89.3%, 89.3%, and 72.5%, 73.06%, 72.04%, respec-

tively. Under the RBF kernel, McDonald’s BL SVM

achieved even higher F1 scores, reaching 90.71%

(Class 1), 88.17% (Class 2), and 74.41% (Class 3),

surpassing baseline SVM, Dir SVM, and BL SVM.

Similarly, using the Polynomial kernel, McDonald’s

BL SVM demonstrated substantial improvements,

particularly in Class 2 (F1 score: 89.92%) outper-

forming baseline SVM, Dir SVM, and BL SVM.

McDonald’s BL SVM demonstrated better classiﬁca-

tion performance on the MNIST dataset when com-

pared to benchmarking methods such as Dir SVM,

and baseline SVM for all SVM kernels. Its re-

markable performance with the Linear kernel was

especially noteworthy; McDonald’s BL SVM out-

performed baseline SVM, Dir SVM, and BL SVM,

achieving F1 scores of 97.01% (Class 1), 74.64%

(Class 2), and 76.57% (Class 3). Furthermore, Mc-

Donald’s BL SVM outperformed baseline SVM, Dir

SVM, and BL SVM with F1 scores of 97.96% (Class

1) and 82.66% (Class 3) using the RBF kernel. Mc-

Donald’s BL SVM demonstrated notable gains even

with the Polynomial kernel, especially in Class 1 (F1

score: 97.52%) and Class 2 (F1 score: 72.29%),

demonstrating how well it captures intricate correla-

tions in the data. This increase might be explained

by the McDonald’s Beta-Liouville distribution’s bet-

ter generalization capabilities, which allow it to repre-

ICEIS 2025 - 27th International Conference on Enterprise Information Systems

186

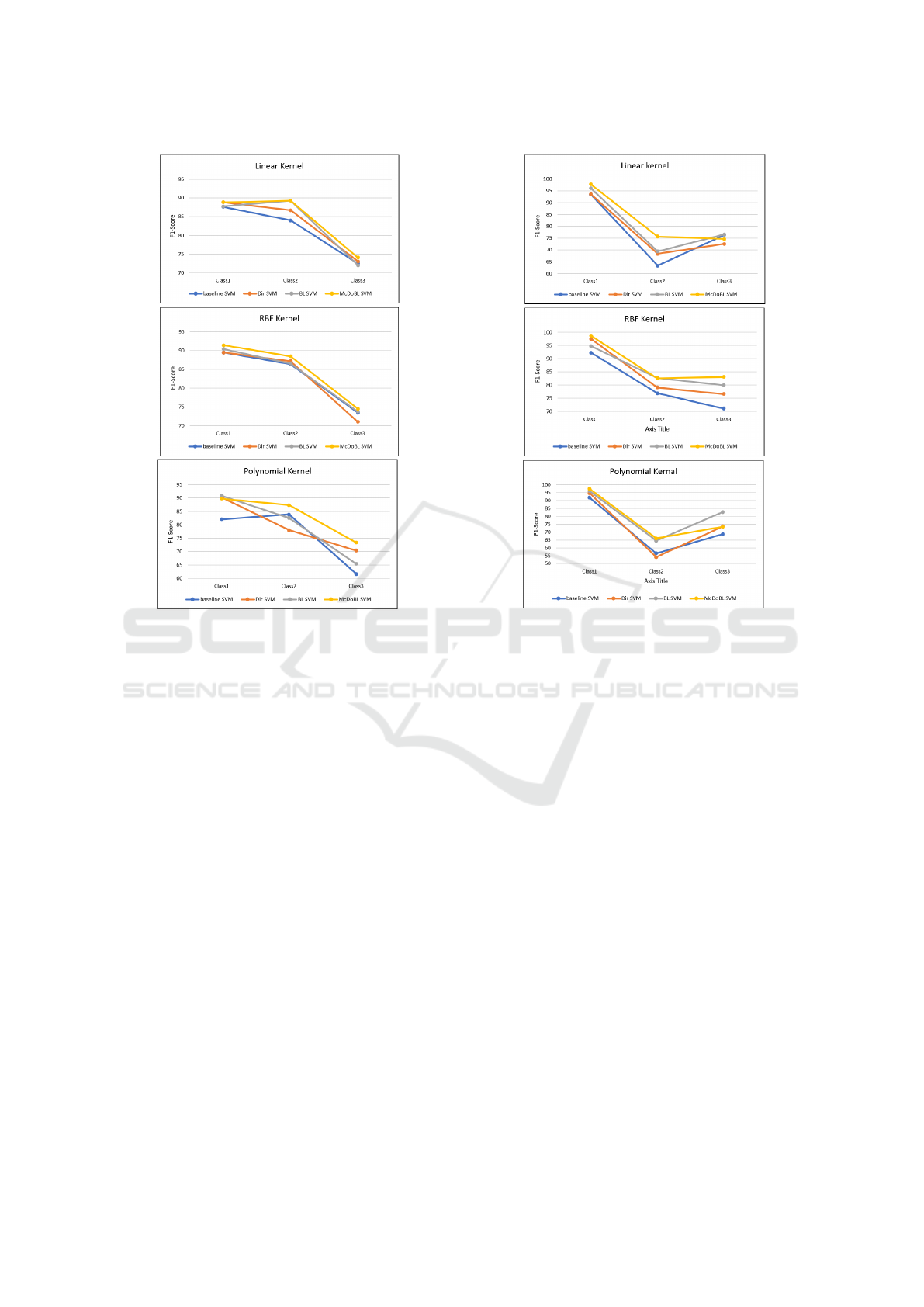
Figure 2: F1 score over subsets for the different approaches

on Fashion MNIST Data Set.

sent data distribution with a higher coherence covari-

ance structure.

Another data set used in our work to measure the per-

formance of our feature mapping strategy for SVM is

the bank data used previously in (Sghaier et al., 2024).

Table 1 shows that McDonald’s BLSVM performs

better than baseline SVM, BLSVM, and DSVM for

all kernels. For linear SVM, McDonald’s BLSVM

achieves the hightest scores marking 99.69 as ac-

curacy and 99.81 as f1 score. Also, McDonald’s

BLSVM provides the highest accuracy of 97.42 and

the highest f1 score of 98.45 when taking into account

the RBF SVM.

6.2 Normality Scores Results

In this part, we apply our suggested McDonald’s BL

normality scores method to the NSL-KDD Cup and

the MNIST image data sets. To simplify the work, we

restrict the label names for the NSL-KDD Cup dataset

to just two classes: the attack class, which consists of

all labels that deviate from the normal class. As a re-

sult, the ﬁnal labels are the attack class and the normal

class. We assess the effectiveness of our approach by

comparing the normality scores based on the McDon-

Figure 3: F1 score over subsets for the different approaches

on MNIST Data Set.

ald’s BL distribution with those based on the Dirichlet

and Beta-Liouville distributions, as well as two base-

line methods: the Convolutional AutoEncoder One-

Class Support Vector Machine (CAE OCSVM) and

the Raw One-Class Support Vector Machine (RAW-

OCSVM) (Deecke et al., 2019),(Zhai et al., 2016).

We have selected Wide Residual Networks

(WRN) (Zagoruyko and Komodakis, 2016) as the

classiﬁer for our architecture. Its width is set to 8,

and its depth to 16. In addition, the OCSVM hyper-

parameters were changed to ν ∈

{

0.1, ··· , 0.9

}

and

γ ∈



−7

, 2

−6

, ··· , 2



Table 2 displays the performance of various ap-

proaches for normality scores, as measured by AU-

ROC, using the MNIST data set. Take note that the

one-vs-all strategy was the evaluation method em-

ployed in our trials. It views one class as abnormal

and the other classes as typical. Based on the out-

comes in the three tables, we can verify that Dirichlet,

McDonald’s Beta-Liouville, and Beta-Liouville per-

form better than the baseline methods. This supports

(our hypotheses) that distributions with higher dis-

criminating power between data speciﬁed on a sim-

plex are those such as McDonald’s Beta-Liouville and

Beta-Liouville.

Uniting Mcdonald’s Beta and Liouville Distributions to Empower Anomaly Detection

187

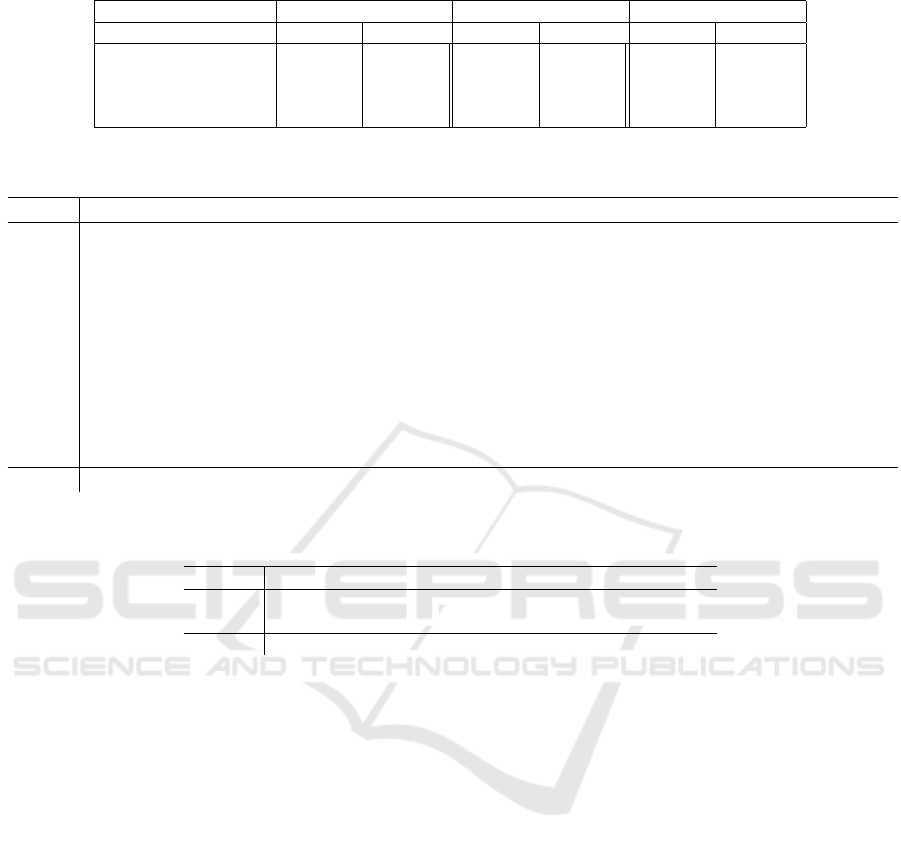
Table 1: F1 score and Accuracy for different kernels on Bank Data Set.

Kernel Linear RBF Polynomial

Approach F1 Score Accuracy F1 Score Accuracy F1 Score Accuracy

Baseline SVM 94.86 91.95 94.97 92.11 90.87 86.22

DSVM 94.77 91.82 97.65 96.08 79.93 72.45

BLSVM 94.77 91.82 97.68 96.15 87.51 81.72

McDonald’s BL SVM 99.81 99.69 98.45 97.42 93.21 89.54

Table 2: AUC of anomaly detection-based normality score techniques for MNIST dataset. In each method, the model was

trained on a single class and tested on the rest. The best performing method in each row appears in bold.

Raw-OC-SVM CAE-OC-SVM Dirichlet Beta-Liouville McDonald’s Beta-Liouville

0 99.54 97.25 91.4 88.99 91.31

1 99.91 99.28 85.5 73.78 93.46

2 88.5 82.33 99.4 99.31 98.65

3 89.07 76.14 96.01 95.96 99.0

4 95.46 79.39 98.72 96.69 99.11

5 91.17 78.35 98.35 97.82 99.65

6 97.06 86.69 99.9 99.9 99.9

7 95.05 86.83 95.58 94.94 95.91

8 86.47 74.41 92.94 93.19 88.29

9 96.3 92.48 99.09 98.91 98.44

mean 93.85 85.31 95.68 93.94 96.37

Table 3: AUC of anomaly detection-based normality score techniques for NSL-KDD Cup dataset. In each method, the model

was trained on a single class and tested on the rest. The best performing method in each row appears in bold.

Dirichlet Beta-Liouville McDonald’s Beta-Liouville

Normal 75.62 75.12 83.12

Attack 76.91 81.59 81.72

mean 76.26 78.35 82.42

As seen in Table 2, the McDonald’s Beta-

Liouville (McDonald’s BL) normality score

(AUC=96.17) for the MNIST data set is better

than the Dirichlet normality score (AUC=95.68),

Beta-Liouville normality scores (AUC=93.94),

RAW OCSVAM (AUC=93.85), and CAE OCSVM

(AUC=85.31). Moreover, McDonald’s BL has the

highest scores for ﬁve of the ten classes (3,4,5,6,7),

achieving an AUC=99.9 for class 6. Even yet, Dirich-

let excels in three classes: 2,4,9, whereas class 8

has the highest AUC=93.19 based on Beta-Liouville

measurement.

The AUC results by Dirichlet, BL, and McDon-

ald’s BL on the NSL-KDD Cup data set are shown

in Table 3. With a 4% difference in AUC from the

nearest score (AUC = 82.42 for McDonald’s BL to

AUC = 78.35 and AUC = 76.26 for BL and Dirich-

let, respectively), McDonald’s BL performs well in

both classes, as this table illustrates. The McDonald’s

BL normalcy score for the attack class yields an AUC

of 81.72, while BL comes in second with 81.59. We

may observe that Dirichlet and BL perform similarly

for the Normal class in the normal class. Additionally,

we observe that McDonald’s BL (83.12, a difference

of 7% from the nearest score) shows a very high score

in comparison to other distributions.

7 CONCLUSION

The development of discriminative algorithms for

proportional data modeling and anomaly detection

tasks was the main objective of this paper. The Mc-

Donald’s Beta-Liouville distribution, which is derived

from the Liouville family and includes the Dirich-

let as a particular example, served as the foundation

for these methods. The McDonald’s Beta-Liouville

distribution, which is used to effectively statistically

represent the properties of the data, is another ad-

vantage of these techniques. This distribution is pri-

marily driven by the large number of data mining,

pattern recognition, and computer vision applications

that naturally generate this type of data. In particu-

lar, we proposed a deep anomaly detection architec-

ture based on normality score that uses McDonald’s

Beta-Liouville to approximate the classiﬁer’s soft-

ICEIS 2025 - 27th International Conference on Enterprise Information Systems

188

max output vector predictions. Three feature map-

ping functions for proportional data have been added

to the SVM learning algorithm in the second and ﬁ-

nal approach. Above all, the ﬁndings of the two

approaches have clearly shown that the McDonald’s

Beta-Liouville can be a good alternative to the re-

cently proposed Beta-Liouville, as it performs better

than the widely used Dirichlet. Nevertheless, signif-

icant drawbacks include presumptions regarding the

alignment of the data distribution, possible difﬁcul-

ties in generalizing to different types of data, and is-

sues with computing complexity in large-scale appli-

cations. Future research may focus on creating hybrid

generative discriminative techniques using SVM ker-

nels produced from McDonald’s Beta-Liouville mix-

ture models.

ACKNOWLEDGEMENT

The completion of this research was made possible

thanks to Natural Sciences and Engineering Research

Council of Canada (NSERC) and Fonds de recherche

du Quebec.

REFERENCES

Amirkhani, M., Manouchehri, N., and Bouguila, N. (2021).

Birth-death MCMC approach for multivariate beta

mixture models in medical applications. In Fujita,

H., Selamat, A., Lin, J. C., and Ali, M., editors,

Advances and Trends in Artiﬁcial Intelligence. Arti-

ﬁcial Intelligence Practices - 34th International Con-

ference on Industrial, Engineering and Other Appli-

cations of Applied Intelligent Systems, IEA/AIE 2021,

Kuala Lumpur, Malaysia, July 26-29, 2021, Proceed-

ings, Part I, volume 12798 of Lecture Notes in Com-

puter Science, pages 285–296. Springer.

Baldominos, A., Saez, Y., and Isasi, P. (2019). A survey

of handwritten character recognition with mnist and

emnist. Applied Sciences, 9(15):3169.

Bouguila, N. (2012a). Hybrid generative/discriminative ap-

proaches for proportional data modeling and classiﬁ-

cation. IEEE Transactions on Knowledge and Data

Engineering, 24(12):2184–2202.

Bouguila, N. (2012b). Inﬁnite liouville mixture models with

application to text and texture categorization. Pattern

Recognit. Lett., 33(2):103–110.

Bouguila, N. and Elguebaly, T. (2012). A fully bayesian

model based on reversible jump MCMC and ﬁnite

beta mixtures for clustering. Expert Syst. Appl.,

39(5):5946–5959.

Bouguila, N. and Ziou, D. (2005a). Mml-based approach

for ﬁnite dirichlet mixture estimation and selection. In

Perner, P. and Imiya, A., editors, Machine Learning

and Data Mining in Pattern Recognition, 4th Interna-

tional Conference, MLDM 2005, Leipzig, Germany,

July 9-11, 2005, Proceedings, volume 3587 of Lecture

Notes in Computer Science, pages 42–51. Springer.

Bouguila, N. and Ziou, D. (2005b). On ﬁtting ﬁnite dirich-

let mixture using ECM and MML. In Wang, P., Singh,

M., Apt

e, C., and Perner, P., editors, Pattern Recogni-

tion and Data Mining, Third International Conference

on Advances in Pattern Recognition, ICAPR 2005,

Bath, UK, August 22-25, 2005, Proceedings, Part I,

volume 3686 of Lecture Notes in Computer Science,

pages 172–182. Springer.

Bouguila, N. and Ziou, D. (2005c). Using unsupervised

learning of a ﬁnite dirichlet mixture model to improve

pattern recognition applications. Pattern Recognit.

Lett., 26(12):1916–1925.

Bouguila, N. and Ziou, D. (2006). Online clustering via

ﬁnite mixtures of dirichlet and minimum message

length. Eng. Appl. Artif. Intell., 19(4):371–379.

Chandola, V., Banerjee, A., and Kumar, V. (2009).

Anomaly detection: A survey. ACM Comput. Surv.,

41(3).

Cortes, C. and Vapnik, V. (1995). Support-vector networks.

Machine Learning, 20:273–297.

Deecke, L., Vandermeulen, R., Ruff, L., Mandt, S., and

Kloft, M. (2019). Image anomaly detection with

generative adversarial networks. In Machine Learn-

ing and Knowledge Discovery in Databases: Euro-

pean Conference, ECML PKDD 2018, pages 3–17.

Springer.

Epaillard, E. and Bouguila, N. (2016). Proportional data

modeling with hidden markov models based on gen-

eralized dirichlet and beta-liouville mixtures applied

to anomaly detection in public areas. Pattern Recog-

nit., 55:125–136.

Epaillard, E. and Bouguila, N. (2019). Variational bayesian

learning of generalized dirichlet-based hidden markov

models applied to unusual events detection. IEEE

Transactions on Neural Networks and Learning Sys-

tems, 30(4):1034–1047.

Erfani, S. M., Rajasegarar, S., Karunasekera, S., and Leckie,

C. (2016). High-dimensional and large-scale anomaly

detection using a linear one-class svm with deep learn-

ing. Pattern Recognition, 58:121–134.

Fan, W. and Bouguila, N. (2012). Online variational ﬁ-

nite dirichlet mixture model and its applications. In

2012 11th International Conference on Information

Science, Signal Processing and their Applications

(ISSPA), pages 448–453.

Fan, W. and Bouguila, N. (2013). Learning ﬁnite beta-

liouville mixture models via variational bayes for pro-

portional data clustering. In Rossi, F., editor, IJ-

CAI 2013, Proceedings of the 23rd International Joint

Conference on Artiﬁcial Intelligence, Beijing, China,

August 3-9, 2013, pages 1323–1329. IJCAI/AAAI.

Fan, W., Bouguila, N., and Ziou, D. (2011). Unsupervised

anomaly intrusion detection via localized bayesian

feature selection. In 2011 IEEE 11th International

Conference on Data Mining, pages 1032–1037.

Uniting Mcdonald’s Beta and Liouville Distributions to Empower Anomaly Detection

189

Fan, W., Sallay, H., and Bouguila, N. (2017). Online

learning of hierarchical pitman–yor process mixture

of generalized dirichlet distributions with feature se-

lection. IEEE Transactions on Neural Networks and

Learning Systems, 28(9):2048–2061.

Fang, K. W. (2018). Symmetric multivariate and related

distributions. CRC Press.

Forouzanfar, D., Manouchehri, N., and Bouguila, N.

(2023a). Bayesian inference in inﬁnite multivari-

ate mcdonald’s beta mixture model. In Rutkowski,

L., Scherer, R., Korytkowski, M., Pedrycz, W.,

Tadeusiewicz, R., and Zurada, J. M., editors, Artiﬁcial

Intelligence and Soft Computing - 22nd International

Conference, ICAISC 2023, Zakopane, Poland, June

18-22, 2023, Proceedings, Part II, volume 14126 of

Lecture Notes in Computer Science, pages 320–330.

Springer.

Forouzanfar, D., Manouchehri, N., and Bouguila, N.

(2023b). Finite multivariate mcdonald’s beta mix-

ture model learning approach in medical applica-

tions. In Hong, J., Lanperne, M., Park, J. W., Cern

T., and Shahriar, H., editors, Proceedings of the

38th ACM/SIGAPP Symposium on Applied Comput-

ing, SAC 2023, Tallinn, Estonia, March 27-31, 2023,

pages 1143–1150. ACM.

Forouzanfar, D., Manouchehri, N., and Bouguila, N.

(2023c). A fully bayesian inference approach for mul-

tivariate mcdonald’s beta mixture model with feature

selection. In 9th International Conference on Control,

Decision and Information Technologies, CoDIT 2023,

Rome, Italy, July 3-6, 2023, pages 2055–2060. IEEE.

Golan, I. and El-Yaniv, R. (2018). Deep anomaly detec-

tion using geometric transformations. In Advances

in Neural Information Processing Systems (NeurIPS),

volume 31.

Hosseinzadeh, M., Rahmani, A. M., Vo, B., Bidaki, M.,

Masdari, M., and Zangakani, M. (2021). Improving

security using svm-based anomaly detection: issues

and challenges. Soft Computing, 25:3195–3223.

Hu, C., Fan, W., Du, J., and Bouguila, N. (2019). A novel

statistical approach for clustering positive data based

on ﬁnite inverted beta-liouville mixture models. Neu-

rocomputing, 333:110–123.

Liu, F. T., Ting, K. M., and Zhou, Z.-H. (2008). Isolation

forest. In 2008 Eighth IEEE International Conference

on Data Mining, pages 413–422.

Manoj, C., Wijekoon, P., and Yapa, R. D. (2013). The mc-

donald generalized beta-binomial distribution: A new

binomial mixture distribution and simulation based

comparison with its nested distributions in handling

overdispersion. International Journal of Statistics and

Probability, 2(2):24.

Nedaie, A. and Najaﬁ, A. A. (2018). Support vector ma-

chine with dirichlet feature mapping. Neural Net-

works, 98:87–101.

Nguyen, H., Azam, M., and Bouguila, N. (2019). Data

clustering using variational learning of ﬁnite scaled

dirichlet mixture models. In 2019 IEEE 28th Inter-

national Symposium on Industrial Electronics (ISIE),

pages 1391–1396.

Oboh, B. S. and Bouguila, N. (2017). Unsupervised learn-

ing of ﬁnite mixtures using scaled dirichlet distribu-

tion and its application to software modules catego-

rization. In 2017 IEEE International Conference on

Industrial Technology (ICIT), pages 1085–1090.

Qiu, C., Pfrommer, T., Kloft, M., Mandt, S., and Rudolph,

M. (2021). Neural transformation learning for deep

anomaly detection beyond images. In Proceedings of

the International Conference on Machine Learning,

pages 8703–8714. PMLR.

Rahman, M. H. and Bouguila, N. (2021). Efﬁcient feature

mapping in classifying proportional data. IEEE Ac-

cess, 9:3712–3724.

Scholkopf, B. and Smola, A. J. (2002). Learning with Ker-

nels: Support Vector Machines, Regularization, Opti-

mization, and Beyond. MIT Press, Cambridge, MA.

Seﬁdpour, A. and Bouguila, N. (2012). Spatial color im-

age segmentation based on ﬁnite non-gaussian mix-

ture models. Expert Syst. Appl., 39(10):8993–9001.

Sghaier, O., Amayri, M., and Bouguila, N. (2023). Mul-

tivariate beta normality scores approach for deep

anomaly detection in images using transformations.

In 2023 IEEE International Conference on Systems,

Man, and Cybernetics (SMC), pages 3428–3433.

Sghaier, O., Amayri, M., and Bouguila, N. (2024).

Libby-novick beta-liouville distribution for enhanced

anomaly detection in proportional data. ACM Trans.

Intell. Syst. Technol., 15(5):107:1–107:26.

Topham, L. K., Khan, W., Al-Jumeily, D., Waraich, A., and

Hussain, A. J. (2022). Gait identiﬁcation using limb

joint movement and deep machine learning. IEEE Ac-

cess, 10:100113–100127.

Wong, T. T. (1998). Generalized dirichlet distribution in

bayesian analysis. Applied Mathematics and Compu-

tation, 97(2–3):165–181.

Xiao, H., Rasul, K., and Vollgraf, R. (2017). Fashion-

mnist: A novel image dataset for benchmark-

ing machine learning algorithms. arXiv preprint

arXiv:1708.07747.

Zagoruyko, S. and Komodakis, N. (2016). Wide residual

networks. arXiv preprint arXiv:1605.07146.

Zamzami, N., Alsuroji, R., Eromonsele, O., and Bouguila,

N. (2020). Proportional data modeling via selection

and estimation of a ﬁnite mixture of scaled dirichlet

distributions. Comput. Intell., 36(2):459–485.

Zhai, S., Cheng, Y., Lu, W., and Zhang, Z. (2016). Deep

structured energy based models for anomaly detec-

tion. In Proceedings of the International Conference

on Machine Learning, pages 1100–1109. PMLR.

Zhang, Y., Nie, X., He, R., Chen, M., and Yin, Y. (2020).

Normality learning in multispace for video anomaly

detection. IEEE Transactions on Circuits and Systems

for Video Technology, 31(9):3694–3706.

ICEIS 2025 - 27th International Conference on Enterprise Information Systems

190