Improving Floating Wind Turbine Stability with Evolutionary

Computation for TMD Optimization

Thayza Melo

, Luciana Faletti Almeida

and Juan G. Lazo Lazo

Research and Postgraduate Department, Centro Federal de Educação Tecnológica Celso Suckow da Fonsesa,

Rio de Janeiro, Brazil

Facultad de Ingeniería, Universidad del Pacífico, Lima, Peru

Keywords: Offshore Wind Turbines, Tuned Mass Damper, Evolutionary Computation, Genetic Algorithms, FAST-SC.

Abstract: Wind turbines in general allow the conversion of wind kinetic energy into electrical energy, but their

installation on land is becoming increasingly complicated, due to wind speed, lower energy generation,

environmental, acoustic and visual aspects, land use, among others. In this sense, offshore wind generation

has advantages such as stronger and more constant winds, lower visual and acoustic impact, greater generation

capacity, development close to large cities, among others. Offshore wind turbines have great potential to

transform the global energy matrix, especially with the use of floating platforms that enable energy generation

in deep waters. However, these systems face significant challenges, such as pendulum loads and movements

induced by winds and waves that cause fatigue to the structure. This work proposes the use of evolutionary

computing techniques, through genetic algorithms, to optimize a passive structural control with tuned mass

damping devices (TMDs), installed in the nacelle of Floating Offshore Wind Turbines (FOWTs) of the Barge

type, aiming to mitigate these pendular effects. The TMDs are configured to act in the fore-aft and lateral-

lateral directions, and the optimization considered the standard deviation of the tower fatigue as a fitness

function, in addition to including stroke limits to adapt to the nacelle dimensions. The optimization was

performed under the free decay condition, i.e., simplified conditions and application of initial inclinations to

the platform. The simulations, conducted in the FAST-SC (Fatigue, Aerodynamics, Structures, and

Turbulence – Structural Control) software, demonstrated a reduction of more than 36% in the structural

fatigue of the tower compared to systems without structural control and an improvement of more than 11%

compared to systems with unidirectional TMD. The results reinforce the effectiveness of passive structural

control with bidirectional TMD in mitigating vibrations and increasing the reliability of floating offshore

turbines, offering an efficient approach to improve the structural reliability of the system.

1 INTRODUCTION

The growing demand for renewable energy sources

has driven the development of offshore wind turbines

as a promising alternative for electricity production.

Although these wind turbines are installed on floating

platforms, designed to exploit stronger and more

consistent winds in deep waters (60m to 900m depth),

they face significant challenges such as wind and

wave-induced pendulum loads (Vijfhuizen, 2006),

shown in Fig. 1. Floating Offshore Wind Turbines

(FOWTs) can have diverse types of bases for

https://orcid.org/0000-0002-0268-5803

https://orcid.org/0000-0001-7149-8350

https://orcid.org/0000-0001-7782-118X

buoyancy, with the Barge being a stable, economical,

and advantageous option for great depths (Villoslada

et al., 2022), therefore chosen for the simulations in

this project.

Research in the field of FOWTs aims to improve

energy production and avoid negative interference

from wind and waves by controlling vibrations and

reducing structural fatigue (Olondriz et al., 2019). To

this end, various forms of structural control have been

explored over the last decade. Passive control using

Tuned Mass Dampers (TMDs) is one of the most

promising for FOWTs when installed in the nacelle,

Melo, T., Almeida, L. F. and Lazo, J. G. L.

Improving Floating Wind Turbine Stability with Evolutionary Computation for TMD Optimization.

DOI: 10.5220/0013171900003905

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 14th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2025), pages 475-484

ISBN: 978-989-758-730-6; ISSN: 2184-4313

475

the uppermost and heaviest part of the wind turbine

(Zuo et al., 2020).

In all projects, the TMD design is optimized to

reduce vibrations and improve wind turbine

performance. Parameters such as stiffness, damping

and mass are adjusted for this purpose. Adjustment

methods include frequency adjustment, genetic

algorithms (GA’s) and surface graphs. The

limitations in the TMD course are little explored,

commonly assuming fixed and simplified values, in

addition to using reduced models of the system in the

optimization loop (Chen et al., 2021). Only one work

(Villoslada et al., 2022) used GA for optimization

including TMD travel limitation and stop

configuration as variables. Although it achieved

satisfactory results in the simulation, it only

considered forward-reverse TMD, did not consider

the side-to-side TMD, nor did it include its variables

in the optimization cycle.

In this context, this work aims to optimize, using

an evolutionary algorithm, a passive structural control

system consisting of two TMDs installed in the

nacelle of a barge-type FOWT, in the fore-aft and

lateral directions. A genetic algorithm is used to

adjust the TMD system parameters, such as mass,

stiffness, damping, stroke limitation, and stop

variables, with the objective of mitigating vibrations

in the structure, platform tower pitch, and turbine

bending mode. In the optimization cycles and FOWT

tests, the simulation is performed with FAST-SC

(Fatigue, Aerodynamics, Structures, and Turbulence

– Structural Control) software, considering the free

decay of the system.

Figure 1: External forces acting on a FOWT (Butterfield

et al., 2007).

This work is organized as follows: Section 2

presents the theoretical framework and literature

review, Section 3 presents the proposed

methodology, Section 4 shows the results obtained,

finally Section 5 addresses the conclusions.

2 LITERATURE REVIEW

Most wind power generation is conducted by three-

blade horizontal-axis wind turbines located in

sparsely populated coastal areas or on onshore fields

(Picolo et al., 2014). These turbines consist of blades,

rotor (hub), gearbox, generator, nacelle, support

tower, and brake system. The nacelle houses essential

components such as the gearbox and generator, while

the support tower elevates the turbine to optimal

heights for energy generation. The brake system

controls blade speed, especially during storms. They

also have a direction sensor to orient the blades to

capture the best frontal wind (Figueiredo, 2019).

2.1 Offshore Wind Turbines and Their

Technologies

In recent years, there has been a gradual shift towards

offshore wind energy due to favourable wind

resources and proximity to coastal urban areas.

Offshore turbines take advantage of higher and less

turbulent wind speeds, providing greater energy

efficiency. They share technology with onshore

turbines with structural adaptations for different

water depths (Costoya et al., 2020). Fixed turbines in

shallow waters present complexity and excessive

costs, as well as environmental impacts and space

limitations. On the other hand, floating turbines in

deep waters (60m to 900m depth) offer reduced costs,

simplified assembly, and less environmental impact,

making them more viable for offshore deployment

(Hu & He, 2017).

FOWTs offer the flexibility of installation at

various ocean depths, up to 900m, expanding the

possibilities for deployment sites. They are

categorized into Barges, Spar Buoys, and Tension

Leg Platforms (Villoslada et al., 2022). The Barge is

stable and mobile, equipped with fin plates to avoid

stresses on the structure, while the Spar Buoy is

challenging for fabrication and installation due to its

weight concentrated at the lowest point. The Tension

Leg Platform is more innovative and riskier,

submerged with a star-shaped geometry. The stability

of the floating base is ensured by anchoring elements

such as mooring and tensioning, with three main

types: catenary, mechanically tensioned moorings,

ICPRAM 2025 - 14th International Conference on Pattern Recognition Applications and Methods

476

and Tension Leg Platform (TLP) anchors (Jonkman,

2007).

Among these options, Barge-type platforms,

stabilized by flexible or catenary mooring, are more

promising and economical for deep waters (Chen et

al., 2021). For this study, the NREL 5MW turbine

supported by the ITI Energy Barge, developed by the

National Renewable Energy Laboratory (NREL) -

USA, was chosen. An illustration of the barge with

the NREL 5MW turbine is shown in Fig. 2.

Figure 2: FOWT NREL 5MW and ITI Energy Barge (G. M.

Stewart, 2012).

2.2 Structural Control

Structural control aims to reduce loads on buildings

and bridges due to waves and earthquakes (G. M.

Stewart, 2012). For wind turbines on barge-type

floating platforms, this control is crucial due to

movements induced by waves and winds, which

generate an inverted pendulum effect and structural

fatigue. There are three categories of control methods

applied to FOWTs: pitch control, active structural

control, and passive structural control. Pitch control

adjusts aerodynamic forces but has disadvantages in

reducing other loads. Active structural control

directly restricts vibrations. Passive structural

control, such as the Tuned Mass Damper (TMD), is

more robust and economical, being widely used in

skyscrapers and offshore platforms (Jonkman, 2007).

The Tuned Mass Damper (TMD) is a common

passive device used in structural control. It consists of

a mass connected to the main structure by a spring

and a damper, tuned to vibrate at the system's loading

frequency. This vibration allows the damper to

dissipate energy in the form of heat, reducing

structural vibrations. In addition to the main variables

(mass, stiffness and damping coefficient), other

design factors influence the performance of the TMD

in FOWTs. The installation position (nacelle, tower

or platform) affects the frequencies and magnitudes

of the loads, while the direction of movement (front-

back, lateral or mixed) depends on the type of

vibration to be attenuated. The range of movement is

limited by the space available for installation, and the

travel limits, composed of additional springs and

dampers, restrict the mass travel.

The optimal tuning of TMD parameters can be

challenging, especially for nonlinear structures such

as offshore wind turbines. The effectiveness of the

TMD is linked to its mass, but the available space in

the nacelle is a significant limitation for its

installation. The introduction of additional stops and

limiters increases the system's complexity, requiring

advanced algorithms and numerical approaches for

defining and optimizing FOWT systems with TMD

(G. Stewart & Lackner, 2013).

2.3 Evolutionary Computation

Evolutionary algorithms have been widely adopted to

optimize TMD parameters due to their ability to

manage the complexity of passive structural control

systems (Villoslada et al., 2022). These algorithms,

inspired by species evolution and genetics, offer an

adaptive search mechanism, utilizing a population of

problem solutions and genetic operators such as

crossovers and mutations to produce results. The

fittest are selected for reproduction each generation,

combining characteristics from the parents. The basic

procedure of the genetic algorithm (GA) involves

population initialization, fitness calculation,

selection, crossover, mutation, and the creation of a

new population until a stopping condition is reached

(Faletti Almeida, 2007), as shown in Fig. 3. The

problem representation is done through a set of

parameters encoded in a chromosome, which is

decoded to build the actual solution (individual).

In the GA process, evaluation is essential to assign

everyone in the population a numerical value

corresponding to their ability to solve the problem.

Crossover involves exchanging parts of the

chromosomes of two individuals to generate novel

solutions, while mutation consists of randomly

changing the values of the genes in the chromosomes,

ensuring diversity in the population (Faletti Almeida,

2007). The evolution parameters that affect the

performance of the genetic algorithm include

population size, crossover rate, mutation rate, and

Improving Floating Wind Turbine Stability with Evolutionary Computation for TMD Optimization

477

generation interval. Proper adjustment of these

parameters is essential for efficient search.

Performance evaluation is done through evolution

curves (Fogel et al., 2000). In this study, genetic

algorithms are used to optimize the parameters of the

passive structural control type TMD in barge-type

FOWTs.

Figure 3: Basic procedure of a Genetic Algorithm (Faletti

Almeida, 2007).

2.4 Related Works

FOWTs have been focus of different recent research

efforts aimed at improving system efficiency,

especially through structural control to avoid negative

interference from wind and waves and to control

vibrations. Studies have examined both passive and

active control for floating wind turbines, highlighting

the use of tuned mass damper devices (Chen et al.,

2021). Most of these devices are installed in the

nacelle of the turbines, although some research has

explored installations in the turbine tower and on

barge-type platforms (Chen et al., 2021). The design

of these devices involves optimizing parameters to

reduce vibrations in the FOWT structure. Simulators

such as FAST, developed by NREL, have been used

to evaluate passive TMD control solutions in different

FOWT configurations (Lackner & Rotea, 2011).

Additionally, linear models have been developed to

investigate the effects of vibration suppression under

a variety of load cases (He et al., 2017).

A new passive structural control method for

FOWTs is proposed in (Liao & Wu, 2021), to

overcome previous limitations in TMD space. The

work includes optimizing a TMD installed in the

nacelle, showing that it can significantly reduce

structural loads and stabilize power output. TMD

parameter tuning is currently done through methods

such as frequency tuning, genetic algorithms, and

surface plots. The use of genetic algorithms to

optimize TMD designs has grown, with promising

results in simulations (Lackner & Rotea, 2011).

Although explored the inclusion of stops in TMD

models, the optimization of these parameters is still

limited, often using simplified system models during

the optimization cycle (Costoya et al., 2020).

Furthermore, few studies address the use of TMDs

both fore-aft and lateral-lateral to mitigate structural

fatigue, neglecting stop variables in the optimization

process and employing simplified FOWT models

(Lackner & Rotea, 2011).

This work proposes the optimization of a passive

structural control system with two TMD devices

(fore-aft and lateral-lateral) installed in the nacelle,

incorporating stroke limitation during the

optimization cycle. The performance of these devices

is evaluated under free decay conditions using the

FAST-SC simulator directly in the optimization

process.

3 METHODOLOGY

3.1 Characterization: FOWT and

Barge

This work uses a 5MW floating offshore wind turbine

developed by the National Energy Laboratory

(NREL). With a horizontal axis, three blades and

variable speed, designed for position against the

wind, with a 126m diameter rotor and 90m hub

height, as shown in Table 1. Widely adopted in

research, this model is supported by organizations

such as Union Upwind and the International Energy

Agency, is considered economically viable for

FOWT's due to their size (Jonkman, 2007).

Mounted on a barge developed in partnership by

the Universities of Glasgow and Strathclyde, together

with ITI Energy, the barge is square and ballasted

with seawater, anchored by eight catenary lines

(Vijfhuizen, 2006), as shown in Table 2. For

structural control, we opted for the TMD device,

installed in the nacelle, composed of a mass

connected to springs and shock absorbers, effective in

reducing vibrations. The TMD, vibrating in phase

opposite to the structure, reduces vibrational energy,

converting it into heat. These systems are tuned to the

natural frequency of the structure, generally its first

most relevant vibrational mode in the system's

response (Villoslada et al., 2022).

ICPRAM 2025 - 14th International Conference on Pattern Recognition Applications and Methods

478

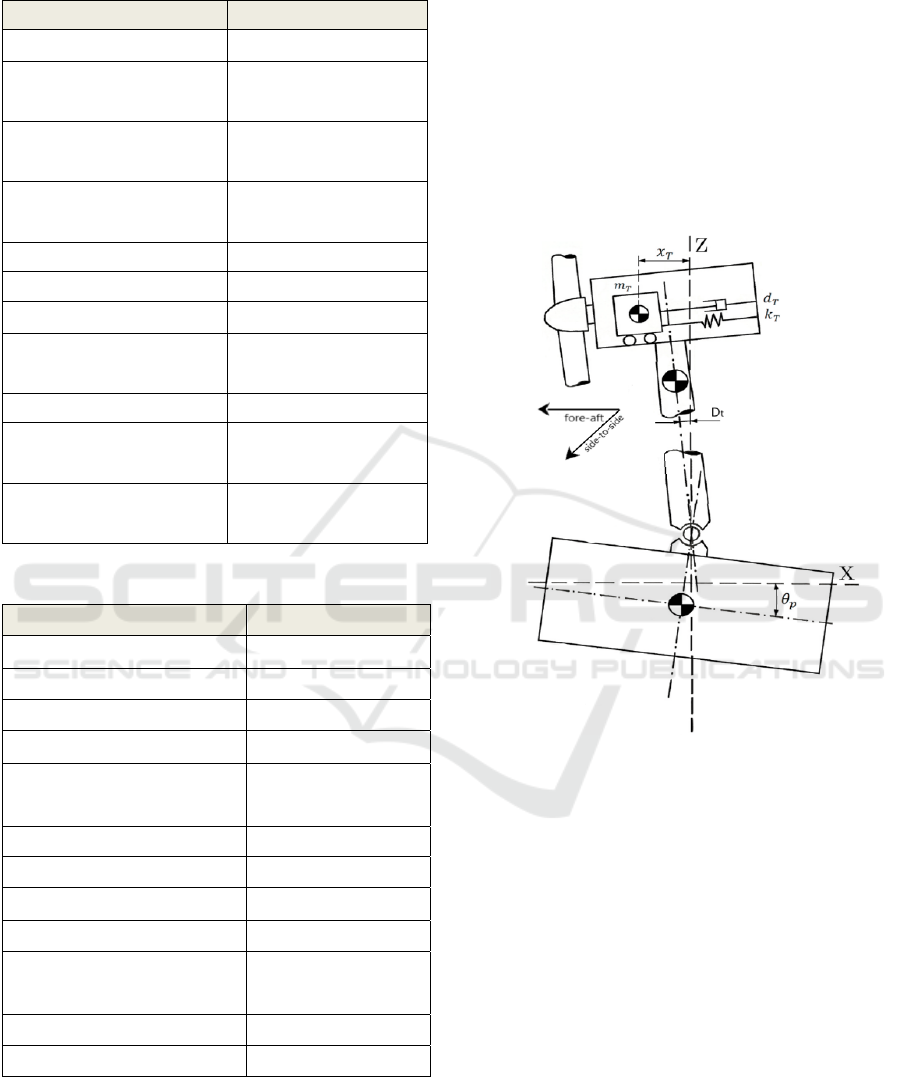
Table 1: FOWT NREL-5MW (Chen et al., 2021).

Parameters Dimensions

Rating 5MW

Rotor Orientation,

Configuration

Upwind, 3 Blades

Control Variable Speed,

Collective Pitch

Drivetrain High Speed, Multiple-

Stage Gearbox

Rotor, Hub Diameter 126m, 3m

Nacelle Dimension 18m x 6m x 6m

Hub Height 90m

Cut-In, Rated, Cut-Out

Wind Speed

3m/s, 11.4m/s, 25 m/s

Cut-In, Rated Rotor Speed 6.9 rpm, 12.1 rpm

Rotor Mass/ Nacelle Mass/

Tower Mass

110tons, 240tons,

347.46tons

Coordinate Location of

Overall CM

(-0.2 m, 0.0 m, 64.0 m)

Table 2: ITI Energy Barge (Vijfhuizen, 2006).

Parameters Dimensions

Size (W × L × H) 40m x 40m x 10m

Moonpool (W × L × H) 10m x 10m x 10m

Draft, Freeboard 4m, 6m

Mass, including Ballast 5,452,000kg

Center of Mass (CM) below

SWL

0.282 m

Roll Inertia about CM 726,900,000 kg⋅m²

Pitch Inertia about CM 726,900,000 kg⋅m²

Yaw Inertia about CM 1,453,900,000 kg⋅m²

Anchor (Water) Depth 150m

Neutral Line Length Resting

on Seabed

250m

Line diameter 0.0809m

Extensional line stiffness 589,000,000 N

3.2 Parametrization of TMD’s

The main parameters of the TMDX (forward-reverse

direction) are: mass mT (kg), where a greater mass

increases inertia and stored kinetic energy, limited by

the total mass of the structure; spring stiffness kT

(N/m); damping dT (N⋅s/m); position xT (m), which

influences design loads and constraints; orientation

(front-back or side, side-side); and travel limits (stops

to limit the movement of the TMDX, affecting loads

and restrictions). The barge model considers platform

compliance, with tower and TMDX degrees of

freedom, in addition to the launch degree. In this

context, the following sub-indices are used: TMDX

(T), tower (t), stops (S) and barge-type platform (p).

The complete TMDX model is illustrated in Fig. 4.

Figure 4: Complete system model for TMDX. Adapted

from (Villoslada et al., 2022).

The TMDX stops, or stops limit the displacement

of the resonant mass, making the installation viable

and realistic. They consist of an additional spring and

a shock absorber that come into action when the mass

deviates a certain distance from the rest position. Stop

parameters include actuation distance (XS), spring

stiffness (kS) and damping coefficient (dS). The

operational logic of the stops follows the same

performance as the FAST simulator, with the spring

always active and the damper only operating when

the mass moves away from the rest position (Fig. 5).

The TMDY, with side-to-side direction, has the

same parameters as the TMDX, but its location is

different, and it is installed to reduce lateral fatigue

on the nacelle. Both are arranged in a "cross" shape in

relation to the center of the nacelle, having different

vertical dimensions.

Improving Floating Wind Turbine Stability with Evolutionary Computation for TMD Optimization

479

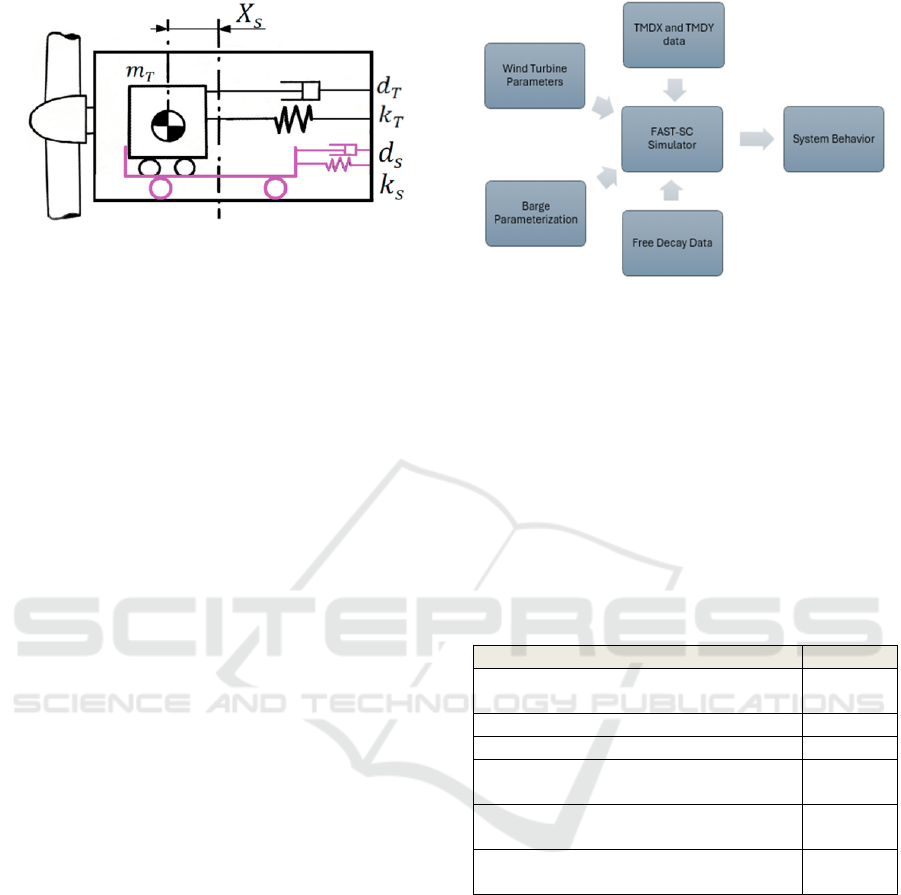
Figure 5: Addition of stops to the TMDX system. Adapted

from (Villoslada et al., 2022).

3.3 FAST-SC Simulator

FAST (Fatigue, Aerodynamics, Structures and

Turbulence) software simulates a 5 MW wind

turbine, using the AeroDyn and HydroDyn modules

to calculate aerodynamics and hydrodynamic loads

on the floating platform. It employs temporal

simulation to solve nonlinear equations, considering

varied factors such as axial and tangential induction,

tip and hub losses, and dynamic stall modeling

(Lackner & Rotea, 2011).

In this simulator, two independent TMDs are

integrated for structural control, this modified version

of the software being called 'FAST-SC'. The

equations of motion are derived using Kane dynamics

(Kane & Levinson, 1985). The TMDs are positioned

in the wind turbine nacelle and consist of mass,

spring, and damper. The position of each TMD,

including the neutral spring position, is defined

relative to the centerline of the top of the tower,

exerting an equal and opposite force on the nacelle.

Each TMD has two stroke limiters to restrict

movement (Kane & Levinson, 1985).

The TMDs oscillate axially in the turbine nacelle

(TMDX) and laterally (TMDY), generating forces. Its

equations of motion, derived from FAST, consider

positions, velocities, accelerations, and forces. In

FAST-SC, TMDX and TMDY are independent and

can be controlled in several ways by the user,

including passive, semi-active, or active control

(Lackner & Rotea, 2011).

The FAST-SC simulator uses an executable file

and a main input file. The latter allows the user to

modify initial parameters to represent the proposed

system, including information about the simulation,

wind turbine, buoyancy base (if applicable) and

TMD’s. It also requires secondary files and libraries

for its proper functioning (Fig. 6).

Figure 6: Simplified FAST-SC flowchart.

In the optimization simulations, simplified system

conditions were used, including free decay of the

structure (wind of 0.5 m/s and without kinematic

wave model). The response to an initial displacement

of 5 degrees in pitch and 10 degrees of initial yaw

rotation on the platform was analyzed. The main

parameters include simulation time (one hundred

seconds), degrees of freedom (DOF’s) of rotation,

pitch, and yaw of the platform, as well as the flexion

modes are set to 'True' and the initial conditions,

shown in Table 3.

Table 3: Main input parameters in FAST.

Parameters Value

RotSpeed (speed rotor initial) 12.1

(rpm)

TmdXDsp (displacement TMDX initial) 1.0 (m)

TmdYDsp (displacement TMDY initial) 1.0 (m)

PtfmRoll (displacement initial rotation

platform)

5 degrees

PtfmPitch (displacement platform initial

step)

5 degrees

PtfmYaw (displacement. platform initial

lurch)

degrees

3.4 Genetic Algorithm Parametrization

In this work, MATLAB software was used with its

optimization libraries to encode the genetic

algorithm. During the GA optimization cycle, each

individual goes through a 100-second simulation in

FAST-SC, with free system decay, to analyze their

response in relation to the tower deflection in x and y

(m) and the barge pitch (degrees). These results make

it possible to evaluate everyone’s performance in

reducing structure fatigue. Each individual is

represented by a chromosome with 14 variables, half

of which are for the TMDX parameters and the other

half for the TMDY parameters. Table 4 contains the

ICPRAM 2025 - 14th International Conference on Pattern Recognition Applications and Methods

480

description of each variable and its lower and upper

limits.

The evaluation function (fa), which determines

the fitness of each individual, is based on the

deflection of the tower (in meters) on the x (Dtx) and

y (Dty) axes, with a weighted average being applied

between both. Due to the greatest fatigue occurring in

the x-axis [11], the total standard deviation of the

evaluation function was calculated according to

equation 1.

𝑓

𝑎

𝜎

(

𝐷𝑡𝑥

)

9 𝜎

(

𝐷𝑡𝑦

)

(1)

Table 4: Lower and upper limits of optimized parameters.

TMD’s Parameters Low Limit Upper

Limit

TmdXMass (mass) 18,000 kg 42,000 kg

TmdYMass (mass) 8,000 kg 12,000 kg

TmdXSpr, TmdYSpr

(spring stiffness)

103 N/m 105 N/m

TmdXDamp, TmdYDamp

(damping)

1,000

N.s/m

20,000

N.s/m

TmdXDwSp (stop

position - positive axis)

7.5 m 8.3 m

TmdXDwSp (stop

position - negative axis)

-8.3 m -7.5 m

TmdYDwSp (stop

position - positive axis)

1.5 m 2.3 m

TmdYDwSp (stop

position - negative axis)

-2.3 m -1.5 m

TmdXSSpr, TmdYSSpr

(stop spring)

104 N/m 106 N/m

TmdXSDamp,

TmdYSDamp (stop

damping)

104 N.s/m 106 N.s/m

Table 5: Main GA evolution parameters.

Parameters 1º 2º 3º 4º

Prossessing

Number

12 11 3 5

Population 50 50 15 15

Max.

Generations

50 50 30 30

Crossover Rate 0.70 0.70 0.70 0.70

Mutation Rate 0.30 0.30 0.30 0.30

Elitization 5 5 2 3

Stopping

Criteria

10-6 10-6 10-6 10-6

Best Individual

(

𝑓

𝑎)

0,2625 0.2714 0,2731 0,2781

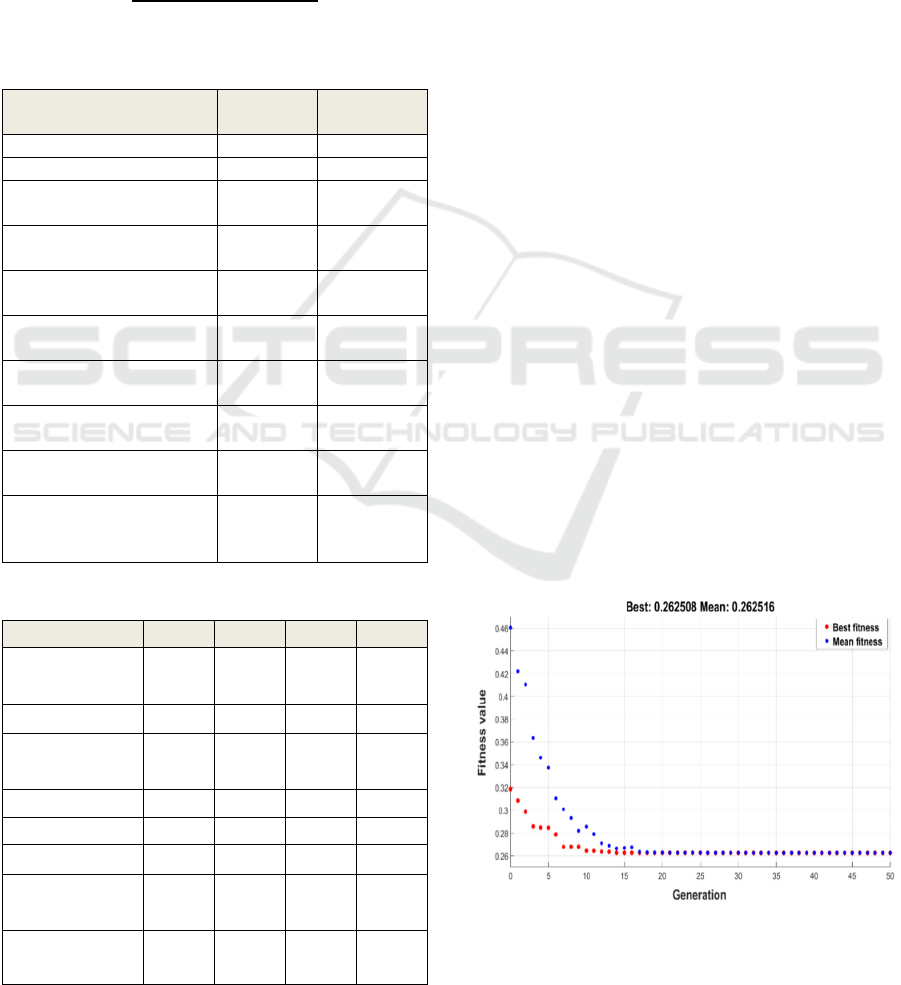
Twenty processing of the genetic algorithm were

done to obtain the best TMD parameterization results.

In Table 5, the main evolution parameters for GA

processing that resulted in the four best results are

presented.

4 RESULTS

The best individual (solution) among the GA

processes was obtained in the 12th process, as shown

in the generation versus evaluation function curve in

Fig. 7. The curve shows that the best individual

reached a value of 0.262508, with an average of

0.262516 per generation.

The graph also shows that GA converged on

satisfactory results from the 17th generation onwards,

demonstrating its effectiveness in identifying the

ideal solution in a relatively short time. This

efficiency is fundamental for studies involving

multiple interdependent variables, such as TMD

parameters, and complex structural analysis

conditions.

The use of GA in this study is justified for several

reasons. Firstly, the problem in question does not

have a defined equation that allows the use of

gradient-based methods, making GA an appropriate

choice due to its ability to explore large solution

spaces without relying on derivatives. In addition, GA

simplifies the mathematical representation of the

system, allowing the optimization process to be

conducted in a more straightforward and intuitive

manner. By operating under free decay conditions

and with reduced degrees of freedom (DOFs), GA can

quickly find the best results for the TMD parameters,

maximizing computational efficiency and reducing

total processing time.

Figure 7: GA behaviour: generations versus evaluation

function.

Improving Floating Wind Turbine Stability with Evolutionary Computation for TMD Optimization

481

These factors demonstrate the robustness and

adaptability of GA as an optimization tool for non-

linear and highly complex systems, such as floating

wind turbines. GA's ability to find optimal solutions

in vast search spaces with multiple constraints

reinforces its relevance for future studies seeking to

optimize structural control devices under different

operating conditions.

The results of the system optimization, with the

best parameterizations for TMDX and TMDY, are

shown in Table 6. The optimization resulted in a

TMDX with a standard deviation of front-to-back

deflection of 0.2511 and a TMDY with a standard

deviation of side-to-side deflection of 0.3655. These

values indicate a significant reduction in the tower's

structural vibrations, directly contributing to reduced

fatigue in the control devices and the overall structure

of the FOWT. This improvement reinforces the

effectiveness of optimized TMDs in mitigating

oscillations in the main axes, extending the useful life

of critical components.

Table 6: Optimized parameters for TMDX and TMDY.

Parameter

TMD

TMDY

Mass (kg

)

40,07

8,93

Spring (N/m

)

3,74

93,82

Damping (N.s/m

)

8,60

1,00

Stop Position (m

)

± 8.

± 2.

Stop Spring (N/m

)

10,00

129,36

Stop Damping (N.s/m

)

389,95

85,95

𝜎

(tower deflection

)

0.251

0.365

In addition, Table 6 shows the main optimized

parameters for the TMDX and TMDY devices, which

play important roles in the structural control of the

FOWT. The 40,076 kg mass of the TMDX allows for

greater inertia to reduce front-to-back vibrations,

while the spring stiffness (3,746 N/m) and damping

(8,607 N.s/m) balance the dynamic response. On the

TMDY, the reduced mass of 8,938 kg is suitable for

lateral-lateral control, with higher spring stiffness

(93,824 N/m) and lighter damping (1,006 N.s/m) due

to the different nature of lateral oscillations.

The stop positions (±8.0 m) for TMDX and ±2.2

m for TMDY) and the respective spring and damping

parameters of the stops ensure that the displacement

of the mass is controlled within safe limits, avoiding

overloads on the devices and the structure. These

values, calibrated for the specific conditions of the

FOWT, demonstrate how optimized parameterization

contributes to a more efficient and reliable system.

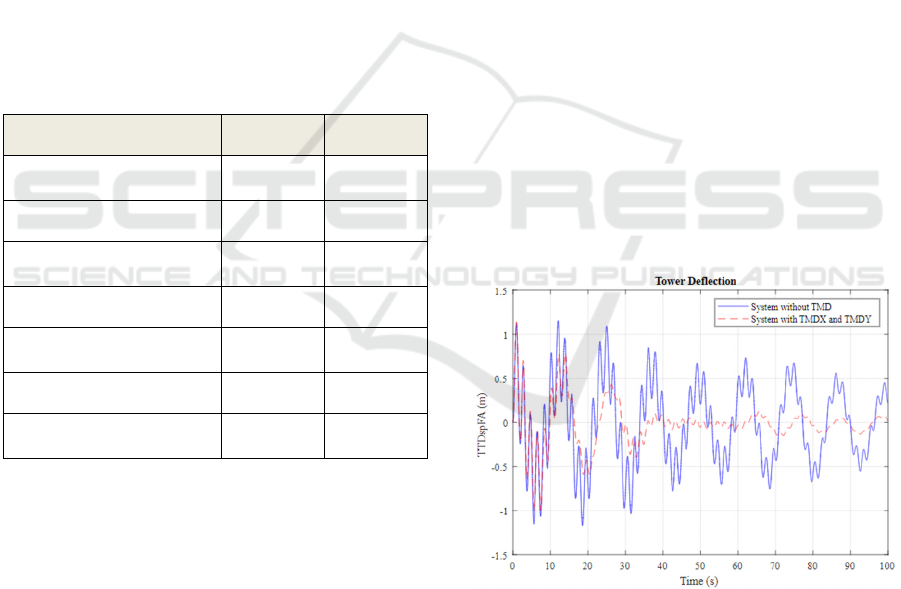
Figures 8 and 9 highlight a significant

improvement in the system's dynamic response after

the inclusion of the optimized TMDX and TMDY.

Figure 8 illustrates the reduction in the displacement

of the fore-aft tower, while Figure 9 shows the

reduction in the inclination of the barge.

When compared to the system without any TMD,

there is a 36.7% reduction in the root mean square

error (RMSE) of the deflection, showing the

effectiveness of the optimized devices. This reduction

is a clear indication of the mitigation of structural

vibrations, which is essential for extending the useful

life of the FOWT and reducing maintenance costs

associated with structural fatigue. This RMSE value

not only reflects a lower oscillation amplitude, but

also demonstrates how the optimized TMDs manage

to balance the dynamic forces imposed on the system.

This result is visibly highlighted in the graphs,

which show a more uniform and consistent

attenuation of vibrations compared to the original

system. The significant decrease in oscillations

reinforces the importance of incorporating optimized

passive control solutions, such as the TMDX and

TMDY, to improve the stability and operational

reliability of floating wind turbines in real operating

conditions.

Figure 8: Tower deflection - system without TMD versus

system with TMDX and TMDY.

ICPRAM 2025 - 14th International Conference on Pattern Recognition Applications and Methods

482

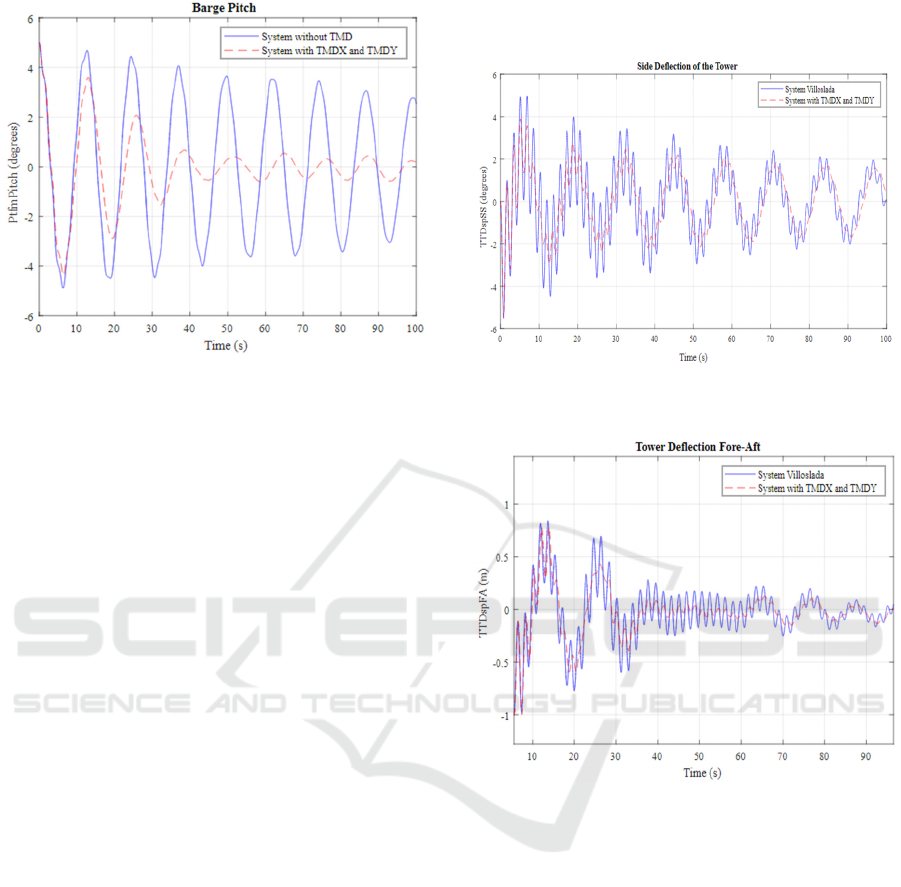
Figure 9: Barge Pitch - system without TMD versus system

with TMDX and TMDY.

For comparison purposes, Figures 10 and 11 show

the graphs of the front-to-back displacement and

lateral displacement of the tower of this system,

compared to the results obtained by Villoslada et al.

(2022), who optimized only the TMDX under similar

initial conditions and free decay.

The analysis shows that the system with

bidirectional TMDs (TMDX and TMDY) performed

11% better in terms of RMSE than the unidirectional

system optimized by Villoslada. This increase in

performance reflects the improved ability of the

bidirectional TMD system to mitigate vibrations in

multiple directions, contributing to a more balanced

reduction in the dynamic forces on the structure.

This superiority of the proposed structural control

system is especially important for floating wind

turbines, which face complex, multi-directional loads

from wind and platform movements. While the

unidirectional TMD system focuses on attenuating

front-to-back oscillations, the use of bidirectional

TMDs allows for a more comprehensive approach,

also reducing lateral oscillations, which are critical

for avoiding structural failures and reducing tower

fatigue.

Figures 10 and 11 visually highlight how the

combination of TMDX and TMDY optimizes the

dynamic response of the tower, resulting in lower

displacement amplitudes in both directions and,

consequently, greater reliability and operational

stability of the system.

There is a significant improvement in the

response of the system that incorporates TMDX and

TMDY compared to the system without any TMD,

achieving a 36.7% reduction in deflection (RMSE:

root mean square error). Furthermore, there was an

11% superior performance (RMSE) compared to the

system developed by Villoslada et al. (2022), which

optimized only TMDX.

Figure 10: Tower deflection - system with TMDX and

TMDY versus results from Villoslada et al. (2022).

Figure 11: Tower Lateral Deflection - system with TMDX

and TMDY versus results from Villoslada et al. (2022).

5 CONCLUSIONS

This study highlights the importance and effectiveness

of passive control in reducing vibrations and pendulum

loads in floating wind systems, making them more

efficient and attractive for energy production. The

main contribution of this work is the comprehensive

consideration of the parameters of the dual TMD

control device in the nacelle, both in the front-to-back

and lateral-to-lateral directions, in the optimization

cycle, demonstrating that the proposed approach

achieves a significant reduction in fatigue (36.7%).

The use of evolutionary computation to

parameterize TMDs is recommended, as the results of

this study reinforce the effectiveness of the genetic

algorithm (GA) as an optimization tool for complex

Improving Floating Wind Turbine Stability with Evolutionary Computation for TMD Optimization

483

systems such as floating wind turbines. From the 17th

generation onwards, GA converged quickly to

satisfactory solutions, demonstrating its ability to

identify the best TMD parameters under free decay

conditions and with reduced degrees of freedom.

In addition, the absence of a defined equation for

the problem justifies the use of GA, which simplifies

the mathematical representation and makes it possible

to explore a wide space of solutions. These factors

highlight the relevance of GA for future applications

in passive structural systems and highly complex

scenarios.

These findings have broad applicability, not

limited to barge-type FOWTs. For example, the

approach can be adapted to other types of floating

platforms, such as Spar Buoys and Tension Leg

Platforms (TLPs), which have different structural

dynamics and operational challenges. In Spar Buoys,

the mass of the TMD could be adjusted to compensate

for the high moment of inertia due to the elongated

structure. In TLPs, TMDs could be used to deal with

the horizontal oscillations generated by the tensioned

anchoring forces.

It is worth noting that the integration of the

proposed methodology into hybrid platforms, which

combine floating elements with fixed foundations,

can be explored, extending its applicability to

different configurations and maritime environments.

Future work could also include simulations and

optimizations under more complex loading

conditions, such as turbulent winds and irregular

waves, as well as considering TMD devices installed

in other parts of the system, such as on the tower or

platform, for an integrated control approach. These

future directions have the potential to broaden the

relevance of the proposed approach and provide more

robust solutions for the next generation of offshore

wind systems.

REFERENCES

Butterfield, S., Musial, W., Jonkman, J., & Sclavounos, P.

(2007). Engineering Challenges for Floating Offshore

Wind Turbines. National Renewable Energy Laboratory.

Chen, X., Kareem, A., Xu, G., Wang, H., Sun, Y., & Hu, L.

(2021). Optimal tuned mass dampers for wind turbines

using a Sigmoid satisfaction function‐based

multiobjective optimization during earthquakes. Wind

Energy, 24(10), 1140–1155.

Costoya, X., deCastro, M., Carvalho, D., & Gómez-

Gesteira, M. (2020). On the suitability of offshore wind

energy resource in the United States of America for the

21st century. Applied Energy, 262, 114537.

Faletti Almeida, L. (2007). Sistema Híbrido de Otimização

de Estratégias de Controle de Válvulas de Poços

Inteligentes sob Incertezas [Doctoral dissertation].

PUC Río.

Figueiredo, A. C. V. S. (2019). Feasibility assessment of

applying a small wind turbine in a guesthouse in

Arraial do Cabo [Doctoral dissertation]. Federal

University of Rio de Janeiro.

Fogel, D. B., Bäck, T., & Michalewicz, Z. (Eds.). (2000).

Evolutionary computation. Institute of Physics

Publishing.

He, E.-M., Hu, Y.-Q., & Zhang, Y. (2017). Optimization

design of tuned mass damper for vibration suppression

of a barge-type offshore floating wind turbine.

Proceedings of the Institution of Mechanical Engineers,

Part M: Journal of Engineering for the Maritime

Environment, 231(1), 302–315.

Hu, Y., & He, E. (2017). Active structural control of a

floating wind turbine with a stroke-limited hybrid mass

damper. Journal of Sound and Vibration, 410, 447–472.

Jonkman, J. M. (2007). Dynamics Modeling and Loads

Analysis of an Offshore Floating Wind Turbine

(NREL/TP-500-41958, 921803; p. NREL/TP-500-

41958, 921803).

Kane, T. R., & Levinson, D. A. (1985). Dynamics, theory

and applications. McGraw-Hill.

Lackner, M. A., & Rotea, M. A. (2011). Passive structural

control of offshore wind turbines. Wind Energy, 14(3),

373–388. https://doi.org/10.1002/we.426

Liao, M., & Wu, Y. (2021). Conceptual design and dynamic

analysis of a novel passive floating offshore wind

turbine structure. Ships and Offshore Structures,

16(10), 1040–1049.

Olondriz, J., Jugo, J., Elorza, I., & and Aron Pujana-Arrese,

S. A.-Q. (2019). A Feedback Control Loop

Optimisation Methodology for Floating Offshore Wind

Turbines. Energies, 12(18), 3490.

https://doi.org/10.3390/en12183490

Picolo, A. P., Rühler, A. J., & Rampinelli, G. A. (2014).

Uma abordagem sobre a energia eólica como

alternativa de ensino de tópicos de física clássica.

Revista Brasileira de Ensino de Física, 36(4), 01–13.

Stewart, G., & Lackner, M. (2013). Offshore Wind Turbine

Load Reduction Employing Optimal Passive Tuned

Mass Damping Systems. IEEE Transactions on Control

Systems Technology, 21(4), 1090–1104.

Stewart, G. M. (2012). Load reduction of floating wind

turbines using tuned mass dampers.

Vijfhuizen, W. J. M. (2006). Design of a wind and wave

power barge [Doctoral dissertation, MS Thesis].

Department of Naval Architecture and Mechanical

Engineering, Universities of Glasgow and Strathclyde.

Villoslada, D., Santos, M., & Tomás-Rodríguez, M. (2022).

TMD stroke limiting influence on barge-type floating

wind turbines. Ocean Engineering, 248, 110781.

Zuo, H., Bi, K., & Hao, H. (2020). A state-of-the-art review

on the vibration mitigation of wind turbines. Renewable

and Sustainable Energy Reviews, 121, 109710.

ICPRAM 2025 - 14th International Conference on Pattern Recognition Applications and Methods

484