Classification of Complaints Text Data by Ensembling Large Language
Models
Pruthweesha Airani, Neha Pipada and Pratik Shah
Indian Institute of Information Technology, Vadodara, India
Keywords:
Natural Language Processing, Machine Learning, Deep Learning, Transformers, Statistical Methods.
Abstract:
Effective and efficient management of consumer complaints requires segregation of complaints based on prod-
ucts, services, etc. categories. In this work, we propose an ensemble classification approach based on statistical
class incidence frequencies from softmax confidence scores of ensemble of classifiers. The classifiers process
the complaint text through Large Language Models (LLMs) followed by discriminating networks. LLMs
along with discriminators are fine-tuned on a large, publicly available dataset of over 162,000 annotated con-
sumer complaint records pertaining to banking services. The proposed ensemble approach utilizes confidence
scores from individual classifiers (LLM embeddings + discriminator network) achieving better accuracy. It is
based on statistical analysis of class-wise precision as a function of confidence score. The individual classi-
fiers built on various SMLMs & LLMs are experimented with, and the results are tabulated for the complaints
classification task.
1 INTRODUCTION
Classification of text data is a challenging problem in
the natural language processing (NLP) domain. Large
language models (LLMs) have been rising in popular-
ity in recent years. Foundation models pre-trained on
a large corpus of unannotated data generally exhibit
good capability to capture semantic essence and con-
text in natural language. However, they don’t spe-
cialize in tasks like classification. The pre-trained
models are typically fine-tuned using a smaller anno-
tated dataset to improve classification accuracy. Pub-
licly available annotated bank consumer complaints
dataset can be used to fine-tune foundational mod-
els for multi-class classification of complaints. The
dataset contains 162,415 records, and 5 distinct class
labels. Various foundation models were fine-tuned
and then ensembled to obtain a verdict for each case.
The high-level architecture of each of the individual
model included the base model of the LLM, followed
by a discriminator block, as outlined in Figure 1.
Classification models often tend to output confi-
dence scores that deviate significantly from the ob-
served class-wise precision values. Analysing the
relationship between class-wise precision and confi-
dence scores provides valuable insights about which
classes a model is overconfident or underconfident
about. These insights may be documented, and later
retrieved to reinterpret the confidence scores obtained
from the models. The reinterpreted scores enable the
ensemble to achieve improved accuracy on unseen
data. The extent to which the computation of preci-
sion as a function of confidence score may improve
accuracy is examined.
2 LITERATURE SURVEY
In recent years, Transformer-based (Vaswani et al.,
2017) language models have revolutionized multi-
class classification tasks. Models like BERT (De-
vlin et al., 2018) and its successors employ atten-
tion mechanisms to effectively understand the context
within the text. Innovations such as RoBERTa (Liu
et al., 2019) which is A BERT-based large language
model, and ALBERT (Lan et al., 2020) have refined
pre-training strategies, resulting in better efficiency
and accuracy. RoBERTa dropped the next-sentence
prediction objective that BERT adopted, during pre-
training, focusing on the masked language modeling
objective, and used Dynamic masking in contrast to
static masking which BERT adopted. ALBERT was
developed with the intention of minimizing model
size by minimising the number of parameters with
techniques like parameter sharing and embedding fac-
torization (Lan et al., 2020). DistilBERT (Devlin
Airani, P., Pipada, N. and Shah, P.
Classification of Complaints Text Data by Ensembling Large Language Models.
DOI: 10.5220/0013173900003890
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 17th International Conference on Agents and Artificial Intelligence (ICAART 2025) - Volume 3, pages 679-686
ISBN: 978-989-758-737-5; ISSN: 2184-433X
Proceedings Copyright © 2025 by SCITEPRESS – Science and Technology Publications, Lda.
679

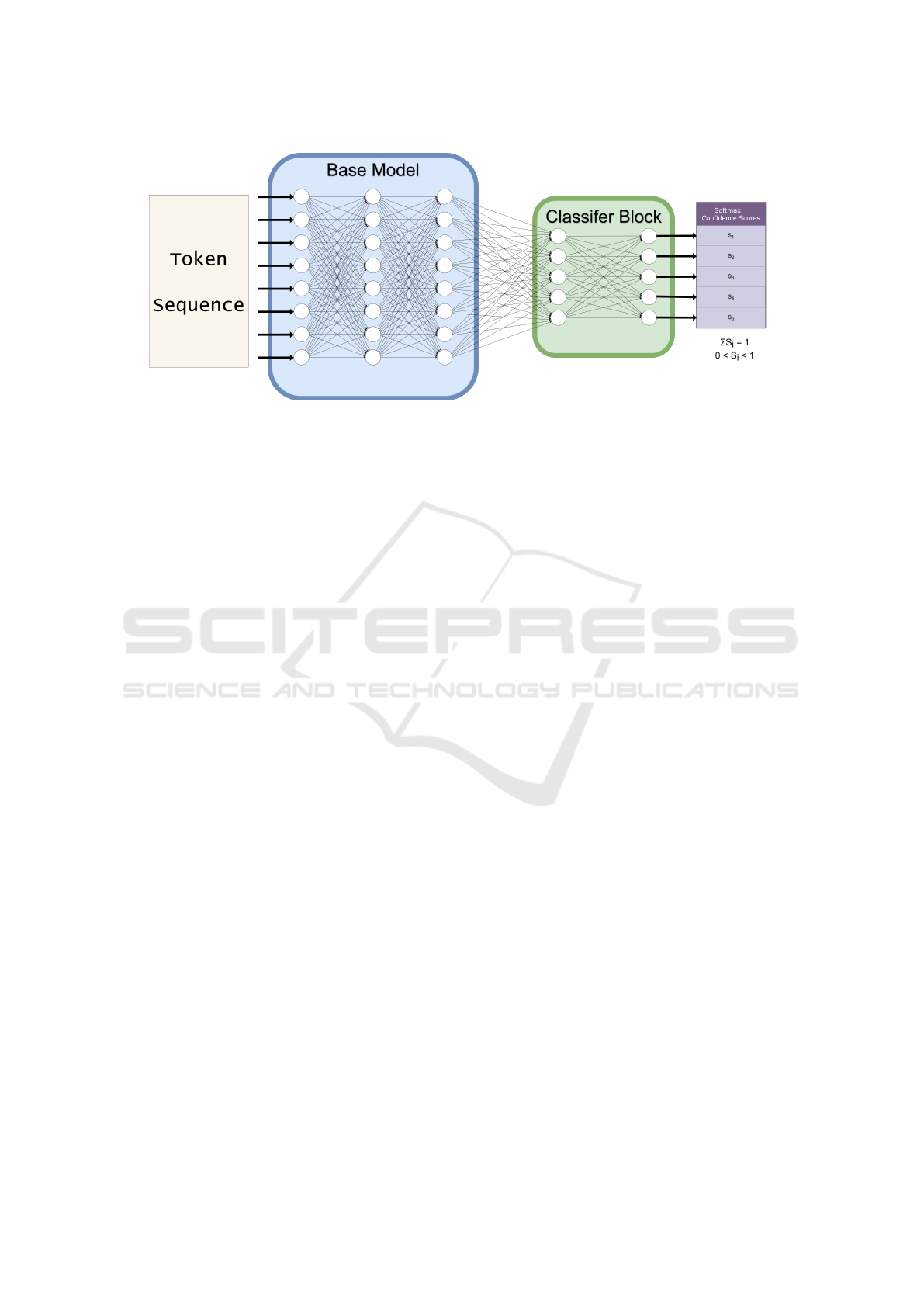
Figure 1: Sequence classifier model with the base model and a classifier block.
et al., 2018) is a version of BERT trained using knowl-
edge distillation (Hinton et al., 2015). DistilBERT re-
portedly retains 97% of BERT’s efficacy across mul-
tiple tasks, while achieving a size reduction of 40%
(Devlin et al., 2018).
Large Language models (LLMs) tend to outper-
form smaller language models by supporting greater
sequence lengths and vocabulary sizes. GTE-large-
en-v1.5 is an English-language long-context text-
representation model based on the architecture of
multilingual text-retrieval model (Zhang et al., 2024)
developed by the Institute of Intelligent Computing,
Alibaba Group. Mistral-7B is a large-language model
(LLM) which features innovations like rolling buffer
cache and sliding window attention (Jiang et al.,
2023) to outperform LLaMa (Touvron et al., 2023)
and other existing models of similar size. MiniGPT4-
7B is A multi-modal model (Zhu et al., 2023), which
can work with images and text, based on BLIP-2 (Li
et al., 2023) and Vicuna (Zheng et al., 2023), in turn
based on LLaMa.
Additionally, techniques like fine-tuning (Dodge
et al., 2020; Doering et al., 2024) and prompt engi-
neering (Reynolds and McDonell, 2021; Vatsal and
Dubey, 2024) enhance these models’ adaptability for
specific classification needs. New approaches, in-
cluding Mixture of Experts (MoE) used in Mistral-7B
(Jiang et al., 2023), present possibilities for improving
efficacy and speed while minimizing computational
demands.
2.1 Our Contribution
The ensemble we developed uses fine-tuned versions
of six foundation models. These models are config-
ured to output softmax confidence scores for the 5-
class classification problem in consideration. We doc-
ument the relationship between confidence scores and
class incidence frequency to populate a lookup table.
We then use the statistical insights thus generated to
develop and refine an ensemble strategy to achieve su-
perior classification accuracy.
3 PROPOSED ENSEMBLE
METHOD
To examine the efficacy of ensemble of classifiers, we
designed an experiment where the inference pipeline
would record the Softmax outputs of all the mod-
els, following which an ensembling strategy would
be developed based on the confidence scores obtained
against a so-called ensemble strategization dataset,
which is disjoint from the training and ensemble
benchmark datasets.
The experiment involves obtaining the datasets
and the pre-trained models, fine-tuning the model pa-
rameters, and a preliminary round of testing the mod-
els to document confidence scores. The development
of the ensemble strategy is based on the relationship
between confidence-scores and class-wise precision.
Once the ensemble strategy has been developed, we
finally benchmark the ensemble on previously unseen
data.
3.1 Deriving Precision as a Function of
Confidence Score
The confidence scores output by the model are
grouped in intervals of 2 percentage points. The pre-
cision for the class in question is calculated for each
of the 2-percentage point width intervals. A lookup
table is built wherein each confidence score interval
is mapped to its corresponding observed class inci-
dence probability vector. These vectors will be used
ICAART 2025 - 17th International Conference on Agents and Artificial Intelligence
680

to reinterpret confidence scores during benchmarking.
R(S) =
5
∑
i=1
(P(c
i
|S
i
).e
i
+ x
5
∑
j=1
(P(c
j
|S
i
).e
j
.δ
i j
)) (1)
The Reinterpreted probability vector function, R
for the input softmax vector S is given by Equation 1,
where
c
i
is the event that the case belongs to class i,
S is the Softmax confidence vector output by the
model for the case in question,
e
i
is the i
th
basis vector in R
5
,
x is the cross-confidence factor,
δ
i j
is the Kronecker delta function.
The cross-confidence factor (x) is a tunable pa-
rameter which determines how much the softmax
confidence score of one class affects the reinterpreted
probability scores for other classes. The most optimal
results were obtained when x was set to 0.4.
3.2 Ensembling
After the Softmax scores from the various models
were compiled, the ensembling strategy was devel-
oped based on precision as a function of confidence
scores. This metric involved comparing the observed
precision of the model in question for confidence
score intervals of 5 percentage points, for each class.
If RoBERTa suggests a 60% confidence in category 1
for a certain case, but the set of all test data points
where RoBERTa awarded 60%(± 1%) confidence
score to category 1 showed a 40% probability of ac-
tually belonging to category 1, one must reinterpret
the confidence scores produced by RoBERTa, to as-
sume a 40% probability of the data point belonging to
category 1.
After the reinterpreted class probabilities are ob-
tained for multiple models for the same data point,
there were several candidate strategies for ensem-
bling. The argmax-of-product strategy involves ini-
tially multiplying the reinterpreted class probability
vectors to obtain a product vector, whose argmax can
be declared as the class predicted by the ensemble.
An analytic hierarchy process (Saaty, 1990) may
also be used to ensemble the models, as described
in Figure 2. The confidence score vectors output by
each model is first multiplied with the model’s over-
all accuracy (which is a scalar). This scaled vector is
then multiplied element-wise with the class-wise pre-
cision vector for the model in question. The resulting
Hadamard product vectors from all models are aggre-
gated to deduce the class with the highest likelihood.
Figure 2: AHP Ensemble; a
i
is the overall accuracy of
model ‘i’ across all classes, against a balanced test dataset.
For instance, suppose, for some data point,
the models RoBERTa, DistilBERT and AL-
BERT respectively produce the probability
vectors S
RoBERTa
= [0.90, 0.02, 0.01, 0.03, 0.04],
S
DistilBERT
= [0.20, 0.70, 0.01, 0.02, 0.07], S
ALBERT
=
[0.70, 0.10, 0.06, 0.09, 0.05]. Given the class-
wise precision vector of RoBERTa is P
RoBERTa
=
[0.90, 0.76, 0.88, 0.90, 0.90], that of DistilBERT is
P
DistilBERT
= [0.88, 0.76, 0.88, 0.85, 0.88], and that of
ALBERT is P
ALBERT
= [0.86, 0.83, 0.86, 0.89, 0.87],
and the overall accuracies, a
RoBERTa
= 0.864,
a
DistilBERT
= 0.859, a
ALBERT
= 0.862, the final
probability vector produced by the AHP network can
be computed using Equation 2.
S
AHP
= ∥
∑
(a
i
· (S
i
◦ P
i
))∥
2
(2)
In this case, substituting applicable terms in
Equation 2 gives us the final probability vector
[0.62, 0.25, 0.03, 0.05, 0.06], with class 1 being the
most likely among all classes.
3.3 Data Description
The dataset was acquired from kaggle.com. The
“Consumer Complaints Dataset for NLP” contains a
total of 162,421 records, out of which 37,949 were
duplicates.
Out of the remaining 124,472 records, 70% were
used for training the model. 10% were used to vali-
date the model, 10% was used to test the individual
models and record the confidence scores for develop-
ing an ensembling strategy. The remaining 10% was
used to benchmark the ensemble strategy developed
in the previous step. The distribution of classes in the
dataset is as detailed in Table 1.
Classification of Complaints Text Data by Ensembling Large Language Models
681

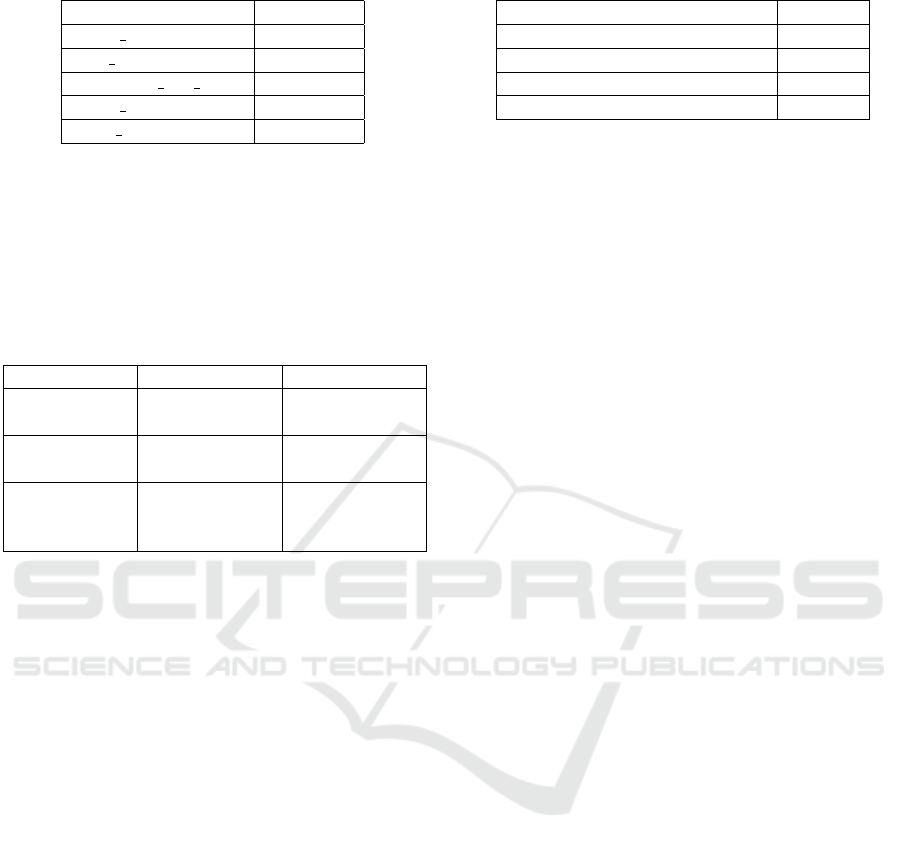
Table 1: Class distribution in the original dataset.
Class Proportion
credit reporting 45.18
debt collection 16.91
mortgages and loans 15.05
credit card 12.04
retail banking 10.82
4 IMPLEMENTATION
The models RoBERTa-base, DistilBERT, ALBERT,
and GTE-en-large were fine-tuned on an NVIDIA
Quadro GP100 GPU with 16GB VRAM.
Table 2: PEFT statistics.
Model MiniGPT4 Mistral-7B
Total
parameters
6,611,542,016 7,117,516,800
PEFT
parameters
4,194,304 6,836,224
PEFT
parameter
proportion
0.0634% 0.0960%
The models miniGPT and Mistral-7B were fine-
tuned on an NVIDIA A40 with 48GB VRAM. These
models were quantized to load in 4-bit precision, and
fine-tuned with a LoRA (Low Rank Adapter) which
minimised the number of trainable parameters as de-
tailed in Table 2.
4.1 Loading Sequence Classification
Model
Foundation models are loaded from HuggingFace
Hub, a platform to publish and access open-source
and/or open-weights models, using the transformers
library (Wolf et al., 2019). In cases where the Auto-
ModelForSequenceClassification function fails to fit
the classifier into the available VRAM efficiently, a
custom lightweight classifier block was appended to
the base model, as shown in Figure 1.
4.2 Fine-Tuning
Once the model weights are loaded into VRAM, the
annotated training data points are used to compute
the loss, and subsequently update the weights in the
model, with a small learning rate, along with the
weights of the discriminator block which was trained
with a higher learning rate.
Table 3: Training Hyperparameters.
Optimizer AdamW
Learning Rate (Full fine-tuning) 1e-5
Training Batch Size 16
Validation Batch Size 16
Dropout probability 0.3
4.2.1 Number of Epochs
Fine-tuning was stopped upon observation of over-
fitting (characterized by training accuracy being sig-
nificantly higher than validation accuracy, or training
loss being significantly lower than validation loss, or
both).
4.2.2 Data Augmentation
The imbalance in the class distribution may incen-
tivize the models to be overconfident about the major-
ity class, leading to inferior accuracy. Synthetic Mi-
nority Oversampling Technique (Chawla et al., 2002)
is a popular way to improve class balance without dis-
carding samples from the majority class. SMOTE is
most effective in scenarios where the each documents
is represented as a bag of words, or TF-IDF, where
the order of tokens is immaterial. While it is possi-
ble to apply SMOTE on the flattened embedding se-
quence representation, it is computationally intensive,
and the curse of dimensionality leads to diminishing
returns. In scenarios where the documents are repre-
sented using word/token embeddings, the generation
of synthetic data points is only possible in the embed-
ding space (or in a feature space that follows the em-
bedding step). We applied white noise to the embed-
ded sequences corresponding to minority class data
points within the training loop rather than before the
loop.
The benefit of this technique is two-fold. It al-
lows us to dynamically produce synthetic data points
in the embedding space without having to consume
disk space or memory for concurrent storage of all
synthetic data points. The other advantage is that
it allows batches to have nearly uniform class dis-
tributions, which yields more consistent loss values,
and consequently, consistent weight updates across
batches. Stratified batching (Chawla et al., 2002) en-
sures that each mini-batch represents the distribution
of classes in the dataset, which can be particularly
useful for imbalanced datasets.
4.2.3 Batch Formation
Mini-batches are stratified based on the class labels of
the samples. This stratification is achieved by ensur-
ing the training dataset has a predetermined, almost
ICAART 2025 - 17th International Conference on Agents and Artificial Intelligence
682

common class distribution in every subsequence of 8
rows. The first 3 entries are of the majority class, fol-
lowed by 5 entries from the 4 minority classes, with
each minority class having at least 1 entry, and at
most, 2 entries.
4.2.4 Selective Generation of Noisy Duplicates
Every batch of 8 data points is first encoded and em-
bedded. The embedding tensors from the minority
classes are multiplied by a so-called noise tensor of
the same shape to synthesize new data points. The
noise tensor contains floating point values between
0.99 and 1.01. Since there are five classes, the first
objective is to iteratively synthesize data points from
the minority class until each of the five classes has
three data points, which amounts to 15 data points.
A non-synthetic data point from any of the classes is
then chosen at random and multiplied with the noise
tensor to synthesize an additional data point to arrive
at a batch size of 16.
4.2.5 Gradient Accumulation
Hardware limitations in the experiment setup pre-
cluded the possibility of sufficiently large training
batch sizes for some models. As a consequence, the
regularizing effect of large batch sizes had to be sim-
ulated using gradient accumulation. The weight up-
date operation was performed after every 4 forward
passes, which allowed simulating a batch size of 16,
while gradients were computed with a batch size of 4.
4.2.6 Validation
After each epoch, the models were validated against
a uniformly distributed validation dataset, which was
disjoint from the training dataset. The validation loss
and accuracy were computed. The validation loss,
along with training loss, was used to make decisions
on whether to continue or terminate the training pro-
cess. In an alternate version of the training loop,
the validation loss was also used to determine which
model checkpoint to fine-tune, after comparing the
validation losses obtained from multiple epochs. The
metrics listed above were also updated on the console
to enable informed manual intervention, if necessary.
4.3 Inference of Individual Models
The inference of the models was performed on a test
dataset which contained 6730 data points, with a uni-
form class distribution, which contained no overlap
with the training data. The test dataset did not con-
tain any synthetic data points. This ensures that the
test dataset is able to benchmark how well the model
generalizes. The test dataset also did not contain any
overlap with the validation dataset, since some of the
model training decisions were dependent on the vali-
dation loss, and in turn, the validation dataset itself.
5 RESULTS AND OBSERVATIONS
The performance of the the individual models as well
as that of the ensemble was compared with the per-
formance of the state-of-the-art BERT model featured
on the kaggle dataset page. The reported accuracy for
the fine-tuned BERT model featured in the notebook
on the kaggle dataset page, was 84.13%.
5.1 Individual Model Benchmark
Results
RoBERTa, DistilBERT and ALBERT exhibit simi-
lar performance across all classes, except Credit re-
porting, as can be observed in Table 4 and Table
5. RoBERTa and DistilBERT also exhibit relatively
lower precision when predicting Credit reporting,
which happens to be the majority class. On the flip-
side, ALBERT seems to exhibit lower recall for the
same class. The overall F-scores of RoBERTa-base,
DistilBERT and ALBERT were similar to one an-
other, as can be observed in Table 6. It is worth not-
ing that ALBERT, with just 11.8 million parameters,
was able to match the efficacy of RoBERTa, which
is over 10 times as large, at 125 million parameters,
and marginally outperform DistilBERT, which has 67
million parameters.
GTE-large, which at 434 million parameters
is about one-sixteenth the size of Mistral-7B and
MiniGPT4-7B, consistently outperforms the larger
models across nearly all classes. This may be at-
tributed to the fact that Mistral and MiniGPT are
decoder-only models, which are better suited for
generative tasks as opposed to encoder-only models
which tend to be better at discriminative tasks. The
sheer size and architectural complexity of the larger
models may also have made them more prone to over-
fitting.
Table 4 provides details about the number of true
positives, false positives and false negatives for each
class, for each of the models. These statistics were
used to generate the F-scores and other metrics in Ta-
ble 5 and Table 6.
Classification of Complaints Text Data by Ensembling Large Language Models
683

Table 4: All model and ensemble classification statistics, class-wise. Support for each class was 1346. Mortg. = Mortgages,
TP = True Positives, FP = False Positives, FN = False Negatives, PV = Argmax-of-Product Ensemble (Vanilla), PR = Argmax-
of-Product Ensemble (Reinterpreted), AR = Analytic Hierarchy Process Ensemble (Reinterpreted), AV = Analytic Hierarchy
Process Ensemble (Vanilla).
Credit Card Credit reporting Debt collection Mortg. and loans Retail Banking
Model TP FP FN TP FP FN TP FP FN TP FP FN TP FP FN
RoBERTa 1060 117 286 1210 372 136 1112 154 234 1211 142 135 1221 131 125
DistilBERT 1092 150 254 1197 386 149 1091 147 255 1149 92 197 1255 171 91
ALBERT 1092 174 254 1128 236 218 1130 177 216 1197 153 149 1256 187 90
GTE 1233 186 113 1116 184 230 1146 161 200 1208 137 138 1269 90 77
Mistral 1146 191 200 1099 233 247 1128 194 218 1228 142 118 1239 130 107
MiniGPT 1183 215 163 1148 285 198 1084 142 262 1213 124 133 1231 105 115
PV-SLM 1099 136 247 1185 327 161 1119 145 227 1196 124 150 1252 147 94
AV-SLM 1095 126 251 1189 320 157 1115 141 231 1196 117 150 1268 163 78
PR-SLM 1143 173 203 1123 216 223 1151 177 195 1218 158 128 1240 131 106
AR-SLM 1136 170 210 1120 205 226 1156 176 190 1226 157 120 1244 140 102
PV-LLM 1195 181 151 1137 228 209 1126 149 220 1225 129 121 1257 103 89
AV-LLM 1194 187 152 1135 233 211 1125 140 221 1224 129 122 1256 107 90
PR-LLM 1223 155 123 1123 163 223 1166 164 180 1236 137 110 1278 85 68
AR-LLM 1210 152 136 1120 155 226 1165 167 181 1239 131 107 1288 103 58
Table 5: All model metrics, class-wise. P = Precision, R = Recall.
Credit Card Credit reporting Debt collection Mortg. and loans Retail Banking
Model P R F1 P R F1 P R F1 P R F1 P R F1
RoBERTa 0.90 0.79 0.84 0.76 0.90 0.83 0.88 0.83 0.85 0.90 0.90 0.90 0.90 0.91 0.91
DistilBERT 0.88 0.81 0.84 0.76 0.89 0.82 0.88 0.81 0.84 0.93 0.85 0.89 0.88 0.93 0.91
ALBERT 0.86 0.81 0.84 0.83 0.84 0.83 0.86 0.84 0.85 0.89 0.89 0.89 0.87 0.93 0.90
GTE 0.87 0.92 0.89 0.86 0.83 0.84 0.88 0.85 0.86 0.90 0.90 0.90 0.93 0.94 0.94
Mistral 0.86 0.85 0.85 0.83 0.82 0.82 0.85 0.84 0.85 0.90 0.91 0.90 0.91 0.92 0.91
MiniGPT 0.85 0.88 0.86 0.80 0.85 0.83 0.88 0.81 0.84 0.91 0.90 0.90 0.92 0.91 0.92
PV-SLM 0.89 0.82 0.85 0.78 0.88 0.83 0.89 0.83 0.86 0.91 0.89 0.90 0.89 0.93 0.91
AV-SLM 0.90 0.81 0.85 0.79 0.88 0.83 0.89 0.83 0.86 0.91 0.89 0.90 0.89 0.94 0.91
PR-SLM 0.87 0.85 0.86 0.84 0.83 0.84 0.87 0.86 0.86 0.89 0.90 0.89 0.90 0.92 0.91
AR-SLM 0.87 0.84 0.86 0.85 0.83 0.84 0.87 0.86 0.86 0.89 0.91 0.90 0.90 0.92 0.91
PV-LLM 0.87 0.89 0.88 0.83 0.84 0.84 0.88 0.84 0.86 0.90 0.91 0.91 0.92 0.93 0.93
AV-LLM 0.86 0.89 0.88 0.83 0.84 0.84 0.89 0.84 0.86 0.90 0.91 0.91 0.92 0.93 0.93
PR-LLM 0.89 0.91 0.90 0.87 0.83 0.85 0.88 0.87 0.87 0.90 0.92 0.91 0.94 0.95 0.94
AR-LLM 0.89 0.90 0.89 0.88 0.83 0.85 0.87 0.87 0.87 0.90 0.92 0.91 0.93 0.96 0.94
Table 6: All model overall metrics. The test dataset size was 6730.
Classified Misclassified Micro-F1 Macro-F1 Weighted average F1
RoBERTa 5814 916 0.864 0.864 0.864
DistilBERT 5784 946 0.859 0.860 0.860
ALBERT 5803 927 0.862 0.862 0.862
GTE 6043 692 0.887 0.887 0.887
Mistral 5840 890 0.868 0.868 0.868
MiniGPT 5859 871 0.871 0.871 0.871
PV-SLM 5851 879 0.869 0.870 0.870
AV-SLM 5863 867 0.871 0.871 0.871
PR-SLM 5875 855 0.873 0.873 0.873
AR-SLM 5882 848 0.874 0.874 0.874
PV-LLM 5940 790 0.883 0.883 0.883
AV-LLM 5934 796 0.882 0.882 0.882
PR-LLM 6026 704 0.895 0.895 0.895
AR-LLM 6022 708 0.895 0.894 0.894
ICAART 2025 - 17th International Conference on Agents and Artificial Intelligence
684

5.2 Ensemble Results
All of the above models yielded, on their own, bet-
ter results than the BERT model. However, accuracy
was improved further by reinterpreting the confidence
scores while ensembling the models, as can be ob-
served in Table 6.
The ensemble of large language models (GTE-
large-en v1.5, Mistral-7B and MiniGPT4-7B) af-
ter reinterpretation of confidence scores, is able to
achieve an accuracy of 89.5%, which is 1.2 percent-
age points better than the vanilla ensemble accuracy
of 88.3%. Note that the vanilla ensemble of the large
language models gave slightly lower accuracy than
GTE-large on its own, which gave 88.7% accuracy.
The ensemble of the smaller language models
(RoBERTa-base, DistilBERT, and ALBERT) also
benefited slightly, with accuracy gaining 0.4 percent-
age points due to the reinterpretation, when using the
argmax-of-product strategy. The reinterpretation im-
proved the AHP Ensemble accuracy by 0.3 percent-
age points.
6 CONCLUSION
The reinterpretation of confidence scores based on
precision as a function of confidence scores, improved
the performance of the ensemble of large language
models by 1.2 percentage points, as can be seen in
the difference between the F-scores of PV-LLM and
PR-LLM in Table 6.
The reinterpretation also had a small positive im-
pact of 0.4 percentage points, on the accuracy of the
ensemble of smaller language models, as can be in-
ferred from the difference between the F-scores of
PV-SLM and PR-SLM in Table 6.
This shows that precision as a function of confi-
dence score is an insightful metric for an ensemble. It
quantifies reliability of model predictions, facilitating
more informed decisions on which prediction to trust.
It gives an edge over simply using the softmax scores
reported by the models to obtain a verdict.
7 LIMITATIONS
The performance of the models, and that of the en-
sembles, was restricted by many factors, including,
but not limited to the dated and primitive method of
data augmentation through addition of noise. SMOTE
is the most-preferred data augmentation method in re-
cent literature pertaining to language models and ma-
chine learning.
The decision to experiment with the addition of
white noise was taken in view of limited VRAM,
which precluded the possibility of SMOTE when
working with a sufficiently large sequence length.
The lack of a comprehensive strategy to tackle class
imbalance may be a limiting factor in this work.
Another limitation is the need for a large portion
of the dataset to be reserved for the development of
the ensemble strategy. The mapping of confidence
scores to class incidence probabilities needs a large
sample size for the reinterpretations to be statistically
significant.
REFERENCES
Chawla, N. V., Bowyer, K. W., Hall, L. O., and Kegelmeyer,
W. P. (2002). Smote: Synthetic minority over-
sampling technique. Journal of Artificial Intelligence
Research, 16:321–357.
Devlin, J., Chang, M., Lee, K., and Toutanova, K. (2018).
BERT: pre-training of deep bidirectional transformers
for language understanding. CoRR, abs/1810.04805.
Dodge, J., Ilharco, G., Schwartz, R., Farhadi, A., Hajishirzi,
H., and Smith, N. (2020). Fine-tuning pretrained lan-
guage models: Weight initializations, data orders, and
early stopping.
Doering, N., Gorlla, C., Tuttle, T., and Vijay, A. (2024).
Empirical analysis of efficient fine-tuning methods for
large pre-trained language models.
Hinton, G., Vinyals, O., and Dean, J. (2015). Distilling the
knowledge in a neural network.
Jiang, A. Q., Sablayrolles, A., Mensch, A., Bamford,
C., Chaplot, D. S., de las Casas, D., Bressand, F.,
Lengyel, G., Lample, G., Saulnier, L., Lavaud, L. R.,
Lachaux, M.-A., Stock, P., Scao, T. L., Lavril, T.,
Wang, T., Lacroix, T., and Sayed, W. E. (2023). Mis-
tral 7b.
Lan, Z., Chen, M., Goodman, S., Gimpel, K., Sharma, P.,
and Soricut, R. (2020). Albert: A lite bert for self-
supervised learning of language representations.
Li, J., Li, D., Savarese, S., and Hoi, S. (2023). BLIP-
2: Bootstrapping language-image pre-training with
frozen image encoders and large language models. In
Krause, A., Brunskill, E., Cho, K., Engelhardt, B.,
Sabato, S., and Scarlett, J., editors, Proceedings of the
40th International Conference on Machine Learning,
volume 202 of Proceedings of Machine Learning Re-
search, pages 19730–19742. PMLR.
Liu, Y., Ott, M., Goyal, N., Du, J., Joshi, M., Chen, D.,
Levy, O., Lewis, M., Zettlemoyer, L., and Stoyanov,
V. (2019). Roberta: A robustly optimized bert pre-
training approach.
Reynolds, L. and McDonell, K. (2021). Prompt program-
ming for large language models: Beyond the few-shot
paradigm.
Saaty, T. L. (1990). How to make a decision: The analytic
hierarchy process. European Journal of Operational
Classification of Complaints Text Data by Ensembling Large Language Models
685

Research, 48(1):9–26. Desicion making by the ana-
lytic hierarchy process: Theory and applications.
Touvron, H., Martin, L., Stone, K., Albert, P., Almahairi,
A., Babaei, Y., Bashlykov, N., Batra, S., Bhargava,
P., Bhosale, S., Bikel, D., Blecher, L., Ferrer, C. C.,
Chen, M., Cucurull, G., Esiobu, D., Fernandes, J., Fu,
J., Fu, W., Fuller, B., Gao, C., Goswami, V., Goyal,
N., Hartshorn, A., Hosseini, S., Hou, R., Inan, H.,
Kardas, M., Kerkez, V., Khabsa, M., Kloumann, I.,
Korenev, A., Koura, P. S., Lachaux, M.-A., Lavril, T.,
Lee, J., Liskovich, D., Lu, Y., Mao, Y., Martinet, X.,
Mihaylov, T., Mishra, P., Molybog, I., Nie, Y., Poul-
ton, A., Reizenstein, J., Rungta, R., Saladi, K., Schel-
ten, A., Silva, R., Smith, E. M., Subramanian, R.,
Tan, X. E., Tang, B., Taylor, R., Williams, A., Kuan,
J. X., Xu, P., Yan, Z., Zarov, I., Zhang, Y., Fan, A.,
Kambadur, M., Narang, S., Rodriguez, A., Stojnic, R.,
Edunov, S., and Scialom, T. (2023). Llama 2: Open
foundation and fine-tuned chat models.
Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J.,
Jones, L., Gomez, A. N., Kaiser, L., and Polo-
sukhin, I. (2017). Attention is all you need. CoRR,
abs/1706.03762.
Vatsal, S. and Dubey, H. (2024). A survey of prompt engi-
neering methods in large language models for differ-
ent nlp tasks.
Wolf, T., Debut, L., Sanh, V., Chaumond, J., Delangue, C.,
Moi, A., Cistac, P., Rault, T., Louf, R., Funtowicz,
M., and Brew, J. (2019). Huggingface’s transformers:
State-of-the-art natural language processing. CoRR,
abs/1910.03771.
Zhang, X., Zhang, Y., Long, D., Xie, W., Dai, Z., Tang, J.,
Lin, H., Yang, B., Xie, P., Huang, F., Zhang, M., Li,
W., and Zhang, M. (2024). mgte: Generalized long-
context text representation and reranking models for
multilingual text retrieval.
Zheng, L., Chiang, W.-L., Sheng, Y., Zhuang, S., Wu, Z.,
Zhuang, Y., Lin, Z., Li, Z., Li, D., Xing, E. P., Zhang,
H., Gonzalez, J. E., and Stoica, I. (2023). Judging
llm-as-a-judge with mt-bench and chatbot arena.
Zhu, D., Chen, J., Shen, X., xiang Li, and Elhoseiny, M.
(2023). Minigpt-4: Enhancing vision-language under-
standing with advanced large language models.
References without a specified journal/conference are from
arxiv.org, and cited using the BibTeX citation featured on
the abstract page.
ICAART 2025 - 17th International Conference on Agents and Artificial Intelligence
686