SIR SQL for Logical Navigation and Calculated Attribute Free

Queries to Base Tables

Witold Litwin

University Paris Dauphine, PSL, France

Keywords: Relational Database Model, SQL, Stored and Inherited Relations.

Abstract SIR SQL stands for SQL with Stored and Inherited Relations (SIRs). Every SIR SQL Create Table makes

definable any base attributes one could have in an SQL Create Table at present. In addition, one can define

inherited attributes (IAs), definable in SQL queries or views only up to now. One may also define foreign

keys (FKs) that are SQL ones or logical pointers in Codd’s original sense. IAs in SIRs with Codd’s FKs

usually provide for logical navigation free (LNF) queries, i.e., without equijoins on FKs and referenced keys.

The same outcome SQL queries to the same base tables without IAs, must include LN avoided.

SIR SQL Create Table may in particular include IAs definable through value expressions also possible in

SQL queries or views only up to now, usually referred to as calculated attributes (CAs). CAs may involve,

e.g., attributes from different tables or aggregate functions, or sub-queries. CAs in SIRs provide for CAF

queries, addressing any CAs in SIRs by name only. In contrast, every SQL query to base tables needing

CAs has to fully define each of these.

The end result is that most of SQL base table queries, requiring LN or CAs schemes at present, become

LNF or CAF queries in SIR SQL. The latter are usually substantially less procedural, i.e., by dozens of

characters. They become also quasi-natural, i.e., with Select clause only naming the selected attributes,

From clause naming a single base table and Where clause, if any, with short Boolean formulae over usual

constraints on some attribute values, at worst. SIR SQL should accordingly significantly boost SQL clients’

productivity. Especially, since most clients are data analysts or application developers, not SQL geeks.

While the problematic of LNF and CAF queries is four decades old, our solution is the first practical one, to

our best knowledge.

Below, we illustrate the problem of LN and of CAs in queries to SQL base tables using Codd’s original

Supplier-Part DB. We then present SIR SQL. We show in depth how SIR SQL LNF and CAF queries to

base tables become possible. We show in particular that Create Table statements defining an SQL DB at

present, usually define also a SIR SQL DB, providing for LNF queries to base tables as free bonus. We

discuss the front-end for SIR SQL that should require, for any popular SQL DBS, a few month

implementation efforts only, validated by proof-of-concept prototype for SQLite3. We accordingly postulate

to upgrade every popular SQL DBS to SIR SQL. 7+ million SQL clients worldwide, of the dominant DB

language, providing for 31B+ US$ market size of SQL apps, will benefit from.

1 THE PROBLEM

Since their inception, five decades ago for the

pioneers, all present SQL DBSs bother the clients,

users and developers, with parts of most of queries

to the base tables, necessary beyond the otherwise

quasi-natural formulation of such queries. The latter

consists of Select with some attributes of a single

base table named in From clause, called addressed

by the query and of Where clause, if any, with, at

worst, short Boolean formulae over usual constraints

on some attributes, e.g., A < 100 And A ≥ 50. The

1st culprit for those cumbersome parts is the logical

navigation (LN) in queries to base tables with

foreign keys and to the referenced tables. Recall that

the term LN or LN joins means equijoins on foreign

and referenced keys, as Codd originally defined

these terms in (Codd, 1978) and results from Codd’s

sheer idea of a foreign key (FK). Actually, the latter

seems implying that for every FK, the LN involving

(or from) the FK, in particular preserves every value

of the FK. I.e., LN always expresses a semi join,

reducing to the inner one, if one wishes so, iff FK

Litwin, W.

SIR SQL for Logical Navigation and Calculated Attribute Free Queries to Base Tables.

DOI: 10.5220/0013199900003929

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 27th International Conference on Enterprise Information Systems (ICEIS 2025) - Volume 1, pages 191-201

ISBN: 978-989-758-749-8; ISSN: 2184-4992

191

respects the referential integrity (RI). The

procedurality that the LN implies, i.e., the necessary

length (number of characters) of the SQL join

clauses defining it, usually adds at least dozens of

characters to the query without. This makes

accordingly, at least linearly, longer query writing

and debugging times. Especially, - when the joins

are the outer ones, (Date, C., J., Darwen, H., 1991).

Not surprisingly, clients usually at least dislike the

LN. In short, queries to base tables requiring LN at

present should possibly be LNF instead.

Figure 1. S_P database.

The 2nd culprit is the impossibility for any SQL

dialect at present, to declare base tables with the

calculated attributes (CAs), defined by value

expressions with, e.g., aggregate functions or sub-

queries or sourced in other tables. If a CA a query

needs could be in the base table, the query could

address it by name only, i.e., the query could be

CAF. Since it cannot be so for any CAs at present,

SQL clients must define the specs of any of those in

the queries. The increase to the query procedurality

may be substantial, e.g., by dozens of characters to

type-in at least. The sheer complexity of some CAs,

those defined by sub-queries especially, also bothers

many, implying particularly careful debugging.

E.g., consider Supplier-Part DB of Codd, Figure

1, the “mother of all the relational DBs”, (Codd,

1978), (Date, 2006). In other words, Supplier-Part

design principles are the ones of most of DBs at

present and properties shown by our examples below

generalize accordingly. We refer to Supplier-Part as

to S_P DB in short. S, P, SP are 1NF stored relations,

(SRs), also called base tables. For Codd, SR means

that none of its stored attributes, (SAs), can be

calculated using the DB scheme and content. Next,

S.S#, P.P# and SP(S#,P#) are the primary keys

(PKs). Finally SP.S# and SP.P# are foreign keys

(FKs) for Codd, originally, (Codd, 1978). I.e., each

is the “logical pointer” to the (unique in S_P) PK

with the same name and, for every FK value, to the,

unique in the referenced table and thus in S_P, tuple

with the same PK value, whenever such a tuple

exists.

A query searching for every supply so and so…

in practice, would most of time address some of SP

attributes together with some attributes of S or P in

its Select and Where clauses. The rationale is that all

the non-key SAs of S and P are conceptual attributes

of SP as well. They should be also SAs of SP. They

are actually not. The normalization anomalies for SP

that would follow and that we discuss more below

are indeed unacceptable for the relational model.

E.g. consider a query searching for the basic data

of smaller supplies, say Q1: “For every supply in

QTY <= 200”, select S#, with SNAME whenever

known, then P# with, also whenever known,

PNAME, and QTY. Q1 could simply formulate in

SQL as:

(Q1) Select S#, SNAME, P#, PNAME, QTY From

SP Where QTY < 200;

Q1 expresses only the necessary projection and

restriction and is, for many, a telegraphic style, but

quasi-natural (language) query. It would suffice if

SNAME and PNAME were attributes of SP.

However, they are not. Hence, Q1 formulates at

present as Q2 below or with an equivalent From

clause, regardless of SQL dialect used:

(Q2) Select S#, SNAME, P#, PNAME, QTY From

SP Left Join S On SP.S#=S.S# Left Join P On

SP.P#=P.P# Where QTY < 200;

The reason is that whatever SP tuple Q1 selects,

nothing in S_P scheme indicates SNAME &

PNAME values Q1 should reference through the

foreign keys, when these values exist. The LN in Q2

does it therefore instead. The “price” is that Q2

becomes twice as procedural and anything, but a

quasi-natural language query.

Next, in practice, every supply has obviously

some weight, say T_WEIGHT, defined as QTY *

WEIGHT, where WEIGHT value is the one

referenced through SP.P# value of the supply, if it is

in P. If T_WEIGHT was of interest to clients and

obviously it would often be in practice, it should be

a CA of SP. Then, e.g., query Q3 providing the ID

and T_WEIGHT of every supply could simply be:

(Q3) Select S#,P#,T_WEIGHT From SP;

Q3 would be a CAF query, with respect to

T_WEIGHT and LNF query with respect to P.

However, as even SQL beginners know,

T_WEIGHT cannot be a CA of SP for any popular

SQL dialect. Hence one has to express Q3 as Q4

with the T_WEIGHT scheme in it, e.g.:

(Q4) Select S#,P#, QTY * WEIGHT As

T_WEIGHT From SP Left Join P On SP.P# = P.P#;

ICEIS 2025 - 27th International Conference on Enterprise Information Systems

192

As one can see, Q4 is more than twice more

procedural than Q3.

Recall finally that the problematic of LNF and of

CAF queries to base tables is anything but new.

Already in early 80ties, Maier & Ullman proposed

the, so-called, universal relation as a solution for the

LNF queries. However, despite its initial popularity,

the concept did not prove practical as yet. For the

CAF queries, Sybase SQL dialect introduced, also in

early 80ties, the virtual (dynamic, computed,

generated….) attributes (VAs). Several other SQL

dialect adopted VAs since. Nevertheless, the result

was and remains only a partial solution, E.g.,

T_WEIGHT cannot be a VA in any SQL dialect we

are aware of. We discuss VAs more later on.

Besides, for decades there were sporadic

proposals for DBs with 1NF only base tables,

including all the conceptual base table attributes we

spoke about, hence providing for LNF queries. None

made to practice, obviously outweighed by

inconveniences of normalization anomalies.

Likewise, it was always known that one may hide

normalized base tables behind multiple

denormalized views providing for LNF and CAF

queries. This approach did not make it neither. Sheer

number of Create View statements necessary to

type-in with multiple replications of base attribute

names, as well as problematic maintenance of views

in sync with alterations to base tables, about always

outweigh the advantages to queries. Altogether, the

problem of a DB supporting LNF and CAF queries

to base tables remained open.

2 OUR SOLUTION

2.1 Overview

The idea is that, since queries to base tables should

be LNF and CAF, for every base table R with

(Codd’s) FKs, for which queries could address some

attributes of R or some referenced through an LN, or

some CAs, Create Table R should predefine the

name of every such attribute and every LN defining

its values. Likewise, every Create Table R should

predefine every CA considered as (conceptual)

attribute of R. The tricky issue is that none of these

additional (pre)definitions should imply any

normalization anomalies in R, with respect to the

existing NF of R. This said, everything that follows

is mere technical details, intended to make the

proposed solution the most practical.

Notice upfront that trivial SAs cannot help, as

pointed out earlier for S_P. Observe also that all the

names of the predefined attributes, as well as all the

LN clauses should possibly be implicit in Create

Table R as issued by the database administrator

(DBA). For every FK in Codd’s sense, all the names

logically pointed to should indeed be already in SQL

meta-tables. One can also easily infer the LN clause

whenever an FK is an SQL one or, is a so-called

primary key named SIR SQL (specific) FK, as we’ll

show. Every statement should then be reasonably,

i.e., within the general SQL framework, the least

procedural for DBA. In particular, - avoiding in this

way errors in otherwise manually copied names or in

LN clauses and the waste of time for their eventual

debugging. Dedicated pre-processing may then add

to the Create Table every missing attribute name and

the LN, for any further processing. Notice finally

that if all the attributes to be predefined and all such

LN clauses are implicit in a Create Table issued by

DBA without any CAs, then any such Create Table

formulates simply as some present one. In other

words, DBA creates then base tables supporting

LNF queries without any additional work with

respect to the one required from DBA at present, to

create “only” base tables without that capability.

From now on, we introduce SIR SQL through the

following steps, described in “for dummies” form.

We published some details separately already, in

depth impossible here within the space limits.

Especially in (Litwin, 2022) that references in turn

main earlier related papers. Our home page, (Litwin,

2025), indexes all our related papers, by title and

abstract at least. The pdf is the bonus, whenever not

copyrighted. There is also ppt for conference papers.

2.2 SIR SQL

SIR SQL stands for SQL supporting Stored &

Inherited Relations (SIRs). SIR construct in general

was largely discussed in our previous papers. For

SIR SQL, any SIR R is simply a 1NF base table R

consisting of some SQL base table enlarged with

IAs, definable as in an SQL Create View or query

only up to now. The SQL table within R bears its

own implicit (default) name R_ and constitutes the

base of R. The name R_ is available to any SIR SQL

statement, as if R_ was stand-alone.

We refer to the attributes of R_ as to base

attributes (BAs) of R. We also refer to the definition

of the IAs within any SIR R as to Inheritance

Expression (IE). With respect to SQL Create Table,

SIR SQL Create Table provides accordingly the

usual SQL Create Table capabilities for R_ and

additional ones for the IE. The latter are basically as

in SQL Create View or queries only at present.

SIR SQL for Logical Navigation and Calculated Attribute Free Queries to Base Tables

193

Likewise, SIR SQL provides for a more general

Alter Table statement. All the other SIR SQL

statements are simply the SQL statement. For most

of the latter, the processing differs however from

their SQL counterparts, as it will appear.

An IE defines every IA A in the attribute list of

SIR SQL Create Table as one can do for A in the

attribute least of an SQL query or view. I.e., A can

have the name of an attribute in the table defined by

From clause or can alias such an attribute or can be a

value expression over some such names or can be a

sub-query… In every case except the 1

one, for SIR

SQL, we qualify A of CA. Some IAs in the list may

also result from the generic SQL ‘*’ character.

While IE attribute list can thus be as in any queries

or views, IE is in contrast, limited with respect to the

two other clauses of an SQL query or view, i.e.,

From and Where clauses. Every From clause should

indeed either be simple From R_ or a sequence of

left or right or inner joins, each on some BA,

perhaps composite, and a key attribute of usually

other table. These joins should further be such that

(i) for every R_ tuple t, there is in the table defined

by From clause, say T, exactly one tuple t’ with t as

a sub-tuple and (ii) T does not have any other tuples.

We will recall the rationale for these assumptions in

what follows.

We qualify From clause in SIR SQL Create Table

formed as above of valid. Otherwise it is invalid. We

also refer to the joins expressed within as to SIR

SQL (predefined) LN (joins). In practice these joins

should be indeed the ones we spoke about. I.e., they

predefine SIR SQL LN (joins) that would be

typically required by SQL queries (at present) if they

addressed the same base tables without IE.

Furthermore, whenever R is a SIR, BAs together

with the table constraints and options form R_

scheme.

Next, in every SIR SQL Create Table R, if there

is any From clause, it then follows the (entire)

attribute list with BAs and IAs and precedes every

eventual table constraint or option. Besides,

whenever Create Table R defines any part of IE, i.e.,

some consecutive IAs or From clause, every such

part should be separated from any of R_ SQL specs

by { } brackets. Each bracket replaces a usual SQL

separator, i.e., ‘,’ or space. IAs may be spread

among BAs or separated by Bas from From clause,

hence more than one pair of { } may be necessary.

The convention facilitates the parsing of the SIR

SQL Create Table statement, as it appeared.

Ex. Suppose S_P.SP declared through the SQL

Create Table of some SQL dialect, e.g., SQLite

SQL:

(1) Create Table SP (S# TEXT, P# TEXT, QTY INT

Primary Key (S#, P#));

Consider then Create Table SP formulated as

follows:

(2) Create Table SP (S# TEXT, P# TEXT, QTY INT

{WEIGHT*QTY As T_WEIGHT, SNAME,

STATUS, S.CITY, PNAME, COLOR, WEIGHT,

P.CITY, From SP_ Left Join S On SP.S#=S.S# Left

Join P On SP.P#=P.P#} Primary Key (S#, P#));

Create Table (2) is a SIR SQL one only, i.e.

impossible to formulate in any present SQL dialect.

It defines SIR SP enlarging SP (1) with IAs defined

within. The attributes and the (only) table constraint

of (1) within (2), define the base SP_. IE is entirely

within a single pair of { }. Also as required, From

clause follows the entire attribute list and precedes

the only SP table constraints that is the Primary Key

constraint.

Let us call S_P1 the DB with S, P and SP (2).

Figure 2, placed at the end of the text, shows

S_P1.SP scheme and content for SIR SQL clients,

given Figure 1. We underlined every key attribute

(and only such attributes), as usual. IAs are italics.

From clause in (2) is valid. Indeed it is first clearly

so for any SP tuple at Figure 2. SP tuples in Figure 1

however implicitly respect the referential integrity

(RI) between SP and S, and P. So does every tuple at

Figure 2.

However, neither in (1) nor in (2) there are no FK

table constraints, as for SP in (Codd, 1978) besides.

Hence, RI is not enforced. One may thus insert to

SP_ (S6, P1, 200). Since the LN in From clause of

(2) consists of left outer joins, the table in SP (2)

From clause would contain one and only one tuple

(S6, P1, 200, null, null, null, null, P1, Nut…). One

may easily see also that this property generalizes to

any tuple breaking the IR with respect to S or P.

The discussed table would not contain further any

more tuples than these resulting from inserts to SP_.

From clause in (2) is thus a valid one. In contrast,

any From clause for SP (2) with any inner join

instead of the outer one, would not fit. The latter

would make From clause valid iff the RI was

enforced. Notice that the outer join expression

would remain valid then anyhow.

Next, observe that the LNF Q1 applies to SP (2).

It is also so for the CAF Q3. The rationale is of

course the presence of the IAs in (2). As the values

of these are calculated only, none of these IAs can

ever create any normalization anomalies, i.e., insert,

update, delete or storage anomalies. These

anomalies would in contrast necessarily occur, if any

of IAs of S_P1.SP was trivially, an SA, as Codd’s

model requires for every BA. Recall that the

ICEIS 2025 - 27th International Conference on Enterprise Information Systems

194

Table S Table P

S# SNAME STATUS CITY P#

PNAME COLOR WEIGHT CITY

S1 Smith 20 London P1 Nut Re

12 London

S2 Jones 10 Paris P2 Bolt Green 17 Paris

S3 Blake 30 Paris P3 Screw Blue 17 Oslo

S4 Clar

20 London P4 Screw Re

14 London

S5 Adams 30 Athens P5 Ca

Blue 12 Paris

P6 Co

19 London

Table SP

P# QTY

-WEIGHT SNAME STATU

S. CITY PNAME COLOR WEIGHT P.CITY

S1 P1 300 3600 Smith 20

ondon

ed 12

ondon

S1 P2 200 3400 Smith 20

ondon

olt Green 1

Paris

S1 P3 400 6800 Smith 20

ondon Screw

lue 1

Oslo

S1 P4 200 2800 Smith 20

ondon Screw

ed 14

ondon

S1 P5 100 1200 Smith 20

ondon Cam

lue 12 Paris

S1 P6 100 1900 Smith 20

ondon Cog

ed 19

ondon

S2 P1 300 3600

ones 10 Paris

ut 12

ondon

S2 P2 400 6800

ones 10 Paris

olt

olt 1

Paris

S3 P2 200 3400

lake 30 Paris

olt Green 1

Paris

S4 P2 200 3400 Clark 20

ondon

olt Green 1

Paris

S4 P4 300 4200 Clark 20

ondon Screw Screw 14

ondon

S4 P5 400 4800 Clark 20

ondon Cam

lue 12 Paris

Figure 2: S-P1 base tables and content. IAs are in italics. IAs content is virtual only. S and P are as in Figure 1.

relational model prohibits the anomalies because of

the annoying side-effects. E.g., in SIR SP, the

redundant with respect to S and P IA values in SP,

e.g., in 6 tuples for SP.S# = ‘S1’ there, Figure 1, do

not cost any additional storage, while they would

obviously do, if they were SAs. Likewise, SP does

not need any updates if a source value varies, e.g.,

S1 name changes to ‘John’, again unlike for the

“trivial” choice. Finally, the latter could in particular

lead to hidden inconsistencies, if a redundant data

manipulation goes awry. E.g., if WEIGHT changes,

but (SA) T_WEIGHT does not for any reasons. Or,

if one inserts tuple (S2, P3, Bolt, Green…), (guess

why?). All these properties of IAs generalize to any

DBs with SIRs. “Better late than never”, through

IAs in base tables, the SIR construct lifts an

intriguing limitation in Codd’s model, (Codd, 1978).

Observe next that S_P1.SP defined by (2),

contains by name and value with respect to S.S# or

P.P#, i.e., the source PKs, every attribute of S_P.

Easy to see thus that not only Q1 formulates as the

substantially less procedural LNF Q2, but that, more

generally, any query Q addressing any attributes of S

or of P through some LN with, perhaps, any

attributes of S_P.SP, formulates as a substantially

less procedural LNF Q’ to S_P1.SP. As for Q1 and

Q2, Q’ consists simply of Q without LN, with,

perhaps, CITY prefixed with S or P, instead of the

non-prefixed one in Q.@

We qualify of explicit every SIR SQL Create

Table R defining every IA and From intended for R

as above discussed. E.g., (2) can be the explicit

Create Table SP for S_P1. We also call then explicit,

IE, IAs, IA list and From clause, e.g., within (2).

Besides, as it will appear, SIR SQL Create Table lets

DBA to omit parts of even entire IE. We speak then

about implicit Create Table, IE…. We qualify of

empty an entirely omitted IE. As it will appear, in

practice, an implicit Create Table should be always

substantially less procedural than the explicit one.

More in depth, a Create Table is implicit iff it (i)

contains any SIR SQL FK qualified in next section

of already mentioned PKN FK or (ii) contains only

some CAs, including IAs simply aliased, but neither

has From clause nor PKN FKs, or (iii) contains SIR

SQL specific generic character ‘#’. Whenever there

is an implicit Create Table for an explicit one, the

DBA is (obviously) expected to take advantage of

the former. Accordingly, every submitted SIR SQL

Create Table is subject to SIR SQL specific pre-

processing. This one 1

finds whether the statement

is effectively implicit. Iff it turns out so, the pre-

processing rewrites the statement to the explicit one.

Every rewriting keeps every BA, table constraint

and option of the submitted Create Table, as well as

every IA and From clause, if there are any. It adds

IAs or parts of, or even entire, From clause, so to

form the explicit Create Table R. If the submitted

Create Table does not turn out to be implicit, the

pre-processing considers it explicit, hence not

needing any rewriting. The further SIR SQL

SIR SQL for Logical Navigation and Calculated Attribute Free Queries to Base Tables

195

processing we discuss later on works on the explicit

statements only.

We discuss later the rewriting rules for PKN FKs.

Notice for now only, with respect to SIR SQL FKs,

that every (present) SQL FK in some SIR R, is SIR

SQL one as well, by default. Besides, a BA in R can

be a SIR SQL FK, without being the former. With

respect to ‘#’, we recall here only that while

modeled on SQL ‘*’, whenever qualified with a base

table name, e.g., R.#, it designates only every non-

PK attribute of R. Likewise, ‘#’ alone designates

only every non-PK attribute of every base table in

From clause. We discussed the rewriting of a Create

Table with ‘#’ previously, (Litwin, 2022), and will

not come back to here.

E.g., we show soon that DBA may create

S_P1.SP through the implicit Create Table

containing only SP_ scheme and the value

expression of T_WEIGHT. Instead of submitting (2),

one expects therefore DBA to submit only:

(3) Create Table SP (S# TEXT, P# TEXT, QTY INT

{WEIGHT*QTY As T_WEIGHT} Primary Key (S#,

P#));

The procedurality difference is 110 characters in

favor of (3). I.e., 86 characters are necessary in SQL

for (3) versus196 for (2), as one can easily double-

check. Such lesser procedurality is an obvious

practical advantage of (3). Recall also that quest for

less procedural and more natural data definition and

manipulation always was and still is the driving

force for the DB research, as well as for the CS

generally. Remember that it is why in particular the

relational DBs succeeded to Codasyl and IMS ones.

If SP did not have T_WEIGHT or any CA more

generally, it will appear that (3) would reduce

simply to (1), i.e., to the SQL Create Table SP for

S_P. For SIR SQL however, the latter would be the

implicit Create Table for S_P1.SP, with empty IE. In

other terms, for SIR SQL, present S_P scheme

defines in fact S_P1. Yet in other words, for SIR

SQL, S_P scheme suffices for the LNF queries that

have to be with LN in any present SQL dialect.@

Next, for every SIR R, there is an SQL view R,

hence with IAs only, defining logically the same

relation as SIR R. We qualify the latter of canonical

view of SIR R and of C-view R, in short. C-view R

results from Create View R with the same attribute

list as in SIR R, except that every R_ attribute is

stripped to its name only, followed by the same

From clause. The difference between SIR R and C-

view R is thus only physical: every SA in SIR R

becomes the IA with the same name and value in

every tuple within C-view R and vice versa. Adding

a C-view R to an SQL DB with R_ as stand-alone

base table, provides then for the same LNF or CAF

queries as SIR R. Provided however that these

queries address the C-view R, instead of the base

table R, necessarily renamed somehow, i.e., to R_.

The rather easy to see drawback of any C-view R

with respect to SIR R, discussed in detail in our

previous papers, is that the former must be more

procedural to specify and to maintain than even the

explicit IE in SIR R. C-view R has to indeed

redefine every SA of R_ as an IA and it constitutes a

separate table to maintain in sync with R_. The

implicit SIR schemes whenever possible, with

possibly an even empty IE, are obviously even more

advantageous. As we just stated, it would be so, e.g.,

for S_P1.SP (3) and of course, even more for (1). In

present terms, every SIR R is thus a view saver for

C-view R.

Finally, as hinted to in the example above, in

practice, every SIR SQL Create Table will extend to

SIRs Create Table of some existing SQL dialect.

Likewise, SIR SQL Alter Table will extend Alter

Table of the dialect. Call kernel (SQL) the dialect

chosen. Some kernels, provide for base tables with

SAs only, as Codd proposed. Any SIR R defined in

SIR SQL extending the dialect will then have the

base R_ with SAs only. Other kernels provide for

the already mentioned VAs as BAs as well. Recall

then, e.g. from our papers on SIRs, that every base

table R with VAs is in fact a limited SIR R. There,

every VA is an IA inherited only from R_ and only

through arithmetic value expression with, perhaps,

scalar functions over SAs or other VAs of R_ and

with implicit ‘From R_’ clause. Accordingly, e.g., as

inheriting also from P, T_WEIGHT could not be a

VA for any present kernels. Nevertheless, despite

their limitations, VAs became popular view-savers,

as we already hinted to.

For SIR SQL consequently, there is no need for a

kernel providing for VAs, although one can still

define any VAs the kernel provides for. Indeed,

regardless of any such kernel and any VAs it could

provide for, SIR SQL dialect for the kernel would

always provide for an equivalent IA with the same

value expression and the implicit ‘From R_’. In

practice, the only syntactical difference would be

that while any VAs define the attribute name first

and the value expression after, the IA scheme would

be the other way around and somewhere within { }

brackets, instead of usual ‘,’ or ‘ ‘. Somehow

consequently, as one could already observe, for SIR

SQL, if VAs are present in a Create Table of SIR R,

they are not considered IAs, since they are not added

to R_ scheme, but are within. In other words, for

SIR SQL, for any SIR R, IAs are only the attributes

ICEIS 2025 - 27th International Conference on Enterprise Information Systems

196

defined in explicit Create Table R as if they were in

C-View R. Unlike we assumed for the general

definition of the SIR construct in our previous

papers. That one was designed for Codd’s relational

model, proposing SAs only in base tables, (Codd,

1978), to recall. Consequently, VAs were there

specifically defined IAs as well.

2.3 SIR SQL Foreign Keys

In our opinion, SQL FK concept differs from Codd’s

original one, (

Codd, 1970), (Date, 2006), (Date, 2021).

Codd defined an FK as a “logical pointer” (LP) to

some table. For SIR SQL, it appeared useful to

merge both concepts. We called the result SIR SQL

FK.

Overview. Accordingly to our intention, an SA in

submitted Create Table R can be SIR SQL FK along

following dimensions, Figure 3. Along one

dimension, FK may enforce RI. We speak

accordingly about RI dimension and RI FK. The

other dimension defines FK as LP. We speak about

LP dimension and LP FK. LP dimension is our

perception of Codd’s FK original concept. Besides,

from now on, FK means SIR SQL FK, unless we

talk specifically about (present) SQL FKs.

FK specs along LP dimension in Create Table R

contribute to IE. One defines accordingly in explicit

and perhaps also implicit Create Table R, LN

through FK and every IA calculated using this LN.

In the wake, it is LP dimension that predefines in

explicit SIR SQL Create Table R, IAs and LN

making LNF and CAF typical queries addressing R.

With respect to RI FKs, one defines every such

FK as if it was an (SQL) FK for kernel SQL dialect.

Whatever is the kernel, one may always define every

such FK through kernel’s dialect for SQL Foreign

Key constraint. Some kernels provide also for

References keyword in FK specs as SA, e.g., SQLite.

In SIR SQL Create Table, one should place every

Foreign Key constraint after IE, hence after the last

‘}’ in practice. The only semantic difference to

kernel’s specs of the same name SQL FK may be

that RI FK references a SIR.

An SA F in submitted SIR SQL Create Table R is

LP FK, iff in explicit Create Table R there is LN on

F and there are some IAs defined using this LN.

Every FK F can be IR FK only or LP FK only or

both. Every LP FK is either primary key named

(PKN) FK, (Litwin, 2022) or LN defined (LND) FK.

PKN FKs do not require LN and IAs in submitted

Create Table R. LND FKs do. For every PKN FK in

submitted Create Table R, the pre-processing adds

LN and IAs transparently. PKN FKs appear in fact

the common practice already, except that they are

defined only as RI FKs. LND FKs should serve less

frequent specific needs we discuss soon.

PKN FKs. An FK F in base table R is PKN iff (i)

F is not PK of R, (ii) there is a base table R

with PK

named F as well and sharing the domain of R.F, (iii)

F is RI FK and R

is the referenced table or (iv) F is

atomic and there is only one R

. In the latter case, if

FK is not RI FK, we speak about natural (PKN) FK,

or NFK in short.

Observe that, by definition then, NFKs do not

enforce RI, i.e., are LP FKs only. RI is thus optional

for PKN FKs. Recall that Codd apparently

considered RI optional for FKs as well. Unlike did

the SQL designers. Observe also that NFKs do not

require any specific declarations in submitted SIR

SQL Create Table, unlike PKN RI FKs. On the other

hand, observe that R

is always necessarily different

from R. Recall finally that some kernels, e.g.,

MySQL provide for referenced keys that are not PKs.

Even if a latter (candidate) key shares the name with

FK, it is not PKN FK.

E.g., consider (3) as submitted SIR SQL Create

Table. Suppose that DBA already created S and P.

Then, S# and P# are PKN FKs. None is RI FK, i.e.,

enforces RI, e.g., through the familiar Foreign Key

SQL table constraint. Each is thus NFK. Hence, e.g.,

insert of (S6, P6, 300) would go through.

A submitted Create Table R is implicit if it

contains PKN FKs. For every PKN FK F, F defines

so-called natural (NI) through F. The term

designates (i) so-called natural IAs (NIAs) and (ii)

LN on F through which the values of every NIA are

computed for queries. Both NIAs and LN are in the

explicit Create Table R only. In other words, the pre-

processing adds these to submitted Create Table R

whenever it finds PKN FKs within.

More in depth, for every PKN FK F1,F2…,

numbered in the (left-to-right) order in R and

referencing respectively R1, R2,…, NIAs

constituting NI through Fi ; i = 1,2… ; have names

and values of all and only non PK attributes of Ri. In

particular, whenever needed, an NIA name can be

the qualified Ri attribute name. Then, for every NIA,

LN on R.F = Ri.F, with vector equality for every

composite F defines its every value and every null.

Also, all the NIAs constituting NI through F1 follow

the last BA or IA specified in implicit Create Table

R. Then, all the NIAs of NI through F2 follow NI

through F1 etc. Finally, for every Fi, NIAs in NI

through Fi are in their source order in Ri.

With respect to every LN defining NI through Fi,

expressed only in the explicit Create Table R, we

recall, if implicit Create Table R has no From clause,

SIR SQL for Logical Navigation and Calculated Attribute Free Queries to Base Tables

197

then pre-processing expresses LN on F1 as: From

R_ Left Join R1 on R_.F1 = R1.F1. Else, it

expresses LN on F1 as: Left Join R1 on R_.F1 =

R1.F1, appending it to From clause in the implicit

Create Table R. Next it appends to From clause

being built up LN for F2, if there is any, expressed

as: Left Join R2 on R_.F2 = R2.F2 etc. We qualify

of, simply, NI, all the resulting NIAs and LN joins

added.

Figure 3 SIR SQL Foreign Keys. RI FK enforces RI. PKN

FKs imply NI, NFKs in particular. LND FKs specify SI.

An FK can be RI FK only or LP FK only, or both.

E.g. Let us follow up on previous example. The

pre-processing of (3), creates (2) as explicit Create

Table SP. IAs following T_WEIGHT together with

From clause form NI. All these IAs are NIAs. IAs

named upon S attributes and LN on S# form NI

through S#. Likewise, IAs sourced in P and LN on

P# form NI through P#.@

LND FKs. An SA F, perhaps composed, is LND

FK iff (i) in submitted Create Table R, for some R

with key C not named F or not a PK, there is LN

(join) on F = C and (ii) in the attribute list, there are

IAs either named upon attributes of R

or being CAs

addressing the latter through value expressions or

simple aliasing. The former IAs may, in particular,

result from R

.# clause we discussed earlier. SA F

that is LND FK does not enforce RI, unless one

declares F also RI FK, Figure 3.

For every LND FK F, we qualify of specific

inheritance (expression) or of SI in short, through F,

the just described IAs and LN, (in submitted Create

Table thus). By the same token, the term SI

designates the result for all the LND FKs in R and

we qualify of specific every IA of SI, SIA in short.

E.g. Suppose that SP DBA prefers IAs sourced in

S named and placed in SP differently from NIAs in

(2). Namely, these IAs should be as in the following

submitted Create Table SP:

Create Table SP (SN TEXT {SNAME, S.CITY

As SCITY} P# TEXT, QTY INT {WEIGHT*QTY

As T_WEIGHT From SP_ Left Join On SP_.SN =

S.S#} Primary Key (S#, P#));

Here, SNAME and SCITY are SIAs. SN is an

LND FK only, hence LP only, i.e., does not enforce

RI. Together, LN and the attributes sourced in S

constitute SI through SN. It is (entire) SI in fact,

since P# provides for NIAs only. Also, STATUS

remains private to S, i.e., only SP clients knowing

that SN and S# share a domain (in Codd’s

vocabulary) may select it and only through the LN in

the query then. We leave the explicit Create Table

SP resulting from the above submitted one as

exercise. @

Summing up on SIR SQL FKs and Codd’s ones.

As we already hinted to, for every SIR R with some

LP FKs, NI or SI values in every R-tuple reflect

Codd’s “logical pointer” idea, (Codd, 1978). Namely,

for every PKN or LND FK, one calculates all these

values using LN. The possibility of such calculus for

queries selecting values of some attributes of R and

of some of the referenced tables was novel by

Codd’s times. It apparently motivated the “logical”

qualifier. The rationale for Codd was that in a “well

designed” DB, all the non-key attributes referenced

by any FK of R, are, conceptually, also attributes of

R. E.g., these were the attributes we spoke about for

S_P.SP, i.e., every non-key attribute of S or of P.

Some of these attributes in R may be furthermore

subject to aliasing or a value expression. For every

tuple of R, if FK has then value matching a value of

the referenced key C, usually PK, then the value of

every such conceptual R attribute, hence of an IA in

R, is the one in the sole eventual tuple with PK=FK

for NI or, following the notation above, with F=C

for SI. For an IA being CA, such a value can further

be subject to a value expression. If FK value in R

tuple does not match any C value, as it can happen

for Codd’s FK, then every such IA is null in the

tuple. In other words, the general form of LN is an

outer semi join. As we have already hinted to, such

form remains valid even if LP FK is also RI FK,

although an inner join does then as well.

However, in Codd’s model, for any base table R,

none of such conceptual attributes could be among

the actual ones of R. As already discussed, they

would necessarily be SAs. Hence, they would

always imply normalization anomalies. The side-

effects of the latter, hinted to above, would, most of

time, offset any practical interest of the LNF queries

with respect the same outcome queries with LN to

the normalized tables. But, as also discussed already,

whenever all these attributes are NIAs instead, none

can ever imply any normalization anomalies. LNF

queries to any R with NI or SI become attractive

again, as it will appear more below. Especially, since

as S_P illustrates as well, most of time in practice, a

base table needs FKs, since most of its conceptual

attributes have to be in referenced tables.

LND

RI F

PKN

LND

ICEIS 2025 - 27th International Conference on Enterprise Information Systems

198

Accordingly, most of queries addressing a table with

FKs will address NI or SI and formulate as quasi-

natural LNF ones. All this is our rationale for FKs in

SIR SQL defined as discussed.

In other words yet, for Codd apparently, at least

originally, not RI, as later for SQL, but NI or SI

were the characteristic property of any FK, e.g., as in

S_P. They were used in queries and views only. For

any base tables with FKs, NI or SI remained in

Codd’s model implicit only, [1,2,3]. In contrast,

while also following on Codd’s intentions, SIR SQL

LP FKs provide for the explicit predefinition of NI

or SI in the base tables. This frees accordingly the

queries to these tables and to referenced ones from

LN formulae.

Next, observe that for SIR SQL, any SQL Create

Table R with PKN FKs, does not define “only” an

SQL base table as at present, i.e., only with the BAs,

table constraints and options. Instead, it defines SIR

R with the same BAs, table constraints and options,

forming base R_ but also with NI. E.g., for SQL

presently, (1) defines “only” SP with attributes as at

Figure 1. But, for SIR SQL, (1) defines in fact SP

(2) without T_WEIGHT. I.e. it defines SP as at

Figure 2, without T_WEIGHT column. Accordingly

for SIR SQL, given S_P content in Figure1, (1)

specifies SP content in Figure 2 without the latter

one.

Observe finally that, as illustrated above by SP

with T_WEIGHT example, the rationale for implicit

schemes is that they are always less procedural than

the explicit ones. Furthermore, whenever base tables

of SIR SQL DB do not contain any CAs and any SI,

DBA may simply issue the present Create Table for

each of these tables. DBA provides in this way for

LNF queries without aDny additional procedurality

to define the IE. Recall, - as it was wished for our

solution. Without “moving a finger” as one says,

DBA makes accordingly SIR SQL clients likely

happier and, for sure, more productive than at

present.

2.4 SIR SQL Create Table Formally

Space limits prohibit discussing here the (boring)

formal definitions of implicit and explicit SIR SQL

Create Table. Please refer to “only a click-away”

research report entitled as this article in (Litwin,

2025)..

2.5 SIR SQL LNF or CAF Queries

Consider a sequence, say S, of Create Table

statements defining an SQL DB, say D. Typically,

some statements in S define base tables with PKN

FKs and some define the referenced tables. Also

typically, one creates every referenced table before

the referencing one. As for S_P, in particular.

Suppose now that S defines a SIR SQL DB D1.

Then, a typical query, say Q1, to D1 base tables

would select some attributes of a table R1 with FKs

and some attributes of referenced table and would be

LNF. For every Q1, the same output query Q2 to D

would require some LN between R1 and some

referenced tables and perhaps among those. Q1

should be then less procedural than Q2 by dozens of

characters. Q1 is accordingly always faster to

conceive. Recall queries Q1 to S_P and Q2 to S_P1

above.

Suppose now that S is a SIR SQL sequence, with

some Create Table defining a CA A, e.g.,

T_WEIGHT. Then, every A that one could

alternatively define as VA A’ of S’ being S except

for A and creating an SQL DB, would not be more

procedural than A’. In any case, A would not be

more procedural than A’’ defined as A, but within

any SQL query to base tables created by S without

CAs and defining an SQL DB. Also, queries to D1

should usually be LNF or CAF. Unlike, could be the

same output queries to the SQL base tables. Recall

queries Q3 and Q4 above.

See the above mentioned research report in

(Litwin, 2025) for more on these advantages of SIR

SQL DBs.

2.6 SIR SQL Canonical Architecture

Let us call SIR (enabled) DBS, any relational DBS

(RDBS) providing for SIR SQL. To implement a

SIR DBS ‘simply’, i.e. through a couple of months

of programming only, stick to the canonical

architecture, we overview now and illustrate at

Figure 4. In the nutshell, SIR DBS consists then

from the front-end, called SIR SQL layer or SIR-

layer in short, reusing as follows any popular kernel

SQL DBS, e.g., SQLite3:

- SIR-layer takes care of every SIR SQL dialect

statement and returns any outcomes. Every SIR SQL

dialect extends to SIRs the kernel SQL dialect.

- The kernel is the actual storage for every SIR

SQL DB, becoming the same name DB for the

kernel SQL.

- SIR-layer forwards to the kernel every Create

Table R submitted without PKN FKs and without

any IA, but perhaps with VAs declared as if they

were intended for the kernel. Any Create Table R

with PKN FKs is for SIR-layer an implicit scheme,

preprocessed accordingly to the explicit one with the

SIR SQL for Logical Navigation and Calculated Attribute Free Queries to Base Tables

199

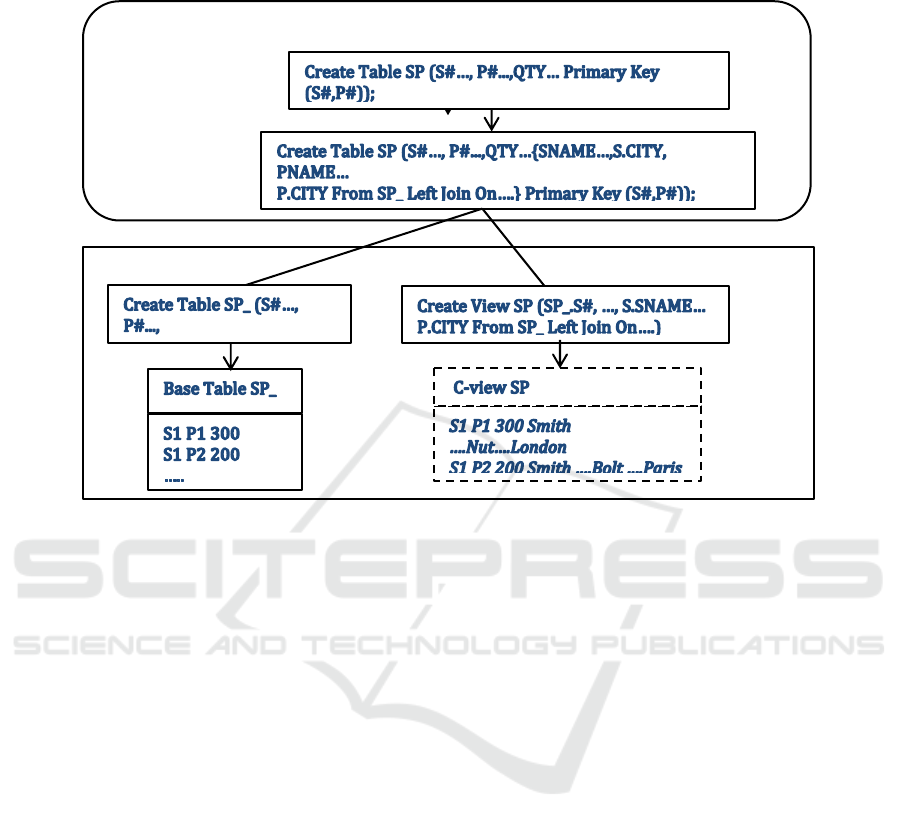
Figure 4. Canonical Implementation of S_P1.SP base table with the actual content within kernel SQL DBS. As for any SQL

view, C-view SP content is basically virtual.

(explicit) NI. The preprocessing infers every NIA

name and LN from kernel’s SYS meta-tables.

Likewise, for every base table R’ referenced through

LND FK spec, the preprocessing infers every IA

name resulting from R’.#. Easy algorithms for all

this, discussed in our previous articles, were

prototyped for SQLite kernel.

Besides, SIR-layer parses every explicit Create

Table R to Create Table R_ and Create View R

defining C-view R. To prevent any name conflicts in

C-view, for the latter, every attribute is qualified with

its source table name, including R_ for every BA.

SIR-layer then forwards both statements as an atomic

transaction to the kernel. Figure 4, at the end of the

article illustrates the result for S_P1.SP processing.

- SIR-layer also forwards to the kernel every (SIR

SQL) Alter Table R that does not contain SIR-

specific clause termed IE clause. It is indeed

supposed kernel SQL Alter Table, addressing thus

base table R that is not a SIR and should remain so.

SIR-layer also forwards any Alter Table R_. IE

clause may be explicit or implicit, even empty. It

always means that R is or should become a SIR. If R

is a SIR already, SIR-layer issues to the kernel Alter

View R with new C-view R produced from IE clause

and, for an implicit IE clause, from the altered R_

scheme and from view R scheme in kernel SYS-

tables. If R is not yet a SIR, SIR-layer similarly

produces and sends to the kernel as an atomic

transaction: Alter Table R renaming R to R_ and

Create View R with C-view R. See (Litwin, 2022)

for more.

- Furthermore, SIR-layer forwards to the kernel

any Drop Table R if R is not a SIR. Otherwise it

issues an atomic transaction with Drop Table R_ and

Drop View R.

- For SIR SQL data manipulation statements,

SIR-layer simply forwards any submitted query to

the kernel. For any SIR SQL update statement, safe

policy for every kernel and every SIR R is to address

R_. E.g., Insert To SP_..., Update SP_... and Delete

From SP_... for S_P1.SP. An update statement

addressing SIR R directly, e.g., Insert To SP…, may

or may not work. It depends on kernel’s view update

capabilities. The kernel would indeed address any

such queries to view R. In particular, no present

kernel provides for any CA updates.

2.7 SIR SQLLite3 Proof-of-Concept

Prototype

SIR-layer in Python and SQLite3 as the kernel

appeared the most suitable for this goal. The actual

Kernel S

L DBS

lici

Schema

lici

Schema

L La

ICEIS 2025 - 27th International Conference on Enterprise Information Systems

200

prototype available at present provides also for self-

running demo. The overall effort was 2-3 months of

makeshift Python’s developer, i.e., the effort

conform to expectations. The demo creates S_P1,

either from the explicit SP scheme or from the

S_P.SP scheme. The latter is assimilated to SIR SQL

implicit scheme with empty IE, resulting from the

natural PKN FKs S# and P#. Then, one manipulates

S_P1, through LNF queries or, after adding

T_WEIGHT CA, through LNF and CAF queries.

Users familiar with Python may easily alter the

demo. E.g., to prepare their own SIR DBS reusing

another kernel: DB2, SQL Server, PostgreSQL,

MySQL… you name it. See (Litwin, 2025) for more

on the prototype.

3 CONCLUSION

Since five decades i.e., since 1974 when IBM

introduced SQL, every SQL DBS requires the

clients to specify most of time in queries to base

tables, LN and CAs, at least other than VAs for

some dialects. The procedurality of LN and of CA

specs is usually substantial, requiring dozens of

characters to type-in and debug, bothering many.

SIR SQL gets rid of this annoyance, most of time

reducing the queries to the LNF and CAF ones. In

particular, the LNF queries to the base table created

through Create Table as generally at present only

become possible. In fact we expect most of SIR SQL

DBAs to define DBs in this way, providing LNF

queries to clients as free bonus, without “moving a

finger”.

For CAF queries, it may suffice to add to Create

Table only the value expressions defining the CAs.

Recall also that SQL base tables at present simply do

not provide for CAs possible with SIR SQL. We

expect future SIR SQL DBs used for data analysis,

e.g., Big Data DBs, to routinely profit from this

capability. Finally, the proof-of-concept prototype

SIR DBS with SQLite as the kernel proved simple to

realize. Although the problem of LNF and CAF

queries is anything but new, our solution is the only

of the kind, to our best knowledge.

In sum, we have shown that if present SQL DBs

had SIR-layers, LNF and CAF queries to base tables

would be the standard and their present equivalents a

bad dream. Also, as it appeared for SQLite, to

provide SIR-layer for a present SQL DBS, should

cost no more than a few months effort, i.e., - peanuts

by industrial standards. We postulate consequently

that DB courses and textbooks take notice of SIR

SQL from now on. This, despite the lack of any SIR

SQL layer fully implemented as yet. After all, same

happened to present relational DBSs.

By the same token, we postulate to upgrade every

popular SQL DBSs to SIR SQL, “better sooner than

later”. Over 7+ million SQL clients worldwide will

benefit from. Bear in mind also that this spread out

makes SQL the most used DB language, (Gaffney,

& al, 2022). (Sobolevskiy, 2915), (Stonebraker,

Pavlo, 2023). Recall finally that SQL crowd makes

70% of all developers and provides for estimated

31B US$ market size of SQL DBSs, (ZipDo, 2024).

REFERENCES

Codd, E., F. (1970). A Relational Model of Data for Large

Shared Data Banks. CACM, 13, 6.

Date, C., J. (2006). An Introduction to Database Systems,

ed. Pearson Education Inc. ISBN 9788177585568,

2006, 968p.

Date, C., J., (2021). E.F. Codd and Relational Theory.

Revised Edition. LULU PRESS, INC., 2021.

Date, C., J., Darwen, H., (1992). Watch out for outer join.

In Date and Darwen Relational Database Writings

1989-1991. ADDISON-WESLEY,

Litwin, W. (2022). Stored and Inherited Relations with

PKN Foreign Keys. In 26th European Conf. on

Advances in Databases and Information Systems

(ADBIS 22). SPRINGER (publ.).

Gaffney, K., P., Prammer, M., Brasfield, L., Hipp, D., R.,

Kennedy,D., Jignesh, M., P., (2022). SQLite: Past,

Present and Future. In PVLDB, 15(12):3535-3547.

Sobolevskiy, M. (2915). How Many SQL Developers Is

Out There: A JetBrains Report, Dec. 23.

ZipDo, (2024). Essential Sql Statistics in 2024.

https://zipdo.co.

Litwin, W., (2025). Home Page.

https://www.lamsade.dauphine.fr/~litwin/witold.html .

Stonebraker, M. Pavlo, A., (2023). What Goes Around

Comes Around… And Around. SIGMOD Record,

June 2024, 53, 2.

SIR SQL for Logical Navigation and Calculated Attribute Free Queries to Base Tables

201