Urban Growth in Metropolitan Regions Using Dynamic Modeling by

Cellular Automata: A Comparative Analysis Between Brazil and

Portugal

Elizabeth Maria Feitosa da Rocha de Souza

, Antonio Alberto Teixeira Gomes

and Vandre Soares Viegas

Federal University of Rio de Janeiro, Department of Geography, Graduate Program in Geography Geosciense Institute,

Rio de Janeiro, Brazil

University of Porto, Faculty of Arts and Humanities, Porto, Portugal

Keywords: Cellular Automata, Spatial Dynamic Models, Urban Areas, Metropolitan Regions.

Abstract: This study synthesizes the outcomes of land use changes obtained through the implementation of dynamic

modeling by cellular automata across two metropolitan regions in Portugal and Brazil. The purpose is to

analyze the primary findings acquired, considering the particularities of each nation and evaluate the

potentialities of the used data. The study examined the metropolitan regions of MRRJ (Rio de Janeiro, Brazil)

and AMP (Porto, Portugal). Modifications were implemented in the DinamicaEgo software to the

fundamental data representing static and dynamic variables for each context. The findings revealed a

substantial increase of urban areas in the MRRJ, and the modeling demonstrated its applicability across the

two contexts, considering the requisite modifications for the data accessible in each country.

1 INTRODUCTION

Cellular models in urban modelling became implicit

in early computer models of the 1960s, e.g., the work

of Chapin and Weiss for North Carolina (Chapin and

Weiss,1968) Waldo Tobler's model for Detroit in

1970 (Tobler, 1970), and the model developed by

Couclelis for Los Angeles in 1989 (Couclelis,1989).

Cellular automata (CA) have emerged as the

prevailing architectural design employed in spatial

simulation models. Cellular automata, as defined by

Stephen Wolfram, are mathematical representations

of physical systems in which time and space are

discrete (Wolfram, 1983). These representations take

the form of a regular uniform grid, where each

location contains a discrete variable. In accordance

with a predetermined set of local rules and the values

of the variables in their immediate vicinity at the

previous time increment, the variables in each cell are

updated simultaneously. CA models have the

capability to emulate various concerns associated

https://orcid.org/0000-0002-2672-8169

https://orcid.org/0000-0002-1764-0659

https://orcid.org/0000-0002-2880-8314

with land use changes. They can be used to create

self-modifiable models for high-resolution urban land

use dynamics, prototypes to simulate land conversion

via integrated Geographic Information Systems (GIS)

(Clarke, et al 1997; White et al, 1997; Wu, 1998) and

have numerous applications for simulating scenarios

involving urban dynamics (Barredo et al, 2003;

White, and Engelen, 1993). The use of dynamic

models can support the definition of environmental

public policies that involve the assessment of land use

and land cover as a fundamental component to unders-

tand changes that may result from combined biophysi-

cal and socioeconomic factors, with both short-term

and long-term impacts (Meyer and Turner, 1992).

In this context, the research aimed to identify

potential scenarios of land use and land cover change

until the year 2050 in the Metropolitan Area of Porto

(AMP) and the Metropolitan Region of Rio de Janeiro

(MRRJ), specifically within the boundaries of

urbanized territories, while observing changes

between classes and specificities.

142

Souza, E. M. F. R., Gomes, A. A. T. and Viegas, V. S.

Urban Growth in Metropolitan Regions Using Dynamic Modeling by Cellular Automata: A Comparative Analysis Between Brazil and Portugal.

DOI: 10.5220/0013205000003935

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 11th International Conference on Geographical Information Systems Theory, Applications and Management (GISTAM 2025), pages 142-149

ISBN: 978-989-758-741-2; ISSN: 2184-500X

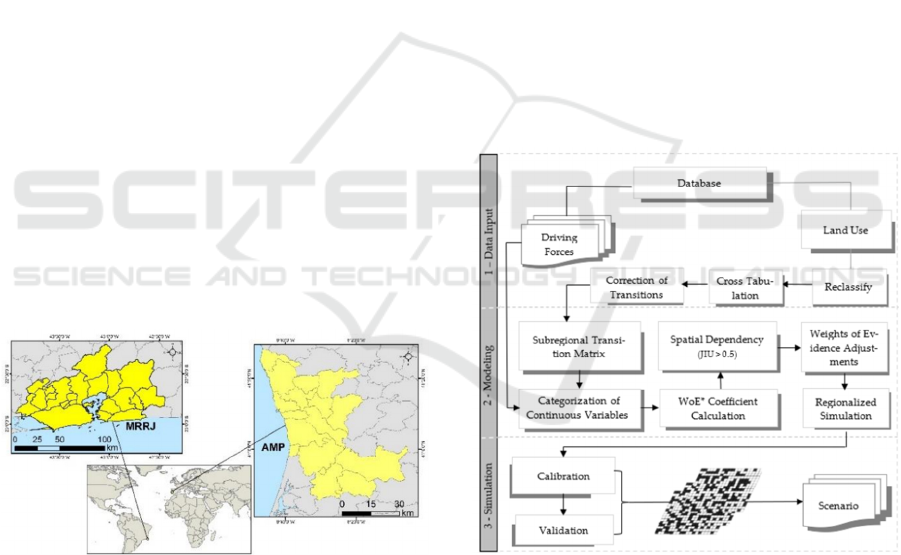
2 STUDY AREA

The study area encompasses two Metropolitan

Regions: Metropolitan Area of Porto (AMP) and the

Metropolitan Region of Rio de Janeiro (MRRJ -

Figure 1). Although referred to by different

acronyms—AMP for the Metropolitan Area of Porto

in Portugal and MRRJ for the Metropolitan Region of

Rio de Janeiro in Brazil—both regions fulfil

analogous roles within their respective national

contexts. In 2021, the Porto Metropolitan Area

(AMP), composed of 17 municipalities, had a

population of approximately 1,7 million inhabitants

distributed across an area of 2,040 km². Meanwhile,

the Rio de Janeiro Metropolitan Region (RMRJ),

consisting of 22 municipalities, was home to around

12 million inhabitants in an area of 6,700 km², with

significantly higher population density due to the

concentration of people in municipalities like Rio de

Janeiro, São Gonçalo, and Duque de Caxias. These

regions represent important urban hubs in their

respective countries, facing distinct challenges in

terms of planning and urban development.

Each area functions as a logistical hub for regional

planning, economic development, and the

coordination of urban services. Both regions

represent densely populated areas that support

integrated infrastructure alongside public policy

frameworks. This functional alignment underscores

the significance of metropolitan regions as

foundational elements in urban planning and

governance in each country.

Figure 1: Study area - Areas considered in the study for

comparison purposes

Situated in southeastern Brazil, the Metropolitan

Region of Rio de Janeiro (MRRJ) is an extremely

urbanized, multifaceted, and diverse region. This

region, which includes the capital city, Rio de Janeiro,

and significant neighbouring municipalities including

São Goncalo, Duque de Caxias, and Niterói, is

renowned for its geographical, historical, and

economic importance. Based on a survey carried out

in 2022 by the Brazilian Institute of Geography and

Statistics (IBGE, 2022), the Metropolitan Region of

Rio de Janeiro is the second most populous

metropolitan area in Brazil, comprising 74% of the

total population of the state of Rio de Janeiro, with an

estimated 12 million inhabitants.

The Metropolitan Area of Porto is the second

largest in Portugal, encompassing 17 municipalities

around the city of Porto. According to data from the

Land Use and Occupation Map - COS2022 (Instituto

Nacional de Estatística, 2022).

The AMP has emerged as a strategic area for

advancing mobility and sustainability projects,

essential for the region's future.

3 MATERIALS AND METHODS

The CA model used in this work is implemented in

the Dinamica EGO (Environment for Geoprocessing

Objects) platform 7.4, a software developed by

researchers from Federal University of Minas Gerais

(UFMG). The methodology used is presented

according to the scheme shown in Figure 2.

Figure 2: Workflow (*WoE – Weights of Evidence).

Simulation models utilize two types of

explanatory variables, divided between Static and

Dynamic. The former remains unchanged at each

temporal step of the model, while the latter changes

with each iteration based on the distance from the

central axis being analyzed.

The first step in the modeling process is

parameterization using the Weight of Evidence

method, following the Bayesian approach. This

Urban Growth in Metropolitan Regions Using Dynamic Modeling by Cellular Automata: A Comparative Analysis Between Brazil and

Portugal

143

involves assigning weights to different input

variables based on their relevance to the specific

problem.

Historical transition matrices are calculated. The

transition matrix describes a system that changes in

discrete increments of time. In the Dinamica EGO

platform, matrices are calculated using a Markovian

model, which combines the Markov Chains technique

with Cellular Automata. Dinamica EGO also employs

Markov chains to determine the amount of change, as

well as cellular automata to reproduce patterns of

these changes from probability maps, which are

calculated using the Weight of Evidence statistical

method (Soares Filho et al, 2002). Cellular automata

(CA)-based models have been widely used due to

their ability to simulate dynamic spatial patterns. The

choice of the CA-Markov model in this study is

justified by its integration of Markov transition

matrices with dynamic spatial modeling, enabling the

capture of land use changes with high temporal and

spatial granularity.

For the desired period—a range of years—two

types of matrices are generated: a global matrix,

representing the transition rates for the entire training

period, and a multistep matrix, which reflects annual

changes. The global matrix aggregates all transitions

across the specified period, while the multistep matrix

allows for more granular modeling by representing

changes on an annual basis.

It is important to clarify which transitions are

being modeled, as this directly influences the

simulation outcomes. In DINAMICA, transitions are

managed through two Cellular Automata (CA)

algorithms: the Patcher, which simulates the

aggregation of land patches, and the Expander, which

models the expansion of existing areas. These

mechanisms ensure that spatial patterns align with the

observed dynamics, providing a robust framework for

projecting future scenarios.

In Dinamica EGO, a set of sub-regional functors

is used to process the data separately in each sub-

region. In this model, transitions are simulated

annually for each of the subdivisions, dividing a map

into parts for separate data processing and then

combining the results. This allows the modeler to

define operations that should be applied only to

specific sub-regions or different parameters and

coefficients. The result is a model that respects the

regional context. In both cases, the transitions of

interest focus on changes to urban, vegetation, and

cultivated areas.

The dynamic variables considered in this study

are exclusively related to land use and land cover in

the years specified for each region: AMP and MRRJ.

These variables reflect temporal changes that directly

influence the projected scenarios and are updated in

each iteration of the model. The static variables, on

the other hand, remain constant throughout the

modeling process and represent potential factors

influencing the observed and projected land use

changes. These variables include hydrography,

transportation systems, and topography, which play a

fundamental role in defining spatial patterns of urban

expansion and enable the simulation of future

scenarios. The dynamic variables include distances

from existing urban areas, which are updated at each

iteration of the model, while static variables, such as

elevation and the hydrographic network, remain

unchanged. Dinamica EGO uses Markov matrices to

determine transition rates and spatial patterns based

on weights of evidence calculated using the Bayesian

method.

In summary, the calibration was conducted using

the Expander and Patcher functions, which simulate,

respectively, the expansion of existing patches and

the formation of new urban patches. To address the

specificities of the study area, the model was

regionalized, dividing the territory into subareas with

distinct characteristics and adjusting parameters for

each region. This process allowed for greater

accuracy in annual simulations, respecting regional

contexts and producing results tailored to the

geographic complexity of each studied area.

Validation was based on spatial similarity between

simulated and observed maps from 2021 (RMRJ) and

2019 (AMP), using fuzzy methods and moving

windows. The simulation was regionalized to account

for local characteristics of the territory, such as

differences between rugged terrain areas and

lowlands. The model annually simulates transitions,

adjusting parameters to reflect local dynamics and

generate accurate predictions of urban expansion.

3.1 Metropolitan Area Porto –

Portugal - Model

The Metropolitan Area of Porto (AMP) was modeled

utilizing the subsequent variables: land use and

occupation, roads and railways, hydrography,

elevation and slope.

The elevation and slope values were derived using

the USGS-provided NASADEM Digital Elevation

Model (30m spatial resolution).

At a 1:10,000 scale, the road network is an

integral component of the National Motorway

Network, while the railway network is an extension

of the National Railway Network.

GISTAM 2025 - 11th International Conference on Geographical Information Systems Theory, Applications and Management

144

The hydrographic network is a 1:200,000 scale

representation of the principal channels and rivers

extracted from the Hydrography Network of

Continental Portugal. Only the main rivers and

channels were considered. While pertinent to the

simulation process, this class is regarded as limiting

in the modeling process for the expansion of the

urbanized class.

In the study, the Land Use and Occupation Map

(COS) for 2015 and 2018 was considered for the

preliminary analysis, focusing on the base period

2015–2018. The primary categories analyzed were

vegetated cover, agricultural regions, and urbanized

areas. To project future scenarios, the model

incorporated simulations for specific years: 2030,

2040, and 2050. A cross-tabulation analysis was

conducted using the converted matrix dataset,

maintaining the same spatial resolution to assess

changes over time and validate the model's outputs.

3.2 Metropolitan Region in Rio De

Janeiro/Brasil - Model

In MRRJ, the initial and final maps come from the

time series provided by Mapbiomas (collection 7.1),

including the years 2016 and 2021, that is, a period of

05 years, con-sidered sufficient to identify areas of

urban expansion.

The MapBiomas 7.1 collection includes annual

land use and land cover data for the period 1985 to

2021. The secondary data taken from the platform

have some spatial inconsistencies in the thematic

classifications, often due to noise and main-ly in

classes and transversal themes, e.g., agriculture and

pasture. Currently, there are 30 classes available,

from macro-classes 1 - Forest; 2 - Non-Forest Natural

Formation; 3 - Farming; 4. Non vegetated area; 5 –

Water. The static variables were obtained from

official Brazilian agencies (hydrography, road

system, and topography).

The first stage of adjusting the Mapbiomas data

consists of correcting incorrect transitions that

normally occur in the form of isolat-ed pixels and

have no correspondence in the real world, for

example, a pixel classified as urban infrastructure

should not transition to the water class.

The established rule was that no pixel originally

classified as urban infrastructure (class 24) - Areas

with significant density of buildings and roads -

should transition to other classes. After the correc-

tion, the other subclasses other than urban

infrastructure were converted to the “Others” class,

maintaining binary use maps.

Finally, the last phase involves data calibration,

validation, and scenario observation. The maximum

value of the Fuzzy similarity index is considered,

using exponential decay for window sizes of 3x3,

5x5, 7x7, 9x9, and 11x11 as a validation method. The

index varies from 0 to 1, where 1 indicates perfect

spatial agreement.

Kernel Density Estimation was applied in the

study to enhance the identification of change-prone

areas.

4 RESULTS

Regarding the parameterization of the transition

algorithms, Expander and Patcher, the model

achieved better validation results with a higher

percentage assigned to the Expander algorithm:

0.92% (RMRJ) and 0.87% (AMRJ).

Considering the threshold mentioned in (Soares

Filho et al, 2002), where values close to 0.6 in the

similarity index with exponential decay indicate

adequate spatial congruence between simulated and

real maps, it is reasonable to conclude that, in terms

of suitable similarity, the period from 2015 to 2018

(AMP) and from 2016 to 2021 (MRRJ) showed

satisfactory adjustments, especially in the 3x3

window.

4.1 Metropolitan Region in Rio De

Janeiro/Brasil

To Metropolitan Region of Rio de Janeiro Based on

the model, the following areas are identified as

particularly promising for urban expansion in 2050:

Situated west of the Capital, on the boundary between

the Santa Cruz and Guaratiba communities.

Additional noteworthy localities within the Capital

comprise Campo Grande, Vila Militar, Campo dos

Afonsos, Vargem Grande, and Recreio dos

Bandeirantes. These are areas with available spaces

for urban occupation and increased construction.

Furthermore, the Baixada Fluminense encompasses

municipalities Duque de Caxias, Magé, Nova Iguacu,

and Seropedica, all of which exhibit substantial

prospects for development.

In the East Fluminense, Maricá, Niterói, and São

Goncalo are the municipalities that are undergoing

the most significant urban development. In the

Mountain subregion, Petrópolis municipality

observes noteworthy urban expansion in the vicinity

of the central area, which encompasses the Vila

Militar and Valparaíso neighborhoods. In the

southern region, notable residential areas include

Urban Growth in Metropolitan Regions Using Dynamic Modeling by Cellular Automata: A Comparative Analysis Between Brazil and

Portugal

145

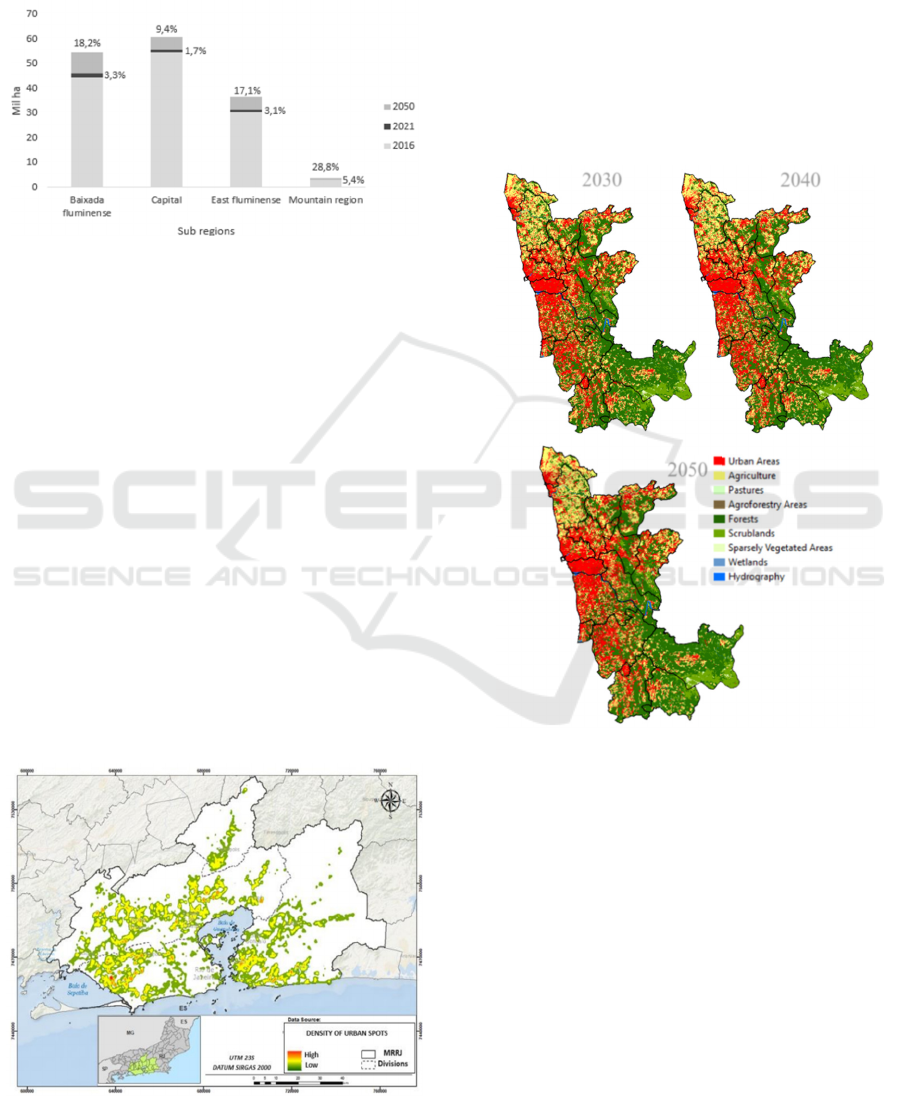
Independência and Quitandinha. Notable are the

regions of Mosela to the west and Bonsucesso and

Itaipava to the north. The aforementioned regions

symbolize the anticipated epicenters of urban growth

as predicted by the model for the year 2050 (Figure 3).

Figure 3: Urbanization by subregion through 2050,

represented graphically by absolute and relative values.

Kernel density estimation (Figure 4) was

employed to depict urban expansion in 2050. This

interpolator enables the determination of the

magnitude of a particular occurrence throughout an

entire region (Freire, 2015). Druck et al, (2004)

describe how the Kernel density estimator creates a

surface whose value is proportional to the sample

intensity per unit area and fits a two-dimensional

function to the considered events in order to estimate

the point intensity of the process across the entire

study region. Kernel Density estimates the intensity

of events (in this case, urbanization) per unit of area,

generating a continuous surface that highlights

regions with higher concentrations of change. This

technique complemented the analysis based on

transition matrices, enabling the mapping of regions

with significant urban change. The use of this

methodology was essential due to the high variability

in land use in the MRRJ, providing a more detailed

Figure 4: Urban Expansion Scenario for 2050 in MRRJ.

view of urbanization hotspots and enhancing future

scenarios for urban planning and environmental

management.

Municipalities outside the capital (Rio de Janeiro)

highlight a current trend of urban expansion and

demand for housing and new developments.

4.2 Metropolitan Area Porto - Portugal

The Figure 5 highlights the results obtained after

modeling for the years 2030, 2040, and 2050 with a

detailed analysis of the evolution.

Figure 5: Future Landuse Scenarios for AMP in 2030, 2040,

and 2050.

A 2.66 percent increase in urbanized territories is

observed across the entire study area from 2030 to

2040, and a 2.55 percent increase from 2040 to 2050.

The projected increases for agricultural regions are

1.13% and 1.08%, correspondingly. On the contrary,

a decline in forested regions is noted, fluctuating by

approximately 1.8% during both time periods.

The Figure 6 delineates the regions where

anticipated alterations occur during the examined time

frames. There is a total of 2274 polygons. From 2023

to 2040, there is a projected total of 1097 regions

undergoing changes, namely involving the conversion

of brush areas into urbanized zones and the

transformation of brush areas into agricultural land.

2030

2040

2050

GISTAM 2025 - 11th International Conference on Geographical Information Systems Theory, Applications and Management

146

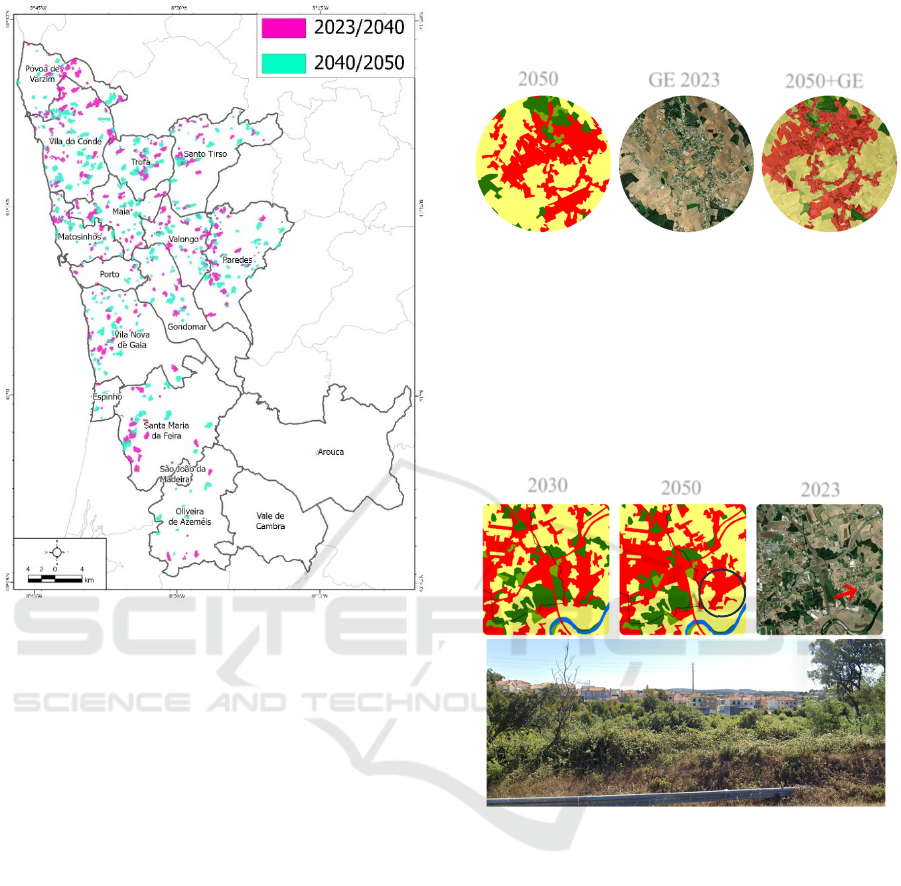
Figure 6: Regions with alterations in landuse during 2023 –

2040 and 2040 and 2050.

There is a significant concentration of expansion

near the cities of Vila Nova de Gaia, Matosinhos, and

Gondomar, which are already densely urbanized

areas close to the metropolitan center of Porto. This

growth suggests a continuous trend of urbanization in

peri-urban areas and an expansion into zones with

existing infrastructure.

In the period from 2040 to 2050, growth appears

more dispersed, with new urbanization points

emerging in regions such as Paredes, Santo Tirso, and

Oliveira de Azeméis, indicating a possible gradual

decentralization of the observed expansion. This

pattern suggests a potential saturation of central areas

and a search for new development zones on the

periphery of the AMP, leading to a more balanced

growth between municipalities in the northern and

southern parts of the Metropolitan Area. These data

highlight the need for integrated urban planning to

meet the growing demands for infrastructure and

services in these emerging regions.

Figure 7 highlights the projection for the Serra do

Monte area (Northern Region of the AMP), with three

representations: the 2050 projection showing

urbanized area growth; a 2023 GE image as a

reference; and a combination of both, indicating

urban area densification and anticipated changes.

Figure 7: Changes in 2050 for Serra do Monte, Northern

Region of the AMP.

Figure 8 demonstrates the predominant vegetation

scenario near the A28 highway, which may be

impacted by increased urban construction by 2050.

The imagem also highlights an on-site view of the

area. The red arrow indicates the direction of the

photo's viewpoint.

Figure 8: Changes in 2050 for Póvoa de Varzim.

Vila Nova de Gaia, located south of Porto, is

expected to expand residential growth in areas with

exposed soil and available land, as highlighted in

Figure 9.

The results presented for the Metropolitan

Regions of Rio de Janeiro (RMRJ) and the

Metropolitan Area of Porto offer distinct perspectives

regarding urban expansion projections. In the RMRJ,

there is a notable focus on specific expansion areas,

particularly in sub-regions with significant growth,

such as the Baixada Fluminense and the East

Fluminense. In the case of the Metropolitan Area of

Porto, direct changes in land use stand out, detailing

transformations in agriculture and urbanized

territories. The conversion of areas from scrubland

and agriculture into urbanized territories is

emphasized. In both contexts, the results converge by

2030

2050

2023

2050

GE 2023

2050+GE

Urban Growth in Metropolitan Regions Using Dynamic Modeling by Cellular Automata: A Comparative Analysis Between Brazil and

Portugal

147

Figure 9: Changes in 2050 for Vila Nova de Gaia.

highlighting challenges related to urban growth, such

as inadequate infrastructure and environmental

impacts, underscoring the need for sustainable public

policies and careful urban planning in both regions.

5 CONCLUSIONS

This study presents a synthesis of the outcomes

achieved by employing cellular automata to perform

dynamic modeling in multiple metropolitan regions

of Portugal and Brazil. The research centers on the

primary discoveries, taking into account the specific

characteristics of each nation and the data utilized,

while analyzing the metropolitan areas of Rio de

Janeiro (RMRJ) and Porto (AMP). The DinamicaEgo

software was modified with respect to the

fundamental data that represented static and dynamic

variables in each respective context. The findings

unveiled a significant rise in RMRJ, thereby

illustrating the model's versatility in different

settings, contingent upon the data requirements of

each country.

The findings pertaining to urban expansion

projections for the Metropolitan Region of Rio de

Janeiro (RMRJ) and the Metropolitan Area of Porto

(AMP) present unique and discernible viewpoints.

RMRJ places considerable emphasis on particular

expansion zones, particularly in rapidly developing

subregions like Baixada Fluminense and East

Fluminense. Particular attention is paid to explicit

alterations in land use within AMP, which pertain to

agricultural and urbanized regions. Both contexts

emphasis the transformation of agricultural and

scrubland regions into urbanized ones. The findings

converge in that they emphasize the environmental

impacts and insufficient infrastructure associated

with urban expansion, thereby emphasizing the

necessity for sustainable public policies and

meticulous urban planning in both areas.

In future stages of the research, new variables are

intended to be included in the modeling process. The

boundaries of protected areas in the AMP may improve

the delineation of urban areas for future decades.

ACKNOWLEDGEMENTS

We would like to express our sincere gratitude to

CNPq (National Council for Scientific and

Technological Development) and FAPERJ

(Foundation for Research Support of the State of Rio

de Janeiro) for their financial support, which was

essential to the successful development of this

research. Their contributions have played a crucial

role in enabling us to carry out this work.

REFERENCES

Barredo, J.; Kasanko, M.; McCormick, N.; Lavalle, C.

(2003) Modelling dynamic spatial processes:

simulation of urban future scenar-ios through cellular

automata. Landscape and Urban Planning, 64, 145–

160.

Chapin, J.R.; Weiss, S.F. (1968). A probabilistic model for

residential growth. Transportation Research, v.2 p 375-

390.

Clarke, K.; Hoppen, S.; Gaydos, L. (1997) A self-modifying

cellular automaton model of historical urbanization in

the San Francisco Bay area. Environment and Planning

B, 24, 247–261.

Couclelis, H. (1989) Macrostructure and Microbehavior in

a Metropolitan Area. Environment and Planning B,

v.16, p.141-154.

Druck, S., Carvalho, M. S., Câmara, G., & Monteiro, A. V.

M. (2004). Análise Espacial de Dados Geográficos.

Brasília: Embrapa.

Freire, F. H. M. A. (2015). Introdução à Estatística

Espacial. Recuperado de http://www.observatoriodas

metropoles.ufrj.br/download/aulasanalise-espacial.pdf/

Instituto Brasileiro de Geografia e Estatística (IBGE).

(2022). Censo results 2022. Acesso https://censo20

22.ibge.gov.br/panorama/

Instituto Nacional de Estatística (INE). (2022). Land Use

and Occupation Map (COS2022). Lisboa: INE.

2030

2050

2023

GISTAM 2025 - 11th International Conference on Geographical Information Systems Theory, Applications and Management

148

Meyer, W. B., & Turner, B. L. (1992). Human population

growth and global land-use/cover change. Annual

review of ecology and systematics, 23(1), 39-61.

Soares-Filho, B. S., Cerqueira, G. C., & Pennachin, C. L.

(2002). DINAMICA—a stochastic cellular automata

model designed to simulate the landscape dynamics in

an Amazonian colonization frontier. Ecological

Modelling, 154(3), 217-235.

Tobler, W. R. (1970). A computer movie simulating urban

growth in the Detroit region. Economic Geography,

46(2), 234–240.

White, R.; Engelen, G.; Uljee, I. (1997) The use of

constrained cellular automata for high-resolution

modeling of urban land use dy-namics. Environment

and Planning B, 24, 323–343.

White, R.; Engelen, G. (1993). Cellular automata and

fractal urban form: a cellular modelling approach to

the evolution of land use patterns. Environment and

Planning A, 25, 1175–1199.

Wolfram, S. (1983) Statistical mechanics of cellular

automata. Review of modern physics, v. 55, p.601-643.

Wu, F. (1998) SimLand: A prototype to simulate land

conversion through the integrated GIS and CA with

AHP-derived transition rules. International Journal of

Geographical Information Systems, 12(1), 63–82.

Urban Growth in Metropolitan Regions Using Dynamic Modeling by Cellular Automata: A Comparative Analysis Between Brazil and

Portugal

149