Exploring and Evaluating Interplays of BPpy with Deep Reinforcement

Learning and Formal Methods

Tom Yaacov

, Gera Weiss

, Adiel Ashrov

, Guy Katz

and Jules Zisser

Ben-Gurion University of the Negev, Israel

The Hebrew University of Jerusalem, Israel

Keywords:

Behavioral Programming, Deep Reinforcement Learning, Formal Methods.

Abstract:

We explore and evaluate the interactions between Behavioral Programming (BP) and a range of Artiﬁcial In-

telligence (AI) and Formal Methods (FM) techniques. Our goal is to demonstrate that BP can serve as an

abstraction that integrates various techniques, enabling a multifaceted analysis and a rich development pro-

cess. Speciﬁcally, the paper examines how the BPpy framework, a Python-based implementation of BP, is

enhanced by and enhances various FM and AI tools. We assess how integrating BP with tools such as Satisﬁ-

ability Modulo Theory (SMT) solvers, symbolic and probabilistic model checking, and Deep Reinforcement

Learning (DRL) allow us to scale the abilities of BP to model complex systems. Additionally, we illustrate

how developers can leverage multiple tools within a single modeling and development task. The paper pro-

vides quantitative and qualitative evidence supporting the feasibility of our vision to create a comprehensive

toolbox for harnessing AI and FM methods in a uniﬁed development framework.

1 INTRODUCTION

It is commonly agreed that the future of software de-

velopment, especially in reactive systems, relies on

the use of models, advanced analysis techniques, and

artiﬁcial intelligence (AI) (Naveed et al., 2024). How-

ever, while the current state-of-the-art involves vari-

ous analysis tools and techniques, each still uses its

own input language and modeling approach, requir-

ing manual integration to combine results with system

code. Finding a modeling framework that can safely

interweave user code and machine-generated artifacts

while supporting formal analysis is a challenging re-

search problem. This paper examines the Behavioral

Programming (BP) framework (Harel et al., 2012)

and its potential as a uniﬁed modeling abstraction that

glues tools without manual translation, showing its

effectiveness in combining multiple tools throughout

the software development process.

BP is a software engineering paradigm designed

to allow developers to specify the behavior of reactive

systems incrementally and intuitively, aligning with

how they perceive the system’s requirements (Harel

et al., 2012). Its primary strength lies in its abil-

ity to break down intricate speciﬁcations into man-

ageable components that interact through a uniﬁed

protocol, enabling the creation of desired behavior.

This compositional modeling capability can be ap-

plied across various domains (Bar-Sinai et al., 2018)

and integrated with techniques from different disci-

plines (Bar-Sinai and Weiss, 2021).

The beneﬁts afforded by BP to traditional software

engineering have been studied extensively (Elyasaf

et al., 2019; Elyasaf, 2021). In this work, we aim

to complement existing research by focusing on the

problem at hand — namely, the integration of BP with

AI and formal analysis (FM) techniques. Speciﬁcally,

we utilize the BPpy library (Yaacov, 2023), a frame-

work for BP in Python, along with several Python-

based libraries, to explore the interplay and beneﬁts

that arise from these combinations. Ultimately, we

aim to lay the groundwork for constructing a compre-

hensive software engineering toolbox to harness mod-

ern AI and FM techniques.

Our contributions include:

Satisﬁability-Modulo-Theory (SMT): We present an

enhanced communication protocol among modules

for solving complex constraint systems and show it

promotes the efﬁciency of the execution mechanism.

Symbolic Model Checking: We developed a method

that allows the veriﬁcation of large BP models by an-

alyzing each module separately and combining them

symbolically.

Yaacov, T., Weiss, G., Ashrov, A., Katz, G. and Zisser, J.

Exploring and Evaluating Interplays of BPpy with Deep Reinforcement Learning and Formal Methods.

DOI: 10.5220/0013215200003928

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 20th International Conference on Evaluation of Novel Approaches to Software Engineering (ENASE 2025), pages 27-40

ISBN: 978-989-758-742-9; ISSN: 2184-4895

Probabilistic Model Checking: We designed an ap-

proach that facilitates the analysis of probabilistic as-

pects of a behavioral system.

Deep Reinforcement Learning (DRL): We present a

framework that improves the alignment of require-

ments with BP modules, delivering a more efﬁcient

execution mechanism.

While this is not the main focus of the paper, it is

worth noting that beneﬁts go both ways: BP’s effec-

tive system components management can boost these

tools. For instance, BP can serve as a theory for SMT

solvers by dynamically generating candidate runs and

incrementally revealing constraints, like other theo-

ries guide the solver’s reasoning process. In the con-

text of DRL, we leverage the ﬂexibility offered by BP

to specify a system’s behavior only partially, leaving

gaps for the DRL engine to resolve. This approach

can help guide the learning process and safeguard the

resulting execution mechanism from leading to unde-

sirable outcomes. BP’s ﬂexible division of the model

into smaller modules can also aid in symbolic or prob-

abilistic veriﬁcation process and facilitate more natu-

ral and direct modeling. This differs from current al-

ternatives, focusing on a monolithic state-based sys-

tem description.

This study not only focuses on new integrations.

While the symbolic and probabilistic veriﬁcation in-

tegrations presented here are novel, the combina-

tion of SMT and DRL with BP was discussed in

prior research (Katz et al., 2019; Eitan and Harel,

2011; Elyasaf et al., 2019; Yaacov, 2023). To pro-

vide a comprehensive understanding of the beneﬁts of

these integrations, we incorporated ideas from previ-

ous work, introduced new tools, and conducted fresh

evaluations comparing them against current alterna-

tives in BP to assess the effectiveness of all tools in

new dimensions.

As a glimpse into a future research direction, we

also present a small experiment showing the applica-

bility of combining SMT solvers, probabilistic mod-

eling, and DRL in conjunction with BP. The result of

this study provides compelling evidence, in our opin-

ion, of the viability of using BP as a modeling ap-

proach that supports all the aforementioned methods.

The structure of the paper is as follows: We

start with a short introduction to BP and BPpy

in Section 2. Subsequently, each integration is

discussed individually in sections 3 to 6. These

sections include evaluations and analyses. We

do not devote separate sections to related work

and comprehensive conclusions, as relevant refer-

ences and discussion are provided within each sec-

tion. In Section 7, we showcase the combined

use of these integrations. All supplementary mate-

rial is available at https://github.com/bThink-BGU/

Papers-2025-ENASE-BPpyEvaluation.

2 BEHAVIORAL

PROGRAMMING & BPpy

To introduce the reader to the language of BP, we be-

gin by describing the BPpy package and the general

BP principles it implements. In BP, developers spec-

ify scenarios, named b-threads, which are simple se-

quential threads of execution that represent behaviors

the system should include or avoid. Each scenario is

standalone and is usually self-contained, concerning

itself with a speciﬁc aspect of the system—typically,

a single requirement. During runtime, an application-

agnostic execution mechanism interprets and inter-

weaves these b-threads to generate a cohesive system

behavior. Speciﬁcally, the mechanism is based on a

synchronization protocol presented by (Harel et al.,

2010). It consists of each b-thread submitting a state-

ment before selecting each event that the b-program

produces. When a b-thread reaches a point where

it is ready to submit a statement, it synchronizes a

statement with its peers, declaring which events it

requests, which events it waits for (but does not re-

quest), and which events it blocks (prevents from oc-

curring). After submitting the statement, the b-thread

is paused. Once all b-threads have submitted their

statements, we say the b-program has reached a syn-

chronization point. At this point, an event arbiter se-

lects a single event that has been requested and is not

blocked. It then resumes all b-threads that either re-

quested or waited for the selected event. The other b-

threads remain paused, and their statements are used

in the next synchronization point. This process is re-

peated throughout the execution of the program. A

formal deﬁnition of BP semantics is available as an

appendix in the supplementary material.

To make BP’s core concepts more concrete, we

begin with an illustrative example of a b-program (a

set of b-threads) implemented in BPpy. The example

is an adaptation of one of the sample b-programs pre-

sented in the work of (Harel et al., 2012) describing

a system responsible for controlling the mixing of hot

and cold water from two separate taps. Listing 1 de-

picts three b-threads. Each b-thread is implemented

as a Python generator—a function that can pause it-

self and pass data back to its caller at any point, using

the yield idiom. It can then be resumed when re-

invoked with the send method. The statements sub-

mitted by each b-thread are structured as sync class

instances containing events or event sets labeled by

the arguments request, block, waitFor. The exe-

ENASE 2025 - 20th International Conference on Evaluation of Novel Approaches to Software Engineering

cution mechanism in BPpy starts by independently in-

voking each b-thread generator and awaiting its state-

ment yield. Once all the statements have been col-

lected, an event is selected, and the program resumes

its execution based on the aforementioned synchro-

nization protocol.

@t hr ead

def ad d_ ho t () :

for i i n ra nge (3) :

yi eld sy n c ( r e qu es t = BE ve nt ( " HOT " ) )

@t hr ead

def ad d_ co ld ( ) :

for i i n ra nge (3) :

yi eld sy n c ( r e qu es t = BE ve nt ( " CO LD " ))

@t hr ead

def co nt ro l () :

wh ile Tr u e :

yi eld sy n c ( w a it Fo r = BE ve nt ( " HOT " ) )

yi eld sy n c ( w a it Fo r = All () , bl ock = BEv en t (" H OT " ))

Listing 1: The HOT/COLD b-program (Harel et al., 2012).

The ﬁrst two b-threads, add_hot and add_cold,

request the event of pouring a small amount of hot and

cold water, respectively, three times. Unlike many

other programming paradigms, BP offers developers

the ﬂexibility not to be bound by a single predeﬁned

behavior for the system. Instead, the system has the

freedom to select any behavior that aligns with all the

deﬁned b-threads. For instance, a b-program consist-

ing of the two b-threads shown in Listing 1 does not

impose a speciﬁc order for pouring hot and cold wa-

ter. Consequently, its execution can generate all se-

quences that include exactly three occurrences of the

HOT event and three occurrences of the COLD event.

To illustrate further, consider that after running

the initial version of the system for some time, a

safety concern arises, and a new requirement is in-

troduced, stating that it is undesirable to have two

consecutive HOT events. While it is possible to mod-

ify the add_hot b-thread by adding new conditions

and statements, the BP paradigm encourages us to

maintain the alignment between existing b-threads

and their respective requirements and add a new b-

thread. This approach promotes an incremental and

modular development style, where developers can add

or remove behaviors independently without affecting

other b-threads. Thus, we introduce the control b-

thread in Listing 1, which repeatedly waits for the oc-

currence of HOT and then blocks HOT while waiting for

any following event using the All event set.

3 BP ⇔ SMT SOLVERS

BPpy implements SMT solver integration following

the concepts outlined in (Katz et al., 2019). The im-

plementation is based on the Z3-solver (De Moura

and Bjørner, 2008) package, although other solvers

may also be used. In this integration, events are

represented as an assignment over a set of SMT

variables. At each synchronization point, b-threads

specify request/block/waitFor constraints over the

variables in the form of logical statements to be sat-

isﬁed. Once all constraints are collected, the execu-

tion mechanism invokes the solver to ﬁnd a satisfying

assignment to the variables embedded in these con-

straints. Speciﬁcally, the solver ﬁnds an assignment

requested by at least one b-thread that is not blocked.

To introduce this integration, we begin with

an illustration of the Cinderella-Stepmother prob-

lem (Bodlaender et al., 2012). This problem involves

a two-player game with a system of water buckets.

Initially, there are N empty buckets arranged in a cir-

cle, each with a capacity of B water units. In each

turn, Cinderella’s stepmother distributes A water units

across the buckets as she chooses. Subsequently, Cin-

derella empties C adjacent buckets. This cycle of the

stepmother pouring and Cinderella emptying repeats.

The stepmother’s objective is to ﬁll one bucket with

B units, while Cinderella aims to prevent any bucket

from becoming full.

The code in Listing 2 exempliﬁes a solver-based

version of the Cinderella-Stepmother example. It

consists of the main b-thread, which is responsible

for changing the assignments to the buckets list of

integers based on the constraints generated by the

stepmother and cinderella functions. These func-

tions use the last selected assignment, which is re-

turned through the b-thread’s yield command. The

bucket_limit b-thread ensures that the variables

will not exceed the buckets’ capacity B. We note that

bucket_limit does not specify request or wait-for

constraints. Thus, its blocking constraint remains in-

variant throughout the execution of the b-program.

The SMT solver integration allows b-threads to

communicate versatile variable assignments, going

beyond discrete events. Along with its advantages

in enhancing expressiveness, extensively discussed

in (Katz et al., 2019), it can potentially improve BP’s

computational capabilities during execution. This

section aims to validate this assumption by compar-

ing the conventional discrete event mechanism and

the presented SMT-based event mechanism. To assess

this, a set of empirical experiments was carried out

to measure the runtime execution and memory efﬁ-

ciency of a b-program tasked with solving a multiple-

constraint problem using both approaches. The com-

plete code developed for this evaluation is available in

the supplementary material.

Exploring and Evaluating Interplays of BPpy with Deep Reinforcement Learning and Formal Methods

bu ck ets = [ In t (f "b { i} " ) for i in ran ge ( N) ]

def st ep mo th er ( pre v ):

ad ded = S um ([ b - pr e v . ev al ( b) f or b in b uc ke ts ] )

no n_ neg = And ( [ b - pr ev . e v al ( b) >=0 f or b in buc ke ts ] )

re tur n A nd ( ad de d == A , no n_ ne g )

def ci nd er el la ( pre v ):

r = l ist ( ran ge ( N ) ) + li st ( r a ng e (N ) )

def em pty ( r ng ) :

cs = [] # c on st ra in ts li s t

for j i n ra nge ( N ):

if j in r ng :

cs . ap pe nd ( b uc ke ts [ j] == 0)

el s e :

cs . ap pe nd ( b uc ke ts [ j] == pre v . ev a l ( b u ck et s [ j ] ) )

re tur n A nd ( cs )

re tur n O r ([ e m pt y (r [ i: i+ C ]) f or i in r an ge ( N) ])

@t hr ead

def bu ck et _ l i m i t () :

wh ile Tr u e :

yi eld sy n c ( bl oc k = O r ([ b > B for b i n b u ck et s ]) )

@t hr ead

def mai n () :

e= yie ld syn c ( re qu est = And ( [b = =0 f or b in b uc ke ts ] )

for i i n ra nge ( STE PS ) :

e = y ie ld syn c ( re qu e st = st ep mo th er ( e ))

e = y ie ld syn c ( re qu e st = ci nd er el la ( e ))

Listing 2: A BP solver-based implementation to the

Cinderella-Stepmother program.

The evaluation included three use cases. The ﬁrst

is the Cinderella-Stepmother problem, for which we

developed an equivalent discrete implementation and

compared its performance with the solver-based im-

plementation presented in Listing 2. This implemen-

tation generates all the possible states of the buckets

as individual events. We tested the programs with in-

creasing parameter values of B and N. Since the com-

plexity increases very rapidly in the discrete case with

N, we only show here the growth with B.

The second use case is an adaptation of the Lights

Out puzzle game (Anderson and Feil, 1998), which

we refer to as the bit-ﬂip problem. The problem do-

main is a Boolean matrix of dimensions N × M. At

ﬁrst, the matrix is randomly initialized, and in each

move, a single row or column values are ﬂipped.

Also, in each move, one row or column cannot be

ﬂipped, and it is therefore blocked. A potential ob-

jective is to ﬁnd a sequence of bit-ﬂips to transition

the matrix from one conﬁguration to another. This

problem is relevant as Boolean matrices can effec-

tively represent reactive systems such as communi-

cation networks.

For the third example, we implemented the circled

polygon example (see Figure 1). The program’s ob-

jective is to ﬁnd a coordinate outside a regular poly-

gon’s area but inside the circumscribing unit circle.

We tested this problem with an increasing number of

polygon edges. The problem relevance stems from

its multifaceted nature, common in reactive systems

with geometrical constraints involving real-valued pa-

rameters that BP is well-suited to solve (Katz et al.,

2019; Elyasaf, 2021). The discrete implementation

solves this multi-constraint problem by discretizing

the product of the two-dimensional continuous inter-

vals [−1, 1]

(the area enclosing the circle centered

at (0, 0)) incrementally. As the number of edges in

the polygon grows, the area between the polygon and

the circle diminishes, necessitating ﬁner discretiza-

tion and an increase in the number of events to ﬁnd

a solution.

y = x + 1

y = −x + 1

y = x − 1

y = −x − 1

+ y

= 1

(1, 0)

(0, 1)

(0, 0)(−1, 0)

(0, −1)

Figure 1: A circled

polygon problem with

4 edges. The colored

area between the poly-

gon and the circle rep-

resents the area of po-

tential solutions to the

problem.

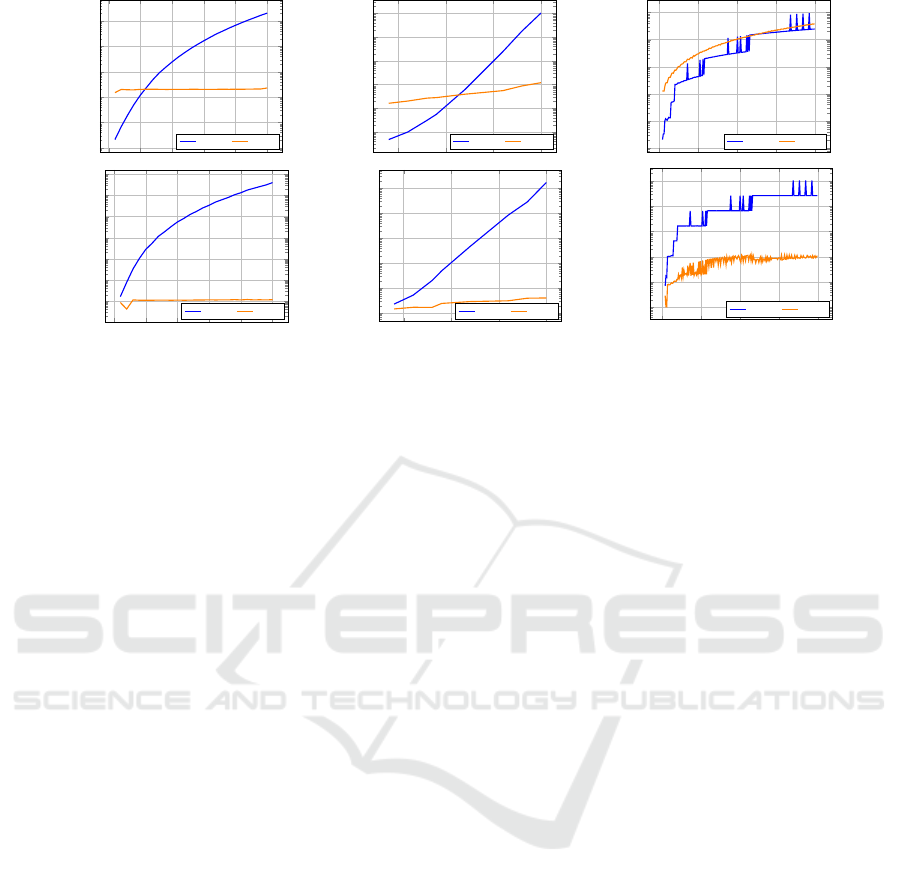
The memory and runtime results for the three use

cases are shown in Figure 2. For the Cinderella-

Stepmother and bit-ﬂip problem, the runtime and

memory performance of the discrete implementation

exponentially increases with B and N × M, respec-

tively. This behavior aligns with expectations, as

increasing parameter values increase the number of

events, which means that more events are being ex-

amined at the synchronization point, and hence, addi-

tional runtime and memory are needed. The runtime

and memory usage of the solver-based Cinderella-

Stepmother implementation remained constant as the

problem size increased, while the solver-based bit-

ﬂip implementation increased exponentially but with

a signiﬁcantly smaller slope.

For the circled polygon problem, both implemen-

tations exhibit a signiﬁcant increase in runtime as the

complexity rises, contrasting with previous results.

We attribute this latter increase to the fact that we

now have many equations over real-valued variables;

this may be because, in this model, the SMT engine

runs the theory module many times. Interestingly, the

runtime of the discrete implementation remains simi-

lar or lower until n = 164, after which it spikes sig-

niﬁcantly. This behavior stems from varying com-

plexities, where some instances are straightforward

for the discrete implementation, while others require

ﬁner discretization. Regarding memory usage, the

solver-based implementation maintains a distinct ad-

vantage, stabilizing around n = 100. Nevertheless,

the memory values surpass those of previous exam-

ples, underscoring the problem’s complexity for the

solver. Conversely, the discrete version memory us-

age increases with ﬁner discretization as complexity

rises, with spikes similar to the runtime analysis, in-

dicating the discussed unexpected behavior.

ENASE 2025 - 20th International Conference on Evaluation of Novel Approaches to Software Engineering

Runtime (ms.)

Discrete Solver

Runtime (ms.)

Discrete Solver

100

150

200

Runtime (ms.)

Discrete Solver

−2

−1

Memory usage (KB)

Discrete Solver

(a) Cinderella-Stepmother

(N=5,C=2,A=5).

−2

−1

N X M

Memory usage (KB)

Discrete Solver

(b) bit-ﬂip.

100

150

200

Number of Edges (n)

Memory usage (KB)

Discrete Solver

Figure 2: The runtime and memory of the discrete and solver-based implementations for the three problems. The values on

the y-axis were converted to log

scale due to the variance in the original scales.

In summary, our study encompassed a perfor-

mance evaluation contrasting discrete and solver-

based implementations across the domains of

Boolean, Integer, and Real variables, with various

types of constraints and different levels of complex-

ities. The experiments conﬁrmed the anticipated su-

periority of the solver-based approach. Additionally,

we showcased the adaptability of BP’s SMT solvers

integration in tackling various problem scenarios.

The potential use of BP to enhance SMT capabil-

ities has been explored in prior studies (Harel et al.,

2013). While SMT solvers are crucial for various ap-

plications like software veriﬁcation and program syn-

thesis, their incompleteness can hinder their effective-

ness. Integrating BP with SMT can enhance system

robustness and reliability, potentially leading to more

advanced automated theorem-proving tools for spe-

ciﬁc theories like arithmetic and arrays. As mentioned

in the introduction, BP can serve as a theory for de-

ciding behavioral constraints in a setting where we try

to ﬁnd runs that satisfy a set of constraints modeled as

a composition of b-threads.

Qin et al. utilized SMT in conjunction with BIP

models, employing it to prune unsatisﬁable transitions

in Open Automata derived from Open pNets (Qin

et al., 2020). Their work emphasizes formal analy-

sis rather than enhancing the underlying mechanism.

In contrast, our approach integrates SMT into BP to

introduce a decision mechanism for dynamically se-

lecting events, thereby increasing its expressiveness

and adaptability.

4 BP ⇔ SYMBOLIC MODEL

CHECKING

This section introduces a new method for verifying b-

programs by translating them into the SMV symbolic

speciﬁcation language (McMillan, 1993). A signif-

icant advantage of this method is its ability to ver-

ify software written in languages like Python, where

the states of the b-threads, modeled as generators,

are not readily clonable (Yaacov, 2023). We evalu-

ate the efﬁciency of symbolic model checking in BP

programs and compare it with the current best prac-

tices in BP veriﬁcation, which rely on explicit model

checking, involving an exhaustive enumeration of the

state space.

As in other modeling paradigms, veriﬁcation is a

subject of considerable work. Some introduced model

checking methodologies and accompanying tools for

verifying safety and liveness properties in behavioral

programs (Harel et al., 2011; Bar-Sinai and Weiss,

2021). Other studies have explored the potential ben-

eﬁts of BP’s compositionality in scalable veriﬁcation

and its applications (Harel et al., 2013). See also (Qin

et al., 2020) for a similar approach using the BIP

modeling framework. However, previous work on BP

veriﬁcation primarily concentrated on explicit model

checking. As systems grow in size and complexity,

the limitations of explicit model checking become ap-

parent, necessitating the adoption of symbolic veriﬁ-

cation techniques as an imperative alternative.

BPpy’s symbolic model checker takes a unique

approach by utilizing the inherent compositional-

ity of behavioral programs. It independently ex-

Exploring and Evaluating Interplays of BPpy with Deep Reinforcement Learning and Formal Methods

plores the state space of each b-thread and ana-

lyzes the product space symbolically, avoiding the ex-

plicit enumeration of all states. More speciﬁcally,

when applying symbolic model checking in BPpy,

b-programs are automatically translated to an SMV

model (McMillan, 1993) and veriﬁed symbolically

using PyNuSMV (Busard and Pecheur, 2013). The

translation maps each b-thread to an SMV module,

which reﬂects the space explored using Depth First

Search (DFS). For instance, consider the module pre-

sented in Listing 3, which represents the add_hot b-

thread in Listing 1. Within each b-thread module,

there exists a local variable called state, capturing

the current state of the b-thread. Additionally, each

module incorporates local Boolean variables for each

event that the associated b-thread may either request

or block. For example, since the add_hot b-thread

requests the HOT event, its corresponding module con-

tains the Boolean variable HOT_requested, which

dynamically changes based on the current state.

MO DUL E add _h ot ( e ve nt )

VAR

st ate : 0 .. 4 ;

HO T_ re qu es t e d : b oo le an ;

IN I T

st ate = 0

AS SIG N

HO T_ re qu es t e d :=

ca s e

st ate = 2 | s t at e = 1 | s t at e = 0 : T R UE ;

st ate = 3 : FA LS E ;

TR U E : FA LS E ;

es a c ;

ne x t ( st at e ) :=

ca s e

ne x t ( ev en t ) = HO T : sta te + 1;

TR U E : st at e ;

es a c ;

Listing 3: The add_hot b-thread translation to SMV.

Listing 4 depicts the main module of the translated

SMV model derived from HOT/COLD b-program

discussed in Section 2. In the translated model, this

main module functions as the event arbiter for the b-

program and implements BP semantics. It initiates

an enumerated variable event, representing the cur-

rently selected event. The event variable can take

any of the events requested across all b-threads, in ad-

dition to two auxiliary events, BPROGRAM_START and

BPROGRAM_DONE, marking the program’s start and end

of execution, respectively. Further, the main module

activates all the b-threads of the program as module

instances. It tracks each b-thread instance, requested

and blocked variables, by using the DEFINE opera-

tor. To capture the b-program’s dynamics, the sys-

tem deﬁnes a transition relation that allows the next

event value to be any currently enabled event. If

no such event exists, the b-program terminates, and

the system transitions to a sink state where event =

BPROGRAM_DONE. This setting facilitates the detec-

tion of possible violations related to the termination

of the b-program, such as deadlocks or early termina-

tion scenarios.

MO DUL E main

VAR

ev ent :{ B PR OGR AM _S TA R T , BP R OG RA M_D ON E , HOT , COL D };

bt0 : add _h ot ( e ve n t ) ;

bt1 : add _c ol d ( ev en t );

bt2 : con tr ol ( e ve n t ) ;

IN I T

ev ent = BP RO GR AM _S T A R T

DE FIN E

HO T_ re qu es t e d := bt0 . H O T _ r e qu es te d ;

HO T_ bl oc ke d : = bt2 . H OT _b lo ck ed ;

CO LD _r e q u e s te d := bt1 . C OL D_ re q u e s t ed ;

CO LD _b lo ck ed := b t2 . C OL D_ bl oc ke d ;

HO T_ en ab le d : = H O T _ r eq ue st ed & ! H OT _b lo ck ed ;

CO LD _e na bl ed := CO LD _r eq ue st ed & ! C OL D_ bl oc ke d ;

TR ANS

ne x t ( ev en t ) != B P R O G RA M_ ST AR T & (! HO T_ en ab le d - > n ext (

ev ent ) ! = HOT ) & (! C O L D _ e na bl ed -> ne xt ( e ven t ) !=

CO L D ) & ( H OT _e na bl ed | CO LD _e na bl ed -> n ext ( e ve nt ) !=

BP RO GR AM _D O N E ) & ( eve nt = BP RO GR AM _D ON E - > nex t (

ev ent ) = B P R O GR AM _D ON E )

Listing 4: The translated main module of the HOT/COLD

b-program discussed in Section 2.

We now turn to a performance evaluation for the

aforementioned approach. All programs and tools

used for evaluation in this study are available in the

supplementary material. The evaluation involved sev-

eral b-programs, including 1) The HOT/COLD exam-

ple presented in Section 2 with an increasing num-

ber of portions (N) and cold b-threads (M); 2) The

Dining Philosophers b-program presented in (Elyasaf

et al., 2023); and 3) The Tic-Tac-Toe game presented

in (Elyasaf et al., 2023). For this evaluation, all the

speciﬁcations we considered hold (i.e., no violations

are discovered through model checking) to examine

how quickly the various approaches can traverse the

entire search space. We compared the results against

similar b-programs veriﬁed using BPjs (Bar-Sinai and

Weiss, 2021), a Java-based tool for running and an-

alyzing behavioral programs written in JavaScript,

which is the current best practice in BP veriﬁcation.

The symbolic veriﬁer in BPpy can function in two

modes: Binary Decision Diagrams (BDD) and SAT-

based Bounded Model Checking (BMC), where the

model is unrolled for a ﬁxed number of steps and is

checked for violations that can occur within that num-

ber of steps or fewer. We compared these modes to

the BPjs veriﬁer in unbounded and bounded modes,

respectively. The results are available in Table 1.

In terms of memory consumption, both symbolic

model checkers outperformed the explicit veriﬁer, es-

pecially the BDD-based veriﬁer, exhibiting improved

efﬁciency. This result aligns with expectations, given

that the program’s state space is symbolically rep-

resented through BDDs or logical formulas rather

than being explicitly enumerated. Regarding veriﬁ-

cation time, we observed that the BDD-based model

ENASE 2025 - 20th International Conference on Evaluation of Novel Approaches to Software Engineering

Table 1: The average time and memory (over 10 repe-

titions) required to verify b-programs in BPpy and BPjs.

The Binary Decision Diagrams (BDD) and SAT-based

Bounded Model Checking (BMC) modes implemented in

BPpy are compared against the BPjs veriﬁer in unbounded

and bounded modes, respectively.

Unbounded Bounded

time

memory

time

memory

N,M |E|

|S|

BDD BPjs BDD BPjs BMC BPjs BMC BPjs

HOT/

COLD

30,1 2 121 2.9 5.1 0.08 0.24 3.8 5.2 0.09 0.23

60,1 2 122 3.5 5.3 0.08 0.29 5.0 5.3 0.13 0.29

90,1 2 182 4.2 5.6 0.08 0.34 7.9 5.4 0.19 0.36

30,2 3 1022 3.5 10.0 0.08 0.78 5.2 8.4 0.10 1.03

60,2 3 3842 4.4 50.9 0.09 1.21 18.3 22.6 0.18 1.64

90,2 3 8462 5.3 215.6 0.11 1.32 99.1 102.0 0.37 1.65

30,3 4 11437 3.9 398.8 0.08 1.19 5.4 223.9 0.10 1.61

60,3 4 158901 5.1 t.o. 0.11 t.o. 22.7 t.o. 0.20 t.o.

90,3 4 519151 7.4 t.o. 0.13 t.o. 121.5 t.o. 0.46 t.o.

Dining

Phil.

3,- 12 106 4.6 6.1 0.12 0.29 5.5 4.5 0.08 0.25

6,- 36 30862 t.o. 56.8 t.o. 0.97 8.0 5.0 0.09 0.30

9,- 54 3299501 t.o. o.m. t.o. o.m. 11.2 5.8 0.10 0.36

TTT 3,- 21 69502 t.o. 1852.1 t.o. 10.01 26.1 750.6 0.15 7.98

the number of program events,

the number of program states,

in sec-

onds,

in GB, o.m. out of memory (16GB), t.o. timeout (60 minutes)

checker excelled in the examples where the total num-

ber of events remained relatively small. However,

as the number of events increased, the veriﬁcation

time for the BDD-based model checker experienced

a signiﬁcant surge. Conversely, when considering

the bounded option, BMC demonstrated greater re-

silience to a growing number of events in the b-

program, positioning itself as a more robust approach.

The translation of B-programs into SMV mod-

els, utilizing their inherent compositionality, shows

promise for achieving scalability and efﬁciency in

veriﬁcation. Our future research will focus on en-

hancing the translation process to improve the veri-

ﬁcation of programs with a larger number of events.

Also, we aim to extend the symbolic model checking

support to various execution mechanisms and proto-

cols, including the one outlined in Section 3.

5 BP ⇔ PROBABILISTIC

MODELING

This section discusses BP as a modular language for

modeling and analyzing probabilistic systems, en-

hancing its semantics for compositional modeling of

probabilistic and non-deterministic behaviors. Tradi-

tionally, randomness in BP is introduced through a

random function for event selection, with the sync

node’s standard event selection protocol being an

example. However, this is limited as it only al-

lows uniform distributions. Since we want to al-

low non-uniform distribution, we take the alternative

approach of allowing a random behavior of the b-

threads. We want to deﬁne randomness in a way that

allows both execution (sampling) and model check-

ing. This poses a non-trivial challenge because, dur-

ing model checking, the analysis needs to consider

all possible paths with their probabilities. Thus, we

introduce the choice idiom, illustrated in Listing 5,

where a dictionary maps values to probabilities for

deﬁning categorical distributions in b-threads. These

distributions can be sampled during the execution of

a b-program or transformed for analysis.

def co in _f li p () :

si d e = y i el d c ho ice ({ " he ads " : 0.4 , " t ai ls " : 0.6 })

yi eld sy n c ( r e qu es t = BE ve nt ( s ide ) )

Listing 5: Uneven coin ﬂip using the choice statement.

The proposed BP model combines non-

determinism and probability for different modeling

purposes. Non-determinism is handled through sync

points with multiple events, while probabilities are

speciﬁed using choice. Non-determinism arises in

systems when there is a decision to make. Prob-

abilities are used to model uncontrolled random

events. Thus, during analysis, non-determinism

is typically addressed by analyzing contingencies,

while probabilities are computed for each path.

Executing programs with choice statements in-

volves random selection based on a speciﬁed dis-

tribution, facilitating naive sampling. Model anal-

ysis is done by translation into the PRISM lan-

guage (Kwiatkowska et al., 2011), a tool for analyzing

probabilistic systems with a module-based approach.

The translation process, largely similar to the one dis-

cussed for SMV in Section 4, has been automated

and integrated into BPpy. Supplementary material in-

cludes technical details about this process, code, and

documentation. We utilize the mdp model type in

PRISM to analyze systems that involve a combination

of non-determinism and probabilistic behavior.

We compared sampling and formal analysis to

evaluate translation performance. Experiments timed

the analysis of parametrized versions of three mod-

els. Sampling involved running models repeatedly

and monitoring outcomes. Formal veriﬁcation trans-

lated the model into PRISM format and veriﬁed it us-

ing Storm probabilistic model checker (Hensel et al.,

2022). All programs and tools used for this evaluation

can be found in the supplementary material.

The ﬁrst model, the classic Monty Hall problem,

which is infamous for its counter-intuitive solution,

is described as follows: “A game host hides a prize

behind one of three doors. The contestant guesses

which door has the prize. The host then opens one

Exploring and Evaluating Interplays of BPpy with Deep Reinforcement Learning and Formal Methods

door with no prize. The contestant can stick with

their choice or switch.” Our evaluation parameter-

ized the total number of doors, prizes, and doors

ruled out, as proposed in (Depuydt and Gill, 2012).

The model presented in Listing 6 consists of three

b-threads. The ﬁrst b-thread, named hide_prizes,

determines where to hide prizes, requests the hiding

events, blocks the opening of the doors with hidden

prizes until the opening phase is complete, and waits

for the contestant to open a door. It checks if the cho-

sen door contains a prize and accordingly announces

a win or lose event. We added the repeat, replace

, and sorted parameters to the choice statement to

ease the use of the idiom in cases where repeated sam-

pling is required. The make_a_guess b-thread waits

for the end of the hiding phase, guesses a door, and

then blocks its opening. The open_doors b-thread

waits for the guess and then requests to open doors

while blocking the already opened doors. Then, it re-

quests the event that marks the end of the host door

opening phase and the event for the door the contes-

tant eventually opens.

@t hr ead

def hi de _p ri ze s ( doo rs , p ri ze s_ nu m ):

pr ize s = y iel d c ho ic e ({ i : 1/ len ( d oor s ) fo r i in doo rs } ,

re pea t = p r iz es_ nu m , r ep la ce = Fa l se , s ort ed = T rue )

for hid e in pri ze s :

yi eld sy n c ( r e qu es t = BE ve nt ( f" hid e { hid e }" ) )

yi eld sy n c ( r e qu es t = BE ve nt ( " d on e_ hi di ng " ) )

do nt _o pe n = [ B Ev en t (f " op en { d} " ) f or d in p ri ze s ]

yi eld sy n c ( bl oc k = don t_ o pe n , w a it Fo r = BE ve nt ( " d on e_ op en in g " )

do o r = y i el d s ync ( w ai tF or = a ll _o pe n )

yi eld sy n c ( r e qu es t = BE ve nt ( " win " if int ( d o or . n ame [4 :]) in

pr ize s else " los e ") )

@t hr ead

def ma ke _a _ g u e s s () :

yi eld sy n c ( w a it Fo r = BE ve nt ( " d on e_ hi di ng " ) )

yi eld sy n c ( r e qu es t = BE ve nt ( f" gue ss {0} " ))

yi eld sy n c ( bl oc k = BE ven t ( f" o pen {0} " ) )

@t hr ead

def op en _d oo rs ( d oors , do or s_ op en ed _ n u m ) :

yi eld sy n c ( w a it Fo r =[ BE v en t ( f " g ues s {d } ") f or d in d oo rs ])

bl oc ked = []

for _ i n ra nge ( do or s_ o p e ne d_ nu m ) :

e = y ie ld syn c ( re qu e st = all _op en , b lo c k = b lo c ke d )

bl oc ked += [ e]

yi eld sy n c ( r e qu es t = BE ve nt ( " d on e_ op en in g " ))

yi eld sy n c ( r e qu es t = al l_o pen , blo ck = b lo cke )

Listing 6: A BPpy model of the Monty Hall problem.

The experiment included generating instances of

the b-program from Listing 6 for all parameter combi-

nations up to 10 doors. For sampling, we executed the

program 10,000 times to track the win event occur-

rence and used PRISM and Storm for model checking

to calculate the probability of reaching the win state.

The analysis time is the entire duration of Storm.

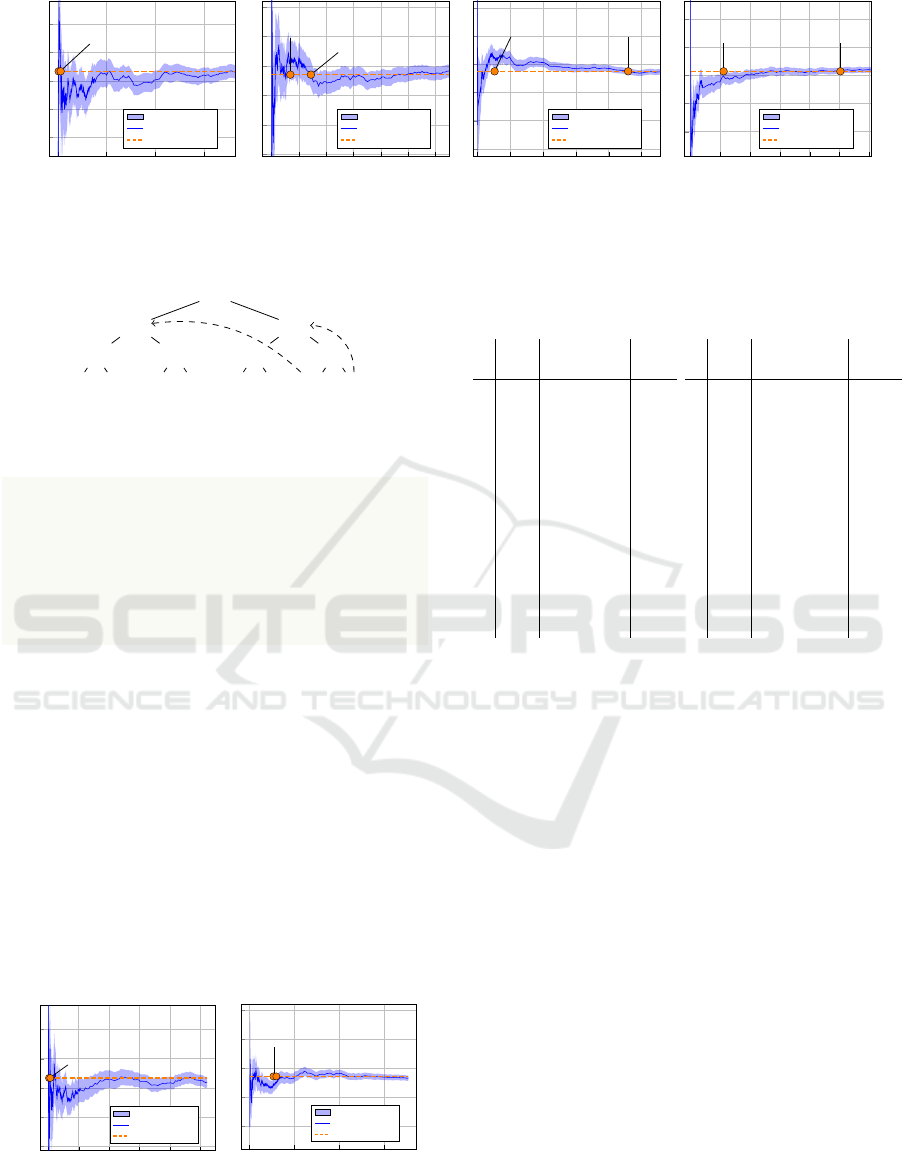
The results of applying two analysis methods to

the Monty Hall model with different parameter values

are shown in Figure 3. The blue line and halo depict

the mean and standard error of collected samples over

time. The dashed orange line shows the exact com-

putation value, and the orange circles mark the time

of translation to PRISM and the subsequent analysis.

These ﬁndings indicate that exact analysis yields re-

sults before sampling variance reaches acceptable er-

ror margins in all examined cases.

Table 2 provides a breakdown of the runtime for

the exact analysis in the proposed approach for the

Monty Hall model with 10 doors, distinguishing be-

tween PRISM model construction and Storm analy-

sis. An expected correlation exists between the time

spent on model translation and overall computation

time. The primary source of complexity appears to be

the number of doors opened, as the modeling process

times out entirely after 6 doors. This is likely due to

numerous different paths that do not merge, unlike the

situation with the number of prizes.

Table 2: Runtime in seconds for exact analysis with various

parameter combinations for the Monty Hall model with 10

doors. The table presents PRISM model construction times

on the left and Storm analysis times on the right.

Opened

Prizes 1 2 3 4 5 6

1 0.6/0.1 1.1/0.5 9.4/8.4 114.7/536.3 4120.6/t.o. t.o./t.o.

2 2.2/1.3 4.1/3.8 8.7/46.0 112.0/1401.4 3798.0/t.o. t.o./t.o.

3 6.5/5.9 7.6/18.3 13.2/136.3 122.1/t.o. 4376.5/t.o. t.o./t.o.

4 13.9/19. 15.5/52.8 21.0/252.7 123.3/t.o. 3874.2/t.o.

5 21.1/29.4 22.2/64.2 28.6/197.2 135.5/t.o.

6 17.8/19.9 18.2/34.5 24.7/77.5

7 10.1/6.4 10.9/8.4

8 8.3/1.4

t.o. timeout (two hours)

Our second evaluation involves modeling a fair

n-sided dice using fair coins, following Knuth’s al-

gorithm (Knuth, 1976) featured in PRISM. This al-

gorithm uses rejection sampling to minimize the ex-

pected coin tosses by simulating a uniform distribu-

tion over powers of two with fair coins. For example,

in the case of a six-sided die (see Figure 4), three coin

tosses yield 8 possibilities. If the resulting value of

the tosses is smaller than six, the algorithm accepts

it. Otherwise, the algorithm repeats the process as if

starting with the remainder. More complex cases may

involve multiple trees for simulation.

The BP model for this algorithm tracks coin ﬂips

through b-threads representing nodes in the sequence.

Each node waits for its parent. Then, depending on

its place in the tree, it either returns the dice value or

performs a toss and requests the corresponding next

node. This results in a simple model where all b-

threads can be generated by a single function shown

in Listing 7.

Results from the dice program analysis in Table 3

and Figure 5 align with our observations from smaller

ENASE 2025 - 20th International Conference on Evaluation of Novel Approaches to Software Engineering

0 2 4

0.62

0.64

0.66

0.68

0.7

Finished translation to PRISM

and computation

Time (s)

Sampling mean

Standard error

Sampling mean

Exact probability

(a) d = 3, p = 1, o = 1.

0 2 4

8 10 12

0.2

0.22

0.24

0.26

0.28

0.3

Finished translation

to PRISM

Finished

computation

Time (s)

Standard error

Sampling mean

Exact probability

(b) d = 9, p = 2, o = 1.

0 10 20 30 40

0.82

0.84

0.86

0.88

0.9

0.92

Finished translation

to PRISM

Finished

computation

Time (s)

Standard error

Sampling mean

Exact probability

0 20 40

80 100 120

0.6

0.62

0.64

0.66

0.68

Finished translation

to PRISM

Finished

computation

Time (s)

Standard error

Sampling mean

Exact probability

(d) d = 10, p = 5, 0 = 2.

Figure 3: A comparison of the sampling-based analysis and the exact analysis for the Monty Hall model with different values

of doors (d), prizes (p), and doors opened (o)..

1,0

2,0

4,0

8,0 8,1

4,1

8,2 8,3

2,1

4,2

8,4 8,5

4,3

8,6 8,7

Figure 4: An illustration of the process simulating a six-

sided dice using coin ﬂips.

@t hr ead

def nod e (u , x ) : # u : lay er si ze , x : in dex in l aye r

wh ile Tr u e :

yi eld sy n c ( w a it Fo r = BE ve nt ( f" n {u } _{ x} " ))

if u < n : # i nne r n ode

fl i p = y i el d c ho ice ({ 0:0 .5 , 1 :0. 5} )

yi eld sy n c ( r e qu es t = BE ve nt ( f" n {u * 2} _ {2* x + fl ip } ")

el s e : # l ast la ye r

if x >= n :

yi eld sy n c ( r e qu es t = BE ve nt ( f" n {u - n} _{ x %n } ") )

el s e :

yi eld sy n c ( r e qu es t = BE ve nt ( f" re sul t_ { x }" ) )

Listing 7: B-thread deﬁnition of any single node in the BP

model of Knuth’s algorithm (Knuth, 1976).

Monty Hall versions, where the exact analysis outper-

forms sampling. One difference from the previous ex-

ample was that translation, rather than computation,

was the more time-consuming part of the exact analy-

sis due to more b-threads and fewer commonly shared

events. This example is notable due to the unlimited

number of times it may repeat before yielding a re-

sult, making it particularly suited for exact analysis,

which explores the full possibility space simultane-

ously. We can observe that in more complex cases

like Figure 5b, the exact analysis still performs well

due to oversampling advantages.

0.12

0.14

0.16

0.18

0.2

Finished translation to PRISM

and computation

Time (s)

Sampling mean

Standard error

Sampling mean

Exact probability

(a) n = 6.

500

1,000

1,500

0.02

0.04

0.06

0.08

Finished translation to PRISM

and computation

Time (s)

Standard error

Sampling mean

Exact probability

(b) n = 29.

Figure 5: Comparison of the sampling-based and exact

analysis for the n-sided dice model.

Table 3: Exact analysis of various sizes for a dice. Some

require multiple trees which repeat the same structure.

n States

Trans./Comp.

time (s)

Result n States

Trans./Comp.

time (s)

Result

6 64 0.129/0.21 0.1667 19 1868 46.931/6.056 0.0526

7 68 0.141/0.053 0.1429 20 512 3.179/0.418 0.05

8 38 0.132/0.053 0.125 21 440 3.009/0.399 0.0476

9 292 1.361/0.214 0.1111 22 1200 20.060/2.451 0.0455

10 216 0.821/0.147 0.1 23 968 12.796/1.522 0.0435

11 596 5.095/0.635 0.0909 24 376 1.592/0.233 0.0417

12 168 0.423/0.097 0.0833 25 2744 101.133/12.561 0.04

13 848 9.941/1.191 0.0769 26 1704 39.804/5.134 0.0385

14 144 0.440/0.097 0.0714 27 2668 96.446/12.325 0.0370

15 148 0.443/0.099 0.0667 28 368 1.664/0.239 0.0357

16 78 0.451/0.097 0.0625 29 4448 265.348/33.184 0.03448

17 752 8.300/0.999 0.0588 30 304 1.705/0.237 0.03333

18 592 5.272/0.663 0.0556

Our last case study is a variation of the bit-ﬂip sce-

nario discussed in Section 3. In this variation, diago-

nals are initiated randomly, and the actions are taken

at each step, where each consecutive row or column

can be ﬂipped. The goal here is to ﬁnd a sequence

that results in the board having the same (or as close

as possible for odd-size boards) number of bits turned

on and off.

The translation part in the exact analysis of the

bit-ﬂip model was more challenging than in previous

cases, starting at relatively small matrix sizes. This

is due to the large number of board conﬁgurations in

this scenario. Each of the possible 2

n×m

possibilities

adds both an event and a state in each b-thread, re-

sulting in an exponential number of options that must

be explored in all of the b-threads during translation.

However, when considering all b-threads as a uniﬁed

b-program during exact analysis, the number of pos-

sible outcomes is relatively small.

We conducted a sampling-based analysis by mea-

suring 9, 999 runs or as many as possible within an

hour, as seen in Table 4. Sampling outperformed ex-

act analysis, supporting double the translation’s grid

size before slowing down. We suspect the difﬁcul-

ties stem from the sync events being a product of rel-

atively costly computations. Section 3 and Section 7

Exploring and Evaluating Interplays of BPpy with Deep Reinforcement Learning and Formal Methods

present an alternative analysis approach to the discrete

event selection mechanism used here by integrating

SMT solvers, which aims to address this issue.

Table 4: Sampling results of the discrete bit-ﬂip model with:

average, standard measurement error, number of samples

(Samp.), and average time per sample in seconds (Time).

Dim Mean SEM Sam. Time Dim Mean SEM Sam. Time

2x2 0.263 0.004 9999 0.002 3x3 0.441 0.005 9999 0.023

2x3 0.264 0.004 9999 0.004 3x4 0.178 0.004 9999 0.295

2x4 0.309 0.005 9999 0.008 3x5 0.329 0.014 1062 3.39

2x5 0.309 0.005 9999 0.041 3x6 0.197 0.052 61 59.934

2x6 0.241 0.004 9999 0.237 3x7 0.4 0.25 5 885.183

2x7 0.124 0.007 2476 1.454 4x4 0.209 0.024 292 12.34

2x8 0.081 0.013 456 7.903 4x5 0.143 0.167 7 554.663

2x9 0.13 0.051 46 79.496

The presented examples cover a wide range of

parameter values and diverse model types, spanning

from models with few states and minimal transitions,

such as the dice problem, to highly interconnected

ones in bit-ﬂip. Our methods show promise in differ-

ent problem domains, especially in smaller systems.

Modeling probabilistic systems with both non-

deterministic and probabilistic behavior has been ad-

dressed in various ways previously. Some mod-

els focus on representing systems with probabilis-

tic transitions (Puterman, 1990; Stoelinga, 2004),

while others are designed to represent systems with

non-deterministic choices (Rabin and Scott, 1959;

Savitch, 1970). For systems exhibiting both non-

deterministic and probabilistic behavior, models such

as PRISM (Kwiatkowska et al., 2011) are commonly

used. These models allow for a rich representation of

system dynamics, enabling the analysis and veriﬁca-

tion of system properties. The advantages of model-

ing randomness in BP have not been explored before.

The only reference to randomness we know of is in

event selection strategies (Harel et al., 2010).

6 BP ⇔ DRL

This section explores the interplay between BP and

deep reinforcement learning (DRL), focusing on how

it can enhance the alignment of requirements with BP

modules for more effective execution. We illustrate

how DRL’s advanced data processing and interpreta-

tion abilities can aid in designing complex systems

in BP. Subsequently, we discuss how BP’s structured

way of encoding rich behavioral speciﬁcations can

enhance DRL-driven solutions. This is demonstrated

using BPpy’s integration with Gymnasium (Towers

et al., 2023), a widely recognized API standard for

reinforcement learning (RL) environments.

The combination of RL and BP was ﬁrst intro-

duced by (Eitan and Harel, 2011), which enhanced

the semantics of live sequence charts (LSC), a visual

language for BP, by incorporating reinforcements and

applying learning algorithms. In recent years, this

combination has gained growing interest, with several

studies conducted with the assistance of BPpy. These

studies explored different ways this learning mecha-

nism can be combined with BP’s execution (Elyasaf

et al., 2019; Yaacov et al., 2024).

To illustrate how DRL can enhance the efﬁciency

of execution mechanisms in BP, we begin with an

evaluation of the Blueberry Pancake Maker exam-

ple presented in (Bar-Sinai, 2020). In this exam-

ple, a pancake batter is made from dry and wet

mixtures using a mixer controlled by a b-program.

The ﬁrst two b-threads in Listing 8 prepare batter

for n pancakes by adding n mixtures without spec-

ifying the order, which can lead to improper bat-

ter thickness. To prevent damage to the mixer,

we need to control the order of mixture additions.

The thickness_meter b-thread monitors thickness

changes, while the range_arbiter b-thread ensures

the thickness stays within [−b, b]. Next, we add

blueberries to the mix. To prevent the blueber-

ries from bursting during the mixing process, 75%

of the total mixture of batter should be added, and

the batter itself should be relatively thin. The b-

threads enough_batter and batter_thin_enough

block the blueberry addition event until these condi-

tions are met. Depending on the sequence in which

the dry and wet mixtures are added, scenarios may

arise where the AddBlueberries event, requested

by the blueberries b-thread, remains blocked by

batter_thin_enough throughout the program’s ex-

ecution. Such a situation would inevitably violate the

system requirements, as it would result in a pancake

mixture with no blueberries.

To address the risk of missing blueberries, one op-

tion is to deﬁne a speciﬁc sequence for their addition.

However, this becomes progressively more compli-

cated with larger systems and various requirements.

For instance, if dry and wet mixtures are not con-

sistently ready for addition, determining a strict se-

quence becomes more challenging and prone to er-

rors. Thus, our aim is to design ﬂexible b-programs

to allow for all valid behaviors.

To address the complexity in specifying that blue-

berries must eventually be added, we used the in-

tegration between BPpy and Gymnasium introduced

in (Yaacov, 2023). This integration encapsulates a b-

program as an RL environment, allowing developers

to delineate the program’s target objectives or opti-

mization criteria by incorporating the localReward

ENASE 2025 - 20th International Conference on Evaluation of Novel Approaches to Software Engineering

@t hr ead

def a d d _d ry _m ix tu re (n ) :

for i i n ra nge ( n ):

yi eld sy n c ( r e qu es t = D ry Mi xt u re () )

@t hr ead

def a d d _w et _m ix tu re (n ) :

for i i n ra nge ( n ):

yi eld sy n c ( r e qu es t = W et Mi xt u re () )

@t hr ead

def t h i ck ne ss _m et er () :

wh ile Tr u e :

e = y ie ld syn c ( wa it F or = mi xt ur e_ ad d )

if e == Dry Mi xt ur e () :

yi eld sy n c ( r e qu es t = T hi ck ne ss Up () , blo ck = mi xt ur e_ ad d )

el s e :

yi eld sy n c ( r e qu es t = Th ic kn ess Do wn , bl ock = mi xt ur e_ ad d )

@t hr ead

def ra n g e _ a rb it er ( b ):

th ic kn es s = 0

wh ile Tr u e :

e = y ie ld syn c ( wa it F or = an y_ th ic k )

th ic kn es s += 1 if e == Th ic kn es sU p () els e -1

if a b s ( th ic kn es s ) >= b :

bl oc k_e = Dr yM ix tu re () if thi ckn ess >0 els e W et Mi xt ur e ()

yi eld sy n c ( bl oc k = blo ck_e , w ait Fo r = m ix tu re _a dd )

el s e :

yi eld sy n c ( w a it Fo r = m ix tu re _a dd )

@t hr ead

def bl ue be rr ie s ( ) :

yi eld sy n c ( r e qu es t = A dd Bl ue be rr i e s ( ) )

@t hr ead

def en o u g h _ ba tt er ( n ):

for j i n ra nge ( i nt (( n * 3) / 2) ):

yi eld sy n c ( w a it Fo r = mi xt ure _a d d , b lo ck = A dd Bl u e b e r ri es () )

@t hr ead

def b a t te r_ th in _ e n ou gh ( n ):

th ic kn es s = 0

wh ile Tr u e :

if t hi ck ne ss >= 0:

e= yie ld syn c ( wa it For = an y _t h ic k , bl oc k = A dd Bl ue be rr ie s () )

el s e :

e= yie ld syn c ( wa it For = an y_ th ic k )

th ic kn es s += 1 if e . na me == " T hi ck ne ss Up " el s e -1

Listing 8: The Blueberry Pancake Maker b-program (Bar-

Sinai, 2020).

parameter. This parameter can be integrated into

any yield statement, complementing traditional re-

quirements and facilitating learning through RL algo-

rithms. Embedding these reward-based criteria within

BPpy streamlines the modeling of intricate systems,

fostering more intuitive and efﬁcient development

practices. Listing 9 demonstrates how rewards are

added to the blueberries b-thread, reﬂecting the

system’s preference for eventually adding blueberries.

@t hr ead

def bl ue be rr ie s ( ) :

yi eld sy n c ( r e qu es t = A dd Bl ue be rr i e s ( ) , lo ca lR ew ar d = - 0 .0 0 01 )

yi eld sy n c ( w a it Fo r = All () , lo ca lR ew ar d =1)

Listing 9: The updated blueberries b-thread which the

localReward parameter.

Our evaluation focused on the task of ﬁnding a

deterministic event selection mechanism to generate

a single execution trace adhering to system require-

ments. We compared two mechanisms. The ﬁrst uses

a DRL algorithm, wherein the state space is repre-

sented by local variables of the b-threads, serving as

input to the agent’s neural network. The learning al-

gorithm was aborted upon successful task completion,

producing a correct sequence of events in its predic-

tions. Speciﬁcally, we employed the Maskable PPO

algorithm (Huang and Onta

on, 2022) implemented

in the Stable Baselines3 package (Hill et al., 2018),

with a standard multilayer perception (MLP) network

with two hidden layers of size 64. The second mecha-

nism we evaluated uses an explicit program synthesis

approach, in which a valid execution trace is found by

exploring the program’s state space. This is consid-

ered the current standard approach, as it has been dis-

cussed previously, and is supported by existing tools.

The runtime and memory usage of the two mech-

anisms for ﬁnding a single execution trace are pre-

sented in Table 5. Tests were conducted with n ∈

{200, 300, 400, 500} and b ∈ {25, 50, 75, 100}. As ex-

pected, the runtime and memory of the synthesis ap-

proach increase with the problem size, especially n.

In contrast, the DRL approach’s runtime and memory

remain relatively stable. This can be attributed to the

fact that increasing n and b doesn’t change the num-

ber of program variables, keeping the neural network

complexity constant. This demonstrates that DRL can

be particularly beneﬁcial when system complexity is

due to variable value range rather than quantity.

Table 5: Comparison of average (over 10 repetitions) of

runtime and memory of the DRL and program synthesis ap-

proaches for ﬁnding a single valid execution trace.

Time

Memory

Time

Memory

n b DRL Syn. DRL Syn. n b DRL Syn. DRL Syn.

200

25 17 123 1.79 0.06

400

25 16 555 1.79 0.11

50 19 142 1.79 0.06 50 18 569 1.79 0.12

75 19 149 1.79 0.06 75 16 558 1.79 0.12

100 18 163 1.79 0.06 100 17 591 1.79 0.12

300

25 16 333 1.79 0.08

500

25 15 894 1.79 0.15

50 20 312 1.79 0.08 50 18 927 1.79 0.15

75 19 339 1.79 0.09 75 19 873 1.79 0.15

100 20 333 1.79 0.09 100 16 903 1.79 0.16

in seconds,

in GB

We also evaluated the Cinderella-Stepmother

problem from Section 3. In this variation, the DRL

mechanism needs to effectively handle a counter-

strategy of the stepmother described in (Shevrin

and Yossef, 2020), where in each round, the step-

mother maintains two buckets, which Cinderella can-

not empty at once, evenly ﬁlled. Once the stepmother

reaches a round in which one of the buckets can be

entirely ﬁlled, it does so and wins. The results of this

example experiment are provided as an appendix in

the supplementary material. The evaluation yielded

results similar to the pancake maker example. The ap-

pendix also contains early results for the task of ﬁnd-

Exploring and Evaluating Interplays of BPpy with Deep Reinforcement Learning and Formal Methods

0 0.2 0.4

0.6

0.8 1

·10

Learning time steps

Mean Reward

PPO

Random

Greedy

(a) 3 × 3.

0.5

1.5

·10

Learning time steps

PPO

Random

Greedy

(b) 4 × 4.

0.5

1.5

2.5

·10

Learning time steps

PPO

Random

Greedy

0 1 2 3 4

·10

100

Learning time steps

PPO

Random

Greedy

(d) 6 × 6.

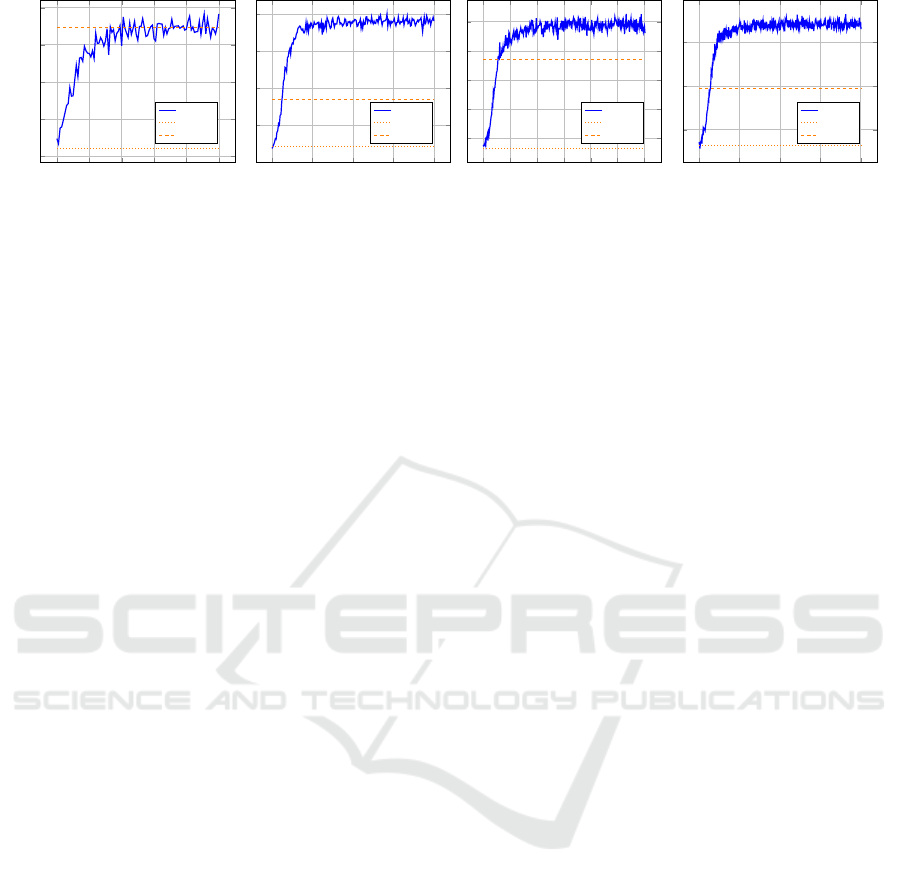
Figure 6: Mean reward of the PPO algorithm for the bit-ﬂip two-player game on square matrices of sizes 3 × 3, 4 × 4, 5 × 5,

and 6 × 6. The results are compared with random and greedy baseline strategies.

ing a non-deterministic event selection mechanism

that adheres to system requirements for the two ex-

amples. The results show that in both cases, the al-

gorithms converged to accurate strategies after a short

training time.

The evolving DRL ﬁeld presents challenges in

the safety, robustness, and interpretability of poli-

cies. Previous research suggests using BP to encode

expertise for enhancing training and system reliabil-

ity (Yerushalmi et al., 2023; Ashrov and Katz, 2023).

We note that BPpy supports knowledge encoding by

modifying rewards, features, and actions before re-

laying them to the learning algorithm or environment,

enhancing system safety and ease of training.

7 BP ⇔ (DRL+Probabilities+SMT)

In the previous sections, we saw four integrations of

BP with other mechanisms. As our vision is to use

BP as a unifying modeling language suited for com-

bining these methods, we demonstrate the interplay of

the different mechanisms described in the preceding

sections. Speciﬁcally, we show how the integrations

with SMT solvers, probabilistic modeling, and DRL

can be used together to create a comprehensive envi-

ronment that facilitates both modeling and analysis.

For this demonstration, we use a variation of the

bit-ﬂip problem described earlier: A two-player game

over a Boolean matrix of dimensions N × M. The ini-

tial state of the matrix resembles a chessboard with

alternating positive and negative bits. Our opponent

randomly ﬂips rows and columns, while our objec-

tive is to devise a strategy that involves strategically

ﬂipping rows or columns to turn on as many bits as

possible simultaneously. We can randomly ﬂip bits

or implement a greedy strategy that selects the row or

column with the highest number of bits to turn on in

each round. However, as we will demonstrate later, a

better strategy that is more challenging to implement

manually can be achieved using DRL.

Section 3 and Section 5 demonstrate how the dis-

crete implementation of the problem can be challeng-

ing for execution and analysis as the matrix size in-

creases. This section uses a solver-based implemen-

tation combined with the choice idiom presented in

Section 5 to model the opponent’s behavior. The

complete program used for the following evaluation,

along with a description of the code, is available in an

appendix in the supplementary material.

We ran the PPO algorithm (Huang and Onta

on,

2022) to learn a strategy for the task. The learned

strategy was compared against two baseline strate-

gies. The ﬁrst strategy randomly selects rows and

columns to ﬂip, while the second greedily selects the

row/column with the highest number of bits to turn

on in each round. The mean expected reward of these

strategies was computed using the choice idiom. Re-

sults are presented in Figure 6. We observe that the

PPO algorithm rapidly obtained a strategy that can

plan ahead and achieve better (or equal in the 3 × 3

case) results than the greedy approach in all matrix

sizes examined.

The bit-ﬂip demonstration shows how BP can

serve as a “Swiss army knife” for modeling and anal-

ysis: Starting with a problem that was challenging

to execute in a discrete program and upgrading it to

utilize solvers. Subsequently, DRL can be applied to

achieve a more effective strategy, and it can be evalu-

ated and compared using probabilistic analysis.

The integration of SMT, probabilistic model

checking, DRL, and BP holds great potential, as

the ﬁrst three are already closely linked. Many

probabilistic model checking problems are solved

using SMT-based constraint solving or linear opti-

mization, while DRL algorithms address scalability

issues in these problems. Tools like PRISM and

STORM demonstrate this synergy, combining solvers

and DRL. Extending this integration to BP could en-

able adaptive decision-making with formal guaran-

tees for complex systems.

ENASE 2025 - 20th International Conference on Evaluation of Novel Approaches to Software Engineering

8 CONCLUSION

In conclusion, our study focused on integrating BP

with a variety of techniques to establish a compre-

hensive framework for specifying and analyzing re-

active systems. Moving forward, our future work will

delve deeper into use cases involving multiple inte-

grations and explore more complex and extensive ex-

amples. Additionally, we plan to focus on evaluating

the usability of our proposed framework and assess

how well it aids in programming to increase adoption

and enhance accessibility.

ACKNOWLEDGEMENTS

This work of Weiss, Yaacov, and Zisser was partially

supported by funding from the Israel Science Founda-

tion (ISF) grant number 2714/19. The work of Ashrov

and Katz was partially funded by the European Union

(ERC, VeriDeL, 101112713). Views and opinions ex-

pressed are however those of the author(s) only and

do not necessarily reﬂect those of the European Union

or the European Research Council Executive Agency.

Neither the European Union nor the granting author-

ity can be held responsible for them.

REFERENCES

Anderson, M. and Feil, T. (1998). Turning lights out with

linear algebra. Mathematics Magazine.

Ashrov, A. and Katz, G. (2023). Enhancing Deep Learning

with Scenario-Based Override Rules: a Case Study.

In MODELSWARD.

Bar-Sinai, M. (2020). Extending Behavioral Programming

for Model-Driven Engineering. PhD Thesis, Ben-

Gurion University of the Negev, Israel.

Bar-Sinai, M. and Weiss, G. (2021). Veriﬁcation of Live-

ness and Safety Properties of Behavioral Programs

Using BPjs. In Leveraging Applications of For-

mal Methods, Veriﬁcation and Validation: Tools and

Trends.

Bar-Sinai, M., Weiss, G., and Shmuel, R. (2018). BPjs:

an extensible, open infrastructure for behavioral pro-

gramming research. In MODELS.

Bodlaender, M. H. L., Hurkens, C. A., Kusters, V. J., Staals,

F., Woeginger, G. J., and Zantema, H. (2012). Cin-

derella versus the wicked stepmother. In Theoretical

Computer Science.

Busard, S. and Pecheur, C. (2013). PyNuSMV: NuSMV as

a Python Library. In NASA Formal Methods.

De Moura, L. and Bjørner, N. (2008). Z3: An efﬁcient SMT

solver. In TACAS.

Depuydt, L. and Gill, R. D. (2012). Higher Variations of the

Monty Hall Problem (3.0 and 4.0) and Empirical Def-

inition of the Phenomenon of Mathematics, in Boole’s

Footsteps, as Something the Brain Does. Advances in

Pure Mathematics, 02.

Eitan, N. and Harel, D. (2011). Adaptive behavioral pro-

gramming. In ICTAI.

Elyasaf, A. (2021). Context-Oriented Behavioral Program-

ming. Information and Software Technology, 133.

Elyasaf, A., Sadon, A., Weiss, G., and Yaacov, T. (2019).

Using Behavioural Programming with Solver, Con-

text, and Deep Reinforcement Learning for Playing a

Simpliﬁed RoboCup-Type Game. In MODELS.

Elyasaf, A., Yaacov, T., and Weiss, G. (2023). What Petri

Nets Oblige us to Say: Comparing Approaches for

Behavior Composition. IEEE Transactions on Soft-

ware Engineering, 49.

Harel, D., Kantor, A., Katz, G., Marron, A., Mizrahi, L.,

and Weiss, G. (2013). On composing and proving the

correctness of reactive behavior. In EMSOFT.

Harel, D., Lampert, R., Marron, A., and Weiss, G. (2011).

Model-checking behavioral programs. In EMSOFT.

Harel, D., Marron, A., and Weiss, G. (2010). Programming

Coordinated Behavior in Java. In ECOOP.

Harel, D., Marron, A., and Weiss, G. (2012). Behavioral

programming. Communications of the ACM, 55.

Hensel, C., Junges, S., Katoen, J.-P., Quatmann, T., and

Volk, M. (2022). The probabilistic model checker

Storm. International Journal on Software Tools for

Technology Transfer, 24.

Hill, A., Rafﬁn, A., Ernestus, M., Gleave, A., Kanervisto,

A., Traore, R., Dhariwal, P., Hesse, C., Klimov, O.,

Nichol, A., Plappert, M., Radford, A., Schulman, J.,

Sidor, S., and Wu, Y. (2018). Stable Baselines.

Huang, S. and Onta

on, S. (2022). A Closer Look at Invalid

Action Masking in Policy Gradient Algorithms. In

FLAIRS.

Katz, G., Marron, A., Sadon, A., and Weiss, G. (2019). On-

the-ﬂy construction of composite events in scenario-

based modeling using constraint solvers. In MODEL-

SWARD.

Knuth, D. (1976). The complexity of nonuniform random

number generation. Algorithm and Complexity, New

Directions and Results.

Kwiatkowska, M., Norman, G., and Parker, D. (2011).

PRISM 4.0: Veriﬁcation of Probabilistic Real-Time

Systems. In CAV.

McMillan, K. L. (1993). The SMV System. Symbolic

Model Checking.

Naveed, H., Arora, C., Khalajzadeh, H., Grundy, J., and

Haggag, O. (2024). Model driven engineering for ma-

chine learning components: A systematic literature re-

view. Information and Software Technology, 169.

Puterman, M. L. (1990). Markov decision processes. In

Stochastic Models, volume 2. Elsevier.

Qin, X., Bliudze, S., Madelaine, E., Hou, Z., Deng, Y., and

Zhang, M. (2020). Smt-based generation of symbolic

automata. Acta Informatica, 57.

Rabin, M. O. and Scott, D. (1959). Finite automata and

their decision problems. IBM Journal of Research and

Development, 3.

Exploring and Evaluating Interplays of BPpy with Deep Reinforcement Learning and Formal Methods

Savitch, W. J. (1970). Relationships between nondetermin-

istic and deterministic tape complexities. Journal of

computer and system sciences, 4.

Shevrin, I. and Yossef, M. (2020). Spectra example:

Cinderella-stepmother problem.

Stoelinga, M. (2004). An Introduction to Probabilistic Au-

tomata. Bulletin of the EATCS, 78.

Towers, M., Terry, J. K., Kwiatkowski, A., Balis, J. U.,

Cola, G., Deleu, T., Goul

ao, M., Kallinteris, A., KG,

A., Krimmel, M., Perez-Vicente, R., Pierr

e, A., Schul-

hoff, S., Tai, J. J., Tan, A. J. S., and Younis, O. G.

(2023). Gymnasium.

Yaacov, T. (2023). BPpy: Behavioral programming in

Python. SoftwareX, 24.

Yaacov, T., Elyasaf, A., and Weiss, G. (2024). Keeping

Behavioral Programs Alive: Specifying and Execut-

ing Liveness Requirements. In International Require-

ments Engineering Conference.

Yerushalmi, R., Amir, G., Elyasaf, A., Harel, D., Katz, G.,

and Marron, A. (2023). Enhancing Deep Reinforce-

ment Learning with Scenario-Based Modeling. SN

Computer Science, 4.

ENASE 2025 - 20th International Conference on Evaluation of Novel Approaches to Software Engineering