Grammar Veriﬁcation for Students:

A Grammar Design Recipe with Veriﬁcation Steps

Marco T. Morazán

Computer Science Department, Seton Hall University, 400 South Orange Ave, South Orange, NJ, U.S.A.

Keywords:

Context-Free Grammars, Grammar Design, Grammar Correctness, Formal Languages Education.

Abstract:

Formal Languages and Automata Theory courses introduce students to grammars as formal systems to gener-

ate words in a language. Although grammars appear conceptually simple, students struggle to develop them

given that production rules are nondeterministically applied, which leads to uncertainty about grammar cor-

rectness. This struggle may be mitigated by offering students a framework for grammar design. This article

advocates that such a framework may be provided using a design recipe in a programming-based approach to

Formal Languages and Automata Theory. It puts forth a novel initiative to include grammar veriﬁcation in

such courses. The proposed approach is outlined and illustrated using an extended example. Reﬂections on

expectations and on why the initiative can be successful are presented.

1 INTRODUCTION

In most Formal Languages and Automata Theory

(FLAT) textbooks and, therefore, courses, students are

exposed to regular (rg) and/or context-free grammars

(cfg) (e.g., (Vázquez and Sáiz, 2022; Hopcroft et al.,

2006; Linz, 2011; Martin, 2003; Morazán, 2024;

Rich, 2019; Sipser, 2013; Sudkamp, 2006)). As any

FLAT instructor has witnessed, many students strug-

gle developing grammars. Sipser, for example, states

that context-free grammars are even trickier to con-

struct than ﬁnite automata (Sipser, 2013). To help

students, Sipser outlines techniques to help students

construct grammars that include divide-and-conquer

for languages that are the union of simpler languages,

a transformation algorithm for languages that are reg-

ular (i.e., build a dfa and transform the dfa to a

grammar), and the use of recursion (e.g., generate

the beginning and ending terminal symbols of a word

and recursively generate the middle symbols). Rich

(Rich, 2019), in contrast, offers 3 strategies to develop

context-free grammars: generate related word regions

in tandem (e.g., the beginning and the end), generate

unrelated regions using divide-and-conquer, and use

recursion. Neither Sipser nor Rich, however, offer a

systematic methodology to develop grammars. Most

textbooks, in fact, expect students to learn by example

with no attention to systematic design principles nor

to grammar correctness.

A new trend in FLAT education takes a design-

and programming-based approach (Morazán, 2024).

In this approach, students are presented with a de-

sign recipe for grammars and a domain-speciﬁc lan-

guage, FSM (Morazán and Antunez, 2014), embedded

in Racket (Flatt et al., 2024), to easily implement

their designs. In addition to directly constructing rgs

and cfgs, students can also employ unit testing to

validate grammars and can implement the algorithms

they develop as part of their constructive proofs. An

undeniable beneﬁt of this approach is that FSM ap-

peals to Computer Science students trained to write

programs and provides immediate feedback on gram-

mar implementation, such timely feedback has proven

useful in other areas of Computer Science when ex-

posing students for the ﬁrst time to a body of work

(Race, 2001; Venables and Haywood, 2003).

A design recipe is a series of steps, each with a

speciﬁc outcome, that guides students from a prob-

lem description to a well-designed and validated pro-

gram. This approach was ﬁrst pioneered by Felleisen

et al. for a ﬁrst introduction to programming course

(Felleisen et al., 2018) and later expanded by the

author to the ﬁrst two introduction to programming

courses (commonly referred to in the USA as CS1 and

CS2) (Morazán, 2022a; Morazán, 2022b).

The initiative presented in this article builds on

previous work done to integrate design and program-

ming into FLAT education (Morazán, 2024), which in-

cludes design recipes for building state machines and

for building grammars. There is, however, a sharp

662

Morazán, M. T.

Grammar Veriﬁcation for Students: A Grammar Design Recipe with Veriﬁcation Steps.

DOI: 10.5220/0013216500003932

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 17th International Conference on Computer Supported Education (CSEDU 2025) - Volume 2, pages 662-669

ISBN: 978-989-758-746-7; ISSN: 2184-5026

contrast between these two design recipes. The for-

mer includes steps for machine veriﬁcation whilst the

latter does not include veriﬁcation steps for gram-

mars. This article proposes that grammar veriﬁcation

ought to also be part of FLAT courses just as machine

veriﬁcation. This is appropriate in FLAT courses, be-

cause of the emphasis placed on proving construction

algorithms correct. In essence, a grammar deﬁnes a

program to construct words in a language. As such,

it ought to be veriﬁed much like students verify pro-

grams when studying Discrete Mathematics (Akerkar

and Akerkar, 2007) or Software Engineering (Blan-

chard et al., 2024; Huisman and Wijs, 2023). To this

end, the design recipe for grammars is extended with

veriﬁcation steps. These new steps guide students to

establish grammar correctness.

The article is organized as follows. Section 2

brieﬂy presents grammar design using FSM. Section 3

discusses the proposed new veriﬁcation steps to help

students establish grammar correctness. Section 4 of-

fers reﬂections on expectations and on why the pro-

posed initiative is likely to be well-received by stu-

dents. The article ends with concluding remarks in

Section 5.

2 GRAMMAR DESIGN USING

FSM

2.1 Constructors and Observers

FSM provides constructors to build rgs and cfgs:

make-rg: N T R S → rg

make-cfg: N T R S → cfg

N denotes the set of nonterminal symbols (i.e., syntac-

tic categories). T denotes the set of terminal symbols

(i.e., the input alphabet). R denotes the set of produc-

tion rules. S denotes the starting nonterminal. Each

production rule has a left and righthand side. The left

hand side always consists of a single element in N. For

an rg, the righthand consists of one or two elements.

Only S may generate, ε, the empty word. Any non-

terminal may generate a terminal symbol or a termi-

nal symbol and a nonterminal symbol. For a cfg, the

righthand side consists of an arbitrary number of sym-

bols in {N ∪ T ∪ {ε}}

. We denote the language

generated by a grammar G as L(G).

There is a generic observer to extract each gram-

mar component. For instance, grammar-rules, given

a grammar, returns the grammar’s production rules.

In addition, grammar-derive, given a grammar and

a word, returns the word derivation if the word is in

the grammar’s language. Otherwise, it returns a string

1. Pick a name for the grammar and specify the al-

phabet

2. Deﬁne each syntactic category and associate each

with a nonterminal clearly specifying the starting

nonterminal

3. Develop the production rules

4. Write unit tests

5. Implement the grammar

6. Run the tests and redesign if necessary

Figure 1: The Design Recipe for Grammars.

indicating that the word is not in the grammar’s lan-

guage.

2.2 The Design Recipe for Grammars

The design recipe for grammars is displayed in Fig-

ure 1 (Morazán, 2024). It has 6 steps and each re-

quires a concrete outcome to advance grammar con-

struction. Step 1 requires specifying the name for

the grammar and its input alphabet. Step 2 requires

the deﬁnition of syntactic categories, the mapping

of these syntactic categories to nonterminal symbols,

and the clear identiﬁcation of the starting nontermi-

nal. The deﬁnition of syntactic categories requires

identifying what needs to be generated by each.

Step 3 requires specifying the production rules.

These rules are designed based on what is generated

by each syntactic category as deﬁned in Step 2. Stu-

dents must reason abstractly in terms of the mean-

ing of each syntactic category and not in terms of in-

put alphabet elements. Step 4 requires writing unit

tests. For rgs, tests must include words that are in

and are not in the grammar’s language. For cfgs,

tests must include words in the language. Words

that are not in the language must be tested with cau-

tion, given that some derivations may be inﬁnite. The

unit tests are written using the syntax provided by

RackUnit (Welsh and Culpepper, 2024). Tests writ-

ten for w /∈L(G) determine that the string returned by

grammar-derive corresponds to a string indicating

that w is not in L(G). Tests written for w∈L(G) deter-

mine that the last element of the derivation returned

by grammar-derive corresponds to w.

Step 5 requires implementing the grammar based

on the results for the previous steps. Finally, Step 6

requires running the tests and redesigning if errors are

detected or if tests fail. We note that debugging is

performed in the context of design. That is, students

are encouraged to revisit the steps of the design recipe

to reﬁne their programs.

Grammar Veriﬁcation for Students: A Grammar Design Recipe with Veriﬁcation Steps

663

1 ;; Syntactic Category Documentation

2 ;; S: generates words with number of b > number of a, starting nonterminal

3 ;; A: generates words with number of b ≥ number of a

4 (define numb>numa (make-cfg '(S A)

5 (A → ε) (A → bA)

6 (A → AbAaA) (A → AaAbA) )

8 (check-equal? (grammar-derive numb>numa '(a b)) "(a b) is not in L(G).")

9 (check-equal? (grammar-derive numb>numa '(a b a)) "(a b a) is not in L(G).")

10 (check-equal? (grammar-derive numb>numa '(a a a a a)) "(a a a a a) is not in L(G).")

11 (check-equal? (last (grammar-derive numb>numa '(b b b))) 'bbb)

12 (check-equal? (last (grammar-derive numb>numa '(b b a b a a b))) 'bbabaab)

13 (check-equal? (last (grammar-derive numb>numa '(a a a b b b b))) 'aaabbbb)

Figure 2: A cfg for L = {w|w∈(a b)

∗

∧ w has more bs than as}.

2.3 Illustrative Example

To illustrate the result of applying the steps of the de-

sign recipe for grammars, consider implementing a

grammar over the alphabet {a, b} for the language

containing all words with more bs than as. A solu-

tion is displayed in Figure 2. The results for Step 1,

name and alphabet, are part of the implementation as

displayed, respectively, on lines 4 and 5.

To document the syntactic categories for Step 2,

students must think about what needs to be generated.

The starting nonterminal, S, must generate words that

have more bs than as. This is an invariant prop-

erty that any production rule for S must guarantee.

This means that S may generate a b with words on

either side that have a number of bs that is greater

than or equal to the number of as. Students observe

that the words on either side of S deﬁne a differ-

ent (sub)language and, therefore, needs to be repre-

sented with, A, a new syntactic category. The invari-

ant property, generate words with a number of bs that

is greater than or equal to the number of as, must

be guaranteed by any production rule for A. Words in

L(A) are generated as follows:

• generate ε

• generate an a and a b in any order with words in

L(A) before and after both of them

• generate an arbitrary number of bs

Students observe that no new (sub)languages need to

be generated and, therefore, only two syntactic cate-

gories are needed. The results for this step are dis-

played on lines 1–3 in Figure 2.

The production rules to satisfy Step 3 are devel-

oped based on the results from Step 2. S generates

words with more bs than as using the rules displayed

on line 6 in Figure 2. A generates word with a number

of bs greater than or equal to the number of as using

the rules displayed on lines 7–8.

A sample of unit tests for words both in and not in

L are developed to satisfy step 4 of the design recipe.

7 For each syntactic category design and implement an

invariant predicate to determine if a given word satis-

ﬁes the role of the syntactic category

8 For words in L(G) prove that the invariant predicates

hold for every derivation step.

9 Prove that L = L(G)

Figure 3: Veriﬁcation Steps for Grammars

These are displayed on lines 11–16 in Figure 2. The

FSM code in Figure 2 illustrates how Step 5 is satisﬁed.

Finally, Step 6 is satisﬁed by running the code and

observing that no errors are thrown and that no tests

fail.

3 GRAMMAR VERIFICATION

STEPS

3.1 Proposed Expanded Design Recipe

The design recipe for grammars provides students

with a framework for grammar implementation and

validation. In addition, it provides a lingua franca

for students and instructors to discuss grammar de-

sign. This design- and programming-based approach

makes Automata Theory more relevant to Computer

Science students and provides instructors with a

framework to understand/grade grammars developed

by students. The design recipe for grammars does

not, however, address guiding students through the

process of veriﬁcation, which is at the heart of FLAT.

This means that students are left unsure about the cor-

rectness of their implementation. Therefore, design

recipe steps for grammars veriﬁcation are proposed.

The proposed grammar veriﬁcation steps, 7–9, are

displayed in Figure 3. Step 7 asks students to develop

an invariant predicate for each syntactic category sat-

isfying the following signature:

word → Boolean

CSEDU 2025 - 17th International Conference on Computer Supported Education

664

1 ;; word → Boolean

2 ;; Purpose: Determine if the given word ought to be

generated by S

3 (define (S-INV w)

4 (let [(as (filter (λ (s) (eq? s 'a)) w))

5 (bs (filter (λ (s) (eq? s 'b)) w))

]

6 (> (length bs) (length as))))

8 (check-equal? (S-INV '()) #f)

9 (check-equal? (S-INV '(a b a)) #f)

10 (check-equal? (S-INV '(a a a a)) #f)

11 (check-equal? (S-INV '(b)) #t)

12 (check-equal? (S-INV '(a a a b b b b)) #t)

13 (check-equal? (S-INV '(b b a a b a b)) #t)

15 ;; word → Boolean

16 ;; Purpose: Determine if the given word ought to be

generated by A

17 (define (A-INV w)

18 (let [(as (filter (λ (s) (eq? s 'a)) w))

19 (bs (filter (λ (s) (eq? s 'b)) w))

]

20 (>= (length bs) (length as))))

22 (check-equal? (A-INV '(a a b)) #f)

23 (check-equal? (A-INV '(a a a a)) #f)

24 (check-equal? (A-INV '(b b a a a b a)) #f)

25 (check-equal? (A-INV '()) #t)

26 (check-equal? (A-INV '(b)) #t)

27 (check-equal? (A-INV '(a a b a b b)) #t)

Figure 4: Invariant predicates for numb>numa.

Each predicate determines if the given word satis-

ﬁes the conditions speciﬁed in Step 2 of the design

recipe for its syntactic category. Step 8 asks students

to prove that the invariant predicates hold for each

derivation step. This is done by induction on the num-

ber of derivation steps. Step 9 ask students to prove

that the language of the grammar is correct. This is

achieved by building on the proof developed for Step

8. That is, students assume that the invariant predi-

cates for the nonterminals in the righthand side of a

production rule hold and show that the use of the rule

means that the invariant predicate for the nonterminal

on the left hand side of the rule holds.

3.2 Illustrative Example

To illustrate the development of answers for the new

steps of the proposed expanded designed recipe, we

shall continue with the design started in Section 2.3.

To satisfy Step 7, students are expected to write an

invariant predicate for, S and A, the grammar’s two

syntactic categories. For both predicates, the as and

the bs of the given word may be extracted. For S,

the length of the bs must be greater than the length

of the as. For A, the length of the bs must be greater

than or equal to the length of the as. A sample im-

plementation of the results for this step are displayed

in Figure 4. Observe that students are expected to de-

sign the predicates. Among other things, this means

that each predicate must have a signature, a purpose

statement, and unit tests using words that ought and

that ought not be generated by the syntactic category.

For Step 8, the proof that invariant predicates hold

for any derivation is done by induction on the height

of a derivation tree for an arbitrary word w. A sam-

ple proof that students are expected to produce is dis-

played in Figure 5. The minimum height is 1, which

is always the base case and means that any produc-

tion rule used must use the starting nonterminal. For

numb>numa, this means the only possible derivation

tree is generated using S → b. An argument must

be made that the generated word satisﬁes S-INV. To

establish this, the righthand side of each rule is ana-

lyzed to establish that the generated word has more

bs than as. For the inductive step, students must ana-

lyze any rule that may be used after the ﬁrst produc-

tion rule and establish that the generated word satis-

ﬁes the invariant predicate for the nonterminal on the

left hand side of the used production rule. Once again,

to establish this students analyze the righthand side of

the production like done for the base case. The de-

tailed arguments are found in Figure 5. The reader can

appreciate that the induction is not beyond the grasp

of an advanced undergraduate Computer Science stu-

dent that has taken an introduction to Discrete Math-

ematics course.

For Step 9, we denote the language targeted as

L, the constructed grammar as G, and the language

for the constructed grammar as L(G). The proof for

grammar correctness builds on the proof in Step 8. It

is divided into two lemmas. The ﬁrst establishes that,

for an arbitrary word, w∈L if and only if w∈L(G). The

second establishes that, for an arbitrary word, w /∈L if

and only if w /∈L(G). A sample proof students are ex-

pected to develop is displayed in Figure 6. We note

that proving that predicate invariants always hold sim-

pliﬁes the argument for grammar correctness. Stu-

dents build an argument based on invariant predicates

holding after every derivation step. Once again, the

reader can appreciate that the proof is not beyond the

grasp of an advanced undergraduate Computer Sci-

ence student.

4 REFLECTIONS

The primary expectation for the proposed initiative

to include grammar veriﬁcation in FLAT education is

Grammar Veriﬁcation for Students: A Grammar Design Recipe with Veriﬁcation Steps

665

Theorem 1. For numb>numa invariant predicates hold.

Proof. Base case: n = 1.

If a single rule is used, it must be (S → b).

This rule generates the word b, which is a word that has more bs than as. Thus, S-INV holds.

Inductive Step:

Assume: State invariant predicates hold for n=k. Show: State invariant predicates hold for n=k+1.

n=k+1 means that any rule other than (S → b) is used. We establish that invariant predicates hold for each:

(S → AbA)

The generated word is obtained by concatenating a word with |b| ≥ |a|, the word b, and a word with |b| ≥ |a|.

The generated word, therefore, has at least one more b than as. Thus, S-INV holds.

(A → ε)

The generated empty word has an equal number of as and bs. Thus, A-INV holds.

(A → AbAaA)

The generate word is obtained by concatenating a word with |b| ≥ |a|, the word b, a word with |b| ≥ |a|, the

word a, and a word with |b| ≥ |a|. The generated word, therefore, has |b| ≥ |a|. Thus, A-INV holds.

(A → AaAbA)

The generate word is obtained by concatenating a word with |b| ≥ |a|, the word a, a word with |b| ≥ |a|, the word

b, and a word with |b| ≥ |a|. The generated word, therefore, has |b| ≥ |a|. Thus, A-INV holds.

(A → bA)

The generate word is obtained by concatenating the word b and a word with |b| ≥ |a|. The generated word,

therefore, has |b| > |a|. Thus, A-INV holds.

Figure 5: Proof for invariant predicates.

to improve student understanding. This better under-

standing is to be evidenced in at least two ways. The

ﬁrst involves the development of predicate invariants.

Such development is evidence that students have rea-

soned carefully about what a syntactic category repre-

sents and understand their formal role enough to for-

mulate a validation predicate. The predicates students

developed are not intended to statically reﬂect their

understanding. Students will also be able to provide

them as input to a dynamic visualization tool to simu-

late the construction of the derivation tree for a given

word generated by the grammar. The visualization

tool shall indicate for each derivation step, using node

coloring, if the invariant for the expanded nonterminal

holds. In this manner, students will be able to debug

their grammars when words not in the target language

are generated by a grammar.

The second involves the development of a correct-

ness proof. Such a development reﬂects that students

understand the relationship between syntactic cate-

gories. In the vernacular, we can say that they under-

stand how the pieces of the puzzle ﬁt together. Such a

development is evidence that students understand the

derivation process. An additional beneﬁt is that such

a development further hones their proof-development

skills. The development of these skills are usually not

emphasized enough in undergraduate Computer Sci-

ence education and grammar development in a FLAT

course presents a perfect opportunity to do so.

It is well-known that mental resistance to formal

methods (i.e., proofs) exists (Gries, 1987; Zingaro,

2008). A natural question to ask is: Why do we be-

lieve we can be successful with the proposed initia-

tive? Indeed, this is an important question that cannot

be fully answered until the initiative is deployed in

the classroom and student perceptions are measured.

Nonetheless, we have reason to believe that the ini-

tiative is likely to be successful. This cautious opti-

mism is based on data collected from two US-based

universities, Seton Hall University (SHU) and Worces-

ter Polytechnic Institute (WPI), using the design-based

methodology (Morazán, 2024) to teach their FLAT

CSEDU 2025 - 17th International Conference on Computer Supported Education

666

Lemma 1. w∈L ⇔ w∈L(numb>numa).

Proof.

(⇒) Assume w∈L.

This means that w has |b| > |a|. Given that the production rules can generate more bs than as in any order, there

is a sequence of derivation steps whose yield is w. Thus, w∈L(numb>numa).

(⇐) Assume w∈L(numb>numa).

Given that predicate invariants always hold, this means that w has |b| > |a|. Thus, w∈L.

Lemma 2. w /∈L ⇔ w/∈L(numb>numa).

Proof. (⇒) Assume w /∈L.

This means that w has |a| ≥ |b|. Given that predicate invariants always hold, this means that S cannot generate w.

Thus, w/∈L(numb>numa).

(⇐) Assume w/∈L(numb>numa)

This means that S does not generate w. Given that the grammar can generate word elements in any order and that

predicate invariants always hold, w must have |a| ≥ |b|. Thus, w /∈L.

Theorem 2. L = L(numb>numa).

Proof. The proof follows from Figures 6 to 6.

Figure 6: Proof for L = L(numb>numa).

courses. In these courses, students employed a de-

sign recipe for state machines that includes veriﬁca-

tion steps similar to the ones proposed in this article.

That is, students wrote proofs for state predicate in-

variants holding and for machine correctness.

The two courses enrolled a total of 106 students,

11 at SHU and 95 at WPI. A total of 53 students vol-

unteered to participate in the survey, 10 from SHU and

43 from WPI, making the overall response rate among

registered students 50% (the response rate among reg-

istered students is 91% at SHU and 45% at WPI). The

day the survey was administered, a total of 43 stu-

dents attended class at WPI (31 in-person and 12 re-

motely) and 10 students attended class at SHU (all in-

person). This attendance rate is typical for both in-

stitutions. The responses, therefore, reﬂect the per-

ceptions of students that regularly attend class and

not the perceptions of all students registered for these

courses. Among the respondents, 14 (26%) self iden-

tiﬁed as female, 36 (68%) self identiﬁed as male, and

the remaining 3 (6%) self identiﬁed as: 1 nonbinary,

1 agender, and 1 declined to respond. Finally, stu-

dents at both institutions received neither payment nor

beneﬁts for participating in the survey. Using a Lik-

ert scale (Likert, 1932) to respond, 1 (Strongly Dis-

agree) to 5 (Strongly Agree), with 3 as a neutral re-

sponse, these students were presented with the fol-

lowing statements related to proofs:

Q1: I feel empowered by knowing how to

reason and write proofs about formal

languages.

Q2: Writing programs in FSM helped me

develop constructive proofs.

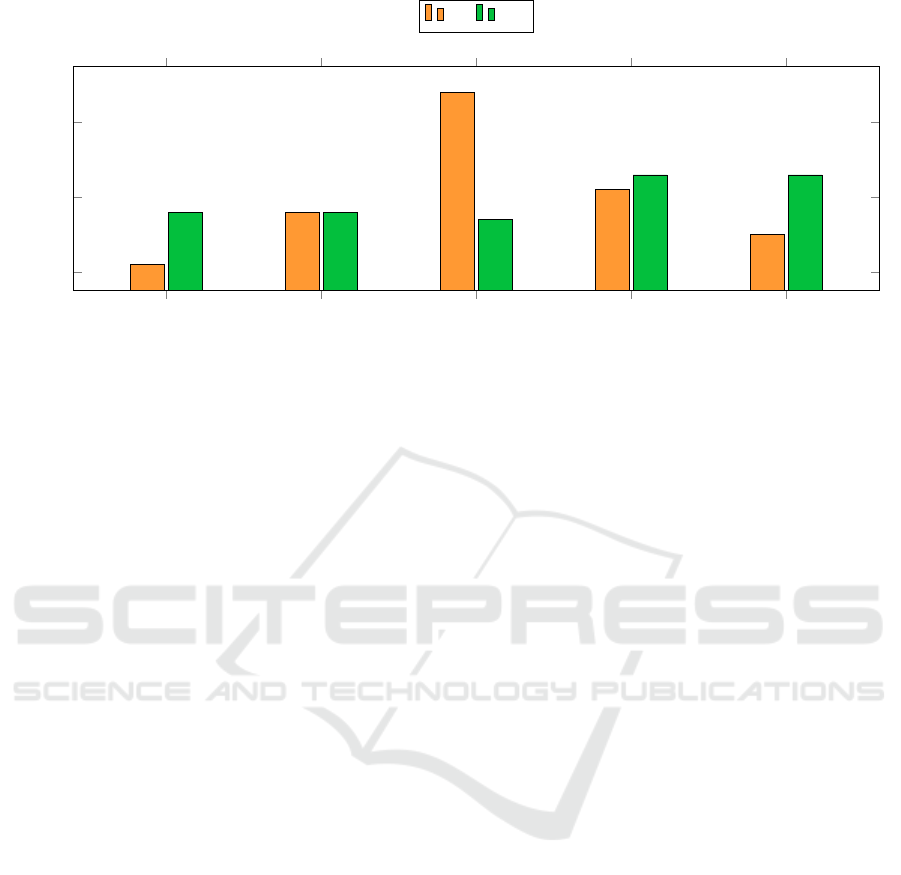
The distribution of responses is displayed in Figure 7.

For Q1, we observe that 70% of respondents tend

not to disagree with the statement (responses 3–5).

For Q2, we observe that 63% of respondents tend

not to disagree with the statement (responses 3–5).

These results are very encouraging and indicate that

the design- and programming-based approach used is

making inroads in dismantling the mental resistance

to formal methods. The success achieved with ma-

chine veriﬁcation is the basis for our cautious opti-

mism regarding the success of the proposed initiative.

5 CONCLUDING REMARKS

This articles presents a novel initiative to include

grammar veriﬁcation in Formal Languages and Au-

tomata Theory education. The design and devel-

opment process is illustrated using a programming-

based approach that requires students to document

the role of their syntactic categories, to develop in-

variant predicates based on these roles, and to pro-

vide a proof of grammar correctness. As the reader

can appreciate, none of these requirements are beyond

the abilities of an advanced undergraduate Computer

Grammar Veriﬁcation for Students: A Grammar Design Recipe with Veriﬁcation Steps

667

1 2 3 4 5

0.1

0.2

0.3

0.11

0.18

0.34

0.21

0.15

0.18 0.18

0.17

0.23 0.23

Score from 1 (Strongly Disagree) to 5 (Strongly Agree)

Proportion of Respondents

Q1 Q2

Figure 7: Empirical data on machine proofs.

Science student. Although the proposed initiative is

based on a programming-based approach to Formal

Languages and Automata Theory, the design steps are

transferable to courses still using a pencil-and-paper

approach. That is, grammar design is not restricted to

programming-based courses.

We are cautiously optimistic that the proposed

initiative can be successful for two reasons. The

ﬁrst, as mentioned above, is that none of the ver-

iﬁcation steps are beyond an advanced undergradu-

ate student that has taken an introduction to Discrete

Mathematics course. The second, is that classroom

work done with veriﬁcation of state machines has

been successful and well-received by students. To-

gether, these reasons suggests that any Formal Lan-

guages and Automata Theory instructor can success-

fully make grammar veriﬁcation interesting and palat-

able to Computer Science students.

REFERENCES

Akerkar, R. and Akerkar, R. (2007). Discrete Mathematics.

Pearson Education India.

Blanchard, A., Marché, C., and Prévosto, V. (2024). For-

mally Expressing what a Program Should Do: the

ACSL Language. In Kosmatov, N. and Signoles, J.,

editors, Guide to Software Veriﬁcation with Frama-

C - Core Components, Usages, and Applications.

Springer.

Felleisen, M., Findler, R. B., Flatt, M., and Krishnamurthi,

S. (2018). How to Design Programs: An Introduction

to Programming and Computing. MIT Press, Cam-

bridge, MA, USA, Second edition.

Flatt, M., Findler, R. B., and PLT (2024). The Racket Ref-

erence. PLT. Last accessed: June 2024.

Gries, D. (1987). The Science of Programming. Springer-

Verlag, Berlin, Heidelberg, 1st edition.

Hopcroft, J. E., Motwani, R., and Ullman, J. D. (2006). In-

troduction to Automata Theory, Languages, and Com-

putation (3rd Edition). Addison-Wesley Longman

Publishing Co., Inc., USA.

Huisman, M. and Wijs, A. (2023). Concise Guide to

Software Veriﬁcation - From Model Checking to An-

notation Checking, 2. Texts in Computer Science.

Springer, Cham, Switzerland, First edition.

Likert, R. (1932). A Technique for the Measurement of

Attitudes. Archives of Psychology, 140:1–55.

Linz, P. (2011). An Introduction to Formal Languages and

Automata. Jones and Bartlett Publishers, Inc., USA,

Fifth edition.

Martin, J. C. (2003). Introduction to Languages and the

Theory of Computation. McGraw-Hill, Inc., New

York, NY, USA, 3 edition.

Morazán, M. T. (2022a). Animated Problem Solving - An

Introduction to Program Design Using Video Game

Development. Texts in Computer Science. Springer,

First edition.

Morazán, M. T. (2022b). Animated Program Design - In-

termediate Program Design Using Video Game Devel-

opment. Texts in Computer Science. Springer, Cham,

Switzerland, First edition.

Morazán, M. T. (2024). Programming-Based Formal Lan-

guages and Automata Theory - Design, Implement,

Validate, and Prove. Texts in Computer Science.

Springer, Cham, Switzerland, First edition.

Morazán, M. T. and Antunez, R. (2014). Functional Au-

tomata - Formal Languages for Computer Science

Students. In Caldwell, J. L., Hölzenspies, P. K. F.,

and Achten, P., editors, Proceedings 3rd International

Workshop on Trends in Functional Programming in

Education, TFPIE 2014, Soesterberg, The Nether-

lands, 25th May 2014, volume 170 of EPTCS, pages

19–32, Australia. Open Publishing Association.

Race, P. (2001). Using feedback to help stu-

dents learn. https://phil-race.co.uk/wp-

content/uploads/Using_feedback.pdf. Last accessed:

June 2024.

CSEDU 2025 - 17th International Conference on Computer Supported Education

668

Rich, E. (2019). Automata, Computability and Complexity:

Theory and Applications. Pearson Prentice Hall.

Sipser, M. (2013). Introduction to the Theory of Computa-

tion. Cengage Learning, USA, 3rd edition.

Sudkamp, T. A. (2006). Languages and Machines - An In-

troduction to the Theory of Computer Science. Pear-

son Education, Inc., Third edition.

Vázquez, E. G. and Sáiz, T. G. (2022). Introducción

a la Teoría de Autómatas, Gramáticas y Lenguajes.

Grado en Ingeniería Informática. Editorial Universi-

taria Ramón Areces, Second edition.

Venables, A. and Haywood, L. (2003). Programming Stu-

dents NEED Instant Feedback! In Proceedings of the

Fifth Australasian Conference on Computing Educa-

tion - Volume 20, ACE ’03, page 267–272, AUS. Aus-

tralian Computer Society, Inc.

Welsh, N. and Culpepper, R. (2024). RackUnit: Unit Test-

ing. PLT Racket, v8.12 edition. Last accessed: June

2024.

Zingaro, D. (2008). Another Approach for Resisting Stu-

dent Resistance to Formal Methods. SIGCSE Bull.,

40(4):56–57.

Grammar Veriﬁcation for Students: A Grammar Design Recipe with Veriﬁcation Steps

669