ARP∆: Hardware-Accelerated Ray-Traced Photon Differentials
Adrian De Barro
a
, Keith Bugeja
b
and Sandro Spina
c
Department of Computer Science, University of Malta, Msida, Malta
Keywords:
Photon Mapping, Global Illumination, Ray Tracing Hardware, Photon Differentials, Photon Density
Estimation, Photon Footprints, Anisotropic Scattering, Rendering Performance, Ray Differentials, Real-Time
Rendering.
Abstract:
Photon mapping is a widely used rendering technique that provides biased but consistent global illumination
through particle and radius-based density estimation. In this work, we enhance photon mapping by integrating
photon differentials, representing each photon as a beam connected to its neighbours. Our proposed method,
ARP∆, dynamically adjusts bandwidth by leveraging changes in both the photon’s position and direction,
allowing for adaptive control based on the photon’s path through the scene. Additionally, ARP∆ combines
multiple photon differential strategies to enable efficient global illumination on ray tracing hardware, seam-
lessly transitioning to progressive photon mapping in highly anisotropic conditions. Experimental results
demonstrate that ARP∆ achieves image quality comparable to state-of-the-art photon mapping techniques,
validating its effectiveness in producing high-fidelity renders.
1 INTRODUCTION
Photon Mapping and its variants, known for their bi-
ased yet consistent solution to the rendering equation,
are often preferred over unbiased path-based meth-
ods, due to their tendency to produce blurry rather
than noisy output until convergence. These meth-
ods excel in handling caustics from specular-diffuse-
specular ray paths, which are challenging for path-
based approaches. While the kernel estimation in
photon mapping introduces bias and variance, these
can be mitigated with high photon emissions, assum-
ing unlimited memory. Progressive approaches ad-
dress this by using infinite photon counts within finite
memory.
Advancements in GPUs have enabled real-time
implementations of photon mapping, leveraging ras-
terisation pipelines and compute shaders. The work of
Evangelou et al. Evangelou et al. (2021) and subse-
quent extension to progressive photon mapping Kern
et al. (2023) have effectively utilised progressive den-
sity estimation with ray tracing hardware. By adapt-
ing the concept of ray differentials Igehy (1999), pho-
ton differentials facilitate adaptive bandwidth selec-
tion at the photon level, striking a balance between
a
https://orcid.org/0000-0002-3087-9218
b
https://orcid.org/0000-0002-3111-1251
c
https://orcid.org/0000-0001-7197-410X
bias and variance, based on the photon’s trajectory.
In this paper, we introduce Hardware-Accelerated
Ray-Traced Photon Differentials (ARP∆), a novel ap-
proach to global illumination using photon differen-
tials optimised for ray tracing hardware. The key con-
tributions are:
• the integration of multiple photon differential
techniques to achieve global illumination; and
• the adaptation of photon differentials for efficient
use on ray tracing hardware.
2 BACKGROUND
Ray differentials Igehy (1999) extend a parametrised
ray into a beam by differentiating it, estimating its
relationship with neighbouring rays as it propagates.
Each ray, r, combines position, p, and direction, d,
differentiated with respect to the tangent space de-
scribed by vectors u and v as:
∂r
∂u
= (
∂p
∂u
,
∂d
∂u
),
∂r
∂v
= (
∂p
∂v
,
∂d
∂v
). (1)
Positional and directional derivatives describe tangent
space changes and beam angular spread, respectively.
Ray differentials are advantageous over Cone and
Beam Tracing for maintaining simplicity in tracing
300
De Barro, A., Bugeja, K. and Spina, S.
ARPÎ
ˇ
T: Hardware-Accelerated Ray-Traced Photon Differentials.
DOI: 10.5220/0013216800003912
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 20th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2025) - Volume 1: GRAPP, HUCAPP
and IVAPP, pages 300-307
ISBN: 978-989-758-728-3; ISSN: 2184-4321
Proceedings Copyright © 2025 by SCITEPRESS – Science and Technology Publications, Lda.

Figure 1: Test scenes rendered using ARP∆, our locally adaptive hardware ray-traced photon mapper. From left to right:
Caustic Glass (C-G), Crytek Sponza (C-S), Veach Bidir (V-B) and Water Caustics (W-C).
procedures as they work seamlessly with standard ray
tracing frameworks, relying on simple ray-casting op-
erations without requiring additional geometric com-
plexity or higher-order intersection calculations.
Photon differentials Schjøth et al. (2007) apply ray
differentials to density estimation, generating ellip-
soidal footprints at intersection points. For point emit-
ters, initial photon area and flux are adjusted upon
surface interaction. This formulation only supports
point light emitters, with no initial change in posi-
tional differentials. On absorption, the photon foot-
print forms an ellipse, its area derived from the par-
allelogram cross section formed by the positional dif-
ferentials. Photon differentials differ from traditional
photon mapping by considering all elliptical footprint
intersections at a point x
p
rather than relying on k-
nearest neighbors (k-NN) for computing illumina-
tion. Intersection tests and irradiance contributions
are determined via transformations into filter space,
considering the intersected footprints’ total radiance
at scene points.
3 LITERATURE REVIEW
Photon mapping Jensen (1996) has been widely used
for delivering accurate global illumination under dif-
ferent scenarios. For each pixel, it maintains a search
radius that limits the maximum distance to search
for (using k-NN) contributing photons in the photon
map. Photon mapping requires an infinite amount
of memory to converge on a solution. Haschisuka
et al. Hachisuka et al. (2008) address this limita-
tion by introducing a multi-pass approach for pho-
ton mapping, while also progressively reducing the
search radius by some factor α. Progressive photon
mapping introduces a temporal dependence between
frames that was rectified by Knaus et al. Knaus and
Zwicker (2011), essentially allowing multiple scatter-
ing phases to occur in parallel. Suykens and Willems
Suykens and Willems (2001) expanded ray differen-
tials to encompass full ray paths, adding new differen-
tials for sampled events. Initially, Schøjt et al. Schjøth
et al. (2007) confined photon differentials to paths that
could be represented by ray differentials. This was
later broadened by Fabianowski and Dingliana Fabi-
anowski and Dingliana (2009) to incorporate diffuse
interreflections and footprint extraction from BVHs.
They achieved this without requiring new differen-
tials, instead interpreting diffuse reflections as absorp-
tion and re-emission events. Early implementations
were limited to point lights, but Frisvad et al. Frisvad
et al. (2014) widened the scope of photon differentials
to include a variety of light sources. They also intro-
duced screen-space splatting, albeit without address-
ing diffuse interreflections. Purcell et al. Purcell et al.
(2003) were the first to implement an entire photon
mapping solution on the GPU. McGuire McGuire and
Luebke (2009) employed the GPU for both the initial
scattering and final gathering of the photon mapping
process. Mara et al. Mara et al. (2013) present various
density estimation techniques for screen-space photon
mapping.
Smal and Aizenshtein Smal and Aizenshtein
(2019) combine the rasterisation pipeline with mod-
ern ray tracing hardware to achieve real-time global
illumination (GI). Reflective Shadow Maps handle the
initial photon scattering, while ray tracing propagates
photons through the scene. This method bypasses
acceleration structures, splatting indirect illumination
directly onto the frame buffer. Kim Kim (2019)
employ projection volumes, similar to Jensen’s pro-
jection map Jensen (2004). These volumes enclose
caustic-generating elements, projecting their bound-
ing box opposite to the directional light to form an im-
portance map for caustic generation. Absorbed pho-
tons are compressed into single pixels, followed by
denoising to diffuse caustic energy. Yang and Ouyang
Yang and Ouyang (2021) extend Kim’s approach to
deliver real-time caustics. They introduce two meth-
ods: Adaptive Anisotropic Photon Scattering, which
uses photon differentials and adaptive photon emis-
ARPÎ
ˇ
T: Hardware-Accelerated Ray-Traced Photon Differentials
301

sion to generate detailed caustic patterns, and Ray-
Guided Water Caustics, tailored for caustics above
and below water surfaces. Both approaches rely on
the frame buffer for photon contributions.
Evangelou et al. Evangelou et al. (2021) reverse
the photon search problem by exploiting acceleration
structures provided by hardware ray tracing, and their
method is used as the basis for Kern et al.’s Kern
et al. (2023) progressive photon mapping implemen-
tation. Moreau Moreau and Doggett (2022) leverage
Evangelou’s inverse-radius approach to accelerate the
rendering of indirectly visible caustics. In contrast,
techniques like those presented by Yang and Ouyang
are unable to render indirect caustics due to their re-
liance on screen-space methods. Unlike Kern et al.,
who focus on accelerating photon maps, Moreau and
Doggett store pixel-world-space regions of interest,
referred to as collection points. During the photon
scattering process, photons interacting with diffuse
surfaces contribute to the collection points they inter-
sect. This object-space radiance estimation enhances
temporal coherence, as the radiance approximation is
independent of screen-space constraints.
4 METHOD
Previous work using photon differentials did not pro-
vide a comprehensive global illumination solution.
Existing solutions either utilised custom acceleration
structures or relied on screen-space splatting, forego-
ing the use of an acceleration structure. Drawing in-
spiration from the work of Fabianowski et al. Fabi-
anowski (2011); Fabianowski and Dingliana (2009),
Frisvad et al. Frisvad et al. (2014), Evangelou et al.
Evangelou et al. (2021) and Kern et al. Kern et al.
(2023), we leverage the acceleration structures pro-
vided by ray tracing hardware to develop ARP∆, a
locally adaptive global illumination technique based
on photon differentials.
PPM leverages per-pixel statistics, shrinking the
search radius as more photons are detected near a
query point in the scene. This mechanism enables
PPM to adaptively select bandwidth on a per-pixel
basis. Probabilistic Progressive Photon Mapping in-
troduced by Knaus Knaus and Zwicker (2011) moves
away from per-pixel information towards a uniform
radius for all pixels per iteration, facilitating the par-
allelisation of the scattering process. Following this,
Evangelou et al. and subsequently Kern et al. reverse
this process. Instead of employing k-nearest neigh-
bours method to retrieve all photons within a circular
region equal to the current global radius, they repre-
sent each photon as a sphere with the global radius
specified for the respective frame iteration. While
this method enhances performance, the approach can-
not make use of locally adaptive bandwidth, leading
to potentially biased or noisy intermediate results un-
til convergence. For this reason, we have adopted
photon differentials. Although our approach does not
utilise screen-space statistics, it achieves local band-
width adaptivity through the resulting change in the
differential vectors which represent the photon’s foot-
print at point of intersections.
Footprints that exhibit anisotropy can pose chal-
lenges when incorporated into acceleration structures.
These may result in excessively large bounding boxes,
especially for highly anisotropic footprints that occur
when the positional differentials have a small separa-
tion angle. To address this issue, problematic foot-
prints are culled and replaced with progressive pho-
tons at runtime, ensuring overall performance is main-
tained.
Table 1 provides definitions for the mathematical
notations used throughout this paper, while Figure 2
summarizes the key steps for adopting photon differ-
entials on ray tracing hardware.
Table 1: List of symbols.
Symbol Definition
α Angle subtended by two positional differ-
ential vectors in tangent space
p Position vector of a ray or photon
d Direction vector of a ray or photon
∂
∂u
Partial derivative with respect to u
∂
∂v
Partial derivative with respect to v
r Ray represented as position and direction
x
p
Intersection position vector of a photon on
a surface
⃗n
p
Photon’s surface intersection normal
M
−1
p
Inverse transform from footprint’s tangent
space to filter space
M
p
Tangent space transform of the footprint
⃗p Position vector of a photon intersection
⃗
d
′
New reflection direction vector
v Virtual travel distance of a photon
t Travel distance of a photon to the next sur-
face
D
u
Positional differential vector in direction u
D
v
Positional differential vector direction v
ω
′
New direction vector in a photon path
h
max
Maximum allowed length of the major dif-
ferential
f Threshold fraction for degenerate removal
S Smoothing parameter, a scaling factor ap-
plied to photon differential footprints
S
c
Caustics photon map smoothing parameter
S
g
Global photon map smoothing parameter
GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications
302

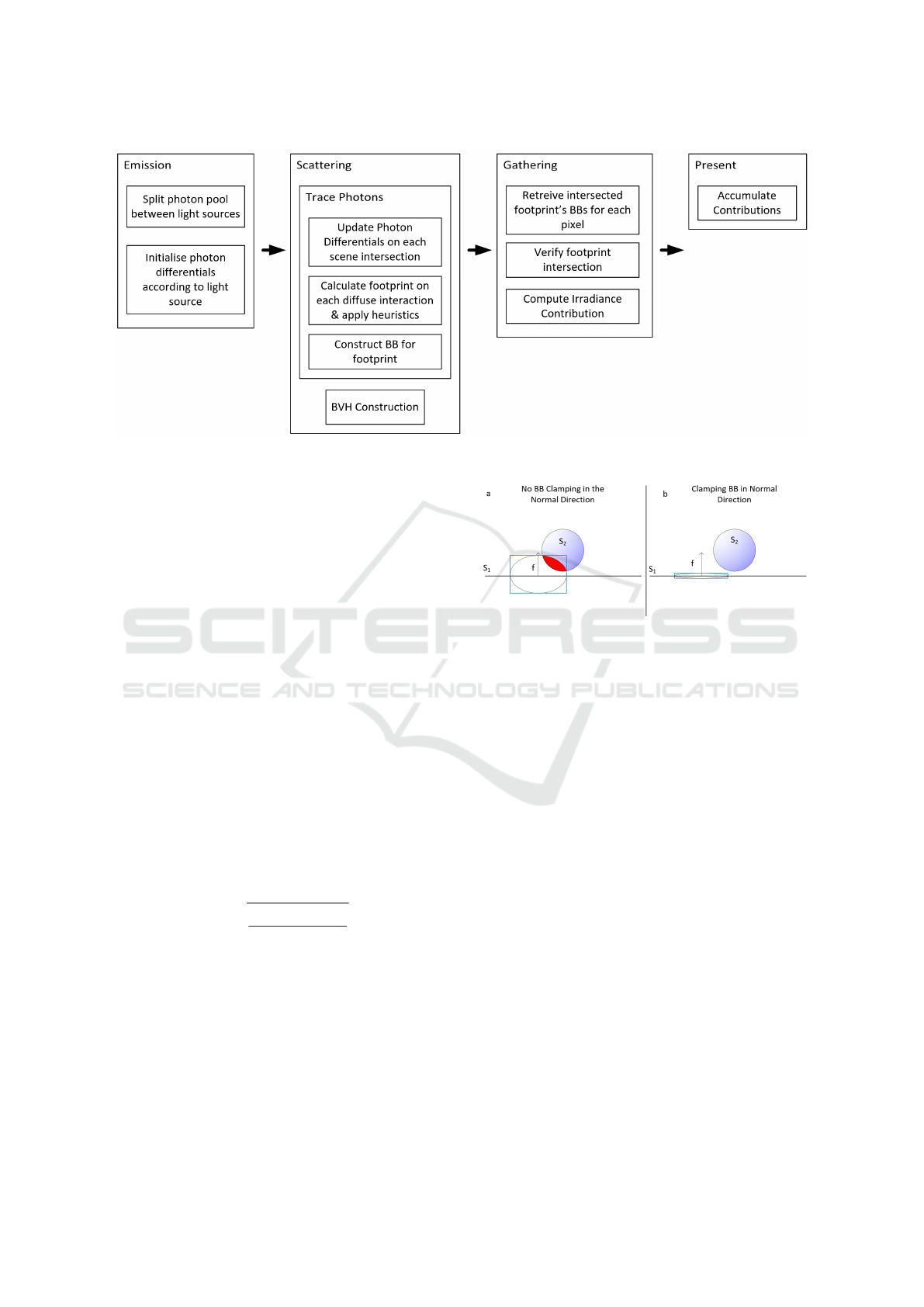
Figure 2: Pipeline illustrating the primary steps for incorporating photon differentials into ray tracing hardware.
4.1 Emission and Propagation
Our method adopts a framework similar to that of
Frisvad et al. Frisvad et al. (2014) for its effective han-
dling of various light sources. However, to achieve a
full global illumination solution, we address diffuse
interreflections, which are not accounted for in Fris-
vad et al.’s model. Suykens Suykens (2002) treats
each diffuse interreflection as a random event, requir-
ing new differentials for every diffuse reflection. This
increases the computational load significantly due to
the need for constant updates and management of a
list of differentials and the complex calculation of
photon footprints as a Minkowski sum.
In order to only track a singular set of photon
differentials, we integrate Fabianowski Fabianowski
(2011) absorption and re-emission heuristic into Fris-
vad et al.’s framework. At each photon intersection
point ⃗p, we construct a tangent plane for the new re-
flection direction
⃗
d
′
, setting the length of the tangent
and bi-tangent to match those used during the initial
light source emission. We calculate the virtual dis-
tance v a photon travels before re-emission using:
v =
s
∥
D
u
x × D
v
x
∥


D
φ
ω
′
× D
θ
ω
′


, (2)
where v is a the square root of the ratio of po-
sitional differentials at the intersection point to the
initial directional differentials on emission. This en-
sures that upon re-emission, the photon’s positional
differentials retain the same footprint size as at their
previous intersection. The virtual distance v is then
added to the travel distance t at the next surface inter-
section. Interested readers can refer to Fabianowski’s
work Fabianowski (2011) for further details.
Figure 3: For a photon with an elliptical footprint f , inter-
secting surface S
1
, (a) uses an un-clamped bounding box in
the normal direction which results in light leaks to surface
S
2
(shaded in red), while (b) clamps the bounding box in
the normal direction to reduce the chances of light leaks.
4.2 Photon Map
Two photon maps are used, one for global illumina-
tion and the other for caustics. At each diffuse inter-
section, we add the photon’s current state to the ac-
celeration structure. Exploiting the ray tracing hard-
ware’s acceleration structures, we treat each footprint
as a bounding box (BB). This involves using half the
position differentials to determine the BB’s extents,
thereby identifying its minimum and maximum lim-
its. In practice, these differentials form an ellipsoid,
with its maximum height at the footprint’s centre be-
ing half the minor differential. Since the footprint is
ellipsoidal, it might inadvertently contribute to sur-
faces close by in the normal direction. To prevent this,
the maximum BB height along the normal direction is
set to the current progressive radius.
4.3 Gathering
Inspired by Evangelou et al. (2021), our gathering
process differs from the standard k-NN method by us-
ing photon differentials and footprints integrated with
ARPÎ
ˇ
T: Hardware-Accelerated Ray-Traced Photon Differentials
303

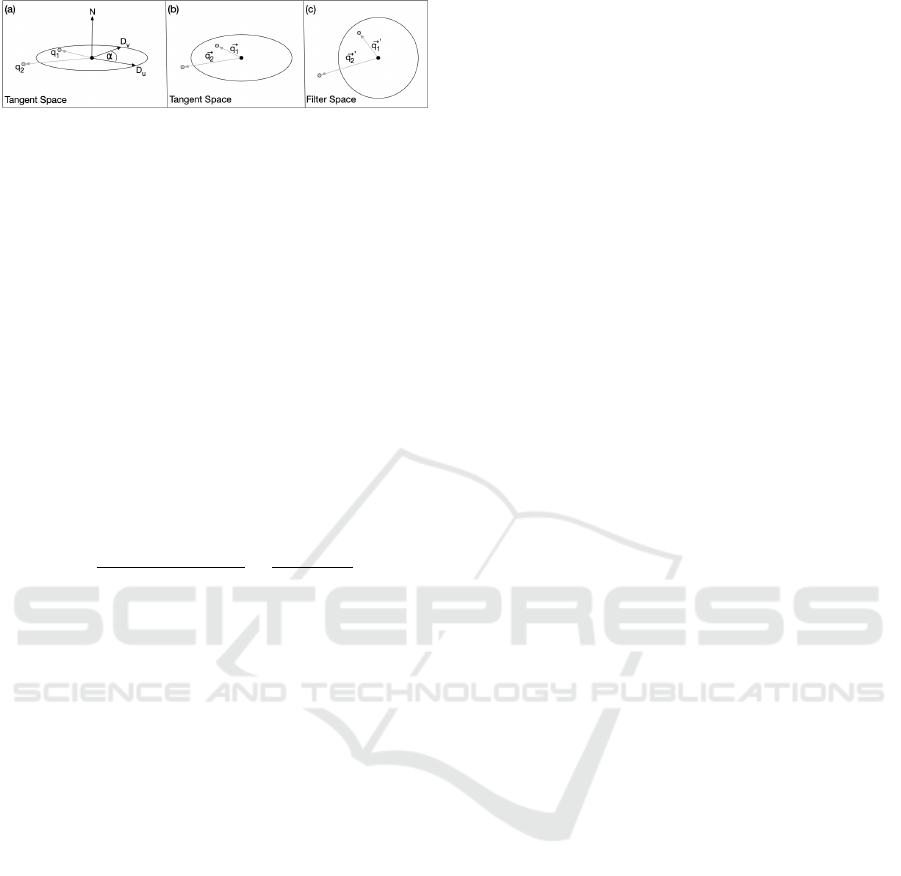
Figure 4: Transformation from tangent space to filter space.
(a) In tangent space, the footprint is defined by the normal
vector and positional differentials. Vectors connecting the
footprint’s center to the query points q
1
and q
2
are const-
nructed. (b) Tangent space is shown along the −N direction
for clarity. (c) Vectors ⃗q
1
and ⃗q
2
are transformed into filter
space using M
−1
p
. q
1
intersects the footprint since ⃗q
1
′
has a
magnitude smaller than one.
the BVH. We construct a ray originating at the scene’s
query point to detect all intersecting BBs. To confirm
the ray’s presence within the footprint, we transform
the footprint into filter space and then check for an
intersection with a unit circle. As suggested by Fabi-
anowski and Dingiliana Fabianowski and Dingliana
(2009), this involves computing the inverse matrix of
the ellipsoid. Since this is impractical for real-time
settings, we adopt Frisvad et al.’s method that directly
computes the first two rows of M
−1
p
:
M
−1
p
=
2
D
u
x
p
· (D
v
x
p
×⃗n
p
)
·

D
v
x
p
× ¯n
p
¯n
p
× D
u
x
p

, (3)
where D
u
and D
v
are the positional differentials at the
intersection point, x
p
is the world-space intersection
point,⃗n
p
is the intersection normal and M
−1
p
is the in-
verse of matrix M
p
, the matrix representing the foot-
print space. The transform M
−1
p
maps the anistropic
footprint into a unit circle. To determine if a query
point intersects a footprint, a vector from the foot-
print’s center to the query point is constructed and
transformed into filter space using M
−1
p
. If the mag-
nitude of this transformed vector is less than or equal
to one, the query point resides within the footprint.
Figure 4 illustrates the transformation from tangent
space to filter space, and demonstrates how intersec-
tions with query points are identified.
4.4 Smoothing Parameters
A smoothing parameter is employed to adjust the size
of all footprints Schjøth et al. (2007). Initial attempts
to use a unified smoothing parameter for both caustic
and global photon maps proved ineffective, as caus-
tic and global ellipsoids often demand distinct scal-
ing factors for optimal results. To resolve this, two
independent scaling factors S
c
(caustics photon map)
and S
g
(global photon map) are introduced. On ab-
sorption, photons are classified as either caustic or
global, scaled by the respective smoothing parameter
and added to the corresponding photon map.
4.5 Heuristics
Dealing with sizeable ellipsoidal footprints in accel-
eration structures is difficult. Their limited illumina-
tion contribution contrasts sharply with their exten-
sive bounding boxes. This difference often causes in-
effective spatial partitioning in the BVH and more fre-
quent point-ellipse intersection tests. Some ellipsoids
from caustics generate extended, non-axis aligned
footprints, requiring an unduly large BB that substan-
tially increase redundant intersection queries.
To address these shortcomings, we employ four
heuristics: H Max Limit, Dampened Adaptation and
Degenerate Removal Fabianowski (2011) and Bound-
ing Box Culling heuristic adapted from Kaplanyan
and Dachsbacher (2013). The H Max Limit heuris-
tic clamps the positional differentials of a footprint to
a set length h
max
, while Dampened Adaptation raises
the major positional differential ∂P to ∂P
1/4
. The mi-
nor differential is dampened by the same ratio. De-
generate Removal is a heuristic identifying ellipsoids
with a footprint height below a small threshold frac-
tion f of their base. Fabianowski Fabianowski (2011)
identify and exclude differentials that are degenerate;
in ARP∆ they are replaced by a photon whose band-
width is equal to the current progressive radius. The
respective progressive radius is determined according
to the current frame index and an initial radius di-
mension. Bounding Box Culling removes any non-
degenerate ellipsoids with a bounding box larger than
5% of the total scene area and replaces them with a
progressive photon.
5 RESULTS
ARP∆ was developed using Falcor Kallweit et al.
(2022), building upon the implementation by Kern et
al. Kern et al. (2023). Four different scenes were cho-
sen on the basis of their illumination properties, each
with S
c
and S
g
parameters, obtained experimentally:
Caustic-Glass (C-G) Kern et al. (2023) with 0.55 and
1.00, Crytek Sponza (C-S) McGuire (2017) with 1.00
and 0.87, Veach-Bidir Room (V-B) with 0.26 and 0.66
Bitterli (2016), and Water Caustic (W-C) with 0.50
and 0.77. Reference images were generated using
RTPM Kern et al. (2023) by accumulating each view
for a total of 100,000 iterations and scattering one
million photons per iteration. Initial progressive pho-
ton mapping radii were set to 0.01 for caustic photons
and 0.05 for global photons. These were determined
experimentally. Similar to Kern et al. Kern et al.
(2023) and Frisvad et al. Frisvad et al. (2014) we eval-
uate ARP∆ in terms of performance (average iteration
GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications
304

Reference ARP∆-50K RTPM-50K ARP∆-250K RTPM-250K ARP∆-1000K RTPM-1000K
C-S
V-B
Figure 5: Renders and the corresponding SSIM heatmaps at the ten-second mark for C-S and V-B, for all three experiment
configurations (E-50K, E-250K and E-1000K).
Scene Method
E-1000K E-250K E-50K
SSIM NI ATI (ms) SSIM NI ATI (ms) SSIM NI ATI (ms)
C-G
ARP∆ 0.992 802 12.8 0.993 1485 6.8 0.981 1713 6.5
RTPM 0.998 1863 5.4 0.997 1832 5.4 0.990 1861 5.5
C-S
ARP∆ 0.988 1449 6.9 0.980 1581 6.7 0.932 1515 6.4
RTPM 0.986 1668 6.2 0.956 1658 6.1 0.831 1684 5.9
V-B
ARP∆ 0.969 884 11.3 0.974 1535 6.4 0.966 1645 5.8
RTPM 0.976 1268 7.0 0.938 1790 5.5 0.790 1778 5.6
W-C
ARP∆ 0.989 449 22.7 0.992 971 10.3 0.977 1616 6.1
RTPM 0.941 1386 6.9 0.993 1819 5.7 0.980 1845 5.3
Table 2: Image quality results under time-normalised constraints (10s) for ARP∆ and RTPM. Iteration counts up to the 10
second mark (NI) and the respective average time per iteration (ATI) in milliseconds, are also reported.
time) and image quality using the SSIM (Structural
Similarity Index Measure) metric.
Three experiments, E-1000K, E-250K and E-50K,
were conducted to evaluate ARP∆ across a range of
photon densities: E-1000K with one million photons
per iteration for high-density scenarios, and E-250K
and E-50K, with photon counts reduced to a quarter
and a twentieth of E-1000K’s respectively per itera-
tion, to evaluate performance at lower photon densi-
ties. Ten second runs were conducted for the three
experimental setups, both with ARP∆ and RTPM (see
Table 2). Figure 5 shows the SSIM error heatmaps
for the Cytek-Sponza (C-S) and the Veach-Bidir (V-
B) scenes. For each scene, the experiments were
conducted with uniform smoothing parameters and
consistently applied all the heuristics mentioned in
§4.5, ensuring standardisation across different scenar-
ios. All results were rendered at a resolution of 1920
× 1080 on an NVIDIA RTX 2080 Ti.
6 DISCUSSION
The results show that our method can achieve accu-
rate global illumination with effective convergence,
even at reduced sampling frequencies. We attribute
these results to the local adaptive nature of the pho-
ton footprints. However, optimising this bandwidth
can be computationally demanding, leading to lower
frame rates, as observed in the Water Caustics scene
during the E-1000K experiment. This scene has dense
photon regions and varying AABB sizes which in-
crease the point-ellipsoid queries computed during
the gathering process. Variance underneath the glass
egg in the Veach-Bidir scene was still noticeable af-
ter 10,000 iterations of accumulation (Figure 6, left).
This observation corroborates the limitations previ-
ously noted by Frisvad et al. Frisvad et al. (2014).
Additionally, a minor reduction in SSIM accuracy
was noted in the Crytek-Sponza scene, attributable to
larger initial differential magnitudes stemming from
decreased photon counts. This impacted the precision
ARPÎ
ˇ
T: Hardware-Accelerated Ray-Traced Photon Differentials
305

Figure 6: Qualitative comparison of caustics under E-
1000K (top-left: RTPM, 100,000 iterations; bottom-left:
ARP∆, 10,000 iterations; right: RTPM and ARP∆, 500 iter-
ations).
of shadows, as the smoothing parameters remained
unchanged.
Photon differentials, in contrast to progressive
techniques, enable the rendering of sharp and well-
defined caustics, as demonstrated in Figure 6 and Ta-
ble 2. Progressive methods often result in blurry caus-
tics before reaching convergence, noticeable in the
Water-Caustics and Caustic-Glass scenes (see Figure
6, right). While reducing the initial radius can mit-
igate this blurriness, it also increases variance. By
integrating progressive photon mapping with photon
differentials, we effectively address the challenge of
extremely anisotropic photons by defaulting to pro-
gressive photons when such cases are detected. We
posit that large photon footprints and their corre-
sponding large bounding volumes hinder balanced
BVH construction. Preliminary tests indicate that us-
ing the culling heuristic boosts computational effi-
ciency.
7 CONCLUSION & FUTURE
WORK
This paper presents a new approach to global illu-
mination using photon differentials optimised for ray
tracing hardware. When facing problematic ellipsoid
footprints, we switch to progressive photon mapping
to ensure the accuracy of our solution. The results
demonstrate high-quality physically based rendering
at real-time rates. Future research should focus on
automating the smoothing parameters based on pho-
ton density, illumination type, photon path and scene
geometry.
REFERENCES
Bitterli, B. (2016). Rendering resources. https://benedikt-
bitterli.me/resources/.
Evangelou, I., Papaioannou, G., Vardis, K., and Vasilakis,
A. A. (2021). Fast radius search exploiting ray trac-
ing frameworks. Journal of Computer Graphics Tech-
niques (JCGT), 10(1):25–48.
Fabianowski, B. (2011). Interactive Manycore Photon
Mapping. PhD thesis, Trinity College (Dublin, Ire-
land). School of Computer Science & Statistics.
Fabianowski, B. and Dingliana, J. (2009). Interactive
global photon mapping. Computer Graphics Forum,
28(4):1151–1159.
Frisvad, J. R., Schjøth, L., Erleben, K., and Sporring, J.
(2014). Photon differential splatting for rendering
caustics. Computer Graphics Forum, 33(6):252–263.
Hachisuka, T., Ogaki, S., and Jensen, H. W. (2008). Pro-
gressive photon mapping. ACM Trans. Graph., 27(5).
Igehy, H. (1999). Tracing ray differentials. In Proceedings
of the 26th Annual Conference on Computer Graph-
ics and Interactive Techniques, SIGGRAPH ’99, page
179–186, USA. ACM Press/Addison-Wesley Publish-
ing Co.
Jensen, H. W. (1996). Global illumination using photon
maps. In Pueyo, X. and Schr
¨
oder, P., editors, Ren-
dering Techniques ’96, pages 21–30, Vienna. Springer
Vienna.
Jensen, H. W. (2004). A practical guide to global illu-
mination using ray tracing and photon mapping. In
ACM SIGGRAPH 2004 Course Notes, SIGGRAPH
’04, page 20–es, New York, NY, USA. Association
for Computing Machinery.
Kallweit, S., Clarberg, P., Kolb, C., Davidovi
ˇ
c, T., Yao,
K.-H., Foley, T., He, Y., Wu, L., Chen, L., Akenine-
M
¨
oller, T., Wyman, C., Crassin, C., and Benty, N.
(2022). The Falcor rendering framework. https:
//github.com/NVIDIAGameWorks/Falcor.
Kaplanyan, A. S. and Dachsbacher, C. (2013). Adaptive
progressive photon mapping. ACM Trans. Graph.,
32(2).
Kern, R., Br
¨
ull, F., and Grosch, T. (2023). Accelerated pho-
ton mapping for hardware-based ray tracing. Journal
of Computer Graphics Techniques (JCGT), 12(1):1–
28.
Kim, H. (2019). Caustics Using Screen-Space Photon Map-
ping, pages 543–555. Apress, Berkeley, CA.
Knaus, C. and Zwicker, M. (2011). Progressive photon
mapping: A probabilistic approach. ACM Trans.
Graph., 30(3).
Mara, M., Luebke, D., and McGuire, M. (2013). Toward
practical real-time : Efficient gpu density estimation.
In Proceedings of the ACM SIGGRAPH Symposium
on Interactive 3D Graphics and Games, I3D ’13, page
71–78, New York, NY, USA. Association for Comput-
ing Machinery.
McGuire, M. (2017). Computer graphics archive. https:
//casual-effects.com/data.
McGuire, M. and Luebke, D. (2009). Hardware-accelerated
global illumination by image space photon mapping.
GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications
306

In Proceedings of the Conference on High Perfor-
mance Graphics 2009, HPG ’09, page 77–89, New
York, NY, USA. Association for Computing Machin-
ery.
Moreau, P. and Doggett, M. (2022). Real-time rendering
of indirectly visible caustics. In Sousa, A. A., De-
battista, K., and Bouatouch, K., editors, Proceedings
of the 17th International Joint Conference on Com-
puter Vision, Imaging and Computer Graphics Theory
and Applications, volume 1 of GRAPP, page 39–48,
Set
´
ubal, PRT. INSTICC, SciTePress.
Purcell, T. J., Donner, C., Cammarano, M., Jensen, H. W.,
and Hanrahan, P. (2003). Photon mapping on pro-
grammable graphics hardware. In Proceedings of the
ACM SIGGRAPH/EUROGRAPHICS Conference on
Graphics Hardware, pages 41–50. Eurographics As-
sociation.
Schjøth, L., Frisvad, J. R., Erleben, K., and Sporring, J.
(2007). Photon differentials. In Proceedings of the
5th International Conference on Computer Graphics
and Interactive Techniques in Australia and Southeast
Asia, GRAPHITE ’07, page 179–186, New York, NY,
USA. Association for Computing Machinery.
Smal, N. and Aizenshtein, M. (2019). Real-Time Global
Illumination with Photon Mapping, pages 409–436.
Apress, Berkeley, CA.
Suykens, F. (2002). On Robust Monte Carlo Algorithms for
Multi-Pass Global Illumination. PhD thesis, Depart-
ment of Computer Science, KU Leuven, Celestijnen-
laan 200A, 3001 Heverlee, Belgium.
Suykens, F. and Willems, Y. D. (2001). Path differentials
and applications. In Proceedings of the 12th Euro-
graphics Conference on Rendering, EGWR’01, page
257–268, Goslar, DEU. Eurographics Association.
Yang, X. and Ouyang, Y. (2021). Real-Time Ray Traced
Caustics, pages 469–497. Apress, Berkeley, CA.
ARPÎ
ˇ
T: Hardware-Accelerated Ray-Traced Photon Differentials
307