Navigating Points of Interest: The Dog-Walker Pathﬁnding Algorithm

Natsuki Tsutsui

and Shohei Yokoyama

Graduate School of System Design, Tokyo Metropolitan University, Hino, Tokyo, Japan

Keywords:

Geographic Information System, Pathﬁnding Algorithm, Flickr.

Abstract:

Navigating complex environments that encompass both road networks and points of interest (POIs) demands

innovative pathﬁnding solutions. Traditional algorithms, such as Dijkstra’s, primarily focus on ﬁnding the

shortest path between nodes on a graph and are not designed to handle the additional complexity of scattered

POIs. This paper introduces the dog-walker pathﬁnding algorithm, a novel approach that integrates the discov-

ery of waypoints and greedy routing into a single process. By simulating the dynamics between two agents—a

dog motivated by POIs and a walker navigating a graph—the algorithm dynamically identiﬁes routes that con-

nect key locations and pass through areas rich in POIs. This method leverages road networks and POIs to

provide routes from the start point to the end point tailored to user preferences. Owing to the minimal data

requirements for POIs, this method can be easily integrated with various data sources, including X( formerly

Twitter), Google Maps, and Instagram. In this study, we develop an agent-based online algorithm inspired by

the dogwalker. We veriﬁed the algorithm using POI data obtained from Flickr and Google Maps, demonstrat-

ing its application in real-world scenarios such as recommending tourist routes. Demonstrations show that

our algorithm effectively generates routes that align with user preferences, as evidenced by qualitative and

quantitative assessments. Additionally, we demonstrated that our method operates more rapidly than methods

utilizing Dijkstra’s algorithm.

1 INTRODUCTION

Pathﬁnding algorithms are essential for numerous ap-

plications related to real-world mobility. They are

widely used for ﬁnding the shortest route between

two points in large graph data, such as road maps.

Additionally, these algorithms help manage complex

queries such as route optimization, automated driv-

ing, and tourist route recommendations.

In this paper, we introduce the dog-walker algo-

rithm, a novel method designed to ﬁnd routes that

cater to user interests within large graph data spaces

with numerous point of interest(POIs).

The proposed method utilizes data from Open

Street Map

and Flickr

. Figure 1 illustrates the tar-

geted spatial area. By integrating geographical infor-

mation and social media content, this approach en-

riches the analysis and enhances the precision of the

methodological application. In our graph, road net-

work edges are depicted by blue lines, while POIs are

https://orcid.org/0009-0000-2390-5572

https://orcid.org/0000-0002-0550-617X

https://www.openstreetmap.org/copyright/en

https://www.ﬂickr.com

represented by red dots. The algorithm identiﬁes ef-

ﬁcient routes in such spaces, favoring regions with a

high density of POIs.

Traditionally, algorithms such as Dijkstra’s are

used to ﬁnd optimal routes on graphs. However, these

methods are not equipped to handle spaces where

both graphs and POIs coexist, as targeted in this study.

In typical road networks, nodes are placed at inter-

sections, but our usual start and end points, such as

buildings or parking lots, are not directly on the road.

Similarly, most landmarks do not reside directly on

the road.

This concept is particularly suited for applications

using geosocial big data. For instance, consider the

graph as a road network and the POIs as geotagged

photos shared on social media sites. A geotag rep-

resents the latitude and longitude coordinates where

the photo was taken, provided by the GPS of a smart-

phone or other device. Locations with a high den-

sity of geotags are noteworthy. Geotags often exist

independently from the road network and may have a

fuzzy density distribution due to GPS errors.

The objective of the proposed method is to dis-

cover routes on the road network that pass through

Tsutsui, N. and Yokoyama, S.

Navigating Points of Interest: The Dog-Walker Pathﬁnding Algorithm.

DOI: 10.5220/0013238800003935

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 11th International Conference on Geographical Information Systems Theory, Applications and Management (GISTAM 2025), pages 27-38

ISBN: 978-989-758-741-2; ISSN: 2184-500X

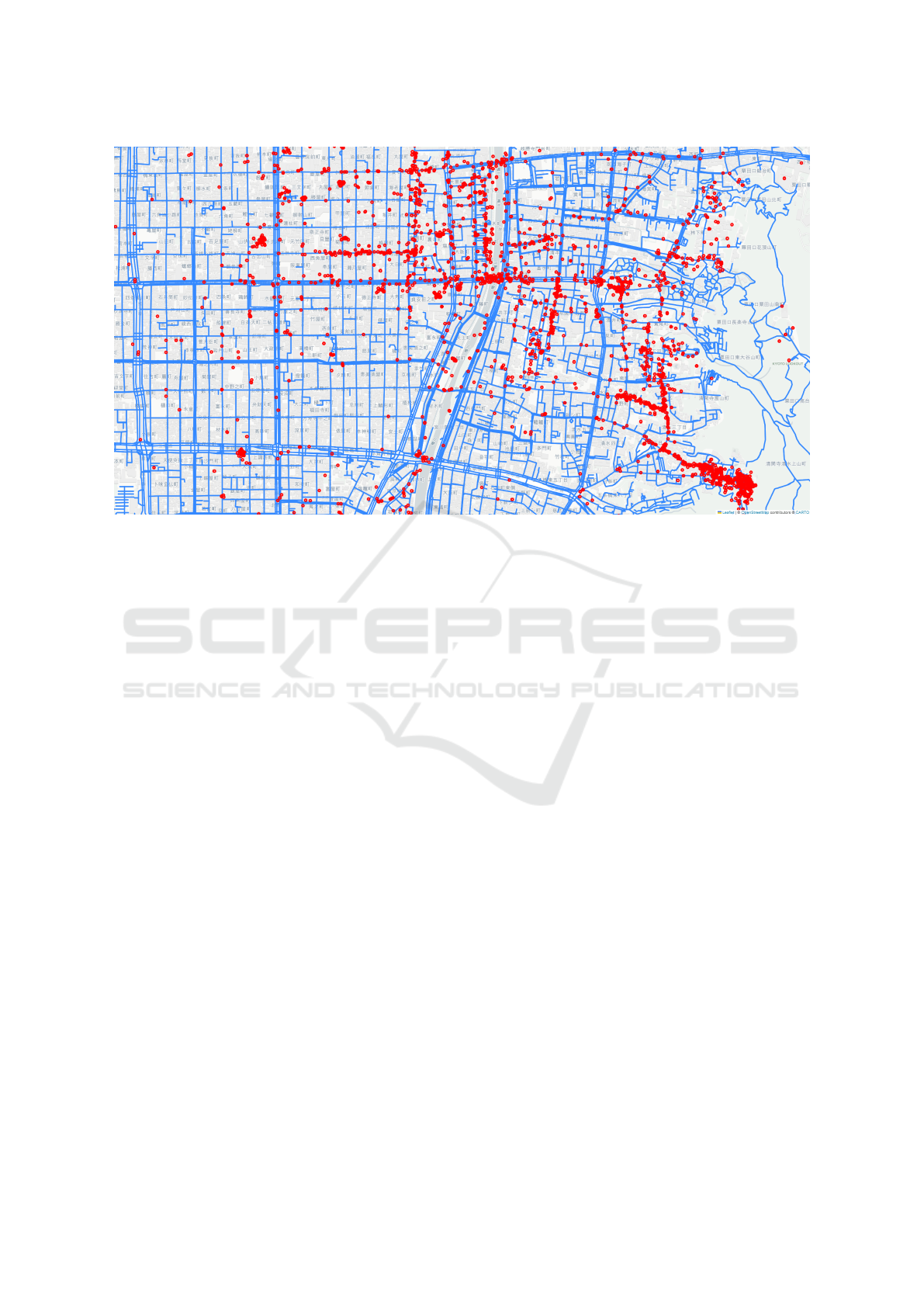
Figure 1: OpenStreetMap data in Kyoto Prefecture, Japan. Blue lines represent road network edges and red dots represent

POIs.

locations with a high density of POIs that are not di-

rectly on the road network but exist in the same space.

This algorithm can be applied to recommend

sightseeing routes based on geosocial data. Con-

ventionally, recommending tourist routes required

two steps: recommending waypoints and discover-

ing routes connecting them. For example, POIs are

density-clustered by DBSCAN, and routes are dis-

covered using nodes in the cluster as waypoints. In

contrast, the proposed method is an online algorithm

that simultaneously discovers waypoints and optimal

routes.

The dog-walker pathﬁnding algorithm works on

the principle of two agents: a dog and a walker. The

walker navigates the graph, while the dog moves in-

dependently within a two-dimensional space, moti-

vated by POIs. The dog and walker are linked by a

lead, with the walker propelled in the direction the

dog wishes to go. The dog, motivated by POIs acting

as food, moves toward areas where POIs are abun-

dant. Once the dog has consumed enough POIs, it

gravitates toward its goal. The path that the walker

takes, led by the dog, is the output of this algorithm,

anticipated to pass through areas with a high density

of POIs.

The contributions of this study are as follows.

1. Identifying waypoints based on POIs.

2. Discovering efﬁcient routes around waypoints.

3. Developing an algorithm that combines the above

two steps.

4. Creating agent-based online algorithms inspired

by the dog-walker concept.

5. Demonstrating a strong relevance to real-world

applications.

In this study, we qualitatively and quantitatively

evaluated the recommended routes assuming user

preferences using geosocial data, and the results in-

dicated that route recommendations were effectively

made.Additionally, we demonstrated that our method

operates more rapidly than methods utilizing Dijk-

stra’s algorithm.

The remainder of this paper is structured as fol-

lows: Section 2 covers related work, Section 3 details

our proposed method, Section 4 presents the experi-

ments, and Section 5 concludes the paper and outlines

future work.

2 RELATED WORK

Research utilizing geotagged social data has explored

not only route recommendations based on user pref-

erences but also methods that consider various fac-

tors such as time, distance, route safety, weather, and

crowding as costs in the calculation. Additionally,

studies have focused on identifying popular tourist

spots using geotagged social data.

Yang et al. (Yang et al., 2011) proposed a ver-

satile and highly accurate method for identifying

tourist spots using geotagged social data collected

GISTAM 2025 - 11th International Conference on Geographical Information Systems Theory, Applications and Management

from Flickr in Paris, Hong Kong, and New York.

This method employs self-tuning spectral lustering,

which does not require parameter settings, allowing

for consistent clustering applicable to cities and loca-

tions with different POI characteristics.

Chen et al. (Chen et al., 2011) proposed a per-

sonal trajectory prediction system based on GPS data,

using a new algorithm called Continuous Route Pat-

tern Mining to extract route patterns. This system pre-

dicts future routes by utilizing route patterns extracted

from an individual’s past trajectory data. Popescu

et al. (Popescu and Grefenstette, 2009) developed a

method to estimate visit times and daily tourist routes

using geotagged social data from Flickr in London,

New York, Paris, and San Francisco. The proposed

method automatically estimates visit times to tourist

locations by utilizing the timestamps and location in-

formation of photos posted by users. Kurashima et

al. (Kurashima et al., 2010) proposed a system that

models the history of places visited by tourists us-

ing geotagged social data from Flickr in New York

and San Francisco. This system recommends travel

routes based on the user’s current location and in-

dividual interests, leveraging data from large-scale

photo-sharing sites for route recommendations, un-

like previous studies that utilized GPS data. Ishizaki

et al. (Ishizaki et al., 2021) introduced an algorithm

called P-UCT that recommends routes best match-

ing user preferences. The method includes gener-

ating evaluators using Support Vector Machine and

route generation using Monte-Carlo Tree Search. Jie

et al. (Bao et al., 2012) developed a system that auto-

matically learns user preferences from location his-

tories and extracts local expert opinions to provide

recommendations. This system utilizes data collected

from Foursquare in New York and Los Angeles. All

of these route recommendation and estimation meth-

ods require user movement records and speciﬁc data

sources, leading to challenges in data acquisition and

the insufﬁciency of necessary data in certain regions.

De et al. (De Choudhury et al., 2010) proposed

a method for generating tourist routes using geo-

tagged social data from Flickr. This method uses

geographic and temporal information to create timed

paths based on each user’s visited locations, stay du-

rations, and travel times. By applying an orienteering

problem algorithm (Tsiligirides, 1984), the system

recommends optimal travel routes. Furthermore, Ma-

jid et al. (Majid et al., 2015) introduced a method for

recommending suitable tourist destinations and travel

routes using geotagged social data from Flickr, tourist

data from Google Places, and historical weather data.

These studies differ from our research in that they re-

quire pre-existing information about tourist spots for

route recommendations. Jain et al. (Jain et al., 2010)

proposed a system called Antourage to recommend

tourist routes using geotagged social data from Flickr.

In this method, users specify a starting point and a

maximum travel distance, and the system suggests

routes that visit popular tourist destinations within

those constraints. The route exploration algorithm

employs the Max-Min Ant System, a metaheuristic

algorithm developed based on the behavior of real

ants, as proposed by Dorigo et al. (Dorigo et al.,

1996) (Dorigo and Gambardella, 1997) (Dorigo and

Di Caro, 1999). It is primarily applied to combina-

torial optimization problems and is particularly effec-

tive for the Traveling Salesman Problem (TSP). This

algorithm consists of pheromone trails, pheromone

updates, probabilistic path exploration, and an itera-

tive process. Antourage recommends tours that visit

popular tourist destinations; however, its optimization

algorithm is time-consuming, making it unsuitable for

online processing.

Kim et al. (Kim et al., 2014) proposed a nav-

igation system called SocRoutes, which uses crime

history data from Chicago and geotagged social data

from X to suggest routes based on the regional con-

text, particularly emotions. Unlike traditional naviga-

tion systems that suggest routes based on the shortest

distance or fastest time, SocRoutes considers emo-

tional context when suggesting routes. Fu et al.

(Fu et al., 2014) introduced TREADS, a travel route

recommendation system that leverages social media

data, speciﬁcally X and Yelp reviews, to recom-

mend safe and interesting travel routes in real time.

TREADS takes into account the user’s interests and

safety, employing text summarization techniques to

provide summaries of X data and Yelp reviews related

to the locations on the recommended route. Quercia

et al. (Quercia et al., 2014) developed a system that

recommends not only the shortest route in urban areas

but also emotionally pleasant routes. They retrieved

the top k-shortest paths and evaluated these routes us-

ing geotagged data based on criteria such as “beau-

tiful,” “quiet,” and “happy.” These route exploration

methods are designed for speciﬁc purposes, unlike

our research, which aims to integrate multiple user

preferences and interests.

Yamashita et al. (Yamashita and Yokoyama, 2022)

proposed a method for recommending routes based

on user preferences by dividing a map into a grid and

assigning weights to the edges of the graph based

on nighttime light data and geotagged tweets from

X. They applied Dijkstra’s algorithm to ﬁnd opti-

mal routes. While this method shares similarities

with our research in terms of integrating various data

sources and recommending routes based on user pref-

Navigating Points of Interest: The Dog-Walker Pathﬁnding Algorithm

erences, it relies on Dijkstra’s algorithm (Dijkstra,

1958), which tends to avoid recommending routes

that signiﬁcantly deviate from the shortest path. In

contrast, our study allows for adjusting the extent to

which POIs are collected based on parameters, thus

recommending more interesting detours.

3 PROPOSED METHOD

This section details the proposed method. Figure 2

provides an overview of our methodology, which is

divided into three phases: dataset, preprocessing, and

main processing.

The dataset phase consists of POI data (Section

3.1) and road network data (Section 3.2). During pre-

processing, we extract speciﬁc POIs from the POI

data (Section 3.3) and remove dead-end nodes from

the road network (Section 3.4), overlaying them onto

the same plane. We then assign POIs to each node

(Section 3.5) and precompute the interest vectors

(Section 3.6). In the main processing phase, we set

start and end points on the preprocessed data, ap-

ply Dijkstra’s algorithm (Section 3.7) to construct

the shortest path tree, and execute the dog-walker

pathﬁnding algorithm (Section 3.8).

Additionally, “POIs-on-map” refers to the situa-

tion where POIs overlap on the road network, while

“Weighted POIs-on-map” indicates a state where data

has been preprocessed, with POIs assigned to each

node.

3.1 Data on POIs

We use geotagged POI data for route searching. The

POI data requires only coordinate information on a

two-dimensional plane (latitude and longitude), mak-

ing it applicable to various data sources.

We utilize geotagged data shared on social net-

working services as POI data. Geotags represent the

coordinates where the data were posted, suggesting

that areas with high geotag density may contain points

of interest. Therefore, our method suggests a route

that includes waypoints densely populated with geo-

tags en route to the destination. We have employed

data from sources such as Flickr and Google Maps

;

however, our methodology is adaptable to various

sources, including Instagram

and X

, allowing for

the integration of different data sources.

https://www.google.com/maps

https://www.instagram.com

https://www.x.com

3.2 Road Network

We deﬁne the road network as a simple undirected

graph with non-negative weights, excluding one-way

streets. The graph is denoted as G = (V, E), where V

represents the set of nodes, and E represents the edges

of the road network. Each edge is represented as an

unordered pair of vertices, u, v ∈ V , where (u, v) ∈ E

and u ̸= v.

The cost between nodes is represented as w(u, v),

where w(u, v) = w(v, u) and w(u, v) > 0. Each node

has associated two-dimensional coordinate informa-

tion; if the coordinates of nodes u and v are x

and x

respectively, then x

̸= x

when u ̸= v.

Furthermore, we denote the straight-line distance

between coordinates x

and x

as l(x

, x

). However,

l(x

, x

) does not necessarily equal w(u, v) because

real-world roads are not composed of straight lines.

3.3 Extraction POIs

The extracted POIs contain various metadata depend-

ing on the dataset. For instance, Flickr provides meta-

data such as latitude and longitude, images, creation

time, text, and tags. Google Maps might include re-

views and store names. These metadata are used to

extract subsets according to user preferences. For in-

stance, data extracted from Flickr using the text “tem-

ple,” can be used by tourists interested in visiting tem-

ples.

In this study, we focus on the dog-walker pathﬁnd-

ing algorithm and do not discuss the method of ex-

tracting data based on user preferences. However, our

method assumes that the POIs, based on user prefer-

ences, only require latitude and longitude, making it

compatible with various datasets.

3.4 Removal of Dead-End Nodes

The proposed method relies on the dog agent moving

toward POIs, which makes it vulnerable at dead-end

nodes. This occurs because the dog agent is drawn

to the POIs regardless of dead ends, leading to a loop

when a waypoint exists beyond the dead-end node.

To ensure efﬁcient navigation, a preprocessing step is

necessary to remove these nodes. Therefore, we re-

moved the dead-end nodes using the existing method

by Jiyoung et al (Pung et al., 2022).

We remove edges connected to nodes of degree

one, ensuring that each node v in the graph G satisﬁes

deg(v) ≥ 2.

Additionally, road networks often represent the

same street with two edges separated by lanes, such

as in multilane roads. Thus, merely deleting nodes

GISTAM 2025 - 11th International Conference on Geographical Information Systems Theory, Applications and Management

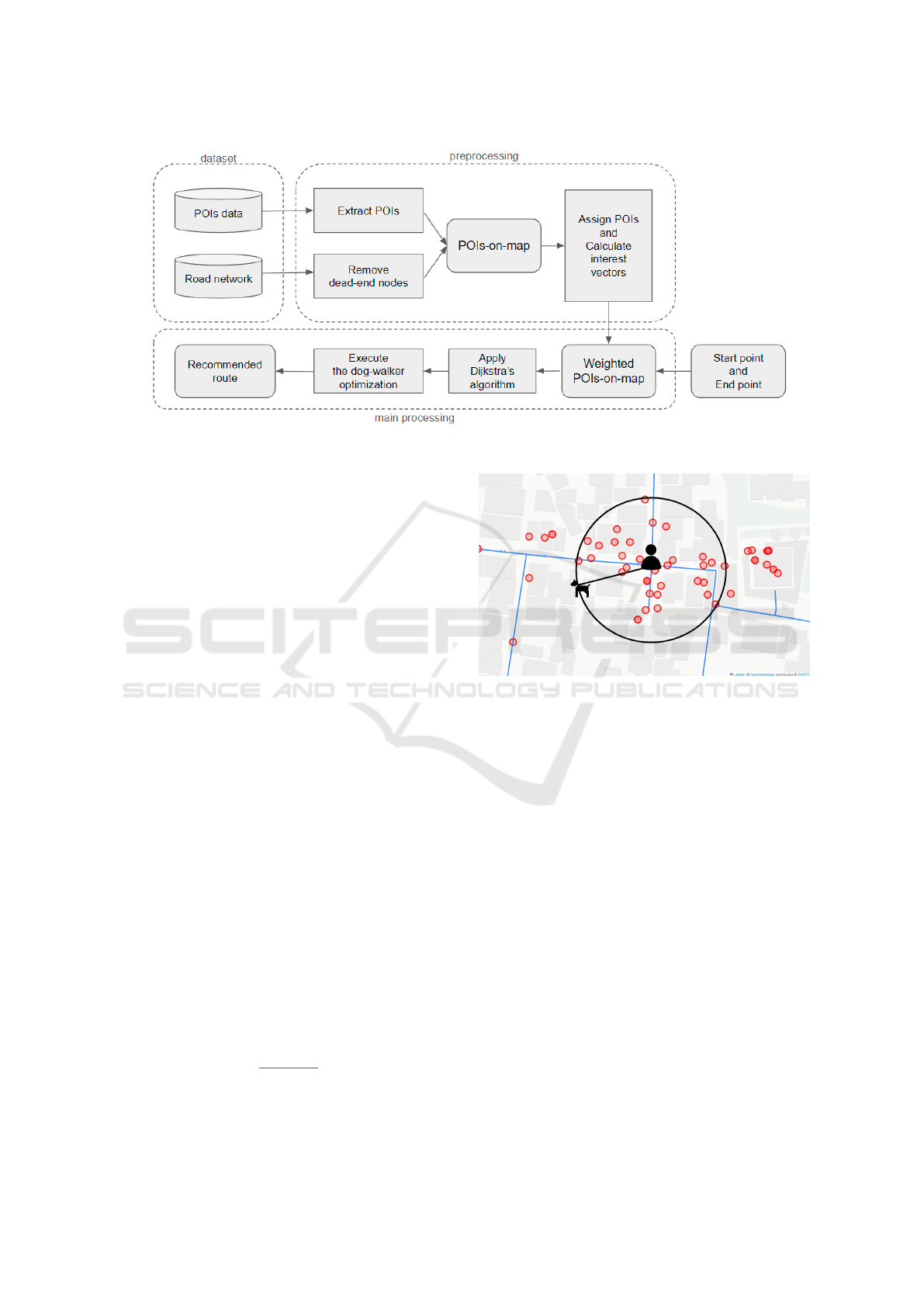
Figure 2: Overview of proposed method.

of degree one does not completely remove dead-end

nodes. However, this issue is peripheral to our core

problem and will not be further discussed here.

The preprocessed road network graph and the ex-

tracted POIs are combined on the same plane as POIs-

on-map, which is then passed on to the subsequent

processing.

3.5 Assigning POIs

For each node, we record a set of POIs within a dis-

tance L[m] (in m). To calculate the distance between a

node and a POI, we use the Haversine formula, which

treats the Earth as a perfect sphere using spherical

trigonometry. If the longitude and latitude of point

A are (φ

, ψ

) and those of point B are (φ

, ψ

), the

distance between points A and B is given by the fol-

lowing formula:

L = R cos

−1

(sinψ

sinψ

+ cos ψ

cosψ

cos∆φ)

(1)

As shown in Figure 3, when an agent reaches a

node, the POIs recorded at that node are considered

to be collected by the dog agent. The nodes that have

been collected in this manner no longer inﬂuence sub-

sequent route searching. This process is detailed fur-

ther in Section 3.8, “Execution of the Dog-Walker

Pathﬁnding Algorithm.”

3.6 Calculation of Interest Vectors

For each node, the sum of the dog’s interest vectors

for all POIs is calculated using the following formula:

(

, x

)

) =

− x

) (2)

∑

p∈P

(

, x

)

) (3)

Figure 3: Collection method of POI by the dog agent in the

proposed route recommendation system. The walker agent

(depicted as a human silhouette) remains at the reached

node, while the dog agent (depicted as a dog silhouette) col-

lects POI (red circles) within a deﬁned radius (black circle)

around the node.

Description 1. Blue lines represent road network

edges and red points represent POI.

Here, P represents the set of POIs, x

is the posi-

tion vector of a POI, x

is the position vector of a node,

and n is a parameter that determines the weight given

to distance. A larger value of n indicates a greater in-

terest in nearby POIs. The dog agent determines its

next node based on this interest vector I

3.7 Application of Dijkstra’s Algorithm

When a user speciﬁes the start and end points in lat-

itude and longitude, the nearest nodes are identiﬁed

and assigned as the respective start and end points.

Subsequently, Dijkstra’s algorithm is applied starting

from the end node to construct the shortest path tree,

recording the parent of each node in the process. This

Navigating Points of Interest: The Dog-Walker Pathﬁnding Algorithm

information enables the walker agent to navigate to-

ward the end node.

This process is initiated after the user provides the

start and end points, thus constituting a part of the on-

line processing phase. As such, Dijkstra’s algorithm

incurs a computational cost of O(N logM), where N

represents the number of nodes and M the number of

edges.

3.8 Execution of the Dog-Walker

Pathﬁnding Algorithm

This section describes the dog-walker pathﬁnding al-

gorithm. In the proposed method, the agent begins at

the start node and follows these steps until it reaches

the end node: (1) retrieve POIs, (2) recalculate the

interest vector, and (3) determine the next node.

3.8.1 Retrieval of POIs

The dog agent collects POIs within a radius of L[m]

from the reached node and stores them in a set. Once

collected, these POIs no longer inﬂuence any node.

The targeted POIs are assigned to nodes during pre-

processing, and except when L is excessively large,

the overall computational complexity remains within

approximately O(|P|). (|P| is the number of POIs)

As the collected POIs no longer have any inﬂu-

ence, it is necessary to recalculate the interest level

when deciding the next node. The method for recal-

culating this interest level is detailed in the following

section.

3.8.2 Recalculate the Interest Vector

When the agent decides the next node, it calculates

the interest vector I

following the formula:

= CI

+ I

(4)

Here, I

represents the dog’s interest vector for

POIs at the current node that have not yet been col-

lected, while I

represents the walker’s interest vec-

tor. Therefore, the interest vector I

for the agent is

determined by the sum of the interest vectors of both

the dog and the walker. Additionally, C is a parameter

that dictates whether the dog or walker has a greater

inﬂuence on decision-making.

As the movement of the node is determined by the

direction of the vector I

, scalar values are essentially

meaningless in this context. Therefore, the parameter

is set for only one of the terms.











∑

p∈P

(

, x

)

) −

∑

q∈Q

(

, x

)

∑

p∈P\Q

(

, x

)

(5)

Here, Q is the set of collected POIs. If the set of

collected POIs is less than half of the total POIs, the

calculation is done by subtracting from the prepro-

cessed interest vectors. If more than half, the interest

vectors of the uncollected POIs are added to ﬁnd the

dog’s interest vector. This yields the same result with

either formula, regardless of the number of collected

POIs. However, for a large number of POIs, or when

few POIs are collected, this can signiﬁcantly reduce

execution time.

Additionally, I

is calculated according to the fol-

lowing formula:

now

min

(

, x

)

) (6)

Here, j denotes the parent node of i, and x

and

represent the coordinates of these nodes, respec-

tively. L

min

is the shortest path length from the origin

to the destination calculated a priori using Dijkstra’s

algorithm, while L

now

denotes the cumulative distance

traveled by the agent from the start node to its current

node. Consequently, as the path length increases, the

walker agent experiences a stronger compulsion to-

ward the end node.

3.8.3 Determining the Next Node

The next node is determined by selecting the node that

has the highest cosine similarity between the direction

vector from the current node to an adjacent node and

the interest vector.

k = argmax

· v

vi, j

||v

i, j

(i, j ∈ E) (7)

Here, v

i, j

represents the direction vector from

node i to node j. If the next node is not the end node,

the agent repeats this process starting from the POI

collection phase.

Our method requires calculating the inﬂuence

from each POI as the agent moves between nodes,

which can be time-consuming for route search. The

worst-case computational complexity of the route

search is the product of the number of nodes tra-

versed and the total number of POIs used. There-

fore, the computational complexity increases propor-

tionally with the number of POIs. However, as the

POIs collected by the agent do not affect subsequent

route searches, the number of POIs that inﬂuence the

search decreases as the search progresses. Moreover,

if the inﬂuence of all POIs and the set of nearby POIs

is precomputed for each node during preprocessing,

the actual execution time becomes signiﬁcantly faster

than the theoretical computational complexity.

GISTAM 2025 - 11th International Conference on Geographical Information Systems Theory, Applications and Management

4 EXPERIMENTS

In this section, we describe the datasets used, and

present the results and analyses of the experiments.

4.1 Datasets

4.1.1 Flickr

Flickr is a photo-sharing platform that allows users

to upload, share, and tag photographs and videos. It

features an extensive database of billions of images,

many of which are geotagged. This geotagged data

have been utilized in a wide range of ﬁelds, including

geographic information system (GIS) research, com-

puter vision, and social sciences for analysis and vi-

sualization purposes.

However, our proposed method does not rely on

user movement histories or images, which enhances

its compatibility with data sources other than Flickr.

In this study, Flickr was chosen because of the ease of

data acquisition and the large scale of its data sources.

4.1.2 Google Maps

Google Maps is a Web-based mapping service that

provides satellite imagery, street maps, panoramic

street views (street views), real-time trafﬁc condi-

tions (Google Trafﬁc), and route planning for walk-

ing, driving, cycling, and public transit. As a rich

source of geographic data, Google Maps been exten-

sively used in various ﬁelds, including urban plan-

ning, transportation, and tourism. Detailed and fre-

quently updated data aid precise planning and analy-

sis of spatial patterns.

In our research, Google Maps was selected as the

second source of POIs data because of the ease of data

acquisition and availability of additional information

such as reviews.

4.1.3 Open Street Map

Open Street Map is a free user-generated database of

map data that offers a comprehensive array of geo-

graphic information, including roads, buildings, and

terrain, from around the world. This platform is an

open-source project that allows map data to be freely

used for both commercial and non-commercial pur-

poses.

Open Street Map data are utilized in a variety of

applications such as location-based services, naviga-

tion tools, urban planning, and transportation system

research.

4.2 Experimental Setting

For our experiments, we used Flickr data spanning

three years, from January 1, 2021 to January 1, 2024.

Data for speciﬁc segments in Times Square, Manhat-

tan, New York, USA, and Kyoto City, Kyoto Prefec-

ture, Japan were gathered from Flickr, Google Maps,

and OpenStreetMap. These datasets includes POIs

and road network data.

From Flickr, we extracted posts within the tar-

geted segments that included relevant keywords in

their descriptions or tags. Data extraction from

Google Maps was conducted manually, selecting ap-

propriate content within the targeted segments. The

acquired road network data consisted of walker path-

ways within the designated segments.

In each experiment, we collected POIs and road

network data within speciﬁed geographical bound-

aries. For Times Square, the collection was within

the latitude range of 40.745149 to 40.767065 and

longitude range of -73.996706 to -73.970711. Sim-

ilarly, in Kyoto, the data were gathered within lati-

tude 34.99054 to 34.99940 and longitude 135.76802

to 135.78408.

The acquired road network data consisted of

walker pathways within the designated segments.

4.3 Experimental Result and Analysis

4.3.1 Experiments with Flickr Data

We conducted experiments using data from Flickr on

Times Square, Manhattan, New York to validate our

proposed method. Figure 4 (a) illustrates the results

of a route search from latitude 40.74510, longitude -

73.99670 to latitude 40.76710, longitude -73.97080,

restricted to posts containing the text ‘cityscape.’ The

blue route represents the shortest path, while the or-

ange route depicts the path determined by our pro-

posed method. Figure 4 (b) illustrates the results of

a route search restricted to posts containing the text

“art” in the same section.

Figure 5 shows the waypoints traversed by the

route determined by our proposed method, as il-

lustrated in Figure 4. The ﬁrst waypoint is along

the 7th Avenue, a well-known and bustling area in

Times Square. The next waypoint spans horizon-

tally at the Top of the Rock observation deck, where

most posts focus on the night view. Furthermore,

for routes tagged with ’art’, after navigating several

smaller waypoints, the route notably passes through a

signiﬁcant waypoint at The Museum of Modern Art

(MoMA).

These ﬁgures demonstrate that the route generated

by our proposed method effectively passes through

Navigating Points of Interest: The Dog-Walker Pathﬁnding Algorithm

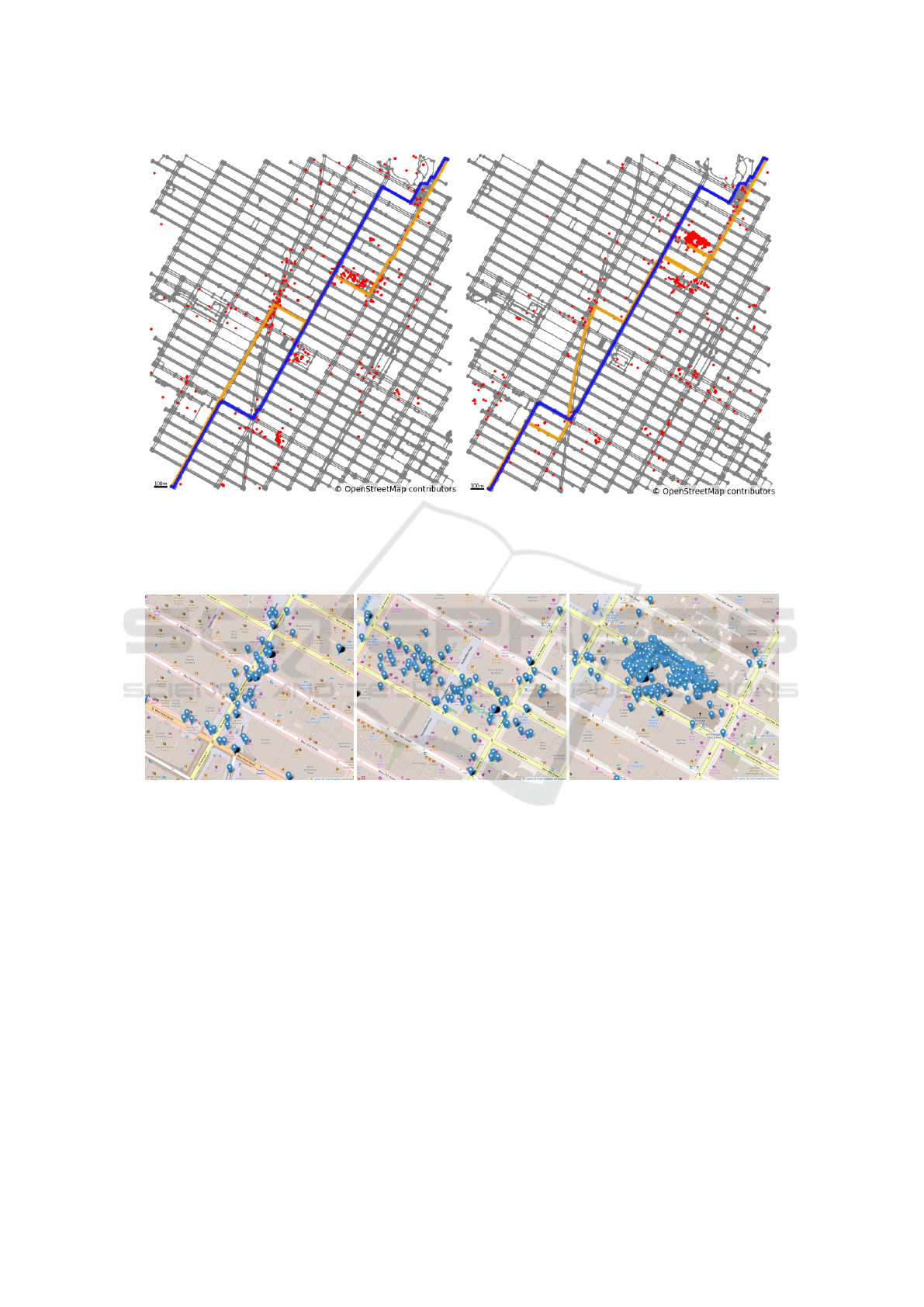
(a) cityscape (b) art

Figure 4: Results of the experiment that used the proposed method with Flickr data in parts of Manhattan, New York, USA.

The gray, blue, and orange lines represent the road network, shortest route, and recommended route derived using the proposed

method. Red dots represent POIs.

(a) 7th Avenue (b) Top of the Rock (c) MoMa

Figure 5: Details of waypoints passed by the proposed method in Times Square.

waypoints associated with the text ‘cityscape’ and

‘art’ within the area.

4.3.2 Experiments with Google Maps and Flickr

Data

In Kyoto City, Kyoto Prefecture, we conducted ex-

periments using data from Google Maps and Flickr

to validate our proposed method. Figure 6 visu-

alizes POIs related to ‘temple’ buildings along the

popular tourist route from Kiyomizu-Gojo Station to

Kiyomizu-dera Temple. In the experiments using

Google Maps data, temples within the segment were

designated as POIs, which are listed in Table 1.

Posts containing the keyword ‘temple’ within the

studied segment were extracted from the Flickr data.

In each ﬁgure, the blue and orange routes depict the

shortest and recommended paths, respectively.

Figure 7 details the waypoints passed by the route

recommended by our proposed method shown in Fig-

ure 6. The ﬁrst encountered waypoint is the Yasaka

Pagoda at Hokan-ji Temple, a renowned photographic

landmark. The next waypoint is Kiyomizu-zaka, a

major street leading to the Kiyomizu-dera Temple.

These ﬁgures demonstrate that the route generated by

our proposed method effectively passes through loca-

tions with POIs while heading toward the end node.

4.3.3 Experiments on Execution Time

We compared the execution times of the proposed

method with those of a baseline method, utilizing the

GISTAM 2025 - 11th International Conference on Geographical Information Systems Theory, Applications and Management

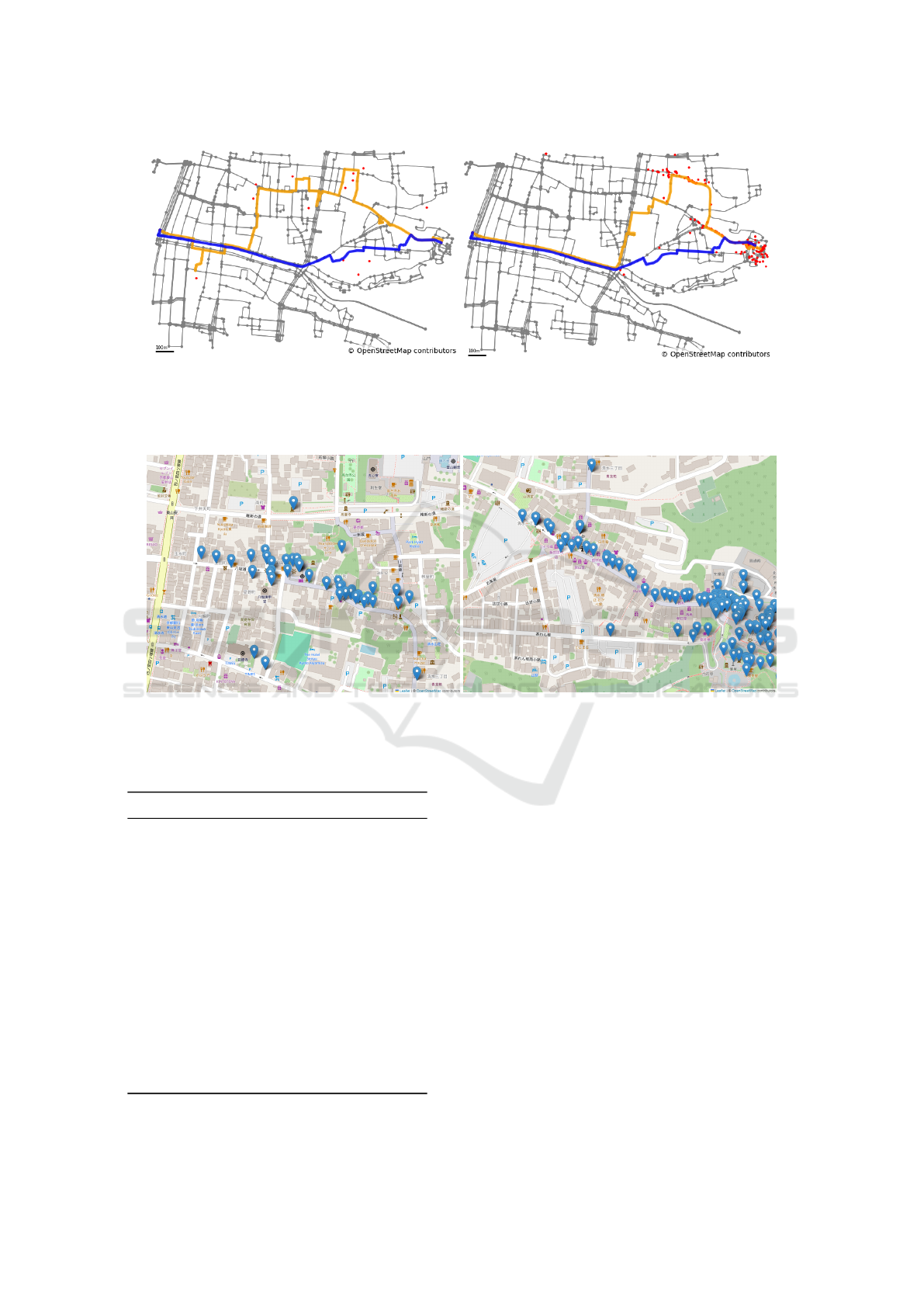
(a) using Google Maps data (b) using Flickr data

Figure 6: Results of the experiment conducted using the proposed method with Google Maps and Flickr data in Kyoto City,

Kyoto Prefecture, Japan. The gray, blue, and orange lines show the road network, shortest route, and recommended route

derived using the proposed method. Red dots represent POIs related to ‘temple.’.

(a) Hokan-ji Temple (b) kiyomizu-zaka

Figure 7: Details of waypoints passed by the proposed method in Kyoto.

Table 1: Coordinates of temples located in the target sec-

tion.

temple name latitude longitude

Rokuharamitsu-ji 34.99722 135.77336

Rokudouchinnou-ji 34.99839 135.77537

Shoumyou-ji 34.99422 135.77081

Kiun-ji 34.99153 135.78051

Jippo-ji 34.99445 135.77829

Honju-ji 34.99464 135.77910

Saifuku-ji 34.99931 135.77395

Nittai-ji 35.02649 135.79178

Daizen-ji 34.99803 135.77891

Hofuku-ji 34.99634 135.77643

Hokan-ji 34.99872 135.77926

Kongo-ji 34.99851 135.77869

Tsumyoji 34.99405 135.77898

Kosho-ji 34.99698 135.78269

Juen-ji 34.99839 135.77116

road network of Times Square and artiﬁcially gener-

ated POIs. The baseline method employed two ap-

proaches: a simple execution of Dijkstra’s algorithm

between the start and end points, and an integrated

approach combining DBSCAN clustering with Dijk-

stra’s algorithm For this comparison, we measured

only the execution time of the main processing after

the user’s start and end points had been provided.

In the proposed method, we generated a shortest

path tree using Dijkstra’s algorithm and subsequently

executed the dog-walker pathﬁnding algorithm, mea-

suring the duration required. For this analysis, we

conﬁgured the proposed method with parameters that

ensured all waypoints were visited, meeting the con-

ditions of the baseline method. In Baseline Method

1, we calculated the execution time of Dijkstra’s al-

gorithm from the start point to the endpoint. In the

baseline method 2, the route from the start to the end

node was calculated multiple times using Dijkstra’s

algorithm to ensure all given waypoints were visited,

Navigating Points of Interest: The Dog-Walker Pathﬁnding Algorithm

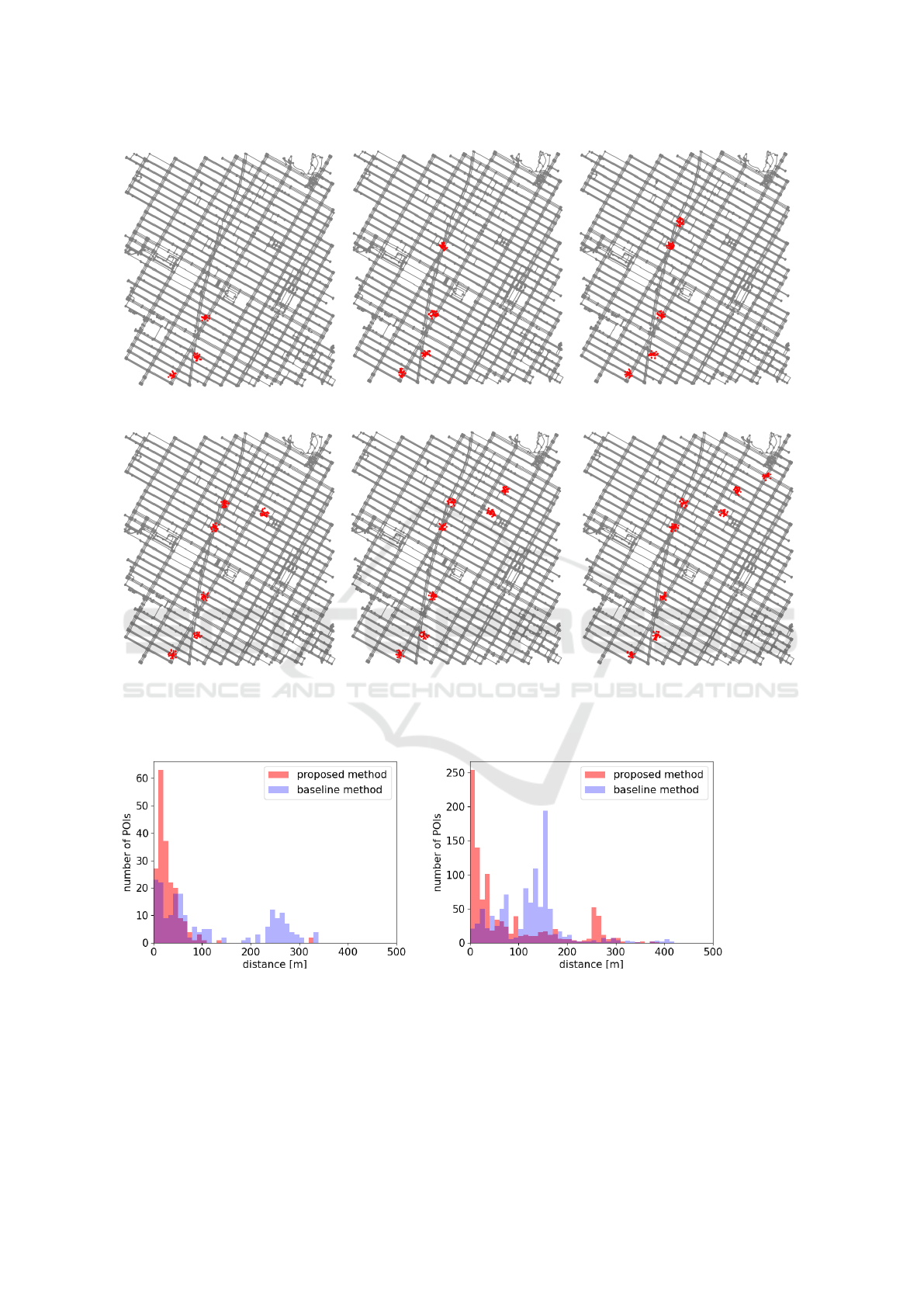
(a) Number of waypoints is 3

(|POIs| = 30)

(b) Number of waypoints is 4

(|POIs| = 60)

(|POIs| = 90)

(d) Number of waypoints is 6

(|POIs| = 120)

(e) Number of waypoints is 7

(|POIs| = 150)

(f) Number of waypoints is 8

(|POIs| = 180)

Figure 8: POIs-on-map using artiﬁcial data.

(a) Manhattan (b) Kyoto

Figure 9: Distribution of the shortest distance between each POI and route.

and we compared the execution times. Here, the pro-

cessing time for DBSCAN in the baseline method was

not included in the computation time because it can

be performed during preprocessing. Thus, the execu-

tion time for the baseline method is proportional to

the time spent on Dijkstra’s algorithm. Additionally,

The waypoints generated for the experiment has 30

POIs each, randomly generated within a 50m radius

from the center point to account for GPS errors.

Figure 8 illustrates the POIs-on-map when the

GISTAM 2025 - 11th International Conference on Geographical Information Systems Theory, Applications and Management

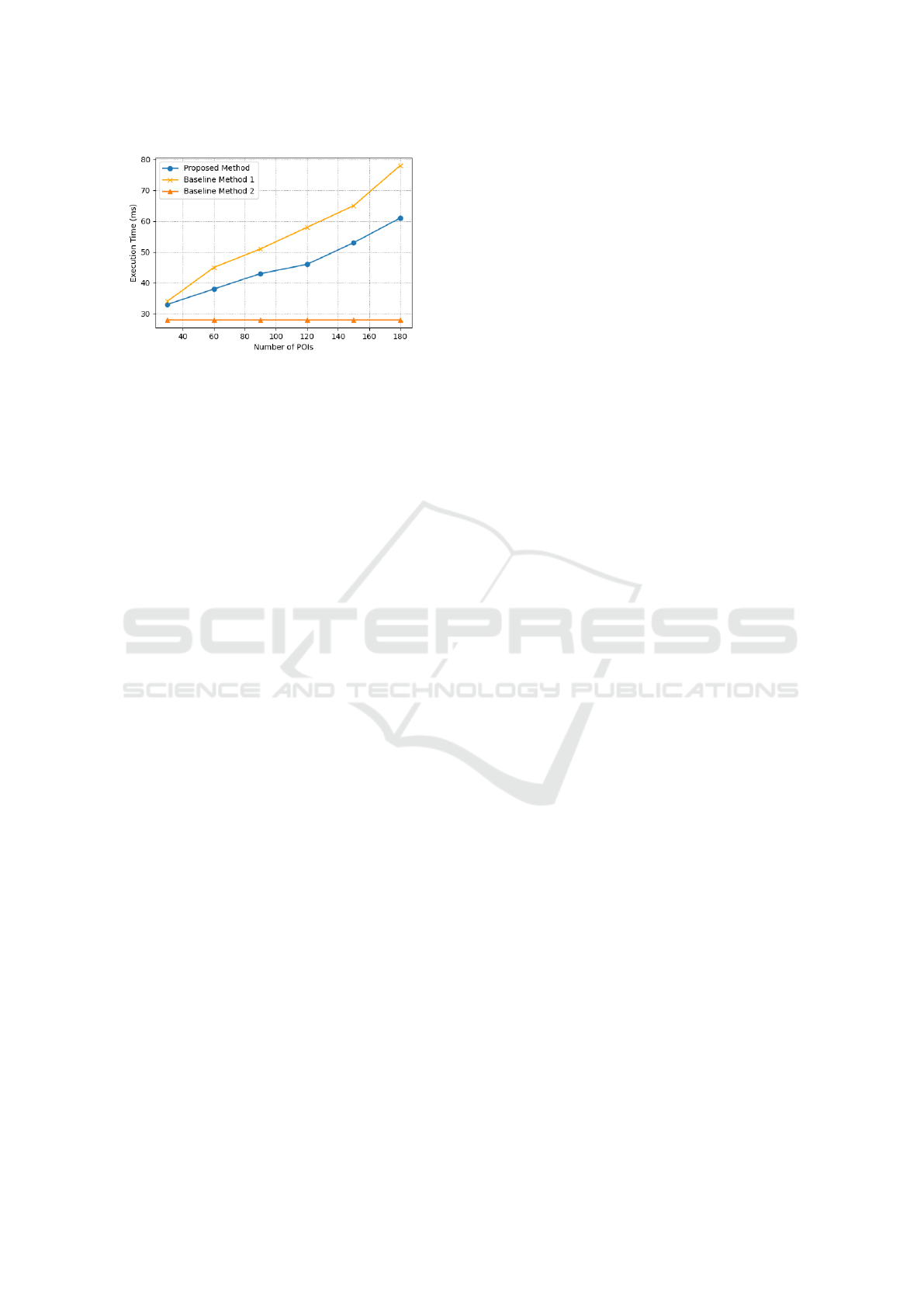
Figure 10: Execution time comparison among proposed and

baseline method.

number of waypoints was varied from 3 to 8.

Figure 10 compares the execution times of the

proposed method and the baseline methods. The ex-

perimental results indicate that, while the execution

time of the proposed method is less efﬁcient than the

simple Dijkstra’s algorithm, it outperforms when ap-

plied to routes involving waypoints.

In scenarios similar to those in Google Maps,

where the number of POIs associated with each way-

point is low, the proposed method’s execution time is

notably shorter. Conversely, as the number of POIs

belonging to each waypoint increases, the difference

in execution time is expected to decrease.

In the baseline method 2, after deciding which size

of waypoints to pass through using parameters, the or-

der of movement must be manually conﬁgured. On

the other hand, the proposed method excels as it in-

tegrates the discovery of waypoints and the determi-

nation of which waypoints to pass through within a

single algorithm, allowing for automatic execution.

4.3.4 Experiments on Route Evaluation

We compared the distances between the proposed

route and each point of interest (POI) with those gen-

erated by the baseline method. Figure 9 (a) presents

a histogram of the distances between the route shown

in Figure 4 (a) and each POI, while Figure 9 (b) cor-

responds to Figure 6 (b). These ﬁgures reveal that the

POIs are more densely clustered around a 50-meter

range in the routes generated by the proposed method

compared to the baseline approach.

5 CONCLUSION & FUTURE

WORK

In this study, we proposed a route recommendation

method designed to effectively navigate through way-

points, conceptualized around the idea of dogwalker.

The algorithm, named dog-walker pathﬁnding algo-

rithm, operates based on the principles of two agents:

a dog and a walker. The walker, serving as a navigat-

ing agent within the graph, moves independently in a

two-dimensional space, separate from the dog. How-

ever, connected by a leash, the walker is propelled to-

ward the direction the dog wishes to explore. Moti-

vated by POIs acting as incentives, the dog tends to

move toward areas abundant in POIs. Once the POIs

are sufﬁciently consumed, the dog moves toward the

goal, pulling the walker along a path that is expected

to pass through high-density POI areas. This path is

the output of our algorithm.

Experiments were conducted in two distinct areas:

Kyoto City in Kyoto Prefecture, Japan, and Manhat-

tan, New York, USA. As a result, it has been demon-

strated that our method can recommend routes that

effectively pass through POIs and operates faster than

the baseline method using Dijkstra’s algorithm. Fu-

ture work will focus on further evaluation and re-

ﬁnement of this method. Generally, evaluating algo-

rithms that use social big data is challenging. In this

paper, we conducted a qualitative evaluation using

Flickr and Google Maps as test datasets. For quanti-

tative evaluation, there are several ideas, such as scor-

ing based on the number of POIs passed or assigning

scores based on reviews from Google Maps for spe-

ciﬁc buildings such as temples. However, these eval-

uations may vary depending on the context and could

be inﬂuenced by parameters, potentially making them

less reliable.

Various possibilities are available for reﬁning our

method, including optimizing parameter settings and

the decision-making processes of the agents. Our

method focuses on proposing an algorithm that effec-

tively passes through waypoints in cases where POIs

and the graph exist on the same plane but do not over-

lap; however, evaluation and algorithmic improve-

ment are important, and hence will be prioritized in

future work. Additionally, there is room for improve-

ment in peripheral issues such as preprocessing the

road network used and reﬁning the data extraction

methods.

REFERENCES

Bao, J., Zheng, Y., and Mokbel, M. (2012). Location-based

and preference-aware recommendation using sparse

geo-social networking data. pages 199–208.

Chen, L., Lv, M., Ye, Q., Chen, G., and Woodward, J.

(2011). A personal route prediction system based

on trajectory data mining. Information Sciences,

181(7):1264–1284.

De Choudhury, M., Feldman, M., Amer-Yahia, S., Gol-

Navigating Points of Interest: The Dog-Walker Pathﬁnding Algorithm

bandi, N., Lempel, R., and Yu, C. (2010). Automatic

construction of travel itineraries using social bread-

crumbs. In Proceedings of the 21st ACM Conference

on Hypertext and Hypermedia, pages 35–44.

Dijkstra, E. (1958). A note on two problems in connexion

with graphs. Numb. Math., 1.

Dorigo, M. and Di Caro, G. (1999). Ant colony optimiza-

tion: a new meta-heuristic. In Proceedings of the 1999

congress on evolutionary computation-CEC99 (Cat.

No. 99TH8406), volume 2, pages 1470–1477. IEEE.

Dorigo, M. and Gambardella, L. M. (1997). Ant colony sys-

tem: a cooperative learning approach to the traveling

salesman problem. IEEE Transactions on evolution-

ary computation, 1(1):53–66.

Dorigo, M., Maniezzo, V., and Colorni, A. (1996). Ant sys-

tem: optimization by a colony of cooperating agents.

IEEE transactions on systems, man, and cybernetics,

part b (cybernetics), 26(1):29–41.

Fu, K., Lu, Y.-C., and Lu, C.-T. (2014). Treads: A safe

route recommender using social media mining and

text summarization. In Proceedings of the 22nd ACM

SIGSPATIAL International Conference on Advances

in Geographic Information Systems, pages 557–560.

Ishizaki, Y., Koyama, Y., Takayama, T., and Togawa, N.

(2021). A route recommendation method consider-

ing individual user’s preferences by monte-carlo tree

search and its evaluations. Journal of information pro-

cessing, 29:81–92.

Jain, S., Seufert, S., and Bedathur, S. (2010). Antourage:

mining distance-constrained trips from ﬂickr. In

Proceedings of the 19th international conference on

World wide web, pages 1121–1122.

Kim, J., Cha, M., and Sandholm, T. (2014). Socroutes:

safe routes based on tweet sentiments. In Proceedings

of the 23rd International Conference on World Wide

Web, pages 179–182.

Kurashima, T., Iwata, T., Irie, G., and Fujimura, K. (2010).

Travel route recommendation using geotags in photo

sharing sites. In Proceedings of the 19th ACM interna-

tional conference on Information and knowledge man-

agement, pages 579–588.

Majid, A., Chen, L., Mirza, H. T., Hussain, I., and Chen,

G. (2015). A system for mining interesting tourist lo-

cations and travel sequences from public geo-tagged

photos. Data & Knowledge Engineering, 95:66–86.

Popescu, A. and Grefenstette, G. (2009). Deducing trip

related information from ﬂickr. In Proceedings of

the 18th international conference on World Wide Web,

pages 1183–1184.

Pung, J., D’Souza, R. M., Ghosal, D., and Zhang, M.

(2022). A road network simpliﬁcation algorithm that

preserves topological properties. Applied Network

Science, 7(79).

Quercia, D., Schifanella, R., and Aiello, L. M. (2014). The

shortest path to happiness: Recommending beautiful,

quiet, and happy routes in the city. In Proceedings

of the 25th ACM conference on Hypertext and social

media, pages 116–125.

Tsiligirides, T. (1984). Heuristic methods applied to orien-

teering. Journal of the Operational Research Society,

35:797–809.

Yamashita, O. and Yokoyama, S. (2022). Preference aware

route recommendation using one billion geotagged

tweets. In Proceedings of the 6th ACM SIGSPA-

TIAL International Workshop on Location-based Rec-

ommendations, Geosocial Networks and Geoadvertis-

ing, pages 1–10.

Yang, Y., Gong, Z., and U, L. H. (2011). Identifying points

of interest by self-tuning clustering. In Proceedings

of the 34th international ACM SIGIR conference on

Research and development in Information Retrieval,

pages 883–892.

GISTAM 2025 - 11th International Conference on Geographical Information Systems Theory, Applications and Management