Penta: Towards Visualizing Compound Graphs as Set-Typed Data

Henry Ehlers

, Mario Kerndler

and Renata G. Raidou

Visualization Group, TU Wien, Favoritenstr. 9-11 / E193-02, Vienna, Austria

Keywords:

Compound Graph, Network Visualization, Set Visualization, Ego Network.

Abstract:

Compound graphs are graphs whose nodes, in addition to topological connections, share group-level relation-

ships. The need to incorporate both topological and group-level relationships makes them inherently chal-

lenging to visualize, especially for large data. We present Penta, a prototypical dashboard that, by combining

elements of compound graph and set visualization, provides a complete view of both types of relationships.

To this end, we employ ﬁve linked views that provide insight into a compound graph’s i) global and set-

local topology using both hypernode and traditional node-link diagrams, respectively, ii) set and entity-level

relationship and identity using similarity matrices linked by a bipartite node-link diagram, as well as iii)

node-centric topology across sets visualized as a layered node-link diagram. We demonstrate the workﬂow

and advantages of Penta in three small-scale case studies, using character co-occurrence networks as well as

biochemical pathway data. While still a prototype, the proposed dashboard shows promise in facilitating a

complete visual exploration of the topology and group-level relationships present in compound graphs, simul-

taneously.

1 INTRODUCTION

A clustered or compound graph is a graph whose

nodes, in addition to topological connections, share

group-level relationships (Vehlow et al., 2015b). In

the context of social networks, for example, nodes

may represent individual people, edges (different

types of) relationships between them, and groups cir-

cles of friends. Given their general utility and ap-

plicability, compound graphs, their visualization, and

their analysis are common across many different do-

mains: from social sciences (Humayoun et al., 2016),

through biochemistry (Paduano and Forbes, 2015)

and neurology (Al-Awami et al., 2014), to transporta-

tion logistics (Ducruet, 2017). Subsequently, various

visualization approaches and systems have been put

forth to tackle the visualization of compound graphs

differently: some of these forgo interactivity in the

interest of scalability (Xia et al., 2015), others com-

bine the two using summarization techniques (Pad-

uano and Forbes, 2015) or linked views (Al-Awami

et al., 2014), while others yet build upon domain-

speciﬁc visual conventions to better serve a particular

user group (Humayoun et al., 2016). Ultimately, all

https://orcid.org/0000-0002-5994-1492

https://orcid.org/0009-0001-4748-8512

https://orcid.org/0000-0003-2468-0664

these approaches address the challenge of simultane-

ously visualizing graph topology and group structure.

A compound graph’s group structure can be con-

ceptualized as a collection of sets; their elements

formed by the graph’s nodes, and their intersections

by nodes present in two or more groups (Pezzotti

et al., 2018). When visualizing or analyzing sets, we

are interested in understanding their relations, such

as containment, exclusions, or intersections, to better

understand the role or importance of their elements

(Alsallakh et al., 2016). However, even when the

underlying data is not a graph, such set-typed data

can become challenging to visualize. Depending on

the complexity and size of the data, such visualiza-

tions often require the use of abstraction (Rodgers

et al., 2015) or summarization (Lamy and Tsopra,

2020) to remain legible. Domain-speciﬁc applica-

tions may additionally require the interactive visual-

ization of meta-data attached to sets’ and their ele-

ments (Lex and Gehlenborg, 2014). Many different

families of techniques and tools have been developed

to tackle these challenges, both for generic set-typed

and application-area-speciﬁc data (Alsallakh et al.,

2016). However, few—if any—of these techniques

can be applied to compound graphs, and fewer still

scale to large datasets, common in modern biochemi-

cal and social network analysis.

Ehlers, H., Kerndler, M. and Raidou, R. G.

Penta: Towards Visualizing Compound Graphs as Set-Typed Data.

DOI: 10.5220/0013242300003912

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 20th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2025) - Volume 1: GRAPP, HUCAPP

and IVAPP, pages 913-921

ISBN: 978-989-758-728-3; ISSN: 2184-4321

913

In this paper, we present Penta, a prototype dash-

board for the visualization of non-hierarchical, non-

disjoint compound graphs as set-typed data. With this

prototypical implementation, we aim to address sev-

eral outstanding gaps in the ﬁelds of both set visual-

ization (Alsallakh et al., 2016) and compound graph

visualization (Vehlow et al., 2015b; Ehlers et al.,

2024a), by combing multiple linked views, (similar-

ity) matrix visualizations, and ego network represen-

tations. More speciﬁcally, the contribution of Penta’s

linked views is that they provide insight into i) the

group’s global and local topology using both hypern-

ode and traditional node-link diagrams, respectively,

ii) set and vertex-centric relationship and identity us-

ing similarity matrices linked by a bipartite node-link

diagram, as well as iii) node-centric topology across

sets visualized as a layered node-link diagram.

2 RELATED WORK

As Penta’s ﬁve linked views draw from conventions

of compound graph visualizations, matrix-based set-

visualization, as well as ego-network visualization,

we here discuss the state-of-the-art of each.

Compound Graph Visualization. Compound

graphs have been visualized in a multitude of ways

(Ehlers et al., 2024a; Vehlow et al., 2015b), us-

ing node attributes, overlays, bipartite node-link

diagrams, multiples, trees, matrices, abstractions,

and hybrid techniques. The most common way of

visualizing group-level memberships in compound

graphs, node attributes take the form of, for example,

colors (Vehlow et al., 2015a) or glyphs (Wang et al.,

2016). Overlay techniques add group-level associa-

tions atop a graph’s embedding, using, for example,

regions (Partl et al., 2013), lines (Alper et al., 2011),

or combinations of the two (Meulemans et al.,

2013). Less common than either overlays or node

attributes, bipartite node-link diagrams represent

both nodes and groups as (different types) of vertices

with topological and group-level-association edges

connecting them (Bigelow et al., 2019). Multiples opt

to visualize each group’s subgraph separately, as seen

in Bach et al.’s Small Multiples (Bach et al., 2015) or

Graph Diaries (Bach et al., 2014). Trees, commonly

visualized alongside a compound graph’s topology,

visualize elements, i.e. vertices, as the leaves of the

tree and their (hierarchical) set-element relationships

as edges (Abello et al., 2006). (Biadjacency) ma-

trices, also visualized separately from a compound

graph’s topology, depict vertex-group memberships

tabularly where each row corresponds to a vertex

and each group to a column (Chuang et al., 2012).

Abstractions do not visualize all sets, elements, and

their relationships but provide a view into one by

abstracting away the others. This broad category

can unsurprisingly include many different types of

approaches (Rodgers et al., 2015; Yoghourdjian et al.,

2018) Finally, hybrid techniques combine any of

these aforementioned techniques to visualize group

membership and topology simultaneously (Angori

et al., 2019; Henry et al., 2007).

Matrices for Set-Typed Data. While several ex-

amples of set visualization and their elements as bi-

adjacency-based matrices can be found in the liter-

ature (Sadana et al., 2014; Lex et al., 2014), simi-

larity-based matrix representations are less common.

We could only identify two examples for the ex-

plicit purpose of similarity-matrix-based set visual-

ization. First, Liu et. al’s Similarity Lattice (Xu

Liu et al., 2005) represents sets’ pairwise Complete-

ness and Intensity similarity as a non-symmetric sim-

ilarity matrix. Second, Intervene (Khan and Math-

elier, 2017) features similarity-based matrix repre-

sentations alongside more conventional biadjacency-

based ones. As also discussed in reviews of both

compound graph visualization (Vehlow et al., 2015b;

Ehlers et al., 2024a) and set visualization (Alsallakh

et al., 2016), the use of (similarity) matrices is a novel

avenue with which to communicate group and entity-

level relationships in both sets and compound graphs.

Ego Network Visualizations. Ego network repre-

sentations visualize graph topology relative to some

selected node of interest—the so-called “ego” (Ehlers

et al., 2024b). Ego networks may be used to simplify

the visualization of a graph’s topology, by only visual-

izing those nodes and edges of immediate importance

to the selected ego. Examples of node-centric visual-

izations of larger graphs can be found across several

domains (Ehlers et al., 2024b). Here, we are particu-

larly interested in the use of layered (tree-like) node-

link diagrammatic representations, as they promise an

intuitive and orderly view into the intrinsically lay-

ered topology of ego networks. Such layered rep-

resentations align nodes along “layers” representing

the distance from the selected ego (Sayers, 2004).

While not related to ego networks directly, similar

ideas of edge scaling and distance-based node em-

bedding can be found in the visualization of phyloge-

netic trees (Shank et al., 2018), evolutionary graphs

(Miller et al., 2011), or synaptic/brain graphs (Al-

Awami et al., 2014). To the best of our knowledge,

such ego network visualizations have not yet found

application in compound graph visualization.

IVAPP 2025 - 16th International Conference on Information Visualization Theory and Applications

914

3 THE FIVE FACETS OF PENTA

Visualizing compound graphs is challenging, as one

needs to visually communicate both graph topology

and group-level relationships simultaneously. Specif-

ically, supporting the following aspects is necessary:

1. viewing all groups’ global topology,

2. investigating the particular set-relative topology

of selected groups,

3. understanding the similarities of all groups and

nodes relative to each other,

4. viewing all selected set-element mappings, and

5. investigating the node-relative topology of the

graph, i.e. topology relative to a selected ego.

To integrate the aforementioned channels of infor-

mation, we propose the prototypical web-based Penta

dashboard, which aims to visualize different facets

of a compound graph’s group structure and topology

in ﬁve linked views. Users are expected to upload

their compound graph’s topology and group-level as-

sociations they wish to investigate to Penta, within

which they then interactively ﬁlter and explore their

dataset. This may entail selecting entities or sets

within its multiple linked views or looking them up

based on their unique identiﬁers. More speciﬁcally, in

accordance with Shneiderman’s (Shneiderman, 1996)

mantra of “Overview First, [...] ﬁlter, then details

on demand” the dashboard aims to funnel users from

a global view of topology, through the topology and

similarity of selected sets, to the immediate topology

of a particular node. Interactive selections of vertices

and sets in any of these ﬁve views are reﬂected in all

other views through brushing and linking (Buja et al.,

1991). Penta, available on GitHub, was developed in

Svelte using D3.js (Bostock et al., 2011).

Global Topology. For some compound graph

G(V, E, S) let V denote its total set of elements/nodes,

E its total set of edges, and S its elements’ non-

hierarchical, non-disjoint group structure. For a set

s ∈ S, node-set pairs (v

,s) and (v

,s) in V

are con-

nected by edges E

⊆ V

× V

, where V

⊆ V × S.

Here, the input graph’s global topology can be either

represented as a force-directed or (as presented here)

a radial node-link diagram (Figure 1b). As straight-

line node-link diagrams do not tend to produce aes-

thetically pleasing or readable results for graphs of

larger sizes and greater complexity (Ehlers et al.,

2023), we do not visualize nodes v ∈ V and their edges

e ∈ E directly. Instead, each set of nodes V

is visual-

ized as its own circular hypernode (Terje Bjørke et al.,

2010). Hovering over such hypernodes reveals their

labels. To communicate which groups of nodes are

present across sets, groups of nodes that form inter-

sections between sets of nodes are represented by sep-

arate, square hypernodes (Figure 1b). Hypernodes’

sizes encode the cardinality of their sets or intersec-

tions, i.e. the more elements a set contains, the larger

the set’s corresponding hypernode.

In the particular example shown in Figure 1b,

seven groups, representing seven Mus musculus

KEGG pathways, are depicted—one circular node per

group. The size of each node represents the num-

ber of genes (nodes) in each pathway. Between these

seven groups, there are ﬁve unique intersections, rep-

resented by ﬁve square nodes. One particular inter-

section, consisting only of a single node with identi-

ﬁer 58810 is highlighted. Said node is the intersec-

tion between the three selected, i.e. colored, groups,

indicated by the edges connecting the intersection’s

square node to the three groups’ circular nodes.

Set-Relative Topology. From the aforementioned

global topological view, hypernodes can be selected,

thereby adding their elements, i.e. vertices, to the

set-relative topological view. This is represented as

a straight-line node-link diagram (Figure 1a), laid out

using D3.js’s particle-based force-directed algorithm

(Bostock et al., 2011). Each added group of nodes is

color-coded, using an appropriate ColorBrewer color

palette (Harrower and Brewer, 2003) used consis-

tently across all views. To ensure colors remain visu-

ally distinct from each other (Healey, 1996), users can

only select up to ten such groups simultaneously. We

highlight intersections between two or more groups

by color-coding them in black. Hovering over any in-

dividual node reveals its label and highlights its corre-

sponding hypernode in the global topological view, as

well as its location in the (to-be-discussed) element-

similarity matrix in a similar way.

In the example shown in Figure 1a, three of the

seven aforementioned Mus musculus KEGG path-

ways have been selected, one colored green, the other

blue, and the ﬁnal one orange. Nodes that form an in-

tersection between any two of the three selected path-

ways are colored dark grey. The selected node 58810,

which forms an intersection between all three selected

pathways, is colored black.

Set and Vertex Similarity. To navigate both sets

and elements, we propose the use of two interactive

similarity matrices—one depicting set similarity and

the other representing vertex similarity (Figure 2c).

Unlike identity matrix representations, which may ne-

cessitate panning and scrolling to navigate owing to

potential asymmetries, a square, symmetric similar-

ity matrix offers a clearer overview of all sets or ele-

Penta: Towards Visualizing Compound Graphs as Set-Typed Data

915

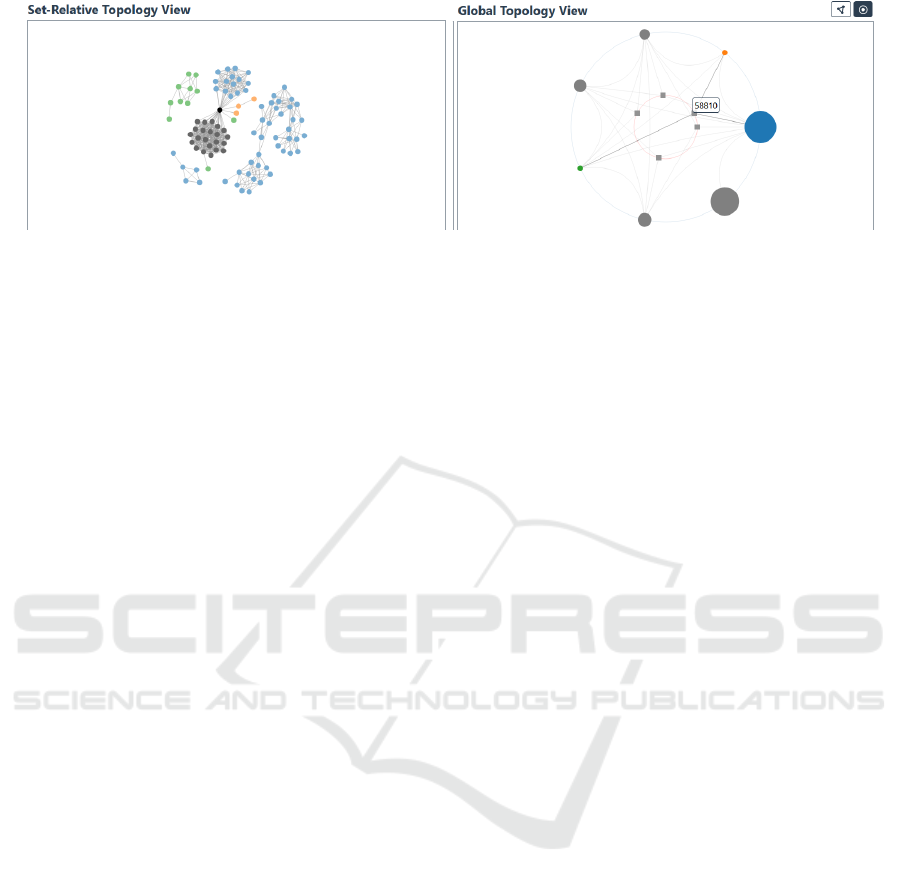
(a) (b)

Figure 1: The (b) global topology view for seven KEGG mouse (MMU) pathways (groups) and their intersections. The (a)

set-relative topology of a selection of three sets from the global topological view, colored in blue, orange, and green in both

views. A notable intersection between these three selected is the entity (vertex) with identiﬁer 58810 which is highlighted in

black on the (a).

ments simultaneously. Moreover, matrix representa-

tions offer overall greater visual clarity and ﬂexibil-

ity over many other approaches for set and element

visualization (Alsallakh et al., 2016). This concep-

tual ﬂexibility includes the straightforward use of

different similarity measures with which to under-

stand groups and elements relationships (Vijaymeena

and Kavitha, 2016). Here, for any two sets A, B ∈ S,

their similarities are computed using the Jaccard dis-

tance J(A,B) = (|A∩B|)/(|A∪B|), chosen for its con-

ceptual simplicity and its applicability to both set and

topological node similarity. To quantify element simi-

larity, the same conceptual approach based on the Jac-

card distance is used: for any two vertices/elements

a,b ∈ V , we can deﬁne their “sets” as A = q(a) and

B = q(b), where q(x), for an element x ∈ V , can take

different forms. We make use of a topological set

deﬁnition: q(x) = {v : ∀v ∈ V,{x,v} ∈ E}, i.e. we

simply deﬁne a node’s set as its immediate neighbor-

hood. In both cases, the similarity is encoded using

a luminance colormap, i.e. white indicating low and

black high similarity. Moreover, a selected set’s rows

and columns are indicated using colored lines. Ad-

ditionally, matrices can be ﬂexibly reordered based

on selected criteria to facilitate the detection of novel

or unexpected relationships between entities (Mueller

et al., 2007). Here, as a proof of concept, we allow the

user to reorder both set and element similarity matri-

ces by either i) a random ordering for the identiﬁca-

tion of unexpected relationships, or ii) an attribute-

based ordering that organizes entities by their lexico-

graphic order, or iii) an agglomerative, hierarchical

clustering-based order to identify clusters of interest

(Kaufman and Rousseeuw, 1990).

In the example shown in Figure 2c, the set-

similarity matrix represents the character similarities

among the ﬁrst four books of the Harry Potter series

(Ravi, 2024). Each set, i.e. book, is represented by

one of the four rows and columns of the matrix, or-

dered lexicographically. Each cell represents the Jac-

card distance between two sets. The darker a cell,

the more similar the two sets are. Instead of space-

consuming conventional labels, colored lines indicate

the identity of each row and column. Here, books two

and three have been selected from the global topo-

logical view (Figure 2a). The vertex-similarity ma-

trix (Figure 2c), shows the similarity between nodes

(characters) as a function of their immediate neigh-

borhood, i.e. the more neighbors two nodes have in

common, the more similar they are. Each row and col-

umn corresponds to a particular character, and each

cell to the similarity between two nodes. Again, sim-

ilarity is mapped to cell brightness.

Set-Node Connection Graph. The previously dis-

cussed similarity matrix representations allow for an

in-depth exploration of within-set and within-element

relationships. However, they do not visualize the set

membership of elements or the mapping of sets to el-

ements (Pezzotti et al., 2018). To link the aforemen-

tioned similarity views, we visually exploit the bipar-

tite relationship between them and visualize said re-

lationship as a “Connection Graph” (Figure 2c). For

matrices, drawing (curved) edges between their rows

(or columns) is conceptually fairly straightforward,

as they already form a one-dimensional projection of

their elements (Misue and Zhou, 2011). More speciﬁ-

cally, given a single selected set S, its projection point

is connected to all its elements’ (x ∈ S) projection

points by curved edges. Alternatively, given a single

selected element x, its projection point is connected to

all sets of which it is a member, i.e. {s : ∀s ∈ S,x ∈ s}.

Edge and label colors utilize the same color palette as

in the global and set topology views.

In this particular example (Figure 2c), the connec-

tion graph shows the mapping of Harry Potter books

IVAPP 2025 - 16th International Conference on Information Visualization Theory and Applications

916

(sets) to the characters of the series (nodes), and vice-

versa. For each book’s character, curved edges are

drawn between the books’ and the character’s row in

their respective similarity matrices. The color of the

curved line corresponds to the color of the set, as de-

picted in both the global and set-relative topological

views (Figures 2a and 2b). If a node, i.e. character,

maps to multiple sets (books), multiple such lines will

be drawn, connecting the one node to multiple sets.

Node Relative Topology. While the global and set-

local topological views of the graph provide a good

starting point for exploring particular sets and their el-

ements, they are insufﬁcient in understanding a node’s

connectivity across all sets. To amend this, we em-

ploy a vertex-centric representation of topology for a

particular selected entity, i.e. an ego network where

the selected vertex forms the “ego” (Ehlers et al.,

2024b). This ego network is generated from the

graph’s global topology based on a selected ego node

of interest and a user-speciﬁed maximum exploration

depth. More speciﬁcally, Penta employs a breadth-

ﬁrst search algorithm to traverse the graph from the

ego node, through its neighbors, its neighbors’ neigh-

bors, and so on, up to the speciﬁed depth, thereby

constructing a tree(-like) data structure that encapsu-

lates the shortest possible paths to all reachable nodes.

This tree is visualized as a layered node-link diagram

(Figure 3c). Its layers, i.e. nodes, are sorted by their

inverse weighted edge distance to the ego, i.e. the

greater the edge weight between any two nodes, the

closer they will be visualized in the tree. This also

allows for Penta to sort a node’s neighbors based on

this edge weight, i.e. the closest neighbor appears at

the top of its branch, and the furthest at the bottom.

In the example of Figure 3, a co-occurrence net-

work of Star Wars characters across the ﬁrst six

movies is shown. The depicted ego network displays

the node-relative topology of one selected character,

namely R2-D2, depicted in the top left of Figure 3c.

The layered node-link diagram shows a character’s

connections across all sets in the dataset. The more

a character interacted with R2-D2, i.e. the larger their

co-occurrence edge weight, the higher up in the lay-

ered node-link diagram it appears, i.e. Anakin inter-

acted more with R2-D2 than Qui-Gon, who interacted

more than Luke. The same ordering system applies to

each layer of this layered node-link diagram. The or-

dering is reinforced by scaling each edge’s horizontal

length based on edge weight, i.e the more two char-

acters interact, the larger their edge weight, and the

closer they appear in the horizontal space.

4 USE CASES

In order to demonstrate the potential utility of Penta,

three small-scale usage scenarios are presented.

Scenario 1: Noticing Notable Nodes. In order to

demonstrate the utility of both the global and set-local

topological view, consider a Mus musculus example

dataset, in which each node represents a gene, each

edge a gene-gene interaction, and groups of genes

represent KEGG pathways in mice (Kanehisa and

Goto, 2000). For seven such pathways, their global

topology is visualized as a hypernode-link diagram

(Figure 1b). Here, three pathways of particular inter-

est, mmu0010, mmu00053 and mmu00040, colored in

blue, green, and orange, respectively, are selected in

the global topological view, their vertices visualized

in the corresponding set-local topology view (Figure

1a). From the global topology view, we can imme-

diately discern the relative sizes of these three sets,

i.e. mmu0010 (blue) is larger than any other pathway

in the dataset, indicated by the area encoding of the

nodes. Moreover, we can immediately see how all our

datasets intersect and the cardinalities of these inter-

sections. More speciﬁcally, a particular intersection

between the three pathways of interest is revealed to

be a single node, namely 58810. The importance of

this particular node across the selected pathways is

also made immediately apparent in the set-relative lo-

cal topological view (Figure 1a), where said node not

only forms an intersection between these three path-

ways but also a bridge between two large clusters of

nodes. Among those, one forms an intersection of its

own between two selected pathways (colored in grey).

The combined use of these two views—hypernode

and traditional node-link diagrams—has enabled an

intuitive and speedy overview of the pathway’s global

and local topology and facilitated the identiﬁcation of

a notable node.

Scenario 2: Such Similarity, Much Wow. In order

to demonstrate the utility of set and node-similarity

matrix views, consider a Harry Potter character co-

occurrence network (Ravi, 2024), in which each node

represents a character, each weighted edge the num-

ber of interactions two characters shared, and each

group one of the ﬁrst four books of the series. In or-

der to determine the similarities between books two

and three, colored orange and red respectively, the

two groups’ hypernodes have been selected from the

global topological view (Figure 2a) and their nodes

and connections added to the local topological view

(Figure 2b), as discussed previously. This view al-

ready sheds some view into the strong overlap in char-

Penta: Towards Visualizing Compound Graphs as Set-Typed Data

917

(a) (b)

(c)

Figure 2: Visualizing Character Interactions Across Harry Potter Books. (a) Global Topology View: Overview of character

interactions across the ﬁrst four books, highlighting recurring characters. (b) Local Topology View: Dense inter-character

connections between books two and three. (c) Set and Vertex-Similarity Analysis: Consistent level of recurring characters

and interactions between books.

acters between the two books, given the many (black)

nodes that form intersections between the two books.

However, viewing the set-similarity matrix (Figure

2c), the darker gray color of books two and three’s

similarity, immediately communicates that these two

books share the greatest set of characters across the

ﬁrst four published books. Following the connection

graph and viewing the vertex similarity matrix, one

can immediately note three interesting blocks of char-

acters, namely i) those that strongly co-occur across

books two and three, ii) those that primarily co-occur

in book two, and iii) those that primarily co-occur in

book three Figure 2c). The interactive dashboard now

allows for individual inspection of character-character

similarity scores. The set and vertex similarity matri-

ces allow us to quickly identify subsets of nodes of

potential interest for follow-up study.

Scenario 3: Me! Me! Me! Me! Here, to ex-

plore the utility of the ego network, consider a co-

occurrence network of Star Wars characters across the

ﬁrst six movies, in which each node represents a char-

acter, each weighted edge the number of interactions

two characters shared, and each group one of the six

movies (Gabasova, 2024). Here, given some prior ex-

ploration of groups and their connectivity, a user has

identiﬁed a particular node of interest, namely R2-

D2, as this particular character forms an intersection

across all six groups (Figure 3a). As the local topo-

logical view (Figure 3b) is too dense to make out said

character’s immediate neighborhood, a user can uti-

lize the vertex-relative ego network view (Figure 3c.

Here, the selected ego, here R2-D2, forms the root

node of the layered tree representation in the top left.

From a simple cursory look, a user can immediately

identify the ego’s closest neighbors, here Anakin, Qui-

Gon, and Luke, thanks to the vertical ordering of the

IVAPP 2025 - 16th International Conference on Information Visualization Theory and Applications

918

(a) (b)

(c)

Figure 3: Analyzing the Star Wars Character Network. (a) Global Topology View: Comprehensive visual map of the

Star Wars character network, highlighting key characters across all movies. (b) Local Topology View: View into the dense

interrelationships of characters across the ﬁrst six movies. (c) Ego-Network of R2-D2: Central role and extensive connections

of R2-D2 within the Star Wars narrative.

ego’s neighbors by edge weight, i.e. R2-D2’s closest

neighbors are located at the top of the tree. More-

over, thanks to the horizontal ordering of nodes based

on cumulative proximity to the ego, one can addition-

ally notice that, while Piett and Ozzel are both a hop-

distance of three away from R2-D2, Piett is closer

once edge weights are factored in. This node-relative

topological view facilitated by the ego network allows

for an in-depth look at the selected ego’s (immediate)

neighborhood in an intuitive and fast manner.

5 SUMMARY AND TAKE-AWAY

The prototypical Penta dashboard offers a holistic

approach to visualizing compound graph data, en-

abling users to analyze both topological and group-

level relationships across multiple datasets. Through

our three case studies, Penta demonstrates its abil-

ity to highlight both global and local graph struc-

tures effectively. For example, in the ﬁrst scenario,

Penta allows users to quickly identify key intersec-

tions and pathways, such as important genes within

Penta: Towards Visualizing Compound Graphs as Set-Typed Data

919

biological networks. The second scenario showcases

Penta’s utility in visualizing co-occurrence networks,

revealing shared character groups across Harry Potter

books. Lastly, the third scenario focuses on individ-

ual nodes within a Star Wars network, where users

can explore character relationships based on interac-

tion frequency. Overall, Penta’s prototypical imple-

mentation already promises to be a valuable tool for

researchers looking to interpret compound graph re-

lationships in larger datasets.

6 CONCLUSION AND FUTURE

WORK

In this paper, we have presented the prototypical im-

plementation of Penta, a novel approach to the holis-

tic visualization of compound graph data. We further

demonstrated the use and effectiveness of our tool on

three use case scenarios, which indicate Penta’s util-

ity in making sense of a compound graph’s topol-

ogy, both on a local and global level, as well as

group structure. In future work, we hope to i) im-

plement additional similarity measures with which

to view set and vertex relationships(Vijaymeena and

Kavitha, 2016), ii) implement additional clustering

algorithms with which to sort similarity matrices

(Koutrouli et al., 2020), iii) allow for the integration

of node and edge attribute data to go beyond purely

topological analyses, and iv) improve the scalability

of multiple views through, for example, latent vari-

able space scatter plots (Pezzotti et al., 2018).

REFERENCES

Abello, J., van Ham, F., and Krishnan, N. (2006). ASK-

GraphView: A Large Scale Graph Visualization Sys-

tem. IEEE Transactions on Visualization and Com-

puter Graphics, 12(5):669–676. Conference Name:

IEEE Transactions on Visualization and Computer

Graphics.

Al-Awami, A. K., Beyer, J., Strobelt, H., Kasthuri, N.,

Lichtman, J. W., Pﬁster, H., and Hadwiger, M. (2014).

NeuroLines: A Subway Map Metaphor for Visualiz-

ing Nanoscale Neuronal Connectivity. IEEE Trans-

actions on Visualization and Computer Graphics,

20(12):2369–2378.

Alper, B., Riche, N., Ramos, G., and Czerwinski, M.

(2011). Design Study of LineSets, a Novel Set Vi-

sualization Technique. IEEE Transactions on Visual-

ization and Computer Graphics, 17(12):2259–2267.

Conference Name: IEEE Transactions on Visualiza-

tion and Computer Graphics.

Alsallakh, B., Micallef, L., Aigner, W., Hauser, H., Miksch,

S., and Rodgers, P. (2016). The State-of-the-Art of Set

Visualization. Computer Graphics Forum, 35(1):234–

260.

Angori, L., Didimo, W., Montecchiani, F., Pagliuca, D.,

and Tappini, A. (2019). ChordLink: A New Hybrid

Visualization Model. In Graph Drawing and Net-

work Visualization: 27th International Symposium,

GD 2019, Prague, Czech Republic, September 17–20,

2019, Proceedings, pages 276–290, Berlin, Heidel-

berg. Springer-Verlag.

Bach, B., Henry-Riche, N., Dwyer, T., Madhyastha, T.,

Fekete, J.-D., and Grabowski, T. (2015). Small Mul-

tiPiles: Piling Time to Explore Temporal Patterns

in Dynamic Networks. Computer Graphics Forum,

34(3):31–40.

Bach, B., Pietriga, E., and Fekete, J.-D. (2014). GraphDi-

aries: Animated Transitions andTemporal Navigation

for Dynamic Networks. IEEE Transactions on Visu-

alization and Computer Graphics, 20(5):740–754.

Bigelow, A., Nobre, C., Meyer, M., and Lex, A. (2019). Ori-

graph: Interactive Network Wrangling. In 2019 IEEE

Conference on Visual Analytics Science and Technol-

ogy (VAST), pages 81–92.

Bostock, M., Ogievetsky, V., and Heer, J. (2011). D³ Data-

Driven Documents. IEEE Transactions on Visual-

ization and Computer Graphics, 17(12):2301–2309.

Conference Name: IEEE Transactions on Visualiza-

tion and Computer Graphics.

Buja, A., McDonald, J., Michalak, J., and Stuetzle, W.

(1991). Interactive data visualization using focusing

and linking. In Proceeding Visualization ’91, pages

156–163.

Chuang, J., Manning, C. D., and Heer, J. (2012). Ter-

mite: visualization techniques for assessing textual

topic models. In Proceedings of the International

Working Conference on Advanced Visual Interfaces,

AVI ’12, pages 74–77, New York, NY, USA. Associ-

ation for Computing Machinery.

Ducruet, C. (2017). Multilayer dynamics of complex spa-

tial networks: The case of global maritime ﬂows

(1977–2008). Journal of Transport Geography,

60:47–58.

Ehlers, H., Marin, D., Wu, H.-Y., and Raidou, R. (2024a).

Visualizing Group Structure in Compound Graphs:

The Current State, Lessons Learned, and Outstanding

Opportunities. pages 697–708.

Ehlers, H., Pahr, D., Filipov, V., Wu, H.-Y., and Raidou,

R. G. (2024b). Me! Me! Me! Me! A study and com-

parison of ego network representations. Computers &

Graphics, 125:104123.

Ehlers, H., Villedieu, A., Raidou, R. G., and Wu, H.-Y.

(2023). Improving readability of static, straight-line

graph drawings: A ﬁrst look at edge crossing resolu-

tion through iterative vertex splitting. Computers &

Graphics, 116:448–463.

Gabasova, E. (2024). evelinag/StarWars-social-network.

original-date: 2015-12-15T00:33:54Z.

Harrower, M. and Brewer, C. A. (2003). ColorBrewer.org:

An Online Tool for Selecting Colour Schemes for

Maps. The Cartographic Journal, 40(1):27–37.

Healey, C. (1996). Choosing effective colours for data vi-

sualization. In Proceedings of Seventh Annual IEEE

Visualization ’96, pages 263–270.

IVAPP 2025 - 16th International Conference on Information Visualization Theory and Applications

920

Henry, N., Fekete, J.-D., and McGufﬁn, M. J. (2007).

NodeTrix: a Hybrid Visualization of Social Networks.

IEEE Transactions on Visualization and Computer

Graphics, 13(6):1302–1309.

Humayoun, S. R., Ezaiza, H., AlTarawneh, R., and Ebert,

A. (2016). Social-Circles Exploration through Inter-

active Multi-Layered Chord Layout. In Proceedings

of the International Working Conference on Advanced

Visual Interfaces, AVI ’16, pages 314–315, New York,

NY, USA. Association for Computing Machinery.

Kanehisa, M. and Goto, S. (2000). KEGG: Kyoto Ency-

clopedia of Genes and Genomes. Nucleic Acids Re-

search, 28(1):27–30.

Kaufman, L. and Rousseeuw, P. (1990). Agglomerative

Nesting (Program AGNES). In Finding Groups in

Data, Wiley Series in Probability and Statistics, pages

199–252. John Wiley & Sons, Ltd.

Khan, A. and Mathelier, A. (2017). Intervene: a tool for

intersection and visualization of multiple gene or ge-

nomic region sets. Pages: 109728 Section: New Re-

sults.

Koutrouli, M., Karatzas, E., Paez-Espino, D., and

Pavlopoulos, G. A. (2020). A Guide to Conquer the

Biological Network Era Using Graph Theory. Fron-

tiers in Bioengineering and Biotechnology, 8:34.

Lamy, J.-B. and Tsopra, R. (2020). RainBio: Propor-

tional Visualization of Large Sets in Biology. IEEE

Transactions on Visualization and Computer Graph-

ics, 26(11):3285–3298. Conference Name: IEEE

Transactions on Visualization and Computer Graph-

ics.

Lex, A. and Gehlenborg, N. (2014). Sets and intersections.

Nature Methods, 11(8):779–779.

Lex, A., Gehlenborg, N., Strobelt, H., Vuillemot, R., and

Pﬁster, H. (2014). UpSet: Visualization of Intersect-

ing Sets. IEEE Transactions on Visualization and

Computer Graphics, 20(12):1983–1992. Conference

Name: IEEE Transactions on Visualization and Com-

puter Graphics.

Meulemans, W., Riche, N. H., Speckmann, B., Alper, B.,

and Dwyer, T. (2013). KelpFusion: A Hybrid Set Vi-

sualization Technique. IEEE Transactions on Visual-

ization and Computer Graphics, 19(11):1846–1858.

Conference Name: IEEE Transactions on Visualiza-

tion and Computer Graphics.

Miller, R., Mozhayskiy, V., Tagkopoulos, L., and Ma, K.-L.

(2011). EVEVis: A multi-scale visualization system

for dense evolutionary data. In 2011 IEEE Sympo-

sium on Biological Data Visualization (BioVis)., pages

143–150.

Misue, K. and Zhou, Q. (2011). Drawing Semi-bipartite

Graphs in Anchor+Matrix Style. In 2011 15th In-

ternational Conference on Information Visualisation,

pages 26–31. ISSN: 2375-0138.

Mueller, C., Martin, B., and Lumsdaine, A. (2007). A com-

parison of vertex ordering algorithms for large graph

visualization. In 2007 6th International Asia-Paciﬁc

Symposium on Visualization, pages 141–148.

Paduano, F. and Forbes, A. G. (2015). Extended LineSets:

a visualization technique for the interactive inspection

of biological pathways. BMC Proceedings, 9(6):S4.

Partl, C., Lex, A., Streit, M., Kalkofen, D., Kashofer, K.,

and Schmalstieg, D. (2013). enRoute: dynamic path

extraction from biological pathway maps for explor-

ing heterogeneous experimental datasets. BMC Bioin-

formatics, 14(19):S3.

Pezzotti, N., Fekete, J.-D., H

ollt, T., Lelieveldt, B. P., Eise-

mann, E., and Vilanova, A. (2018). Multiscale Visu-

alization and Exploration of Large Bipartite Graphs.

Computer Graphics Forum, 37(3):549–560.

Ravi, N. (2024). nikhil-ravi/harry-potter-interactions.

original-date: 2023-11-05T01:37:30Z.

Rodgers, P., Stapleton, G., and Chapman, P. (2015). Visual-

izing Sets with Linear Diagrams. ACM Transactions

on Computer-Human Interaction, 22(6):27:1–27:39.

Sadana, R., Major, T., Dove, A., and Stasko, J. (2014). On-

Set: A Visualization Technique for Large-scale Bi-

nary Set Data. IEEE Transactions on Visualization

and Computer Graphics, 20(12):1993–2002.

Sayers, C. (2004). Node-centric RDF Graph Visualization.

Shank, S. D., Weaver, S., and Kosakovsky Pond, S. L.

(2018). phylotree.js - a JavaScript library for appli-

cation development and interactive data visualization

in phylogenetics. BMC Bioinformatics, 19(1):276.

Shneiderman, B. (1996). The eyes have it: a task by data

type taxonomy for information visualizations. In Pro-

ceedings 1996 IEEE Symposium on Visual Languages,

pages 336–343. ISSN: 1049-2615.

Terje Bjørke, J., Nilsen, S., and Varga, M. (2010). Visual-

ization of network structure by the application of hy-

pernodes. International Journal of Approximate Rea-

soning, 51(3):275–293.

Vehlow, C., Beck, F., Auw

arter, P., and Weiskopf, D.

(2015a). Visualizing the Evolution of Communi-

ties in Dynamic Graphs. Computer Graphics Forum,

34(1):277–288.

Vehlow, C., Beck, F., and Weiskopf, D. (2015b). The State

of the Art in Visualizing Group Structures in Graphs.

Eurographics Conference on Visualization (EuroVis) -

STARs, page 20 pages.

Vijaymeena, M. and Kavitha, K. (2016). A Survey on Sim-

ilarity Measures in Text Mining. Machine Learning

and Applications: An International Journal, 3(1):19–

28.

Wang, X., Liu, S., Liu, J., Chen, J., Zhu, J., and Guo, B.

(2016). TopicPanorama: A Full Picture of Relevant

Topics. IEEE Transactions on Visualization and Com-

puter Graphics, 22(12):2508–2521.

Xia, J., Gill, E. E., and Hancock, R. E. W. (2015). Net-

workAnalyst for statistical, visual and network-based

meta-analysis of gene expression data. Nature Proto-

cols, 10(6):823–844.

Xu Liu, Ming Luo, and Ben Shneiderman (2005). Visual-

ization of Sets.

Yoghourdjian, V., Dwyer, T., Klein, K., Marriott, K., and

Wybrow, M. (2018). Graph Thumbnails: Identifying

and Comparing Multiple Graphs at a Glance. IEEE

Transactions on Visualization and Computer Graph-

ics, 24(12):3081–3095.

Penta: Towards Visualizing Compound Graphs as Set-Typed Data

921