Symmetry Detection and Symmetrization in Cellular Automata

ıt Gregor and Ivana Kolingerov

Department of Computer Science, Faculty of Applied Sciences,

University of West Bohemia, Technick

a 8, Plze

n, Czech Republic

Keywords:

Symmetry, Cellular Automata, Symmetrization.

Abstract:

Symmetry is the important property of many geometric objects. Our work analyzes the symmetry in two-

dimensional objects created using the cellular automata in the context of the initial conﬁgurations and rules

of the automata. Symmetry of basic geometric shapes, such as circles, rectangles, and curves, mapped into

the cells of the automaton, is analyzed in this paper. Also, the symmetry of random objects is analyzed.

This paper also describes the method for centroidal symmetry detection and axial symmetry detection in the

cellular automata, and it also brings the approach of using the cellular automata for object symmetrization by

comparing it with objects in the library of symmetrical objects.

1 INTRODUCTION

Symmetry is an important feature of geometric ob-

jects. A symmetrical object is invariant to some geo-

metric transformation. In 2D space, the two simplest

cases are as follows: if the transformation is rotation,

the symmetry is called a centroid symmetry. If the ge-

ometric transformation is reﬂection, the symmetry is

called an axis symmetry.

Due to the importance of symmetry, many meth-

ods of its detection have been developed for static

data, both for geometric objects and for digitized pic-

tures.

Not so many methods have been developed for

dynamic data, i.e., for the data that changes in time

somehow. In the case of raster representation, a suit-

able tool seems to be a kind of cellular automaton, as

it has dynamics as its core substance. The challenge

is to know in advance whether a given initial conﬁg-

uration leads to a symmetric output after a sequence

of steps and which does not. What is more, it is im-

portant to collect knowledge on how to modify some

initial conﬁgurations to get a symmetric output. This

can be used for the correction of distorted geometric

shapes, shape editing, or sketch-based modeling.

This paper is the ﬁrst step in the analysis of cel-

lular automata in the described direction - symme-

try detection and symmetrization in dynamic raster

data. The analysis is done on simple planar geometric

shapes represented in a raster.

In Section 2, previous methods for symmetry de-

tection in dynamic data will be described. Section

3 focuses on describing the proposed cellular au-

tomata symmetry detection and symmetrization meth-

ods. Section 4 provides the results of the experiments.

Section 5 concludes the paper.

2 RELATED WORK

A cellular automaton (CA) is a one-, two-, three-, or

even more-dimensional structure consisting of a reg-

ular grid of cells (Adamatzky, 2010). Each cell can

be in one of a ﬁnite set of states (usually only two,

dead or alive). CA develops over time; each cell stays

in the same state or changes according to some rules,

considering its 4- or 8-neighborhood. The most often

used rule is Conaway’s rule (Vayadande et al., 2022):

If the two or three neighbours of the live cell are alive,

the cell will survive in the next iteration. If exactly

three neighbours of the dead cell are alive, the cell

will live in the next iteration. In all other cases, the

cell will die or stay dead in the next iteration.

A CA can be run with many other rules to serve

various purposes. For example, (Rosin, 2006) tried

to ﬁnd the best rule from a large set of rules to pro-

cess a digital image. CA can be used for image pro-

cessing (Rosin et al., 2014). Although a CA seems

to have a large potential for symmetry detection and

symmetrization, the only method in this area known

to us was proposed in (Javaheri Javid et al., 2014) -

a fast detection algorithm to ﬁnd symmetry axes us-

Gregor, V. and Kolingerová, I.

Symmetry Detection and Symmetrization in Cellular Automata.

DOI: 10.5220/0013250000003912

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 20th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2025) - Volume 1: GRAPP, HUCAPP

and IVAPP, pages 317-322

ISBN: 978-989-758-728-3; ISSN: 2184-4321

317

ing a CA and a swarm intelligence algorithm with a

stochastic diffusion search.

After each iteration of the cellular automata, there

should be detected if the symmetry exists or not.

This can be done with many methods for the process-

ing of the raster data. (Mestetskiy and Zhuravskaya,

2020) use the asymmetry measure computed using the

Fourier descriptor of an object boundary. (Wang et al.,

2015) compare locally afﬁne invariant features based

on edges to detect symmetry.

As for the problem of symmetrization, one ap-

proach for the transition from the asymmetric patterns

to complex symmetric patterns (symmetrization) was

published in (S

anchez and Lopez-Ruiz, 2006) and

uses a stochastically coupling the proportion of pairs

of sites located at the equal distance from the centre

of the lattice.

3 THE PROPOSED METHOD

Let us describe the proposed methods for the symme-

try detection and symmetrization of simple objects in

CA. We will consider the central and axis symmetry.

The approach to ﬁnding local symmetry will also be

described.

3.1 Symmetry Detection

Let us have some population of live cells in a CA in

some given time of development, which is to be in-

spected for its symmetry. The candidate on the centre

of the central symmetry C is calculated as the mean

position of all live cells. For each point P, a vector

V = P − C is constructed. Then, the opposite vector

is determined as V

= [−V

, −V

], and the cell in

the position C +V

is checked whether it is live. If

not, the point C is not the centre of the central sym-

metry of this cell pair and the algorithm ends. In this

way, all live cells are checked. If an opposite sym-

metric cell is found for all of them, the population is

central symmetric with the centroid C. Cells that were

found as the opposite symmetric cells do not have to

be processed because their opposite cells will always

be one of the already processed cells.

Now, the proposed method of detection of the ax-

ial symmetry will be described. It uses the centroid

C computed in the previous step. Candidate axes,

which pass through the point C, are generated. These

axes are generated with the angle between the hori-

zontal axis and the symmetry axis from 0 to 180 de-

grees with the step 0.1 degree. For each axis and

then for each cell P, the orthogonal line to the axis,

which passes through point P, is computed. Then,

the intersection I of the line and the axis is computed.

After that, the normal vector to the axis is computed

as N = P − I. An opposite vector N

is determined

as N

= [−N

, −N

], and if the cell on the position

I + N

is not alive, the candidate axis is not the axis

of the symmetry, and the algorithm can jump to the

next axis. If all points meet the condition, the candi-

date axis is the axis of the symmetry.

These methods can be applied to all live cells from

a CA to detect global symmetry. The local symmetry

can also be found using a clustering algorithm, such

as K-means, as the ﬁrst step. The resulting clusters

can be processed separately by symmetry detection

algorithms.

3.2 Symmetrization

The proposed symmetrization method is based on the

library of symmetrical patterns. This library contains

basic symmetrical objects, such as horizontal and ver-

tical lines, rectangles, and circles of different sizes.

The method is based on the computation of distance

between objects from the library and the current con-

ﬁguration. This distance is computed as the difference

between the live and dead cells in the conﬁguration

and the object from the library.

Before the symmetrization starts, the algorithm

for symmetry detection is applied to verify there is

neither a symmetry centroid nor a symmetry axis. In

each step, the size of the current population is com-

puted as the size of the bounding box of all live cells.

The distances for objects from the library, which have

a similar size with toleration 2 in each dimension, will

be computed. If the minimal size is lower than some

threshold, the current conﬁguration of the CA will be

replaced by the symmetric pattern from the library.

The symmetrization ends when the symmetry detec-

tion algorithm ﬁnds some symmetry axis or a centroid

of the central symmetry.

The symmetrization can be done globally on the

whole population or locally on clusters.

4 EXPERIMENTS AND RESULTS

Let us present the experiments with the symmetry de-

tection and the symmetrization method. The method

was developed in the C# programming language, and

the experiments ran on the computer with the Proces-

sor AMD Ryzen 7 7730U (8 cores with simultane-

ous multithreading, 2 GHz, 4.5 GHz turbo) with inte-

grated Radeon graphics and 16 GB RAM. The exper-

iments were processed on the operating system Win-

dows 11 Home.

GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications

318

First, let us concentrate on testing the behaviour of

CA if the initial conﬁguration is symmetric and ran-

dom. Second, the functionality of the developed sym-

metrization method will be veriﬁed. Comparison with

other state-of-the-art methods was not made because

the authors of this paper are not aware of any existing

work in this direction.

All experiments will be processed with the cel-

lular automata with the basic rule called Conway’s

Game of Life and with other three rules, selected ac-

cording to the experimental results. Rules, which will

be used for all experiment, are as follows:

1. Conway’s Game of Life: The live cell will be

alive in the next iteration if it has two or three live

neighbors, and the dead cell will be alive in the

next iteration if it has exactly three neighbors. In

other cases, the cell will be dead.

2. The live cell will be alive in the next iteration if it

has two up to four live neighbours, and the dead

cell will be alive in the next iteration if it has three

or four live neighbours. In other cases, the cell

will be dead in the next iteration. This rule leads

to the fast-growing number of live cells.

3. The live cell will be alive in the next iteration if it

has one or two living neighbors, and the dead cell

will be alive in the next iteration if it has exactly

two neighbours. In other cases, the cell will be

dead in the next iteration. This rule leads to the

fast-growing number of live cells in the following

iterations but is slower than the second rule.

4. The live cell will be alive in the next iteration if it

has three or four neighbours, and the dead cell will

be alive in the next iteration if it has exactly four

neighbours. In other cases, the cell will be dead in

the next iteration. This rule leads to the death of

most of the cells in the following iterations.

4.1 Symmetric Initial Conﬁgurations

In this experiment, the tested initial conﬁgurations

represented simple symmetric objects, such as line

segments, circles, and curves of various sizes. Ex-

periments were executed on many objects; in the fol-

lowing text, only some interesting results will be de-

scribed.

Fig.1 shows nine pairs of images in which the ﬁrst

image represents a circle of some size, and the second

image represents the stable state in which the circle

converges after some iterations. For these symmetri-

cal circles, all the following iterations were symmetri-

cal, including the stable states. Also, other tested ob-

jects, such as line segments and symmetrical curves,

were symmetrical in all the following populations.

Figure 1: Nine pairs of images representing the circle on the

ﬁrst position of the pair and the stable state, into which the

CA converges in the second image of the pair.

In Fig.2 on the left, an initial conﬁguration rep-

resenting the letter S is shown; on the right, there is

the central symmetric state after 80 iterations with the

second rule. The other objects were also tested with

the second rule, such as circles and line segments of

various sizes. For these initial conﬁgurations, the fol-

lowing iterations were also symmetrical.

Figure 2: Initial conﬁguration representing the letter S and

the state after 80 iterations with the second rule.

The next described initial conﬁguration was a ver-

tical line segment, which can be seen in Fig.3. This

conﬁguration was tested with the third rule, resulting

in symmetric populations in each iteration. Also, for

the third rule, all symmetrical initial conﬁgurations

led to symmetry in all iterations.

Figure 3: Initial conﬁguration representing a vertical line

segment and the state after 45 iterations with the third rule.

Let us show the results for the last rule. The ini-

tial conﬁguration can be seen in Fig.4, resulting in a

symmetric stable state after ﬁve iterations.

Symmetry Detection and Symmetrization in Cellular Automata

319

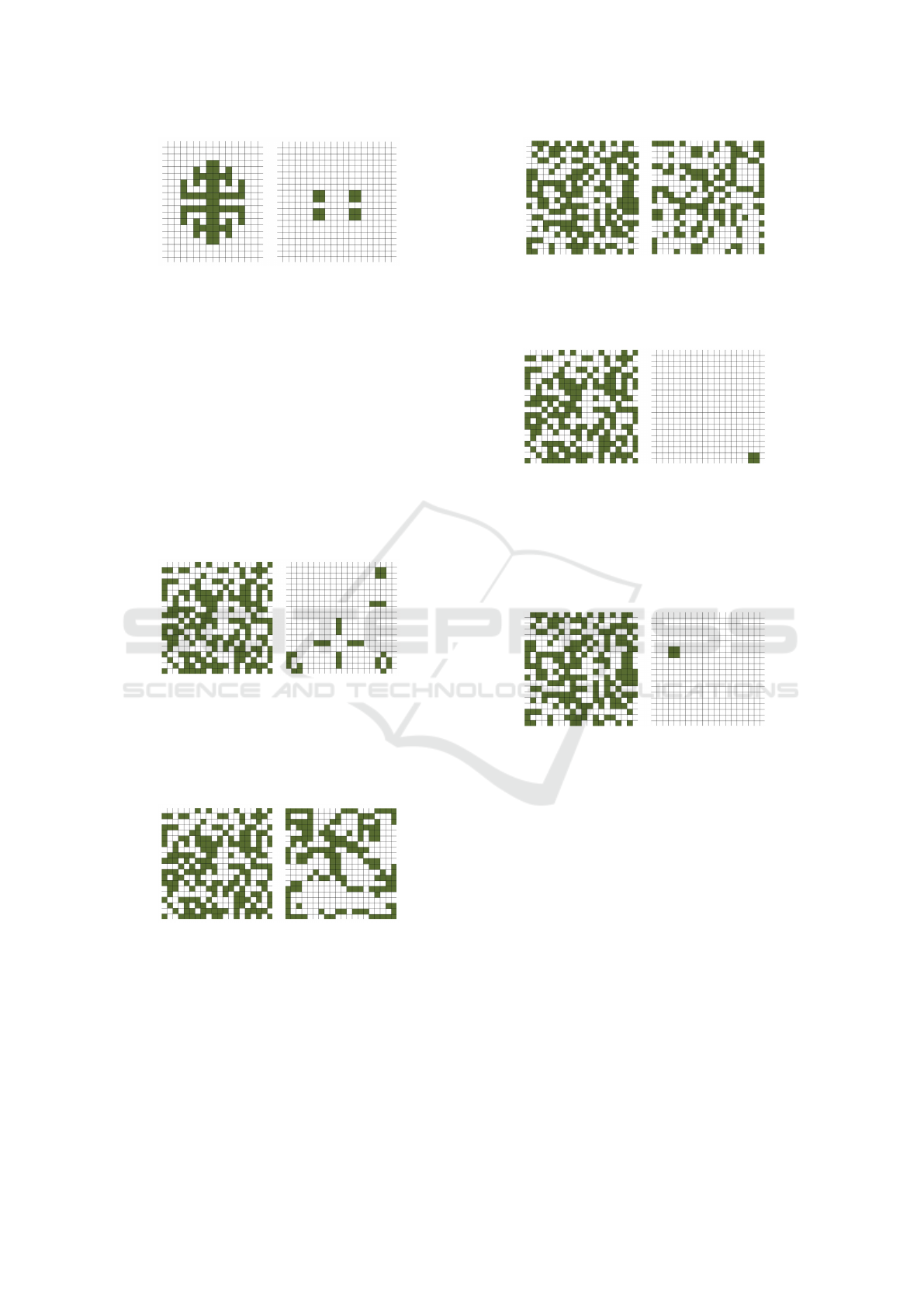
Figure 4: Symmetric initial conﬁguration and the stable

state after 5 iterations with the fourth rule.

We can conclude from this group of experiments

that when the initial conﬁguration was symmetric, it

stayed symmetric in all following iterations, but we

have no proof of the general validity of this statement.

4.2 Random Initial Conﬁgurations

In this experiment, the tested initial conﬁgurations

were random.

Fig.5 depicts a random initial conﬁguration and

the stable state after 61 iterations with the ﬁrst rule.

The stable state is not symmetrical, but some struc-

tures have a local symmetry.

Figure 5: Random initial conﬁguration and the stable state

after 61 iterations.

The same initial conﬁguration tested with the sec-

ond rule can be seen in Fig.6. On the right, we can see

the state after 109 iterations, which is not symmetric,

nor does it contain locally symmetric structures.

Figure 6: Random initial conﬁguration and the state after

109 iterations with the second set of rules.

The second random initial conﬁguration was

tested with the third rule, as shown in Fig.7. After

90 iterations (on the right), the population is not sym-

metric, and it does not contain any local symmetric

structures.

For the last rule, two initial random conﬁgurations

will be shown. The ﬁrst one can be seen in Fig.8 on

the left, and, on the right, see the symmetric stable

Figure 7: Random initial conﬁguration and the state after

90 iterations with the third rule.

state after 6 iterations. However, this is a trivial stable

state, a block.

Figure 8: First random initial conﬁguration and the sym-

metric stable state after 6 iterations with the fourth rule.

The second random initial conﬁguration with the

symmetric stable state after 4 iterations can be seen

in Fig.9. Both random conﬁgurations with the fourth

rule were ﬁnished with the globally symmetric stable

state, a block again.

Figure 9: Second random initial conﬁguration and the sym-

metric stable state after 4 iterations with the fourth rule.

4.3 Almost Symmetric Initial

Conﬁgurations

This part of the experiment tests the behavior of sim-

ple symmetric objects with some noisy points.

The ﬁrst tested initial conﬁguration, which rep-

resents the horizontal line segment with two noisy

points, can be seen in Fig. 10. It resulted in a sym-

metric stable population after 7 iterations with the ﬁrst

rule, again a block.

The second tested conﬁguration, which represents

the rectangle with three noisy points, did not result

in a globally symmetric population, but there are two

clusters, which are both locally symmetric. This ini-

tial conﬁguration with the stable locally symmetric

state can be seen in Fig.11. It was also tested with

the ﬁrst rule.

The initial conﬁguration representing the horizon-

GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications

320

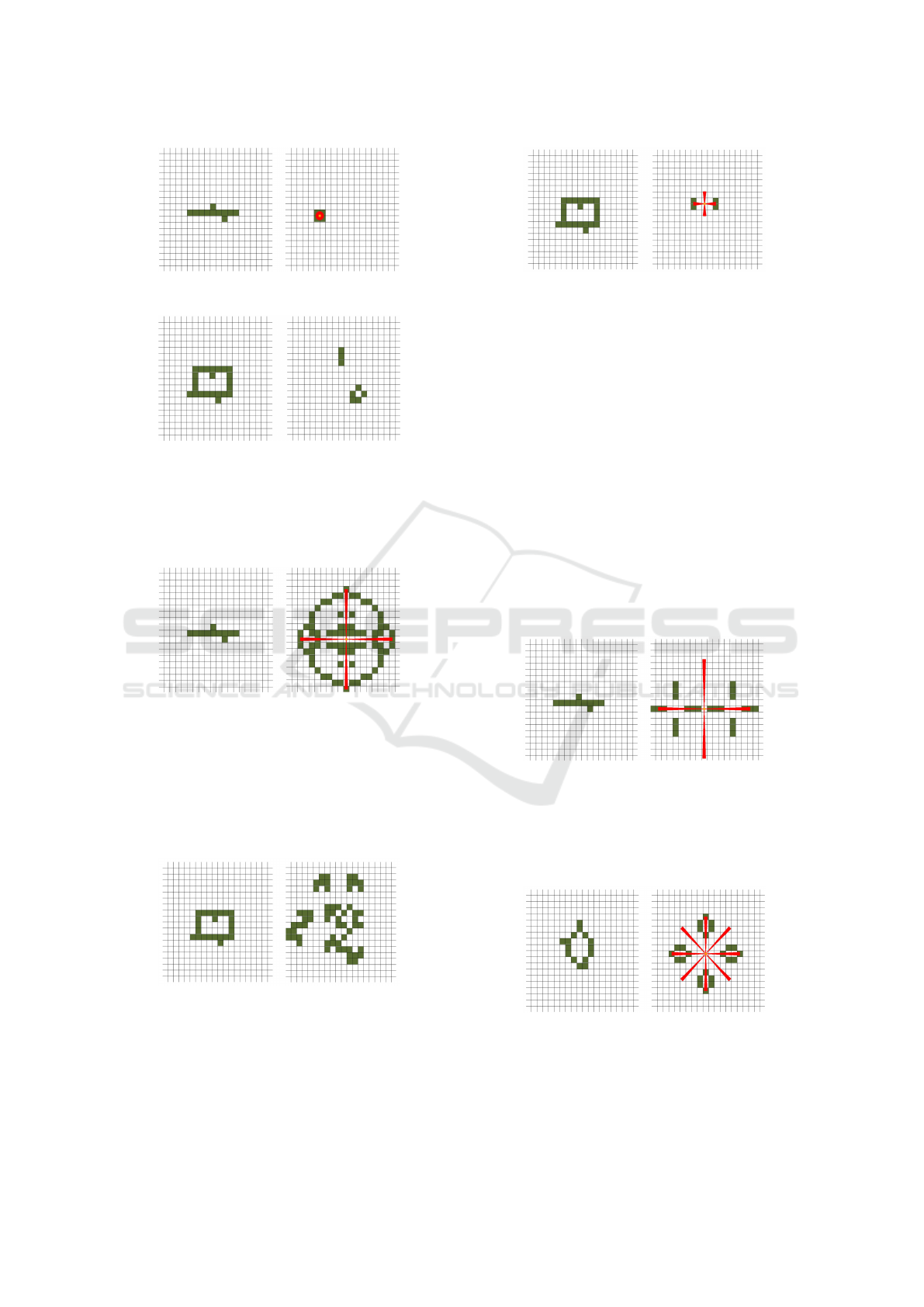
Figure 10: Noisy horizontal line segment and the population

after 7 iterations with the ﬁrst rule.

Figure 11: Noisy rectangle and the locally symmetric state

after 4 iterations with the ﬁrst rule.

tal line segment with two noisy points was also tested

with the second rule. It led to the symmetric popula-

tions. In Fig.12 can be seen the symmetric population

after 9 iterations.

Figure 12: Noisy horizontal line segment and the state after

9 iterations with the second rule.

In Fig.13, the initial conﬁguration representing the

rectangle with three noisy points can be seen; it was

tested with the third rule. The population after six iter-

ations can be seen in the right part of the ﬁgure. This

rule for the tested object did not lead to a symmetric

conﬁguration.

Figure 13: Noisy rectangle with the state after 6 iterations

with the third rule.

The rectangle was also tested with the fourth rule.

The fourth rule with this object resulted in the death

of all cells, but the last population before death, which

can be seen in Fig. 14, was symmetric.

Figure 14: Noisy rectangle with the symmetric population

after 4 iterations with the fourth rule.

A conclusion from the experiments can be drawn

that the horizontal line segments resulted in symmet-

ric populations in the next iterations. The rectangle

did not usually result in globally symmetric popula-

tions, but sometimes it resulted in locally symmetric

populations.

4.4 Symmetrization

This part of the work focuses on the symmetrization

of non-symmetric conﬁgurations. Firstly, the algo-

rithm will be tested on almost symmetric objects and

random conﬁgurations.

Fig.15 on the left depicts an object representing a

horizontal line segment with noise, and the resulting

symmetric stable state is on the right. The object was

symmetrized successfully.

Figure 15: Horizontal line segment with two noisy points

with the symmetric state after 7 iterations with the ﬁrst rule.

In Fig.16, the object representing the hexagon

with three noisy points can be seen. On the right,

the stable symmetric state is shown; here, the sym-

metrization was also successful.

Figure 16: Noisy hexagon with the symmetric population

after 9 iterations with the fourth set of rules.

Fig.17 presents the random initial conﬁguration

and the resulting conﬁguration after 61 iterations.

Global symmetrization was unsuccessful because

Symmetry Detection and Symmetrization in Cellular Automata

321

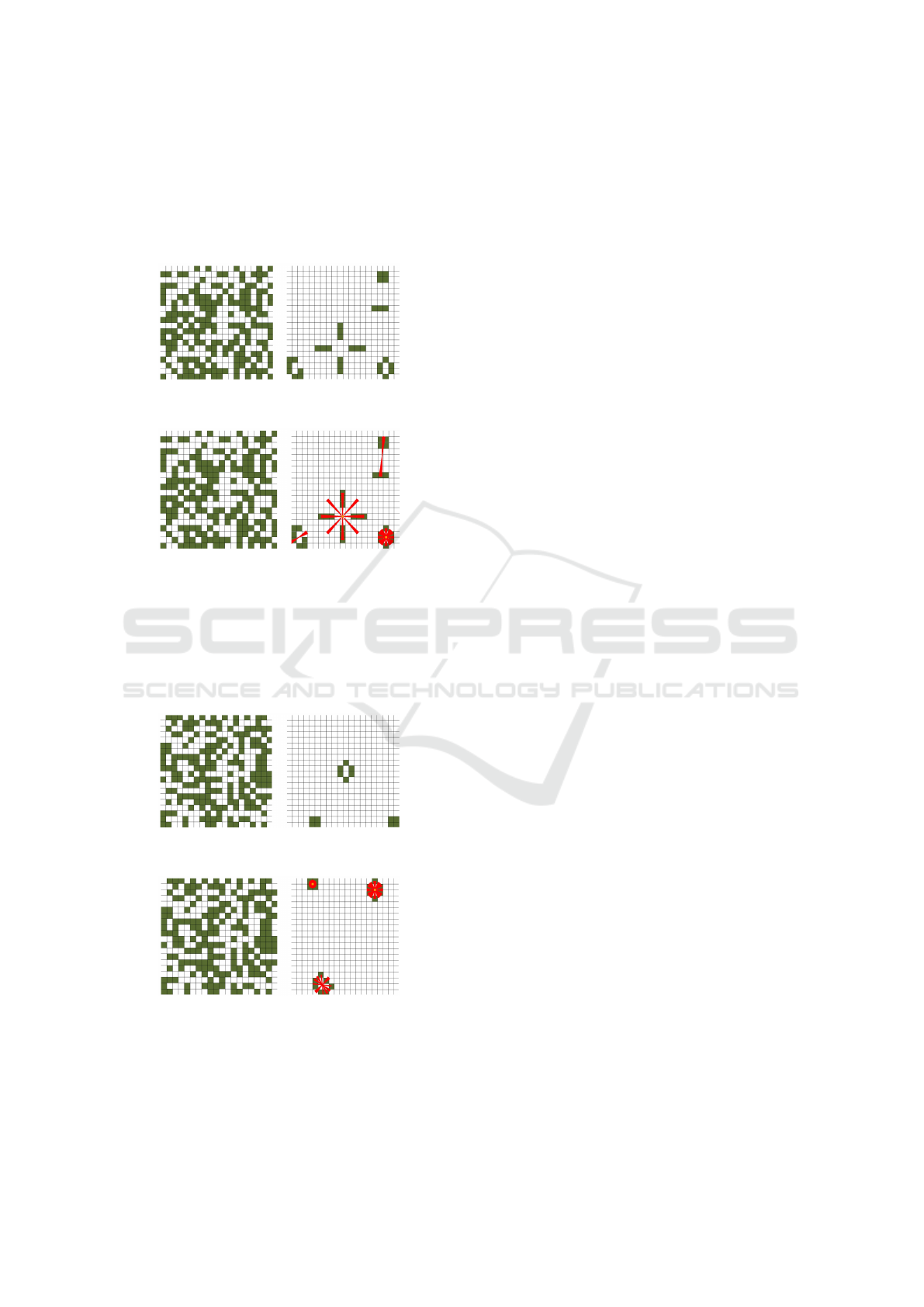
the resulting stable state is not globally symmetric.

Fig.18 depicts the ﬁnal symmetric state with the local

symmetrization. It was successful because all clusters

have some symmetry axis or centroid, but the appear-

ance of the stable state is the same as in the previous

Fig. 17.

Figure 17: Random conﬁguration and the stable state after

61 iterations with the ﬁrst rule.

Figure 18: Random conﬁguration with the stable locally

symmetric population after 61 iterations with the ﬁrst rule.

In Fig.19, we demonstrate another random initial

conﬁguration with the stable state after 161 iterations.

The global symmetrization was not successful. Fig.20

is the stable locally symmetric state after 99 iterations.

The local symmetrization was successful and brought

a different result than the global symmetrization.

Figure 19: Random conﬁguration and the stable state after

161 iterations with the ﬁrst rule.

Figure 20: Random conﬁguration with the stable locally

symmetric population after 99 iterations with the ﬁrst rule.

The conclusion from this part of the experiments

is that when the initial conﬁguration of CA is almost

symmetric, with the simple shape, the symmetriza-

tion works. When the conﬁguration is random, only

the local symmetrization works well, but the global

symmetrization does not.

5 CONCLUSION

This paper made the ﬁrst steps to analyze the usage

of cellular automata in symmetry detection and sym-

metrization of simple planar geometric shapes rep-

resented in a raster. Two simple algorithms were

proposed and tested with some promising and some

discouraging results. In the future, attention should

be devoted to developing rules that help maintain or

strengthen the symmetry of the conﬁguration.

ACKNOWLEDGEMENTS

This research was supported by the Czech Science

Foundation under the research project 21-08009K;

V.Gregor was also supported by the Ministry of Edu-

cation, Youth and Sports under the Students Research

project SGS-2022-015.

REFERENCES

Adamatzky, A. (2010). Game of Life Cellular Automata.

Springer-Verlag London Limited.

Javaheri Javid, M. A., al Rifaie, M. M., and Zimmer, R.

(2014). Detecting symmetry in cellular automata gen-

erated patterns using swarm intelligence. In Dediu,

A.-H., Lozano, M., and Mart

ın-Vide, C., editors, The-

ory and Practice of Natural Computing, pages 83–94,

Cham. Springer International Publishing.

Mestetskiy, L. and Zhuravskaya, A. (2020). Mirror sym-

metry detection in digital images. In Proceedings of

the 15th International Joint Conference on Computer

Vision, Imaging and Computer Graphics Theory and

Applications (VISIGRAPP 2020) - Volume 4: VIS-

APP, pages 331–337. INSTICC, SciTePress.

Rosin, P. (2006). Training cellular automata for image pro-

cessing. IEEE Transactions on Image Processing,

15(7):2076–2087.

Rosin, P., Adamatzky, A., and Sun, X. (2014). Cellular Au-

tomata in Image Processing and Geometry. Springer

International Publishing.

anchez, J. and Lopez-Ruiz, R. (2006). Symmetry pattern

transition in cellular automata with complex behavior.

Chaos Solitons & Fractals.

Vayadande, K., Pokarne, R., Phaldesai, M., Bhuruk, T., and

Kumar, P. (2022). Simulation of conway’s game of

life using cellular automata. International Research

Journal of Engineering and Technology.

Wang, Z., Tang, Z., and Zhang, X. (2015). Reﬂection sym-

metry detection using locally afﬁne invariant edge cor-

respondence. IEEE Transactions on Image Process-

ing, 24(4):1297–1301.

GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications

322