Exhaustive Model Identification on Process Mining
Takeharu Mitsuda
1
, Hiroyuki Nakagawa
1,2
, Haruhiko Kaiya
3
, Hironori Takeuchi
4
, Sinpei Ogata
5
and
Tatsuhiro Tsuchiya
1
1
Osaka University, Japan
2
Okayama University, Japan
3
Kanagawa University, Japan
4
Musashi University, Japan
5
Shinshu University, Japan
Keywords:
Process Mining, Process Discovery, HeuristicsMiner.
Abstract:
HeuristicsMiner is a process mining technique, which can construct a process model representing dependency
relations of each activity from event logs. HeuristicsMiner is notable for its ability to output a process model
that removes noise from the input data by allowing the user to set multiple parameters. However, it is difficult
for users to understand the characteristics of each parameter and to identify parameter values that enable
them to obtain ideal process models. In this study, we propose a method for identifying all possible process
models that can be generated from an input event log in HeuristicsMiner. We extract the conditions under
which the dependencies in the input logs are represented in the output model, and then create a process model
transition table based on these conditions to identify these models. We applied this method to several large logs
and mined process models using the combinations of parameter values obtained, and confirmed that process
models were efficiently obtained without excesses or deficiencies.
1 INTRODUCTION
Process mining is a technique for extracting beneficial
information from business process data called event
logs. Process models, which can be represented by
diagrams such as Petri nets can be generated by fo-
cusing on the sequence of executed activities. Over
the past few decades, a number of process mining al-
gorithms have been developed. One of the algorithms
for process mining is HeuristicsMiner, which is more
tolerant of noise in event logs than conventional algo-
rithms.
Most of the process mining algorithms, including
HeuristicsMiner require to determine multiple param-
eter values. In order to obtain a process model that
correctly and concisely represents the current situa-
tion, it is important to find appropriate values for these
parameters. However, finding good parameter values
to generate a process model that the user desires is
not easy because the effects of these parameter values
are not intuitively understandable. Also, since some
parameters can be specified using continuous values,
there are countless combinations, making it difficult
to mine all models to be generated.
In this study, we propose a method for identify-
ing all possible process models that can be generated
from an input event log in HeuristicsMiner without
excess or deficiency. We also implement the pro-
posed method as a plug-in of a process mining tool
ProM and apply it to a large event log to confirm that
the proposed method can correctly identify all possi-
ble process models. The user’s parameter adjustment
work can be omitted by mining the parameter value
combinations obtained with this method. This allows
the user to obtain a useful process model more effi-
ciently than before.
2 BACKGROUNDS
2.1 Process Mining
Process mining is a part of data mining techniques,
which transforms logs collected from daily business
work into models, and utilizes them for improvements
Mitsuda, T., Nakagawa, H., Kaiya, H., Takeuchi, H., Ogata, S. and Tsuchiya, T.
Exhaustive Model Identification on Process Mining.
DOI: 10.5220/0013270400003928
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 20th International Conference on Evaluation of Novel Approaches to Software Engineering (ENASE 2025), pages 449-456
ISBN: 978-989-758-742-9; ISSN: 2184-4895
Proceedings Copyright © 2025 by SCITEPRESS – Science and Technology Publications, Lda.
449

Table 1: An example event log W
1
.
Case Activity Time
case 1 activity A 2024-10-01 00:18
case 1 activity E 2024-10-01 01:53
case 2 activity A 2024-10-01 20:52
case 2 activity C 2024-10-02 13:07
case 3 activity A 2024-10-03 04:56
case 4 activity A 2024-10-03 06:57
case 4 activity B 2024-10-04 05:38
case 3 activity C 2024-10-04 06:19
case 5 activity A 2024-10-05 03:11
case 5 activity B 2024-10-05 18:45
case 4 activity C 2024-10-06 03:53
case 4 activity D 2024-10-06 21:34
case 5 activity C 2024-10-07 08:28
case 2 activity B 2024-10-08 02:12
case 2 activity D 2024-10-08 11:58
case 3 activity B 2024-10-09 11:05
case 5 activity D 2024-10-10 10:07
case 1 activity D 2024-10-11 09:09
case 3 activity D 2024-10-11 22:43
of efficiency (van der Aalst, 2016). Using process
mining techniques, records stored in enterprise sys-
tem can be utilized for business improvements, such
as detection of irregular activities in business and ad-
justments of current business flow. Process mining is
now being studied for use in improving business op-
erations in a wide range of industries, including soft-
ware development (Keith and Vega, 2017), medicine
(Mans et al., 2008), and semiconductor manufactur-
ing (Rozinat et al., 2009).
In process mining, business activities recorded by
information systems are referred to as “event logs”.
Table 1 shows an example of an event log in its sim-
plest configuration, which includes the case, activity,
and time attributes. The logs often contain additional
attributes, such as the resource attribute, which indi-
cates the organization or person that performed the
event. Because the log contains a large amount of
data, discovering and analyzing data patterns hidden
in the log requires techniques that specialize in pro-
cess mining.
2.2 Process Discovery Algorithm
The process discovery is a set of process mining tech-
niques that build models from the history of actual op-
erations stored in event logs, allowing accurate mod-
els to be used for workflow management.
The initial technique of process discovery from
control-flow perspective is the α algorithm (van der
Aalst et al., 2004). The algorithm regards that if an
event is always followed by another event it is likely
to have a relation between both tasks. It classifies the
relation between directly following (in sequence) and
parallelism, and the result is represented as the Petri-
net model. Today the α algorithm is said to be the
most basic implementation of the process discovery
algorithm, and many extentions of the α algorithm
exist (Medeiros et al., 2004) (Wen et al., 2007) (Wen
et al., 2010).
However, the algorithm has difficulty in correctly
handling event logs stored in practical systems. This
is because the algorithm presupposes the input log
as perfect information, which means the log doesn’t
include any noise. In practical situation the log of-
ten has noise such as errors, low frequent activities,
low frequent activity sequences and exceptions. This
noise prevents the algorithm from correctly classify-
ing the relation between activities.
2.3 HeuristicsMiner
2.3.1 Overview
The HeuristicsMiner (Weijters et al., 2006) is a pro-
cess discovery algorithm which is less sensitive to
noise. When it generates an output model, it considers
not only the sequence of activities, but also on the fre-
quency with which following relations are observed in
the log. This allows the algorithm to output a model
that accurately reflects the workflow.
The HeuristicsMiner employs following three
steps to generate a model. The first step calculates
measures which evaluates relations between activities
and generates a model called “dependency graph”.
The second step determines for each split and join
in the dependency graph whether it is an AND or an
XOR relationship. The third step mines long-distance
dependency relations, which could not be mined by
the previous steps. This study focuses on metrics and
thresholds that are mainly used in the first step.
2.3.2 Metrics
In HeuristicsMiner, a relation in which two activities
tend to be executed consecutively is called a depen-
dency relation. HeuristicsMiner employs a depen-
dency measure to express and evaluate those relations
between activities.
Let a and b be activities recorded in log W , and
|a >
W
b| represents the total number of times b oc-
curs immediately after a. The value of a ⇒
W
b can be
calculated as shown below:
a ⇒
W
b =
|a >
W
b| − |b >
W
a|
|a >
W
b| + |b >
W
a| + 1
(a ̸= b) (1)
An increased value of a ⇒
W
b suggests that there is a
dependency relation between the activities a and b.
ENASE 2025 - 20th International Conference on Evaluation of Novel Approaches to Software Engineering
450

However, the metric a ⇒
W
b is unable to evaluate
the relations correctly when short loops are included
in the input log. There are two loop patterns which
cannot be mined by the metric: length-one loops (the
same activity is recorded consecutively) and length-
two loops (two different activities are recorded al-
ternately). To recognize these patterns as a depen-
dency relation, HeuristicsMiner introduces two addi-
tional metrics for loop patterns. Let |a >>
W
b| be the
total number of times b occurs immediately before a
and immediately after a. The values of a ⇒
1W
a and
a ⇒
2W
b can be calculated as shown below:
a ⇒
1W
a =
|a >
W
a|
|a >
W
a| + 1
(2)
a ⇒
2W
b =
|a >>
W
b| + |b >>
W
a|
|a >>
W
b| + |b >>
W
a| + 1
(3)
The “relative to best” is a metric that represents
the relative importance of its dependency to others.
For any activity a and any activity x present in the
log, the maximum value of a ⇒
W
x is denoted as
dep
max
(a). For any pair of activities (a, b), the rel-
ative to best value is calculated as follows:
rtb(a, b) = dep
max
(a) − (a ⇒
W
b) (4)
If the value of relative to best for a pair of activities
is less than the value of the relative to best threshold,
the dependency between activities is not represented
in the dependency graph.
Note that the value of relative to best only af-
fects normal dependencies, and it will not affect short
loops.
2.3.3 Parameters
HeuristicsMiner can be configured with several pa-
rameters. The set values of those parameters deter-
mine which dependencies between each activity are
represented in the dependency graph. By adjusting
the values of these parameters as needed, users can
obtain a high-quality process model for their particu-
lar use. The parameters of HeuristicsMiner that have
a particularly large impact on the output model are
listed below.
Dependency Threshold. The dependency thresh-
old is a parameter used to determine which depen-
dencies to represent in the dependency graph by com-
paring them to the dependency value of each depen-
dencies. The value of this parameter has a strong in-
fluence on the number of dependencies being repre-
sented in the dependency graph.
Relative-to-Best Threshold. The relative-to-best
threshold is a parameter used to determine which de-
pendencies to represent in the dependency graph by
comparing them to the relative-to-best value of each
dependencies. The value of this parameter affects on
the number of dependencies connected from each ac-
tivity in the dependency graph, thereby working to ad-
just the graph density.
2.4 Problem
HeuristicsMiner has a number of parameters, includ-
ing the thresholds described in Section 2.2. Users
must specify those parameters before execution. It
is difficult to uniquely determine the values of these
parameters to generate a useful model, as they are af-
fected by the user’s usage, the size of the input logs,
the amount of noise, etc. Therefore, users need to
keep checking the output model and manipulating the
parameters until the model they want is output.
One possible improvement to reduce the burden of
parameter setting on users is to mine all possible pro-
cess models for the input log in advance and present
them to users for selection. This method allows users
to easily obtain process models without understand-
ing the concept of parameters. However, Heuristic-
sMiner cannot mine all process models in advance
because there are countless combinations of param-
eter values. In order to implement this method in
HeuristicsMiner, it is necessary to develop a method
to extract all combinations of parameter values corre-
sponding to each output model.
2.5 Related Works
A number of studies have been conducted on the ap-
plication of meta-heuristics to process discovery with
the objective of improving model output (Montasser
and Helal, 2023). With regard to the improvement of
the output of HeuristicsMiner, Burattin et al. (Burat-
tin and Sperduti, 2010) explored the use of Heuristics
Miner++ (Burattin, 2015), a derivative of Heuristic-
sMiner, and assumed that there are only a finite num-
ber of values for parameters that affect the model con-
struction. It was demonstrated that when the set of
activities in log W can be represented as A
W
, there
are at most |A
W
|
i
(i ∈ N ) valid parameter value com-
binations, which is finite. Additionally, a method
for generating an optimal process model was pro-
posed, which involved conducting a local search in
the search space with each parameter representing a
phase. Moreover, research has been conducted on
frameworks that run multiple process mining meth-
ods and meta-heuristics simultaneously, with the ob-
Exhaustive Model Identification on Process Mining
451

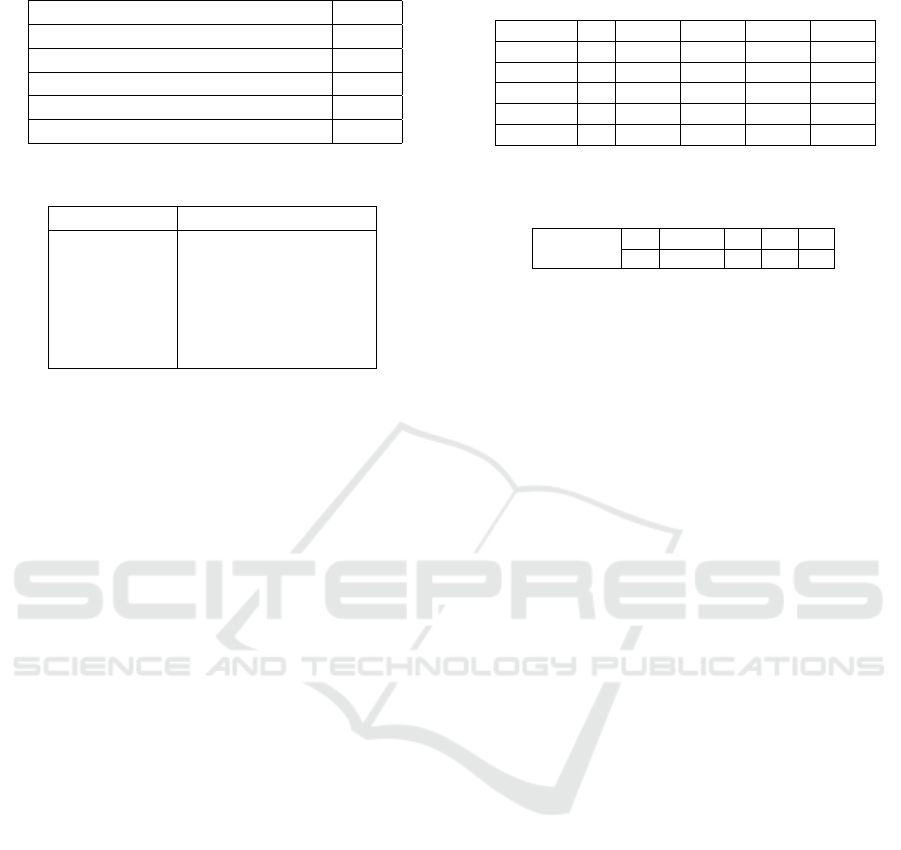
Table 2: Parameters and their values fixed in this study.
Parameter name Value
Positive observations threshold 1
AND-threshold ∞
All-tasks connected False
Ignore loop dependency thresholds False
Long distance dependency False
Table 3: The summary of log W
2
.
Case Sequence of activities
case 1 to 3 A, B, B, D
case 4 to 9 A, B, C, B, D
case 10 to 18 A, B, C, D
case 19 to 27 A, C, B, D
case 28 to 30 A, D
case 31 to 42 A, E, D
jective of generating more satisfactory models (Au-
gusto et al., 2021).
These metaheuristics are capable of deriving supe-
rior approximate solutions in a shorter time than other
algorithms. However, the solutions derived by meta-
heuristics, including local search, are locally optimal
and cannot be guaranteed to be optimal over the entire
parameter space. Consequently, in order to output an
optimal model for a metric, it is necessary to construct
the model without the use of metaheuristics.
3 PROPOSED MODEL
IDENTIFICATION METHOD
3.1 Overview
In order to address the issue identified in the preced-
ing section, we propose a method that identifies all
possible process models that can be output from an in-
put log using a process model transition table. For the
sake of simplicity, only the values of the Dependency
threshold (dep-TH) and the Relative to best thresh-
old (rtb-TH) are manipulated in this method, while
the values of the other parameters are fixed at specific
values as indicated in Table 2.
This section describes steps of the proposing
method, with the case of mining the event log W
2
shown in Table 3 as an illustrative example. Note
that cases with the same pattern of the sequence of
activities are aggregated into a single row. The log W
2
includes 156 records of event, and involves with 42
cases and 5 activities.
The proposed method consists of two steps. First,
we identify the conditions for parameters when de-
pendency relations in the input log appear in the out-
Table 4: Matrix in which the value of Formula (1) is
recorded.
a ⇒
W
b A B C D E
A 0.947 0.900 0.750 0.857
B 0.947
C 0.900
D
E 0.857
Table 5: Matrix in which the value of Formula (2) is
recorded.
a ⇒
1W
a
A B C D E
0.750
put model and list them in the list called “dependency
output list.” Using the list, we generate the table
called “process model transition table,” which is used
to mark cells in order to filter out duplicate models
that can be constructed from the input log.
3.2 Extraction of Dependency Output
Range
This step identifies the parameter value conditions un-
der which the dependencies between activities in the
event log are output to the process model.
First, we create 4 matrices that record the values
of each metrics denoted in Formula (1) through For-
mula (4). The matrices generated for each log W
2
are presented in Table 4 through Table 7. To im-
prove readability, dependencies that have never been
logged (which are never shown in the graph because
they do not meet the positive observation threshold
condition) and dependencies that have a dependency
value of zero are omitted.
We then list all the dependencies recorded in the
matrices, along with the conditions under which the
dependencies appear in the graph. The list is referred
to as the dependency output list, and the list for log
W is shown in Table 8. The procedure for obtain-
ing conditions for each dependency varies by type of
dependency; length-one-loop dependencies, length-
two-loop dependencies, and other dependencies. De-
tails on how to obtain these conditions are described
in the following sections for each type of dependency.
3.2.1 Length-One-Loop Dependency
Length-one-loop dependency is represented in the
graph when the dep-TH value is smaller than or equal
to the value of a ⇒
1W
a. The value of rtb-TH does not
determine whether the dependencies are represented
or not.
ENASE 2025 - 20th International Conference on Evaluation of Novel Approaches to Software Engineering
452

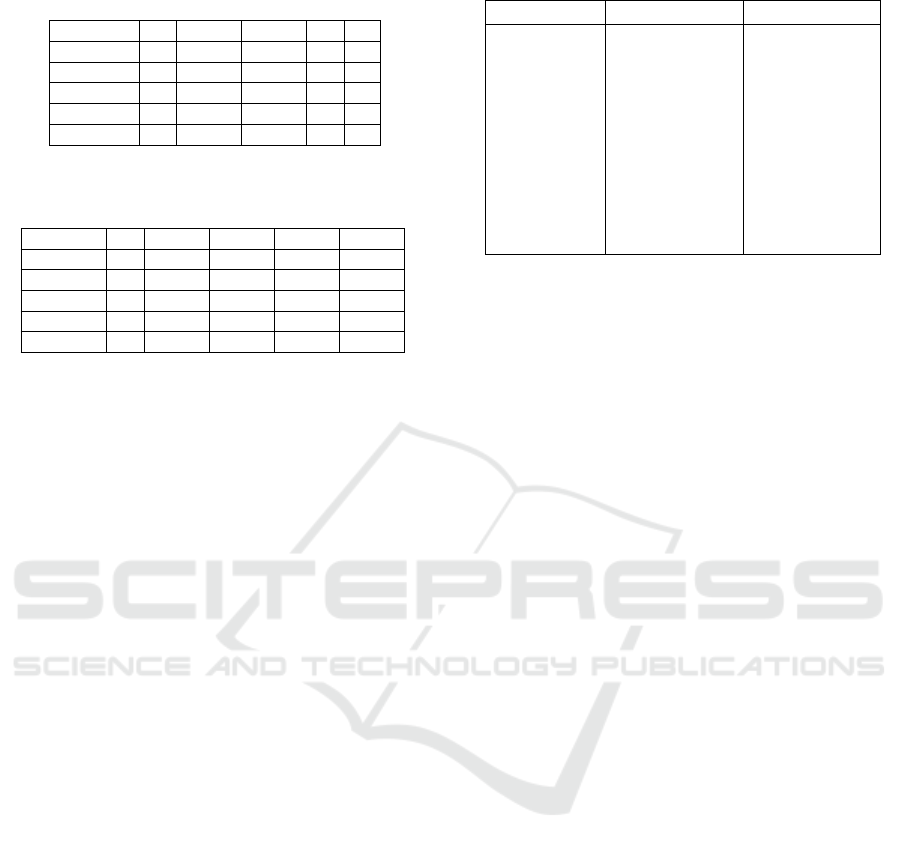
Table 6: Matrix in which the value of Formula (3) is
recorded.
a ⇒
2W
b A B C D E
A
B 0.857
C 0.857
D
E
Table 7: Matrix in which the value of Formula (4) is
recorded.
rtb(a, b) A B C D E
A 0.000 0.047 0.197 0.090
B 0.000
C 0.000
D
E 0.000
3.2.2 Length-Two-Loop Dependency
When an activity is executed repeatedly and forms a
length-one-loop dependency, and another activity is
executed at the same time, it may be misinterpreted
that the two activities have dependencies. To avoid
this, HeuristicsMiner represents length-two-loop de-
pendencies only when there are no length-one-loop
dependencies in the related activities.
Considering the special condition above, length-
two-loop dependency is represented in the graph
when the dep-TH value is smaller than or equal to the
value of a ⇒
2W
b and neither a ⇒
1W
a nor b ⇒
1W
b
appear in the dependency graph. For instance, Ta-
ble 8 records dep-TH range condition of b >>
W
c as
(0.750, 0.857]. Length-one-loop dependency between
activities b and c is only represented when dep-TH is
greater than 0.750, because activity b is considered
to have length-one-loop dependency when dep-TH is
smaller than or equals to the value.
As with length-one-loop dependencies, the value
of rtb-TH does not determine whether the dependen-
cies are represented or not.
3.2.3 Non-Loop Dependency
In this section, the term “non-loop dependency” refers
to a dependency that is not “length-one-loops” or
“length-two-loops.” The conditions under which
“non-loop dependencies” are represented in the out-
put model are contingent upon both dep-TH and rtb-
TH.
The dep-TH condition for a non-loop dependency
to be represented in the dependency graph is that the
value of dep-TH is greater than or equal to a ⇒
W
b.
It should be noted, however, that if length-two-loop
dependency between a and b is considered to exist,
the output model may not change whether non-loop
Table 8: Dependency output list for log W
2
.
dependency dep-TH rtb-TH
b >
W
b (0.000, 0.750] [0.000, 1.000)
b >>
W
c (0.750, 0.857] [0.000, 1.000)
c >>
W
b (0.750, 0.857] [0.000, 1.000)
a >
W
b (0.000, 0.947] [0.000, 1.000)
a >
W
c (0.000, 0.900] [0.047, 1.000)
a >
W
d (0.000, 0.750] [0.197, 1.000)
a >
W
e (0.000, 0.923] [0.024, 1.000)
b >
W
d (0.000, 0.947] [0.000, 1.000)
c >
W
d (0.000, 0.900] [0.000, 1.000)
e >
W
d (0.000, 0.923] [0.000, 1.000)
dependency from a to b exist or not. The presence or
absence of a length-two-loop in the dependency graph
is contingent upon the relationship between the values
of a ⇒
2W
b, a ⇒
1W
a, and b ⇒
1W
b. Consequently,
the condition for the emergence of a dependency from
a to b is influenced by the interplay between four met-
ric values, including a ⇒
W
b.
In contrast to the dep-TH condition, the rtb-TH
condition for a non-loop dependency is simple; non-
loop dependency is represented in the graph when the
rtb-TH value is greater than or equal to the value of
r(a, b).
3.3 Generation of Process Model
Transition Table
In this step, a process model transition table is cre-
ated based on the dependency output list created in
the Section 3.2. This table shows all output models
that can be output when the values of the parameters
are continuously changed.
The output model may undergo a change only
when a parameter value crosses the values of parame-
ters appearing in the dependency output list derived
from the input logs. In contrast, the output model
never undergoes a change with any other values. This
property is utilized to generate a two-dimensional ar-
ray, wherein each column represents the value of dep-
TH appearing in the dependency output list and each
row represents the value of rtb-TH appearing in the
dependency output list. Each cell of the array can then
be represented as one of the output models.
Table 8 contains four values within the range (0, 1)
for dep-TH and two values within the range [0, 1) for
rtb-TH. The process model transition table created
based on this list is shown in Table 9.
However, it should be noted that some of the cells
shown in Table 9 represent the same models. For
example, cells (1) through (5) in Table 9 represents
different pairs of parameter values, but the resulting
process models produced by the HeuristicsMiner are
Exhaustive Model Identification on Process Mining
453

Table 9: Process model transition table for log W .
rtb-TH
dep-TH
0.947 0.923 0.900 0.857 0.750
0.000 (1) (5)
0.024 (2)
0.047 (3)
0.197 (4)
Table 10: Process model transition table for log W (with
markings).
rtb-TH
dep-TH
0.947 0.923 0.900 0.857 0.750
0.000 x
0.024 x
0.047 x x
0.197 x x x x
exactly the same.
In order to identify the elements that represent
identical output models, we focus on the cells con-
tained in each row and column of this table. We mark
the cells that correspond to a model that are identi-
cal to another model. For example, let us assume that
we focus on the column in Table 9 where dep-TH is
0.947. Based on the conditions recorded in Table 8,
the dependencies that can be represented in the model
when dep-TH is set to 0.947 are a >
W
b and b >
W
d.
The conditions for rtb-TH for these two dependencies
to appear in the model are [0.000, 1.000) for both,
as indicated in Table 8. Consequently, regardless of
the value of rtb-TH, the two dependencies are always
represented in the model, and the output model re-
mains unchanged. Therefore, the elements shown in
(1) through (4) in the process model transition table
correspond to the same process model. In this case,
we mark against cells (2) through (4), except for cell
(1), which is the uppermost.
The execution of the procedures for each column
and row of the Table 9 results in the generation of
the Table 10. The cells marked with an “x” in the
Table 10 are those cells which have been marked to
indicate that they correspond with the same process
model as the other cells. The cells not marked in this
table represent output models that do not overlap with
other models. In the example in log W
2
, the 25 pos-
sible combinations at the outset of this step were re-
duced to 12. By recording the values of the parame-
ters of these cells and mining them by inputting them
into HeuristicsMiner in sequence, the process model
obtained by HeuristicsMiner can be obtained without
excess or deficiency.
4 EXPERIMENT
In this section, we apply the proposed method to a
large event log in order to confirm its effectiveness.
We then mine process models from the generated pro-
cess model transition table using HeuristicsMiner. In
order to confirm that the proposed method can iden-
tify process models without excess or deficiency, we
will demonstrate that there are no duplicate models in
the output models.
4.1 Experimental Procedures
We developed a ProM plug-in named “PMenum” to
excecute our proposed method and automatically gen-
erate process model transition table
1
. The plug-in
works in ProM 6.13 (ProM, 2023), which is an open-
source software for process mining distributed free of
charge under the GPL license.
Using the plug-in, we generated process model
transition tables from three different large-scale event
logs. Additionally, we outputted each process model
associated with each cell of the process model tran-
sition table we obtained. Since the HeuristicsMiner
is not available in ProM 6.13, we used the Flexible
Heuristic Miner (Weijters and Ribeiro, 2011) instead,
which is an extended version of the HeuristicsMiner.
The group of process models generated by Flex-
ible Heuristic Miner was divided into two categories
according to whether the cell on the process model
transition table to which each model is associated
is marked or not. For the group of models asso-
ciated with unmarked cells (hereafter referred to as
the “unique model group”), we conducted a verifica-
tion process to ascertain that no model in the group
matched any of the models in the group. For the group
of models associated with the marked cells (hereafter
referred to as the “duplicate model group”), we ver-
ified that all models are consistent with one of the
models in the unique model group.
In this experiment, we used event logs distributed
for the Process Discovery Contest 2023 (PDC2023,
2023). The contest is sponsored by the Task Force
on Process Mining of the IEEE, where event logs
are published in XES Standard format. We randomly
picked 3 test logs from the distributed data set.
A summary of the basic metrics of each log used
in this experiment is presented in Table 11. Each log
comprises 1000 cases, although the number of activ-
ity types and the presence or absence of loops varies
between logs.
1
The implementation of the PMenum is uploaded to the
following webpage: https://github.com/tmitsuda/PMenum
ENASE 2025 - 20th International Conference on Evaluation of Novel Approaches to Software Engineering
454

Table 11: Summary of logs used in the experiment.
Log cases events event types
Log A
(pdc2023 000000.xes)
1,000 20,000 28
Log B
(pdc2023 010000.xes)
1,000 37,490 34
Log C
(pdc2023 020000.xes)
1,000 55,377 36
Table 12: Summary of process model transition table ob-
tained by the proposed method.
Log Column Row Cell
Unmarked
cell
Log A 173 166 28,718 472
Log B 220 247 54,340 733
Log C 232 287 66,584 1,147
4.2 Experimental Results
The summary of the process model transition table
obtained by applying the proposed method to the
event logs in Table 11 is shown in Table 12. The num-
ber of columns referred in the Table 12 represents the
number of cells in the horizontal direction of the pro-
cess model transition table and is equal to the number
of the dependency values that appear in the depen-
dency output list. The number of rows referred in the
Table 12 represents the number of cells in the vertical
direction of the process model transition table and is
equal to the number of the relative to best values that
appear in the dependency output list. The product of
the number of columns and the number of rows is the
number of cells in the process model transition table,
which is shown in the column “cell” of the Table 12.
According to the test result conducted using the three
logs, the proposed algorithm can detect 98.4% of the
duplicate process models on average.
Observing the process model transition table ob-
tained by the proposed method, it can be confirmed
that unmarked cells are aligned in a linear pat-
tern. This is because the relative-to-best value repre-
sents the difference in the dependency value between
the dependency relation with the largest dependency
value for each activity and the dependency with the
smallest dependency value, and thus the dependency
relation with the smallest dependency value is likely
to have a larger value of relative-to-best.
The validation against the unique model group
described in Section 4.1 was performed, and it was
confirmed that all models did not match any of the
unique model group models. In other words, the mod-
els identified by the proposed method are not exces-
sive. Furthermore, when the validation was tested on
the duplicate model group, it was confirmed that all
the models were consistent with one of the models in
the unique model group. In other words, the number
of models identified by the proposed method is suffi-
cient. Therefore, we can conclude that the proposed
method is capable of identifying process models with-
out excess or deficiency.
5 DISCUSSION
As HeuristicsMiner’s parameters can be set with con-
tinuous values, there are infinite combinations of pa-
rameter values, rendering it challenging to enumer-
ate the output models that can be mined by Heuris-
ticsMiner. Using the process model transition table,
all possible process models generated from the input
log can be enumerated. This enables the identification
of the model that scores the best metric value, as the
method outputs a list of all process models that can be
output by the input log. Also, the marking procedure
to the process model transition table conducted in the
proposed method can drastically reduce the choice of
models. This will help users to pick their ideal model
easier, and other systems can reduce their calculation
time of process discovery.
In the conventional HeuristicsMiner plug-in im-
plemented in ProM, the user must adjust parameter
settings while referencing the output results. Further-
more, changing parameter values does not always re-
sult in the anticipated change in the process model,
necessitating a significant amount of time to output
the process model that the user desires. However,
by utilizing the list of output models obtained by this
method, it is possible to create a tool that allows the
user to change the output model and select an appro-
priate model without manipulating parameters. For
example, the process model visualizer implemented
in PMenum can sequentially display process mod-
els that can be generated from input logs by simply
clicking a button. Since it doesn’t require any prior
knowledge of HeuristicsMiner’s parameters, the tool
is friendly for users who are not familiar with process
mining.
6 CONCLUSION
This study proposed a method for obtaining parame-
ter combinations that output different process models
for HeuristicsMiner, one of the process discovery al-
gorithms, without excess or deficiency. The proposed
method can narrow down the number of valid parame-
ter combinations to a finite number, thus enabling the
user to obtain process models with fewer man-hours.
Exhaustive Model Identification on Process Mining
455

In the experiment, the proposed method was applied
to three large-scale event logs, and it was demon-
strated that effective parameter combinations could be
obtained without excess or deficiency.
In this study, we focused on only two of the pa-
rameters used in HeuristicsMiner for model identi-
fication. Adapting this approach to other discovery
techniques and more parameters would make the pro-
cess discovery more efficient. There are many other
parameter-based process discovery techniques such as
Fuzzy Miner (G
¨
unther and van der Aalst, 2007), each
with different characteristics and analytical capabil-
ities. In our future work, we would like to support
other techniques in this way so that users can use more
algorithms with little knowledge of process discovery
and are more likely to encounter models that more ac-
curately reflect their business flow.
It is also necessary to consider a method for se-
lecting ideal process models from the set of models
obtained from the input logs identified by the pro-
posed method. The experiment has shown that this
method can significantly reduce the number of can-
didate models. However, when the input logs are
large and the process model transition table contains
many cells, it is still difficult to find the model that the
user wants from the set of models generated by this
method. A possible method to assist users in select-
ing a process model is to use metrics such as precision
rate and recall rate to further narrow down the candi-
date models, and the specific procedure for this needs
to be studied. In addition, if a tool with an interac-
tive interface can be developed to present the model
the user is seeking in a question-and-answer format,
it will be easier to obtain a process model. In this
way, it is important to develop tools that can be easily
handled even by users without knowledge of process
discovery, in order to popularize process mining.
REFERENCES
Augusto, A., Dumas, M., La Rosa, M., Leemans, S. J. J.,
and vanden Broucke, S. K. L. M. (2021). Optimiza-
tion framework for dfg-based automated process dis-
covery approaches. Software and Systems Modeling,
20:1245–1270.
Burattin, A. (2015). Heuristics Miner for Time Inter-
val, pages 85–95. Springer International Publishing,
Cham.
Burattin, A. and Sperduti, A. (2010). Automatic determina-
tion of parameters’ values for heuristics miner++. In
IEEE Congress on Evolutionary Computation, pages
1–8.
G
¨
unther, C. W. and van der Aalst, W. M. P. (2007).
Fuzzy mining – adaptive process simplification based
on multi-perspective metrics. In Business Process
Management, pages 328–343, Berlin, Heidelberg.
Springer Berlin Heidelberg.
Keith, B. and Vega, V. (2017). Process mining applications
in software engineering. In Trends and Applications in
Software Engineering, pages 47–56, Cham. Springer
International Publishing.
Mans, R., Schonenberg, H., Leonardi, G., Panzarasa, S.,
Cavallini, A., Quaglini, S., and van der Aalst, W.
(2008). Process mining techniques: An application
to stroke care. Studies in health technology and infor-
matics, 136:573–578.
Medeiros, A., Dongen, B., van der Aalst, W., and Wei-
jters, A. (2004). Process mining for ubiquitous mo-
bile systems: An overview and a concrete algorithm.
In Ubiquitous Mobile Information and Collaboration
Systems, volume 3272, pages 151–165.
Montasser, R. K. and Helal, I. M. A. (2023). Process discov-
ery automation: Benefits and limitations. In 2023 In-
telligent Methods, Systems, and Applications (IMSA),
pages 496–501.
PDC2023 (2023). Process discovery contest
2023. https://icpmconference.org/2023/
process-discovery-contest/.
ProM (2023). Prom tools. https://promtools.org/
prom-6-13/.
Rozinat, A., Jong, I., Gunther, C., and van der Aalst, W.
(2009). Process mining applied to the test process of
wafer scanners in asml. Systems, Man, and Cybernet-
ics, Part C: Applications and Reviews, IEEE Transac-
tions on, 39:474–479.
van der Aalst, W. (2016). Process Mining: Data Science in
Action. Springer Berlin, Heidelberg.
van der Aalst, W., Weijters, T., and Maruster, L. (2004).
Workflow mining: discovering process models from
event logs. IEEE Transactions on Knowledge and
Data Engineering, 16(9):1128–1142.
Weijters, A. and Ribeiro, J. (2011). Flexible heuristics
miner (fhm). In Journal of Applied Physiology - J
APPL PHYSIOL, pages 310–317.
Weijters, A., van der Aalst, W., and Alves de Medeiros, A.
(2006). Process mining with the HeuristicsMiner al-
gorithm. BETA publicatie : working papers. Technis-
che Universiteit Eindhoven.
Wen, L., van der Aalst, W., Wang, J., and Sun, J. (2007).
Mining process models with non-free-choice con-
structs. Data Min. Knowl. Discov., 15:145–180.
Wen, L., Wang, J., van der Aalst, W., Huang, B., and Sun, J.
(2010). Mining process models with prime invisible
tasks. Data & Knowledge Engineering, 69:999–1021.
ENASE 2025 - 20th International Conference on Evaluation of Novel Approaches to Software Engineering
456